The Role of Working Memory Capacity and Interference Resolution Mechanisms in Task Switching

Abstract

Theories of task switching have emphasized a number of control mechanisms that may support the ability to flexibly switch between tasks. The present study examined the extent to which individual differences in working memory (WM) capacity and two measures of interference resolution, response-distractor inhibition and resistance to proactive interference (PI), account for variability in task switching, including global costs, local costs, and N-2 repetition costs. 102 young and 60 older adults were tested on a battery of tasks. Composite scores were created for WM capacity, response-distractor inhibition, and resistance to PI; shifting was indexed by rate residual scores which combine response time and accuracy and account for individual differences in processing speed. Composite scores served as predictors of task switching. WM was significantly related to global switch costs. While resistance to PI and WM explained some variance in local costs, these effects did not reach significance. In contrast, none of the control measures explained variance in N-2 repetition costs. Furthermore, age effects were only evident for N-2 repetition costs, with older adults demonstrating larger costs than young adults. Results are discussed within the context of theoretical models of task switching.

In everyday life, we often shift our attention between tasks, putting previous goals temporarily aside to focus on the current task. Despite being a seemingly effortless process, task switching incurs costs in both time and accuracy relative to continuing with the same task. Accordingly, accounts of task switching have sought to specify the cognitive control processes involved in minimizing switch costs, including, for example, the ability to update the contents of working memory with the current task set (i.e., the current task goal and response to be made) and the ability to resolve interference from conflicting information required by a prior task but not the current one (see Kiesel et al., 2010, for a review). While aspects of task switching are hypothesized to depend on other cognitive processes, to our knowledge prior studies have not tested these accounts using an individual differences approach in which variation in working memory and interference resolution have been related to multiple aspects of task switching. The goal of the present study was to take such an approach.

The measures of working memory and interference resolution presented here were reported in a previous study (Pettigrew & Martin, 2014) in which we examined whether these constructs differed as a function of age. In the present study, using data from the same participants, we created composite scores for working memory (WM) capacity, response-distractor inhibition, and proactive interference (PI) resolution in order to relate these constructs to different aspects of task switching. Some prior evidence suggests that response-distractor inhibition and PI resolution are distinct aspects of interference resolution (Friedman & Miyake, 2004; though see Pettigrew & Martin, 2014), with the former referring to resolution of interference elicited from information in the external environment and the latter referring to resolution of interference from no longer relevant information in memory; these constructs, therefore, might play different roles in task switching.¹

Task Switching

In the present study, we examined three measures of task switching: global switch costs, local switch costs, and N-2 repetition costs. Global switch costs refer to worse performance observed during mixed blocks relative to pure (or single task) blocks. In contrast, local switch costs refer to worse performance observed for switch relative to repeat trials within a mixed block. Though global and local costs would seemingly reflect similar demands of switching, they formed separate factors in latent variable analysis (Kray & Lindenberger, 2000) and are thought to draw on different cognitive processes, as discussed below. Another type of cost, termed the N-2 repetition cost or backward inhibition (Mayr & Keele, 2000), has been documented in paradigms involving three different tasks, where worse performance is found when switching back to a more recently abandoned task (ABA) relative to switching to a less recently performed third task (CBA). Below, we discuss the control mechanisms hypothesized to be associated with each of these costs.

Global switch costs (e.g., Jersild, 1927; Rogers & Monsell, 1995; Spector & Biederman, 1976) were the earliest reported measure of task switching (e.g., plus-minus task; Jersild, 1927). However, some have argued that this measure does not reflect switching per se, but rather the working memory demands of keeping multiple task in an active, accessible state in mixed blocks (in comparison to a pure block where only one task is relevant) (Rogers & Monsell, 1995). Global costs have been hypothesized to measure the ability to update, manipulate, and maintain multiple tasks in WM (e.g., Mayr, 2001; Rogers & Monsell, 1995). In line with the WM account for global switch costs, Baddeley, Chincotta, and Adlam (2001; see also Emerson & Miyake, 2003; Spector & Biederman, 1976) found that global switch costs were larger in uncued than cued shifting conditions, in which participants must use their own resources (presumably WM) to keep track of the relevant task across trials. Furthermore, concurrent articulatory suppression, thought to disrupt rehearsal processes, has been found to have detrimental effects on measures of global task switching when self-cueing demands are high (e.g. Baddeley et al., 2001; Bryck & Mayr, 2005; Emerson & Miyake, 2003). These findings support the idea that global switch costs involve working memory resources for keeping multiple tasks sets in mind as well as keeping the current task active and suggest that individual differences in working memory capacity should relate to the size of global switch costs.

However, Rubin and Meiran (2005) have proposed that interference resolution – described as the ability to manage competition between activated tasks due to the presence of ambiguous stimuli that are associated with multiple tasks – plays a strong role in the task decision process within mixed blocks and is common to both switch and repeat trials (see also Allport et al., 1994). This suggests a contribution of interference resolution to mixed block performance, and predicts a relationship between global costs and measures of interference resolution.

Local switch costs are thought to more directly reflect the switching process itself as the subject changes between tasks (Rogers & Monsell, 1995). The two main theoretical accounts of local switch costs are interference resolution and task set reconfiguration, which make different predictions regarding the association between local costs and the control mechanisms examined here.

Allport and colleagues (Allport, Styles, & Hsieh, 1994; Allport & Wylie, 2000; Wylie & Allport, 2000; see also Altmann & Gray, 2008; Badre & Wagner, 2006) have proposed a critical role for interference resolution in local switch costs. Their account assumes continued priming from previously activated task features (i.e., task set inertia); when a task repeats, this activation is beneficial but when a task switches, this activation results in interference. Because this interference is hypothesized to derive from previously formed stimulus-response-task set bindings that persist in memory (e.g., Allport et al., 1994; Waszak, Hommel, & Allport, 2003), it may be considered a type of proactive interference. Support for this interference account comes from various sources. For example, Allport and colleagues (Allport & Wylie, 2000; Waszak, Hommel, & Allport, 2003; Wylie & Allport, 2000) found larger switch costs for stimuli that were previously associated with a competing task. Evidence of interference from previously relevant task features also comes from findings of asymmetrical switch costs: when one task is more dominant than another (e.g., as with word reading vs. color naming in the Stroop task), larger switch costs are obtained when switching to the dominant, easier task (word reading) than when switching to the less dominant task (color naming) (Allport et al., 1994; see Meuter & Allport, 1999, for similar results in bilingual language switching). Asymmetrical switch costs result because more inhibition is required to overcome interference from the dominant task, causing greater difficulty when having to switch back to that task (Allport et al., 1994; Allport & Wylie, 2000; Meuter & Allport, 1999; but see Yeung & Monsell, 2003, for a different account of asymmetrical switch costs, and Koch et al., 2010 for discussion). A complete review of the role for interference resolution in local switch costs is beyond the scope of this paper, but can be found elsewhere (Vandierendonck, Liefooghe, & Verbruggen, 2010). For the purposes of the present study, this account of local switch costs predicts a relationship between the ability to resist PI and the size of local switch costs.

The other prominent account of local costs focuses instead on control mechanisms involved in changing task-set and stimulus-response mappings, often termed “task set reconfiguration” (Rogers & Monsell, 1995). Under this account, local costs are hypothesized to reflect an active process that involves the retrieval and updating of task sets at the point of a task switch (Kray & Lindenberger, 2000; Mayr, 2001; Meiran, 2000; Rogers & Monsell, 1995; Rubinstein, Meyer, & Evans, 2001). Though there are multiple proposals regarding task set reconfiguration (e.g., Rogers & Monsell’s (1995) endogenous control; Rubinstein et al.’s (2001) goal shifting; Meiran’s (2000) stimulus set biasing; Mayr & Kliegl’s (2000) retrieval of task information from long-term memory), they all assume a function that clears the focus of attention of the previously relevant task and replaces it with newly relevant task features and stimulus-response mappings. According to this view of local switch costs, there is no explicit connection to interference resolution, but we might expect a relation between local costs and working memory capacity to the extent that task set retrieval and implementation utilize WM resources.

Lastly, N-2 repetition costs (Mayr & Keele, 2000; for a review, see Koch et al., 2010) are thought to reflect the application of inhibition as a mechanism for disengaging from no-longer-relevant tasks at the point of a task switch. The measurement of N-2 repetition costs requires mixed blocks containing three tasks (e.g., tasks A, B, and C), in order to compare triad task sequences (e.g., ABA vs. CBA) that differ in how recently task A was performed. Mayr and Keele (2000) found worse performance in the ABA sequence (the N-2 repetition trial) relative to the CBA sequence (N-2 switch trial), suggesting more difficulty in switching back to a recently abandoned task (ABA). Mayr and Keele (2000; see also Gade & Koch, 2005, 2007; Schuch & Koch, 2003; Schneider & Verbruggen, 2008) interpreted the presence of N-2 repetition costs as reflecting backwards inhibition – the aftereffects of having previously applied inhibition to a no-longer-relevant task. Of note, backward inhibition may be an important component of local switch costs (Mayr & Keele, 2000) as discussed above with respect to the explanation for asymmetrical switch costs and clearing the focus of attention at the point of a task switch, functioning to overcome residual activation (i.e., interference) of no-longer-relevant task features. To the extent that backward inhibition is elicited as a consequence of top-down control mechanisms that overcome interference from task features in the external environment or representations in memory, it might be associated with response-distractor inhibition or resistance to PI, respectively. However, it has been proposed that N-2 repetition costs reflect a more automatic process such as lateral inhibition, which may be applied during response selection (Gade & Koch, 2005, 2007; Schuch & Koch, 2003; Schneider & Verbruggen, 2008; cf. Houghton, Pritchard, & Grange, 2009) or self-inhibition, applied immediately after task execution (Grange, Juvina, & Houghton, 2012; cf. Koch et al., 2010). Such automatic processes may be theoretically distinct from both the inhibition of prepotent responses and resolution of PI. The present study provides a test of this distinction: if N-2 repetition costs reflect an automatic form of inhibition (lateral or self-inhibition), we would not predict an association between N-2 repetition costs and either PI resolution or response-distractor inhibition.

To summarize, theoretical accounts make different predictions regarding the contribution of control mechanisms to various measures of task switching. Because the control mechanisms discussed here are impaired in healthy aging (i.e., reduced WM capacity and increased interference with age) (e.g., May, Hasher, & Kane, 1999; Hasher & Zacks, 1988; Pettigrew & Martin, 2014), the inclusion of both young and older the two age groups may provide additional variability for detecting relationships between the task switching measures and control mechanisms. Given the theoretical accounts discussed above, we hypothesized working memory would account for variance in global switch costs, and resistance to PI would be related to local switch costs. In contrast, we hypothesized no association between N-2 repetition costs and the control mechanisms included, if these costs reflect an automatic form of inhibition rather than interference resolution via top-down control.

Method

As noted earlier, the participants, the working memory measures, and the proactive interference and response-distracter inhibition measures were previously reported in Pettigrew and Martin (2014). Specifics about the participants and these procedures are reiterated here to enhance readability, though in the interest of space, only brief task descriptions are provided. Participants were also tested on a flanker task (e.g., Eriksen & Eriksen, 1974; not described below); however, these data were not included in the present study, as Pettigrew and Martin (2014) found that this task did not significantly load with the other response-distractor inhibition tasks.

Participants

A total of 167 participants were tested on the tasks detailed below, including 105 young adults and 62 older adults. For the young adult sample, 67 were recruited through the Rice University subject pool and received credit towards course requirements for research participation; the remaining 38 were recruited from the Houston community through Craig’s List (houston.craigslist.org). Data from three young adults were excluded: two participants failed to complete both testing sessions, and another was not a fluent speaker of English. The remaining 102 young adults consisted of individuals between the ages of 17 and 32 (M > = 21, SD > = 3). The older adult sample included 62 members of the Houston community who had expressed prior interest in participating in Psychology experiments. Data from two older adults were excluded: one participant failed to complete both testing sessions and another’s testing was discontinued due to possible cognitive impairment as indicated by a score of less than 26 on the Mini-Mental State Examination (MMSE; Folstein, Folstein, McHugh, & Fanjiang, 2001); all other older adults scored 26 or above (Table 1). The remaining 60 older adults consisted of individuals between the ages of 64 and 87 (M > = 71, SD > = 5).

Table 1.

Demographic variables and performance on control composite scores as a function of age.

	Young	Old
n	102	60
Age	21.2 (3.08)	71.0 (4.96)	p < .001*
MMSE	-	28.83 (1.12)	-
Education	14.0 (1.69)	16.0 (2.81)	p < .001*
WAIS Vocabulary (/66)	52.1 (7.3)	51.8 (7.53)	p = .81
Symbol-digit coding (speed; /35)	24.8 (4.45)	16.3 (3.17)	p < .001*
Response-distractor inhibition composite	−0.15 (0.50)	0.25 (0.76)	p < .001*
Resistance to PI composite	−0.32 (0.43)	0.54 (0.70)	p < .001*
WM composite	0.23 (0.64)	−0.40 (0.82)	p < .001*

Note. For the digit symbol task and WM composite, higher scores reflect better performance. For the inhibition and resistance to PI composite scores, higher scores reflect worse performance (i.e., larger interference effects).

^*Significant group differences, p < .05.

Procedure

Prior to starting the experimental tasks, participants completed the informed consent process, a demographics form, and background questionnaire to screen for confounding disorders such as neurological trauma or other impairment that might affect cognitive functioning. Older adults also completed the MMSE (Folstein et al., 2001) to screen for possible mild cognitive impairment or dementia. Study completion involved two separate two-hour sessions, with approximately 1–2 weeks between sessions. Breaks were provided between blocks within tasks and between tasks, as needed. All tasks were completed in the same order, with one exception: a few participants received the automated operation span task at a different time during the testing session due to computer availability.

Materials and Task Descriptions

All tasks included practice trials for task familiarization and learning of stimulus-response mappings. The experimental tasks fall into four categories: shifting tasks, response-distractor inhibition tasks, resistance to PI tasks, and working memory tasks.

Shifting Tasks

All participants completed a cued shifting task that involved switching between three tasks. Some participants also completed a second shifting task that included the same three tasks, but only involved switching between two tasks at any given time. Due to time constraints and being added to the design later in time, data for this latter task were only collected on a subset of young (n = 94) and older (n = 20) adults; only data from the young adults are reported.

Both shifting tasks utilized a cued shifting paradigm with targets consisting of a number (one, two; number task) of shapes (circle or diamond; shape task) of varying sizes (small (1.5”×1.5”) or large (3”×3”); size task). Each trial started with an explicit cue indicating the relevant task for a given trial, reading “Number”, “Shape”, or “Size” (see Jost, De Baene, Koch, & Brass (2013) for a discussion of cue manipulations). Explicit cues minimize task demands associated with memorizing arbitrary cue-task associations or the need to keep track of task sequences (e.g., Baddeley et al., 2001; Emerson & Miyake, 2003). Thus, any relation to working memory capacity would not be due to these aspects of shifting present in some paradigms. The target appeared 200 milliseconds (ms) after cue onset, displayed below the cue in the center of the screen. Both the cue and target remained on the screen until a button press was made, and the next trial started after a fixed 200 ms response-cue interval. The circle, small, and one target dimensions were mapped to the left response key; the diamond, large, and two target dimensions were mapped to the right response key. Shifting tasks were programmed on a Macintosh computer running PsyScope (Cohen, MacWhinney, Flatt, & Provost, 1993).

Shifting between three tasks

In the three-task shifting paradigm, participants completed a total of six experimental blocks, including three pure task blocks (i.e., one for each of the three tasks: number, shape, size) followed by three mixed task blocks. In the pure task blocks, participants responded to a single task throughout the duration of the block. Each pure block contained 42 trials, with the first two trials of each block excluded as warm-up. The order of the pure blocks was counterbalanced across participants. In mixed blocks, the relevant task depended on the cue presented at the start of the trial, with the relevant task changing every trial (i.e., every trial was a task switch). Each experimental mixed block contained 99 trials, with the first three trials of each block excluded as warm-up. For both pure and mixed blocks, targets were selected pseudo-randomly with the constraint that no exact stimulus repetitions were allowed. Additionally, within the mixed blocks, task sequence was also constrained by the following: a) all three tasks occurred equally often, b) there were no direct task repetitions, c) each task triad (e.g., size, shape, number; shape, size, number; etc.) appeared equally often within a block, and d) there was an equal number of N-2 task switches (CBA) and N-2 task repetitions (ABA). One practice block consisting of 16 trials preceded each experimental pure task block; additionally, one practice mixed block consisting of 40 trials preceded the first experimental mixed block. This task allowed for the measurement of two dependent variables (DV): global switch costs, measured as mixed vs. pure block performance, and N-2 repetition costs, measured as N-2 repeat vs. N-2 switch trials within the mixed block.

Shifting between two tasks

A subset of participants also completed a two-task shifting paradigm (in a different session than the three-task shifting), which included an additional set of three mixed blocks using the same number, shape, and size tasks just described. The mixed blocks in this task included both switch and repeat trials for calculating local switch costs. In this version of the task, only two of the three tasks were relevant within a given mixed block: for the first block, the two relevant tasks were form and size; for the second block, form and number; and for the third block, size and number. Prior to each experimental mixed block, participants completed a practice block of 10 trials. Each experimental mixed block contained 35 trials, with the first 3 trials of each block excluded as warm-up. Unlike three-task shifting, task repetitions were allowed, though exact stimulus repetitions were not. Half of the trials were repeat trials and the other half switch trials. For the subset of young adult participants (n = 94) whose data are reported, the DV was local switch costs, measured as switch vs. repeat trials.

Response-Distractor Inhibition Tasks

Picture-word interference task (PWI)

In the picture-word interference task (e.g., Lupker, 1979; Schriefers, Meyer & Levelt, 1990), participants named a picture while ignoring a super-imposed distractor word. In the interference condition, the picture and distractor word were semantically related (i.e., picture and word come from the same category); in the no interference condition, the picture and distractor word were semantically unrelated. The interference effect was measured as RT for interference vs. no interference trials. One young adult’s PWI data were missing due to experimenter error.

Nonverbal (NV) Stroop task

In the nonverbal Stroop task (Hamilton & Martin, 2005), participants responded to the direction of an arrow (left, right; via button press) that was presented on the left, center, or right side of the screen. In the interference condition, arrow direction and location were incongruent (left-pointing arrow on the right side of the screen); in the no interference condition, the arrow was presented in a directionally neutral location (i.e., the center of the screen). This task also contained congruent trials (e.g., left-pointing arrow on the left side of the screen) that were not included as part of the DV. The interference effect was measured as RT for interference vs. no interference trials.

Stroop task

In the Stroop task (Stroop, 1935), participants named the color of the target, which was either a word (in the incongruent and congruent trials) or string of asterisks (in the neutral condition). In the interference condition (incongruent trials), color words appeared in a color different from the written word (e.g., blue written in red). In the no interference condition (neutral trials), participants named the color of a string of asterisks. This task also contained congruent trials (color words appeared in the same color as the written word) that were not included as part of the DV. The interference effect was measured as RT for interference vs. no interference trials. One older adult’s Stroop data were missing due to color blindness.

Resistance to Proactive Interference Tasks

Recent negatives task

In the recent negatives probe task (e.g., Monsell, 1978), participants heard a list of three words followed by a probe word, then indicated whether the probe word was in the previous list by pressing “yes” or “no” keys. This task contained three trial types. In the interference condition, referred to as recent negative trials, the probe word was not presented in the most recent list (list n), but it was presented in the previous trial (list n-1), requiring a “no” response. In the no interference condition, or non-recent negative trials, the probe word was not presented in any of the most recent lists, also requiring a “no” response. This task also contained positive trials (i.e., the probe word was presented in the most recently presented list (list n), requiring a “yes” response) that were not included as part of the DV. The interference effect was measured as RT for interference vs. no interference trials, demonstrating a participant’s susceptibility to interference from previously relevant list items.

Cued recall task

In the cued recall task (Tolan & Tehan, 1999; similar to Friedman & Miyake, 2004), participants saw one or two lists of four sequentially presented words that they were instructed to read silently or aloud. Following a filler task that involved making verbal magnitude judgments, participants saw a category cue and were asked to recall the category exemplar from the most recently presented list. In the no interference condition, participants saw only a single list before receiving a category cue (i.e., one-list trials). In the interference condition, participants saw two four-item lists, though only the second list contained an item from the cued category. This task also contained two-list trials in which both the first and second lists both contained cued category exemplars; these trials were not included as part of the DV. The interference effect was measured as accuracy for interference vs. no interference trials.

Release from proactive interference task

In the release from PI task (a variant of the task used by Peterson & Peterson, 1959; similar to Friedman & Miyake, 2004), participants were presented with ten blocks of lists. Each block contained four lists of eight sequentially presented words: the first three lists contained items from the same semantic category, whereas the fourth list contained items from a different semantic category. Participants read each list item aloud, then completed a filler task that involved sequential counting by number and letter (e.g., “H-39, I-40, J-41…”); after the filler task, participants recalled as many of the just-presented list items as possible. As in Pettigrew and Martin (2014), the dependent variable was the number of list 1 intrusions made during list 2 recall.

Working Memory Tasks

Automated operation span

In the automated operation span task (Ospan; Turner & Engle, 1989; Unsworth, Heitz, Schrock, & Engle, 2005), participants saw a math operation to verify (true/false) followed by a letter to remember. Following several math operation-letter pairs, participants saw an array of twelve letters with boxes next to them, at which point they recalled the previously presented letters in serial order by clicking the relevant boxes. The dependent variable was the operation span defined as the sum of all perfectly recalled sets (Unsworth et al., 2005). Ospan data were missing from two older adults due to experimenter or computer error.

Backwards digit span

In the backwards digit span task from the Weschler Adult Intelligence Scale-Revised (WAIS-R; Weschler, 1981), participants heard a series of numbers which they recalled in backwards order, starting with the most recently presented item. Participants completed two trials at each list length, continuing until either errors were made on both trials at a given list length or the maximum list length (8 items) was completed. The dependent variable was the total number of trials correctly recalled.

Sternberg recognition task

In the Sternberg recognition task (McElree & Dosher, 1989; Nee & Jonides, 2008), participants saw a list of five serially presented words (presented for 500 ms each). The last word was followed by a 300 ms mask, and then a probe word. Participants indicated whether the probe word was in the most recently presented list (yes/no). The dependent variable was overall accuracy across all trials. Data were missing for two older adults due to unwillingness to complete this task because of frustration with the speed of item presentation.

Data Processing and Missing Data

For all interference resolution RT measures, RTs from errors and/or voice key errors were removed and outlying RTs were also excluded, including all RTs < 250 ms and > 10,000, and RTs falling more than 2.5 standard deviations beyond an individual’s mean, by condition. As mentioned in the Method, seven data points were missing, though no individual subject was missing data for more than one task. Given the small number of missing points, and to avoid excluding these subjects altogether, missing values were replaced with the mean for that age group.

Composite Scores for Control Mechanisms

To examine whether control mechanisms were differentially associated with measures of task switching, we created separate standardized composite scores for WM capacity, response-distractor inhibition, and resistance to PI by averaging performance across the three tasks within each domain. For the WM composite, WM task DVs (for the operation span, backwards digit span, and Sternberg recognition) were z-scored then averaged, with higher values indicating larger WM capacities (i.e., better performance). For the interference tasks, we regressed the interference condition on the no interference condition and saved the standardized residuals, which were used as the task’s DV. The only exception to this was for the release from PI task, which used the z-scored proportion of list 2 intrusions as the DV; as discussed in Pettigrew & Martin (2014), intrusions were found to be more reliable than the interference residual for this task. Where necessary, interference measures were reverse scored so larger values indicated more interference (i.e., worse performance). For the response-distractor inhibition composite, the mean of the residual interference effects for the PWI, NV Stroop, and Stoop tasks was computed. For the resistance to PI composite, the mean of the recent negatives and cued recall residual interference effects and the release from PI z-scored intrusion effect was computed.

Dependent Variable for Task Switching Measures

Shifting performance was measured with rate residual scores, which incorporate both response time (RT) and accuracy data in a single score (Hughes, Linck, Bowles, Koeth, & Bunting, 2014). As described in Hughes et al. (2014), rate residual scores were based on the rate of correct responding per second for each trial type. Prior to calculating response rates, outlying RTs (RTs 2.5 standard deviations beyond an individual’s mean performance, by condition) were replaced with that participant’s cutoff. Rate residual scores were computed separately, but in the same manner, for global costs, local costs, and N-2 repetition costs. Blocks were divided into a comparable number of subsets of trials (though the subsets had a different number of trials, given the different block lengths). For global costs, pure and mixed blocks were each divided into 8 sets of trials (pure block subsets contained 15 trials; mixed block subsets contained 36 trials). For local costs, repeat and switch trials were each divided into 6 sets of trials (each repeat and switch trial subset contained 8 trials). For N-2 repetition costs, N-2 repeat and N-2 switch trials were each divided into 8 sets of trials (each N-2 repeat and N-2 switch trial subset contained 17–19 trials). The rate of correct responding was calculated for each subset “by dividing the number of correct responses per trial type by the time taken to make all of the responses, whether accurate or inaccurate (summing the RTs for that trial type)” (p. 709). Using these rates of correct responding, rate residual scores were calculated: for each subset, the difficult shifting condition was regressed on the easy shifting condition (i.e., for global costs, mixed block subset 1 was regressed on pure block subset 1). For global costs and N-2 repetition costs, a total of 8 residuals were calculated per subject; for local costs, a total of 6 residuals were calculated per subject. Each subject’s subset residuals were then averaged to produce rate residual scores, with more negative residuals indicating larger switch costs.

Alternative scoring methods for task switching – such as rate residual scores – have been argued to provide a more accurate measure of task switching ability because they incorporate the two measures in which switch costs can occur (i.e., latency and accuracy) (Draheim & Engle, 2014; Hughes et al., 2014). Previous work has also suggested that these scores are more reliable and valid than traditional RT difference scores (Hughes et al., 2014). Additionally, because rate residual scores use regression residuals in which performance on the “easier” (or baseline) shifting condition was regressed from the more difficult shifting condition, these scores also allowed us to control for individual differences in other factors that might influence task performance (e.g., Cerella, 1990; Cronbach & Furby, 1970; Faust, Balota, Spieler, & Ferraro, 1999), such as baseline resources or processing speed (Salthouse, 1994; Salthouse & Babcock, 1991).

Analyses

Multiple regression was used to examine the relationship between the task switching measures and control mechanisms. For each switch cost – i.e., global costs, local costs, and N-2 repeittion costs – rate residuals scores were regressed on the three control composites of WM capacity, response-distractor inhibition, and resistance to PI. Given the age-heterogeneous sample, these regressions also included additional predictors: age (dichotomous: young, old) and the control mechanism by age interactions (product). The interactions were included to determine whether shifting-control associations differed as a function of age. (Age terms were not included in the local cost model because it only contained young adult data.)

In the above analyses, none of the age×control mechanism interactions were significant (all ps > .27), suggesting that the association between control mechanisms and shifting measures did not differ for young and older adults. Interactions terms were removed from the regression models and the below results reflect the main effects only. Though the analyses focused on shifting rate residual scores, mean RTs and error rates are also reported in Table 2, and regression analyses using RT and error difference scores are reported in the Appendix for comparison.

Table 2.

Mean (standard deviation) performance on shifting measures by age and condition. More negative rate residual scores indicate larger switch costs.

	Response times			Error rates			Rate residual scores
Global switch costs
Age	Pure	Mixed	RT cost	Pure	Mixed	Error cost	Global Cost
Young	487 (83)	1109 (257)	622 (214)	.03 (.03)	.04 (.04)	.01 (.03)	0.06 (0.80)
Old	732 (189)	1715 (652)	983 (546)	.02 (.02)	.04 (.06)	.03 (.06)	−0.10 (0.93)
Local switch costs
Age	Repeat	Switch	RT cost	Repeat	Switch	Error cost	Local Cost
Young	717 (154)	800 (161)	82 (94)	.04 (.04)	.05 (.05)	.01 (.05)	0.01 (0.62)
N-2 repetition costs
Age	N-2 switch (CBA)	N-2 repeat (ABA)	RT cost	N-2 switch (CBA)	N-2 repeat (ABA)	Error cost	N-2 Repetition Cost
Young	1084 (263)	1137 (260)	53 (71)	.04 (.04)	.04 (.04)	.003 (.02)	0.14 (0.45)
Old	1670 (645)	1764 (663)	94 (102)	.04 (.06)	.05 (.06)	.01 (.02)	−0.22 (0.38)

Where possible, we estimated DV reliabilities with a split-half reliability adjusted by the Spearman-Brown formula. For the shifting dependent variables, split-half reliabilities were calculated by splitting trial subsets into two halves (odd/even); rate residual scores were then calculated for each half, and reliabilities calculated by correlating these halves. For the interference resolution composites, reliability values reflect the split-half reliability of the composite score. For both the shifting DVs and the interference resolution composites, we also report reliabilities for each age group, calculated as just mentioned but separately for young and older adults. Because trial-by-trial Ospan data was inaccessible (i.e., only a summary score was available), WM composite reliability was estimated by averaging previously published reliability values: for Sternberg recognition, split-half reliability = .95 (Pettigrew & Martin, 2014); for Ospan, split-half reliability = .78 (Unsworth et al., 2005); for backwards digit span, test-retest reliability = .83 (Weschler, 1981).

Results

Participant demographics and scores on various cognitive and composite measures are shown in Table 1. Shifting scores, including RT, accuracy, and rate residual scores by age and condition are shown in Table 2. Older adults were more educated, though the two age groups were matched on scores of crystallized intelligence as measured by the vocabulary subtest of the WAIS-III (Weschler, 1997). Otherwise, the older adults showed relatively standard patterns of age-related differences, including slower processing speed (as measured by the symbol-digit coding task of the MMSE; Folstein et al., 2001), reduced working memory capacity, and increased interference (as measured by the two interference resolution composites). Shifting DV and control composite reliabilities are shown in Table 3. Reliabilities were variable, being quite good for global costs and the working memory and response-distractor inhibition composite scores, but quite low for N-2 repetition costs; reliability for local costs and the resistance to PI composite score fell in between. Intercorrelations among the shifting rate residual scores, control composite scores, and age (dichotomous) are shown in Table 4.

Table 3.

Reliabilities for the shifting dependent variables and composite measures. Shifting reliabilities reflect split-half reliabilities of rate residual scores.

Measure	Reliability (all subjects)	Reliability (young)	Reliability (old)
Global costs	.95	.94	.96
Local costs (n = 94 young)	-	.67	-
N-2 repetition costs	.44	.46	.51
Response-distractor inhibition composite	.78	.77	.81
Resistance to PI composite	.59	.29	.69
WM composite	.85	-	-

Table 4.

Intercorrelations between shifting variables (rate residual scores), control composite scores, and age. More negative rate residual scores indicate larger switch costs.

	1	2	3	4	5	6	7
1. Global costs	-	.57*	0.38*	−0.07	−0.09	0.26*	−0.09
2. Local costs	-	-	.12	.06	−.17	.18	-
3. N-2 repetition costs	-	-	-	−0.07	−0.25*	0.26*	−0.38*
4. Response-distractor inhibition composite	-	-	-	-	0.22*	−0.27*	0.30*
5. Resistance to PI composite	-	-	-	-	-	−0.35*	0.61*
6. WM composite	-	-	-	-	-	-	−0.40*
7. Age (dichotomous)	-	-	-	-	-	-	-

^*p ≤ .005

Note. For the cells shaded in gray, n = 94 young adults.

Global Switch Costs

Global costs

Subjects demonstrated significant global switch costs, as measured by RT difference scores (M cost = 755 ms, SD = 410), t(161) = 23.43, p < .001. Figure 1a shows the RT plot of mixed block performance against single block performance for both young and older adults. Although the slope is somewhat higher for the older than the younger adults, the correlation between rate residual scores and age was not significant (see Table 4), and global rate residual scores did not differ between older adults (-.10) and younger adults (.06), t(160) = 1.20, p = .23. Global rate residual scores were only correlated with one individual differences measure, the working memory composite. Similar results were observed in the multiple regression: working memory had a highly significant regression weight (p = .002), with the positive coefficient indicating that higher WM capacity was associated with more positive rate residual scores (i.e., smaller global switch costs). In contrast, neither response-distractor inhibition nor resistance to PI were significantly associated with mixed block performance (both ps > .90).²

Figure 1.

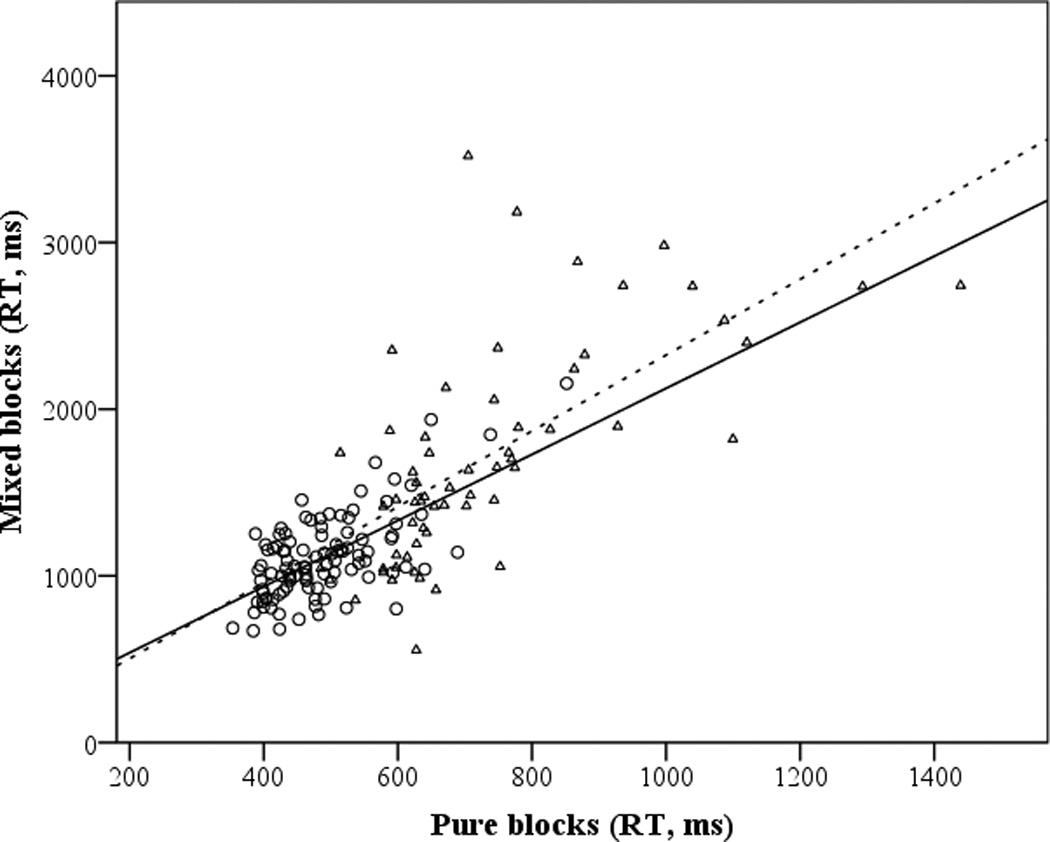
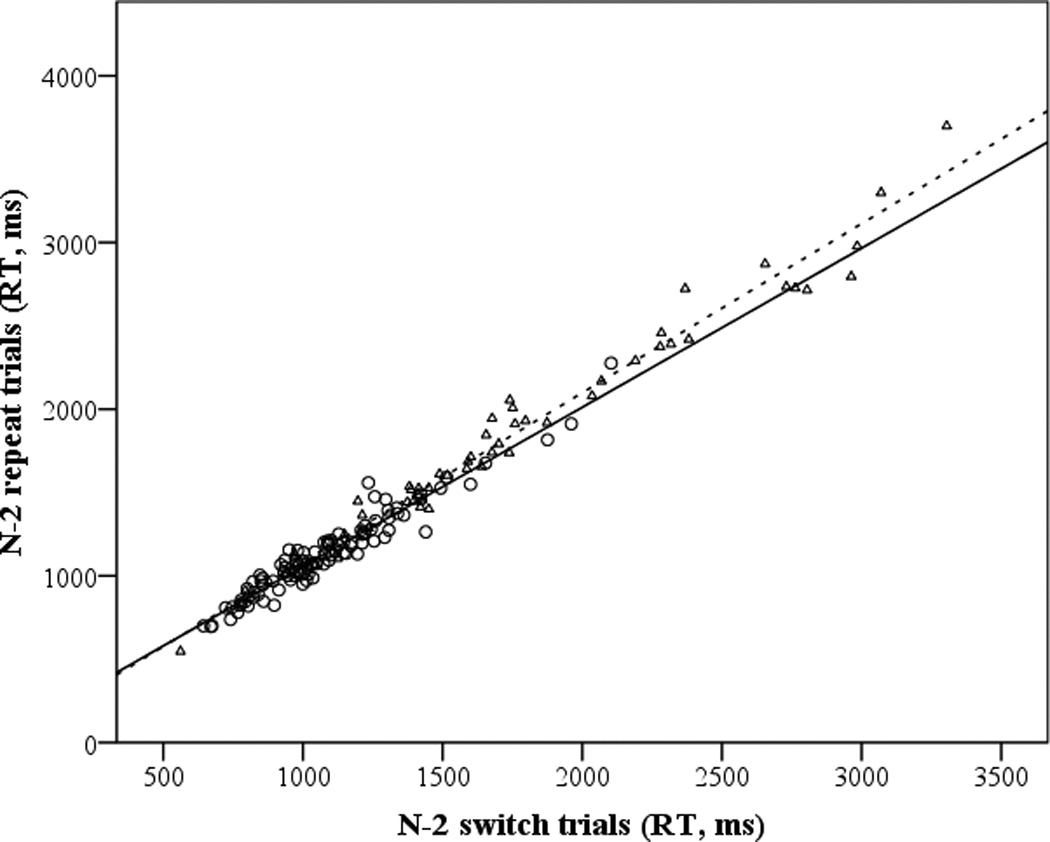
Scatterplots and fit lines for the global (1a) and N-2 (1b) shifting response times, by condition and age group. Young adults are indicated by circles (solid line) and older adults by triangles (dashed line).

Local Switch Costs

Local costs

The subset of young adults (n = 94) that completed this task demonstrated significant local switch costs, as measured by RT difference scores (M cost = 82 ms, SD = 94), t(93) = 8.52, p < .001. As shown in Table 4, local rate residual scores were not significantly correlated with any of the control composite measures. The multiple regression revealed the same pattern of null effects: local costs were not significantly associated with any of the control measures, though the association with both resistance to PI (p = .10) and WM (p = .10) were marginal, with the negative weight for resistance to PI and the positive weight for WM suggesting individuals with lower PI and higher WM capacity demonstrate a trend towards better rate residual scores (i.e., smaller local switch costs). In contrast, response-distractor inhibition was not significant (p = .42).

N-2 Repetition Costs

N-2 repetition costs

On average, subjects demonstrated small but significant N-2 repetition costs, as measured by RT difference scores (M cost = 68 ms, SD = 86), t(161) = 10.15, p < .001. Across age groups, there was a substantial correlation between N-2 repeat and N-2 switch trial performance (r = 0.987, p < .001). Figure 1b displays the RT plot of N-2 repeat vs. N-2 switch trial performance for young and older adults, with a slightly higher slope for the older adults. N-2 repetition rate residual scores were significantly larger for older adults (−.21) relative to younger adults (.14), t(160) = 5.19, p < .001 . N-2 rate residual scores were also significantly correlated with age and the resistance to PI and WM composite scores (all ps < .005; Table 4), with the respective correlation directions indicating that better rate residual scores (i.e., smaller N-2 repetition costs) were associated with younger age, lower PI, and higher WM capacity. In the multiple regression results, however, only the weight for age was significant (p < .001; Table 5): none of the control mechanisms explained additional variance in N-2 rate residual scores, though the effect of WM was marginal (p = .09).

Table 5.

Regression results examining the association between cognitive control mechanisms and shifting measures. More negative rate residual scores indicate larger switch costs.

Cost	Predictor	B	S.E. B	β	p
Global switch costs	Age	.02	.18	.01	.90
	Inhibition	−.005	.11	−.004	.96
	Resistance to PI	−.001	.12	−.001	.99
	WM	.29	.09	.27	.002*
Local switch costs	Inhibition	.11	.13	.08	.42
	Resistance to PI	−.25	.15	−.17	.10
	WM	.17	.10	.17	.10
N-2 repetition costs	Age	−.32	.09	−.34	< .001*
	Inhibition	.05	.06	.08	.33
	Resistance to PI	−.004	.06	−.01	.94
	WM	.08	.05	.14	.09

^*p < .05

Note. S.E. = standard error

Discussion

Accounts of everyday cognition have proposed an important role for executive control and working memory in situations requiring flexible, organized behavior (e.g., Baddeley, 1986; Miller & Cohen, 2001; Norman & Shallice, 1986). The present study examined the extent to which individual differences in control measures, including WM capacity and the interference resolution mechanisms of response-distractor inhibition and resistance to PI, explain variability in measures of task switching, and whether these relationships differ in young and older adults. To our knowledge, this is the first time this type of individual differences approach has been taken with multiple theoretically distinct measures of task switching. Variance in global switch costs was related to WM capacity, whereas none of the control measures explained variance in local costs or N-2 repetition costs. There were no interactions with age, suggesting that control mechanisms do not differentially relate to measures of task switching in young and older adults. Additionally, age effects were only evident for N-2 repetition costs, with older adults demonstrating larger costs than young adults. These results are discussed in greater detail below.

Global Switch Costs

WM capacity, reflecting the temporary maintenance and manipulation of information in WM, was a significant predictor of global switching. Individuals with larger WM capacities demonstrated smaller global costs in line with accounts suggesting global switch costs reflect the ability to maintain, coordinate, and manipulate multiple tasks in WM (Mayr, 2001; Rogers & Monsell, 1995). Oberauer and colleagues (2003) have suggested that WM reflects multiple mechanisms, including “storage in the context of processing” (p. 189), as well as the ability to coordinate elements into structures (i.e., binding). We believe this delineation of WM translates well to mixed block performance. For example, high capacity individuals may be better able to bind task features together (i.e., binding stimulus values to response alternatives) (Oberauer et al., 2003; Oberauer, 2005) to create more distinct representations of what should be done in the context of a given task. Coherent bindings may also allow high capacity individuals to maintain more stable task representations and better utilize task representations in a flexible manner when the focus of attention must be updated at the point of a task switch.

Given that performance in mixed blocks involves keeping multiple task sets in an accessible state – while also maintaining them as distinct representations – it may seem surprising that resistance to PI was not a significant predictor of global costs. Of note, the present study used a cued shifting paradigm in which each trial began with an explicit task cue that indicated the relevant task for that trial (e.g., “Shape”). Although multiple mappings between stimuli and responses need to be created, maintained, and utilized, explicit cues may function to reduce interference between tasks relative to situations in which cues are implicit (i.e., symbolic) or subjects must keep track of task alternation on their own (e.g., Baddeley et al., 2001; Emerson & Miyake, 2003; Spector & Biederman, 1976). Therefore, it remains to be seen whether resistance to PI would play a stronger role in global switch costs when WM mechanisms are otherwise utilized for interpreting task cues or remembering task sequences.

We found no effect of age on global rate residual scores; of note, the effects of age remained non-significant in a regression that excluded the control measures (i.e., with age as the only predictor, β = 0.06, p = .37), indicating no difference in global switch costs between young and older adults with differences in processing speed taken into account. While a number of previous studies have found larger global switch costs for older relative to young adults (Kray & Lindenberger, 2000; Mayr, 2001; Mayr & Liebscher, 2001; Meiran, Gotler, & Perlman, 2001; Reimers & Maylor, 2005; Verhaeghen & Cerella, 2002; Wasylyshyn, Verhaeghen, & Sliwinski, 2011), results have been inconsistent (e.g., Kray, Li, Lindenberger, 2002; Mayr & Kliegl, 2000). Kray et al. (2002; see also Mayr, 2001) have proposed that these contrasting findings may be a product of the degree to which distinct task sets contain non-overlapping elements and can be easily differentiated; when tasks can be more easily differentiated (e.g., in the presence of an explicit cue, as in the present study), interference between tasks may be low, and age effects on global switch costs may be minimal (but see Wasylyshyn et al., 2011, for a meta-analysis suggesting no effect of task manipulations on age effects in global task switching).

Local Switch Costs

Interference and task set reconfiguration accounts of local switch costs make different predictions concerning the association between local switch costs and control mechanisms. In the regression analyses, the weights for both WM capacity and proactive interference were marginally significant (both ps = .10), perhaps due to the moderate DV reliability and reduced power as these analyses only included a subset of young adults (though the sample size was quite large, n = 94). While these caveats make it difficult to rule out either the WM capacity or interference resolution accounts, the findings would be consistent with theories of task switching that postulate the contribution of multiple factors (e.g., Vandierendonck et al., 2010), as discussed below.

As reviewed in the Introduction, accounts of task switching provide some possibilities for what roles WM and resistance to PI may play in local costs. However, theoretical models of local costs generally assume two stages: an endogenous stage that can occur prior to stimulus onset (e.g., during a cue-stimulus interval (CSI)) and an exogenous stage that cannot be completed until after stimulus presentation (Rogers & Monsell, 1995). While accounts of the endogenous component differ in their specifics (Goschke, 2000; Mayr & Kliegl, 2000; Meiran, 2000; Rubinstein et al., 2001), they emphasize the need to clear WM of the no-longer-relevant task in order to update the focus of attention with the currently relevant task set. Rubinstein et al. (2001), for example, have suggested that the endogenous component reflects “goal shifting”, which involves “inserting and deleting [task] goals in declarative WM” (p. 770). From these accounts, the endogenous portion of local switch costs may involve memory mechanisms such as the retrieval and updating of task representations from the activated portion of LTM (rather than maintaining multiple task sets in WM; see Mayr & Kliegl, 2000, for a similar idea), as well as interference resolution for overcoming activation of previously relevant task features, which was hinted at in the present results.

In contrast, the exogenous stage is thought to reflect a component of the local switch cost that cannot occur until after stimulus onset, reflecting the extent to which a response is influenced by irrelevant stimulus features and response mappings (Rogers & Monsell, 1995; see also Vandierendonck, Liefooghe, & Verbruggen, 2010). This component is measured by residual switch costs that remain after an extended CSI. Rubinstein et al. (2001; cf., De Jong, 2000; Meiran, 2000) have described this stage as “rule activation”, involving an additional control process associated with clearing previous stimulus-response (S-R) rules from procedural memory, and loading the newly-relevant rules. In line with interference accounts of switch costs, a number of authors have suggested that interference might play a critical role in delaying responses during this stage (Goschke, 2000; Rubinstein et al., 2001; Vandierendonck et al., 2010), for example, in resisting interference from irrelevant task features (e.g., Friedman & Miyake, 2004; Rubin & Meiran, 2005). Accordingly, it remains possible that the interference resolution may show a stronger relationship with residual switch costs (cf., Badre & Wagner, 2006), rather than local costs measured from short CSIs as in the present study. This endogenous/exogenous distinction also highlights an important limitation of our study – we did not manipulate CSI. In light of the various theories of task switching, the differential role for control mechanisms at short vs. long CSIs warrants additional study. For example, variance in local switch costs at short CSIs may be explained by measures more sensitive to task set retrieval (such as cue-based retrieval; e.g., Unsworth & Engle, 2007), versus measures of interference resolution at long CSIs.

Mixing costs, measured as the difference between task repeat trials in mixed blocks and pure task blocks (e.g., Rubin & Meiran, 2005), may provide another measure for examining the influence of bottom-up interference from irrelevant stimulus features and/or responses inherent to bivalent stimuli (i.e., interference that is conceptually similar to response-distractor inhibition). For example, Rubin and Meiran suggested mixing costs involve a task decision process (referred to above as “goal shifting”; Rubinstein et al., 2001) that is susceptible to interference from the bivalent target features, and that resolution of this interference occurs on both switch and repeat trials (which is consistent with our finding of no association between response-distractor inhibition and local switch costs). In contrast, this interference resolution is unlikely to play a role in pure block trials, during which tasks may be executed in an almost automatic fashion (Rubin & Meiran, 2005). This suggestion of a role for interference resolution in mixing costs may seem at odds with our finding of no significant association between global switch costs and response distractor inhibition. However, as discussed above, mixed blocks may involve a number of WM functions, including the maintenance of stable task representations and the retrieval and updating of task representations at the point of a task switch, that help to avoid interference; these WM demands may be more influential to overall mixed block performance (which includes both switch and repeat trials) than the need to resolve interference from bivalent target features. Mixing costs, in contrast, may provide a clearer picture of the role for control mechanisms when WM demands are minimized (relative to switch trials), and may therefore provide additional information on the role for bottom-up interference from bivalent targets. Unfortunately, the present study was not optimally designed to examine mixing costs, as pure task blocks and repeat trials were included in separate testing sessions.

It should also be noted that our task switching procedure used explicit cues for which each task switch was also accompanied by a cue switch (i.e., change in explicit cue). It has been suggested that local costs in part reflect retrieval processes associated with changes in explicit cues, and to a lesser extent changes in task (e.g., Logan & Bundensen, 2003; Mayr & Kliegl, 2003). However, the present study confounds these and does not allow us to determine whether the control mechanisms differently relate to task switches vs. cue switches. This is an important limitation that could be addressed in future research in a number of ways. For example, a similar individual differences approach could be used with (1) a 2:1 cue-to-task mapping paradigm in order to determine whether retrieval mechanisms or interference resolution play a stronger or differential role in these two processes (e.g., Mayr & Kliegl, 2003), or (2) a predictable switching paradigm in which cue processing is not involved.

N-2 Repetition Costs

We found no association between N-2 repetition costs the control mechanisms examined herein, raising the possibility that N-2 repetition costs (i.e., backward inhibition) reflect a distinct control mechanism (see Mayr & Keele, 2000, for a discussion). To our knowledge, this is the first study that has examined whether this measure is related to other more common measures of interference resolution.

The N-2 repetition cost is hypothesized to reflect the cost of overcoming inhibition that was applied to a recently executed task (Mayr & Keele, 2000; see also e.g., Gade & Koch, 2005, 2007; Koch et al. 2010; Schuch & Koch, 2003; Schneider & Verbruggen, 2008). Given the lack of significant association with the interference resolution mechanisms included herein, this cost may reflect an automatic form of inhibition, such as lateral inhibition (Mayr & Keele, 2000) or self-inhibition (Grange et al., 2012) that functions to clear or disengage the focus of attention when it needs to be updated with new information (Bao, Li, Chen, & Zhang, 2006; Costa & Friedrich, 2012; Mayr & Keele, 2000; see Hasher et al. (1999) and Oberauer (2001) for a similar distinction). This explanation is in line with theoretical interpretations (Mayr, 2001; Mayr & Keele, 2000) that “backward inhibition during sequential selection of mental sets is functionally dissociated from inhibition that is used to keep task-irrelevant information from interfering with task-appropriate settings” (Mayr, 2001, p. 100), and could be further tested in future research by collecting multiple backward inhibition measures and modeling whether they load on a factor that is distinct from other aspects of interference resolution. This may be an important future step given our ability to detect relationships with other constructs was limited by the low reliability of the N-2 repetition rate residual score.

Older adults demonstrated significantly larger N-2 repetition costs relative to the young adults, in contrast to previous studies examining age differences in this measure (Lawo, Philipp, Schuch, & Koch, 2012; Li & Dupuis, 2008; Mayr, 2001). Nonetheless, the results are in line with those of Mayr (2001), who found that older adults demonstrate larger N-2 repetition costs – though his effect failed to reach significance with log-transformed RTs (p = .07). Our results raise the possibility that age effects in N-2 repetition costs exist – though they may be quite small and difficult to detect with small sample sizes. Although there are multiple possible explanations for these age effects, we propose that backward inhibition is a relatively automatic process (as mentioned above; see also Grange et al., 2013; Koch et al., 2010; Mayr, 2001; Mayr & Keele, 2000; Schuch & Koch, 2003; Vandierendonck et al., 2010), with young and older adults applying similar amounts of inhibition to previously relevant task sets. Instead, age effects reflect individual differences in the ability to select or retrieve inhibited representations, with this being a more time consuming process for older adults (i.e., more difficulty in overcoming inhibition). Consistent with this, recent studies have suggested that older adults have no problem removing information from the focus of attention, but they make more errors both accessing information that is outside the focus of attention (Verhaeghen & Basak, 2005) and rejecting intrusions from irrelevant information that is in an activated state in long-term memory (Oberauer, 2001, 2005). Importantly, if we assume that selection mechanisms are applied, at least to some degree, on both switch and repeat trials alike, but that these selection mechanisms are simply slower in older adults, this account is also able to accommodate the lack of age effects on local switch costs (e.g., Reimers & Maylor, 2005; Verhaeghen & Cerella, 2002; Wasylyshyn et al., 2011).

Limitations and Future Directions

The present study should be interpreted within the context of its limitations, which also indicate areas for future research. A number of limitations were mentioned above, including the fact that we did not manipulate the cue-stimulus interval and our shifting paradigms were not designed to measure mixing costs, which may each provide more information about the influence of bottom-up interference from irrelevant stimulus features and/or responses inherent to bivalent stimuli. Furthermore, while our WM and interference resolution measures were indexed by composite scores, we only had a single measure of each task switching DV. Therefore, it will be important to expand upon these findings in future work, using either multiple measures for each switch cost, composite scores, or by manipulating task features (e.g., the number of cue-to-task mappings; CSI; cue ambiguity). Future research, for example, could manipulate cue ambiguity (which might result in more task set competition and create a larger role for interference resolution) and use longer cue-stimulus intervals (which may allow for a better understanding of control mechanisms in endogenous vs. exogenous reconfiguration processes). Furthermore, the present study included an age heterogeneous sample; though we believe this allowed for more variability in performance in our task switching and control measures, future work could ask similar questions in a larger sample of individuals from either age group.

Appendix

Regression results examining the association between cognitive control mechanisms and shifting measures, separately for RT and error difference scores. For these analyses, RTs were processed as follows: RTs from error trials and trials following errors were removed, and outlying RTs were excluded (including all RTs < 250 ms and > 10,000 ms, as well as RTs falling more than 2.5 standard deviations beyond an individual’s mean, by condition). As with the rate residual score results, none of the age×control mechanism interactions were significant (all ps > .10). Interaction terms were therefore removed from the models and the below results reflect the main effects.

Table A1.

regression analyses using RT and error difference scores

	Response times
Cost	Predictor	B	S.E. B	β	p
Global switch costs	Age	225.88	76.59	.28	.004*
	Inhibition	−31.75	46.89	−.05	.50
	Resistance to PI	57.93	52.38	.10	.27
	WM	−155.26	40.47	−.29	< .001*
Local switch costs	Inhibition	−12.15	20.08	−.06	.55
	Resistance to PI	38.02	22.78	.18	.10
	WM	−.73	15.14	−.01	.96
N-2 repetition costs	Age	50.93	17.87	.29	.005*
	Inhibition	−14.96	10.94	−.11	.17
	Resistance to PI	−14.98	12.22	−.12	.22
	WM	−12.66	9.44	−.12	.18
	Error rates
Cost	Predictor	B	S.E. B	β	p
Global switch costs	Age	−.004	.009	−.05	.63
	Inhibition	−.002	.006	−.02	.77
	Resistance to PI	.01	.006	.19	.052
	WM	−.01	.005	−.21	.01*
Local switch costs	Inhibition	−.01	.01	−.10	.34
	Resistance to PI	.01	.01	.10	.35
	WM	−.009	.008	−.13	.23
N-2 repetition costs	Age	.000	.005	−.009	.93
	Inhibition	.001	.003	.04	.66
	Resistance to PI	.009	.003	.25	.01*
	WM	.004	.003	.14	.12

^*p < .05

Note. S.E. = standard error