A Random Utility Model of Delay Discounting and Its Application to People With Externalizing Psychopathology

Abstract

Previous studies have demonstrated that working memory capacity plays a central role in delay discounting in people with externalizing psychopathology. These studies used a hyperbolic discounting model, and its single parameter—a measure of delay discounting—was estimated using the standard method of searching for indifference points between intertemporal options. However, there are several problems with this approach. First, the deterministic perspective on delay discounting underlying the indifference point method might be inappropriate. Second, the estimation procedure using the R² measure often leads to poor model fit. Third, when parameters are estimated using indifference points only, much of the information collected in a delay discounting decision task is wasted. To overcome these problems, this article proposes a random utility model of delay discounting. The proposed model has two parameters, one for delay discounting and one for choice variability. It was fit to choice data obtained from a recently published data set using both maximum-likelihood and Bayesian parameter estimation. As in previous studies, the delay discounting parameter was significantly associated with both externalizing problems and working memory capacity. Furthermore, choice variability was also found to be significantly associated with both variables. This finding suggests that randomness in decisions may be a mechanism by which externalizing problems and low working memory capacity are associated with poor decision-making. The random utility model thus has the advantage of disclosing the role of choice variability, which had been masked by the traditional deterministic model.

Delay discounting is the tendency to place less value on rewards that are delayed in time. It has been demonstrated in both animals and humans (Chung & Herrnstein, 1967; Frederick, Loewenstein, & O’Donoghue, 2002; Rachlin, Raineri, & Cross, 1991) and is frequently interpreted as an indication of impulsivity (e.g., Ainslie, 1974, 1975; McLeish & Oxoby, 2007). Previous studies have shown that delay discounting is associated with various maladaptive behaviors, such as drug use and pathological gambling (see Reynolds, 2006, for a review), addiction (see MacKillop et al., 2011, for a review), and externalizing problems (e.g., Finn, Gunn, & Gerst, 2015). These findings have informed the view that excessive delay discounting is a trans-disease process that contributes to various interconnected psychopathological issues (Bickel, Jarmolowicz, Mueller, Koffarnus, & Gatchalian, 2012).

One critical issue in understanding the relationship between delay discounting and psychological/psychopathological variables is an accurate description of the choice data obtained in delay discounting studies. Most previous studies have used Mazur’s (1987) hyperbolic discounting model to fit the choice data and obtain a measure of delay discounting. Because this model entails a discounting rate that declines over time, it is able to capture the phenomenon of preference reversal frequently observed in empirical studies (e.g., Ainslie & Herrnstein, 1981; Christensen-Szalanski, 1984; Green, Fisher, Perlow, & Sherman, 1981) and thus fits the observed data better than the discounted utility model, which utilizes an exponential discount function (Samuelson, 1937). However, both the hyperbolic discounting model and the discounted utility model take a deterministic perspective on delay discounting and therefore ignore choice variability in empirical data. Recently, Dai and Busemeyer (2014) have shown that intertemporal choice—like risky choice (Rieskamp, 2008)—is essentially probabilistic. To provide a more realistic account of the observed data, models of delay discounting should therefore take choice variability into account.

The purpose of this article is threefold: (1) to propose a probabilistic random utility model of delay discounting, (2) to demonstrate specific parameter estimation methods for this model, and (3) to apply the model to a published data set on delay discounting in a clinical population. To this end, we first present a random utility model of delay discounting that separates payoff devaluation from choice variability in empirical data. This model assumes that the utility assigned to each option may vary from trial to trial, leading to variability in choice between the same pair of options presented repeatedly. Consequently, it captures the probabilistic nature of intertemporal choice and can thus be expected to provide a better description of the empirical data. Second, we describe two interrelated parameter estimation methods for the random utility model. These methods differ in important respects. Consistent results from the two methods would provide converging evidence for the respective findings. Third, we apply the random utility model to the delay discounting data reported for people with externalizing psychopathology in Finn et al. (2015). The proposed model not only replicates previous findings but also reveals that choice variability is significantly associated with both externalizing problems and working memory capacity. We conclude by discussing the importance of adopting a probabilistic perspective on delay discounting and by outlining the implications of our findings for understanding decision-making in people with externalizing psychopathology.

A Random Utility Model of Delay Discounting

A number of discounting models have been proposed to account for the choice data observed in delay discounting studies. Mazur’s (1987) hyperbolic discounting model appears to be the most popular model among psychologists. According to this model, when a given amount (A) of payoff is delayed by t time units, its (present) value (V) equals

$$V=\frac{A}{1+kt}.$$ (1)

The model further assumes that people prefer the payoff with a higher (present) value or discounted utility when choosing between payoffs at different times. In other words, it takes a deterministic perspective on delay discounting in the sense that each payoff, immediate or delayed, has a fixed value and the preference between payoffs at different times is determined solely by these fixed values. As a result, someone choosing repeatedly between a pair of payoffs should always choose the same option.

Yet the long history of empirical research on preferential choice in general and recent work on intertemporal choice in particular challenge this widely adopted assumption. For example, Rieskamp (2008) has shown that preferential choice is essentially probabilistic. As a form of preferential choice, intertemporal choice should also be probabilistic. The results of three experiments conducted by Dai and Busemeyer (2014) provide strong support for the probabilistic perspective on intertemporal choice. Because most studies on delay discounting have used binary choice tasks to elicit delay discounting rates, the observed data should also be investigated from a probabilistic perspective. In this article, we therefore propose a random utility model of delay discounting with a probabilistic view on intertemporal choice.

Random utility models are a class of probabilistic choice models that have been widely used in the risky choice literature to address the issue of choice variability; they can be easily adapted to examine intertemporal choice. The major difference between a deterministic utility model, such as the hyperbolic discounting model, and the corresponding random utility model lies in the way utility is assigned to a given option. A deterministic interpretation of utility implies that any option has a fixed utility across repeated trials. In a random utility model, by contrast, the utility of a given option has a random component and can vary from trial to trial. Consequently, people’s preferences between identical pairs of options may change over time. Both classes of models, however, assume that the option with the higher utility at a given instant will be chosen. According to a random utility model, the probability of choosing option A from a pair of options {A, B} is

$$\mathrm{P}(\mathrm{A}\mid \{\mathrm{A},\mathrm{B}\})=Pr({\mathrm{U}}_{\mathrm{A}}>{\mathrm{U}}_{\mathrm{B}}\mid \{\mathrm{A},\mathrm{B}\}),$$ (2)

in which U_A and U_B are the random utilities of options A and B, respectively.¹

By specifying the joint distribution function of the random utilities, one can derive the choice probability in Equation 2 and then apply such models in real situations. In this article, we assume that the random utilities follow a bivariate normal distribution with independent components, a typical setting for binary choice scenarios. We further assume that the random utilities of all options have the same variances within and across trials. The resultant random utility model is actually a Thurstone Case V model (Thurstone, 1927), which entails that

$${\mathrm{U}}_{\mathrm{A}}-{\mathrm{U}}_{\mathrm{B}}~\mathrm{N}(d,{\mathrm{\sigma }}^2),$$ (3)

in which d = μ_A − μ_B is the difference in mean utility between the two options and σ is a measure of the variability in utility difference. With Equation 3, we have

$$P(A\mid \{A,B\})=\mathrm{\Phi }(\frac{d}{\mathrm{\sigma }}),$$ (4)

in which Φ represents the cumulative distribution function of a standard normal distribution. Finally, we use the traditional hyperbolic discount function (Mazur, 1987) to determine the mean utility of each option. Consequently, for a pair of one smaller-but-sooner (SS) option and one larger-but-later (LL) option typically used in delay discounting studies,

$$d=\frac{A_l}{1+{kt}_l}-\frac{A}{1+{kt}_s},$$ (5)

in which (A_s, t_s) represent the reward amount and delay duration of the SS option and (A_l, t_l) represent the corresponding quantities for the LL option. The proposed model can be viewed as a probabilistic generalization of the widely used hyperbolic discounting model. By replacing d in Equation 4 by the expression in Equation 5, we obtain the probability of choosing the LL option as opposed to the SS option. The probability of choosing the SS option is simply one minus the probability of choosing the LL option.

It is worth noting that there are two parameters in the random utility model: k and σ. The former is inherited from the hyperbolic discounting model as a measure of degree of delay discounting; the latter is unique to the random utility model and can be interpreted as a measure of the utility variance of each payoff. According to the random utility model, this variability or noise in utility is the root of choice variability. The parameter σ can therefore also be viewed as a measure of choice variability. In summary, the discounting parameter k and the choice variability parameter σ reflect different aspects of intertemporal choice and, according to the random utility model, together determine how people behave in delay discounting tasks with binary choices.

Parameter Estimation Methods for the Random Utility Model

Due to the probabilistic nature of the random utility model, its parameter estimation methods are fundamentally different from those suitable for deterministic models. When using the hyperbolic discounting model, researchers usually focus on indifference points between intertemporal options and run a nonlinear regression to find the value of the k parameter that produces the highest R² value. In other words, this fitting procedure employs only a fraction of the information available from the data. Furthermore, it tends to produce relatively low R² values—especially for clinical individual data, which tend to be more variable than data from psychologically healthy individuals. This weakens the utility of the deterministic hyperbolic discounting model and the credibility of conclusions drawn from it. In the probabilistic random utility model, in contrast, responses to all choice questions enter the parameter estimation procedure, and both degree of delay discounting and choice variability are taken into consideration. In other words, more information from the empirical data is utilized to obtain a more robust estimate of the k parameter as well as an additional measure of choice variability, σ. Next, we describe two approaches to estimating parameters for the random utility model of delay discounting proposed here: maximum-likelihood estimation and Bayesian estimation.

Maximum-likelihood estimation (MLE)

Maximum-likelihood estimation is a procedure commonly used in frequentist statistics to estimate parameters of statistical models (Busemeyer & Diederich, 2010). It can also be applied to choice models with a random component such as the random utility model. Specifically, the random utility model predicts the choice probability of each option in a question, and the likelihood of the actual choice sequence across all questions is simply the product of the predicted choice probabilities of all options actually chosen. The goal of MLE is to find parameter values for each participant that produce the highest likelihood of his/her observed data, and these values are treated as the best estimates of the parameters. Statistical software such as Matlab and R can be used to find maximum-likelihood parameter estimates for each participant given his/her data and the random utility model. ²

Bayesian estimation

Bayesian parameter estimation shares certain features with MLE but is built on a fundamentally different approach to statistics, namely, the Bayesian philosophy (Lindley, 2000). On the one hand, like MLE, it uses the predicted choice probabilities of the options actually chosen to evaluate the likelihood of individual data. On the other hand, unlike MLE, it also takes account of prior beliefs in the credibility of each parameter value. By updating appropriate prior beliefs with information from the current data (i.e., its likelihood), researchers can generate posterior beliefs and then obtain parameter estimates that are more comprehensive and robust than those from MLE. Appropriate prior beliefs can be generated either by considering the generally accepted knowledge of the parameters (Kruschke, 2010) or by using so-called objective priors (Berger, 2006).

Both prior and posterior beliefs in parameter credibility are usually represented by probability distributions of the parameters, and measures of central tendency for the posterior distributions can be used as point estimates for respective parameters. In our application of Bayesian parameter estimation to the random utility model, we adopt a normal prior distribution for the natural logarithm of parameter k with a mean of −5 and a standard deviation of 2, and a uniform prior distribution for the choice variability parameter between 0 and 50. Furthermore, for each parameter, we use the posterior mean (i.e., the expected a posteriori [EAP] estimate) as its point estimate. We chose the respective prior distributions for the following reasons: First, previous studies using the hyperbolic discounting model (e.g., Kirby & Maraković, 1996) have suggested that most participants have a log(k) value between −9 and −1 and that the distribution across participants is about normal with an approximate mean of −5. Second, to the best of our knowledge, no previous study has employed the random utility model of delay discounting. As a result, a uniform distribution on the choice variability parameter seems a natural choice. Finally, the amount of the delayed option in Finn et al. (2015) was fixed at 50 dollars. An upper limit of 50 on the choice variability parameter therefore seems reasonable for the target data set. As in the context of MLE, statistical software such as Matlab and R can be used to run Bayesian parameter estimation for each participant given his/her data and the random utility model.

Relationships Among Delay Discounting, Working Memory Capacity, and Externalizing Psychopathology Found Using Traditional Analysis

The associations among externalizing psychopathology (EXT), reduced working memory capacity (WMC), and delay discounting (as a measure of impulsivity) have attracted a great deal of research attention (e.g., Barkley, Edwards, Laneri, Fletcher, & Metevia, 2001; Bechara & Martin, 2004; Finn, Rickert, & Lucas, 2009). Recently, Finn et al. (2015) advanced this line of research by examining the impact of WMC on impulsive decision-making in a sample of young adults who varied in degree of EXT. Participants performed a delay discounting task in either a “WM load” or a “no load” condition. The results showed that (1) WM load led to higher discounting rates across all levels of EXT, (2) EXT was associated with higher discounting rates and lower WMC, and (3) lower WMC was also associated with higher discounting rates.

As in most delay discounting studies, Finn et al. (2015) fit the deterministic hyperbolic discounting model (Mazur, 1987) to individual indifference points to estimate the discounting parameter for each participant. A specific transformation of the resultant estimates, i.e., log₁₀(k), was then used as the dependent variable. In general, the results tallied with those from previous studies. However, this widely adopted method of analyzing delay discounting data ignores the probabilistic nature of the data and may result in misleading conclusions. In this article, we instead fit the probabilistic random utility model to all choice responses for each participant. In this way, both degree of delay discounting and degree of choice variability can be estimated and related to EXT and WMC. Our approach thus uses the full data set and can be expected to yield more stable and credible results.

Reanalysis of Finn et al.’s (2015) Data

Method

Participants

The participants in Finn et al.’s (2015) study were 623 young adults (292 females; mean age = 21.4 years, SD = 2.6; mean years of education = 14.0 years, SD = 1.8) with various EXT symptoms (problems with alcohol, nicotine, marijuana, other drugs, childhood conduct, and adult antisocial behavior). Participants were recruited via advertisements in local and student newspapers and around the community. Respondents were screened via telephone to decide whether they fulfilled the study inclusion criteria and their test sessions were rescheduled if they met any of the test session exclusion criteria on the day of testing (e.g., self-reported use of alcohol or drugs within the past 12 hours). The authors targeted a sample of 25% participants with relatively low EXT problems, 50% with moderate levels of EXT problems, and 25% with very high levels of EXT problems (see Finn et al. for more information on sample characteristics and inclusion and exclusion criteria for the study).

Assessment procedures and materials

EXT problem counts were established using the Semi-Structured Assessment for the Genetics of Alcoholism (SSAGA-II; Bucholz et al., 1994). Specifically, problem counts were calculated for each participant as the number of positively endorsed items out of 120 tapping alcohol problems, 188 tapping drug problems, 47 tapping marijuana problems, 34 tapping conduct problems, and 58 tapping antisocial problems. The latent EXT factor was constructed using maximum-likelihood factor analysis of Blom-transformed problem counts. Blom-transformation was used to address the issue of non-normally distributed problem counts (van den Oord et al., 2000); the only problem counts this method did not effectively normalize were drug problem counts because of zero-inflation. Maximum-likelihood estimation yielded one factor (eigenvalue = 3.87) accounting for 64.5% of the variance in the problem counts, suggesting high internal consistency.

WMC was assessed with the Operation Word Span test (OWS; Conway & Engle, 1994) and a modified version of the Auditory Consonant Trigram test (ACT; Brown, 1958). Previous research has found that both tests reflect WM-related capacities to regulate attention and resist distraction while processing information from long and short-term memory buffers (Endres et al., 2011; Endres et al., 2014; Engle et al., 1999; Unsworth & Engle, 2007). The OWS test requires participants to solve a simple mathematical operation while remembering a word (e.g., 6/3 + 2 = 4 DOG) on each trial and subsequently (after 2 to 6 trials) to recall the words in order of presentation. Performance on the OWS test was measured in terms of the number of words correctly recalled. In the original ACT test, participants have to recall three-consonant nonsense strings after counting backward for varying durations of time. In Finn et al.’s (2015) study, four- and five-consonant nonsense strings were also included. On each trial, the experimenter reads a string of consonants aloud at a rate of one letter per second, followed by a three-digit number. The participant is required to count backward by threes from that number for either 18 or 36 s before recalling the original consonant string. For all string lengths in Finn et al.’s study, two strings were followed by an 18-s delay interval and two by a 36-s delay interval. Performance on the modified ACT test was measured in terms of the total number of correctly recalled consonants across all string lengths and delay intervals.

The delay discounting task was presented on a computer. The text was presented in font size 18 (choice stimuli) and 24 (instructions and question prompts in trials). Instructions for the task were first presented verbally. Once the participant was seated comfortably (approx. 24 inches from the computer), task instructions were then presented again on the computer screen for as long as needed, followed by a series of choice trials. On each trial, participants chose between an immediate reward (an amount of money ranging from $2.50 to $47.50 in $2.50 increments) and $50 at one of six time delays (1 week, 2 weeks, 1 month, 3 months, 6 months, and 1 year). The task was run in six blocks, one for each delay. Each block contained ascending and descending immediate value trials. The ascending sequences stopped when participants switched from choosing the delayed option to choosing the immediate one or chose the immediate $2.50 option right away. The descending sequence stopped when participants switched from the immediate option to the delayed one or chose the delayed option against an immediate $47.50 option right away. The participants were informed in advance that they would receive the amount they chose on one randomly selected trial.

In addition, participants were randomly assigned to either a “WM load” condition or a “no load” condition. In the no load condition each trial started with the presentation of the choice options for 3.5 s, then the screen went blank for 10 s (a fixation cross was presented at the center of the screen) followed by a choice prompt (NOW or LATER), after which the participant made a choice. In the load condition, each trial started with the presentation of the choice options, then a 3-digit number was presented for 1 s, followed by a flashing “#” for 9 s, during which time the participant counted backward from that number in threes. In total, 108 different three-digit numbers were used. The choice prompt was then presented in the same way as in the no load condition. After making a choice, participants were prompted to recall and type the 3-digit number. They were instructed to “be as accurate as possible” in counting backward and in recalling the number on each trial. Participants in the load condition appeared to have no difficulty following the instructions. Overall accuracy in recalling the 3-digit number was 85%, which was unassociated with EXT factor scores. The number of trials for each participant varied depending on switch points.

Data analysis

Using the guidelines of Johnson and Bickel (2008), Finn et al. (2015) excluded the data of 81 participants (13%) from further analysis. We followed the same guidelines and thus used the same data as Finn et al. The following results are therefore based on a sample of 542 participants, of whom 272 were in the “no load” condition and 270 in the “WM load” condition.

To examine both delay discounting and choice variability, we used the random utility model of delay discounting and two interrelated parameter estimation methods—MLE and Bayesian estimation—to reanalyze Finn et al.’s (2015) data. Because of the increased number of parameters and parameter estimation methods, we adopted a somewhat simplified way of analyzing the associations among degree of delay discounting, degree of choice variability, EXT, and reduced WMC. Specifically, we examined the correlations among EXT factor scores, sum scores of WMC measures (i.e., sums of OWS and ACT scores), and parameter estimates from the random utility models using either MLE or Bayesian estimation.

As mentioned above, the EXT factor scores were computed using maximum-likelihood factor analysis of Blom-transformed EXT problem counts. With the final sample of 542 participants, the maximum-likelihood factor analysis again led to a single factor model that accounted for 64.5% of the variance in the problem counts. A multiple-group SEM analysis established measurement invariance for the factor loadings for the EXT factor across the no load and load conditions (Finn et al., 2015). Furthermore, Finn et al. found that none of the indicators of the EXT factor was associated with delay discounting beyond its covariance with other indicators. Similarly, the two measures of WMC were shown to produce the same association patterns among delay discounting, WMC, and EXT, no matter whether they were used as indicators of a latent variable on WMC or as separate measures of WMC. It thus seems appropriate to use the EXT factor score and the sum score of WMC measures to demonstrate the associations among EXT, WMC, delay discounting, and choice variability. We also compared relevant variables between the WM load condition and the no load condition to examine the impact of WM load on delay discounting and choice variability.

Results

Maximum-likelihood estimation

Table 1 shows (as values before slashes) Spearman’s rank-order correlation coefficients among EXT factor scores, sum scores of WMC measures, and parameter estimates given by MLE for the load and no load conditions. We used Spearman’s rho because most variables in the analysis failed to pass the Kolmogorov–Smirnov test of normality. Most of the variables showed significant intercorrelations; the only nonsignificant association—which was between EXT factor scores and estimates of parameter σ in the WM load condition—only marginally failed to reach the level of statistical significance (p = .059, two-tailed). When the data from participants in both conditions were pooled, all associations were statistically significant at the .01 level (see Table 2). The directions and sizes of associations among the k parameter estimates, EXT scores, and WMC scores were virtually the same as those found by Finn et al. (2015) using the traditional hyperbolic discounting model and a nonlinear fitting procedure with R². This is readily seen by comparing Table 1 with Table 3, which shows Spearman’s correlation coefficients between EXT factor scores, sum scores of WMC measures, and traditional estimates of the k parameter. The similarity of these two sets of results is not surprising, because the two parameter estimation methods led to almost perfectly correlated estimates of the k parameter (Spearman’s rho = .99 for data within and across WM load conditions, ps < .01). However, the k estimates from traditional analysis tended to be higher than those from MLE (Wilcoxon signed-rank test, z = 5.01, p < .01, effect size = 0.22). More important, the additional parameter in the random utility model—i.e., the choice variability parameter σ—proved to be positively associated with EXT in the no WM load condition (see Table 1) and when the data were pooled across the two WM load conditions (see Table 2), and negatively associated with WMC within and across the two WM load conditions (see Tables 1 and 2). This suggests that participants with more externalizing problems and lower working memory capacity tended to choose more randomly than those with less externalizing problems and higher working memory capacity.

Table 1.

Summary of Intercorrelations for EXT Factor Scores, Sum Scores of WMC Measures, and Parameter Estimates from the Random Utility Model as a Function of WM Load Condition

Measure	1	2	3	4
1. EXT	–	−.19*/−.19*	.32*/.32*	.22*/.22*
2. WMC	−.20*/−.20*	–	−.16*/−.16*	−.19*/−.18*
3. k	.33*/.32*	−.27*/−.27*	–	.48*/.44*
4. σ	.12/.12	−.17*/−.17*	.23*/.19*	–

Note. Intercorrelations for the no load condition (n = 272) are presented above the diagonal; intercorrelations for the WM load condition (n = 270) are presented below the diagonal. Values before slashes indicate Spearman’s rank-order correlation coefficients for maximum-likelihood estimates; values after slashes indicate those for Bayesian EAP estimates. EXT = externalizing psychopathology; WMC = working memory capacity.

^*p < .01.

Table 2.

Summary of Intercorrelations for EXT Factor Scores, Sum Scores of WMC Measures, and Parameter Estimates from the Random Utility Model for Data Pooled Across WM Load Conditions

Measure	1	2	3	4
1. EXT	–	−.20*/−.20*	.32*/.31*	.15*/.15*
2. WMC	–	–	−.20*/−.20*	−.16*/−.16*
3. k	–	–	–	.38*/.34*
4. σ	–	–	–	–

Note. Intercorrelations for all participants pooled across WM load conditions (n = 542) are presented above the diagonal. Values before slashes indicate Spearman’s rank-order correlation coefficients for maximum-likelihood estimates; values after slashes indicate those for Bayesian EAP estimates. EXT = externalizing psychopathology; WMC = working memory capacity.

^*p < .01.

Table 3.

Summary of Intercorrelations for EXT Factor Scores, Sum Scores of WMC Measures, and Traditional Estimates of the k Parameter as a Function of WM Load Condition

Measure	1	2	3
1. EXT	–	−.19*	.32*
2. WMC	−.20*	–	−.16*
3. k	.34*	−.28*	–

Note. Intercorrelations for the no load condition (n = 272) are presented above the diagonal; intercorrelations for the WM load condition (n = 270) are presented below the diagonal. EXT = externalizing psychopathology; WMC = working memory capacity.

^*p < .01.

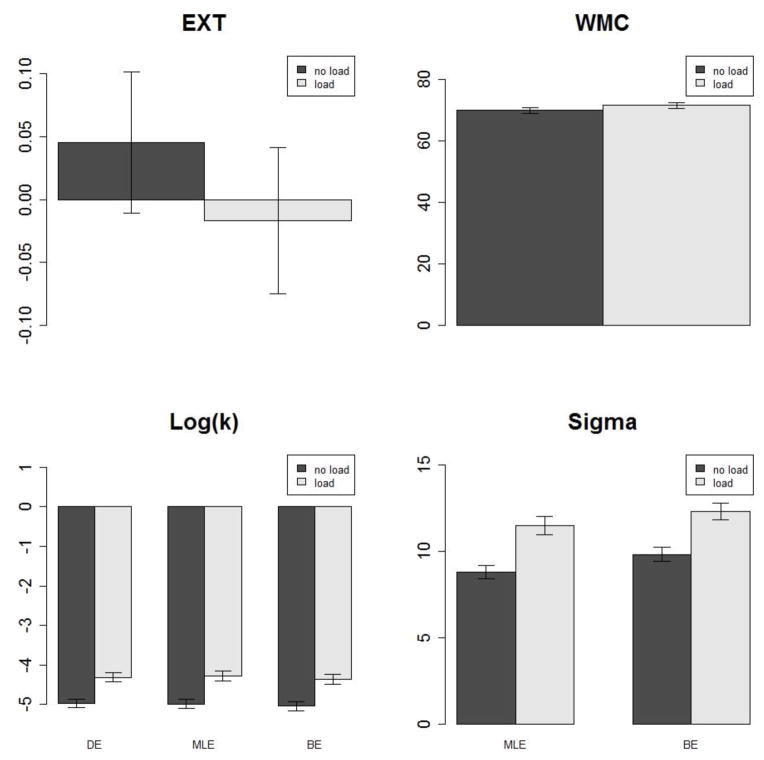
In addition, there were significant differences between participants in the two WM load conditions in terms of estimates of both parameters in the random utility model, but not in the EXT or WMC measures. Specifically, participants in the WM load condition had higher median estimates on both parameters (median ln(k) = −4.42, median σ = 9.50) than those in the no load condition (median ln(k) = −5.18, median σ = 7.23; Wilcoxon rank-sum tests, ps < .01, effect sizes = 0.18 and 0.21, respectively). In contrast, the two groups did not differ in terms of EXT or WMC scores (Wilcoxon rank-sum tests, p = .46 and .27, respectively). Stated otherwise, introducing WM load into the delay discounting task led to higher delay discounting rates and more random choice behavior. The impact of WM load on delay discounting rates was thus the same as found by Finn et al. (2015). See Figure 1 for descriptive results in both conditions.

Figure 1.

Average results for EXT factor scores, sum scores of WMC measures, and parameter estimates of the random utility model as a function of WM load condition. Each error bar represents 1 standard error above and below the mean. EXT = externalizing psychopathology; WMC = working memory capacity; DE = deterministic estimates; MLE = maximum-likelihood estimates; BE = Bayesian EAP estimates.

Bayesian estimation

The results given by Bayesian parameter estimation were virtually the same as those given by MLE. Table 1 shows (as values after slashes) Spearman’s rank-order correlation coefficients among EXT factor scores, sum scores of WMC measures, and parameter estimates using Bayesian parameter estimation in both WM load conditions. Again, most of the variables showed significant intercorrelations, and the only nonsignificant association—which was between EXT factor scores and estimates of parameter σ in the WM load condition—again only marginally failed to reach the level of statistical significance (p = .057, two-tailed). When the data from participants in both conditions were pooled, all associations were statistically significant at the .01 level (see Table 2). The directions and sizes of associations among the k parameter estimates, EXT scores, and WMC scores were again virtually the same as those found by Finn et al. (2015), and individual k parameters estimated using the Bayesian approach correlated with those from traditional estimation almost perfectly (Spearman’s rho = .99 for data within and across WM load conditions, ps < .01). However, the k estimates from traditional analysis tended to be higher than those from Bayesian estimation (Wilcoxon signed-rank test, z = 8.02, p < .01, effect size = .34). As for MLE, the additional choice variability parameter in the random utility model was again positively associated with EXT in the no WM load condition (see Table 1) and when the data were pooled across the two WM load conditions (see Table 2), and negatively associated with WMC within and across the two WM load conditions (see Tables 1 and 2). Finally, there were significant differences between participants in the two WM load conditions in terms of estimates of both parameters in the random utility model using Bayesian parameter estimation (Wilcoxon rank-sum tests, ps < .01, effect sizes = 0.17 and 0.21, respectively). The directions of the differences were the same as those found with MLE (WM load condition, median ln(k) = −4.51, median σ = 10.50; no load condition, median ln(k) = −5.20, median σ = 8.07).

Discussion

In this article, we presented a random utility model of delay discounting, described two interrelated approaches to estimating parameters from such a model, and applied the model to data from a previous study investigating the associations among WMC, EXT, and impulsive decision making. The random utility model extends the traditional hyperbolic discounting model by introducing a random component into the discounted utility of each option. This extension turns the deterministic hyperbolic discounting model into a probabilistic choice model that can accommodate choice variability in empirical data. The extra parameter, σ, can be viewed as a measure of choice variability or randomness resulting from the uncertainty of discounted utilities. This piece of information is virtually ignored in the deterministic model and thus has not been properly studied in previous research. Furthermore, using the deterministic model to analyze empirical data with choice variability may result in misleading conclusions to the extent that estimates of the discounting parameter could be distorted by the noise in choice data. This is especially worrying in the context of clinical data, which tend to be more variable than those from psychologically healthy people.

One potential concern with the present analysis is the high participant exclusion rate of 13% and its impact on the results. Specifically, 81 of the 623 participants in the original sample were excluded both in our analysis and in Finn et al. (2015) for three reasons suggested by Johnson and Bickel (2008). Six participants were excluded because their choices in the delay discounting task were variable and unsystematic, suggesting preferences for later rewards against earlier ones of the same amount. Although this choice pattern is inconsistent with the general concept of delay discounting, the relevant data can in principle be fit by the random utility model. The remaining 75 participants were excluded because they showed either no delay discounting at all (i.e., always choosing the LL option) or extreme discounting of delayed payoffs (i.e., always choosing the SS option). Neither the traditional hyperbolic discounting model nor the random utility model with MLE can be fit to the choice data of these participants to obtain precise parameter estimates. Consequently, we would have to assign expedient estimates to such participants. For instance, we could use k = 0.0001/day for never-discounters, k = 3/day for total-discounters, and σ = 0.01 for both types of participants. In contrast, the random utility model can be properly fit to the same data set using Bayesian estimation. We reran all analyses with the Bayesian EAP parameter estimates and (partly arbitrary) maximum-likelihood parameter estimates for all 623 participants and found virtually the same results. Specifically, all significant correlations and group differences obtained in the smaller sample were still significant with little change to their magnitudes—with the exception of the correlation coefficient between WMC and σ in the WM load condition, which changed from −0.17 to about −0.06 and became nonsignificant. In summary, there are good reasons for excluding the 81 participants, and the results were generally unchanged when they were included in the analysis.

Our results have five key implications. First, the relationships among EXT, WMC, and delay discounting rate found in previous research using the traditional model were replicated in the present analysis, which considered both degree of delay discounting and variability in choice. The random utility model separates these two influential components of participants’ choice behavior in the delay discounting task and thus provides a pure measure of each of them. The results from the random utility model thus substantiate those from the deterministic model.

Second, although our analysis corroborated previous conclusions on the associations between the discounting parameter on the one hand and EXT and WMC on the other, it also revealed that the traditional estimation method based on the deterministic model tends to produce an overestimation of the k parameter. Stated otherwise, ignoring choice variability in actual data leads to biased estimates of the discounting parameter. This problem may be negligible in terms of correlations among relevant variables in the present study, but it may become substantial in other analyses (e.g., comparing discounting rates across groups), resulting in misleading conclusions. In any case, researchers would be well advised to use the random utility model to reach more trustworthy conclusions concerning the discounting parameter.

Third, the extra parameter in the random utility model (i.e., the choice variability parameter σ) was positively associated with EXT in the no WM load condition and when data were pooled across the two WM load conditions, and negatively associated with WMC within and across the two WM load conditions, suggesting an additional mechanism for poor decision-making in participants with EXT and low WMC. Because the traditional hyperbolic discounting model is silent on the issue of choice variability, the relationship among EXT, WMC, and choice variability is totally masked in traditional analysis. Our results suggest that people with more externalizing problems and lower WMC tend to choose more randomly in the delay discounting task (and potentially in other choice tasks) in addition to discounting future payoffs more heavily. In other words, people with EXT and reduced WMC behave not only more impulsively but also more randomly—at least in the normal (i.e., no WM load) condition. Our results also suggest an additional cognitive deficit, or impairment, that may contribute to the self-regulatory problems associated with EXT and reduced WMC. This variability or relative lack of consistency in the decision process may contribute to behavior problems such as drug abuse and antisocial behavior, independent of increased impulsivity (discounting). Of course, neither the design of the study nor the current analysis is sufficient to establish a causal relationship between the variables. More research is needed to examine the possible causal pathways among EXT, reduced WMC, delay discounting rate, and choice variability.

More generally, the choice variability parameter provides an informative measure of randomness in choice behavior to delay discounting researchers, especially clinical psychologists interested in impulsivity and its relationship with other factors and constructs. This additional measure can be easily acquired by fitting the random utility model to data from previous studies on delay discounting, as long as the response to each choice question is recorded in the data set. In other words, researchers can now extract more information from the same data, which makes them better equipped to formulate more comprehensive theories of delay discounting. It is worth noting that the major advantage of adopting the random utility model is to extract more—and more credible—information from the same data sets and not to increase model fit, as is usually the case with more complicated deterministic models.

Fourth, our results shed new light on an ongoing debate regarding the impact of WM load on decision making, namely, whether load increases choice randomness and/or impulsivity (Hatfield-Eldred, Skeel, & Reilly, 2015). The initial study by Hinson, Jameson, and Whitney (2003) suggested that WM load leads to more impulsive choice behavior in a delay discounting task. A reanalysis and new studies by Franco-Watkins and colleagues (Franco-Watkins, Pashler, & Rickard, 2006; Franco-Watkins, Richard, & Pashler, 2010) favored the alternative explanation that WM load leads to increased randomness or inconsistency in choice. Hatfield-Eldred et al. (2015) recently compared the two explanations using a different decision task and found evidence in favor of Hinson et al.’s (2003) theory.

We used a sophisticated mathematical tool—the probabilistic random utility model—to analyze individual delay discounting data in both WM load conditions. With its two separate parameters, the random utility model allows the impact of WM load on impulsivity to be distinguished from that on choice randomness. Our results suggest that WM load leads to simultaneous increases in impulsivity and choice randomness. Two major factors may contribute to these results. First, the present sample was much larger than those used in previous studies, making it statistically more powerful to detect potential impacts of WM load on impulsivity and choice variability. Second, the random utility model suggests that people may choose one option more often than the other, with moderate probabilities varying across choice pairs (e.g., 70% versus 30% for one choice pair and 80% versus 20% for another), whereas the explanation built on random choice implies that people either choose the option with a higher discounted utility for sure or choose totally at random (i.e., choose either option with a one-half probability). Results of recent studies on the probabilistic nature of intertemporal choice (Dai & Busemeyer, 2014) have favored the pattern of gradual change in choice probability suggested by the random utility model, as opposed to the abrupt change in choice probability implied by the random choice explanation. The random utility model thus appears to provide a more appropriate description of the choice variability observed in data. Consequently, its findings with regard to the effect of WM load may provide more subtle and detailed insights.

Fifth and finally, the results obtained using MLE were essentially the same as those obtained using Bayesian parameter estimation. As noted earlier, Bayesian parameter estimation considers not only the likelihood of the observed data (as MLE does) but also prior beliefs in the credibility of each parameter value. In most cases, this difference between MLE and Bayesian estimation leads to different parameter estimates. This also applies in the current analysis, in which an informative prior was selected for the logarithm of the k parameter and the posterior mean (i.e., EAP) was used as the point estimate. Despite the difference in estimation approaches and resultant parameter estimates, the two analyses yielded the same results in terms of the interrelations among EXT, WMC, delay discounting rates, and choice variability, as well as the differences between the two WM load conditions in parameter estimates. In other words, the two estimation methods provided converging evidence for the relationships among the relevant variables. This example demonstrates the value of applying both estimation methods to probabilistic choice models to reach robust conclusions.

Conclusion

Empirical data on delay discounting have long been analyzed from a deterministic perspective that virtually ignores the issue of choice variability. We presented a probabilistic random utility model of delay discounting and applied it to a published delay discounting data set from people with externalizing psychopathology. The results showed that (1) people with more externalizing problems and lower WMC tended to have higher discounting rates and that WM load also led to higher discounting rates; (2) people with more externalizing problems and lower WMC also tended to choose more randomly; likewise WM load led to more random choices; and (3) maximum-likelihood and Bayesian parameter estimation for the random utility model produced essentially the same results, testifying to the robustness of the respective conclusions.