Examining the Variability of Sleep Patterns during Treatment for Chronic Insomnia: Application of a Location-Scale Mixed Model

Abstract

Study Objectives:

The purpose of this study was to introduce a novel statistical technique called the location-scale mixed model that can be used to analyze the mean level and intra-individual variability (IIV) using longitudinal sleep data.

Methods:

We applied the location-scale mixed model to examine changes from baseline in sleep efficiency on data collected from 54 participants with chronic insomnia who were randomized to an 8-week Mindfulness-Based Stress Reduction (MBSR; n = 19), an 8-week Mindfulness-Based Therapy for Insomnia (MBTI; n = 19), or an 8-week self-monitoring control (SM; n = 16). Sleep efficiency was derived from daily sleep diaries collected at baseline (days 1–7), early treatment (days 8–21), late treatment (days 22–63), and post week (days 64–70). The behavioral components (sleep restriction, stimulus control) were delivered during late treatment in MBTI.

Results:

For MBSR and MBTI, the pre-to-post change in mean levels of sleep efficiency were significantly larger than the change in mean levels for the SM control, but the change in IIV was not significantly different. During early and late treatment, MBSR showed a larger increase in mean levels of sleep efficiency and a larger decrease in IIV relative to the SM control. At late treatment, MBTI had a larger increase in the mean level of sleep efficiency compared to SM, but the IIV was not significantly different.

Conclusions:

The location-scale mixed model provides a two-dimensional analysis on the mean and IIV using longitudinal sleep diary data with the potential to reveal insights into treatment mechanisms and outcomes.

Citation:

Ong JC, Hedeker D, Wyatt JK, Manber R. Examining the variability of sleep patterns during treatment for chronic insomnia: application of a location-scale mixed model. J Clin Sleep Med 2016;12(6):797–804.

INTRODUCTION

The sleep disturbance experienced by individuals with insomnia tends to have considerable variability across nights.^1,2 This experience is not captured by the mean level of sleep across nights, but instead requires examination of the intra-individual variability (IIV), or night-to-night variability of sleep. A recent review revealed inconsistent methodology among studies that examined IIV in sleep. The authors found that most studies of IIV used methods such as within-subject standard deviations, coefficient of variance, or mean square of successive differences. Furthermore, these analyses frequently did not control for the mean values when examining IIV.³ Therefore, the authors recommended a two-dimensional approach when analyzing longitudinal sleep data that includes the mean as one dimension and the IIV as a second dimension.³

BRIEF SUMMARY

Current Knowledge/Study Rationale: Sleep disturbance can vary considerably across nights but traditional statistical methods are not optimized to examine both the mean and variability of sleep patterns. We used a novel statistical technique called the location-scale mixed model to simultaneously analyze the mean and intra-individual variability (IIV) on sleep diary data collected for a randomized controlled trial for chronic insomnia.

Study Impact: Mindfulness-based stress reduction (MBSR) and mindfulness-based therapy for insomnia (MBTI) exhibited different patterns of change on mean levels and IIV of sleep efficiency during the course of treatment compared to the control condition. The location-scale mixed model can serve as an efficient statistical technique for analyzing intensive longitudinal sleep data.

Recently, a novel statistical technique called the location-scale mixed model has emerged which appears particularly well-suited for examining the mean and IIV as different dimensions of the sleep experience. This model was developed for the analysis of intensive longitudinal data, and is an extension of a traditional linear mixed model (aka multilevel or hierarchical linear modeling; HLM) that accounts for the clustering of observations within subjects, but additionally allows the between-subjects (inter-individual) and within-subject (intra-individual) variances to be modeled in terms of covariates. In contrast to previous approaches that quantified IIV by calculating a within-subject standard deviation as the outcome in a second-stage analysis,^4,5 the location-scale mixed model can be used to simultaneously examine the effect of covariates on the mean and variance of an outcome. This approach has two advantages. First, by allowing subjects to have different numbers of observations, the degree of precision of each person's mean and variance is directly taken into account in the location-scale mixed model. The second stage approach of calculating within-subject standard deviations assumes that each person's variability is known with the same degree of precision, which can be violated with missing data. Second, by modeling the mean and variance simultaneously, the location-scale mixed model provides an estimate on the variance that is adjusted for the effects on the mean structure. This attribute makes it possible to examine the effect of a covariate (e.g., treatment condition) on the IIV of an outcome measure, over and above the effect of the covariate on the mean of the outcome measure. Whereas the traditional HLM model only allows subjects to influence their mean (i.e., random intercept or random location effect), the location-scale mixed model also accounts for how subjects influence their variance (i.e., random scale effect).⁶ The location-scale mixed model has been used to examine the relationship between variability and outcomes in other areas using ecological momentary assessment data,^7–11 but has not yet been applied to sleep research.

Similar to the concept of frequent sampling in ecological momentary assessments, sleep diaries assess daily sleep/wake patterns and are typically collected throughout the course of behavioral treatments for insomnia. The large number of repeated measures per subject is an example of intensive longitudinal data and provides an opportunity to apply sophisticated modeling techniques, such as the location-scale mixed model, which can examine IIV of sleep as it relates to treatment process and outcomes. Such analyses can be used to examine whether behavioral treatments improve the stability of sleep (i.e., decrease IIV) above and beyond the improvements in the mean level of sleep. Also, these analyses can be used to inform treatment process by examining changes in IIV during different stages of treatment that correspond to the delivery of various treatment components (e.g., sleep restriction therapy, stimulus control).

The purpose of this paper is to introduce the location-scale mixed model as a potential tool for examining the variability of sleep patterns in longitudinal data. As an illustration, we applied the model to data collected from sleep diaries during a three-arm randomized controlled trial for chronic insomnia. The study compared Mindfulness-Based Stress Reduction (MBSR), a standard meditation-based program designed to reduce stress, Mindfulness-Based Therapy For Insomnia (MBTI), a tailored intervention integrating mindfulness meditation and behavior therapy for insomnia, and a self-monitoring (SM) control.¹² Mindfulness meditation is a self-regulation technique that uses focused, present-moment awareness to promote mind-body calmness and relaxation. While our previous paper reported on the changes in mean levels of the a priori main outcomes, total wake time and pre-sleep arousal,¹² this report applied the location-scale mixed model to examine the mean and IIV of sleep efficiency (i.e., percent of time asleep relative to the time in bed), a commonly used index of sleep quality that has also been used as a primary outcome variable for self-reported sleep in behavioral clinical trials on insomnia.^13–15 The data analyses were guided by two research questions. First, do mindfulness meditation programs (standard or tailored) have an impact on sleep efficiency? It was hypothesized that participants receiving MBSR and MBTI would show higher mean levels and less IIV at post-treatment relative to baseline levels. Second, do the behavioral components delivered in MBTI have an impact on sleep efficiency compared to a control group receiving no treatment? It was hypothesized that participants in the MBTI group would show higher mean levels and lower IIV following delivery of the behavioral components compared to the control group at the same time point.

METHODS

We used the location-scale mixed model to conduct secondary analyses on sleep diary data from a three-arm randomized controlled trial conducted at Rush University Medical Center between November 2008 and February 2012. Details of the study design and main outcomes have been previously reported.¹² In brief, 54 adults (74.1% female, 25.9% male, mean age = 42.9 years) who met research diagnostic criteria for an insomnia disorder¹⁶ were randomized to one of three study arms: (1) MBSR (n = 19), (2) MBTI (n = 19), or (3) SM (n = 16). The MBSR arm consisted of 8 weekly, 150-minute group sessions plus one 6-hour meditation retreat held between the 5^th and 7^th sessions following standard delivery of MBSR.¹⁷ The MBSR groups focused on mindfulness meditation practice and the enactment of mindfulness principles in daily life. In addition to the in-class meditation training, participants were provided with digital audio materials to practice meditation at home for at least 30 minutes per day, at least 6 days per week starting from the first session. No specific strategies for sleep or bedtime schedules were delivered as part of MBSR. MBTI featured mindfulness meditation practice that followed the same requirements for home practice starting from the first session. MBTI consisted of the same amount of total contact and the same in-class and at-home meditation practices as MBSR. In addition, MBTI included specific behavioral strategies for insomnia (sleep hygiene,¹⁸ sleep restriction therapy,¹⁹ stimulus control²⁰) delivered within the context of mindfulness principles. Sleep hygiene was introduced in the second session, sleep restriction was introduced in the third session, and stimulus control was introduced in the fourth session. As part of sleep restriction, sleep schedules were discussed and modified weekly based on standard recommendations,¹⁹ starting from the fourth session. Each week, participants were provided with the instructions for reviewing their sleep diaries and making adjustments to their sleep schedules with the MBTI instructor available for guidance if needed. The SM arm consisted of self-monitoring using daily sleep diaries for 8 consecutive weeks with no intervention and no regular contact, except for occasional telephone or email reminders to complete the sleep diaries. Sleep diaries were submitted every 2 weeks, and reminders were provided if patients did not submit diaries on time. Please see Table 1 for details about each session in the MBSR and MBTI arms.

Table 1.

Treatment sessions.

In each of the 3 arms, participants completed prospective sleep diaries recorded on paper each morning for a total of 70 days. These included 7 consecutive days prior to the start of the treatment/monitoring period (baseline week assessment), 56 consecutive days during the 8-week treatment/monitoring period, and 7 consecutive days during the post week assessment. Sleep parameters derived from the sleep diaries included sleep onset latency, wake after sleep onset, total sleep time (TST), and time in bed (TIB). Sleep efficiency (SE) was a percentage calculated as (TST / TIB) × 100 served as the dependent variable in this report.

Model Specifications

The location-scale mixed model for sleep efficiency y, of subject i (i = 1,2,3,…, N subjects) on day j (j = 1,2,3,…, n_i days) is given as:

where x_ij is a vector of independent variables and β is the corresponding vector of regression coefficients. The independent variables can be at the subject level, vary across days, or be interactions of the subject-level and day-level variables. The random subject effect υ_i indicates the influence of the subject i on her/his sleep measures. These random effects are assumed to be normally distributed with zero mean and variance σ²_υ. The errors ε_ij are also assumed to be normally distributed with zero mean and variance σ²_ε and independent of the random effects. Here, σ²_υ represents the between-subjects (BS) variance and σ²_ε represents the within-subjects (WS) variance, or IIV. The location-scale mixed model allows both of these variances to be modeled in terms of independent variables using log link functions, which is identical to the link function used in Poisson regression to ensure a positive count outcome from the estimated model. Similar to what is done in Poisson regression, we calculated standard deviation (SD) ratios by exponentiating the estimated coefficients (note that in Poisson regression, the exponentiated coefficients represent count ratios) to represent the covariate effects on the WS variance. These SD ratios represented the ratio of within-subject standard deviations (WSSD) per unit change of the covariate. As such, an SD ratio greater (lesser) than one represented increased (decreased) variability with increased levels of the covariate. Additionally, a random subject effect is included in the WS variance specification, which permits this variance to vary at the subject level, above and beyond the influence of regressors.^8,10 Thus, an important aspect of the model is that it allows independent variables (treatment arm) to influence the BS and WS variances of the sleep measurements, in addition to their effects on the mean of the sleep measurements.

Data Analysis

In all analyses, the daily repeated observations were treated as nested within subjects. Treatment condition (i.e., treatment arm) and time were entered as the independent variables, and sleep efficiency was treated as the dependent variable. Four levels were created for the effects of time. The baseline assessment (days 1 to 7) was used as the reference point for the other time comparisons. Early treatment/monitoring included the first 2 treatment/monitoring weeks (days 8 to 21). Late treatment/monitoring included the last 6 weeks (days 22 to 63). The post assessment included days 64 to 70, which occurred immediately after the last treatment session or last monitoring week. Days 8 to 63 were consecutive but the time interval between day 7 (end of baseline) and day 8 (start of treatment/ monitoring) varied for each person based on the time between when he/she presented for screening and the start of the group. The rationale for dividing early treatment versus late treatment was to account for the impact of the main behavioral components (sleep restriction and stimulus control). Sleep restriction, which involved scheduled bed times and rise times, was introduced at the third treatment session (day 21), and stimulus control, which also emphasizes a scheduled rise time, was introduced at the fourth treatment session (day 28). Distinguishing between early and late treatment provided an opportunity to examine the trajectory of sleep efficiency before and after the delivery of these behavioral components in MBTI.

For the effect of treatment arm, we used SM as the reference cell and included indicator variables for the two treatments (i.e., MBSR vs. SM and MBTI vs. SM). In addition, we obtained estimates from the model to compare MBSR and MBTI. Group × time interactions were also included to examine differential patterns of change over time by treatment arm. As previously mentioned, in addition to mean levels, the location-scale mixed model also allows these independent variables to influence the within-subject variance in order to assess their effects on night-to-night variability. Estimation of the model parameters was performed using the MIXREGLS program (Information on running the Location Scale Mixed Models using MIXREGLS can be found at: http://www.jstatsoft.org/article/view/v052i12).²¹ All analyses were conducted on an intent-to-treat basis.

In addition to the location-scale mixed model, we also conducted an analysis using the more traditional random-intercept mixed model with the same variables as the location-scale mixed model above. Results from the random-intercept mixed model are presented in Table 2 to provide a comparison to the results of the location-scale mixed model.

Table 2.

Comparison of output for random intercept mixed models versus location-scale mixed model.

RESULTS

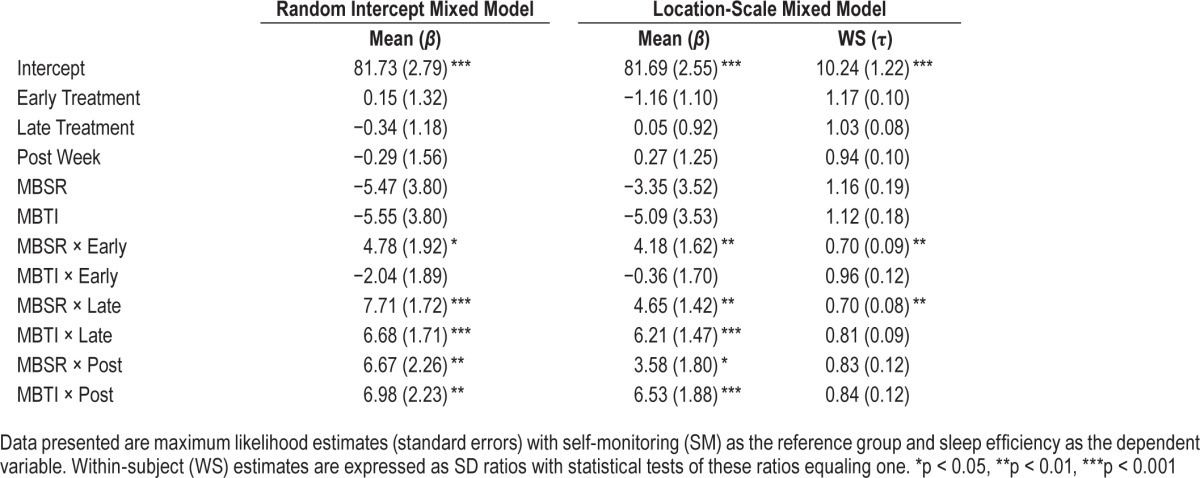
A total of 2,855 observations were available for the 54 subjects. The median number of daily measurements was 62 (out of 70 total), which represents a median percentage of 11.4% missing data per subject. The majority of missing data were due to 6 participants who did not provide data beyond baseline (i.e., randomized, but did not attend treatment sessions). As a result, there were more observations per subject in the SM control (median = 68.5) compared to MBSR (median = 57) or MBTI (median = 57), p < 0.05. However, the model estimates the parameters using full information maximum likelihood and allows missing data to vary between the groups and any other covariates in the model, and therefore provides valid results under the assumption of missing at random (MAR).²² At baseline, the mean (and WSSD) for SE by group was: 78.34% (13.81) for MBSR, 76.59% (13.30) for MBTI, 81.69% (11.87) for SM (see Figure 1).

Figure 1. Sleep efficiency.

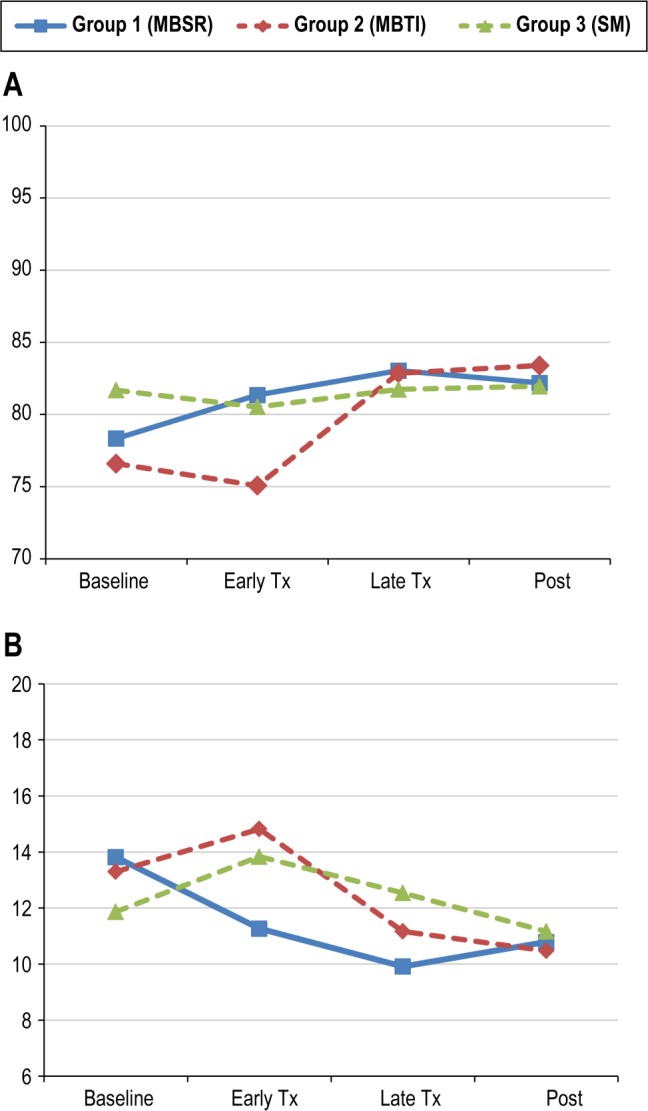
Model-based estimates of group means (A) and within-subject standard deviations (B) for sleep efficiency across the 4 time periods. Note that the location-scale mixed model compares the change from baseline as opposed to the values at each time point. (B) Significant interactions can be seen as the differential change in within-subject standard deviations from baseline to early treatment between MBSR vs SM and MBSR vs MBTI and from baseline to late treatment between MBSR vs SM.

Mean Levels

Using the location-scale mixed model, results for the mean levels revealed that after adjusting for variance, the MBSR group had a larger increase in sleep efficiency from baseline (i.e., better sleep) relative to the SM group at early (beta = 4.18, p < 0.01), late (beta = 4.65, p < 0.01), and post week (beta = 3.58, p < 0.05). Simple effects for MBSR across time revealed significant increases in sleep efficiency from baseline at early (p < 0.01), late (p < 0.001), and post (p < 0.01). The MBTI group did not show a significant change in sleep efficiency from baseline relative to the SM group at early treatment (beta = −0.36, p = 0.83), but did show a larger increase from baseline to late (beta = 6.21, p < 0.0001) and post (beta = 6.53, p < 0.001) relative to the SM group. Simple effects for MBTI across time revealed significant increases in sleep efficiency from baseline at late (p < 0.0001) and post (p < 0.0001) but not at early treatment (p = 0.24). When comparing MBSR versus MBTI, the MBSR group showed a larger increase in sleep efficiency from baseline to early treatment (beta = 4.54, p < 0.01) relative to MBTI. No significant changes from baseline were found between MBSR and MBTI at late treatment (p = 0.32) or post (p = 0.12). These results are consistent with the results of the random-intercepts mixed model, which assumed a constant within-subject variance. As shown in Table 2, both models detected a significant increase from baseline (p < 0.05) in sleep efficiency for MBSR relative to SM at early, late, and post week and for MBTI relative to SM at late and post week. Figure 1A presents model-based estimates of the group means across the four time periods.

Within-Subject Variance

Results for the modeling of the within-subject variance (i.e., IIV) revealed that after adjusting for mean levels, MBSR had a significantly larger decrease in IIV (i.e., less variability) from baseline to early (SD ratio = 0.70, p < 0.01) and late treatment (SD ratio = 0.70, p < 0.01), but not to post (SD ratio = 0.83), when compared to SM. The observed SD ratio of 0.70 indicates that there was a 30% reduction in the IIV of SE in the MBSR group compared to the control group at early and late treatment. Simple effects for MBSR across time revealed signifi-cant decreases in IIV at early (p < 0.05), late (p < 0.001), and post week (p < 0.05). No significant differences between MBTI and SM in the changes from baseline were found at early (SD ratio = 0.96, p = 0.72), late (SD ratio = 0.81, p = 0.067), or post (SD ratio = 0.84, p = 0.23). Simple effects for MBTI across time revealed significant decreases in IIV at late (p < 0.05) and post (p < 0.05), but not at early treatment (p = 0.23). When comparing MBSR versus MBTI, the MBSR group showed a larger decrease in IIV (i.e., less variability in sleep efficiency) from baseline to early treatment (SD ratio = 1.37, p < 0.05). No significant differences between MBSR and MBTI in changes from baseline were found at late (p = 0.17) or post (p = 0.20). Figure 1B presents model-based estimates of the within-subject standard deviations for each group across the four time periods

Figure 2 illustrates 3 patterns of change in sleep efficiency across the entire study period. These 3 subjects (one from each arm) were chosen to display examples of a consistently low IIV, a change in IIV over time, and a consistently high IIV based on their random effect scale estimates (i.e., estimates of within-subject variance). Figure 2A displays data from a participant in the MBSR arm who has the lowest scale estimate and displays low IIV in sleep efficiency across the entire study period. This represents a “consistent sleeper” whose sleep efficiency was generally stable from night-to-night throughout the study period. Figure 2B displays data from a participant in the MBTI arm with a larger scale estimate who exhibits a pattern of increased levels of sleep efficiency and decreased IIV (increased stability) from baseline through treatment and into post-treatment. This represents a participant who responded to treatment with improvements in both the level and stability of sleep efficiency occurring primarily after the initiation of sleep restriction on day 21. Figure 2C displays data from a participant in the SM control condition with the largest scale estimate who has high IIV (low stability) throughout the study period. This represents an “inconsistent sleeper” who has high night-to-night variability throughout the study period. Although other patterns of change over time are possible, these figures illustrate three potential patterns that are likely to arise across time and reflect the information captured by the random scale effect.

Figure 2. Daily sleep efficiency data for three individual participants across the entire study period.

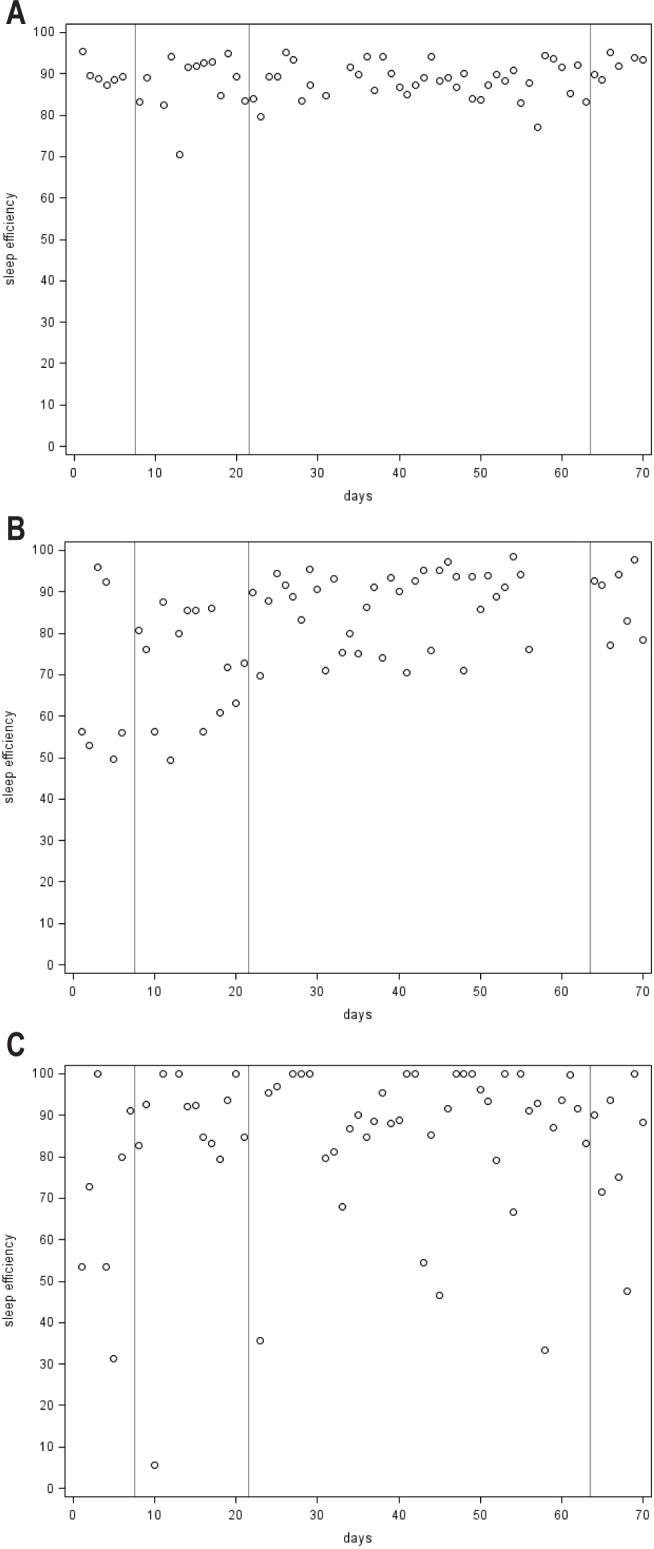
(A) Subject in MBSR condition with low variability (high stability) in sleep efficiency. (B) Subject in MBTI with decreased variability (increased stability) in sleep efficiency during treatment. (C) Subject in SM condition with high variability (low stability) in sleep efficiency. The baseline period is from day 1 to the first line marked (day 7). Early treatment/monitoring is from day 8 to the second line marked (day 21). Late treatment/ monitoring period is from day 22 to the third line marked (day 63). The post treatment/monitoring period is from day 64 to day 70.

DISCUSSION

The goal of this paper was to demonstrate the application of the location-scale mixed model for conducting two-dimensional analyses on mean levels and IIV using daily sleep diary data. We selected sleep efficiency data from a recently completed randomized controlled trial for chronic insomnia to demonstrate how this statistical technique can be applied to these two dimensions to examine treatment outcome and process. Compared to traditional statistical methods, this method can yield greater precision and efficiency as an analytic tool for intensive longitudinal sleep data.

In our example, the location-scale mixed model provided estimates on mean levels that were similar to the random intercepts mixed model, indicating congruence with this traditional statistical approach. The findings revealed significant increases in the mean levels of sleep efficiency for MBSR, rising from 78.3% at baseline to 82.2% at post, and for MBTI, rising from 76.6% at baseline to 83.4% at post. A particular strength of this study was the inclusion of the SM arm, which controlled for the effects of completing sleep diaries with no active treatment. For both treatment arms, the pre-to-post changes in mean levels of sleep efficiency were significantly larger than the preto-post change observed for the SM control. These findings provide evidence to support the efficacy of MBSR and MBTI on improving the level of sleep efficiency at post-treatment.

A unique advantage of the location-scale mixed model is the simultaneous modeling of mean and variance, providing an estimate of the IIV after adjusting for the mean structure. Both MBSR and MBTI showed significant pre-to-post decreases in IIV, which is similar to two previous studies on CBT-I that found significant pre-to-post reductions in night-to-night variability of sleep patterns.^23,24 However, when these two treatment groups were compared to the SM control, the pre-to-post changes were not significantly different. Although the pattern was in the hypothesized direction, the decrease in IIV from baseline to post for the two treatment arms was not significant, above and beyond the effects of completing diaries without treatment. This finding indicates the importance of interpreting the change in IIV relative to a control condition. In terms of treatment outcomes, it appears that MBSR and MBTI have a greater magnitude of effect on the mean levels of sleep efficiency compared to the IIV.

Another advantage of the location scale mixed model is the precision gained by generating estimates based upon all available data collected during the entire study period. By allowing for different number of observations per subject (i.e., using all available data), intent-to-treat analyses are able to be conducted and missing data did not seem to have an adverse impact on the model. Unlike previous studies that only examined pre-to-post comparisons, the location scale mixed model can generate estimates of sleep efficiency during the course of treatment. This provides an opportunity to examine changes in sleep patterns during the course of treatment, potentially yielding insights into treatment mechanisms. Between group comparisons revealed that MBSR was associated with more rapid effects on sleep efficiency compared to both MBTI and the SM control. Specifically, MBSR was associated with a greater increase in mean levels of sleep efficiency and a reduction of 30% in IIV of sleep efficiency relative to the SM control, which emerged early in treatment and continued during the late treatment period. MBSR also showed a greater increase in mean levels of sleep efficiency and reduction in IIV relative to MBTI during the early treatment phase, but not later in treatment. These findings point towards different trajectories in sleep patterns that arise during the course of MBSR and MBTI, with preliminary indications that MBSR produces a stable increase in sleep efficiency that begins early in treatment and continues into late treatment.

Additionally, we examined the impact of the behavioral components of MBTI during treatment. The hypothesized pattern of significant increases in the mean levels of sleep efficiency and significant decreases in the IIV did emerge after the delivery of the main behavioral components in MBTI (sleep restriction and stimulus control), but the changes in IIV were not significantly different compared to the SM control. One possible explanation for the lack of significant findings is that sleep restriction, which aims to optimize mean levels of sleep efficiency, involves weekly modifications to the sleep schedule. These weekly adjustments might have led to the null findings on IIV during late treatment. Furthermore, stimulus control was introduced the following week and both behavioral strategies could have been used by participants in subsequent weeks. Although it is typical in behavioral treatments for insomnia to add stimulus control to sleep restriction, the study design precluded the ability to examine the impact of each treatment component independently. Notably, the overall pattern of changes in sleep efficiency for MBTI shown in Figure 1 (mean levels increasing during late treatment) is similar to the patterns commonly observed for CBT-I, whereby sleep may initially worsen before there is improvement later in treatment and beyond treatment termination.

The present report was intended to provide an example of how the location scale mixed model could be applied to sleep diary data. We selected a simple model for illustrative purposes, but more sophisticated models can include covariates (e.g., age, partner status, BMI) to examine the impact of these variables on the mean and IIV of sleep efficiency or other sleep parameters. Such analyses can be used to test specific hypotheses and develop a theoretical framework for the antecedents and consequences of IIV, as recommended by Bei et al.³ Furthermore, the model could be used to explore different trajectories of change in IIV over time by treating time as a polynomial factor rather than a linear factor. This could yield important patterns regarding the patient's sleep experience during the course of treatment. One limitation of the location-scale mixed model is that it does not take into account the impact of poor sleep efficiency on one night relative to sleep efficiency on the following night. Therefore, examining the temporal relationship between good nights and bad nights of sleep would require other statistical methods, as demonstrated by Perlis et al.^2,25 Also, the present analyses were conducted on self-report data, but the model can also be applied to objective longitudinal data collected from actigraphy or consumer-based wearable technologies. Finally, the power to detect significance is not yet established for the location-scale mixed model. The sample size in this example was relatively small for between subjects-comparisons (i.e., comparisons between treatment conditions) and the number of within-subject observations at baseline and post week (7 days) were smaller than the number of within-subject observations for early (14 days) and late treatment (42 days). These factors might have led to reduced power to detect differences between groups in the change from baseline to post-treatment. Further work is needed to develop a method for conducting power analyses for the location-scale mixed model.

In summary, the location-scale mixed model is a novel statistical tool that can be applied to longitudinal daily sleep diaries collected as part of a randomized controlled trial or in a clinical case replication series. The present findings provide preliminary support for the hypothesis that mindfulness-based interventions can lead to increased levels and stabilization of sleep efficiency. Further research is needed in larger samples to confirm these findings and examine mechanisms through which standard mindfulness programs (i.e., MBSR) and tailored mindfulness programs (i.e., MBTI) lead to improvement in sleep patterns. Research using a priori hypotheses that includes the location-scale mixed model with a study design that isolates treatment components could clarify the impact of sleep restriction and stimulus control on the variability of sleep patterns in the context of MBTI or CBT-I. In addition, assessing IIV of sleep during treatment for insomnia has important clinical implications. For example, when delivering sleep restriction, modifications to the sleep schedule are currently informed only by the mean level of sleep efficiency. However, consideration of IIV in addition to mean level of sleep efficiency merits further investigation as a potential measure of treatment response and decision-making in the context of behavioral treatments for insomnia. The location-scale mixed model could provide a novel statistical tool for further research in this area.

DISCLOSURE STATEMENT

This was not an industry supported study. This research project was supported by a grant from the National Institutes of Health, National Center for Complementary and Alternative Medicine, awarded to the first author (K23AT003678). Dr. Manber receives royalties from New Harbinger and Guilford Press. This activity is unrelated to the current manuscript. Dr. Wyatt serves as a consultant for Philips Respironics, which is unrelated to this study. Dr. Ong receives royalties from the American Psychological Association Books and serves as a consultant for Big Health, Inc. Dr. Hedeker has indicated no financial conflicts of interest.

ABBREVIATIONS

CBT-I

cognitive-behavioral therapy for insomnia

HLM

hierarchical linear modeling

IIV

intra-individual variability

MBTI

Mindfullness-Based Therapy for Insomnia

MSBR

Mindfullness-Based Stress Reduction

SD

standard deviation

SM

self-monitoring

TIB

time in bed

TST

total sleep time

WS

within-subject

WSSD

within-subject standard deviation