Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 Apr 6;6:23494. doi: 10.1038/srep23494

Optical phase conjugation assisted scattering lens: variable focusing and 3D patterning

Jihee Ryu 1,*, Mooseok Jang 2,*, Tae Joong Eom 3,a, Changhuei Yang 2,b, Euiheon Chung 1,c
PMCID: PMC4877672  PMID: 27049442

Abstract

Variable light focusing is the ability to flexibly select the focal distance of a lens. This feature presents technical challenges, but is significant for optical interrogation of three-dimensional objects. Numerous lens designs have been proposed to provide flexible light focusing, including zoom, fluid, and liquid-crystal lenses. Although these lenses are useful for macroscale applications, they have limited utility in micron-scale applications due to restricted modulation range and exacting requirements for fabrication and control. Here, we present a holographic focusing method that enables variable light focusing without any physical modification to the lens element. In this method, a scattering layer couples low-angle (transverse wave vector) components into a full angular spectrum, and a digital optical phase conjugation (DOPC) system characterizes and plays back the wavefront that focuses through the scattering layer. We demonstrate micron-scale light focusing and patterning over a wide range of focal distances of 22–51 mm. The interferometric nature of the focusing scheme also enables an aberration-free scattering lens. The proposed method provides a unique variable focusing capability for imaging thick specimens or selective photoactivation of neuronal networks.

Light focusing is typically achieved through a lens or curved mirror with a fixed focal length. The focusing optics numerical aperture (NA) defines the depth of focus (DOF) as1

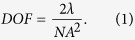graphic file with name srep23494-m1.jpg

Equation (1) assumes a circular aperture; 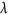Inline graphic is wavelength of light. For micron-scale light focusing with visible light (focus size of 1–5 microns at 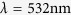Inline graphic), the NA has to be in the range of 0.05–0.27, which leads to a depth of focus of 14–360 microns. Thus, for most biomedical applications that require three-dimensional (3D) optical interrogation, the specimen target section needs to be precisely aligned to the focal plane.

This problem can be circumvented with a variable-focus lens. The most common design is the zoom lens, in which the focal length is adjusted with a moving element(s). However, this approach may not be suitable for lens configurations that require exact alignment, such as an objective lens. This limits zoom lens applications in biological microscopy. Another notable approach to variable focusing is to electrically modulate the morphology or refractive index of lens element. One prominent example is the fluid lens, in which the radius of curvature of a fluid drop is modulated by external voltage2,3,4,5. However, the aberration and limited numerical aperture of fluid lens restricts its applications2.

A wavefront-shaping technique provides versatile light focusing without physical modification to the optical element6,7,8,9. Instead, the spatial light modulator (SLM) is employed to shape the incident wavefront on the lens aperture so that a spot or multiple spots can be created at the desired location(s) in three-dimensional space. A notable strength of this technique is the ability to create multiple foci simultaneously or sequentially. This enables, for example, optical stimulation of multiple locations on a neuron6,8,9, or creation of optical traps in arbitrary three-dimensional configurations7. However, the controllable degrees of freedom in a SLM are not sufficient to address every possible nuance of the optical wavefront over the large aperture (>1 cm). In fact, when the 1-megapixel SLM (1,000 × 1,000 pixels) is placed onto a 1 × 1 cm2 aperture, the maximum possible deflection angle through the SLM is only ~1.5 degrees [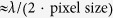Inline graphic]. Thus, the achievable focusing range is correspondingly limited.

An alternative technique was proposed by Vellekoop et al., which exploits light scattering to achieve interferometric focusing10. In this approach, the feedback-based wavefront-shaping method is used to focus light through scattering layer by progressively achieving constructive interference of the scattered light field at a chosen point10,11,12. This “scattering lens” enables diffraction-limited focusing (given by aperture size and focal length) that is immune to aberration10. Furthermore, it is demonstrated that the focus reconstructed behind the scattering media can be laterally13,14,15 or axially16,17 displaced by the optical memory effect18,19. However, in previous works, the backing objective lens placed in between the scattering lens and the spatial light modulator significantly limits the effective aperture size of the scattering lens, which in turn limits the variable focusing capability of the scattering lens. For instance, Yang et al. has demonstrated that the spot reconstructed through a scattering layer can be axially displaced over the range of ~300 μm for three dimensional fluorescence imaging16.

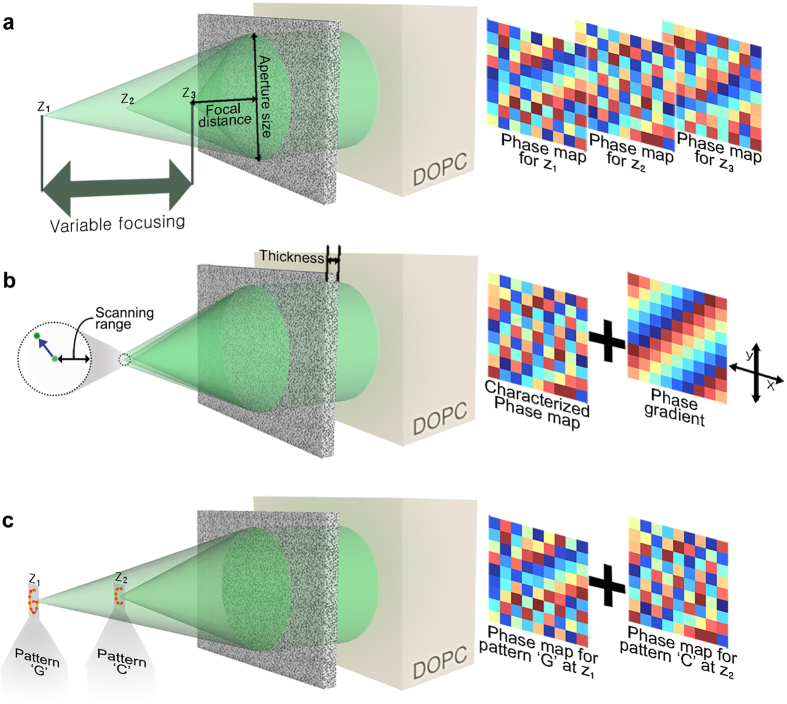
In this study, we report an optical phase conjugation (OPC)-assisted scattering lens that generates micron-sized focal spot over a wide range of focal distances (22–51 mm, Fig. 1a). The scattering lens also enables three-dimensional light patterning in micron resolution over a volume enclosed by a ~20 μm × 20 μm circle at 22 mm focal distance and a ~50 μm × 50 μm circle at 51 mm focal distance (Fig. 1c). The optical phase conjugation system is implemented with a pixel-to-pixel aligned sensor and SLM20,21. The sensor in the digital OPC (DOPC) system is first used to characterize the randomized wavefront originated from the reference spot behind the scattering lens. Then, SLM plays back the phase-conjugated (time-reversed) wavefront, which is focused back to the reference spot through the scattering lens. In the characterization step, multiple wavefronts are captured at different axial positions of the reference spot and used for variable focusing. As demonstrated in the previous studies13,14,15,16,17, a memory effect is used for lateral scanning (Fig. 1b). The OPC-assisted method enables coordination of much larger numbers of optical modes with shorter lens characterization time than the previous feedback algorithm scheme10,13. This OPC-assisted scattering lens will find applications in the areas of optical imaging and selective photoactivation.

Figure 1. Schematic of the optical phase conjugation-assisted scattering lens.

Figure 1

Open in a new tab

(a) Variable focusing with the OPC-assisted scattering lens. The scattering lens generates a focal spot at different focal distances by playing back the phase-conjugated version of the wavefront recorded at different focal distances z1, z2, and z3. (b) Lateral scanning of the focal spot. The focal spot can be laterally moved based on the short-range correlation (memory effect). In this case, a linear phase gradient is added to the recorded wavefront. The gradient amplitude determines the amount of displacement and the direction determines the direction of spot movement. (c) Arbitrary 3D patterning. Arbitrary 3D patterns, such as ‘C’ and ‘G’ at two different planes, can be created using a scattering lens by superposing multiple wavefronts that individually optimize the optical modes inside ‘C’ and G’.

In this paper, we provide a detailed description of the experimental setup and procedure. We present experimental data on the focal spot size and usable range of the scattering lens, and demonstrate sequential and simultaneous light patterning in three-dimensional space. Finally, we discuss the limitations and practicality of the proposed scheme.

Results

Principle

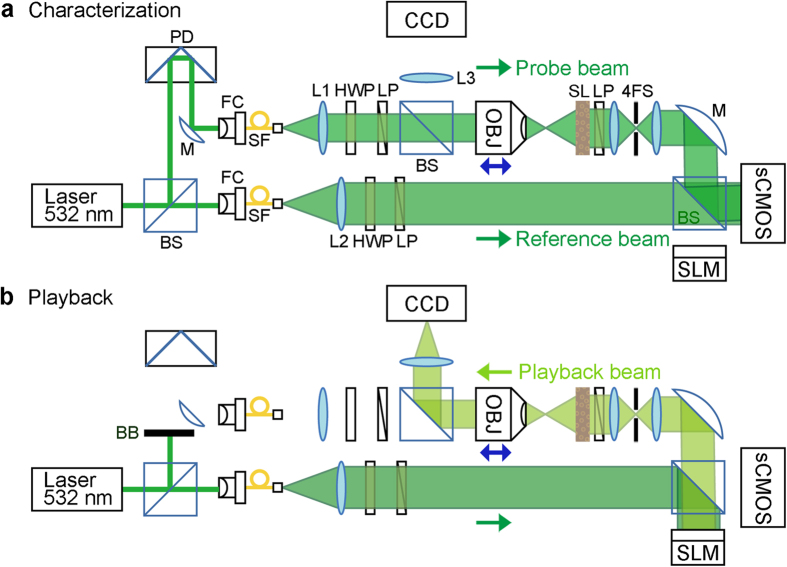
The experimental configuration for lens characterization is shown in Fig. 2. The probe beam is focused through an objective lens and scattered by a scattering lens, which is a 5.6 μm thick layer of ZnO particles (white paint) sprayed onto a standard glass microscope slide. Based on the scattering coefficient of the white pigment (~1.3 μm−1)13,22, we estimate that the light is scattered an average of ~7 times and create a Lambertian scattering from the other side of the scattering lens. The DOPC system, which is imaged onto the scattering lens surface through the 4-f system (with 1.2× magnification), collects the scattered wavefront. Here, the collimated reference beam interferes with the scattered probe beam so that the complex wavefront can be measured with an off-axis holographic method23. The iris in the 4-f system selects the off-axis component to be recorded and played back. The linear polarizer and wave plate are used to match the polarization angle of the probe beam and reference beam. We repeatedly characterize the scattering lens at focal distances ranging from 22–51 mm by translating the objective lens along the optical axis. We then conjugate the recorded wavefront and play it back from the SLM. The same reference beam used for the holographic measurement serves as a playback beam. The reconstructed focal spot or pattern is then imaged onto the CCD camera through an objective lens and tube lens (L3). The probe beam is blocked during this process.

Figure 2. Illustration of experimental setup.

Figure 2

Open in a new tab

The scattering lens is characterized and then used to generate a focal spot or focal pattern. (a) Characterization. A narrow beam from a 532-nm pulsed diode-pumped solid-state laser is split into a probe beam and a reference beam. Both beams are spatially filtered through a single-mode fiber and collimated with a plano-convex lens. The probe beam is focused through the objective lens (magnification ×10, NA 0.25) and scattered through the scattering lens. The diffused wavefront is captured by the DOPC system, which is optically placed on the scattering lens surface through the 4-f system (1.2× magnification). The collimated reference beam interferes with the diffused probe beam for the off-axis holography method. The linear polarizer and half-wave plate match the polarization of both beams. (b) Playback. The phase-conjugated copy of the recorded wavefront is calculated and displayed on SLM. Then, the playback beam (the reference bean reflected off the SLM) is focused through the scattering lens by the time-reversal symmetry. The focal plane of the scattering lens is imaged onto the CMOS camera through the objective lens and tube lens for visual observation of the focal spot. Sample beam is blocked in this process. BS, beam splitter; PD, path delay part; M, mirror; FC, fiber coupler; SF, single mode fiber; L1, 300 mm lens; L2, 200 mm lens; L3, 500 mm lens; LP, linear polarizer; HWP, half-wave plate; OBJ, objective lens; SL, scattering lens; 4FS, 4-f system (from SL, 150 mm lens, iris, and 125 mm lens); sCMOS, scientific complementary metal oxide semiconductor; SLM, spatial light modulator; CCD, charge-coupled device; BB, beam blocker.

The focusing fidelity is quantified by the enhancement factor, which is defined as the ratio between the intensity contained in the focal spot and the average background intensity. In contrast to conventional focusing schemes, background is inevitable in the interferometric approach. This is attributed to partial measurement of the wavefront emerging from the scattering lens. In other words, the deviation from the perfect phase conjugation randomly contributes to the background while the portion of playback field overlapped with the perfect phase-conjugated field forms a converging spherical wavefront (aberration free due to the time-symmetry of Green function)10. If only the input field phase is controlled in the time-reversal process, the enhancement factor (alternatively, peak-to-background ratio) has the following relation to the number of controllable input modes (N)11:

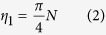graphic file with name srep23494-m5.jpg

where the subscript 1 denotes that a single optical mode (i.e. focal spot) is reconstructed through the time-reversal process. In our experiment, N was ~40,000 (see Methods for the determination of N). Thus, from Eq. (2), we estimate the theoretical 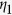Inline graphic of ~31,000.

When we generate a light pattern composed of K optical modes, we add K input wavefronts that independently optimize each optical mode behind the scattering lens. Therefore, 1/K energy from the input side contributes to the light intensity at each optical mode in the desired light pattern. Mathematically, the enhancement factor of the light pattern (here, the ratio between the average intensity contained in each focal spot and the average background intensity) is given by

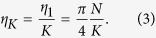graphic file with name srep23494-m7.jpg

Focal spot size at different focal distances

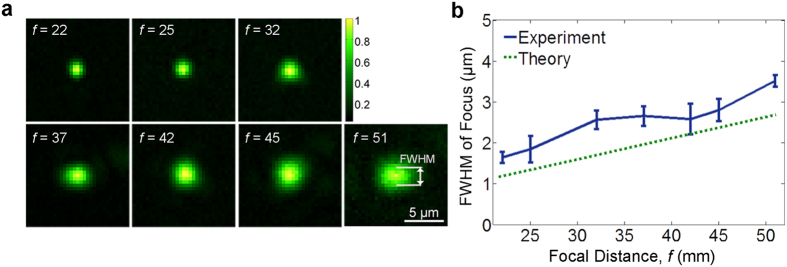
We first demonstrate the variable-focusing capability of the OPC-assisted scattering lens (Fig. 1a). The scattering lens is characterized for focal distances ranging from 22–51 mm. Then, we play back each captured wavefront to create the focal spot at each focal distance. The lateral intensity distribution and the full width at half maxim (FWHM) of the reconstructed focal spot at different focal distances is presented in Fig. 3 (axial intensity profiles are presented in Supplementary Fig. S1). FWHM ranges from ~1.5−3.5 μm, which corresponds with NA of ~0.08–0.18. The focal spot size linearly increases with increasing focal distance. Because the aperture size of scattering lens is fixed, the effective NA is inversely proportional to focal distance. The theoretical relation is given by

Figure 3. Variable focusing through OPC-assisted scattering lens.

Figure 3

Open in a new tab

(a) Images of focal spot at different focal distances. Each image is normalized with respect to peak intensity. (b) Theoretical and experimental full width at half maximum (FWHM) of the focal spot at different focal distances.

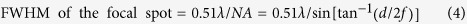graphic file with name srep23494-m8.jpg

where d is the aperture size of scattering lens (~10 mm with 1.2× magnification of the 4-f system). We expect the deviation from the theoretical prediction is mostly from the marginal distortion of the reference wavefront. The distortion can lead to inaccurate wavefront measurement and playback, which was performed based on the assumption that the reference wavefront is perfectly flat. With the presence of short-range correlation, the unwanted distortion in the wavefront may contribute to the light intensity in the vicinity of the original spot. We also note that the misalignment and aberration of the tube lens (L3) may cause an additional blurring in detection point spread function. The enhancement factor η1 ranges between 2,500–8,000, depending on alignment quality. It corresponds to the 8~25% of the theoretical η1 from Eq. (2).

Lateral scanning range at different focal distances

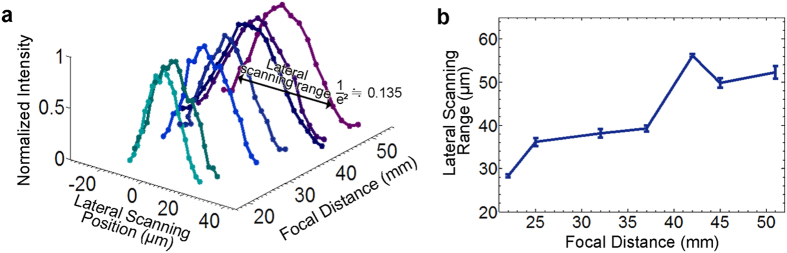
Similar to the previous studies13,14,15,16,17, the focus was laterally shifted by merging the captured wavefront with the linear phase gradient (Fig. 1b). Figure 4a plots the normalized peak intensity of the focal spot at different lateral scanning positions and focal distances. The lateral scanning range, which is obtained as full width at 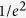Inline graphic, was measured to be 28~56 microns (Fig. 4b). As theoretically expected (see Supplementary Note 1 for details), the angular scanning range was not affected by focal distance (experimental data provided in Supplementary Fig. S2). Consequently, the lateral scanning range linearly scaled with the focal distance.

Figure 4. Lateral scanning range of the OPC-assisted scattering lens.

Figure 4

Open in a new tab

(a) Normalized peak intensity of the focal spot at different lateral scanning positions and focal distances. (b) Theoretical and experimental full width at 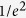Inline graphicof the intensity profile at different focal distances.

Demonstration of light patterning

We demonstrate arbitrary light patterning based on the superposition principle. First, we sequentially create multiple focal points at different focal distances by adding multiple phase gradient maps into a single phase-conjugate wavefront (Fig. 5a). The synthesized wavefronts are shown in Fig. 5b. We observe a noticeable deformation in the focal spot and ghost spots in some patterns. These unwanted effects could be significantly suppressed by controlling the amplitude term in addition to the phase term. With the imperfect wavefront modulation and reduction in the short-range correlation, the enhancement factor ηK is reduced ~20 times as the number of reconstructed focal spots increases from 1 to 11. We demonstrated the generation of the light pattern composed of up to 83 multiple foci and presented in Supplementary Fig. S3.

Figure 5. Sequential generation of multiple focal spots at different focal distances.

Figure 5

Open in a new tab

The focal distance is changed from 15 to 35 mm with 5-mm intervals. The wavefronts at each focal distance were recorded. Then, the phase maps for multiple foci were synthesized and played back separately. (a) Images of multiple foci at different focal distances. Each image is normalized with respect to peak intensity. (b) Phase map shown for each focal distance. The phase map is cropped into 20 × 20 pixel images for display.

In practice, the maximum number of possible optical modes depends on the application. For example, if the scattering lens is used for selective optogenetic stimulations, 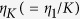Inline graphic of 100 is required for 5-fold modulation of the maximum neural response24. In this case, the maximum number of possible optical modes that can be optimized through the scattering lens is >20.

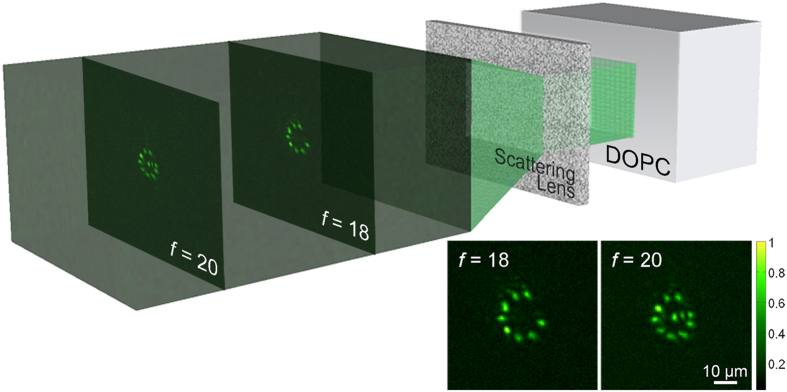
The simultaneous generation of 3D arbitrary patterning through the scattering lens is illustrated in Fig. 6. The phase maps for ‘C’ and ‘G’ are synthesized separately based on two wavefronts captured at two different focal distances (18 and 20 mm). Then, the two phase maps are superposed and displayed on the SLM. We confirmed that the patterns ‘C’ and ‘G’ are created 18 and 20 mm behind the scattering lens through the translating objective lens.

Figure 6. Simultaneous generation of arbitrary patterns at different focal distances.

Figure 6

Open in a new tab

Volumetric 3D image shows the intensity distribution at different focal distances. The image is normalized with respect to the peak intensity. Insets present the patterns ‘C’ and ‘G’ generated at focal distances of 18 and 20 mm, respectively.

Discussion

This paper has demonstrated that the OPC-assisted scattering lens can serve as a variable focusing lens. Although the scattering layer does not essentially increase the number of controllable degrees of freedom (which is determined solely by the SLM), it provides a great deal of flexibility in selecting a focal distance by redistributing the intrinsic controllable degrees of freedom in SLM into a full angular spectrum. The 10 × 10 mm2 wide aperture provides a micron-scale focal spot with variable focal length from 22–51 mm. Short-range correlation enables lateral shift of the spot with simple modification of the characterized wavefront. Using a digital wavefront shaper, we superposed multiple wavefronts to generate the arbitrary light pattern in three-dimensional space. Similar to other lenses equipped with wavefrant shaping methods10,13,16,25,26, the OPC-assisted scattering lens corrects aberrations. The larger the lens aperture, the more flexibility the lens will provide. In principle, larger apertures are achievable with higher magnification of the relay system between the DOPC plane and the scattering lens. In Supplementary Fig. S4, we present the curve depicting the trade-off between NA and focal distance of the scattering lenses at various aperture sizes. For the sake of comparison, a scatter plot of NA and working distance of commercially available objective lenses is also provided.

We achieved variable focusing with the multiple wavefronts characterized with the point sources at a different distance from the scattering lens. Alternatively, variable focusing can be achieved through the longitudinal memory effect with a single wavefront solution. As demonstrated in the previous studies16,17, the wavefront solution synthesized with a quadratic phase profile can be used for longitudinal scanning. However, we note that in our experimental configuration the longitudinal correlation range (in geometrical optics approximation, 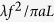Inline graphic where f is focal distance, a is aperture size, and L is the thickness of scattering lens) is an order of magnitude shorter than the variable focusing range we demonstrated in our study.

In our system, the lateral focusing range is approximately 25–50 μm when it is defined as full width at 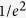Inline graphicof the peak intensity (without lateral scanning). However, the η1 corresponding to the peak intensity is ~2,500–8,000, and η1 will be sufficiently high for most applications even with a 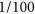Inline graphic reduction. Thus, in practice, the usable field of view of our scattering lens can be extended to ~40–100 μm. The lateral scanning range can be further improved by attaining full short-range correlation with better alignment between the SLM image plane and scattering layer or by increasing the number of characterization points on the transverse plane.

The scattering lens is ineffective in terms of power transmission. The power transmission depends on the type and thickness of scattering layer and the number of controllable optical modes. For instance, in our experiment, ~10−7–10−8 of total power impinged on the input side was delivered to the focal spot. Although the power transmission is not effective through a scattering layer, considering the optical power distribution within the usable field of view, more than 50% of the power is focused to the target spot(s). The absolute power delivered to the focal spot(s) can be arbitrarily controlled by adjusting the power of the playback beam.

The OPC-assisted scattering lens provides great flexibility for variable-light focusing and light patterning, and can be used for a broad range of optical applications. First, it can serve as illumination optics for fluorescence microscopy. It has a unique capability in focusing light through thick specimens such as CLARITY-cleared tissue27. In the imaging applications, an array of focal spots along with fast scanning from a galvo mirror and digital micromirror device (in place of liquid crystal SLM), will significantly improve the imaging speed. In addition, axial resolution can be further extended with an isotropic focusing scheme, which can be simply achieved in the current setup by allowing the reference spot (probe beam) to interfere with the reconstructed focal spot (playback beam)25,28. In addition to its application in imaging, the scattering lens can be a powerful tool for manipulating particles and activating biomolecules or materials. For example, it can be combined with optogenetics technology for interrogating three-dimensional neuronal networks at cellular resolution29.

In practice, a potential difficulty in using the scattering lens is that the characterization step requires a high-quality objective lens and is time-consuming when the number of characterization points is large. One direction worth pursing for future research is to develop a strategy for self-characterization of scattering lenses30.

Methods

Setup

A pulsed laser beam (532 nm wavelength, 5 ns pulse width, 2 kHz repetition rate, 7 mm coherence length) generated from the Q-switched laser (FQS-200-1-Y-532, Elforlight) was split into a probe beam and a reference beam. The probe beam was focused through the objective lens (magnification ×10, NA 0.25, PLN 10X, Olympus) and transmitted through the scattering layer. The transmitted probe beam was relayed to the CMOS sensor or the DOPC system through the 4-f system and interfered with the reference beam. The diameter of the iris placed in between two lenses of 4-f system was around 3 mm. The phase map of the probe beam is calculated through the off-axis method and stored in a computer. The characterization step is repeatedly performed at multiple locations of the reference spot along the optical axis. The motorized stage was used to precisely position the objective lens. Then in the playback step, the SLM (Pluto, Holoeye) of the DOPC system displayed the conjugated wavefront to generate a single or multiple spots through the scattering layer. Although we used a pulsed laser in our experiment, a continuous wave laser (with a single longitudinal mode) would be a more preferable choice as it typically has a longer coherence length.

DOPC system is optimized through the digital auto-alignment method31. Through the experiment, we achieved the experimental enhancement factor for single focus 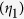Inline graphic and multiple foci 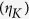Inline graphic corresponded with 4–25% of the theoretical values. We speculate the discrepancy may be due to the cross talk between SLM pixels and the loss of sub-pixel nuance in a speckle field. 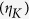The reduction in the short-range correlation further decreases the enhancement factor of multiple foci Inline graphic.

The objective lens was also used to visualize the focal plane of the scattering lens. Imaging magnification from the focal plane of the scattering lens to the CCD sensor (Prosilica GC655, Allied Vision) was characterized by a Ronchi ruler (200 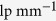Inline graphic, Edmund Optics).

Determination of the number of controlled optical modes

The number of pixels we controlled in the experiment was 1654 × 1080. Once the separation between the off-axis component and the zero order component in Fourier space is optimized, we cropped the elliptical region (major axis of ~150 pixels and minor axis of ~85 pixels) in the Fourier space to extract the phase conjugation component. We estimated the number of controllable degrees of freedom as the number of pixels in the cropped Fourier component, which is around ~40,000.

Diffuse sample preparation

The scattering lens was prepared by spray painting ZnO particles onto a standard microscope slide. The ZnO layer thickness was 5.6 μm. The thickness was measured by the surface profiler (Alpha-step IQ, KLA-Tencor, Milpitas, CA, USA).

Determination of spot size and scanning range

The one-dimensional intensity profile of the focal spot is extracted from the image of the focal spot captured from the CCD sensor. The intensity profile was fitted to the one-dimensional Gaussian profile. The spot size was then determined as the FWHM of the fitted Gaussian profile.

The one-dimensional scanning profile was acquired by sampling the peak intensity of the focal spot at different lateral scanning positions. The scanning profile was normalized and fitted to the functional form of 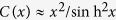Inline graphic18,19. Then, the full width at 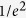Inline graphicof the fitted curve was determined as the lateral scanning range.

Additional Information

How to cite this article: Ryu, J. et al. Optical phase conjugation assisted scattering lens: variable focusing and 3D patterning. Sci. Rep. 6, 23494; doi: 10.1038/srep23494 (2016).

Supplementary Material

Supplementary Information
srep23494-s1.pdf (289.8KB, pdf)

Acknowledgments

We thank Kiri Lee for helpful discussions. This research was supported by the GIST-Caltech Research Collaboration Project through a grant provided by GIST in 2015, the Institute of Medical System Engineering (iMSE) in the GIST, the Bio & Medical Technology Development Program of the National Research Foundation of Korea (2011-0019633), the New Growth Power Equipment Competitiveness Reinforcement Program (10047580), the Industrial Strategic Technology Development Program (10047943) of the Ministry of Trade, Industry & Energy of Korea, the National Institutes of Health (1DP2OD007307-01), and the National Institutes of Health BRAIN Initiative (1U01NS090577-01).

Footnotes

Author Contributions J.R. and M.J. contributed equally to the work. M.J. conceived the experiments. J.R. carried out the experiments. J.R. and M.J. analysed the data. All authors contributed to writing the manuscript. T.J.E., C.Y. and E.C. supervised the project.

References

  1. Born M. & Wolf E. Principles of optics: electromagnetic theory of propagation, interference and diffraction of light. (Cambridge university press, 1999). [Google Scholar]
  2. Commander L. G., Day S. E. & Selviah D. R. Variable focal length microlenses. Opt. Commun. 177, 157–170 (2000). [Google Scholar]
  3. Berge B. & Peseux J. Variable focal lens controlled by an external voltage: An application of electrowetting. Eur. Phys. J. E 3, 159–163 (2000). [Google Scholar]
  4. Sato S. Liquid-Crystal Lens-Cells With Variable Focal Length. Jpn. J. Appl. Phys. 18, 1679–1684 (1979). [Google Scholar]
  5. Kuiper S. & Hendriks B. H. W. Variable-focus liquid lens for miniature cameras. Appl. Phys. Lett. 85, 1128–1130 (2004). [Google Scholar]
  6. Anselmi F., Ventalon C., Begue A., Ogden D. & Emiliani V. Three-dimensional imaging and photostimulation by remote-focusing and holographic light patterning. Proc. Natl. Acad. Sci. 108, 19504–19509 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Curtis J. E., Koss B. A. & Grier D. G. Dynamic holographic optical tweezers. Opt. Commun. 207, 169–175 (2002). [Google Scholar]
  8. Nikolenko V. SLM microscopy: scanless two-photon imaging and photostimulation using spatial light modulators. Front. Neural Circuits 2, 1–14 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  9. Szabo V., Ventalon C., De Sars V., Bradley J. & Emiliani V. Spatially Selective Holographic Photoactivation and Functional Fluorescence Imaging in Freely Behaving Mice with a Fiberscope. Neuron 84, 1157–1169 (2014). [DOI] [PubMed] [Google Scholar]
  10. Vellekoop I. M., Lagendijk A. & Mosk A. P. Exploiting disorder for perfect focusing. Nat. Photonics 4, 320–322 (2010). [Google Scholar]
  11. Vellekoop I. M. & Mosk A. P. Focusing coherent light through opaque strongly scattering media. Opt. Lett. 32, 2309–2311 (2007). [DOI] [PubMed] [Google Scholar]
  12. Vellekoop I. M. Feedback-based wavefront shaping. Opt. Express 23, 12189–12206 (2015). [DOI] [PubMed] [Google Scholar]
  13. Vellekoop I. M. & Aegerter C. M. Scattered light fluorescence microscopy: imaging through turbid layers. Opt. Lett. 35, 1245–1247 (2010). [DOI] [PubMed] [Google Scholar]
  14. Hsieh C.-L., Pu Y., Grange R., Laporte G. & Psaltis D. Imaging through turbid layers by scanning the phase conjugated second harmonic radiation from a nanoparticle. Opt. Express 18, 20723–20731 (2010). [DOI] [PubMed] [Google Scholar]
  15. Van Putten E. G. et al. Scattering Lens Resolves Sub-100 nm Structures with Visible Light. Phys. Rev. Lett. 106, 193905 (2011). [DOI] [PubMed] [Google Scholar]
  16. Yang X., Hsieh C.-L., Pu Y. & Psaltis D. Three-dimensional scanning microscopy through thin turbid media. Opt. Express 20, 2500–2506 (2012). [DOI] [PubMed] [Google Scholar]
  17. Ghielmetti G. & Aegerter C. M. Scattered light fluorescence microscopy in three dimensions Abstract. Opt. Express 20, 110–115 (2012). [DOI] [PubMed] [Google Scholar]
  18. Feng S., Kane C., Lee P. & Stone A. Correlations and fluctuations of coherent wave transmission through disordered media. Phys. Rev. Lett. 61, 834–837 (1988). [DOI] [PubMed] [Google Scholar]
  19. Freund I., Rosenbluh M. & Feng S. Memory effects in propagation of optical waves through disordered media. Phys. Rev. Lett. 61, 2328–2331 (1988). [DOI] [PubMed] [Google Scholar]
  20. Yaqoob Z., Psaltis D., Feld M. S. & Yang C. Optical Phase Conjugation for Turbidity Suppression in Biological Samples. Nat. Photonics 2, 110–115 (2008). [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Cui M. & Yang C. Implementation of a digital optical phase conjugation system and its application to study the robustness of turbidity suppression by phase conjugation. Opt. Express 18, 3444–3455 (2010). [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Vellekoop I. & Mosk A. P. Universal Optimal Transmission of Light Through Disordered Materials. Phys. Rev. Lett. 101, 120601 (2008). [DOI] [PubMed] [Google Scholar]
  23. Cuche E., Marquet P. & Depeursinge C. Spatial filtering for zero-order and twin-image elimination in digital off-axis holography. Appl. Opt. 39, 4070–4075 (2000). [DOI] [PubMed] [Google Scholar]
  24. Lin J. Y., Lin M. Z., Steinbach P. & Tsien R. Y. Characterization of Engineered Channelrhodopsin Variants with Improved Properties and Kinetics. Biophys. J. 96, 1803–1814 (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Jang M., Sentenac A. & Yang C. Optical phase conjugation (OPC)-assisted isotropic focusing. Opt. Express 21, 8781-8792 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Booth M. J., Neil M. A. A., Juskaitis R. & Wilson T. Adaptive aberration correction in a confocal microscope. Proc. Natl. Acad. Sci. USA 99, 5788–5792 (2002). [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Chung K. et al. Structural and molecular interrogation of intact biological systems. Nature 497, 332–337 (2013). [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Hell S. & Stelzer E. H. K. Properties of a 4Pi confocal fluorescence microscope. J. Opt. Soc. Am. A 9, 2159–2166 (1992). [Google Scholar]
  29. Deisseroth K. Optogenetics. Nat. Methods 8, 26–29 (2011). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Wang K. et al. Rapid adaptive optical recovery of optimal resolution over large volumes. Nat. Methods 11, 625–628 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Jang M., Ruan H., Zhou H., Judkewitz B. & Yang C. Method for auto-alignment of digital optical phase conjugation systems based on digital propagation. Opt. Express 22, 14054–14071 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Information
srep23494-s1.pdf (289.8KB, pdf)

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES