Combined registration and motion correction of longitudinal retinal OCT data

Abstract

Optical coherence tomography (OCT) has become an important modality for examination of the eye. To measure layer thicknesses in the retina, automated segmentation algorithms are often used, producing accurate and reliable measurements. However, subtle changes over time are difficult to detect since the magnitude of the change can be very small. Thus, tracking disease progression over short periods of time is difficult. Additionally, unstable eye position and motion alter the consistency of these measurements, even in healthy eyes. Thus, both registration and motion correction are important for processing longitudinal data of a specific patient. In this work, we propose a method to jointly do registration and motion correction. Given two scans of the same patient, we initially extract blood vessel points from a fundus projection image generated on the OCT data and estimate point correspondences. Due to saccadic eye movements during the scan, motion is often very abrupt, producing a sparse set of large displacements between successive B-scan images. Thus, we use lasso regression to estimate the movement of each image. By iterating between this regression and a rigid point-based registration, we are able to simultaneously align and correct the data. With longitudinal data from 39 healthy control subjects, our method improves the registration accuracy by 50% compared to simple alignment to the fovea and 22% when using point-based registration only. We also show improved consistency of repeated total retina thickness measurements.

1. INTRODUCTION

Optical coherence tomography (OCT) has become widely used in ophthalmology since it provides high resolution three-dimensional data of the retina and the contained structural layers that make it up. As such, both gross pathologies, like retinal detachments, and smaller changes, such as ganglion cell layer thinning, are detectable using OCT. Often, these smaller retinal changes are observed in population studies where, for example, the average thickness of specific layers are significantly different in one population versus another. However, tracking small changes in a single patient over short time intervals is significantly more challenging for a variety of reasons including the limited resolution of the scanner, the accuracy of the segmentation algorithms, the positioning of the eye, and movement of the eye during a scan. Therefore, to improve the consistency and accuracy of longitudinal thickness measurements, it is critical to both register the scans for alignment and apply motion correction in the absence of eye tracking.

While OCT scanner technology is rapidly evolving, with modern scanners having eye and pupil tracking to address the issue of alignment and eye motion, retrospective studies are often performed on data acquired from older scanners without these improvements. In these systems, measurements are made spatially relative to the position of the center of the fovea only, providing just a single landmark for aligning data from the same subject acquired at different times. Using this simplistic strategy, alignment errors due to eye motion and head rotation are still possible.

Research on registration or alignment of OCT data and motion correction have typically been done separately from one another. Since we are only concerned with longitudinal data acquired from the same subject in our work, the registration problem primarily consists of aligning the blood vessel patterns as seen in a fundus view of the retina. These vessels can be thought of as fixed landmarks that do not change over time. For the specific purpose of longitudinal analysis, there have only been a small number of papers on the alignment of OCT data.^1–4 The two works of Niemeijer et al.^{1, 2} provide longitudinal registration as a motivating example, but do not include experiments to show improved longitudinal stability or accuracy. In Wu et al.,³ blood vessel points are extracted from an OCT fundus projection image and registered between scans using the coherent point drift algorithm.⁵ This work was later used to evalute the change in thickness over time in patients with macular edema.⁶ In our own prior work,⁴ we registered longitudinal data using intensity-based registration of OCT fundus projection images.

To address the problem of motion correction, several algorithms have been developed that require a pair of orthogonally acquired scans,^{7, 8} data which is not frequently acquired. Another method, which does not require multiple scans, uses a particle filter to track different features between images.⁹ In work by Montuoro et al.,¹⁰ eye motion was corrected using a single scan by estimating the lateral translation between successive B-scan images by maximizing the phase correlation. The variability of this method is quite large, however, due to the images having slightly different features despite being close together.

As an alternative to acquiring multiple scans (orthogonal or otherwise) at the same visit, we propose to use data from successive longitudinal visits to simultaneously register and motion correct the data. With such a framework, more accurate measurements can be made without the need to acquire multiple scans at each visit. Perhaps the closest related work to our own is that of Vogl et al. where they combined previous work on motion correction and point-based registration to align data in succession before doing a longitudinal analysis.⁶ By simultaneously doing these two steps, we are able to overcome any drawbacks found in doing the correction and registration steps separately since we take advantage of complementary information found in successive scans.

2. METHODS

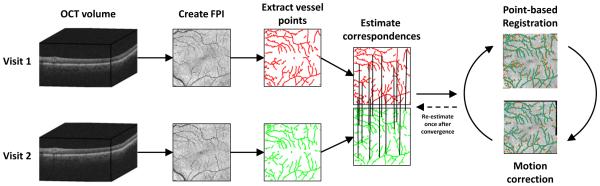
An overview of our method is presented in Fig. 1. We begin with two OCT volumes acquired from the same subject at different times. A fundus projection image (FPI) is created from each volume by projecting the intensities along each A-scan (vertically) to the x-y plane. The blood vessel patterns are shown clearly in the FPI since the vessels create a shadow below their location. A set of points representing the vessels are then extracted and correspondences between the two point sets are estimated. Finally, we iterate between a point-based registration (using a rigid + scale transformation) to align the data and a lasso regression to do motion correction. With the data in alignment, any measurements made on the two scans, for instance thickness values, will be in correspondence and thus more accurate than if the data was misaligned.

Figure 1.

Overview of the algorithm for motion correction and registration of OCT data from two visits. The final iterations between point-based registration and motion correction are carried out until convergence. Note that correspondences are estimated for every point and only a reduced set are shown for display purposes.

2.1 Fundus projection image

Alignment of the OCT data relies on accurate extraction of the blood vessel points. Segmentation of blood vessels in OCT images is a significantly more challenging problem than in color fundus images due to the lower resolution and speckle noise in OCT data. To extract the blood vessel locations from the 3D OCT scans, we need to project the data to 2D, creating FPIs which show the blood vessels across the retina. To do this, we average the intensities along each A-scan over different regions of the retina, combining the fact that the vessels produce a hyperintense area in the inner retina, while their shadows produce a hypointense area in the outer retina.

We generate a single FPI, f(x, y), as a linear combination of FPIs created separately on the inner and outer retina, formed as f (x, y) = f_o(x, y) + α (1 − f_i(x, y)), where f_o and f_i are created by averaging voxels found in the outer and inner retina, respectively. Specifically, f_o is the average intensity from the bottom boundary of the inner nuclear layer (INL) to Bruch’s membrane (BrM). To create f_i, we average the pixel intensities in the ganglion cell and inner plexiform (GCIP) layer between 40% and 80% of the distance between the bottom boundary of the retinal nerve fiber layer (RNFL) to the top of the INL. Each FPI is then normalized to have intensities between 0 and 1. Note that the final FPI is created using the term 1 − f_i, which changes the bright values of the inner retina to be compatible with the dark vessels in the outer retina. The layer boundaries needed to compute each FPI are found using our previously developed automated layer segmentation algorithm.¹¹ Figure 2 shows an example of the FPI generation, showing f_o, 1 − f_i, and the resulting combined FPI f. We see that while f_i has more noise, it has better contrast for some of the smaller vessels. We empirically chose a value of α = 0.5, which provides a good balance between noise and vessel contrast.

Figure 2.

FPIs generated from (a) the outer retina, (b) the inner retina, and (c) their combined FPI.

2.2 Blood vessel segmentation and point extraction

Before registration of the data, we need to extract the blood vessel points from the FPIs. These points are extracted from a binary segmentation of the vessels. An overview of the process is shown in Fig. 3. To do the segmentation, we first resize each FPI to have a roughly isotropic size of 256 × 256 pixels. Next, we process the images by applying background subtraction to reduce inhomogeneity in the images, followed by using a Frangi filter to enhance the vessel structures and reduce the noise.¹² Background subtraction was done by subtracting the image with the morphological closure of the image using a disk structuring element with a radius of 7 pixels. The resulting processed image was rescaled to have intensity values between 0 and 1 and then thresholded at a value of 0.09 to create a binary image containing the vessels. Any connected components with an area of less than 15 pixels were removed to again filter out noisy results. To create the final segmentation, we applied a morphological closing with a disk structuring element with a radius of 2 pixels to the binary image to connect small discontinuities in the vessels. Finally, the vessel points are extracted from the binary skeleton of the segmentation. These skeleton points are used instead of the segmentation directly which both reduces the number of points used for the registration and provides less ambiguity for finding correspondences.

Figure 3.

The processing pipeline for segmenting and extracting blood vessel points from the FPI.

2.3 Vessel registration and lasso regression

To solve the point-based registration problem, we define our two point sets as ${\left\{{\mathbf{p}}_i\right\}}_{i\in \mathcal{ℐ}}$ and ${\left\{{\mathbf{q}}_i\right\}}_{i\in \mathcal{ℐ}}$, where $\mathcal{ℐ}$ = { 1, … n} and n is the number of points. We require that the point correspondences are known meaning that p_i and q_i correspond to the same vessel point for every i. Since the segmentation results in two sets of points without known correspondences, we must first estimate the correspondences between them. To do this, we use the coherent point drift (CPD) algorithm, a deformable point-based registration method.⁵ CPD uses the EM algorithm to find correspondences and is quite robust to the frequent outliers and noisy points we see in our data. Since these correspondences may still have errors, we run the registration and motion correction algorithm twice, estimating correspondences using CPD at the start of both iterations.

While the CPD result aligns the data well, its non-rigid transformation violates the assumption that the transformation between OCT scans acquired from the same subject should be rigid, with an additional scale component to account for camera position. While the deformations introduced by eye motion are non-rigid, they are modeled in a separate way as described later. The rigid plus scale transformation allows rotation, translation, and scaling of the points. A point p_i = (p_i,x, p_i,y)^T from one FPI is related to a point q_i = (q_i,x, q_i,y )^T through the relation p_i = sRq_i + t where s is the scale, R is a 2 × 2 rotation matrix parameterized by a single rotation angle, and t is the translation.

To model the motion correction problem, we assume eye motion results in the displacement of a B-scan’s position relative to the previous one. This assumption is appropriate since images are acquired one at a time, in raster order. We denote the displacement of B-scan image j as γ_j for the first OCT scan and β_j for the second. Note that we assume the same number of B-scan images for each scan, and thus j ∈ {1, …, n_B } for both, where n_B is the number of B-scans. As we are concerned with motion in both the x and y plane (the axes of the FPI), γ_j and β_j each have an x and y component.

To combine the registration and motion correction problems together, we look to minimize the following cost function

$$C=\sum _{i=1}^n\parallel \left({\mathbf{p}}_i+\sum _{j=1}^{\lfloor p_i,y\rfloor }{\gamma }_j\right)-s\mathrm{R}\left({\mathbf{q}}_i+\sum _{j=1}^{\lfloor q_i,y\rfloor }{\beta }_j\right)-\mathbf{t}{\parallel }^2+\lambda \sum _{j=1}^{n_B}(\mid {\gamma }_j\mid +\mid {\beta }_j\mid ).$$ (1)

The term ${\Sigma }_{j=1}^{\lfloor p_{i,y}\rfloor }$ γ_j represents the overall displacement of vessel point p_i based on the cumulative displacement of each B-scan up to that point. Since each point may not lie exactly on a B-scan due to the resizing of the FPI, we use the floor operator ⌊·⌋ in the limit of the summation. The coefficient λ encourages displacement values to be 0 as it gets larger since the L1 norm induces sparsity. It is important to note that if we used a global displacement model instead of a cumulative one, the displacements would no longer be sparse. Sparsity is a desired feature for two reasons. First, eye motion tends to be abrupt during a scan, with infrequent, large displacements. Second, the estimation of displacements for both scans is rather ill-posed. A displacement in one image can be counteracted by an opposite displacement at the same location in the other image (e.g., if γ_j = −β_j and s and R are close to identity). If no displacement truly exists at that point, the sparsity constraint will encourage both coefficients to be zero.

The problem of minimizing Eq. 1 is solved by iterating between solving for the transformation parameters and solving for the displacements until convergence, which usually occurs within 20 iterations. We use a value of λ = 1, empirically set with a preference to keep many of the coefficients set to zero. By careful inspection of Eq. 1, we see that by fixing the displacements and solving for s, R, and t, we have a simple least-squares point-based registration problem. The second term can be ignored as it does not depend on the transformation parameters. In other words, we minimize the reformulated function

$$\tilde{C}=\sum _{i=1}^n\parallel {\tilde{\mathbf{p}}}_i-s{\mathrm{R}}_{{\tilde{\mathbf{q}}}_i}-\mathbf{t}{\parallel }^2,$$ (2)

where ${\tilde{\mathbf{p}}}_i$ and ${\tilde{\mathbf{q}}}_i$ are the motion corrected vessel points. This minimization can be solved in closed form, e.g., using singular value decomposition or Procrustes alignment.¹³ Next, by fixing the transformation parameters, Eq. 1 can be rearranged such that the displacements are estimated by solving a lasso, or L1 regularized regression problem.¹⁴ Specifically, the first term can be rewritten as $\parallel \mathbf{y}-\mathrm{X}\alpha {\parallel }_2^2$ where y = p_i − sRq_i − t, X = − [I₂ ⊗ X₁ −sR ⊗ X₂], α = [γ^T β]^T, and the x and y components of vectors are stacked such that $\mathbf{y}={\left[{\mathbf{y}}_x^{\mathrm{T}}{\mathbf{y}}_y^{\mathrm{T}}\right]}^{\mathrm{T}}$. I₂ is a 2 × 2 identity matrix while the design matrices X₁ and X₂ are n ×|n_B with a structure such that the first ⌊p_i⌋ columns of row i have a value of 1 and the remaining columns have a value of 0. Thus, Eq. 1 reduces to

$$C=\parallel \mathbf{y}-\mathrm{X}\alpha {\parallel }_2^2+\lambda \parallel \alpha {\parallel }_1$$ (3)

which is in the form of a lasso regression and we solve using the Glmnet software package.^{14, 15}

As a final note, we use a phase correlation motion correction method both to initialize the displacements and to use as weights in the lasso regression.¹⁰ Since many of the smaller resulting displacements are due to noise, we ignore any displacement estimates smaller than 3 pixels (≈ 35 µm). We denote the estimated initial translations of a B-scan j as ${\widehat{\gamma }}_{j,x}$ and ${\widehat{\beta }}_{j,x}$, with only the x-component of the displacement estimated. To incorporate these as weights in the lasso regression, we modify the second term of Eq. 1 as

$$\lambda \sum _{j=1}^{n_B}({\nu }_j\mid {\gamma }_{j,x}\mid +\mid {\gamma }_{j,y}\mid +{\eta }_j\mid {\beta }_{j,x}\mid +\mid {\beta }_{j,y}\mid )$$ (4)

with Gaussian-shaped weights ${\nu }_j=\text{exp}-\frac{{\widehat{\gamma }}_{j,x}^2}{2{\sigma }^2}$ and ${\eta }_j=\text{exp}-\frac{{\widehat{\beta }}_{j,x}^2}{2{\sigma }^2}$, where σ = 10. These weights act to reduce the lasso penalty when it takes a small value, thus reducing the sparsity constraint when we have confident initial estimates.

3. EXPERIMENTS AND RESULTS

To examine both the accuracy and consistency of our method, we looked at data from 26 healthy control subjects. Both eyes of all subjects were scanned twice, with the second scan occurring within an hour of the first. In total, 42 of the 52 possible pairs of images were used (considering both eyes), with some pairs not included due to a missing acquisition or poor image quality. Macular OCT data was acquired using a Zeiss Cirrus scanner (Carl Zeiss Meditec Inc., Dublin, CA), with each scan covering a 6 × 6 mm area centered at the fovea. Each scan has 1024 pixels per A-scan, 512 A-scans per B-scan, and 128 B-scans. For each pair of scans, landmark points were manually selected on FPIs at corresponding vessel bifurcations and corners to generate ground truth data for exploring the accuracy of the registration. An average of 37 points were selected from each pair of images, with a range of 18 to 45 points, depending on the complexity of the vessel pattern in each eye.

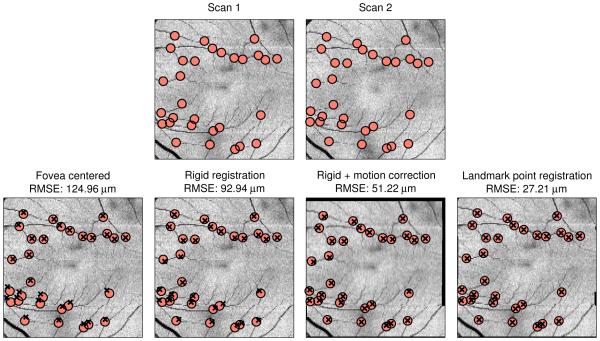
First, we looked at the accuracy of our method. To do this, we compared the average root mean square error (RMSE) of the manually selected landmark points after registration. Three methods of registering the data were compared: 1) alignment to the center of the fovea^∗, 2) the proposed method without motion correction (registration only), and 3) the proposed method (registration plus motion correction). We also ran our method after replacing the automatically segmented vessel points p_i and q_i with the manually selected landmark points. This result provides both an indicator of the best possible performance for our method and also an estimate for how accurately the landmark points can be localized in an FPI. The results are shown in Table 1. Our method showed a significant improvement in accuracy as compared to both of the other methods when using a paired t-test (p < 0.01). Differences between errors when using the segmented points versus the manual points are due to the accuracy of both the vessel segmentation and the correspondence estimation using CPD. An example showing the landmark point alignment after registration using the four methods is shown in Fig. 4.

Table 1.

Root mean square error (μm) of the manually selected blood vessel landmark positions after registration using different methods. Standard deviations are in parentheses.

Fovea alignment	Rigid registration	Rigid reg. + motion correction	Proposed using manual points
59.0 (30.5)	38.3 (19.3)	29.7 (10.8)	19.2 (3.3)

Figure 4.

(Top row) FPIs from two successive scans with corresponding manually selected landmark points overlaid. (Bottom row) Landmark points from Scan 2 overlaid on Scan 1 after registration using different methods. Manual points are marked as red circles and registered points are marked as black ×’s.

An important application of our method is the measurement of retinal thicknesses in longitudinal data. Since the time between scans in our dataset is minimal, we expect the difference in thickness between them to be close to zero. To explore this, we applied a previously developed automated segmentation algorithm to all of the data, segmenting a total of eight layers.¹¹ Looking only at the total retina thickness, we computed the average value within a 5 × 5 mm area centered at the fovea for each scan. The results are shown in Table 2, where we computed the average signed and unsigned change in thickness between the two successive scans. Our method was significantly better (closer to 0) than the other methods when looking at the unsigned values (p < 0.05). Note that we did not compare to the result of our method when using the manual landmark points here since the sparse nature of these points means we are not able to accurately localize B-scan motion (there are fewer landmark points than B-scan images). Thus, the thickness maps are likely to be incorrectly registered in areas where there are no landmark points. Looking at individual layers, we saw no difference when comparing the registration with and without the motion correction, but we did see thickness differences that were significantly closer to zero in the RNFL and GCIP layers when comparing the two registration methods versus fovea alignment (p < 0.05).

Table 2.

Average signed and unsigned difference in total retinal thickness (μm). Standard deviations are in parentheses.

		Fovea centered	Rigid registration	Rigid reg. + motion correction
	Signed	−0.10 (0.82)	−0.08 (0.55)	−0.14 (0.46)
	Unsigned	0.67 (0.48)	0.45 (0.34)	0.37 (0.31)

Finally, in Fig. 5, we show FPIs before and after registration for two subjects with each row showing a different subject. The uncorrected FPIs from the first and second temporal scan are shown in Figs. 5(a) and 5(b), respectively. The same images are shown in Fig. 5(c) and 5(d) after motion correction and registration. Note that motion correction is applied to both scans, while registration is only applied to the second. Figure 5(e) shows the segmented boundaries from each scan after motion correction and registration overlaid on the first corrected FPI only. Motion artifacts are highlighted by arrows and have been corrected after running our algorithm.

Figure 5.

FPIs (a, b) before and (c, d) after motion correction and registration. Motion artifacts are indicated by arrows. In (e), segmented blood vessel points from the first (red) and second (green) scans are overlaid.

4. CONCLUSIONS AND FUTURE WORK

We have developed a method for simultaneous registration and motion correction of longitudinal macular OCT data. Our method has better accuracy when registering longitudinal data compared to only registration, and enables more consistent thickness measurements between scans. While the motion correction did not show significant improvements when looking at specific layer thicknesses, the registration did prove to be important when compared against data aligned only to the fovea. The cohort of data included in our experiments was a healthy one with a minimal amount of motion artifacts. If scans with motion were explicitly included, we expect to see more improvement within each layer when using our method. A critical step for the registration of the data is the segmentation and extraction of the blood vessel points. Currently, this step leads to many points without correspondences, depending on the contrast of the vessels in each FPI. Thus, in future work, we will continue work on improving the segmentation of the vessels. There are also several parameters in the method, including the sparsity coefficient λ, and weight parameter σ, that need to be estimated in a more rigorous cross-validation framework. While the value of λ seems to be rather sensitive for accurately estimating motion, the value of σ is much more robust. Finally, we hope to look at simulated deformation experiments to further validate our methodology, in addition to running the method on data from non-healthy patients where motion may be more severe.