A Penalized Latent Class Model for Ordinal Data

Abstract

Latent class models provide a useful framework for clustering observations based on several features. Application of latent class methodology to correlated, high-dimensional ordinal data poses many challenges. Unconstrained analyses may not result in an estimable model. Thus, information contained in ordinal variables may not be fully exploited by researchers. We develop a penalized latent class model to facilitate analysis of high-dimensional ordinal data. By stabilizing maximum likelihood estimation, we are able to fit an ordinal latent class model that would otherwise not be identifiable without application of strict constraints. We illustrate our methodology in a study of schwannoma, a peripheral nerve sheath tumor, that included three clinical subtypes and 23 ordinal histological measures.

1 Introduction

Schwannomas are benign nerve sheath tumors that occur in one of three clinical settings: as isolated sporadic tumors, in the setting of neurofibromatosis 2 (NF2) or in a recently described disease called schwannomatosis. Patients with these three conditions have different genetic predispositions and prognoses. Distinguishing schwannomatosis from NF2 patients and patients with sporadic tumors remains a clinical challenge (Polliani, et al., 2005). Diagnostic criteria have only very recently been established for schwannomatosis (MacCollin, et al., 2005). In addition, some patients meet the clinical criteria for more than one subset (Baser, et al., 2006). As a result, it is of interest to define unique histological characteristics of schwannomas arising in the different clinical subsets that could aid in diagnosis. The data in this study consist of 16 ordinal and 7 binary histological characteristics of schwannomas, all of which are grouped into nine broad histological features (Table 1). Our first goal is to ascertain whether the patients cluster into a small number of classes that have similar histology; the second is whether these data-driven classes correspond to current clinical diagnosis. The presence of both ordinal and binary data types requires a methodology that can handle mixed data. Furthermore, we wish to incorporate subject matter knowledge, such as histological subsets, into the data analysis.

Table 1.

Schwannoma data

Feature Group	Variable	Type (number categories)
Pattern	*Antoni A	ordinal (4)
	Antoni B	ordinal (4)
	Verocay Bodies	ordinal (4)
	Lobularity	ordinal (4)
	Myxoid Stroma	ordinal (4)
	*Fascicular	ordinal (4)
	Whorling	ordinal (4)
Blood Vessels	Hemosiderin	ordinal (4)
	Thrombosis	ordinal (4)
	Clustered-small	ordinal (4)
	Clustered-medium/large	ordinal (4)
	HyalinizedWalls	ordinal (4)
Inflammation	Macrophages	ordinal (4)
	Chronic Inflammation	ordinal (4)
Axons	Periphery	binary
	Intratumoral	binary
	Splayed	binary
	Bundled	binary
Other	Nerve Edema	binary
Other	Nerve Inflammation	binary
Other	Intraneural Growth Pattern	binary
Other	Protein Pools	ordinal (4)
Other	Cysts	ordinal (4)

List of schwannoma histological variables and associated feature group. The four ordinal categories correspond to 0, 1, 2, or 3 of that feature. An asterisk (*) indicates that the lowest ordinal level (0) was not observed. For all latent class analyses, the two highest ordinal values were collapsed to give C = 3 levels.

High-dimensional data such as the schwannoma data are becoming quite common in biomedical applications. Preliminary analyses indicated that the 23 variables are highly correlated, making multivariate regression techniques unattractive. One multivariate approach to classification analysis is the use of latent class modeling. Since its introduction decades ago (e.g., Lazarsfeld, 1950, McHugh, 1956), latent class modeling has been successfully used for classification in the presence of correlated outcomes. It has been applied to the analysis of psychosocial, biomarker, inter-rater, educational testing, quality-of-life, and genetic data (e.g., Bartholomew and Knott, 1999; Agresti and Lang, 1993; Dayton and Macready, 1988; Bandeen-Roche, et al., 1997; Houseman, et al., 2006). The latent classes (or clusters) are determined by similar responses to several observed binary, nominal, ordinal, or continuous variables, conditional on class membership. A common assumption is that, conditional on class membership, probabilities of response are homogenous over individuals and variables are independent. Thus the unobservable latent classes are assumed to account for the observed association in the variables.

Constrained likelihood methods of parameter estimation have been developed when the number of observed variables is a substantial fraction of the number of observations and local identifiability of model parameters is questionable. Use of equality and inequality constraints of class-specific and latent class parameters enable a parsimonious representation of the latent class model. For example, some authors have set conditional probabilities given latent class membership to be equal for certain variables (Lazarfeld and Henry, 1968; Hoitjink, 1998), and others have constrained them to increase or decrease across classes (Agresti and Lang, 1993; Croon, 1990). This approach is appealing when there are natural constraints for the particular application. However, when the natural constraints are not absolute, this approach offers no flexibility.

Houseman, et al. (2006) developed a penalized approach to categorical latent class parameter estimation for binary data. This allowed them to fit an otherwise unidentifiable latent class model with nominal latent classes, to moderate-dimensional genetic data. Such a model has not yet been developed for ordinal data, which are quite common in biomedical applications such as the aforementioned schwannoma study. Penalization is preferable to the use of explicit parameter constraints in the absence of subject matter knowledge that yields natural restrictions on the probabilities. Even in the presence of natural constraints, the approach allows for more flexibility and large penalties can mimic the application of constraints.

Histological classification for different tumor types uses both a binary system (present, absent) and quantitative 3-level systems (mild, moderate, marked, or few, some, many) depending on the tumor type and the feature. The way to determine the best system is to see which is best at predicting the correct diagnosis by comparing the prediction to the gold standard diagnosis. Many histological classifications evolve with time as researchers compare different different scoring system. The ordinal scoring considered for the schwannoma data performed well at predicting the correct diagnosis, providing a biological rationale for the treatment of latent classes as ordinal. From a statistical point of view, it is natural to consider ordinal latent classes when considering ordinal variables. Agresti and Lang (1993) comment that, ”When observed categorical scale is ordinal, one can further improve model parsimony and obtain simpler interpretations by fitting latent class models that utilize the ordinality.” As the motivating schwannoma data contain a large number of variables relative to subjects, it was not possible to fit an unrestricted, locally identifiable, ordinal latent class model with more than two classes using the approach of Agresti and Lang (1993). We encountered problems with the estimation of parameters for variables for which not every ordinal level was represented. Moreover, the penalized latent class model developed by Houseman, et al. (2006) could not be fit to the dichotomized histological scores, due to the loss of information resulting from dichotomizing the ordinal variables. As a result, the schwannoma data require a new technique for latent class modeling that enables stable parameter estimation. In this paper we develop a penalized estimation method that accommodates both ordinal and categorical variables in conjunction with ordinal latent classes, which are typically assumed when the observed variables are ordinal, and is estimable even in the presence of missing ordinal levels.

Section 2 provides an introduction to latent class models for nominal categorical data and Section 3 presents the latent class model for ordinal data using the linear-by-linear latent class model proposed by Agresti and Lang (1993). Section 4 proposes a penalized latent class model for ordinal data, and Section 5 discusses reparameterization, penalty selection, and selection of starting values for the optimization algorithm. Section 6 presents results of a simulation study and is followed by analysis of the schwannoma data in Section 7. Section 8 concludes with a discussion.

2 Latent Class Model for Unordered Categorical Variables

Since this paper extends penalization from the binary to ordinal setting, this section first presents the latent class model for the case where observed variables are unordered. For each subject i, i = 1, 2, ...,N, we observe M categorical variables, (Y_i1, ..., Y_iM). In the latent class literature, these variables have been called observed, indicator, manifest, item, or response variables. This discussion will adhere to the term variables. We refer to the realization of a variable as a response. Let η_j denote probability of membership of a subject to unobserved latent class j. Let K_i denote the latent class to which subject i belongs, with K_i taking values from 1, ..., J. Note that η_j = P(K_i = j) and ${\sum }_{j=1}^J{\eta }_j=1$. The variables Y_im take on values from {1, ...,C_m} where C_m ≥ 2. We denote the probability distribution of Y_im given latent class as π_mj, with π_mj(c) = P(Y_im = c|K_i = j). Note that we could assume a regression model for this probability to allow for nonexchangeable subjects (Bandeen-Roche, et al, 1997), but to simplify the presentation, we do not do so. For unordered categorical variables, we can parameterize the π_mj(c) as

$${\pi }_{mj}(c)=\frac{exp({\beta }_{\mathit{mjc}})}{1+{\sum }_{l=1}^{C_m-1}exp({\beta }_{\mathit{mjl}})}\text{and}{\pi }_{mj}(C_m)=\frac{1}{1+{\sum }_{l=1}^{C_m-1}exp({\beta }_{\mathit{mjl}})}.$$ (2.1)

The β’s are unknown latent class-specific parameters whose collection is denoted as β = (β₁₁′, ..., β_MJ′), where each β_mj’ is a vector of length C_m – 1 (one parameter for each of C_m – 1 possible responses). Let

$$Y_{im}(c)=\{\begin{array}{ll}1\hfill & \text{if}\text{the}\text{response}\text{level}\text{on}\text{variable}m\text{is}c,\text{i.e.},\text{if}{Y}_{im}=c\hfill \\ 0\hfill & \text{otherwise.}\hfill \end{array}$$

Based on the standard assumption that within latent class, variables are independent, the joint probability of Y_i is expressed as

$$\varphi (y_i)=Pr(Y_{i1}=y_{i1},\dots ,Y_{iM}=y_{im})=\sum _{j=1}^J{\eta }_j\prod _{m=1}^M\prod _{c=1}^{C_m}{\pi }_{mj}{(c)}^{y_{im}(c)},$$ (2.2)

and the log-likelihood for all n observations is

$$L=\sum _{i=1}^{n}log\left\{\sum _{j=1}^J{\eta }_j\prod _{m=1}^M\prod _{c=1}^{C_m}{\pi }_{mj}{(c)}^{y_{im}(c)}\right\}.$$ (2.3)

The model can be fit by maximizing the log likelihood in (2.3) with respect to parameters η_j and β_mj. The log likelihood is easily differentiated to obtain the score equations. Setting the right-hand side of each score equation equal to zero yields the estimating equations for the θ̂ = (η̂₁, ..., η̂_J–1, β̂₁₁′, ..., β̂β_MJ′), which can be expressed as functions of the posterior probabilities of latent class membership, given the observed data. The posterior probabilities are:

$$P(K_i=j\mid Y_i=y_i)={\eta }_j\prod _{m=1}^M\prod _{c=1}^{C_m}{\pi }_{mj}{(c)}^{y_{im}(c)}/\varphi (y_i).$$ (2.4)

The probabilities in (2.4) can be used for the classification of subjects into latent classes, using for example, highest posterior probability, and are calculated in the Expectation step of the Expectation-Maximization (E-M) algorithm (Dempster, et al., 1977). Considering latent class membership as missing data, the score equations can be solved using a variant of the E-M algorithm, which involves iterating between these posterior probabilities and maximum likelihood estimates. In the context of latent class models, this estimation approach is explained in Goodman (1974) and Bartholomew and Knott (1999).

3 Latent Class Model for Ordinal Responses

One way to model ordinal variables is via an adjacent categories logit model. This model specifies a common effect of response level across latent classes. This is a computationally simpler model than alternative models, as it does not involve cumulative probabilities. The linear-by-linear latent class model implies a stochastic ordering of response distributions for ordered classes (Agresti and Lang, 1993):

$$log\left(\frac{{\pi }_{mj}(c)}{{\pi }_{mj}(c+1)}\right)={\alpha }_{mc}+{\delta }_m{s}_{j}c=1,\dots ,C_m-1;m=1,\dots ,M;j=1,\dots ,J,$$ (3.1)

where s_j is a score corresponding to class j. In the absence of any other motivation for class scores, in this paper, we take s_j = j. Conditional on class, α_mc+δ_m is the log odds of response level c relative to c + 1 in latent class 1. δ_m is the log odds ratio of response level c versus c + 1 for a unit increase in ordinal latent class score s_j for variable m. It follows from (3.1) that

$${\pi }_{mj}(c)=\frac{exp({\alpha }_{mc}+{\delta }_m{s}_j)}{1+{\sum }_{l=1}^{C_m-1}exp({\alpha }_{ml}+{\delta }_m{s}_j)}\text{and}{\pi }_{mj}(C_m)=\frac{1}{1+{\sum }_{l=1}^{C_m-1}exp({\alpha }_{ml}+{\delta }_m{s}_j)}.$$ (3.2)

Note that this model is more parsimonious than that given in equation (2.1) because the probabilities are functions of parameters, δ_m and α_mc, that do not depend on latent class. In the ordinal setting the probabilities relate to latent class only through the class score s_j. Although s_j = j throughout this paper, if different subject matter considerations arose, another possibility would be to allow for unequal spacing of latent classes through the score s_j. It is possible to allow s_j to vary between 0 and 1. An example is to standardize the latent class score, s_j = (j – 1)/(J – 1). In this case the scale of δ_m is the same for any chosen J, thereby making the penalty parameter roughly comparable across models with different numbers of classes. This model formulation can accommodate a combination of ordinal and binary variables, such as in the schwannoma example. The log-likelihood contribution for the i^th subject for a latent class regression model with M ordinal and binary variables is written as

$$L_i=log\left\{\sum _{j=1}^J{\eta }_j\prod _{m=1}^M\prod _{c=1}^{C_m}{\pi }_{mj}{(c)}^{y_{im}(c)}\right\}.$$ (3.3)

As for the case of unordered categorical variables, the E-M algorithm, with a Newton-Raphson maximization step, can be used to solve for α, δ, and η, treating the latent variable indicators, k_i, as missing.

4 Penalized Ordinal Latent Class Model

A potential drawback of the ordinal latent class model for high-dimensional data is its large number of parameters. For example, if C_m = C there are M × (C–1) intercepts, M slopes, and J–1 prevalence parameters. The schwannoma data contain 16 ordinal variables with C = 3 (the two highest categories were collapsed to give C = 3 since very few values of ’4′ were actually observed) and 7 binary variables (C = 2), resulting in 64 parameters for a 3-class model. Not surprisingly, with only 84 subjects, we could not obtain a fit using the ordinal latent class model of Agresti and Lang (1993). Estimation of α for variables in which not every response level was observed was particularly problematic in the unpenalized version of the model. Thus when M is a substantial fraction of n, we propose use of a penalized log-likelihood of the form

$$L_c(\alpha ,\delta ,\eta ,{\mathrm{\Lambda }}_1,{\mathrm{\Lambda }}_2)=L(\alpha ,\delta ,\eta )-C(\alpha ,\delta ,{\mathrm{\Lambda }}_1,{\mathrm{\Lambda }}_2),$$ (4.1)

where C(α, δ,Λ₁,Λ₂) is a penalty that depends on δ and α, Λ₁ is a diagonal penalty matrix for the α parameters, and Λ₂ is a diagonal penalty matrix for the δ parameters. Specifically, we consider a ridge penalty of the form, C(α, δ,Λ₁,Λ₂) = α′Λ₁α + δ′Λ₂δ. Maximization of (4.1) directly penalizes α and δ from the model in equation (3.1), with the goal of biasing these estimates toward the null.

Since a one unit change in response level on a binary variable is considered to be qualitatively different from a one unit change in response level on an ordinal variable, we differentially penalize ordinal and binary variables. Thus we allow the diagonal elements of Λ₁ and Λ₂ to differ according to which type of variable that diagonal element penalizes. In the presence of ordinal outcomes, we consider separate penalties for the intercepts and slopes from equation (3.1). The ridge penalty produces an additional term in the score functions for the unpenalized likelihood represented as, ( $\frac{\partial L}{\partial {\alpha }_{mc}},\frac{\partial L}{\partial {\delta }_m}$):

$$\frac{\partial L_c}{\partial {\alpha }_{mc}}=\frac{\partial L}{\partial {\alpha }_{mc}}+\frac{\partial C}{\partial {\alpha }_{mc}},\frac{\partial L_c}{\partial {\delta }_m}=\frac{\partial L}{\partial {\delta }_m}+\frac{\partial C}{\partial {\delta }_m},$$

where $\frac{\partial C}{\partial {\alpha }_{mc}}=2{\sum }_{j=1}^J{\alpha }_{mc}{\lambda }_{1\mathit{mjc}},\frac{\partial C}{\partial {\delta }_m}=2{\sum }_{j=1}^J{s}_j{\delta }_m{\lambda }_{2mj}$, and λ_1mjc and λ_2mj represent the diagonal smoothing parameters of the penalty matrices for δ and α, respectively. In the interest of computational efficiency, we set the penalties to be constant for all j and c. Since we penalize ordinal and binary variables differently, let ${\lambda }_{1m}^o,{\lambda }_{2m}^o$ and ${\lambda }_{1m}^b,{\lambda }_{2m}^b$ be the respective diagonal penalty parameters of Λ₁ and Λ₂ that penalize the ordinal and binary variables. The penalties are allowed to differ for ordinal versus binary variables, but are the same for all ordinal, and for all binary variables, respectively, so hereafter, the ’m’ subscript is dropped. The reparameterization in Section 5 will require a modest expansion of this notation. The penalized likelihood is maximized by an adaptation of the E-M algorithm. Paralleling the ML strategy developed by Bandeen-Roche, et al. (1997), the estimation technique includes a Newton-Raphson step for maximization:

1. Fix J, ${\lambda }_1^o,{\lambda }_2^o,{\lambda }_1^b,{\lambda }_2^b$ and compute posteriors P̃_ij for each subject i.

2. Apply Newton-Raphson to obtain (α̃, δ̃) using a weighted adjacent categories logit model with P̃_ij as weights.

3. Set η̃_j equal to ${\sum }_{i=1}^n{\stackrel{\sim }{P}}_{ij}/n$.

4. Iterate steps 1 through 3 until a convergence criterion is met.

Conditional on the penalties ${\lambda }_1^o,{\lambda }_2^o,{\lambda }_1^b,{\lambda }_2^b$, and the number of classes, J, an estimate of the variance of the estimator (α̂, δ̂, η̂, ) is obtained by Taylor expansion. Fixing the penalty, the variance is $H_c^{-1}nV{H}_c^{-1}$, where H_c is the Hessian matrix of L_c, and V is the asymptotic variance of the score component ( $\frac{\partial L_i}{\partial \alpha },\frac{\partial L_i}{\partial \delta },\frac{\partial L_i}{\partial \eta }$), which is estimated empirically from the data, as in Houseman, et al. (2006).

5 Orthogonal Reparameterization, Penalty Selection, and Starting Values

In the schwannoma study there is a natural grouping of the histological variables into 9 broad features of tumor cells. Six features contain ordinal and 3 contain binary variables, as seen in Table 1. Because of this structure, we choose an orthonormal reparameterization to directly contrast these broad features and apply the penalty to the reparameterized parameters, allowing important feature contrasts to be penalized less than detail contrasts. In the strictly binary setting, such a reparameterization improved the predictive power of the model (Houseman, et al., 2006). It is desirable to leave a term unpenalized so that classes can be distinguished in mean response, i.e., so that there is a parameter that represents the average α and δ over all m. This is accomplished by allowing the first vector of the orthonormal matrix to be a vector of constants. Hereafter, the term “feature contrasts” refers to vectors of the orthogonal contrast matrix that contrast the 9 groups of variables, or features, and the term “detail contrasts” refers to the supplemental vectors of the M × M orthonormal matrix. To motivate the transformation, first note that equation (3.2) can be written as

$${\pi }_{mj}(c)=\frac{exp(x_m^{\prime }{\alpha }_m+x_m^{\prime }\delta s_j)}{1+{\sum }_{l=1}^{C_m-1}exp(x_m^{\prime }{\alpha }_l+x_m^{\prime }\delta s_j)}\text{and}{\pi }_{mj}(C_m)=\frac{1}{1+{\sum }_{l=1}^{C_m}exp(x_m^{\prime }{\alpha }_l+x_m^{\prime }\delta s_j)},$$ (5.1)

where x_m is a unit vector of length M with a 1 in the m^th place, α_c is a length M vector, and δ is the length M vector (δ₁, ..., δ_M)’. In order to implement penalization, we generalize x to include any set of vectors {x_m} such that $x_m^{\prime }{x}_l=1$ if m = l and zero otherwise. Let U = (x₁, ..., x_M) represent an orthonormal matrix of dimension M ×M, such that U′U = I. The matrix U can is chosen such that elements represent contrasts between features of interest. In the presence of mixed variable types as in the schwannoma example, to accommodate M₁ ordinal, and M₂ binary variables, allow U to have a block diagonal structure, where the first block contains M₁ orthogonal contrasts and the second contains M₂ orthogonal contrasts. More specifically, the first block of U contains the 6 orthogonal contrasts of interest for ordinal variables (an “intercept” term that allows for a mean response plus 5 feature contrasts), which are supplemented using Gram-Schmidt orthogonalization with 10 detail contrasts, for a total of M₁ = 16 vectors. Similarly, the second block of U contains the 3 orthogonal contrasts of interest for binary variables, which are supplemented with 4 detail contrasts. Penalization is then performed on the transformed parameters, Uα and Uδ. The penalty term is then: C(α, δ,Λ₁,Λ₂) = α′U′Λ₁Uα + δ′U′Λ₂Uδ, where the feature-based parameterization of the linear model allows us to further decompose Λ₁ and Λ₂ in order differentially penalize features and details, and ordinal and binary variables. To illustrate this, let the diagonal penalty matrix ${\mathrm{\Lambda }}_1=a_r^o{\stackrel{\sim }{\mathrm{\Lambda }}}_r^o+a_s^o{\stackrel{\sim }{\mathrm{\Lambda }}}_s^o+a_r^b{\stackrel{\sim }{\mathrm{\Lambda }}}_r^b+a_s^b{\stackrel{\sim }{\mathrm{\Lambda }}}_s^b$, where ${\stackrel{\sim }{\mathrm{\Lambda }}}_r^o$ is an M₁ × M₁ diagonal matrix with ones on the diagonals corresponding to ordinal feature contrasts and zeros elsewhere, ${\stackrel{\sim }{\mathrm{\Lambda }}}_s^o$ is an M₂ × M₂ diagonal matrix with ones on the diagonals corresponding to the ordinal detail contrasts and zeros elsewhere. Similarly, ${\stackrel{\sim }{\mathrm{\Lambda }}}_r^b$ is a diagonal matrix with ones on the diagonals corresponding to binary feature contrasts and zeros elsewhere, and ${\stackrel{\sim }{\mathrm{\Lambda }}}_s^b$ is a diagonal matrix with ones on the diagonals corresponding to the binary detail contrasts and zeros elsewhere. We can decompose the penalty matrix for δ in the same way; ${\mathrm{\Lambda }}_2=a_t^o{\stackrel{\sim }{\mathrm{\Lambda }}}_t^o+a_u^o{\stackrel{\sim }{\mathrm{\Lambda }}}_u^o+a_t^b{\stackrel{\sim }{\mathrm{\Lambda }}}_t^b+a_u^b{\stackrel{\sim }{\mathrm{\Lambda }}}_u^b$. If $a_r^o<a_s^o$ and $a_r^b<a_s^b$, then the penalty matrix Λ₁ constrains α for the detail contrasts more than the feature contrasts. The same logic holds for $a_t^o<a_u^o,a_t^b<a_u^b$, Λ₂, and δ.

Because we separately penalize intercepts versus slopes, features versus details, and ordinal versus binary variables, there are a total of 8 penalties, which necessitates a careful search methodology in the interest of computational efficiency. To accomplish this, we first fit the model with only ordinal data, which requires that we search over 4 penalty parameters. Treating as fixed the optimal penalties obtained for the ordinal variables, we then fit a full model including the binary data, and search for the remaining penalties. In our experience, we have found that results depend little on the exact value of the penalties and more on their magnitude.

The choice of smoothing parameter(s) can be informed by using an analog to the Bayesian Information Criterion (BIC), adapted to the present latent class setting:

$$\text{BIC}=tr(H_c^{-1}nV)\text{log}(n)-2L(\eta ,\alpha ,\delta )$$

The criterion penalizes models with more parameters, which are calculated as an effective degrees of freedom, $df=tr(H_c^{-1}nV)$, where V is an estimate of the asymptotic variance of the score component. In high dimensions, nV should be estimated empirically from the data. BIC has previously been used in latent class model selection for non-nested models, such as those with varying J (Lin and Dayton, 1997), and tends to give consistent results. Houseman et al. (2005) showed that BIC was superior to several other information criteria in selecting the number of latent classes. Thus we use BIC in the schwannoma application for selecting both the number of classes and the smoothing parameters.

Several authors have addressed the sensitivity of the maximum of the log-likelihood, L, in equation (4.1) to the choice of initial values supplied to the optimization algorithm (Bandeen-Roche et al., 1997; Huang, et al., 2004). The model proposed in section (3.1) is not globally identifiable and in our experience, the E-M algorithm may converge to multiple maxima. We have found via simulation that when there exists large separation between class-specific probabilities, it is usually sufficient to obtain reasonable estimates for class-specific probabilities from a univariate adjacent categories logit regression of observed variables Y_i against an estimate of latent class membership K_i. To estimate K_i, we have had success using various clustering algorithms including K-means and hierarchical clustering. In this paper we use the divisive hierarchical clustering function DIANA, which is part of the R library “cluster”. For each of these algorithms, the number of clusters is set to the number of classes, J, for the model we wish to fit. Posterior weights are input directly into the E-M algorithm by slightly perturbing the cluster assignment. In the case where the log-likelihood from equation (4.1) is flat, i.e., where conditional probabilities do not vary markedly over ordered latent classes, several E-M iterations using starting values obtained from different clustering procedures should be used to assess convergence to a local maximum, as different starting values often converge to different maxima. The proper solution can be determined by observing to which solution the algorithm converges for various starting values, and noting whether the Hessian matrix of the penalized likelihood, H_c, is positive definite, as this indicates whether that model is identifiable at this point in the parameter space. For the schwannoma application, we used this suggested method. For the following simulations, it was sufficient to obtain starting values from the DIANA algorithm only.

6 Simulations

To study the behavior of our proposed methodology for data similar to the schwannoma data, we conducted a simulation study. Since three clinical subsets of schwannoma were of interest, we simulated a 3-class model. Table 2 reports results obtained from fitting a penalized 3-class ordinal model to each of 250 simulated data sets, each with n = 100 subjects, M = 10 observed variables, and C = 3 ordinal categories. In these simulations we did not use the feature parameterization, but instead used an orthogonal polynomial transformation, and we chose to penalize only the reparameterized δ_m’s for computational simplicity. Similar to the schwannoma reparameterization, this allows us to penalize the differences from a common delta. We left the α’s unpenalized. The model was fit for 6 different values of one smoothing parameter applied to the reparameterized δ_m’s, for two simulation settings: one in which all δ_m’s equal −1.1, and one in which δ_m’s vary uniformly within [−1.2, −0.8]. We chose these cases to observe the effect of the smoothing parameter under two scenarios: one when the latent class-variable association is equal across variables (case 1), and the other when it differs across variables (case 2). Both cases result in substantially different classes, characterized either by the same (case 1) or different (case 2) effects of each variable conditional on latent class. Case 1 is quite similar to the inter-rater agreement example analyzed by Agresti and Lang (1993). Case 2 corresponds to what we would expect to see with the schwannoma data; the 23 variables have different associations with latent class. We would expect the methodology to be more beneficial in improving prediction when there is variation in association with latent class across variables. As expected, in both cases the introduction of the penalty decreases root mean square error (MSE) and likelihood loss (LL) (e.g., Houseman, et al, 2005). In case 1, both measures decrease monotonically and plateau near λ₂ = 0.5 (note that there is no superscript on λ₂, which represents the diagonal elements of the penalty matrix Λ₂ from section 4, since only ordinal variables are simulated). Since we penalize the difference from a common δ toward zero, a high penalty on this parameter is synonymous with constraining all slopes to be equal, thus we expected a general decline in these measures for data simulated according to equal δ_m’s. The slight increase in MSE in case 1 for λ₂ = 5 might be due to the fact that although starting values obtained for each simulated data set led to convergence for small λ₂, they may not for a penalized model with a large λ₂, as this model is quite different from the unrestricted model under which the data were generated. As λ₂ increases, it may be necessary to use a variety of different starting values; however, this was not feasible in the simulation study. In case 2, there is a more marked reduction in MSE and LL than for case 1. This decrease plateaus near λ₂ = 0.1, which implies that a small penalty is optimal in this case. As expected, in case 2, for higher penalties, both measures slowly increase as the model becomes too simplistic to describe the data. The trend in MSE and LL demonstrates the bias-variance tradeoff, as controlled by the smoothing parameter, λ₂, and shows that these data benefit from the introduction of a small-valued penalty.

Table 2.

Summary of evaluation criteria for simulations with penalized δ

λ1	Case 1: Equal δ			Case 2: Varying δ
	MSE	LL	N	MSE	LL	N
0.001	0.208	18.45	248	0.240	19.48	244
0.01	0.192	18.40	247	0.217	19.38	244
0.1	0.171	18.34	249	0.185	19.25	244
0.5	0.152	18.30	249	0.184	19.21	245
1.0	0.147	18.30	249	0.187	19.21	246
5.0	0.150	18.28	247	0.192	19.20	249

Summary of evaluation criteria applied to 3-class penalized ordinal latent class analysis of 250 simulated data sets. Six penalties were considered for two cases: one in which the components of δ were the same and another in which they varied. For both cases, M = 10, J = 3, and C = 3. N represents the number of simulated data sets out of 250 that converged to a maximum for each of the two cases.

MSE = root mean squared error, {Σ_j(η̂_j – η_j)² +Σ_jΣ_mΣ_c(π̂_mj(c) – π_mj(c))²}^1/2

LL = likelihood loss, –{Σ_jΣmΣc η_j [π_mjlogπ̂_mj + (1 – π_mj(c))log(1 – π̂_mj(c))]}

The study demonstrates the benefit of penalization when the effect size differs across observed variables, similar to the situation observed in the schwannoma data, and gives us an indication of the size of the penalty on δ that might be optimal for the schwannoma data. Since the methodology penalizes the differences from a common delta, there is a steep decline in MSE for unequal δ_m’s, as the methodology pushes these toward a common value. For very large values of λ₂ (greater than 10, not shown here), the classes became too similar, and presumably the model became too simplistic to estimate parameters (i.e., it is estimating a common slope across all M variables). This was evidenced by the fact that with a large λ₂, many more simulations failed to converge to the expected maximum for the 3-class model, implying that a 2- class model was more appropriate. Thus for our application, we consider λ₂ ≤ 5.

There were a few simulated data sets for which the starting values converged to a solution whose Hessian was not positive definite as indicated by N in Table 1. For example, at the smallest penalty value of 0.001, 2 simulated datasets under Case 1 conditions, and 6 simulated datasets under Case 2 conditions, did not converge to a maximum. Application of mid-ranged values of the penalty stabilized estimation in Case 1, and a slightly higher penalty stabilized estimation in Case 2, showing that penalization is effective even in the case where M is moderate compared to the sample size, n.

7 Application

In this section, we consider data on 84 peripheral schwannomas obtained from 59 patients previously characterized clinically and by molecular analysis as sporadic, NF2-associated, and schwannomatosis-associated tumors (Poliani, et al., 2006). The tumors were obtained from the Neurofibromatosis clinic at Massachusetts General Hospital. Twenty-six ordinal and binary histological variables were measured in the schwannomas and 23 variables (16 ordinal and 7 binary, see Table 1) showed enough variation to be considered in our analysis.

It is desirable to fit a 3-class model since there are three schwannoma diagnoses of interest. The penalized latent class model from Houseman, et al. (2006) with J = 3 could not be fit to the binary version of the schwannoma data (with responses of 1, 2, or 3 combined into one level). An adequate solution could not be obtained for the several starting values that were supplied. Instead results implied that either a 1 or 2-class model was more appropriate. We also applied the unpenalized ordinal latent class model to the data and could not obtain a fit. Again, despite several initial values supplied to the algorithm, an adequate 3-class model with positive-definite Hessian matrix could not be obtained. Thus not only was it essential to fully utilize the ordinality of the variables in order to fit the desired 3-class model, but penalization in the context of ordinal variables was necessary to obtain a fit. Applying a ridge penalty of 0.0001 for features and 0.001 for details to intercept and slope parameters enabled a sensible ordinal latent class model to be fit to the schwannoma data.

We considered two and three class penalized models (J = 2 and J = 3) for the schwannoma tumor data. Ordinal levels 0, 1, and 2 in the following analysis refer to 0, 1, and (2 or 3) of that particular trait. The 7 binary variables corresponded to a yes or no (1 or 0 respectively) for the presence of the binary characteristics represented in Table 1. As shown in table 1, the histological characteristics of schwannomas are grouped into nine broader categories of histological features including growth pattern, malformed or abnormal blood vessels, inflammation, trapped axons, as well as an “other” category containing five features: nerve edema, nerve inflammation, intraneural growth pattern, and presence of protein pools and cysts. We contrasted these features as described in Section 5. Thus C = 3 for ordinal and C = 2 for binary variables. In order to stabilize estimation, we penalized both the intercepts and slopes in the context of the feature-based parameterization from Section 5. Feature contrasts were penalized less than detail contrasts, requiring a grid search over the feature and detail penalty parameters for α and δ: $a_r^o,a_s^o,a_t^o$, and $a_u^o$, where $a_r^o<a_s^o$ and $a_t^o<a_u^o$. For features, we considered: (0.0001, 0.001, 0.005, 0.01, 0.05, 0.1, 0.2, 0.5, 1, 2), and for details we considered: (0.001, 0.005, 0.01, 0.05, 0.1, 0.2, 0.5, 1, 2, 5), where features were constrained to be less than detail penalties, for both ordinal and binary variables. Given the tradeoff between accuracy and computation time, using a coarse grid of values to search for the smoothing parameters was more efficient than performing an exhaustive search since we have found that the shrinkage depends more on the magnitude of penalty parameters than the exact values. We chose the optimal penalty parameter by minimizing BIC.

In the first stage of model-fitting, we obtained optimal penalty parameters by fitting a penalized latent class model to the ordinal data. Conditional on these penalties, in a second stage, we performed the same grid search for the penalty parameters for the binary variables, with the ordinal variables included in the model. The first stage model fit to the ordinal data only implied that a three class model was a better fit, and that small penalties for features and details were optimal to stabilize estimation; that is, $a_r^o=a_t^o=0.0001$ and $a_s^o=a_u^o=0.001$. Holding these penalties constant, the penalized model fit with both ordinal and binary variables yielded a similar result where the 3-class model was superior to the 2-class model (lowest 3-class BIC = 2605.9, df = 58.0 and lowest 2-class BIC = 2848.9, df = 97.0), and where the optimal penalty parameters for the binary variables were $a_r^b=a_t^b=0.0001$ and $a_s^b=a_u^b=0.001$. This result is supported by the case 2 simulations in Table 2, as the bias introduced by larger penalties becomes too severe when the effect of observed variables on classes differs.

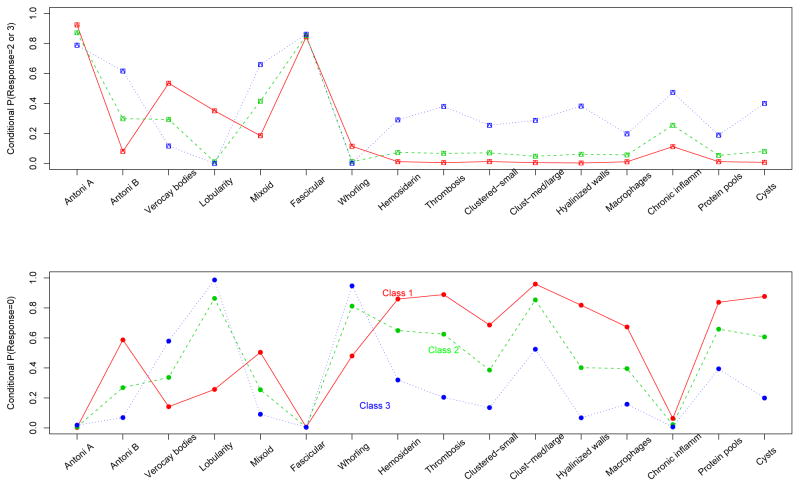
The conditional probabilities of response levels 2 and 3 for the optimal 3-class model are illustrated in the first panel of Figure 1 and probabilities of response level 0 are illustrated in the second panel. The class prevalences are 0.26, 0.38, and 0.36 for classes labelled in the figures as 1, 2, and 3 respectively. Figure 1 shows that membership in the third class is evidenced by a higher conditional probability of observing a response of 2 or 3 than the other two classes, for several of the variables. The variables that lead to this distinction include the five variables in the malformed or abnormal blood vessels group: hemosiderin, thrombosis, clustered-small blood vessels, clustered-medium/large blood vessels, and hyalinized blood vessels, as well as the presence of cysts. A similar, reversed pattern is seen in the second panel of 1 where class 3 is least likely to exhibit none of those features, class 2 is more likely, and class 1 is most likely. The backtransformed δ_m’s (and standard errors as obtained from the formula in Section 4), which demonstrate the strength of association between observed and latent variables are, respectively: −1.05 (0.307), −1.42 (0.351), −1.16 (0.278), −1.14 (0.235), −1.81 (0.348), −1.36 (0.266). It is notable that the results imply a class distinction that is at least partially driven by the five histological variables in the “malformed or abnormal blood vessels” feature group. Class 2 has a very low probability of response 2 or 3 for these variables (~ 0.07 or less for all variables), while these histological variables are not present at all in subjects belonging to class 1 (~ 0 probability for all variables).

Figure 1.

Conditional histological probabilities of response 2 or 3 for ordinal variables among schwannoma patients - best fit with ridge penalty.

Upper panel: Conditional probabilities of observing response 2 or 3 for the 16 ordinal variables obtained from fitting a penalized ordinal latent class model to the schwannoma data. Lower panel: Conditional probabilities of observing response 0 for the 16 ordinal variables obtained from fitting a penalized ordinal latent class model to the schwannoma data. The ridge penalty is applied to α and δ, for each of 16 ordinal and 7 binary variables for schwannoma tumors.

Overall, 66/84 patients had posterior probabilities (equation (2.4)) greater than 0.80, and 73/84 patients had posterior probabilities greater than 0.70; thus in general, most subjects belonged to a latent class with very high posterior probability. To determine how well the above-mentioned variables predict latent class assignment, it was natural to look at the posterior probabilities for those who had these present, and those who did not. For the 10 subjects who scored greater than two on three or more of the six symptoms that most distinguished latent class membership, their posterior probabilities of membership in class 3 ranged from 0.92 to 1.0, and 8 of these actually had a probability of 1.00. Similarly, for the 15 subjects who did not have any of these features present, 9 had a posterior probability of 1.00 of belonging to latent class 1, 2 had probabilities of 0.67 and 0.76, and 4 were more likely to be classified into the second latent class. Thus, there would be a low misclassification rate if one were to base classification on either the presence or absence of these 6 variables.

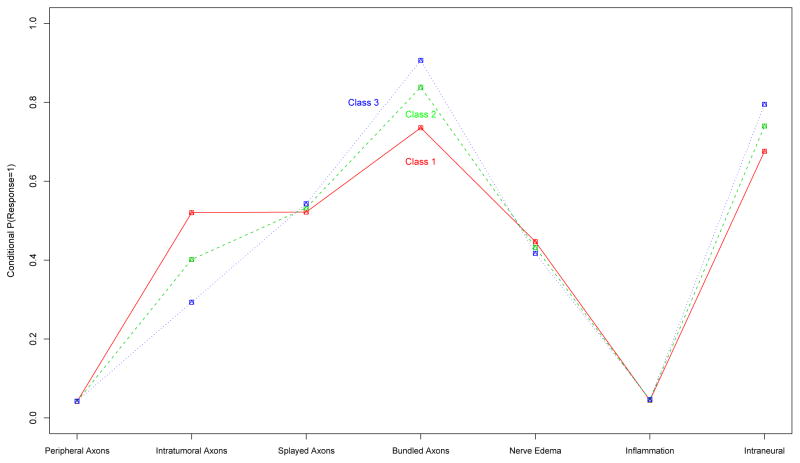
Figure 2 shows the conditional probability of response for each of the binary variables. As none of the binary variable appeared to be associated with latent class, we checked the validity of this result by fitting the model with only the 16 ordinal variables, and used these results to analyze the binary variables. A weighted univariate logistic regression was considered with the binary variable as the dependent variable, ordinal latent class as the independent variable, and posterior probabilities of latent class membership obtained from the ordinal only model, as weights. All resulting logistic regression coefficients were insignificant at the 0.10 type I error rate, suggesting that these variables (peripheral, intratumoral, splayed, and bundled axons, nerve edema, inflammation, and intraneural axons) are not associated with the class structure determined by the 16 ordinal variables. Thus, it is not surprising that when all variables are included together, the binary variables are still unrelated to class structure.

Figure 2.

Conditional histological probabilities of response (success) for binary variables among schwannoma patients - best fit with ridge penalty.

Conditional probabilities of response (success) for 7 binary variables obtained from fitting a penalized ordinal latent class model to the schwannoma data. The ridge penalty is applied to α and δ, for each of the 16 ordinal and 7 binary variables for schwannoma tumors.

Subjects were assigned to classes based on their highest posterior probabilities and we cross-tabulated these with the clinical diagnosis of the three subsets of schwannoma in Table 3. The table indicates that the latent class methodology was best at distinguishing NF2 tumors from the other types but had difficulty discerning schwannomatosis from sporadic tumors. We note that 13 out of 21, or 62% of those diagnosed with NF2 associated tumors were assigned to class 1; thus subjects with NF2 had a high probability of exhibiting the blood vessel feature group ( Figure 1). Coincidentally, 62% of those assigned to Class 1 had NF2 tumors. Classes 2 and 3 were indistinguishable from each other with regard to their compositions of clinical diagnoses. Only 4/32 Class 2 and 4/31 Class 3 tumors were NF2. To formally quantify how well latent classes correlate with clinical subsets, we performed a weighted adjacent categories regression with imputed latent class as the outcome and diagnosis as the predictor. Included in the model were three rows for each tumor, corresponding to diagnosis, each weighted by that tumor’s posterior probability of latent class membership. Results indicated that diagnosis is significantly associated with latent class (p=0.002). While latent classes do not correlate perfectly with clinical diagnosis, the latent class methodology does provide histological profiles of schwannoma patients that offer an additional tool for the diagnosis of a disease that is difficult to diagnose.

Table 3.

Cross-classification of latent class membership with clinical diagnosis

Class	Schwannomatosis	NF2	Sporadic
1	6	13	2
2	19	4	9
3	18	4	9

P-value from weighted ordinal regression model is 0.002

8 Discussion

We have shown that the introduction of a ridge penalty to the feature-based parameterization of class-specific response probabilities allows us to fit an ordinal latent class model to the high-dimensional schwannoma data, which cannot be fit by unconstrained methods for ordinal or binary variables. In the context of ordinal latent class models, the ridge penalty results in a continuous variable selection procedure without imposing unrealistic or inflexible constraints on coefficients employed by existing ordinal latent class models. We note that constraining all variables to be equally associated with latent class, which has been used by several researchers as the constraint of choice for high-dimensional data (Hoitjink, 1998; Meulders, et al., 2002; Agresti and Lang, 1993), is analogous to applying a large penalty to the transformed δ_m’s with unpenalized intercepts. Agresti and Lang (1993) reported results of a constrained ordinal latent class model that was fit to inter-rater agreement data where M = 7, C = 3, and J = 2. In that analysis, δ_m’s were constrained to be equal across all 7 binary variables (raters). Our penalized likelihood approach applied to their data achieved the same results by setting ${\lambda }_2^o=5$ and leaving α unpenalized. The advantage of the penalized likelihood method, however, is that we can allow the data, rather than the researcher, to drive the level of smoothing necessary to obtain a fit. This way, strong assumptions regarding observed variables are not required to obtain an adequate fitting, parsimonious model for high-dimensional data.

In section 3 we introduced a latent class score s_j into equation 3.1. We used s_j = j and considered testing its appropriateness by fitting a penalized latent class model with categorical latent class and ordered variables. This corresponds to unequal spacing between latent classes, and would be the most relaxed score possible. We fit the categorical latent class model for the dichotomized ordinal outcomes but could not achieve convergence for this model. Realizing it was unlikely that we would achieve convergence using ordinal outcomes and assuming categorical latent classes (as this model has many more parameters), we decided a linear score makes sense for both substantive and pragmatic reasons.

We have addressed some challenges in choosing the smoothing parameter for the δ_m coefficients obtained from the model described in Section 4, although some still remain. Latent class literature has addressed joint modeling of binary, nominal, ordinal, and continuous variables (e.g., Moustaki and Papageorgiou, 2005). In biomedical applications, qualitatively different ordinal and nominal variables may be measured. For example, for some schwannoma patients, nominal genotypic data may be available, and NF-2 tumors are thought to be associated with genotype. Our penalized method handles all types of categorical data and applies different penalties to binary versus ordinal data. The problem of how to choose appropriate penalties for nominal parameter estimates, as well as how to relate an ordinal latent class to nominal variables, remains for future investigation. Furthermore, it would be interesting to apply different penalties to parameters representing different response levels. For fitting models with J > 3 in which we allow a regression of fixed covariates on the latent class indicator (as in Bandeen-Roche, et al., 1997), it might also be beneficial to consider a penalty on the resulting η_j, or prevalence parameter. We not that in our application, a sensitivity analysis showed that the choice of penalty parameter does not drastically affect inference or classification.

Our latent class modeling was a form of unsupervised clustering. Following estimation of the model, we evaluated the association between the derived estimated latent classes and clinical diagnosis. Alternatively, a supervised clustering approach would be of interest when the goal is to use the variables to improve prognosis. We could incorporate the clinical outcome into the latent class model, along the lines of Larsen (2004). In this setting, latent class and clinical endpoint conditional on latent class, are jointly modeled. We could accommodate the high dimensionality with a penalty on the parameters resulting from both the latent class part of the model and the survival part of the model. To model the survival outcome, we could consider a Cox model, or even a general class of transformation models (Cheng, 1995).

Inferences from Table 8 hinge on the idea that the “true” diagnosis of these patients is known and that there is no misclassification by physicians. We thus remark that the clinical criteria used for classification into the three clinical subsets were very strict. The NF2 cases satisfied the strictest criteria for clinical diagnosis of NF2 (there are currently four different criteria sets and the most strict ones were used). Similarly, schwannomatosis and sporadic cases satisfied the most strict criteria for clinical diagnosis. They were identified using thin MRI, which is the most sensitive method available. While there is a remote possibility that a patient was misclassified, the techniques and strict criteria used are the best classification based on the available clinical methods to date.

Overall, we have demonstrated that penalized latent class models are effective for classification based on a large number of outcomes and a small to moderate number of subjects, even though they may not correlate well with clinical diagnosis. They are appealing to subject-matter investigators for their clear interpretations. Finally, as they are model-based, they allow for formal comparisons and inference.