Significance
Nearly three decades ago, seismologists discovered peculiarly dense and slow patches just above Earth’s core−mantle boundary (CMB), known as the ultralow velocity zones (ULVZs). The origin of the ULVZs has remained enigmatic because silicate partial melt models face challenges in accounting for the nonubiquitous occurrence of ULVZs and explaining the observed density excess, whereas iron-rich solid models may have difficulty reproducing the sound velocity observations. Here we propose hypotheses involving slab-derived metallic melt as a critical component to explain the density and velocity features of the ULVZs. These hypotheses differ fundamentally from existing models and may provide insights into the influence of the deep carbon cycle on Earth’s dynamics.
Keywords: core mantle boundary, iron−carbon melt, subduction, deep carbon cycle, diffuse scattering
Abstract
Understanding the ultralow velocity zones (ULVZs) places constraints on the chemical composition and thermal structure of deep Earth and provides critical information on the dynamics of large-scale mantle convection, but their origin has remained enigmatic for decades. Recent studies suggest that metallic iron and carbon are produced in subducted slabs when they sink beyond a depth of 250 km. Here we show that the eutectic melting curve of the iron−carbon system crosses the current geotherm near Earth’s core−mantle boundary, suggesting that dense metallic melt may form in the lowermost mantle. If concentrated into isolated patches, such melt could produce the seismically observed density and velocity features of ULVZs. Depending on the wetting behavior of the metallic melt, the resultant ULVZs may be short-lived domains that are replenished or regenerated through subduction, or long-lasting regions containing both metallic and silicate melts. Slab-derived metallic melt may produce another type of ULVZ that escapes core sequestration by reacting with the mantle to form iron-rich postbridgmanite or ferropericlase. The hypotheses connect peculiar features near Earth's core−mantle boundary to subduction of the oceanic lithosphere through the deep carbon cycle.
Ultralow velocity zones (ULVZs) occur as isolated patches near the core−mantle boundary (CMB) and are generally associated with the large low shear velocity provinces (LLSVPs) (1, 2). The nonubiquitous distribution of ULVZs gives evidence for thermal and/or chemical heterogeneities at the base of the mantle (3, 4). The density excess of ULVZs likely arises from iron enrichment (5–7), whereas the velocity anomalies may indicate partial melting (3, 4, 8, 9) or iron enrichment (5–7). Elucidating the origin of ULVZs is therefore important for understanding the thermal and chemical state of the CMB, which, in turn, holds a key to unraveling the evolution history and dynamics of deep Earth.
Given uncertainties in the melting behavior of mantle rocks (10), elastic properties of relevant phases (11, 12), and iron partitioning between them (13, 14), the origin of ULVZs remains enigmatic. Partial melt of silicate composition has been widely considered as the origin of ULVZs because the presence of partial melt reduces shear wave velocity (Vs) effectively, and partial melt was found to be denser than coexisting solids at deep mantle conditions (e.g., refs. 4, 13, 15, and 16). Models involving silicate partial melt face several challenges. First, the solidus temperatures of silicate compositions happen to fall into the ±500 K uncertainty margin of the CMB temperature. Consequently, nonubiquitous partial melting of a silicate composition critically depends on thermal structure of the lowermost mantle, and the presence of chemically distinct components is often invoked to explain the occurrence of patchy melts near the CMB. Given the controversy over the mantle solidus (3, 8–10) and CMB temperatures (17), these models are still under debate and remain to be tested. Second, Nomura et al. (13) found that silicate liquid is, at most, 8% denser than the coexisting solids, and therefore only fully molten pockets can marginally match the density excess of ULVZs, which would then give rise to a vanishing Vs that is too low to match the seismic observations. Similarly, Thomas et al. (18) concluded that residual liquids produced in a whole-mantle magma ocean are not dense enough to remain at the CMB on geological timescales. Furthermore, Thomas and Asimow (19) showed that dense silicate melt must be removed from its equilibrium solid matrix to combine with a denser solid to match the density excess of ULVZs.
Iron-rich solid phases such as wüstite, postbridgmanite, or iron silicide have been proposed as alternative origins of ULVZs (e.g., refs. 5–7, 10, and 20). Candidate sources for iron enrichment include the core or core sediments, residual liquids from a putative basal magma ocean, or subducted banded iron formation. It remains unknown or controversial if iron-rich solids with required composition and properties can be produced near the CMB. For instance, Knittle and Jeanloz (20) attributed ULVZs to FeSi and FeO as core−mantle reaction products although a subsequent study did not produce FeSi from reaction between bridgmanite and molten iron (21). Some of these models showed that simultaneous match of density (ρ), compressional wave velocity (Vp), and Vs can be achieved for certain compositions at 300 K (7), but recent theoretical studies concluded that, at high temperatures, iron-rich wüstite or bridgmanite could not reproduce both Vp and Vs (11, 12).
Seismic tomography revealed that subducted slabs sometimes penetrated the transition zone to reach the CMB (22). Carbonates in the crustal portion of the slab may melt at the mantle wedge or in the transition zone and return to shallow depths (23, 24). On the other hand, the slabs that sank beyond the depth of 250 km are expected to contain metallic iron as a result of stabilization of ferric iron in pyroxene, garnet, or bridgmanite (25–27), plus elemental carbon or carbide through the reduction of carbonates by the metallic iron (28). To assess whether an iron−carbon mixture carried by slabs to the lowermost mantle would contribute to the origin of ULVZs, we investigated the melting behavior of the Fe−C system under the pressures of the lower mantle.
Results and Discussion
X-ray diffraction (XRD) images of mixtures of iron and Fe3C were collected at pressures between 25 GPa and 138 GPa and temperatures up to 3,520 K (Methods and Fig. S1). Upon heating, the Debye−Scherrer rings from Fe3C and hexagonal close-packed ε-Fe powders became sharper and then lost continuity and further evolved to single-crystal spots due to grain growth (Fig. S2). Approaching the eutectic melting temperatures, large single-crystal spots of a given set of lattice planes disappeared and reappeared at different positions in successive XRD images, reflecting fast grain rotation (3, 17). At higher temperatures, an elevated baseline in the integrated XRD spectrum indicated the appearance of a diffuse scattering signal (Fig. 1). At the same time, the volume of solid iron started to plateau with respect to temperature (Figs. S3 and S4), as seen in the melting experiments on pure iron and attributed to preferential absorption of heat by a thin layer of liquid with respect to the overlying solid (17). The simultaneous occurrences of the diffuse scattering signal and volume plateau provide robust evidence for the onset of melting. In the pulsed heating experiments, the intensity of the diffuse scattering signal increased upon further heating, as expected. This is not the case with the continuous heating experiments, probably because melt migrated out of the hot spot. At higher temperatures, the intensities of the observed single-crystal spots of both Fe and Fe3C became smaller (Fig. S2). In two pulsed heating experiments, the reflections of Fe3C eventually disappeared, leaving solid Fe to coexist with the liquid as the liquidus phase. In other pulsed heating and all of the continuously heating experiments, the reflections of crystalline Fe and Fe3C, possibly from solid phases located in the long tails of the X-ray beam away from the laser-heated spot, persisted to the highest attained temperature. The persistence of crystalline diffraction peaks beyond the melting point was also observed in the experiments on iron melting (17).
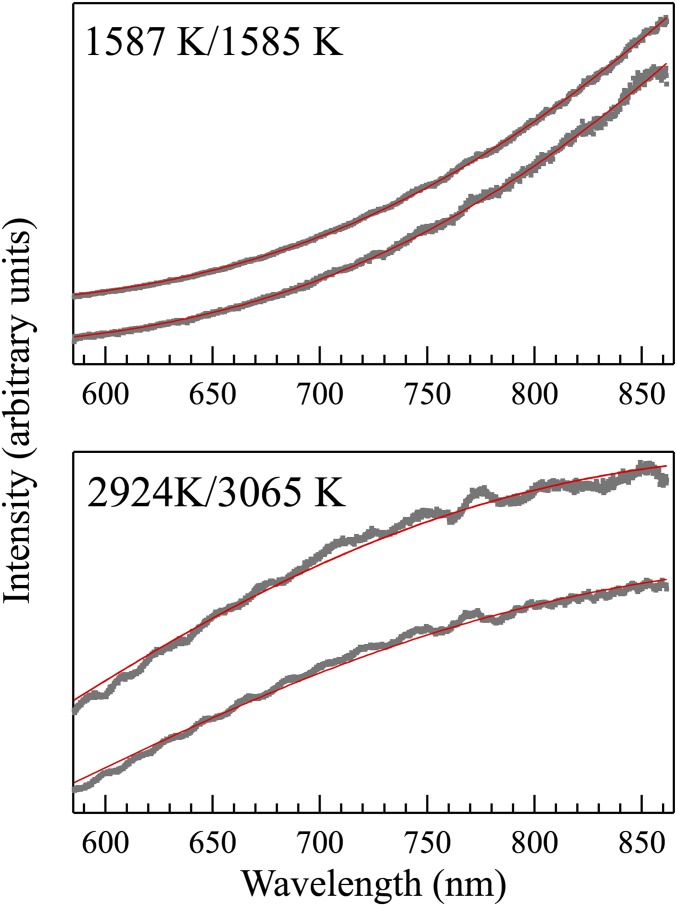
Fig. S1.
Representative thermal radiation spectra (gray dots) and Planck radiation fits (red curves) from downstream (Upper) and upstream (Lower, vertically shifted for clarity) sides in the double-sided laser heating experiment at ∼86 GPa.
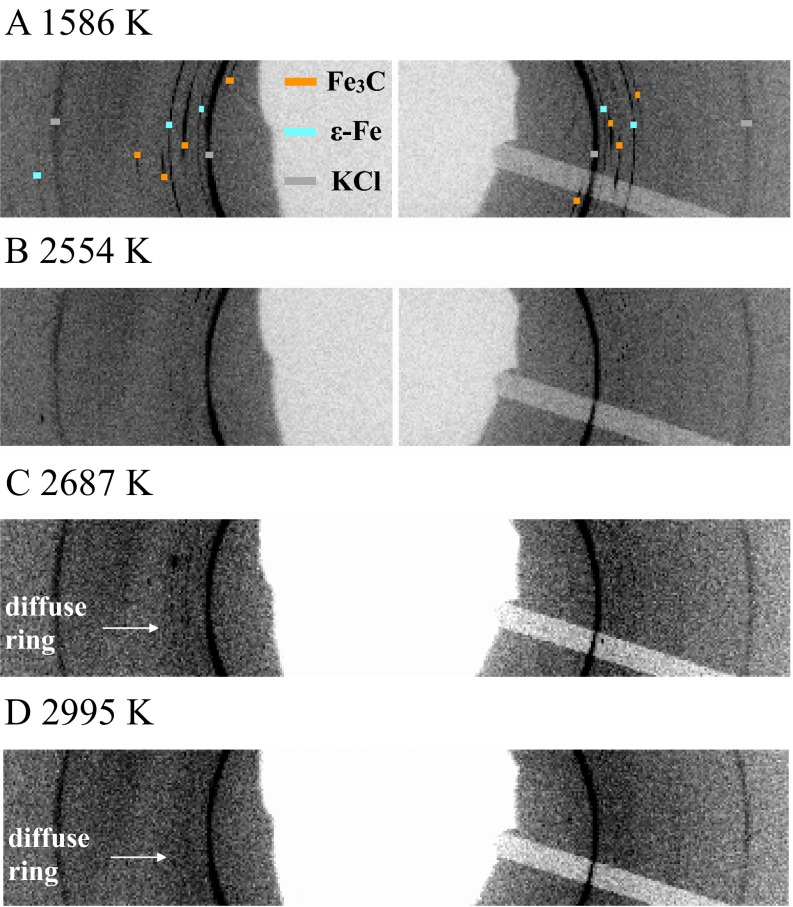
Fig. S2.
XRD images of Fe−Fe3C mixture at 86 GPa, recorded on a PILATUS detector. To better illustrate the appearance of the diffusion rings (white arrows) between 2,554 K and 2687 K, only a section of each full image is shown; 1,586 K (A), 2,554 K (B), 2,687 K (C), and 2,995 K (D). The reflections of Fe3C (orange), iron (blue), and KCl (gray) are marked in the image at 1,586 K. Spotty reflections of solid phases at 2,554 K are present in the excluded section of the image.
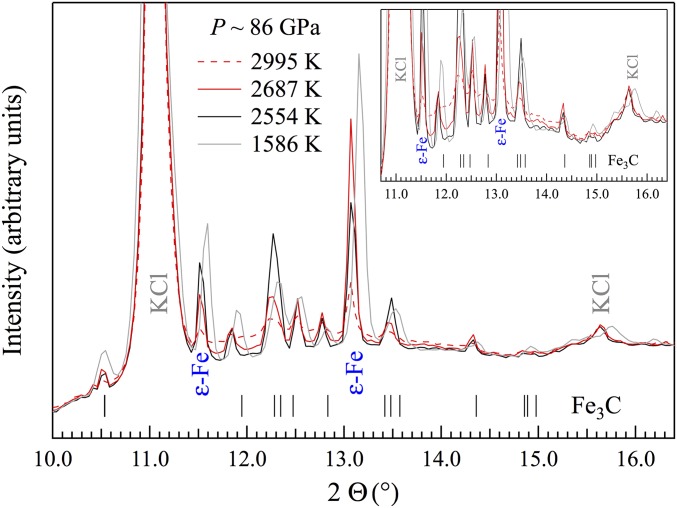
Fig. 1.
Integrated XRD patterns of Fe−Fe3C mixture at ∼86 GPa, with Inset highlighting the evolution of the baseline with increasing temperature. Between 1,586 K (gray) and 2,554 K (black), the baseline barely changed; further heating to 2,687 K (red solid) and 2,995 K (red dashed) led to significantly elevated baselines resulting from diffuse scattering, whereas the intensities of the reflections from Fe3C diminished.
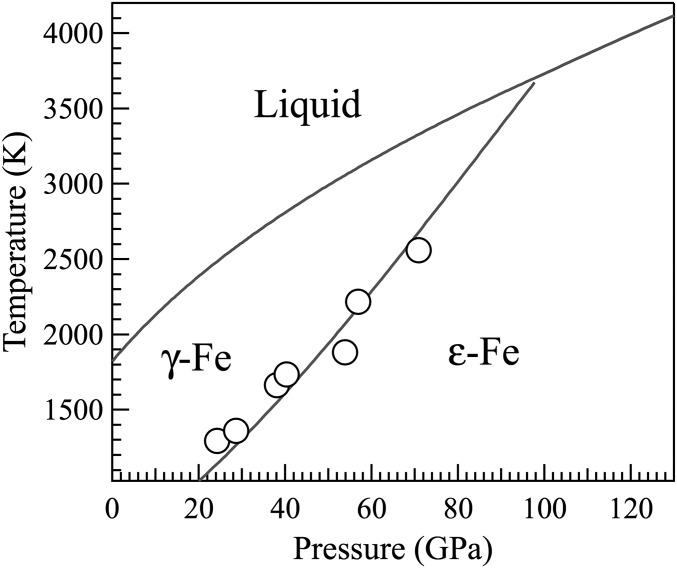
Fig. S3.
The observed ε-Fe to γ-Fe transitions (open circles) are consistent with the known phase diagram of Fe (17). Temperature error bars are smaller than the size of symbol.
Fig. S4.
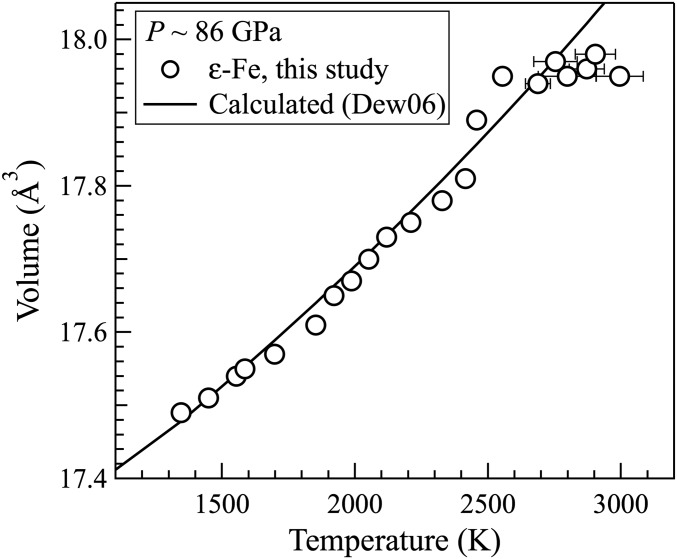
At ∼86 GPa, the measured volume of ε-Fe (open circles) followed the calculated thermal expansion curve [black, Dew06 (57)] up to about 2,500 K, and then became constant upon further heating. The starting temperature of the volume plateau coincides with the first appearance of a diffuse ring in the XRD measurement.
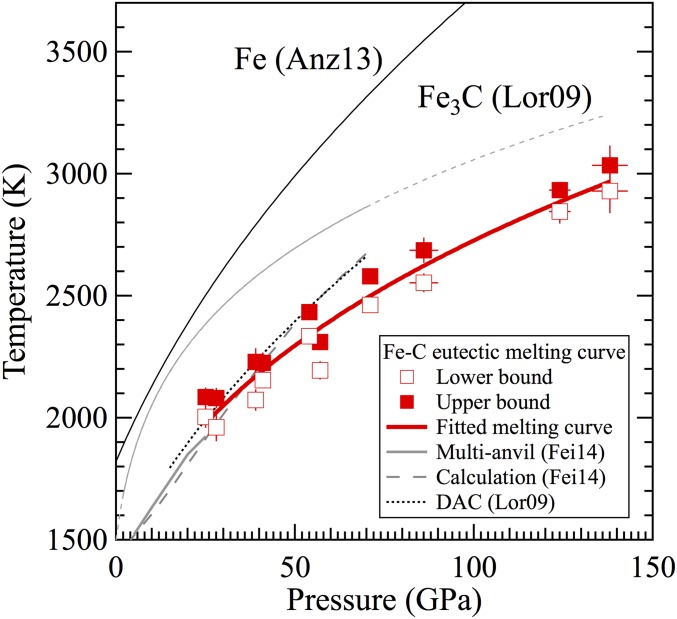
At each pressure, the eutectic melting temperature of the Fe−C system was bracketed by the highest temperature at which the sample contained only solid iron and iron carbide and the lowest temperature at which diffuse scattering signal was observed (Table S1 and Fig. S5). Experiments using the continuous or pulsed heating methods gave consistent results on the melting temperatures. The eutectic melting curve of the Fe−C system constructed from multiple measurements agrees with the existing data to 25 GPa from multianvil studies, where melting was detected by analyzing the recovered run products (29), and with calculated results to 70 GPa (29). The melting temperatures determined in a diamond-anvil cell (DAC) study on the basis of plateaus in the temperature as a function of laser power (30) match the upper bounds of this study (Fig. S5). Fitting the eutectic melting temperatures (T) to the Simon−Glatzel equation yields (T/T0)3.4 ± 0.3 = P/(12 ± 2) + 1, where P is pressure in gigapascals and T0 = 1,426 K is the eutectic melting temperature at ambient pressure (31).
Table S1.
Results of the Fe−C eutectic melting experiments
| Pressure, GPa | Upper bound, K | Lower bound, K | Laser heating mode |
| 25 (1) | 2,085 (38) | 2,004 (45) | Continuous |
| 28 (1) | 2,081 (41) | 1,962 (57) | Continuous |
| 39 (2) | 2,230 (56) | 2,073 (44) | Pulsed |
| 41 (1) | 2,225 (43) | 2,155 (29) | Continuous |
| 54 (2) | 2,433 (14) | 2,335 (33) | Continuous |
| 57 (2) | 2,311 (33) | 2,195 (37) | Pulsed |
| 71 (1) | 2,580 (6) | 2,463 (24) | Pulsed |
| 86 (4) | 2,687 (52) | 2,554 (39) | Pulsed |
| 124 (3) | 2,934 (33) | 2,846 (49) | Pulsed |
| 138 (5) | 3,035 (81) | 2,930 (91) | Pulsed |
Upper bound is the lowest temperature where diffuse scattering was detected. Lower bound is the highest temperature where no diffuse scattering was detected. Numbers in parentheses are uncertainties in the last digits. Temperature uncertainty is estimated from the difference between the downstream and upstream sides in double-sided laser heating experiments. Pressure uncertainty reflects the variations in pressures between 300 K and eutectic melting temperature.
Fig. S5.
The eutectic melting curve of the Fe−C binary system bracketed by the highest temperature where no diffuse scattering was detected (open squares) and the lowest temperature where diffuse scattering was detected (solid squares). The results from this study agree with the those from multianvil experiments up to 25 GPa [Fei14 (29)] and with thermodynamic calculation up to 70 GPa (29). The eutectic melting temperatures determined using the diamond-anvil cell and on the basis of plateau in temperature–power relation up to 70 GPa [Lor09 (30)] match the upper bounds of this study. As pressure increases, the melting curve of Fe [Anz13, (17)] diverges from that of the eutectic curve, whereas the extrapolated melting curve of Fe3C (30) converges toward the eutectic curve.
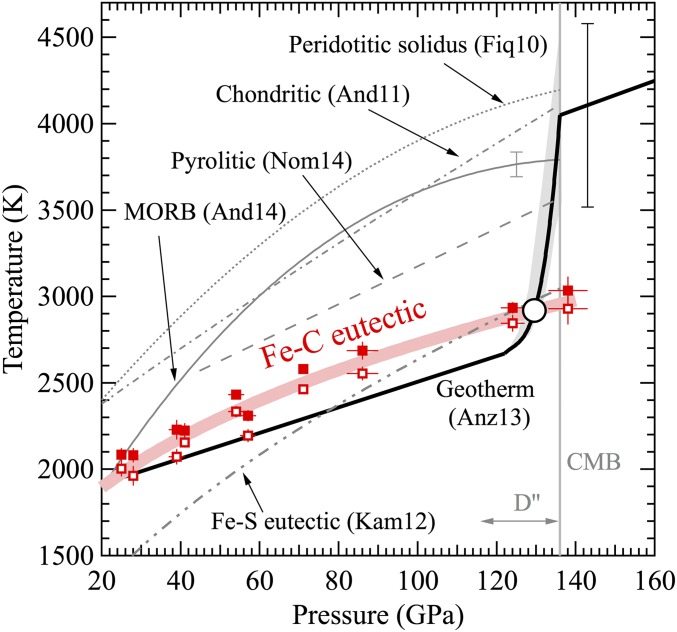
To assess the fate of a slab-derived Fe−C mixture in the mantle, we compare its eutectic melting curve with a simplified one-dimensional geotherm that represents the average temperature as a function of depth for a homogeneous model mantle composition. In reality, the mantle is laterally heterogeneous with regard to temperature. In geodynamical models, slab regions are much cooler than the surrounding regions, and the thermal boundary layer beneath slabs is expected to be quite thin compared with other regions (1). For simplicity, these complications are ignored here. For most of the lower mantle, the eutectic melting temperature of the Fe−C binary system is higher than the present-day mantle geotherm (Fig. 2), implying that an Fe−C mixture would remain solid, unless the presence of nickel and sulfur lowers the solidus sufficiently to induce melting. In the lowermost mantle, the eutectic melting curve intersects with the geotherm, implying that an iron−carbon mixture would melt in the deeper part of the D′′ layer. The model geotherm exhibits a salient feature: It is superadiabatic within the D′′ layer, increasing rapidly toward the outer-core temperature at the CMB at the rate of 50–100 K/GPa. With such a steep gradient, the ±500 K uncertainty in the estimated temperature at the CMB only slightly affects where the eutectic curve and geotherm cross and the iron−carbon mixture begins to melt. The crossing point is at 130 ± 3 GPa and 2,920 ± 150 K, corresponding to 100 ± 50 km depth above the CMB.
Fig. 2.
The eutectic melting curve of Fe−C system (red; this study) intersects the present-day geotherm (thick black curve with gray shaded area indicating uncertainties; ref. 17) at 130 ± 3 GPa and ∼2,920 ± 150 K (open circle). The eutectic melting curve is bracketed by the highest temperature where no diffuse scattering was detected (open squares) and the lowest temperature where diffuse scattering was detected (solid squares). The uncertainties in the crossing temperature and pressure are comparable to the size of the symbol. At the CMB, the eutectic melting temperature of Fe−C system is comparable to that of Fe−S system (32), ∼600 K lower than the solidus temperature of pyrolitic composition (10), ∼800 K lower than that of MORB (3), and 1,100–1,200 K lower than that of chondritic (8) and peridotitic compositions (9).
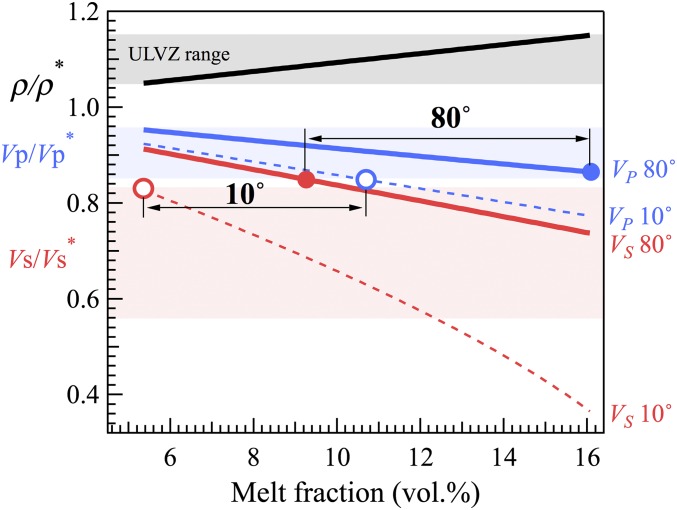
The presence of Fe−C melt in a mantle region is expected to increase its density and reduce its sound velocities, and therefore could potentially produce a ULVZ. The amounts of density excess and velocity reductions depend on a number of factors, including the melt fraction, the contrasts in the density and elastic properties between the interstitial melt and solid skeleton, and the wetting behavior of the melt with respect to the solid matrix (33). Applying models for calculating the compressional and shear wave velocities of liquid−solid composites and using approximate values, we estimated that replacing 1 vol.% solid silicate by Fe−C melt produces about 1% density excess (Supporting Information). Because the Fe−C melt has a similar bulk modulus to the mantle, its influences on the sound velocities arise predominately from its zero shear modulus. Our calculations show that the reduction in shear wave velocity depends strongly on the dihedral angle, at the rate of ∼3% per vol.% melt for a small dihedral angle of 10°, and ∼1% per vol.% melt for a nonwetting dihedral angle of 80°. The reduction in the compressional wave velocity is less sensitive to the dihedral angle and falls into the range of 0.5–1% per vol.% melt. We found that, for a partially molten region containing solid silicate and Fe−C melt, 5–16 vol.% Fe−C melt is needed to reproduce the observed density excess of ULVZs. To simultaneously match the Vs and Vp of ULVZs, 5–11 vol.% melt is needed for a dihedral angle of 10°, and 9–16 vol.% melt is needed for a dihedral angle of 80° (Fig. 3).
Fig. 3.
Density (black), compressional wave velocity (blue), and shear wave velocity (red) ratios between a partially molten region (ρ, Vs, Vp), consisting of solid mantle and Fe−C melt at a given volume fraction (vol.%), and the surrounding mantle (ρ*, Vs*, Vp*) for dihedral angles of 10° and 80°. Double-arrowed lines denote the ranges of melt fraction that match the ULVZs features at dihedral angle = 10° and 80°, respectively, which are constrained by the crossing points (open circles for 10° and closed circles for 80°) between the velocity curves and the seismically observed values of ULVZs (shaded areas).
Previous work suggests that roughly 1 wt.% metallic iron is produced in the crust portion of subducted slabs as a result of disproportionation of ferrous ion in pyroxene and garnet beyond 250 km depth (26, 27) and in bridgmanite when the slab enters the lower mantle (25). The carbon content in the deep mantle slabs may range from 320 ppm to 620 ppm, according to the estimated 2.4–4.8 × 1013 g annual input of carbon to the mantle past the arc (34). Carbonates in the slab may interact with metallic iron to produce elemental carbon or iron carbides (28), making the Fe−C system a viable candidate for partial melt at the CMB. Assuming complete reaction, the estimated abundances of iron and carbon imply that up to 1 wt.% Fe−C melt can be generated in subducted slabs. Depending on its wetting behavior, the Fe−C melt may drain under gravitational force to join the core, or it may be entirely retained in the mantle and could return to shallower depths through convective transport and refreeze. Alternatively, the melt may be concentrated through the shear focusing mechanism, where deviatoric stress in a viscously deforming partially molten rock leads to melt-enriched shear zones (35). In the lowermost mantle, subducted slabs are subject to large dynamic, thermal, and chemical disequilibrium. A slab approaching the CMB may become deformed by viscous drag from the base of the mantle, causing it to fold up near regions of mantle upwelling (36). Consequently, the iron−carbon melt produced in the slab may concentrate near the edge of LLSVP (1, 37). With the lateral extent spanning hundreds of kilometers, the volume of folded subducted slabs at the CMB could be 20 times larger than a typical ULVZ (36) and therefore would be able to supply sufficient Fe−C melt to form ULVZs.
The composition of the Fe−C melt is uncertain because the eutectic composition of the Fe−C binary at the CMB remains controversial: Wood (38) predicted a very iron-rich eutectic melt, which was apparently confirmed by Lord et al. (30), but was inconsistent with more recent results by Fei and Brosh (29). In this study, the starting composition contains roughly equal fractions of iron and Fe3C, correspondingly to about 3 wt.% carbon. Neither Fe3C nor Fe7C3 appeared as the liquidus phase, suggesting that the eutectic composition likely contained more than 1 wt.% carbon. The lack of tight constraints on the eutectic composition does not seem to affect the calculated melt fractions, because the density and sound velocities of Fe−C liquid containing 0–4.1 wt.% carbon at CMB pressure were found to vary only slightly, from 10.5 g/cm3 to 10.1 g/cm3 and 7.95 km/s to 8.15 km/s, respectively (39).
The wetting behavior of Fe−C melt in the lower mantle is not known. If Fe−C melt behaves like Fe−S melt, which has a dihedral angle below 20° in the deep mantle (40), then at least 5 vol.% melt is needed to match the seismic features of ULVZs (type A in Fig. 4). On the other hand, if the Fe−C melt does not wet the grain boundaries, then as much as 9 vol.% melt is needed to reproduce the ULVZ properties (type B in Fig. 4). Yoshino et al. (41) found that, in the nonwetting case with large dihedral angles, the percolation threshold of Fe−S melt in solid olivine is 5 vol.% and that the presence of silicate partial melt raises the threshold to 13 ± 2 vol.%. Given that the solidus of pyrolite (10) lies slightly above the lower bound estimate of temperature at the CMB (Fig. 2), low-degree melting of silicate is plausible. Iron-rich deep melt could produce yet another type of ULVZ through reaction with solid phases (type C in Fig. 4). In the conductive thermal boundary layer at the interface of the core and mantle, chemical reaction is controlled by diffusion and was found to be exceedingly slow in bridgmanite, at the rate of a few meters per billion years (42). Diffusion may proceed much faster for ferropericlase, yet chemical exchange between the core and mantle is still limited to 1–10 km for lattice diffusion and 100 km for grain boundary diffusion over the entire geological history (43). After the Fe−C melt is concentrated into isolated patches as in the previous cases, it may react with the new silicate matrix because of chemical disequilibrium resulting from changes in composition and/or temperature associated with its transport from slab to the edge of LLSVP. For instance, it could recombine with Fe3+ in bridgmanite or postbridgmanite to produce Fe2+, which would then be preferentially incorporated into postbridgmanite or coexisting ferropericlase phase. This process could serve as an alternative mechanism to generate ULVZs consisting mostly of iron-rich solid phases (6, 7), with or without residual metallic melt. In this scenario, iron enrichment in solid phases and the presence of melt could both contribute to the velocity reductions.
Fig. 4.
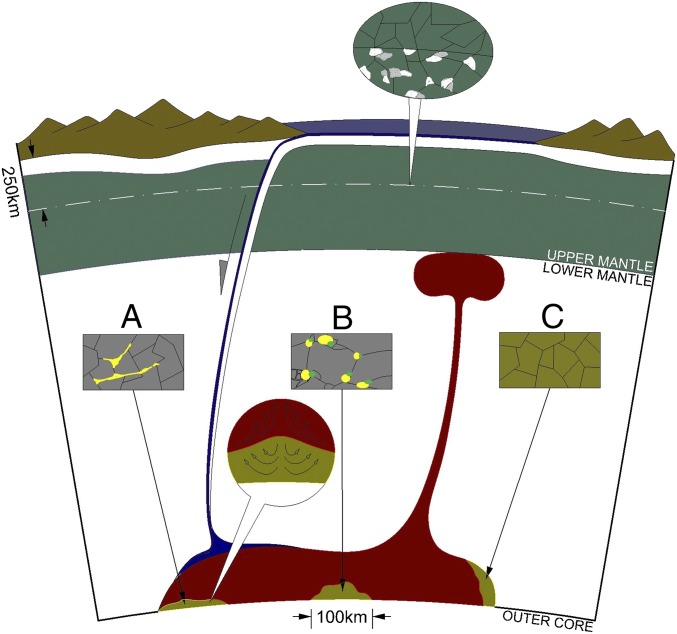
Cartoon illustration of three types of ULVZs involving slab-derived iron−carbon (Fe−C) melt (heights are exaggerated). The upper oval-shaped balloon shows that, at a depth beyond 250 km in the mantle, metallic iron (white) is produced by the disproportionation of ferrous iron in pyroxene and garnet, whereas the dominant carbon species are elemental carbon or iron carbides (gray). Three rectangular boxes represent (box A) ULVZs containing 5–11 vol. % Fe−C melt (yellow) that wets the solid silicate matrix (gray), (box B) ULVZs containing 9–16 vol.% nonwetting Fe−C melt (yellow) coexisting with a small degree of silicate melt (green) in solid silicate matrix (gray), and (box C) ULVZs containing solid phases (yellow-shaded gray) that have become iron-rich through reaction with Fe−C melt. The lower round balloon indicates that dynamic stirring through viscous coupling with the upwelling mantle may prevent or slow down the draining of dense Fe−C melt to the core.
The location and shape of a metallic ULVZ depend on how it forms and evolves over time. For instance, type-A ULVZs require smaller melt fractions and therefore may form at shallower depths when the melting curve just crosses the geotherm, whereas type-B ULVZs require a larger fraction of Fe−C melt and a small degree of silicate melt, and therefore likely form at greater depths when the mantle temperature exceeds the eutectic point by a considerable amount. Alternatively, the depth of formation may be governed by the dynamic process that concentrates Fe−C melt into small regions. Where and how a ULVZ forms will influence its size and shape. Given the same initial volume, type-A ULVZs tend to be shorter and broader because an Fe−C melt that wets the solid matrix will drain readily to reduce the height and it spreads out laterally to increase the width. Type-B ULVZs are likely taller and narrower because nonwetting Fe−C melt does not drain downward or spread laterally as long as the melt fraction stays below the percolation threshold. Type-C UVLZs rely on chemical diffusion to deliver iron to solid phases from Fe−C melt, after it has been accumulated into small patches through mantle convection dynamics. These ULVZs are expected to be relatively tall and narrow as well, because the width is limited by the rate of chemical diffusion, whereas the height is constrained by slow or negligible draining of Fe−C melt to allow chemical reaction with the silicate matrix. Depending on the dynamic process of subduction, including the descending rate, details of deformation, and extent of chemical exchange, alloying elements such as sulfur, silicon, or oxygen may be incorporated into Fe−C melt, and, if so, their presence will modify the melting point and influence the origin and nature of ULVZs. Detailed modeling may shed light on the origin and evolution of metallic ULVZs by considering the melting, wetting, and chemical behavior of relevant compositions, as well as viscosity, density contrast with surrounding mantle, and convective vigor.
Given its chemical affinity, keeping a significant fraction of dense metallic melt from draining into the core may be problematic. After accumulating in an upwelling region, the dense metallic melt may be stirred by the overlying convective mantle through viscous coupling, which keeps it entrained in the solid matrix against draining into the core (44). In type-A ULVZs, the Fe−C melt wets the solid matrix and therefore drains readily and will ultimately merge into the core. In type-B ULVZs, the Fe−C melt may stay trapped in solid matrix, provided that the melt fraction is below the percolation threshold. In type-C ULVZs, the Fe−C melt gets incorporated into crystalline structures through chemical reaction and therefore escapes core sequestration.
The platinum group element (PGE) record in komatiites with different ages suggests that meteoritic veneer was progressively mixed into Earth's deep mantle until the early Archean (45). Billions of years ago, metallic melts may have formed over a wider range of depths than today and facilitated the mixing of the postulated “late veneer” into the lower mantle. The PGE record also suggests that the highly siderophile element (HSE) contents of the mantle remained constant within ±40% since the late Archean (45). Assuming that Fe−C melt in type-A ULVZs is fully equilibrated with the solid matrix and therefore has scavenged all of the HSEs in its source region, then up to 40% of the mantle could have lost its HSEs to the core through the draining of Fe−C melt. With an estimated 1 wt.% Fe−C in the mantle, loss of Fe−C from 40% of the mantle corresponds to 0.8% growth in core mass at the expense of 0.4% reduction in mantle mass, which is equivalent to about 10 km expansion in core radius over Earth's history.
The idea that an iron-rich melt is responsible for the ULVZs has been considered previously, but existing models assumed that the core is the source of iron (e.g., refs. 4, 15, and 46). It has been shown that the capillary rise height of the outer core liquid is only 20 m (47), which is too thin for ULVZs. A more recent study suggested that core fluid could reach up to 1 km through a suction mechanism (48), which is still much thinner than ULVZs. Compared with existing models, the slab metal models are particularly appealing for a number of reasons. An iron−carbon mixture in the slab will definitely melt near the CMB as discussed above. With limited presence of slabs at the CMB, nonubiquitous occurrence of these types of ULVZs is expected. An Fe−C melt is twice as dense as the surrounding mantle, hence the slab metal models can readily explain the density anomaly of ULVZs. Nomura et al. (10) advocated for a CMB temperature near the lower limit of the currently accepted range (17), which requires a chemically distinct component as the origin of ULVZ. McNamara et al. (1) reached the same conclusion on the basis of geodynamics considerations. The slab metal models provide a plausible source of such chemical heterogeneity. Aside from giving rise to various types of ULVZs, the presence of metallic melt may provide an explanation for the enhanced and perhaps laterally varying electrical conductivity in the lowermost mantle (47, 49, 50). The hypotheses involving metallic melt can be tested by investigating the wetting behavior of Fe−C melt under deep mantle conditions, the dynamic behavior of Fe−C melt within the D′′ layer, and the chemical reactivity between Fe−C melt and solid phases near the CMB.
Methods
Experiments were conducted at the Advanced Photon Source (APS), using laser-heated DACs and synchrotron XRD techniques. The starting material was an equal portion mixture of iron powder (99.9%; Alfa Aesar) and Fe3C powder, sandwiched between KCl pellets. Laser heating and XRD measurements were performed at beamline 16-ID-B of the APS, Argonne National Laboratory (ANL). The onset of melting was detected on the basis of simultaneous occurrences of diffuse scattering signal and volume plateau of iron. The density and sound velocities of a partially molten region of the mantle containing Fe−C melt at a given volume fraction were calculated following the equilibrium geometry model (33) for a representative nonwetting dihedral angle of 80° and a wetting dihedral angle of 10°. Details of the experiments and calculations are found in Supporting Information.
SI Methods
High pressures were generated using symmetric-type DACs with pairs of 300-μm culet anvils for experiments up to ∼60 GPa, and 370-μm/250-μm/8° beveled anvils for experiments between ∼70 GPa and 138 GPa. Rhenium gaskets were preindented to about 27 GPa and then drilled using an electric discharge machine to create 150- to 180-μm-sized sample chambers. The starting material, an equal portion mixture of iron powder (99.9%; Alfa Aesar) and Fe3C powder, synthesized as described in ref. 51, was pressed in a DAC to form 7-μm-thick flakes that are 70–130 μm in lateral dimensions. A flake of mixture and 5-μm-sized ruby spheres were loaded into the sample chamber and sandwiched by two 10-μm-thick KCl pellets, which served as thermal and chemical insulation layers, pressure transmitting media, and pressure standard. To remove moisture, the samples were brought to a pressure of 10 microtorr for 30 min and then closed inside the DAC using the Consortium for Materials Properties Research in Earth Sciences/Geo Soil Enviro Consortium for Advanced Radiation Sources (COMPRES/GSECARS) gas-loading system at the APS at ANL.
Laser-heating and XRD measurements were performed at beamline 16-ID-B of the APS. A double-sided yttrium-lithium-fluoride (YLF) laser-heating system with 24- to 34-μm-sized flat top beam, either in a continuous or pulsed mode, was used to generate high temperatures (52). In situ angle-dispersive XRD measurements used monochromatic X-ray with a wavelength of 0.4066 Å and a focused beam size of 4 × 7 μm2 (FWHM). Diffracted X-rays were recorded for 1 s on a MAR165 CCD detector or a 2D Pilatus 1M pixel array X-ray detector. The sample-to-detector distance and the tilt angle and rotation angle of the detectors relative to the incident X-ray beam were calibrated by diffraction of cerium dioxide (CeO2) at ambient conditions. The 2-D XRD images were integrated to 1-D spectra using software Fit2D (53), and peak fitting was performed using the software FullProf.
At each target pressure, a fresh region of the sample was heated, and XRD image and temperature reading (Fig. S1) were collected simultaneously during the heating cycle. X-ray beam, laser heating spot, and temperature measurement spot were aligned by X-ray induced fluorescence from ruby spheres or KCl pressure medium. Pressure was monitored on the basis of the thermal equation of state of KCl (54). Two different heating paths were adopted: For experiments using the MAR165 CCD detector, the sample was heated continuously, with the laser power gradually increased until melting was detected. At 100–1,000 K above the incipient melting, the sample was either quenched by turning off the laser power or gradually cooled to ambient temperature by reducing the laser power. XRD images were collected at every 30–50 K; for experiments using the PILATUS detector, the sample was exposed to the laser beam for 1 s at a given power and then quenched by blocking the laser beam using a high-speed shutter. Limiting the sample's exposure to the laser beam through pulse modulation helps to protect diamonds and limit diamond−sample reaction (52).
The validity of the temperature measurements was confirmed by observing the hexagonally close-packed ε-Fe transforming to face-centered cubic γ-Fe: The phase boundary between ε-Fe and γ-Fe observed in this study (Fig. S3) at pressures up to ∼71 GPa is consistent with ref. 17. At higher pressures, experiments were terminated at temperatures below the iron phase transition.
SI Assessing the Influence of Metallic Melt on Density and Sound Velocities
For a partially molten region (pm) of the mantle containing Fe−C melt (melt) at a given volume fraction (ϕmelt), its density is
| [S1] |
Its sound velocities (Vspm and Vppm) can be calculated following the method described in ref. 33. The bulk and shear moduli of the partially molten region (Kpm and Gpm) depend on that of the melt-free mantle (Kmantle and Gmantle) and that of the solid skeleton (Kske and Gske), which is the solid framework with vacuum pores to replace the melt in a partially molten region, through the following relations:
| [S2] |
| [S3] |
| [S4] |
where and depend on the wetting behavior of the melt in the grain boundaries, decreasing almost linearly with increasing dihedral angle from about 6 at 10° to about 3 at 80° (33).
Taking approximate values for relevant parameters from the Preliminary Reference Earth Model (PREM) model with Kmantle = 655.6 GPa, Gmantle = 293.8 GPa, and Kmelt ≈ Kcore = 644.1 GPa at the CMB pressure (55), we found that the presence of Fe−C melt has little effect on the bulk modulus of the partially molten zone: Kpm /Kmantle is 0.998 regardless of the melt fraction and dihedral angle. This is because Kmelt and Kmantle are rather similar and hence the term ϕmelt ⋅ (1 − Kmantle /Kmelt) in Eq. S3 becomes negligible and Kpm /Kmantle remains nearly 1. In contrast, Gpm /Gmantle, which is the same as Gske /Gmantle because neither vacuum pore nor melt can support shear, varies strongly with the melt fraction and dihedral angle. At small dihedral angle of 10°, Gpm /Gmantle drops to zero at about 19 vol.% melt. Even with a nonwetting dihedral angle of 80°, Gpm /Gmantle vanishes at 43 vol.% melt.
Accordingly, the sound velocities of the partially molten region can be calculated through the following relations:
| [S5] |
| [S6] |
With ρmantle = 5.566 g/cm3 (55) and ρmelt = 10.764 g/cm3 (56), the volume fraction of melt (ϕmelt) that is needed to reproduce the observed 5–15% density excess of ULVZs falls between 5% and 16%. In other words, replacing 1 vol.% solid silicate by Fe−C melt produces about 1% density excess. To simultaneously match the Vs and Vp of ULVZs, we found that the 5–11 vol.% melt is needed for a dihedral angle of 10°, and 9–16 vol.% melt is needed for a dihedral angle of 80° (Fig. 3). The ranges of melt fractions are subject to uncertainties in the input density and moduli values and may vary by up to 4 vol.% for 10% relative variations in the input parameters.
Acknowledgments
The authors thank Michael Walter and Allen McNamara for raising many insightful and important questions and providing thoughtful and constructive reviews; Dave Walker, Max Schmidt, Paul Tackley, Paul Asimow, Jennifer Jackson, Mingming Li, Zeyu Li, Bin Chen, Guoyin Shen, Yue Meng, Jin Liu, and Fuxiang Zhang for helpful discussions; and Liang Li for drafting the cartoon. This research was partially supported by NSF Grants AST 1344133 and EAR 1219891, NASA Grants NNX10AG97G and NNX15AG54G, and Sloan Foundation Deep Carbon Observatory Grant G-2015-14085. Portions of the work were performed at HPCAT (Sector 16), Advanced Photon Source (APS), Argonne National Laboratory.
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1519540113/-/DCSupplemental.
References
- 1.McNamara AK, Garnero EJ, Rost S. Tracking deep mantle reservoirs with ultra-low velocity zones. Earth Planet Sci Lett. 2010;299(1-2):1–9. [Google Scholar]
- 2.Thorne MS, Garnero EJ, Jahnke G, Igel H, McNamara AK. Mega ultra low velocity zone and mantle flow. Earth Planet Sci Lett. 2013;364:59–67. [Google Scholar]
- 3.Andrault D, et al. Melting of subducted basalt at the core-mantle boundary. Science. 2014;344(6186):892–895. doi: 10.1126/science.1250466. [DOI] [PubMed] [Google Scholar]
- 4.Williams Q, Garnero EJ. Seismic evidence for partial melt at the base of Earth’s mantle. Science. 1996;273(5281):1528–1530. [Google Scholar]
- 5.Dobson DP, Brodholt JP. Subducted banded iron formations as a source of ultralow-velocity zones at the core-mantle boundary. Nature. 2005;434(7031):371–374. doi: 10.1038/nature03430. [DOI] [PubMed] [Google Scholar]
- 6.Mao WL, et al. Iron-rich post-perovskite and the origin of ultralow-velocity zones. Science. 2006;312(5773):564–565. doi: 10.1126/science.1123442. [DOI] [PubMed] [Google Scholar]
- 7.Wicks JK, Jackson JM, Sturhahn W. Very low sound velocities in iron-rich (Mg,Fe)O: Implications for the core-mantle boundary region. Geophys Res Lett. 2010;37(15):L15304. [Google Scholar]
- 8.Andrault D, et al. Solidus and liquidus profiles of chondritic mantle: Implication for melting of the Earth across its history. Earth Planet Sci Lett. 2011;304(1-2):251–259. [Google Scholar]
- 9.Fiquet G, et al. Melting of peridotite to 140 gigapascals. Science. 2010;329(5998):1516–1518. doi: 10.1126/science.1192448. [DOI] [PubMed] [Google Scholar]
- 10.Nomura R, et al. Low core-mantle boundary temperature inferred from the solidus of pyrolite. Science. 2014;343(6170):522–525. doi: 10.1126/science.1248186. [DOI] [PubMed] [Google Scholar]
- 11.Muir JMR, Brodholt JP. Elastic properties of ferrous bearing MgSiO3 and their relevance to ULVZs. Geophys J Int. 2015;201(1):496–504. [Google Scholar]
- 12.Muir JMR, Brodholt JP. Elastic properties of ferropericlase at lower mantle conditions and its relevance to ULVZs. Earth Planet Sci Lett. 2015;417:40–48. [Google Scholar]
- 13.Nomura R, et al. Spin crossover and iron-rich silicate melt in the Earth’s deep mantle. Nature. 2011;473(7346):199–202. doi: 10.1038/nature09940. [DOI] [PubMed] [Google Scholar]
- 14.Sinmyo R, Hirose K. Iron partitioning in pyrolitic lower mantle. Phys Chem Miner. 2013;40(2):107–113. [Google Scholar]
- 15.Rost S, Garnero EJ, Williams Q, Manga M. Seismological constraints on a possible plume root at the core−mantle boundary. Nature. 2005;435(7042):666–669. doi: 10.1038/nature03620. [DOI] [PubMed] [Google Scholar]
- 16.Rost S, Garnero EJ, Williams Q. Fine-scale ultralow-velocity zone structure from high-frequency seismic array data. J Geophys Res. 2006;111(B9):B09310. [Google Scholar]
- 17.Anzellini S, Dewaele A, Mezouar M, Loubeyre P, Morard G. Melting of iron at Earth’s inner core boundary based on fast X-ray diffraction. Science. 2013;340(6131):464–466. doi: 10.1126/science.1233514. [DOI] [PubMed] [Google Scholar]
- 18.Thomas CW, Liu Q, Agee CB, Asimow PD, Lange RA. Multi-technique equation of state for Fe2SiO4 melt and the density of Fe-bearing silicate melts from 0 to 161 GPa. J Geophys Res. 2012;117(B10):B10206. [Google Scholar]
- 19.Thomas CW, Asimow PD. Direct shock compression experiments on premolten forsterite and progress toward a consistent high-pressure equation of state for CaO-MgO-Al2O3-SiO2-FeO liquids. J Geophys Res. 2013;118(11):5738–5752. [Google Scholar]
- 20.Knittle E, Jeanloz R. Earth’s core-mantle boundary: Results of experiments at high pressures and temperatures. Science. 1991;251(5000):1438–1443. doi: 10.1126/science.251.5000.1438. [DOI] [PubMed] [Google Scholar]
- 21.Takafuji N, Hirose K, Mitome M, Bando Y. Solubilities of O and Si in liquid iron in equilibrium with (Mg,Fe)SiO3 perovskite and the light elements in the core. Geophys Res Lett. 2005;32(6):L06313. [Google Scholar]
- 22.Grand SP. Mantle shear-wave tomography and the fate of subducted slabs. Philos Trans A Math Phys Eng Sci. 2002;360(1800):2475–2491. doi: 10.1098/rsta.2002.1077. [DOI] [PubMed] [Google Scholar]
- 23.Kelemen PB, Manning CE. Reevaluating carbon fluxes in subduction zones, what goes down, mostly comes up. Proc Natl Acad Sci USA. 2015;112(30):E3997–E4006. doi: 10.1073/pnas.1507889112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Thomson AR, Walter MJ, Kohn SC, Brooker RA. Slab melting as a barrier to deep carbon subduction. Nature. 2016;529(7584):76–79. doi: 10.1038/nature16174. [DOI] [PubMed] [Google Scholar]
- 25.Frost DJ, et al. Experimental evidence for the existence of iron-rich metal in the Earth’s lower mantle. Nature. 2004;428(6981):409–412. doi: 10.1038/nature02413. [DOI] [PubMed] [Google Scholar]
- 26.Rohrbach A, et al. Metal saturation in the upper mantle. Nature. 2007;449(7161):456–458. doi: 10.1038/nature06183. [DOI] [PubMed] [Google Scholar]
- 27.Stagno V, Ojwang DO, McCammon CA, Frost DJ. The oxidation state of the mantle and the extraction of carbon from Earth’s interior. Nature. 2013;493(7430):84–88. doi: 10.1038/nature11679. [DOI] [PubMed] [Google Scholar]
- 28.Rohrbach A, Schmidt MW. Redox freezing and melting in the Earth’s deep mantle resulting from carbon-iron redox coupling. Nature. 2011;472(7342):209–212. doi: 10.1038/nature09899. [DOI] [PubMed] [Google Scholar]
- 29.Fei YW, Brosh E. Experimental study and thermodynamic calculations of phase relations in the Fe−C system at high pressure. Earth Planet Sci Lett. 2014;408:155–162. [Google Scholar]
- 30.Lord OT, Walter MJ, Dasgupta R, Walker D, Clark SM. Melting in the Fe−C system to 70 GPa. Earth Planet Sci Lett. 2009;284(1-2):157–167. [Google Scholar]
- 31.Okamoto H. The C–Fe (carbon–iron) system. J Phase Equilibria. 1992;13(5):543–565. [Google Scholar]
- 32.Kamada S, et al. Melting relationships in the Fe−Fe3S system up to the outer core conditions. Earth Planet Sci Lett. 2012;359:26–33. [Google Scholar]
- 33.Takei Y. Effect of pore geometry on VP/VS: From equilibrium geometry to crack. J Geophys Res. 2002;107(B2):2043. [Google Scholar]
- 34.Dasgupta R, Hirschmann MM. The deep carbon cycle and melting in Earth’s interior. Earth Planet Sci Lett. 2010;298(1-2):1–13. [Google Scholar]
- 35.Kohlstedt DL, Holtzman BK. Shearing melt out of the Earth: An experimentalist’s perspective on the influence of deformation on melt extraction. Annu Rev Earth Planet Sci. 2009;37:561–593. [Google Scholar]
- 36.Hutko AR, Lay T, Garnero EJ, Revenaugh J. Seismic detection of folded, subducted lithosphere at the core-mantle boundary. Nature. 2006;441(7091):333–336. doi: 10.1038/nature04757. [DOI] [PubMed] [Google Scholar]
- 37.Li M, McNamara AK, Garnero EJ. Chemical complexity of hotspots caused by cycling oceanic crust through mantle reservoirs. Nat Geosci. 2014;7(5):366–370. [Google Scholar]
- 38.Wood BJ. Carbon in the core. Earth Planet Sci Lett. 1993;117(3-4):593–607. [Google Scholar]
- 39.Badro J, Côté AS, Brodholt JP. A seismologically consistent compositional model of Earth’s core. Proc Natl Acad Sci USA. 2014;111(21):7542–7545. doi: 10.1073/pnas.1316708111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Shi CY, et al. Formation of an interconnected network of iron melt at Earth’s lower mantle conditions. Nat Geosci. 2013;6(11):971–975. [Google Scholar]
- 41.Yoshino T, Walter MJ, Katsura T. Connectivity of molten Fe alloy in peridotite based on in situ electrical conductivity measurements: Implications for core formation in terrestrial planets. Earth Planet Sci Lett. 2004;222(2):625–643. [Google Scholar]
- 42.Yamazaki D, Kato T, Yurimoto H, Ohtani E, Toriumi M. Silicon self-diffusion in MgSiO3 perovskite at 25 GPa. Phys Earth Planet Inter. 2000;119(3-4):299–309. [Google Scholar]
- 43.Van Orman JA, Fei YW, Hauri EH, Wang JH. Diffusion in MgO at high pressures: Constraints on deformation mechanisms and chemical transport at the core-mantle boundary. Geophys Res Lett. 2003;30(2):1056. [Google Scholar]
- 44.Hernlund JW, Jellinek AM. Dynamics and structure of a stirred partially molten ultralow-velocity zone. Earth Planet Sci Lett. 2010;296(1-2):1–8. [Google Scholar]
- 45.Maier WD, et al. Progressive mixing of meteoritic veneer into the early Earth’s deep mantle. Nature. 2009;460(7255):620–623. [Google Scholar]
- 46.Lay T, Garnero EJ, Williams Q. Partial melting in a thermo-chemical boundary layer at the base of the mantle. Phys Earth Planet Inter. 2004;146(3-4):441–467. [Google Scholar]
- 47.Poirier JP, Malavergne V, Mouël JLL. Is there a thin electrically conducting layer at the base of the mantle? In: Gurnis M, Wysession ME, Knittle E, Buffet BA, editors. The Core-Mantle Boundary Region. Am Geophys Union; Washington, DC: 1998. pp. 131–137. [Google Scholar]
- 48.Kanda RVS, Stevenson DJ. Suction mechanism for iron entrainment into the lower mantle. Geophys Res Lett. 2006;33(2):L02310. [Google Scholar]
- 49.Holme R, de Viron O. Characterization and implications of intradecadal variations in length of day. Nature. 2013;499(7457):202–204. doi: 10.1038/nature12282. [DOI] [PubMed] [Google Scholar]
- 50.Buffett BA. Constraints on magnetic energy and mantle conductivity from the forced nutations of the Earth. J Geophys Res. 1992;97(B13):19581–19597. [Google Scholar]
- 51.Walker D, Dasgupta R, Li J, Buono A. Nonstoichiometry and growth of some Fe carbides. Contrib Mineral Petrol. 2013;166(3):935–957. [Google Scholar]
- 52.Meng Y, Hrubiak R, Rod E, Boehler R, Shen G. New developments in laser-heated diamond anvil cell with in situ synchrotron x-ray diffraction at High Pressure Collaborative Access Team. Rev Sci Instrum. 2015;86(7):072201. doi: 10.1063/1.4926895. [DOI] [PubMed] [Google Scholar]
- 53.Hammersley AP, Svensson SO, Hanfland M, Fitch AN, Hausermann D. Two-dimensional detector software: From real detector to idealised image or two-theta scan. High Press Res. 1996;14(4-6):235–248. [Google Scholar]
- 54.Dewaele A, et al. High-pressure−high-temperature equation of state of KCl and KBr. Phys Rev B. 2012;85(21):214105. [Google Scholar]
- 55.Dziewonski AM, Anderson DL. Preliminary Reference Earth Model. Phys Earth Planet Inter. 1981;25(4):297–356. [Google Scholar]
- 56.Shimoyama Y, et al. Density of Fe-3.5 wt% C liquid at high pressure and temperature and the effect of carbon on the density of the molten iron. Phys Earth Planet Inter. 2013;224:77–82. [Google Scholar]
- 57.Dewaele A, et al. Quasihydrostatic equation of state of iron above 2 Mbar. Phys Rev Lett. 2006;97(21):215504. doi: 10.1103/PhysRevLett.97.215504. [DOI] [PubMed] [Google Scholar]