Straining soft colloids in aqueous nematic liquid crystals

Significance

Liquid crystals (LCs) are anisotropic, viscoelastic fluids that can be used to direct colloids (e.g., metallic nanorods) into organized assemblies with unusual optical, mechanical, and electrical properties. In past studies, the colloids have been sufficiently rigid that their individual shapes and properties have not been strongly coupled to elastic stresses imposed by the LCs. Herein, we explore how soft colloids (micrometer-sized shells formed from phospholipids) behave in LCs. We reveal a sharing of strain between the LC and shells, resulting in formation of spindle-like shells and other complex shapes and also, tuning of properties of the shells (e.g., barrier properties). These results hint at previously unidentified designs of reconfigurable soft materials with applications in sensing and biology.

Abstract

Liquid crystals (LCs), because of their long-range molecular ordering, are anisotropic, elastic fluids. Herein, we report that elastic stresses imparted by nematic LCs can dynamically shape soft colloids and tune their physical properties. Specifically, we use giant unilamellar vesicles (GUVs) as soft colloids and explore the interplay of mechanical strain when the GUVs are confined within aqueous chromonic LC phases. Accompanying thermal quenching from isotropic to LC phases, we observe the elasticity of the LC phases to transform initially spherical GUVs (diameters of 2–50 µm) into two distinct populations of GUVs with spindle-like shapes and aspect ratios as large as 10. Large GUVs are strained to a small extent (R/r < 1.54, where R and r are the major and minor radii, respectively), consistent with an LC elasticity-induced expansion of lipid membrane surface area of up to 3% and conservation of the internal GUV volume. Small GUVs, in contrast, form highly elongated spindles (1.54 < R/r < 10) that arise from an efflux of LCs from the GUVs during the shape transformation, consistent with LC-induced straining of the membrane leading to transient membrane pore formation. A thermodynamic analysis of both populations of GUVs reveals that the final shapes adopted by these soft colloids are dominated by a competition between the LC elasticity and an energy (∼0.01 mN/m) associated with the GUV–LC interface. Overall, these results provide insight into the coupling of strain in soft materials and suggest previously unidentified designs of LC-based responsive and reconfigurable materials.

The majority of living materials are soft. This characteristic emerges from noncovalent interactions that lead to the formation of supramolecular structures that reorganize in response to subtle chemical and mechanical cues (1). The regulation of mechanical strain in particular and the engineering of responses to it across a hierarchy of spatial scales (from the molecular to the supramolecular to the cellular level) are increasingly understood to be one of the central sciences of living systems (2, 3).

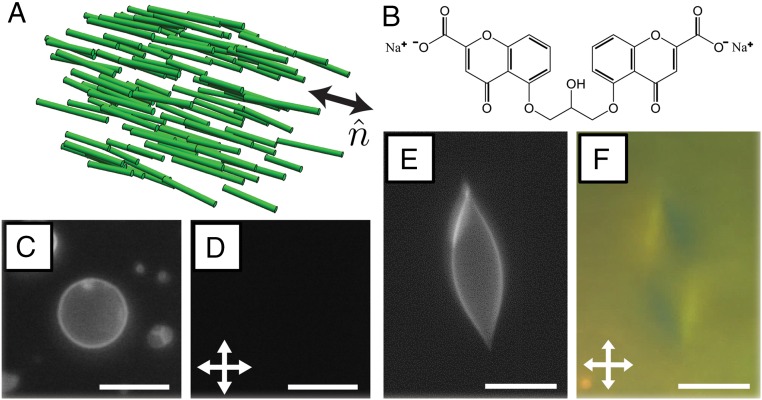
Inspired in part by the functionality of biological materials, a wide range of soft synthetic materials has been assembled by noncovalent interactions of molecular and macromolecular components (1, 4). In particular, liquid crystals (LCs) (Fig. 1A), which are phases that combine the molecular mobility of liquids with the long-range orientational ordering of crystalline solids, have provided the basis for a spectrum of responsive materials, including systems where electrical fields and mechanical strain compete to control electrooptical properties (5, 6). More recently, micro- and nanometer-sized colloidal particles dispersed in LCs have been used to form tunable self-assembled structures for photonic crystals and metamaterials (7). In the systems studied to date, however, the colloids have been “hard” compared with the LC, leading to mechanical straining of the LC but not the colloids (8).

Fig. 1.

(A) Schematic illustration of the long-range orientational order of a nematic LC, which can be characterized by a local director $\widehat{n}$. (B) The chemical structure of a DSCG molecule. (C and E) Fluorescence and (D and F) crossed polar micrographs of GUVs in 15% (wt/wt) DSCG at (C and D) 48 °C (isotropic phase) and (E and F) at 25 °C (nematic phase). (Scale bars: 10 µm.)

In this paper, we move beyond these past studies and consider the more complex situation in which soft colloids are dispersed in LCs, such that a coupling exists between colloid shape and LC strain. Specifically, we have used micrometer-sized synthetic giant unilamellar vesicles (GUVs) as model soft colloids and dispersed them in LCs. We hypothesized that elastic stresses arising from deformation of the LC would strain the GUVs, potentially giving rise, for example, to anisometric GUV shapes, expansion of the surface area of GUV membranes, and temporary poration and/or permanent rupture of the GUV bilayers. To test this hypothesis, we used the lyotropic chromonic LC phase formed from aqueous solutions of disodium cromoglygate (DSCG) (Fig. 1B). We used DSCG, because it is not amphiphilic, and thus, we predicted that it would not disrupt the lipid bilayers of GUVs (in contrast, many surfactants that form lyotropic phases solubilize lipid bilayers). DSCG molecules stack into anisometric assemblies when dissolved in water (9–11) and form mesophases in a manner that depends on temperature and the concentration. We note here that the ordering of nematic DSCG and other chromonic LCs has been explored in confined spherical (12) and cylindrical geometries (13) as well as surrounding rigid spherical inclusions (14).

The results described in this paper yield fundamental insights into the ways in which elastic stresses are coupled to particle shape in soft matter systems, hinting at previously unidentified designs of LC-based responsive and/or active materials. In addition, we note that recent experiments suggest that curvature strain within bacterial and mitochondrial membranes may locally concentrate certain families of lipids to regions of highest membrane curvature. The elastically strained GUVs described in this paper may provide the basis of an experimental platform to further investigate biophysical questions relating to membrane curvature strain (2). Our results also have the potential to provide insights into the recent observation that elastic stresses imparted by LCs can alter bacterial cell shape (15).

Results

Our initial experiments characterized the shapes of GUVs formed on hydrating a dried lipid film [consisting of a ternary mixture of 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC), 1,2-dioleoyl-sn-glycero-3-phosphoethanolamine-N-[methoxy(polyethylene glycol)-2000] (ammonium salt) (DOPE-PEG2000) and N-(4,4-difluoro-5,7-dimethyl-4-bora-3a,4a-diaza-s-indacene-3-propionyl)-1,2-dihexadecanoyl-sn-glycero-3-phosphoethanolamine triethylammonium salt (BODIPY-DHPE)] within a 15% (wt/wt) DSCG solution in its isotropic phase at 48 °C (as detailed in Materials and Methods). At this concentration, we found that DSCG formed a nematic phase below ∼30 °C and an isotropic phase above ∼42 °C, with two-phase coexistence at intermediate temperatures. A small amount (≤2 mol %) of PEG lipid was included in the lipid mixtures to increase steric repulsion between lipid layers on hydration and facilitate the formation of GUVs (16). On inspecting the distribution of the fluorescent probe (BODIPY-DHPE) in samples at 48 °C (prepared such that the DSCG remained in its isotropic phase at all times), we found many approximately spherical lipid domains (Fig. 1C), consistent with the formation of GUVs. We measured the GUVs to have diameters ranging from 2 to 20 µm, although we occasionally found GUVs with diameters as large as 50 µm in our samples. We confirmed the DSCG solutions both inside and outside of the GUVs to be isotropic phases at this temperature by characterizing the samples between crossed polars and observing extinction of transmitted light (Fig. 1D). We note here that we frequently observed small regions of heightened fluorescence near the membranes of some GUVs (Fig. 1C), which we attribute to the presence of small lipid aggregates that associate with the GUVs. We did not observe these fluorescent aggregates to influence the shapes of the GUVs, and they were not observed to change with time (other than because of photobleaching). Additional information regarding GUV lipid and fluorophore miscibility can be found in SI Appendix.

Although the majority of GUVs adopted spherical shapes in isotropic phases of 15% (wt/wt) DSCG, we hypothesized that the GUVs would be strained by cooling of the DSCG solution into its nematic phase because of elastic stresses associated with the deformation of the LC within and outside each GUV. To explore this hypothesis, we quenched a dispersion of vesicles in a 15% (wt/wt) DSCG solution at a rate of ∼10 °C/min from 48 °C (isotropic phase) to 25 °C (pure nematic phase) (Movie S1). On inspection of the sample at 25 °C, we found that the GUVs within the nematic phase had adopted nonspherical, sometimes highly elongated shapes (Fig. 1E). The shapes were stable for the duration of our observations (several hours). Additionally, by inspecting these samples between crossed polarizers, we observed birefringent textures consistent with a nematic LC phase present both inside and outside of the GUVs (Fig. 1F) (discussed in further detail below). We also observed the nonspherical GUVs to align with their major axes parallel to the local orientation of the LC. By heating samples back to 48 °C (isotropic phase), we found that the elongated GUVs reverted to spherical shapes (Movie S2).

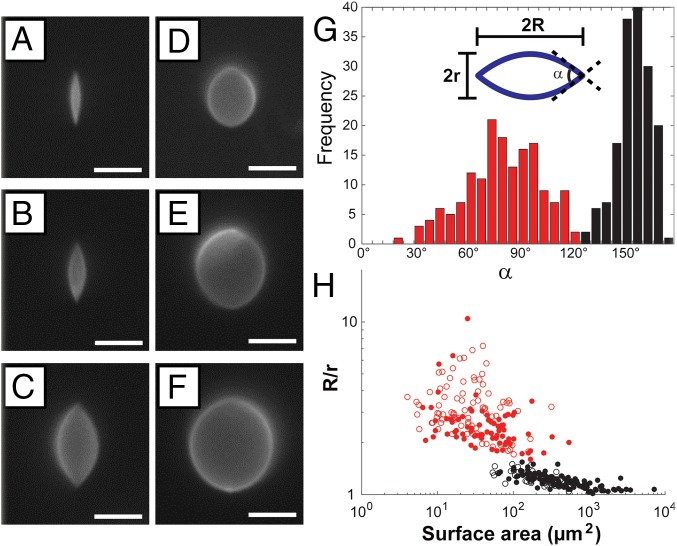
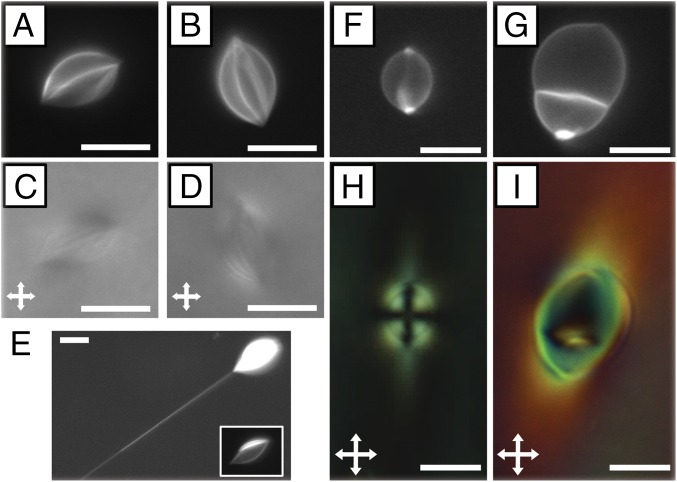
In addition to the highly elongated GUVs of the type shown in Fig. 1 E and F, we also observed a population of GUVs in nematic DSCG with only slightly elongated shapes and approximately rounded poles. Examples of the two populations of GUVs are provided in Fig. 2 A–C (highly strained) and Fig. 2 D–F (slightly strained). By performing confocal microscopy, we confirmed that both populations of GUVs possessed prolate shapes and were symmetric with respect to rotation around their major axes (Movie S3). We analyzed fluorescence micrographs of the GUVs (obtained with the focal plane at the GUV midplane containing the major axis) using a custom MATLAB code (SI Appendix) to quantify the aspect ratio (R/r, where R is the semimajor axis, and r is the semiminor axis), surface area, volume, and cusp angle ($\text{α}$) (defined in Fig. 2G). Inspection of the measured distribution of GUV cusp angles in nematic DSCG (Fig. 2G) supports our conclusion regarding the formation of two populations of strained GUVs separated by a critical cusp angle of $\text{α}\hspace{0.17em}\approx$ 130°.

Fig. 2.

Characterization of the two populations of GUVs that formed in nematic DSCG. Fluorescence micrographs of (A–C) highly elongated, cusped GUVs and (D–F) weakly strained GUVs with approximately rounded poles. (G) Histogram depicting the distribution of cusp angles ($\text{α}$). (H) GUV aspect ratio (R/r) as a function of GUV surface area. In G and H, data in red and black denote GUVs with $\text{α}<$ 130° and $\text{α}>$ 130°, respectively. In H, filled and open points denote GUVs containing 2 mol % PEG lipid and 0.2 mol % PEG lipid, respectively. (Scale bars: 5 µm.)

We also quantified the change in aspect ratio of the vesicles with size by plotting R/r as a function of GUV membrane surface area (SI Appendix, Eqs. S1 and S3) in nematic DSCG (Fig. 2H). In this plot, we distinguish between the population of GUVs possessing sharp cusps ($\text{α}<$ 130°) and the population exhibiting approximately rounded poles ($\text{α}>$ 130°). Fig. 2H reveals that small GUVs (surface area $<$ 50 µm²) typically adopt highly elongated shapes (R/r > 1.54) with sharp cusps in nematic DSCG, whereas larger GUVs (surface area $>$ 500 µm²) adopt slightly elongated shapes (R/r < 1.54) with approximately rounded poles. We also note that there is far greater scatter within the data for GUVs with $\text{α}<$ 130° and that GUVs with surface areas between 50 and 500 µm² exhibit either cusped or rounded poles. Fig. 2H includes data obtained from analysis of GUVs containing 2 or 0.2 mol % PEG lipid plotted as filled and open circles, respectively. Although the rigidity of lipid bilayers increases with increasing PEG lipid content (17), we did not observe the shapes of GUVs in nematic DSCG to depend on PEG lipid concentration. The trends discussed above in the context of Fig. 2H are also evident in a plot of cusp angle vs. GUV surface area (SI Appendix, Fig. S8).

The above-described data provide evidence that GUVs become strained in nematic DSCG, consistent with our initial hypothesis of the influence of LC elastic stresses on GUV shape. However, our observation of two distinct types of nonspherical shapes was not anticipated. We have organized the remainder of this section into two parts, each focusing on one of the two populations of strained GUVs.

Large GUVs with R/r < 1.54.

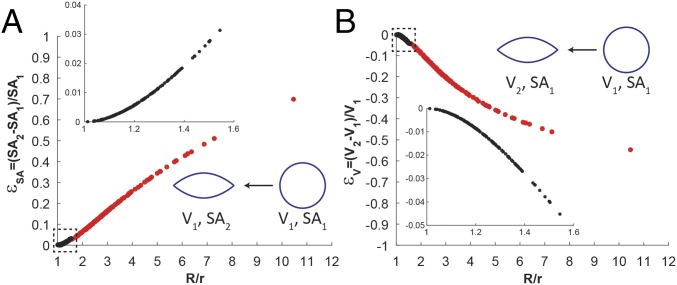
To develop insights into the physical processes leading to the population of large GUVs with R/r < 1.54, we determined first if the transformation from a spherical to an elongated shape involved changes in surface area and/or volume of encapsulated DSCG. Past studies have used micropipette aspiration experiments to establish that the apparent surface area of spherical GUVs prepared from DOPC can expand by up to ∼5% through suppression of thermal undulations and an increase in the average area per lipid molecule (thinning) before rupture at a critical tension of ${\text{τ}}^{\ast }$ = 10 mN/m (18). To assess the likelihood that elastic stresses associated with the nematic LC dilate the GUV surface area and give rise to the population of GUVs with R/r < 1.54, we calculated the fractional expansion of surface area ${\text{ε}}_{\text{SA}}$ required for the nonspherical GUVs in nematic DSCG (with surface area SA₂ calculated from SI Appendix, Eqs. S1 and S3) to encapsulate the same volume as spherical GUVs in isotropic DSCG [with surface area SA₁; ${\text{ε}}_{\text{SA}}=\left(S{A}_2-S{A}_1\right)/S{A}_1$] (Fig. 3A). A modest 3% expansion in membrane surface area can give rise to the most asymmetric GUVs in this population (R/r ∼ 1.54), suggesting that the volume of DSCG encapsulated by GUVs in this population is likely conserved during the DSCG phase transition and straining of the GUV (SI Appendix has additional experimental observations).

Fig. 3.

Fractional changes in surface area and volume calculated to accompany LC-induced GUV shape transformations. (A) Fractional GUV surface area expansion (${\text{ε}}_{\text{SA}}$) calculated for an LC-induced GUV shape transformation at constant internal GUV volume. (B) Fractional change in GUV internal volume (${\epsilon }_{\text{V}}$) calculated for an LC-induced GUV shape transformation at constant GUV membrane surface area. Data in red denote GUVs with cusp angles $\text{α}<$ 130°, and data in black denote GUVs with cusp angles $\text{α}>$ 130°.

Furthermore, we analyzed how an interplay of the LC elastic energy (E_LC) and interfacial membrane energy of the GUV (E_s) might give rise to the equilibrium shapes adopted by GUVs with R/r < 1.54. For this population of slightly elongated GUVs (19), we estimate

$$E_{\text{LC}}=CKR{\left(\frac{r}{R}\right)}^2,$$ [1]

where K is an average elastic constant of the LC [assumed to be 10 pN for 15% (wt/wt) DSCG (20)], and C is a constant. We note that the above estimate of $E_{\text{LC}}$ neglects the unequal magnitudes of the elastic constants of nematic DSCG, a point that we discuss below. We also neglect the membrane bending energy of the GUV in our analysis, because it is negligible compared with E_LC for the GUVs investigated in this paper (SI Appendix). Given our proposal that this population of GUVs forms at constant volume, the major and minor axes of each slightly elongated GUV are related to R₁, the radius of the initially spherical GUV in the isotropic phase of DSCG, by the equation

$$R_1={\left(R{r}^2\right)}^{1/3}.$$ [2]

We describe the interfacial energy required to deform the membrane/interface of the GUV from the initial spherical shape as

$$E_{\text{s}}=\text{τ}S{A}_2,$$ [3]

where $\text{τ}$ is an interfacial energy density that is, in general, a function of R/r, ${\text{ε}}_{\text{SA}}$, and SA₂.

A free energy formulation similar to that described above was previously used to calculate the equilibrium aspect ratio of tactoids arising from the coexistence of nematic and isotropic lyotropic phases (19). Minimizing the total free energy E = E_LC + E_s at constant volume (V) yielded the equation

$$\frac{R}{r}={(\mathrm{CK}/\tau )}^{3/5}{V}^{-1/5}.$$ [4]

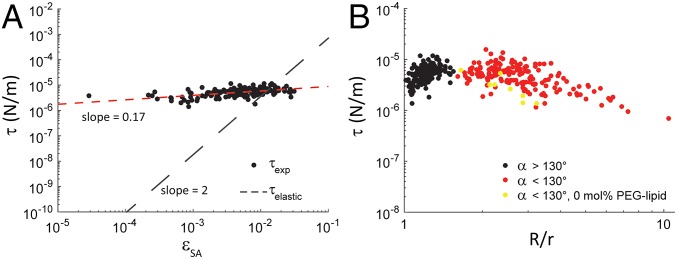
For tactoids, $\text{τ}$ is the interfacial tension between the coexisting nematic and isotropic phases (a constant for a given composition of DSCG). To determine if Eq. 4 might also describe the equilibrium shapes of GUVs in nematic DSCG, we solved Eq. 4 for $\text{τ}$. We evaluated the parameter C in Eqs. 1 and 4 to be ∼6 by solving numerically the Ericksen–Leslie equations with tangential anchoring (see below) for nematic LC inside and outside of prolate spheroidal bodies with aspect ratios matching those that we observed experimentally (SI Appendix shows the numerical calculation). Specifically, we determined how the values of $\text{τ}$ estimated from the experiments (${\text{τ}}_{\text{exp}}$) varied with ${\text{ε}}_{\text{SA}}$, the fractional extension in GUV surface area (at constant volume). Significantly, inspection of Fig. 4A reveals that ${\text{τ}}_{\text{exp}}$ is nearly constant (∼0.01 mN/m) over the entire range of ${\text{ε}}_{\text{SA}}$ values that describe the population of GUVs with R/r < 1.54. In contrast, if the interfacial energy of the GUV was dominated by the elastic energy associated with stretching the GUV membrane, $E_{\text{s}}$ would be given by (21)

$$E_{\text{s}}=\frac{K_{\text{s}}}{2}S{A}_1{\text{ε}}_{\text{SA}}^2,$$ [5]

where K_s is the elastic stretch modulus [K_s ∼ 300 mN/m for DOPC (18)], and $S{A}_1=4\text{π}{R}_1^2$. In this situation, we would expect ${\text{τ}}_{\text{elastic}}\propto {\text{ε}}_{\text{SA}}^2$ (Fig. 4A), where ${\text{τ}}_{\text{elastic}}$ is an interfacial tension that is dominated by an elastic stretching of the GUV membrane.

Fig. 4.

Plots of $\text{τ}$ as a function of fractional GUV surface area expansion (${\text{ε}}_{\text{SA}}$) and GUV aspect ratio (R/r). (A) Log–log plot of ${\text{τ}}_{\text{exp}}$ as a function of ${\text{ε}}_{\text{SA}}$ for the population of GUVs with $\text{α}>$ 130°. The slope of a power law fit to the data is indicated. The relationship between ${\text{τ}}_{\text{elastic}}$ and ${\text{ε}}_{\text{SA}}$ is also shown. (B) Log–log plot of ${\text{τ}}_{\text{exp}}$ as a function of R/r. Data in red and black denote GUVs with cusp angles $\text{α}<$ 130° and $\text{α}>$ 130°, respectively, prepared with 0.2–2 mol % PEG lipid. Data in yellow denote GUVs prepared with 0 mol % PEG lipid, all of which had $\text{α}<$ 130°.

Inspection of Fig. 4A leads to the somewhat surprising conclusion that the interfacial energy of nonspherical GUVs in the LC is not dominated by an energy penalty associated with stretching of the GUV membrane but rather, is dominated by a strain-independent surface energy arising from the presence of an interface between the nematic DSCG and GUV membrane. Moreover, ${\text{τ}}_{\text{exp}}$ has a magnitude similar to the interfacial tension previously measured between coexisting nematic and isotropic DSCG phases (22), although nematic DSCG exists inside and outside the GUVs in our experiment. We return to this point in the following section.

To better understand the nature of the LC-mediated elastic stresses acting on GUVs, we characterized the anchoring and configurations adopted by the nematic phase 15% (wt/wt) DSCG inside and outside the GUVs. We found birefringent “tails” to extend outward from the poles of these GUVs in a direction parallel to the orientation of the far-field director (SI Appendix, Fig. S11 A–C). These tails, which have previously been observed around spherical particles and emulsion droplets with diameters greater than 6 µm that anchor DSCG tangentially (14), are indicative of a twisted configuration of the LC that is favored because of the small twist elastic constant (K₂) of nematic DSCG (20). We conclude also (see below for additional observations) that nematic DSCG is also oriented tangentially at the lipid bilayers of GUVs in our experiments. Consistent with past studies, we found that the tails extending from the two poles of each GUV could exhibit the same handedness of twist (SI Appendix, Fig. S11A) or opposite handedness of twist (SI Appendix, Fig. S11B). However, we did not observe the shapes of GUVs to differ measurably depending on the handedness of the twisted tails.

A recent paper reported that spherical droplets of the chromonic LC, Sunset Yellow, can adopt a twisted bipolar configuration (12). The twisted director configuration is energetically favored over the untwisted configuration when the elastic constants of the LC meet the Williams condition: $K_{33}/K_{11}\le 2.32(1-K_{22}/K_{11})$ (23). Although the elastic constants of Sunset Yellow satisfy this criterion (24), those of nematic DSCG do not (20). In addition, we do not expect the configuration of the LC within the GUV to correspond to a so-called escaped concentric configuration (25) that is observed when the elastic constant for bend (K₃) is smaller than that for splay [K₁; for the DSCG solutions used in our study, the ratio of K₃/K₁ is ∼2.5 (20)]. Other possible internal director configurations have been proposed for nematic LCs confined within spherical droplets with planar surface anchoring (26). Although our observations of the DSCG within the GUVs revealed two point-like features to be commonly located along the minor axis of the GUVs (SI Appendix, Fig. S11 E and F), the birefringence of the LC outside the GUVs made it difficult to determine the origin of these optical features.

Small GUVs with R/r > 1.54.

Next, we address the population of small, highly elongated GUVs (R/r $>$ 1.54) with cusped poles ($\text{α}<$ 130°) in nematic phases of DSCG. We consider whether the highly anisometric shapes of GUVs in this population might also develop as a result of an LC-induced expansion of the GUV surface area at constant GUV volume, similar to the population of larger GUVs (R/r < 1.54) described above. Fig. 3A suggests, however, that this will not occur, because the process would require greater than a 50% expansion of membrane surface area for the most asymmetric GUVs in this population. This expansion is far greater than the ∼5% expansion that DOPC membranes can sustain before rupture (18).

Because the internal volume of this population of GUVs is not conserved during the transition from the isotropic phase to the nematic phase, we considered whether the decrease in GUV volume might be accomplished by an efflux of water (27) but not DSCG molecules across the lipid bilayers of the GUVs. This process would result in an osmotic stress acting across the GUV membrane and based on phase diagrams of aqueous solutions of DSCG, lead to an upward shift in the phase transition temperature of the internal DSCG solution relative to the external DSCG solution (10). To determine whether this prediction might be the case, we compared the volume of each elongated GUV in the nematic phase (V₂ calculated from SI Appendix, Eqs. S2 and S4) with the volume of a spherical GUV (V₁) possessing the same surface area. We determined that this shape transformation would require a 50% reduction in volume for GUVs with the highest aspect ratios (Fig. 3B). Such a large change in the volume of water inside the GUV would lead to an easily measured increase in the phase transition temperatures of the DSCG solution internal to the GUV and/or the formation of higher-order phases (10). Inconsistent with this hypothesis, we found that the phase behavior of the DSCG solution inside of elongated and cusped GUVs was similar to the continuous DSCG phase (for example, Movies S4 and S5).

The results described above, when combined, lead us to conclude that an efflux of both water and DSCG must underlie the formation of highly elongated and cusped GUVs (R/r > 1.54). Because lipid bilayers are not highly permeable to small molecules, such as sucrose, glucose (27) ($M_w=342\hspace{0.17em}\text{g}/\text{mol}$ and $M_w=180.16\hspace{0.17em}\text{g}/\text{mol}$, respectively), or the dye 5,6-carboxyfluorescein (28) ($M_w=376\hspace{0.17em}\text{g}/\text{mol}$), the efflux of DSCG ($M_w=512\hspace{0.17em}\text{g}/\text{mol}$) likely does not occur simply by permeation through intact GUV membranes. Past studies, however, have established that a critical level of tension within a membrane can generate transient pores through which both solutes and water can pass (29). These observations and others (see below) lead us to interpret our results to indicate that strain imposed on the membranes of the GUVs by the nematic DSCG leads to an efflux of the DSCG solution from within the GUVs until the membranes relax sufficiently to allow the pores to dynamically reseal (29).

The above proposal is further supported by the following observations. First, inspection of Fig. 4A reveals that, although ${\text{τ}}_{\text{exp}}\gg {\text{τ}}_{\text{elastic}}$ for most GUVs within the population of slightly elongated GUVs with $\text{α}>$ 130°, we calculate ${\text{τ}}_{\text{elastic}}$ to be comparable in magnitude to ${\text{τ}}_{\text{exp}}$ for the smallest and most highly deformed GUVs in this population. This finding is consistent with a cross-over between the two classes of strained GUVs being defined by the stretching of the lipid membranes of small GUVs to the threshold of transient pore formation (where efflux of the DSCG solution is initiated). Second, the observation that the ratio E_LC/E_s scales as 1/R is consistent with our observation that GUVs smaller than a critical size are strained to the point of transient poration because of LC elastic stresses (Fig. 2H). Third, we note the greater scatter in the data for the population of highly elongated and cusped GUVs in Fig. 2H. This scatter is consistent with the stochastic nature of the pore formation and dynamic resealing processes (29).

Next, we determined if the equilibrium shapes adopted by GUVs with $\text{α}<$ 130° are controlled by a similar interplay between the LC elastic and interfacial energies, which was found for the population of GUVs with $\text{α}>$ 130°. By using experimental data in conjunction with Eq. 4 to generate a plot of ${\text{τ}}_{\text{exp}}$ vs. R/r (Fig. 4B), we found that ${\text{τ}}_{\text{exp}}$ varied weakly as a function of R/r for the population of GUVs with $\text{α}<$ 130° (similar to the population of GUVs with $\text{α}>$ 130°) with values that ranged between 0.01 and 0.001 mN/m. The data suggest that the same coupling between LC elastic energy and GUV–LC surface energy dictates the shapes adopted by all of the GUVs that we observe in nematic 15% (wt/wt) DSCG.

A key finding of our experiments is that the shapes of the GUVs are influenced by a shape-independent interfacial tension. The magnitude of the interfacial energy (∼0.01 mN/m) is similar to that which controls the shapes of tactoids of nematic DSCG dispersed in isotropic phases. We propose that the origin of the interfacial energy associated with the GUVs dispersed in nematic DSCG may arise from depletion of the DSCG concentration near the surface of GUV membranes, effectively creating an “interface” between DSCG-rich and DSCG-poor solutions. Consistent with this interpretation, on heating GUV-containing samples, we observed isotropic domains to form first near the surfaces of GUVs (SI Appendix, Fig. S6 C and D). We note that the PEG lipids are not responsible for this phenomenon, because similar results were obtained in GUVs without PEG lipids (SI Appendix).

We also performed detailed observations of the DSCG director inside and outside of elongated GUVs as described in SI Appendix (a schematic illustration of the director configuration inside and around an elongated GUV is found in SI Appendix, Fig. S12D). For reasons of brevity, we do not detail them here other than to note that neither the nematic DSCG inside highly elongated GUVs nor the nematic DSCG outside highly elongated GUVs showed evidence of the presence of twist, consistent with past observations of nematic tactoids with high aspect ratios (9, 22, 30).

Discussion

The results presented in this paper reveal that spherical GUVs suspended in isotropic 15% (wt/wt) DSCG deform into elongated, nonspherical shapes (spindles) on quenching of the solution into a nematic LC phase. The observation that these shape transformations accompany the DSCG phase transition suggests that elastic stresses imparted by the LC drive the GUV elongation and that a key factor that controls the shapes of the GUVs is a strain-induced efflux of DSCG solution from the interior of the small GUVs. Here, we note that a prior study has documented that the addition of high concentrations [$>$ 6% (wt/wt)] of surfactants to isotropic phases of DSCG [5.5% (wt/wt) DSCG solutions at room temperature] generated nematic domains (31). Additional reports describe that similarly high concentrations of nonamphiphilic molecules, such as poly(vinyl alcohol) (32), PEG (33), and spermine (33), condense DSCG solutions and lead to the formation of nematic and columnar phases. Condensation of DSCG into higher-order phases by concentrated surfactant and polymer solutions is likely the result of depletion effects, whereas electrostatic interactions also may contribute in the case of spermine (33). In contrast, our experiments use low lipid concentrations [∼0.04% (wt/wt)], and we emphasize that the DSCG phase behavior is not substantially perturbed by the presence of the low concentrations. We also note that we did not observe nematic LC phases to form inside or outside GUVs prepared by gentle hydration of lipid films within aqueous solutions of 5.5% (wt/wt) DSCG (SI Appendix, Fig. S1).

The observations reported in our paper document the most common behaviors of GUVs in nematic DSCG. We did, however, observe several GUVs to exhibit behaviors that differed from those described above. First, we note that a small fraction (5–10%) of highly strained GUVs possessed optical features near their poles that hinted at the possible presence of a subtle change of membrane curvature (Fig. 1E). Additional studies are needed to determine if this feature is an optical artifact or a more complex local structure of the membrane near the cusp of these GUVs. Second, although most GUVs in our samples (and all of those analyzed above) exhibited a largely uniform fluorescence signal at their boundaries, a smaller population of elongated and cusped GUVs exhibited a striated appearance in fluorescence and optical micrographs (Fig. 5 A–D), consistent with the presence of folds or wrinkles in the lipid bilayer. These wrinkles in the lipid bilayer were always oriented along the major axis of the GUV. Others have reported previously the formation of wrinkles in GUVs possessing excess surface area (34) as well as elastic, polymeric sheets stretched over millimeter-sized liquid droplets (35). Third, we observed what we interpret to be lipid tubes (36, 37) occasionally extending from the poles of elongated and cusped GUVs (both wrinkled and unwrinkled) (Fig. 5E). Lipid tubes have been reported to form when an extensional force is applied to GUVs under high membrane tensions (38). In our experiments, they seem to form as a result of the LC-mediated elastic stresses that drive the transformation in shape of the GUV. Fourth, we sometimes observed domains exhibiting high fluorescence to be localized near one or both of the poles of slightly elongated GUVs (Fig. 5 F and G). We hypothesize that the polar concentration of these lipids may reflect strain induced in the LC and/or the lipid bilayers (2), including curvature strain within the GUV membrane if there is phase separation within the lipid bilayer (2). Finally, we also identified examples of multiple GUVs interacting with one another in nematic DSCG (Fig. 5 G and I) in a manner consistent with processes of budding or fusion of GUVs. Overall, these observations highlight the rich range of behaviors exhibited by soft phospholipid shells in nematic DSCG.

Fig. 5.

Examples of complex GUV shapes and behaviors observed in nematic phases of DSCG. (A and B) Fluorescence micrographs and (C and D) corresponding optical micrographs (crossed polarizers) of wrinkled GUVs containing 2 mol % PEG lipid GUVs [15% (wt/wt) DSCG at 25 °C]. (E) Fluorescence micrograph of a GUV with a lipid tube extending from its pole. E, Inset is a micrograph collected using a shorter exposure time. (F and H) Fluorescence and crossed polars micrographs, respectively, of a GUV with polar regions exhibiting enhanced fluorescence signals. (G and I) Fluorescence and crossed polars micrographs, respectively, of two GUVs that are either fusing or budding. Details are in the text. (Scale bars: 10 µm.)

Conclusions

In conclusion, this paper reveals the profound influence of the elasticity of LCs on the shape and physical properties of soft colloids. Using GUVs as model soft colloids, we observe the GUVs to be strained into two populations of spindle-like structures with size-dependent aspect ratios. Significantly, the population of large, slightly elongated GUVs forms by expansion of lipid membrane surface area at constant GUV volume, whereas the smaller, highly elongated GUVs form through a mechanism that involves a strain-induced transient pore formation in the GUV bilayer. A key conclusion is that the cross-over between the two populations is defined by the stretching of the lipid membranes of small GUVs to the threshold of transient pore formation (where efflux of the DSCG solution is initiated). This result reveals that LC-induced straining of phospholipid shells provides a potentially useful strategy for controlling membrane properties, including their transmembrane transport properties. Another key finding of our study is that the final shapes of both populations of GUV are controlled by a strain-independent energy associated with the area of contact between the GUV and the nematic LC. The magnitude of the interfacial energy is similar to the nematic–isotropic interface of DSCG solutions. Our observation that isotropic domains of DSCG nucleate near the surface of GUVs on heating hints that the concentration of DSCG may be depleted near the GUV membrane surface. We note also that our study has focused on the influence of isotropic to nematic transitions on the GUVs and that additional studies are required to fully elucidate processes that result in the reformation of spherical GUVs accompanying the nematic to isotropic phase transition (as shown in Movie S2). More broadly, the coupling between LC elastic strain and strain within flexible lipid membranes, as described in this study, may provide guidance to the design of reconfigurable soft materials with potential application in sensing and biology. For example, we envision that these elastically strained GUVs might be attractive model cell membranes and could serve as versatile synthetic platforms to investigate further, for example, how curvature strain influences localization of lipids and proteins in biological membranes.

Materials and Methods

Materials.

A list of materials can be found in SI Appendix.

Lyotropic LC Preparation.

Lyotropic LCs containing DSCG were prepared by mixing 15% (wt/wt) DSCG with 85% (wt/wt) water. At this concentration, the DSCG solution is nematic at room temperature and has a nematic–isotropic coexistence temperature range between 29 °C and 35 °C (10). The mixture was shaken for at least 12 h to ensure complete solubility and homogeneity. Before experimentation, the DSCG solution was heated at 65 °C for 10 min to erase any influence of the history of the sample on its properties.

GUV Preparation.

To enable observations of the behaviors of isolated vesicles, dilute dispersions of GUVs were prepared through the gentle hydration of a dried lipid films containing DOPC, 0.2–2 mol % DOPE-PEG 2000 [or 1,2-distearoyl-sn-glycero-3-phosphoethanolamine-N-[poly(ethylene glycol)2000-N′-carboxyfluorescein] (ammonium salt) (DSPE-PEG2000-CF)], and up to 0.5 mol % BODIPY-DHPE (1 mM total lipid concentration). We modified procedures detailed elsewhere (16) to permit hydration of the GUVs in isotropic phases of DSCG (SI Appendix).

Preparation of Optical Cells.

To investigate GUVs prepared in 15% (wt/wt) DSCG, we added a small volume (∼4.5 µL) of the GUV mixture to a cavity created using sheets of Mylar film (∼60 µm in thickness) placed between two glass substrates. After assembly, the chamber was immediately sealed with epoxy glue to prevent water evaporation. Samples were prepared in the isotropic phase at 48 °C and quenched to the nematic phase at 25 °C to investigate the dynamical shape changes of GUVs that accompany this phase transition. The glass surfaces of the substrates caused degenerate, planar anchoring of the nematic DSCG phase.

Microscopy.

Information about the optical microscopes used in this study and our methods can be found in SI Appendix.