The role of ions in the self-healing behavior of soft particle suspensions

Significance

Understanding when a material crystallizes is of fundamental importance in condensed matter. In many materials, the presence of point defects suppresses crystallization. Surprisingly, colloidal hydrogels can overcome this limitation: A small number of large microgels can spontaneously deswell to fit in the crystal lattice of smaller microgels, thus avoiding the occurrence of point defects. We find that this unique particle deswelling is due to an osmotic pressure difference between the inside and the outside of the microgels resulting from the overlap of counterion clouds of neighboring particles. When this pressure difference exceeds the bulk modulus of the large microgels, these shrink, enabling crystallization without point defects.

Abstract

Impurities in crystals generally cause point defects and can even suppress crystallization. This general rule, however, does not apply to colloidal crystals formed by soft microgel particles [Iyer ASJ, Lyon LA (2009) Angew Chem Int Ed 48:4562–4566], as, in this case, the larger particles are able to shrink and join the crystal formed by a majority of smaller particles. Using small-angle X-ray scattering, we find the limit in large-particle concentration for this spontaneous deswelling to persist. We rationalize our data in the context of those counterions that are bound to the microgel particles as a result of the electrostatic attraction exerted by the fixed charges residing on the particle periphery. These bound counterions do not contribute to the suspension osmotic pressure in dilute conditions, as they can be seen as internal degrees of freedom associated with each microgel particle. In contrast, at sufficiently high particle concentrations, the counterion cloud of each particle overlaps with that of its neighbors, allowing these ions to freely explore the space outside the particles. We confirm this scenario by directly measuring the osmotic pressure of the suspension. Because these counterions are then no longer bound, they create an osmotic pressure difference between the inside and outside of the microgels, which, if larger than the microgel bulk modulus, can cause deswelling, explaining why large, soft microgel particles feel the squeeze when suspended with a majority of smaller particles. We perform small-angle neutron scattering measurements to further confirm this remarkable behavior.

Point defects in crystalline materials disrupt the crystal structure and often prevent crystallization. This is the case, for instance, when large particles are introduced in a crystal of smaller particles. Bragg illustrated the consequences of this disruption using soap bubbles (1). In metal melts, a size mismatch of 15% between the atoms suppresses crystallization (2), and, in hard spheres, which constitute an important model system for condensed matter, a polydispersity above $12\text{\%}$ also prevents crystallization (3). Furthermore, the polydispersity in hard sphere crystals does not exceed 5.7%, due to local segregation of dissimilar particles during crystallization (4, 5).

Remarkably, these restrictions do not necessarily apply to suspensions of soft microgels, which are cross-linked polymer particles immersed in a solvent that can exist in either swollen or deswollen states, depending on external conditions like temperature (6) and pH (7). Indeed, microgel suspensions containing a small fraction of larger particles can crystallize without defects by shrinking the larger particles to a size that is identical to that of the smaller and more abundant microgel particles (8). This deswelling was hypothesized to result either from the direct interaction between large and small particles or from the osmotic pressure exerted by the small microgels on the larger ones (2). Here, we show that none of these effects drive this process. Instead, we find that the counterions bound to the microgel periphery as a result of their electrostatic attraction to the peripheral microgel charges can, at sufficiently large concentration of the small microgels, delocalize and explore the available volume outside the particles, hence exerting the required osmotic pressure to cause deswelling of the larger microgels. Interestingly, this same mechanism could also explain similar deswelling behavior in suspensions of DNA-coated colloids with star-shape architecture (9).

We use large and small temperature-responsive poly(N-isopropylacrylamide) (pNIPAM) microgels (10) and study aqueous suspensions with the particles in the fully swollen state at 18 °C < T < 21 °C (11). In these conditions, the radii of the large and small particles are $R_{\text{b}}\approx 180\hspace{0.17em}\text{nm}$ and either $R_{\text{s}}\approx 135\hspace{0.17em}\text{nm}$ or $R_{\text{s}}\approx 120\hspace{0.17em}\text{nm}$, respectively, as determined by small-angle neutron scattering (SANS); see Table S1 for a detailed list of the different particles we use. These are all synthesized according to the same protocol. Furthermore, at fixed temperature, the suspension phase behavior is essentially determined by the suspension volume fraction, ϕ. However, due to microgel deformability and compressibility, the particle volume and, therefore, ϕ are difficult to quantify, particularly at high particle number densities. As a result, we use a generalized volume fraction, ζ, obtained from the polymer mass fraction and a mapping of the dilute suspension viscosity to the hard sphere expectation (Supporting Information and ref. 12). For low ϕ, $\zeta =\varphi$. In contrast, for sufficiently high ϕ, the particles must deform and shrink to fit into the available space. As a result, ζ can take values larger than 1 at sufficiently high concentrations, whereas ϕ is, at most, equal to 1. Note that ζ is always proportional to the particle number concentration.

Table S1.

Radii and size ratios of the small (s) and large (b) particles used in our studies

Figure	$R_{\mathbf{s}}$ DLS	$R_{\mathbf{b}}$ DLS	$R_{\mathbf{s}}$ SAXS	$R_{\mathbf{b}}$ SAXS	$R_{\mathbf{s}}$ SANS	$R_{\mathbf{b}}$ SANS	$R_{\text{s}}/R_{\text{b}}$	Small (s)	Large (b)
1A	$137\pm 1$	$182\pm 2$	$-$	$173\pm 4$	$131\pm 5$	$176\pm 4$	$0.74\pm 0.05$	Protonated	Protonated
1B	$140.4\pm 0.9$	$182\pm 2$	$-$	$173\pm 4$	$135\pm 3$	$176\pm 4$	$0.77\pm 0.03$	Protonated	Protonated
1C	$138\pm 1$	$187\pm 3$	$133\pm 2$	$181.4\pm 0.5$	$133\pm 2$	$180\pm 8$	$0.74\pm 0.04$	Protonated	Protonated
1D	$141\pm 1$	$182\pm 2$	$137.6\pm 0.5$	$173\pm 4$	$133\pm 4$	$176\pm 4$	$0.76\pm 0.04$	Protonated	Protonated
1E	$142.9\pm 0.9$	$182\pm 2$	$138.4\pm 0.7$	$173\pm 4$	$137\pm 4$	$176\pm 4$	$0.78\pm 0.04$	Protonated	Protonated
1F	$142.9\pm 0.9$	$187\pm 3$	$138.4\pm 0.7$	$181.4\pm 0.5$	$137\pm 4$	$180\pm 8$	$0.76\pm 0.06$	Protonated	Protonated
2A (red triangles)	$138\pm 4$	$182\pm 2$	$-$	$173\pm 4$	$117\pm 7$	$176\pm 4$	$0.66\pm 0.05$	Deuterated	Protonated
2A (black plus signs)	n/a	$182\pm 2$	n/a	$173\pm 4$	n/a	$176\pm 4$	n/a	n/a	Protonated
4 (red triangles)	$136.3\pm 0.9$	n/a	$123\pm 2$	n/a	$125\pm 5$	n/a	n/a	Protonated	n/a
4 (black plus signs)	$136.3\pm 0.9$	n/a	$123\pm 2$	n/a	$125\pm 5$	n/a	n/a	Protonated	n/a
4 (purple diamonds)	$142.9\pm 0.9$	$189\pm 3$	$138.4\pm 0.7$	$-$	$137\pm 4$	$181\pm 4$	$0.76\pm 0.04$	Protonated	Deuterated
4 (green asterisks)	$142.9\pm 0.9$	n/a	$138.4\pm 0.7$	n/a	$137\pm 4$	n/a	n/a	Protonated	n/a

We indicate in the first column the figure in the article where the particular samples are used, and also point out whether the particles are protonated and made with NIPAM, or deuterated and made with D₇-NIPAM. Particle sizes are determined with DLS, SAXS, and SANS. “n/a” is used to indicate when a given column does not apply to a given sample, and “$-$” reflects that the corresponding measurement was not performed.

To study the effect of larger pNIPAM particles on the phase behavior of a suspension of smaller pNIPAM particles, we prepare bidisperse suspensions at various number fractions of the large particles, $n_{\text{b}}$, which we calculate from the single-particle masses of both small and large particles and the corresponding total masses in the bidisperse sample. The total ζ of the suspension is obtained as $\zeta ={\zeta }_{\text{s}}+{\zeta }_{\text{b}}$, where ${\zeta }_{\text{s}}$ and ${\zeta }_{\text{b}}$ are calculated from the swollen volumes of the small and large particles, respectively, and the total volume of the suspension (Supporting Information). The small and large pNIPAM species have a polydispersity ≤ 12% and crystallize at ${\zeta }_{\text{f}}\approx 0.59$, consistent with previous experiments with the same type of particles (12).

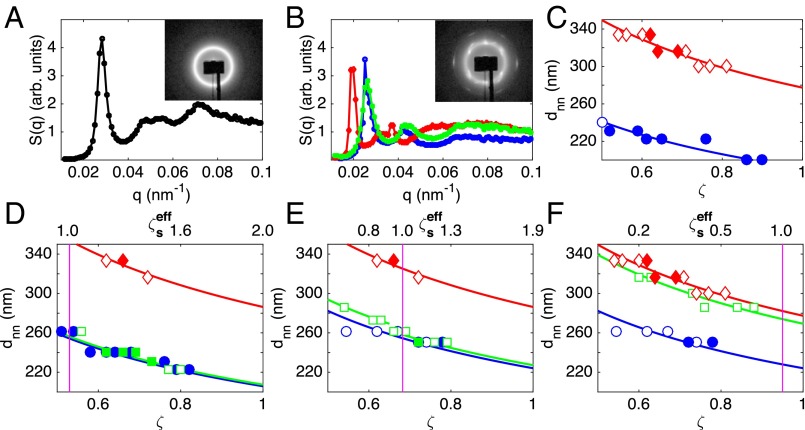
For each $n_{\text{b}}$, a series of suspensions is prepared covering a ζ-range containing both the freezing and melting points of the suspension of small microgels; typically $0.5\lesssim \zeta \lesssim 0.9$. The size ratio of the small and large particles is within the range $0.74<R_{\text{s}}/R_{\text{b}}<0.78$ for all sample series (Supporting Information). We use small-angle X-ray scattering (SAXS) to characterize the phase behavior and elucidate the response of the large particles. We obtain the structure factor, $S\left(q\right)$, by dividing the measured scattered intensity, $I\left(q\right)$, by the form factor, $P\left(q\right)$ (Supporting Information and refs. 11 and 13), which we independently determine with dilute samples. An example of a detector image and the corresponding $S\left(q\right)$ is shown in Fig. 1A for a bidisperse sample in the glassy state with $n_{\text{b}}=\left(1.4\pm 0.1\right)\text{\%}$ and $\zeta =0.76\pm 0.02$. In this case, we use the position of the first peak in $S\left(q\right)$ to obtain the nearest neighbor distance, $d_{\text{nn}}$; we do the same for all liquid and glassy samples. However, for crystalline samples, we find that $S\left(q\right)$ is consistent with a random hexagonal close packed structure for both monodisperse and bidisperse samples; this structure is consistent with what has been reported before for similar and other microgel suspensions and is also realized by hard and charged spheres (14–18). In this case, we obtain the lattice constant and hence $d_{\text{nn}}$ from the position of the second ring of Bragg peaks, which can be clearly seen in the detector image, as shown in Fig. 1B for $n_{\text{b}}=\left(6.6\pm 0.7\right)\text{\%}$ and $\zeta =0.67\pm 0.01$. The second ring of peaks is chosen, as these peaks are true Bragg peaks, whereas the first and third rings are due to Bragg rods (19). The $d_{\text{nn}}\left(\zeta \right)$ curves for monodisperse suspensions of only small or large particles clearly reflect the size difference between the two types of particles, as shown in Fig. 1C.

Fig. 1.

(A) Structure factor, $S\left(q\right)$, of a glassy suspension with $n_{\text{b}}=\left(1.4\pm 0.1\right)\text{\%}$ and $\zeta =0.76\pm 0.02$. (Inset) The detector image. (B) $S\left(q\right)$ of a bidisperse and the two corresponding monodisperse crystalline samples with (green) $n_{\text{b}}=\left(6.6\pm 0.7\right)\text{\%}$ and $\zeta =0.67\pm 0.01$, (blue) $\zeta =0.62\pm 0.01$, and (red) $\zeta =0.63\pm 0.02$. (Inset) The detector image of the bidisperse sample. (C−F) Nearest neighbor distance, $d_{\text{nn}}$, versus generalized volume fraction, ζ, for (blue circles) small-only, (red diamonds) large-only, and (green squares) bidisperse suspensions with (D) $n_{\text{b}}=\left(2.3\pm 0.2\right)\text{\%}$, (E) $n_{\text{b}}=\left(29\pm 3\right)\text{\%}$, and (F) $n_{\text{b}}=\left(79\pm 8\right)\text{\%}$. Crystalline samples are represented by filled symbols. The lines are fits to $d_{\text{nn}}\left(\zeta \right)=a{\zeta }^{-1/3}$, with a as a fitting parameter. In D−F, ${\zeta }_{\text{s}}^{\text{eff}}$ is given by the upper x axis, and the violet vertical line indicates a value of ${\zeta }_{\text{s}}^{\text{eff}}=1$. The swollen radii of the particles used in all shown measurements are listed in Table S1.

Remarkably, we find $d_{\text{nn}}$ in samples with $n_{\text{b}}=\left(2.3\pm 0.2\right)\text{\%}$ to be the same as in monodisperse samples of only small particles, as shown by the squares in Fig. 1D. The decrease of $d_{\text{nn}}$ with ζ reflects isotropic shrinkage of this length scale. Indeed, the data for the small-only and large-only suspensions, as well as that for bidisperse suspensions, follow the functional form expected in this situation: $d_{\text{nn}}=a{\zeta }^{-1/3}$, with a the nearest neighbor distance at $\zeta =1$, which we use as a fitting parameter; this is shown by the curves in Fig. 1 C and D. Note that the curves for the bidisperse sample and the sample comprising only small particles virtually coincide throughout the studied ζ-range. Furthermore, for $n_{\text{b}}=\left(6.6\pm 0.7\right)\text{\%}$, the Bragg peaks of the crystalline bidisperse sample, shown with squares in Fig. 1B, appear at the same q values as the Bragg peaks found in the monodisperse sample of only small particles, shown with circles in Fig. 1B. In the bidisperse sample, the absence of Bragg peaks or a fluid peak reminiscent of a crystal or fluid formed by large particles excludes segregation of small and large particles in these samples. We thus conclude that the large particles deswell and do not significantly disrupt the lattice in crystalline samples, consistent with earlier real-space observations of similar microgel suspensions (8), nor do they disrupt the small-particle arrangement in liquid and glassy samples. Note that, in our experiments, the fraction of large particles is significantly larger than that in prior experiments (8).

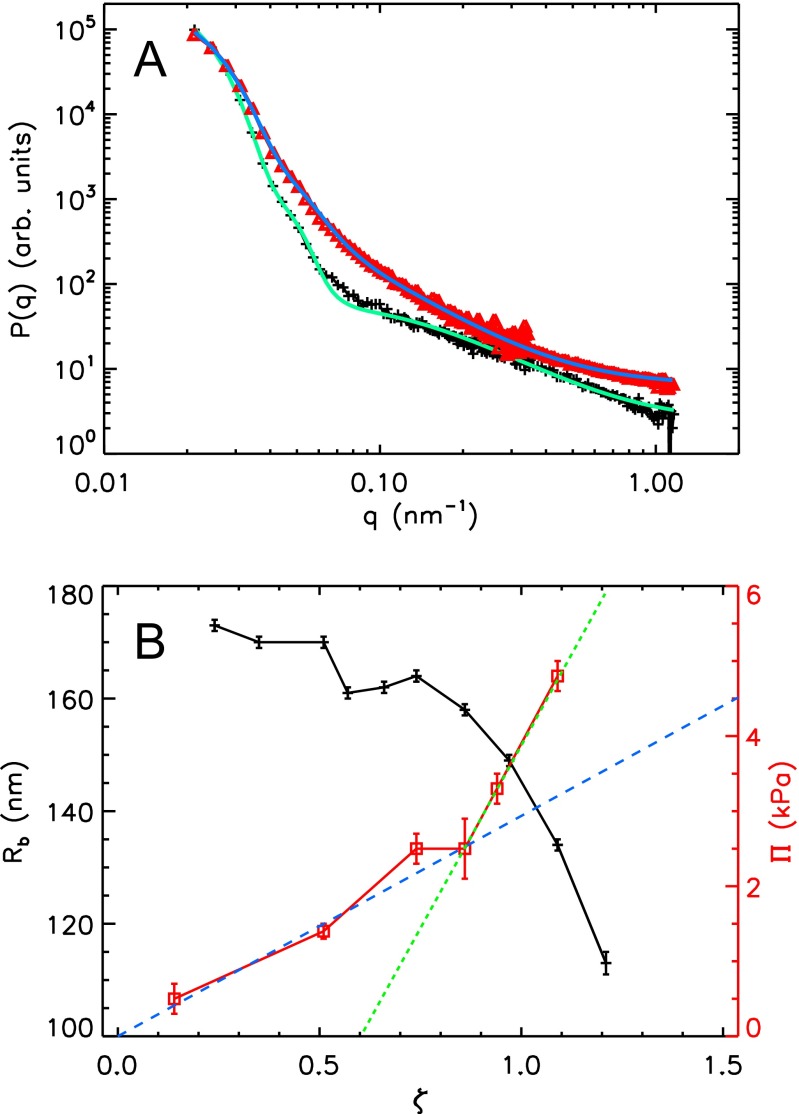
We directly confirm the deswelling of the large particles with SANS using contrast matching to suppress the scattering signal from the small particles (Fig. S1, Supporting Information, and refs. 20 and 21). We thus use deuterated small particles with $R_{\text{s}}=\left(117\pm 7\right)$ nm and large particles with $R_{\text{b}}=\left(176\pm 4\right)$ nm; the resulting size ratio is $R_{\text{s}}/R_{\text{b}}=0.66\pm 0.05$. In this situation, we directly measure the form factor of the large particles, which we fit with a well accepted core−shell model for pNIPAM microgels to obtain the particle radius (Supporting Information, Table S2, and refs. 11 and 13). The result for a bidisperse suspension at $\zeta =0.85\pm 0.05$ and $n_{\text{b}}=\left(2.9\pm 0.3\right)\text{\%}$ is shown by the triangles in Fig. 2A. For comparison, we show with pluses in the same figure the result for a suspension of only large microgels at $\zeta \approx 0.08$, which is dilute enough to directly measure the particle form factor without contrast matching. The corresponding curve shows a faster decay with q, indicating a larger particle size in this case compared with the bidisperse situation. This confirms that the larger microgels have indeed shrunken in the bidisperse suspension. We quantify this behavior in terms of ζ and find that the radius of the larger microgels remains approximately constant and equal to the dilute radius up to $\zeta \approx 0.5$, where it decreases slightly before a more pronounced decrease at $\zeta \approx 0.85$, as shown in Fig. 2B. Note that $R_{\text{b}}=\left(113\pm 2\right)$ nm at $\zeta \approx 1.2$, which coincides with the radius of the small microgels, $R_{\text{s}}=\left(117\pm 7\right)$ nm, measured in dilute conditions and without contrast matching techniques.

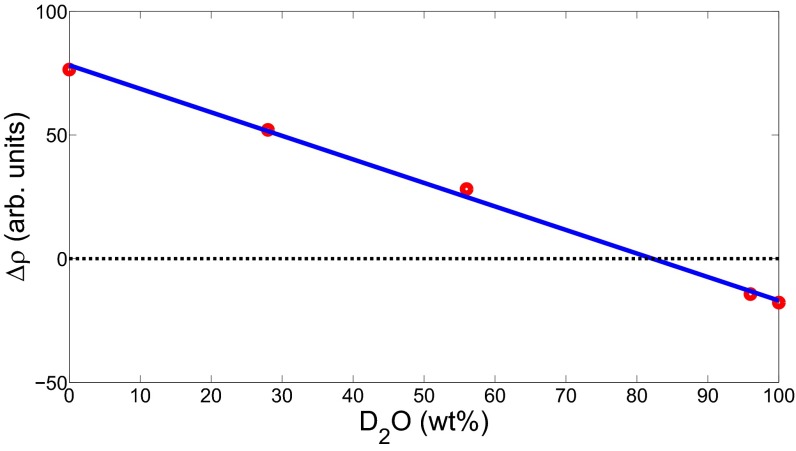
Fig. S1.

Scattering contrast $\mathrm{\Delta }\rho$ (red circles) versus wt% of D₂O. The match point of the deuterated small particles is given by the point, where the linear fit (blue line) to the data crosses $\mathrm{\Delta }\rho =0$.

Table S2.

Form factor parameters obtained from the fits to the SANS measurements using the form factor model given in Particle Form Factor

Sample	Protonated	${\zeta }^{\mathbf{e}\mathbf{f}\mathbf{f}}$	R, nm	$R_{\mathbf{c}}$, nm	σ, nm	${\sigma }_{\mathbf{p}}$, %	ξ, nm
cm1	Large ($2.9\pm 0.3$%)	$2.17\pm 0.04$	113 $\pm$ 2	84 $\pm$ 1	$14.4\pm 0.5$	11 $\pm$ 3	$7.2\pm 0.5$
cm2	Small ($16\pm 3$%)	$2.14\pm 0.03$	95 $\pm$ 5	83 $\pm$ 2	$6\pm 1.5$	10 $\pm$ 2	11 $\pm$ 3

Here, cm1 and cm2 are the samples that show the maximum deswelling. The errors of the parameters have been obtained form the data fit. We also report the percentages of protonated particles and ${\zeta }^{\text{eff}}$.

Fig. 2.

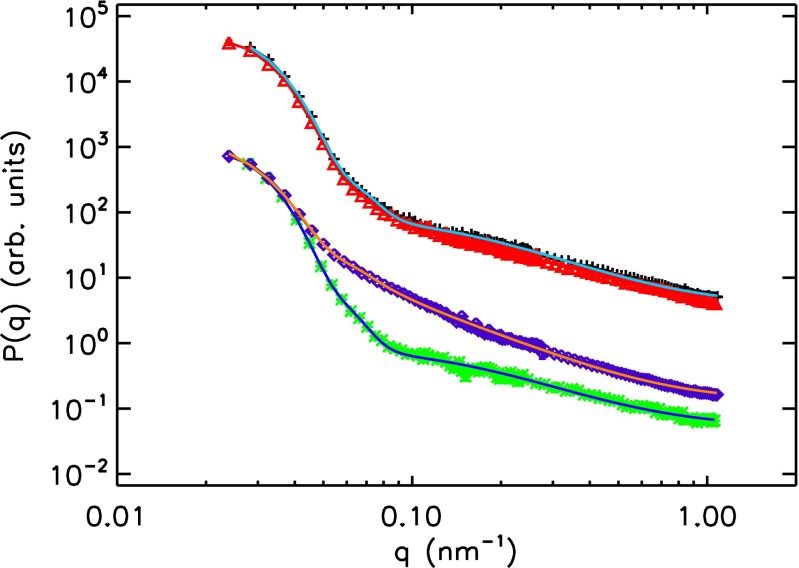
(A) SANS form factors of the large microgels and corresponding fits in (red triangles) a bidisperse sample with $n_{\text{b}}=\left(2.9\pm 0.3\right)\text{\%}$ and $\zeta =0.85\pm 0.05$ and in (black plus signs) a monodisperse large-only sample with $\zeta \approx 0.08$. See Table S1 for fully swollen particle radii. The lines show the form factor fits to the data. (B) SANS radius of the large particles (black plus signs) in the bidisperse sample shown in A and the osmotic pressure (red squares) vs. ζ. The dashed lines are linear fits to $\mathrm{\Pi }\left(\zeta \right)$ for (blue) $\zeta <0.85$ and (green) $\zeta >0.85$ highlighting the change in slope at $\zeta \approx 0.85$.

Interestingly, for bidisperse suspensions with a higher $n_{\text{b}}=\left(29\pm 3\right)\text{\%}$, we find that the $d_{\text{nn}}\left(\zeta \right)\propto {\zeta }^{-1/3}$ behavior only coincides with the corresponding behavior of suspensions with only small particles for $\zeta \gtrsim 0.67$. Below this ζ, the fits of this functional form to the data do not lie on top of each other, as shown in Fig. 1E. This suggests that the large particles only deswell to a size close to that of the small particles for $\zeta \lesssim 0.67$.

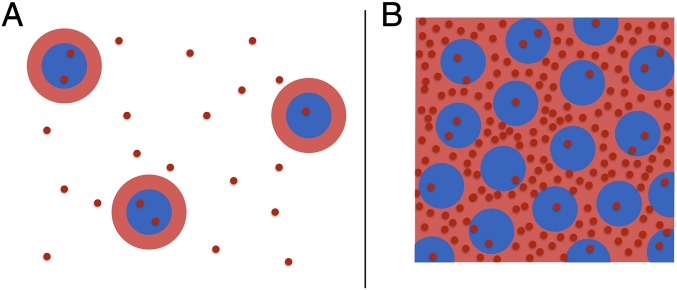
To explain the observed deswelling of the large particles and its dependence on $n_{\text{b}}$, we recall that, despite the fact that NIPAM is not charged, pNIPAM particles contain charged groups at their periphery resulting from the initiator, ammonium persulfate, used in the synthesis (22). As a result, our particles contain ${\text{SO}}_3^{-}$ groups in their outskirts. Correspondingly, there are ${\text{NH}}_4^{+}$ counterions in solution. Interestingly, for the case of ionic microgels, which are charged throughout their bulk, these counterions control the compression of the particles (23). In this case, there is a Donnan potential inside the microgels that confines most of these counterions to the microgel interior. Only those attracted with a strength ≤ k_BT can leave the particles and contribute to the external osmotic pressure to potentially deswell the particles. In our case, however, most of the charge is located in the periphery of the particles rather than throughout their bulk. Hence there is a cloud of bound counterions in the peripheral region of each microgel, as shown schematically in Fig. 3A. In this case and in contrast to the ionic microgel case, those ions that are attracted to the peripheric charged region with a strength ≤ k_BT, distribute both outside and inside the particles, as shown schematically in Fig. 3A. Hence the distribution of these unbound counterions will not result in the osmotic pressure difference between the inside and the outside of the microgel required to explain the deswelling we observe experimentally.

Fig. 3.

Schematics of the microgel particles (blue), their counterion cloud (red rings), and free counterions (red points) (A) in dilute conditions and (B) at high concentration with percolated counterion clouds and bound counterions contributing to the osmotic pressure of the suspension.

To confirm this, we study suspensions of particles with fully swollen radius $R=\left(125\pm 5\right)$ nm at $\zeta \lesssim 0.08$ with added salt. Because we expect the salt ions to distribute both inside and outside of the microgels, they should not induce particle deswelling. We determine the suspension form factor using SANS at concentrations of the salt NaSCN equal to 2.5 mM, 7.1 mM, and 115.3 mM; we then fit the data with the core−shell form factor model and determine the particle radius (Supporting Information). We note that, at the highest salt concentration, the number of salt ions exceeds the number of counterions in our samples. We find that the form factors are virtually identical and are identical to the salt-free case, as shown with black plus signs and red triangles in Fig. 4. Consistent with this, we find $R=\left(125\pm 5\right)$ nm for the case without added salt, and $R=\left(123\pm 3\right)$ nm for the case with the highest salt concentration. These results thus confirm that, indeed, all unbound ions distribute themselves inside and outside the microgels without inducing a significant osmotic pressure difference.

Fig. 4.

SANS form factors and corresponding fits; green asterisks, monodisperse small-only sample at $\zeta \approx 0.08$; purple diamonds, bidisperse sample with $n_{\text{b}}=\left(84\pm 3\right)$%, $\zeta =1.20\pm 0.01$, and a radius $R=\left(95\pm 5\right)$ nm of the deswollen small particles; black plus signs, monodisperse sample at $\zeta \approx 0.08$ with 115.3 mM NaSCN; and red triangles, same as black plus signs but without NaSCN salt. See Table S1 for fully swollen particle radii. The fit for the black plus signs is not shown.

With increasing ζ, however, the distance between particles decreases and, eventually, the clouds of those counterions that are bound to the peripheral charged region with a strength $>k_{\text{B}}T$ overlap. In this concentrated case, the clouds can fill the space between the particles, and these bound counterions can no longer be related to an individual microgel particle, but they rather explore the outside space, thus creating an external osmotic pressure, as schematically shown in Fig. 3B. This external pressure cannot be balanced by the unbound counterions inside the particles, as the counterion density inside remains essentially unchanged. We then hypothesize that the resulting osmotic pressure due to these initially bound and now delocalized counterions is the cause for the deswelling behavior of the large microgels observed experimentally.

To test this, we measure the osmotic pressure, $\mathrm{\Pi }$, of the bidisperse suspension used in the SANS experiments using a membrane osmometer (Wescor 4420). We find that, at low ζ, $\mathrm{\Pi }$ is much larger than what is expected for a fluid of microgels. Furthermore, it increases linearly with ζ up to $\zeta \approx 0.85$, as shown in Fig. 2B with squares. Above this ζ-value and up to the highest ζ we experimentally probe, the behavior of $\mathrm{\Pi }$ is also consistent with a linear growth. However, in this ζ-range, the slope is considerably larger than that at lower ζ, as also shown in Fig. 2B. The observed behavior for $\zeta \lesssim 0.85$ can be understood by realizing that $\mathrm{\Pi }$ is determined by the unbound counterions, as these are much more numerous than the microgel particles (23). Because these ions are only those that can escape the electrostatic attraction to the microgel periphery, their number must be significantly lower than the total number of counterions. By assuming an ideal gas of free counterions, we expect $\mathrm{\Pi }=N_{\text{free}}{k}_{\text{B}}T\zeta /V_{\text{p}}$, with $N_{\text{free}}$ the number of unbound counterions per particle and $V_{\text{p}}$ the volume of a fully swollen microgel particle. We then fit the experimental $\mathrm{\Pi }$ versus ζ, for $\zeta \lesssim 0.85$, and obtain $N_{\text{free}}=\left(8\pm 2\right)\cdot {10}^3$ from the slope of the fit. This corresponds to a counterion density of $\left(9.4\pm 2.6\right)\cdot {10}^{-4}$ nm⁻³ at $\zeta =0.85$, which supports the ideal gas approximation. Furthermore, from the synthesis, we estimate a total number of $N=\left(6.8\pm 0.3\right)\cdot {10}^4$ counterions per particle (Supporting Information). As a result, $N_{\text{free}}/N\approx 11\text{\%}$, which is small, consistent with our expectation. For larger ζ, when the clouds of bound counterions overlap, these ions would then contribute to Π. We interpret the higher slope of $\mathrm{\Pi }\left(\zeta \right)$ for $\zeta \gtrsim 0.85$ as an indication of this fact.

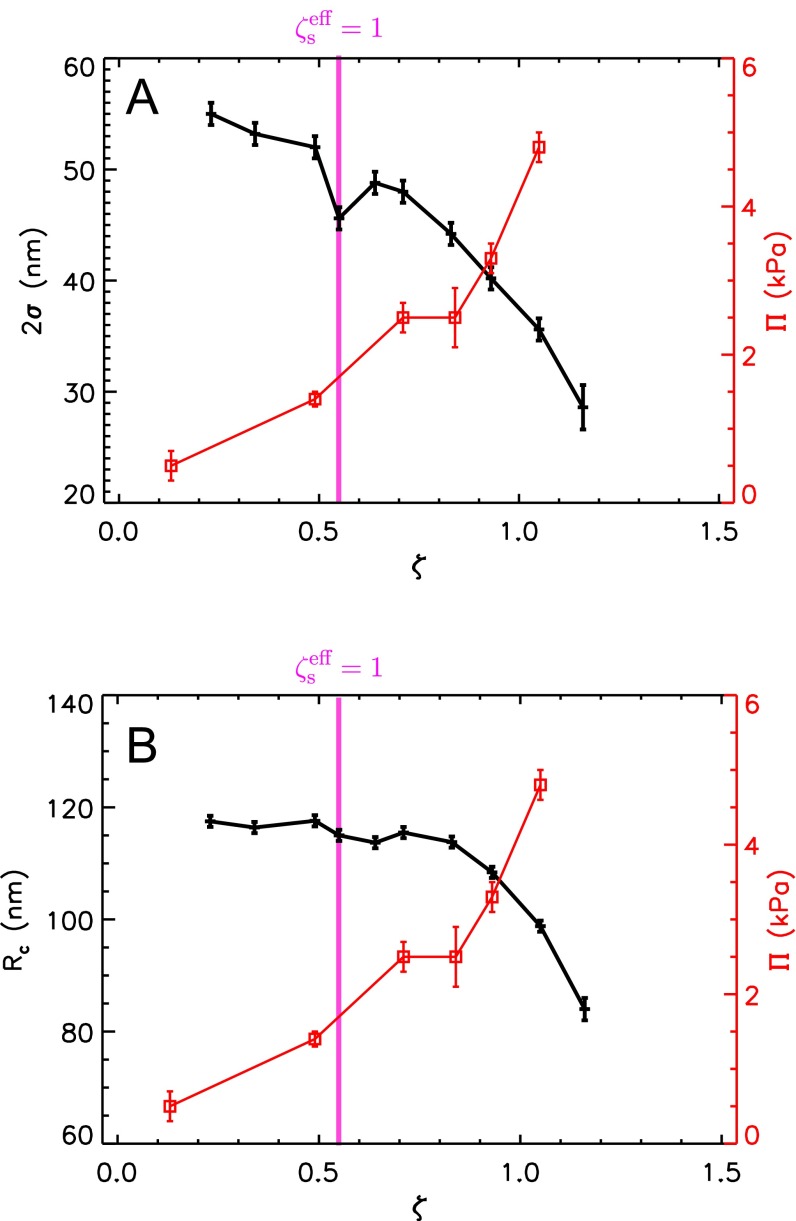
The osmotic pressure behavior is thus supportive of the role played by the bound counterions in our experiments. To further confirm this, we recall that the onset of deswelling in the bidisperse suspension with $n_{\text{b}}=\left(29\pm 3\right)\text{\%}$ occurs at $\zeta \approx 0.67$, highlighted by the vertical line in Fig. 1E, which is close to where $\mathrm{\Pi }$ appreciably changes slope. Indeed, for $\zeta \approx 0.67$, the osmotic pressure difference between the inside and outside of the particles, due to the initially bound counterions, is enough to deswell the fuzzy shell of the particles, as shown in Fig. S2A. As ζ progressively increases, this osmotic pressure difference increases and, eventually, also, the core of the particles gets compressed; this happens at $\zeta \approx 0.85$, as shown in Fig. S2B. Therefore, the change in behavior of the suspension osmotic pressure approximately occurs when the microgel particle appreciably compresses, supporting our interpretation of the results.

Fig. S2.

The ζ-dependence of the width of the fuzzy shell (A) and the core radius (B) of the large particles in a bidisperse sample with $n_{\text{b}}=\left(2.9\pm 0.3\right)\text{\%}$ as determined using SANS with contrast matching. The increase of the osmotic pressure with ζ is shown by the squares and the y axis on the right in both panels.

To further test the proposed mechanism, consider an effective particle consisting of a microgel with radius R and a cloud of bound counterions of thickness $\mathrm{\Delta }r$; the overall particle radius is $R^{\text{eff}}=R+\mathrm{\Delta }r$. We also introduce an effective volume fraction for the small particles in the bidisperse suspensions, ${\zeta }_{\text{s}}^{\text{eff}}={\left(R_{\text{s}}^{\text{eff}}/R_{\text{s}}\right)}^3\hspace{0.17em}{\zeta }_{\text{s}}/\left(1-{\varphi }_{\text{b}}\right)$, where ${\varphi }_{\text{b}}$ is the volume fraction occupied by the large particles. This effective volume fraction corresponds to the volume fraction of the small particles calculated with their effective radius and their accessible volume, which is given by the total suspension volume without the volume occupied by the large particles. Based on our hypothesis, we expect deswelling of the large particles when the space between small particles is filled by the counterion clouds; this corresponds to ${\zeta }_{\text{s}}^{\text{eff}}\gtrsim 1$. By identifying the onset of deswelling in our data for $n_{\text{b}}=\left(29\pm 3\right)\text{\%}$ at $\zeta =0.67$ with the point where ${\zeta }_{\text{s}}^{\text{eff}}\approx 1$, we obtain a value of $\mathrm{\Delta }r=\left(35\pm 4\right)$ nm. Using this value for $\mathrm{\Delta }r$, we can obtain the ζ corresponding to ${\zeta }_{\text{s}}^{\text{eff}}\approx 1$ for other values of $n_{\text{b}}$. For $n_{\text{b}}=\left(2.3\pm 0.2\right)\text{\%}$, we obtain $\zeta \approx 0.53$, which we show with a vertical line in Fig. 1D. Because, in this case, ${\zeta }_{\text{s}}^{\text{eff}}>1$ for all of the studied ζ-range, deswelling is expected throughout, consistent with our observations. In contrast, for $n_{\text{b}}=\left(79\pm 8\right)\text{\%}$, the ζ-value corresponding to ${\zeta }_{\text{s}}^{\text{eff}}\approx 1$ is above any ζ used in the experiments, as shown by the vertical line in Fig. 1F; hence no deswelling is expected. In this case, we find that $d_{\text{nn}}$ is comparable to that in suspensions of only large particles and significantly larger than $d_{\text{nn}}$ in suspensions of only small particles, as shown in Fig. 1F, consistent with our interpretations. Note that the ζ-value associated with the onset of deswelling depends on $n_{\text{b}}$: Although the large particles are found to deswell at ζ below random close packing for $n_{\text{b}}=\left(2.3\pm 0.2\right)\text{\%}$ (Fig. 1D), they do not deswell for any of the accessed ζ, which includes values significantly above random close packing, for $n_{\text{b}}=\left(79\pm 8\right)\text{\%}$ (Fig. 1F). This observation suggests that a direct interaction between large and small particles is not the reason for particle deswelling.

To independently estimate $\mathrm{\Delta }r$, we perform three Monte Carlo simulations of a single microgel particle in water with radius $R=130$ nm, charge $-7\cdot {10}^{4}e$ homogeneously distributed on the surface, and the associated counterions (Supporting Information). Here, e represents the elementary charge. The microgel and its counterions are confined in a spherical volume resulting in microgel volume fractions $\varphi =0.05$, 0.25, and 0.5 for the three simulations. The counterions are treated as mobile, point-like charges with radius 0.007 nm and charge e. Their distribution around the microgel particle is obtained from the simulation, as shown in Fig. S3A. Furthermore, the electrostatic potential, $\psi \left(r\right)$, is obtained from the sum of the potential due to the fixed surface charge and all counterions (see Fig. S3B). We find that most counterions are trapped close to the particle surface, where the potential energy reaches its minimum value. We find the simulation at $\varphi =0.5$ to correspond to the situation with strong overlap of the counterion clouds of neighboring particles and a higher counterion density outside than inside the particle. Following our idea of an effective particle comprising the counterion cloud and resulting in a volume fraction ${\varphi }^{\text{eff}}\approx \varphi {\left[\left(R+\mathrm{\Delta }{r}_{\text{sim}}\right)/R\right]}^3=1$, we obtain the estimate $\mathrm{\Delta }{r}_{\text{sim}}\approx 34$ nm (Supporting Information), which agrees with our experimental value $\mathrm{\Delta }r\approx 35$ nm. We further note that this value is in good agreement with what was found in a dielectric spectroscopy measurement of $\mathrm{\Delta }r$ (22).

Fig. S3.

(A) Counterion density and (B) dimensionless electrostatic potential $e\psi \left(r\right)/k_{\text{B}}T$ versus the distance from the particle center r obtained from Monte Carlo simulations. The simulation data taken at $\varphi =0.05$, 0.25, and 0.5 are shown in blue, red, and green, respectively.

We thus conclude that the deswelling of the large particles in the presence of smaller particles results from the osmotic pressure exerted by the bound counterions, when ζ is large enough for these ions to effectively unbind. However, this osmotic pressure difference should also be felt by the small microgels. To see whether this is the case, we perform a SANS experiment with a sample containing a majority of deuterated large particles, $n_{\text{b}}=\left(84\pm 3\right)$%, with radius $R_{\text{b}}=\left(181\pm 4\right)$ nm and protonated small particles with $R_{\text{s}}=\left(137\pm 4\right)$ nm (Supporting Information). We contrast match the deuterated large particles and probe the form factor of the small microgels in concentrated samples. Indeed, we find that the small particles deswell; from fits of the form factors measured in the bidisperse suspension at $\zeta =1.20\pm 0.01$ (see Table S2) and for a dilute suspension of only small microgels, shown with diamonds and asterisks, respectively, in Fig. 4, we obtain that $R_{\text{s}}$ decreases by $\mathrm{\Delta }{R}_{\text{s}}=\left(42\pm 9\right)$ nm. Interestingly, the effective volume fraction of the large particles, ${\zeta }_{\text{b}}^{\text{eff}}$, in the bidisperse suspension in the experimental conditions is equal to $2.14\pm 0.03$, which is larger than 1, consistent with our expectations based on the counterion-induced deswelling picture. Here, ${\zeta }_{\text{b}}^{\text{eff}}$ is computed for the large particles using the same $\mathrm{\Delta }r$ as determined above for the small microgels.

However, $\mathrm{\Delta }{R}_{\text{s}}$ is smaller than $\mathrm{\Delta }{R}_{\text{b}}=\left(63\pm 6\right)$ nm for a similar ${\zeta }^{\text{eff}}$ (see Table S2). To understand this, recall that the swelling of the microgel not only depends on the osmotic pressure difference between the inside and the outside of the microgels, $\mathrm{\Delta }\mathrm{\Pi }$, but also on a sufficiently small bulk modulus, as, otherwise, the microgels would be too stiff to deswell. In fact, swelling equilibrium for the particles is achieved when the counterion-induced osmotic pressure difference is balanced by the elastic compression of the particles. Hence, swelling equilibrium is expected when $\mathrm{\Delta }\mathrm{\Pi }\approx K\gamma$, with the bulk modulus K and the strain γ, which we estimate as $\mathrm{\Delta }R/R$. Considering a similar $\mathrm{\Delta }\mathrm{\Pi }$ for large and small microgels, we have $K_{\text{s}}{\gamma }_{\text{s}}=K_{\text{b}}{\gamma }_{\text{b}}$, and thus $\mathrm{\Delta }{R}_{\text{s}}=K_{\text{b}}{R}_{\text{si}}\mathrm{\Delta }{R}_{\text{b}}/\left(K_{\text{s}}{R}_{\text{bi}}\right)$, where the subscripts “bi” and “si” denote the radii of the large and small microgels when fully swollen. Because $R_{\text{si}}/R_{\text{bi}}<1$, and we also expect $K_{\text{b}}/K_{\text{s}}\lesssim 1$, we obtain that $\mathrm{\Delta }{R}_{\text{s}}<\mathrm{\Delta }{R}_{\text{b}}$, consistent with our observations. Note that $K_{\text{b}}/K_{\text{s}}\lesssim 1$, because both types of particles are synthesized under identical conditions but the polymerization reaction is stopped earlier for the small particles than for the large particles, implying that the cross-linker concentration has decayed less from the particle center towards the periphery for the small particles than for the large particles.

Our deswelling mechanism is also in good agreement with the deswelling of pNIPAM-based microgels reported in the literature (8, 12, 15, 24, 25). Indeed, using our estimate of $\mathrm{\Delta }r$ to obtain ${\zeta }^{\text{eff}}$, the onset of particle deswelling is observed at $0.9\lesssim {\zeta }^{\text{eff}}\lesssim 1.22$ in all these studies (Supporting Information and Table S3). We stress that we compare rather diverse systems and experiments. In some cases, particles are deuterated and protonated; in some other cases, hard and soft particles are mixed, or a majority of pNIPAM particles is mixed with a small number of large pNIPAM particles copolymerized with acrylic acid. Notably, in a recent form factor study of pNIPAM particles in crowded environments (21), deswelling was first observed at $\zeta \approx 1$, corresponding to ${\zeta }^{\text{eff}}=1.8$, which is higher than our expectation. However, in this SANS experiment, the viscosimetry data show that a majority of soft deuterated particles was mixed with stiffer protonated particles with almost identical size. The softness of the two species is reversed compared to the study presented here: The behavior of the stiffer particles was followed, while the signal of the softer particles was suppressed with contrast matching. Our deswelling mechanism implies, in this case, that the bulk modulus of the protonated microgel was larger than the osmotic pressure difference set by the counterions at ${\zeta }^{\text{eff}}\approx 1$, thus preventing their deswelling. Furthermore, it also implies that the soft deuterated particles would experience deswelling at $\zeta <1$, before deswelling of the stiffer protonated particles. However, the behavior of the deuterated particles was not followed in this earlier work.

Table S3.

Volume fraction, ζ, and swollen particle radius, R, reported in the reference indicated in the first column

Reference	Microgel	ζ	R, nm	$R^{\mathbf{e}\mathbf{f}\mathbf{f}}$, nm	${\zeta }^{\mathbf{e}\mathbf{f}\mathbf{f}}$
8	pNIPAM(-AAc)	0.66	357	392	0.90
15	pNIPAM	0.98	380	415	1.28
15	pNIPAM	1.96	380	415	2.55
24	pNIPAM	0.6	115	150	1.22
25	pNIPAM	0.72	316	351	0.99
25	pNIPAM	0.71	407	442	0.91
25	pNIPAM	0.74	277	312	1.06

The last column gives the effective volume fraction ${\zeta }^{\text{eff}}=\zeta {\left(R^{\text{eff}}/R\right)}^3$ obtained with $R^{\text{eff}}=R+\mathrm{\Delta }r$ and our estimate $\mathrm{\Delta }r=35$ nm. Except for ref. 8, all listed references report deswelling in monodisperse pNIPAM suspensions. In ref. 8, small particles are mixed with larger particles at a small concentration of ∼0.1 wt%.

In conclusion, we have unraveled the self-healing mechanism that allows bidisperse pNIPAM microgel suspensions to crystallize even at high size ratios of large and small particles (8), which would suppress crystallization if the particles were not soft (2). We find charged groups on the periphery of the particles and the corresponding clouds of bound counterions to be the key for the deswelling of the particles. At high concentrations, the counterion clouds fill the space between the particles, and, therefore, a large fraction of the bound counterions becomes effectively free to explore the volume outside the microgels. These ions establish an osmotic pressure difference between the inside and the outside of the particle, which, when larger than the microgel bulk modulus, causes particle deswelling. As pNIPAM microgels synthesized according to the same protocol become softer with increasing particle radius, large particles show a more pronounced deswelling than small particles. Furthermore, because the overlap of the counterion clouds and the associated osmotic pressure difference gradually increase in the range of concentrations around ${\zeta }^{\text{eff}}=1$, the deswelling transition is not sharp but must first affect the softest part of the microgel particles, usually their soft shell. Although the model we present here captures the essential mechanism, more experiments, simulations, and theoretical work is needed to fully justify our interpretations, particularly in the ζ-regime corresponding to ${\zeta }^{\text{eff}}=1$.

Remarkably, the generality of the proposed mechanism changes the role of polydispersity not only for microgel-based suspensions but, presumably, for other soft-particle suspensions. Indeed, it also at least partially explains the deswelling behavior observed with DNA-coated colloids with star-shape architecture (9). We also note that the delocalization of counterions at sufficiently large particle concentrations is reminiscent of the delocalization of electrons in a metal. However, although in the first case the behavior is classical and driven by the increase in entropy of the bound counterions when the individual microgel clouds overlap, in the second case, the effect is quantum mechanical. In both cases, however, the pressure is determined by the delocalized particles: The counterions set the suspension osmotic pressure and ultimately the osmotic pressure difference between the inside and outside of the microgel particles, causing their eventual deswelling, whereas the delocalized electrons in a metal set the pressure and hence the metal bulk modulus.

Microgel Synthesis

We have synthesized pNIPAM microgels using precipitation polymerization. The solvent (ultrapure water), NIPAM (C₆H₁₁NO), the cross-linker N,N′-methylene-bis(acrylamide) (BIS, C₇H₁₀N₂O₂) (26), and the surfactant sodium dodecyl sulfate [SDS, CH₃(CH₂)₁₁OSO₃Na] are mixed together in a reactor. Changing the relative concentration of cross-linker results in microgel particles of different stiffness (23, 27). The surfactant is needed to control the size and the size distribution of the particles (28). To obtain microgels and not macrogels, the synthesis is carried out at 70 °C, since, at this temperature, pNIPAM is insoluble in water (29). After 1 h at 70 °C, the polymerization reaction is initiated by the addition of ammonium persulfate [APS, (NH₄)₂S₂O₈]. Due to the insolubility of pNIPAM in water at 70 °C, the precursor particles formed are not colloidally stable. Thus, they aggregate. However, the charged sulfate groups at the ends of the chains, coming from the initiator (30), mostly remain at the particle/water interface. As the aggregates grow, their surface charge density increases (31), and the growing particles eventually become colloidally stable. These stable particles are referred to as primary particles. Any newly formed colloidally unstable precursor particle joins these primary particles up to when the SDS limits the growth. Thus, the effect of SDS is to provide an additional variable with which to control the particle size. As the particles grow, adsorption of SDS results in colloidally stable microgels that resist aggregation and the capture of other particles. This influence of SDS, in combination with the overall concentrations of monomer and initiator in solution, provides control over the resultant particle size. The reaction is stopped after about 6 h by cooling the reactor down to room temperature. The solution is then filtered through a membrane filter to remove undesired products. Finally, the solution with particles is extensively dialyzed to remove the surfactant and purify the suspension.

For SANS with contrast matching, we use partly deuterated particles. These are synthesized substituting the NIPAM monomer with D₇-NIPAM (C₆D₇H₄NO) and following the same synthesis procedures described above. The only difference is that the reaction is allowed to proceed for 12 h.

We emphasize that we use particles from different syntheses in our study, as the sample quantities required cannot be obtained in a single synthesis. However, all particles are synthesized according to the protocol given above. We provide an overview of their sizes, as obtained with SANS, SAXS, and dynamic light scattering (DLS), the experiment they were used for, whether the particles are protonated or deuterated, and the size ratio, for the case of binary mixtures, in Table S1.

During the synthesis, the cross-linker reacts faster than NIPAM. Therefore, the cross-linker density decays from the particle center towards the periphery. Hence, the microgel core is more cross-linked and stiffer than the fuzzy corona. For particles synthesized according to the same protocol, the particle size affects the particle stiffness: For larger particles, the cross-linker concentration decays more from the center towards the periphery. Therefore, larger microgel particles are softer; this is especially true for their fuzzy corona.

The ${\text{SO}}_3^{-}$ groups from the initiator mainly locate in the outskirts of the microgels and provide the microgel peripheral charge that colloidally stabilizes the particles against aggregation at high temperatures. Associated with these fixed charges, there are ${\text{NH}}_4^{+}$ counterions; these assure the electroneutrality of the suspension. We can estimate the number of counterions per particle from the amounts of the compounds used in the synthesis. The starting solution was composed of 0.995 L of distilled water with 100 mM of monomer (98% NIPAM, 2% BIS). The molar weights of NIPAM and BIS are $M_{\text{NIPAM}}=$ 113 g/mol and $M_{\text{BIS}}=$ 154 g/mol. The used monomer masses were $m_{\text{NIPAM}}=11.02$ g and $m_{\text{BIS}}=0.306$ g, giving a total polymer mass $m_{\text{poly}}\approx 11.33$ g; 5 mL of APS solution was added such that the final concentration of APS in 1 L of solution was 1 mM. The total mass of APS was $m_{\text{APS}}=0.228$ g, and its molar weight is $M_{\text{APS}}=$ 228 g/mol. From our viscosimetry data, we determine the mass of polymer in a particle to be $m_p\approx 6.4\cdot {10}^{-16}$ g. Using this value, we obtain the total number of elementary charges per particle: $N=2N_{\text{A}}{m}_p{m}_{\text{APS}}/(m_{\text{poly}}{M}_{\text{APS}})\approx 6.8\cdot {10}^4$, where the factor 2 accounts for the fact that each APS molecule contains two ${\text{NH}}_4^{+}$ groups, and $N_{\text{A}}=6.022\cdot {10}^{23}$ mol⁻¹ is Avogadro’s number.

Generalized Volume Fraction

A microgel is a cross-linked polymer network immersed in a solvent. In a suitable solvent, microgel particles can swell or deswell in response to variations in external stimuli, e.g., temperature (6, 32, 33), pH (34, 35), hydrostatic pressure (36, 37), or solvent composition (38, 39). In the deswollen state, the microgel particle still contains solvent, whereas no solvent is contained in the collapsed state. We define the swollen and the deswollen states as the largest and smallest size, respectively, the particle can achieve in a given solvent. The equation of state for swelling equilibrium results from the polymer solvent mixing, the elasticity of the polymer network, and the presence of ions.

The pNIPAM-based microgels are temperature-sensitive and show a volume phase transition at T = 32 °C. Our experiments were carried out at a temperature 18 °C < T < 21 °C. Therefore, our particles are in the fully swollen state, and the suspension phase behavior is mainly controlled by the concentration of the particles, which is the case for hard spheres. However, due to their softness and deformability (8, 15, 40–42), the volume of a microgel particle and, therefore, the volume fraction of the suspension, ϕ, is hard to determine. To quantify the concentration, we use the generalized volume fraction

$$\zeta =\frac{N\hspace{0.17em}{V}_{\text{sw}}}{V_{\text{tot}}},$$ [S1]

where N is the number of particles, $V_{\text{sw}}$ is the volume of a single swollen particle, and $V_{\text{tot}}$ is the total volume of the suspension. Note that ζ agrees with ϕ for dilute samples. However, ζ can exceed 1 in concentrated samples, when particles are compressed or are forced to interpenetrate. In contrast, the true volume fraction is limited to $\varphi \le 1$. The number of particles is determined from the total mass of polymer in the sample, $m_{\text{poly}}$, divided by the mass of a microgel particle, $m_p$, with volume $V_{\text{coll}}=4\pi \hspace{0.17em}{R}_{\text{coll}}^3/3$ in the collapsed state,

$$\begin{array}{c}N=\frac{m_{\text{poly}}}{m_p}\approx \frac{m_{\text{poly}}}{{\rho }_{\text{pNIPAM}}\hspace{0.17em}{V}_{\text{coll}}}\\ =\frac{3m_{\text{poly}}}{4\pi R_{\text{coll}}^3\hspace{0.17em}{\rho }_{\text{pNIPAM}}},\end{array}$$ [S2]

where we obtain $m_{\text{p}}$ from the pNIPAM mass density, ${\rho }_{\text{pNIPAM}}=1.269$ g/cm³ (43), because the amount of BIS in the particles is, at most, 2%. In Eq. S1, the total available volume, $V_{\text{tot}}$, is determined under the assumption that microgels in the swollen state are mainly composed of solvent: The mass density of a swollen particle and, therefore, of the total suspension is about equal to the solvent density, ${\rho }_{\text{sol}}$. We then write

$$V_{\text{tot}}\approx \frac{m_{\text{tot}}}{{\rho }_{\text{sol}}},$$ [S3]

where $m_{\text{tot}}$ is the total mass of the sample. In Eq. S1, we also need the volume of a particle in the swollen state: $V_{\text{sw}}=4\pi R_{\text{sw}}^3/3$, with the swollen radius $R_{\text{sw}}$. Using the expression of $V_{\text{sw}}$ together with Eqs. S2 and S3, we can rewrite Eq. S1 as

$$\zeta \approx \frac{m_{\text{poly}}}{m_{\text{tot}}}\frac{{\rho }_{\text{sol}}}{{\rho }_{\text{pNIPAM}}}\frac{R_{\text{sw}}^3}{R_{\text{coll}}^3}=c\frac{{\rho }_{\text{sol}}}{{\rho }_{\text{pNIPAM}}}\frac{R_{\text{sw}}^3}{R_{\text{coll}}^3}.$$ [S4]

When we prepare the samples from freeze-dried powder, we weigh the polymer mass, $m_{\text{poly}}$, and the total mass of the sample, $m_{\text{tot}}$, to obtain the polymer concentration $c=m_{\text{poly}}/m_{\text{tot}}$. The particle radii $R_{\text{coll}}$ and $R_{\text{sw}}$ are obtained from viscosimetry (12) and DLS (44), respectively. The error in ζ is obtained using error propagation through Eq. S4 (45). In this case, the error depends on (i) the errors in $m_{\text{poly}}$ and $m_{\text{tot}}$, which determine c, (ii) the error in $R_{\text{sw}}$, and (iii) the error in $R_{\text{coll}}$.

The generalized volume fraction of bidisperse samples is computed as

$$\zeta ={\displaystyle \sum _{i=1}^2{\zeta }_i},$$ [S5]

where

$${\zeta }_i=c_i\frac{{\rho }_{\text{sol}}}{{\rho }_{\text{pNIPAM}}}\frac{R_{i,\text{sw}}^3}{R_{i,\text{coll}}^3}$$ [S6]

is the generalized volume fraction of the ith batch used to prepare the bidisperse sample, which is obtained from the mass concentration of the ith batch in the bidisperse sample, $c_i$, and the corresponding particle radii in the swollen and collapsed state, $R_{i,\text{sw}}$ and $R_{i,\text{coll}}$, respectively. The error in ζ is given by the sum of the errors in ${\zeta }_i$.

Viscosimetry

Viscosimetry is the most suitable technique to obtain the collapsed radius of a microgel; this is done by measuring the viscosity of the suspension at low concentrations (12, 46). We start by preparing a series of five or six samples with pNIPAM mass concentrations in the range ${10}^{-4}<c<4\cdot {10}^{-4}$. For each sample, we then measure the mean time, t, it takes a given volume of sample, V, to flow through a thin capillary of an Ubbelohde tube viscometer (47) oriented along the gravitational direction. The viscometer is immersed in a water bath at a fixed temperature of (22.00 $\pm$ 0.01) °C. The flow rate, $\mathrm{\Phi }$, can be obtained from the mean velocity of the sample flowing through the capillary, $\langle v\rangle =L/t$, with the capillary length L and its cross section $\pi R^2$. It is also given by the Hagen−Poiseuille law for laminar flow,

$$\mathrm{\Phi }=\pi R^2\frac{L}{t}=\frac{\pi R^4}{8\eta }\frac{\left|\mathrm{\Delta }P\right|}{L},$$ [S7]

where η is the viscosity of the sample and $\left|\mathrm{\Delta }P\right|/L$ is the pressure drop along L. Because |ΔP| is proportional to the density of the sample, ρ, we solve for the kinematic viscosity, $\nu =\eta /\rho$, and obtain

$$\nu =\left(\frac{R^2\left|\mathrm{\Delta }P\right|}{8L^2\rho }\right)t=C\hspace{0.17em}t,$$ [S8]

where C only depends on the geometry of the capillary; in our experiments, $C=3.12\cdot {10}^{-9}$ m² s⁻². From the time t and the sample density, the suspension viscosity follows.

We now have to relate the measured viscosity to the collapsed radius of the microgels. This is done by means of the Einstein−Batchelor equation that describes the behavior of the relative viscosity of a suspension, ${\eta }_r=\eta /{\eta }_{\text{sol}}$, with ${\eta }_{\text{sol}}$ as the solvent viscosity, as a function of its volume fraction (48, 49),

$${\eta }_r=1+2.5\zeta +5.9{\zeta }^2,$$ [S9]

where we have used that for dilute samples $\varphi =\zeta$. Then, using $\zeta =k\hspace{0.17em}c$, with $k=\left({\rho }_{\text{sol}}/{\rho }_{\text{pNIPAM}}\right)\left(R_{\text{sw}}^3/R_{\text{coll}}^3\right)$, we can rewrite Eq. S9 in terms of the polymer mass concentration c, which is used to fit the measured ${\eta }_r\left(c\right)$ data with k as a fitting parameter. From the value of k, we can obtain the collapsed radius as

$$R_{\text{coll}}={\left(\frac{{\rho }_{\text{sol}}}{{\rho }_{\text{pNIPAM}}}\frac{1}{k}\right)}^{1/3}{R}_{\text{sw}},$$ [S10]

where $R_{\text{sw}}$ is obtained using DLS.

Particle Form Factor

As the cross-linker reacts faster than the NIPAM monomer during particle synthesis, the particles have a decaying concentration of cross-linker from the center to the periphery. This gives rise to a core−shell structure where the core is stiffer than the fuzzy corona. This internal structure of a particle is modeled by starting with a homogeneous sphere with radius $R_{\text{c}}$, which is convoluted with a Gaussian with standard deviation σ to obtain a fuzzy corona with decaying density (11, 37). The form factor of such a core−shell particle is given by

$$\begin{array}{l}{P}_1\left(q\right)=[3\frac{\sin \left(q{R}_{\text{c}}\right)-q{R}_{\text{c}}\cos \left(q{R}_{\text{c}}\right)}{{\left(q{R}_{\text{c}}\right)}^3}\\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}{\times \hspace{0.17em}\text{exp}\left(-\frac{{\left(\sigma q\right)}^2}{2}\right)]}^2.\end{array}$$ [S11]

The total particle radius is $R=R_{\text{c}}+2\sigma$. We also take size polydispersity into account by introducing a Gaussian distribution of core radii with standard deviation ${\sigma }_{\text{p}}$. The form factor, including polydispersity, is given by

$$\begin{array}{c}P\left(q\right)=\frac{1}{\sqrt{2\pi }{\sigma }_{\text{p}}\langle R_{\text{c}}\rangle \langle V^2\rangle }{\displaystyle \int d{R}_{\text{c}}\hspace{0.17em}{V}^2\left(R_{\text{c}}\right)}\\ \hspace{0.17em}\times P_1\left(q,R_{\text{c}}\right)\hspace{0.17em}{e}^{-\frac{{\left(R_{\text{c}}-\langle R_{\text{c}}\rangle \right)}^2}{2{\sigma }_{\text{p}}^2{\langle R_{\text{c}}\rangle }^2}},\\ \text{with}\langle V^2\rangle =\frac{1}{\sqrt{2\pi }{\sigma }_{\text{p}}\langle R_{\text{c}}\rangle }{\displaystyle \int d{R}_{\text{c}}\hspace{0.17em}{V}^2\left(R_{\text{c}}\right)}\\ \hspace{0.17em}\times \hspace{0.17em}{e}^{-\frac{{\left(R_{\text{c}}-\langle R_{\text{c}}\rangle \right)}^2}{2{\sigma }_{\text{p}}^2{\langle R_{\text{c}}\rangle }^2}},\end{array}$$ [S12]

where $\langle R_{\text{c}}\rangle$ is the average core radius and $V\left(R\right)=4\pi \hspace{0.17em}{R}^3/3$. Furthermore, structural inhomogeneities of the polymer mesh inside the particle are taken into account with the Lorentzian term

$$I_{\text{chain}}\left(q\right)=\frac{I_{\text{chain}}\left(0\right)}{1+{\left(\xi q\right)}^2},$$ [S13]

where ξ is a measure of the mesh size of the polymer network and $I_{\text{chain}}\left(0\right)$ is the intensity at $q=0$. We fit our form factor data using the model $P_{\text{fit}}\left(q\right)=P\left(q\right)+I_{\text{chain}}\left(q\right)+B$, where B is a constant accounting for the background due to incoherent scattering. This model is used for the form factor measurements done with both SANS and SAXS.

SANS

To directly observe the deswelling of large particles in concentrated microgel suspensions, we use SANS combined with contrast matching. A small number of large protonated particles with radius $R_{\text{b}}=\left(176\pm 4\right)$ nm based on the NIPAM monomer C₆H₁₁NO are added to a majority of deuterated particles with radius $R_{\text{s}}=\left(117\pm 7\right)$ nm based on $D_7$-NIPAM. We determine the scattering length density of the deuterated, small particles from SANS measurements of a series of five dilute samples with varying H₂O/D₂O mixtures as solvent: 0 wt%, 28 wt%, 56 wt%, 96 wt%, and 100 wt% of ${\text{D}}_2\text{O}$. We obtain a mass fraction of 83 wt% D₂O and 17 wt% H₂O at the match point, as shown in Fig. S1. This corresponds to a scattering length density of $5.2\cdot {10}^{-6}$ Å⁻². This H₂O/D₂O mixture is then used as solvent and allows the suppression of the scattering signal from the deuterated particles, further allowing the direct determination of the form factor of the large particles in the sample.

We then prepare concentrated samples with a number ratio of large particles $n_{\text{b}}=\left(2.9\pm 0.3\right)\text{\%}$ spanning the concentration range $0.2<\zeta <1.2$. As shown in Fig. S2, the fuzzy shell starts to deswell first at $\zeta \approx 0.5$, whereas the core is found to deswell at $\zeta \gtrsim 0.85$. This behavior is expected, as the fuzzy shell is softer than the more cross-linked core. Interestingly, we find the fuzzy shell to deswell at a ζ smaller than random close packing, ${\varphi }_{\text{rcp}}\approx 0.64$. This indicates that deswelling is not due to a direct contact between particles, supporting our idea that this compression is due to the contribution of the bound counterions to the suspension osmotic pressure once the counterion clouds of the small microgels fill space.

To follow the deswelling of the small particles at high concentrations, we have also measured samples with a small number of protonated small particles with $R_{\text{s}}=\left(137\pm 4\right)$ nm and a majority of large deuterated particles with radius $R_{\text{b}}=\left(181\pm 4\right)$ nm and a number ratio of $n_{\text{b}}=\left(84\pm 3\right)\text{\%}$. The solvent is chosen to contrast match the large microgel particles, again with an H₂O/D₂O mixture of 17 wt% and 83 wt%, respectively. We find that the small particles deswell with increasing sample concentration. An increase of ζ from 0.08 to 1.2 deswells the small particles by $\mathrm{\Delta }{R}_{\text{s}}=\left(42\pm 9\right)$ nm. In Fig. 4, the difference between the form factors at $\zeta =0.08$ and $\zeta =1.2$ is clearly visible for $q>0.04{\text{nm}}^{-1}$. From the parameter values we obtain after fitting the form factor data with the core−shell model, which we list in Table S2, we see that this is due to the strong compression of the fuzzy shell.

Osmometry

A membrane osmometer (Wescor 4420) was used to measure the osmotic pressure of the samples. The osmometer contains two chambers for the sample suspension and a reference liquid. These are separated by a semipermeable membrane with a pore size of ∼50 nm. A pressure transducer is used to measure the pressure. The osmometer is calibrated by (i) establishing the point of zero pressure, when both chambers are filled with the same solvent, and (ii) using a standard of known osmotic pressure. Our standard is a dextran solution of known polymer concentration and osmotic pressure (50).

After calibration, we measure the osmotic pressure of the bidisperse sample with $n_{\text{b}}=\left(2.9\pm 0.3\right)\text{\%}$, used in the SANS experiments where we follow the deswelling of the large particles, in the ζ-range from 0.12 up to 1.1. The result is shown by the red squares in Fig. 2 and Fig. S2. The sample chamber was filled with the microgel suspension, and the reference chamber was loaded with the solvent, 83 wt% D₂O and 17 wt% H₂O.

For $\zeta \lesssim 0.85$, the osmotic pressure, $\mathrm{\Pi }$, is found to increase linearly with ζ, as expected for an ideal gas of counterions. We estimate the counterion density to be smaller than $\left(9.4\pm 2.6\right)\cdot {10}^{-4}$ nm⁻³ in this ζ-range. This corresponds to a typical distance of $\left(10\pm 1\right)$ nm between the counterions, which is much larger than the Bjerrum length in water, $l_{\text{B}}=0.7$ nm, and therefore supports the assumption of an ideal gas of counterions. For $0.85<\zeta <1.1$, we observe a steeper linear increase of $\mathrm{\Pi }$ with ζ. In this range, any reasonable estimate of the number of counterions contributing to the osmotic pressure still results in an average counterion separation that is much larger than $l_{\text{B}}$. Thus, we expect the ideal gas law to still be a reasonable approximation.

Monte Carlo Simulation

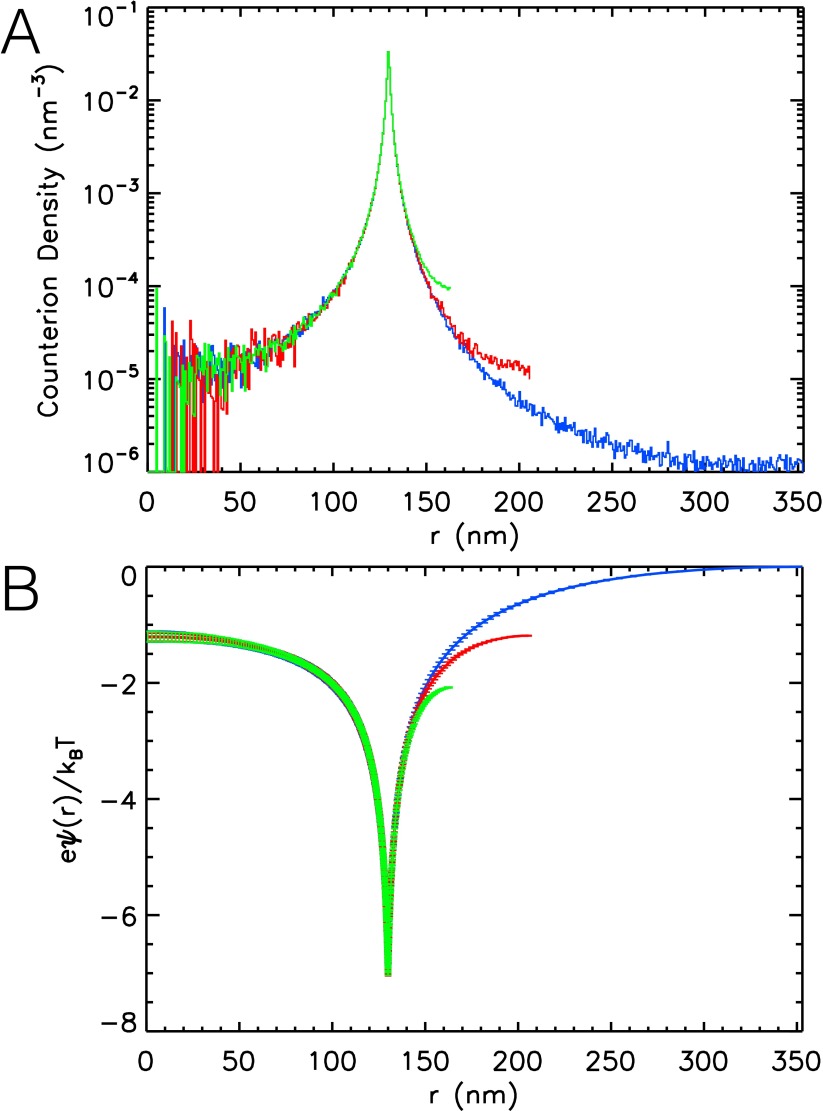
A strict calculation of the counterion density around the charged surface of a microgel involves solving the nonlinear Poisson−Boltzmann equation, which cannot be solved in closed analytical form (51). An analytical solution exists for the linearized Poisson−Boltzmann equation, the Debye−Hückel approximation, which is not applicable in our case, as the electrostatic potential, $\psi \left(r\right)$, close to the surface is too large for this approximation to be valid: $e\psi \left(R\right)>k_{\text{B}}T$ in our experiments, with the elementary charge e. Due to this difficulty, we have performed three Monte Carlo simulations to independently estimate the width of the counterion cloud surrounding a microgel particle.

In the simulations, a single microgel particle is modeled as a spherical surface with radius $R=130$ nm and a fixed surface charge density of $-7\cdot {10}^{4}e/\left(4\pi R^2\right)$. The $7\cdot {10}^4$ counterions with charge e are point-like with a radius of $0.01\hspace{0.17em}{l}_{\text{B}}$, where $l_{\text{B}}$ is the Bjerrum length. The solvent is thus taken into account by using the Bjerrum length of water at room temperature, $l_{\text{B}}=0.7$ nm. We use this length scale as the unit of length in our simulations, and the thermal energy, $k_{\text{B}}T$, as the unit of energy. The simulations only contain one microgel particle and its counterions. The latter are free to arrange around and within the microgel particle and are confined inside a sphere with radius $R_{\text{m}}$; this confining sphere represents an approximate nearest neighbor cage. We choose $R_{\text{m}}=352.87$ nm, 206.36 nm, and 163.79 nm, corresponding to volume fractions of the microgel particle of $\varphi ={\left(R/R_{\text{m}}\right)}^3=0.05$, 0.25, and 0.5, respectively. The counterions are moved by changing their position in a random direction over a randomly chosen distance in the range $\left[0,\delta \right]$. The maximum step length δ is adjusted dynamically for each counterion to ensure that about 50% of the trial moves are accepted for each of them.

After $\sim 3\cdot {10}^7$ Monte Carlo steps, the simulations reach equilibrium: The counterion distribution and the total energy of the system become stationary. We note that one Monte Carlo step corresponds to a trial move for a single counterion. As expected, most counterions are confined to a layer close to the charged surface, as shown in Fig. S3A. The counterion density remains larger than zero up to $R_{\text{m}}$, as a charged sphere cannot truly bind all counterions. For entropic reasons, a small fraction of counterions always escapes the electrostatic attraction. Relative to $\varphi =0.05$, the counterion density at $r=R_{\text{m}}$ is significantly higher for $\varphi =0.25$ and 0.5. This reflects the increasing overlap of counterion clouds from neighboring particles and the increase in osmotic pressure with increasing ϕ.

We measure the dimensionless electrostatic potential $\phi \left(r\right)=e\psi \left(r\right)/k_{\text{B}}T$ by averaging the potential experienced by a test charge, e, placed at 300 random positions for various distances from the particle center; the result is shown in Fig. S3B. For $\varphi =0.05$, we choose $\phi \left(r\right)=0$ at $r=R_{\text{m}}$. The potentials for $\varphi =0.25$ and 0.5 are shifted by adding a constant so that the minimum coincides with the minimum found at $\varphi =0.05$, which corresponds to $\phi \left(R\right)=-6.98\pm 0.10$. The variations of $\phi \left(r\right)$ inside the particle with ϕ are small, whereas $\phi \left(r\right)$ outside the particle is reduced relative to its value inside the particle with increasing ϕ. This reduction of $\phi \left(r\right)$ outside the particle reflects that the counterion density outside the particle increases with increasing ϕ.

At $\varphi =0.05$, the particle is in a dilute environment. We find that $\phi =-1$ at $r_{\text{f}}=R+\left(49\pm 2\right)$ nm. As a result, the counterions located at $r>r_{\text{f}}$ can be taken as those that have escaped from the attraction of the charged surface, whereas the counterions located at $R<r<r_{\text{f}}$ can be taken as bound. This changes at $\varphi =0.25$: The counterions at $r=R_{\text{m}}$ feel a potential $\phi \left(R_{\text{m}}\right)\mathrm{\approx }-1$, and, as a result, all counterions outside the particle appear to be at least weakly bound. This sets the beginning of the overlap of the counterion clouds of neighboring particles. At $\varphi =0.5$, the potential energy at $r\mathrm{=}{R}_{\text{m}}$ is further reduced: $\phi \left(R_{\text{m}}\right)\approx -2$, which is lower than the potential in the center of the particle: $\phi \left(0\right)\approx -1.2$. Although the counterions outside the particle close to $r=R_{\text{m}}$ have a low potential energy, a considerable fraction of them becomes effectively free, because the potential remains at about the same level everywhere between particles, provided the mean distance between particles remains constant. This corresponds to a situation of strong overlap between neighboring counterion clouds.

The counterion density shown in Fig. S3A supports this interpretation: For $\varphi =0.05$, the counterion density outside the particle drops to values below the counterion density in the particle center. This indicates that the osmotic pressure due the counterions inside the particle is somewhat larger than that outside the particle; this osmotic pressure difference adds to the contribution due to polymer−solvent mixing, because, at the experimental temperature, the microgels are in a good solvent. At $\varphi =0.25$, the counterion densities in the center and at $r=R_{\text{m}}$ are about equal, implying an equal osmotic pressure on both sides of the surface. In contrast, at $\varphi =0.5$, the situation is reversed. In this case, the counterion density close to $R_{\text{m}}$ is larger than that in the particle center and, consequently, the osmotic pressure outside the particle is higher than the osmotic pressure inside the particle, implying particle deswelling, provided the osmotic pressure difference is larger than the particle bulk modulus. Our experimental estimate of $\mathrm{\Delta }r$ corresponds to this situation, with the additional restriction that the osmotic pressure difference approximately equals the bulk modulus of the large particles. As the radius $R^{\text{eff}}=R+\mathrm{\Delta }r$ of the hypothetical effective particle gives an effective volume fraction ${\varphi }^{\text{eff}}=1$, we have $R^{\text{eff}}=R_{\text{m}}$ and obtain $\mathrm{\Delta }{r}_{\text{sim}}=R_{\text{m}}-R=33.79$ nm as an estimate for $\mathrm{\Delta }r$ from the simulation at $\varphi =0.5$; this is in excellent agreement with the estimate $\mathrm{\Delta }r\approx 35$ nm from our measurements. It also indicates that, due to particle deswelling, the true volume fraction at the observed onset for deswelling of the large particles, $\zeta =0.67$, is in the vicinity of $\varphi =0.5$.

Comparison with Other Studies

Our model for particle deswelling is in good agreement with the deswelling of pNIPAM-based microgels reported in the literature. In ref. 8, large pNIPAM particles copolymerized with acrylic acid (AAc) shrink in a crowded environment of smaller pNIPAM particles, when $\zeta \ge 0.66$. We compute ${\zeta }_{\text{s}}^{\text{eff}}$ using our estimate of $\mathrm{\Delta }r$ and obtain ${\zeta }_{\text{s}}^{\text{eff}}=0.9$. This value is in reasonable agreement with our model, which predicts particle deswelling for ${\zeta }_{\text{s}}^{\text{eff}}\gtrsim 1$. The fact that we do not obtain exactly ${\zeta }_{\text{s}}^{\text{eff}}=1$ suggests that the width of the counterion cloud for the microgels in this study is somewhat larger than our estimate for $\mathrm{\Delta }r$. In ref. 15, crystals of monodisperse pNIPAM microgels are studied, and deswelling is reported at $\zeta =0.98$ and $\zeta =1.96$. When we compute the values of ${\zeta }_{\text{s}}^{\text{eff}}$ corresponding to these two generalized volume fractions, we find ${\zeta }_{\text{s}}^{\text{eff}}=1.28$ and 2.55, respectively. The observed deswelling occurs for ${\zeta }_{\text{s}}^{\text{eff}}>1$, consistent with our model. For this study, the lowest ζ where deswelling is observed was not reported. Deswelling of monodisperse pNIPAM microgels has also been reported in refs. 24 and 25. In all these works, the onset of deswelling is found in a range $0.9\lesssim {\zeta }^{\text{eff}}\lesssim 1.22$, which is also in good agreement with our model. We stress that we compare rather diverse systems and experiments. In some cases, particles are deuterated and protonated, and in some other cases, hard and soft particles are mixed, or a majority of pNIPAM particles is mixed with a small number of large pNIPAM-AAc particles; we give the details of the systems we consider in Table S3. Despite the variety of systems we compare, our model appears to be consistent with the observed deswelling behavior.

In a form factor study of pNIPAM particles in a crowded environment (21), deswelling was observed to start at $\zeta \approx 1$; this value corresponds to ${\zeta }_{\text{s}}^{\text{eff}}=1.8$, which is higher than our expectations. In this SANS experiment, a majority of deuterated pNIPAM particles was mixed with protonated particles with almost the same size. The viscosimetry data of these particles, which provide the constant k in the expression $\zeta =k\hspace{0.17em}c$, show that k for the deuterated microgels is more than twice the value of k for the protonated microgels. Specifically, $k_{\text{D}}=51\pm 1$, whereas $k_{\text{H}}=22.4\pm 0.6$. Recall that the conversion constant is linked to the ratio of the swollen to collapsed radii, $R_{\text{sw}}/R_{\text{coll}}$. Therefore, a larger k implies a more swollen, relative to the collapsed size, microgel and hence a softer particle. Consequently, in this experiment, the softness of the two species is reversed compared with our study: The behavior of the stiffer protonated particles was probed, while the signal of the softer particles was suppressed with contrast matching techniques. The deswelling of the stiffer particles is observed at a higher volume fraction, but the softer particles must have deswollen first. Indeed, we expect the soft deuterated particles of ref. 21 to deswell for $\zeta <1$, before the deswelling of the stiffer protonated particles. However, the behavior of the deuterated particles was not followed in this study. We emphasize that deswelling is not only determined by the condition ${\zeta }_{\text{s}}^{\text{eff}}\approx 1$ but also by the fact that the osmotic pressure difference between the outside and the inside of the particles, at this point, must be comparable to or larger than the microgel bulk modulus. Whether deswelling happens for a given system thus also depends on the stiffness of the individual particles.