Significance
The extracellular matrix is a complex assembly of structural proteins that provides physical support and biochemical signaling to cells within our tissues. One of the key structural components of the extracellular matrix is collagen, and matrices of collagen exhibit remarkable mechanical properties. Their resistance to deformation is enhanced as deformation is increased over short timescales, a behavior termed strain stiffening, yet they exhibit some characteristics of viscous fluids at longer timescales. Strikingly, we show that the strain stiffening of collagen matrices is coupled with their liquid-like behavior: at greater deformations, these matrices become stiffer but then flow more rapidly to relax this increase in stiffness. These complex mechanical behaviors are likely to be relevant to cellular interactions with these matrices.
Keywords: collagen mechanics, viscoelasticity, force-dependent unbinding, biopolymers, stress relaxation
Abstract
The extracellular matrix (ECM) is a complex assembly of structural proteins that provides physical support and biochemical signaling to cells in tissues. The mechanical properties of the ECM have been found to play a key role in regulating cell behaviors such as differentiation and malignancy. Gels formed from ECM protein biopolymers such as collagen or fibrin are commonly used for 3D cell culture models of tissue. One of the most striking features of these gels is that they exhibit nonlinear elasticity, undergoing strain stiffening. However, these gels are also viscoelastic and exhibit stress relaxation, with the resistance of the gel to a deformation relaxing over time. Recent studies have suggested that cells sense and respond to both nonlinear elasticity and viscoelasticity of ECM, yet little is known about the connection between nonlinear elasticity and viscoelasticity. Here, we report that, as strain is increased, not only do biopolymer gels stiffen but they also exhibit faster stress relaxation, reducing the timescale over which elastic energy is dissipated. This effect is not universal to all biological gels and is mediated through weak cross-links. Mechanistically, computational modeling and atomic force microscopy (AFM) indicate that strain-enhanced stress relaxation of collagen gels arises from force-dependent unbinding of weak bonds between collagen fibers. The broader effect of strain-enhanced stress relaxation is to rapidly diminish strain stiffening over time. These results reveal the interplay between nonlinear elasticity and viscoelasticity in collagen gels, and highlight the complexity of the ECM mechanics that are likely sensed through cellular mechanotransduction.
The composition and architecture of ECM is heterogeneous and varies with tissue type and location. One particularly important ECM protein is type Ι collagen, which is the most abundant ECM component and primarily determines the mechanics of connective tissue (1). Type 1 collagen self-assembles into fibers, and these fibers can form networks in vitro. Studies investigating the mechanical properties of collagen networks have revealed that these networks are nonlinearly elastic and exhibit strain stiffening, or an increase in the elasticity as the strain on the network is enhanced (1–3). This nonlinear elasticity is also a characteristic feature of fibrin gels, which serve as the major component of blood clots, as well as in reconstituted networks of intermediate filaments and cytoskeletal actin networks (2, 4–7). These networks are all composed of semiflexible polymers or fibers, which are relatively rigid, so that the tangent to the contour of the polymer is correlated over long lengths, yet undergo substantial bending fluctuations due to thermal energy. Semiflexible polymers or fibers form networks at low volume fractions (8). Strain stiffening in these networks is thought to arise from either the entropic elasticity of single polymers resisting extension (entropic model) (2, 5), or from alignment of fibers in the direction of strain with a corresponding transition to a regime of elasticity dominated by fiber stretching at higher strains (nonentropic model) (5, 7, 9, 10). Although it has long been known that cells sense and respond to the elastic modulus of ECMs (11–14), recent work has indicated an impact of nonlinear elasticity as well. Studies have found that the nonlinear elasticity of ECM regulates modes of cell motility (15) and differentiation of mesenchymal stem cells (16), alters how far cells are able to sense into the ECM (17), and enables long-range mechanical signaling between cells (18).
In addition to often displaying nonlinear elasticity, most biological gels are viscoelastic and exhibit a time-dependent elastic modulus. These gels undergo stress relaxation in response to an applied strain: the initial stress resisting an applied strain decreases over time due to reorganization processes that relax the stresses in the matrix. In the case of collagen gels typically used for in vitro studies, viscoelasticity and stress relaxation likely arise from unbinding of the weak interactions, such as hydrophobic and electrostatic forces, which hold the fibers in a network (19–21). Interestingly, recent studies have found that viscoelasticity in synthetic hydrogels used as cell culture substrates can influence cell behaviors such as spreading, proliferation, and differentiation (22–25). The nonlinear elasticity of collagen and fibrin is dependent on the history of applied strains, indicating an influence of viscoelasticity on nonlinear elasticity (19). Here, we directly investigate the coupling between viscoelasticity and nonlinear elasticity for various gels, and find that increased strain leads to faster stress relaxation in collagen and fibrin gels. In collagen gels, these results can be explained by force-dependent unbinding of cross-links, and indicate a mechanism whereby strain stiffening is rapidly dissipated.
Results
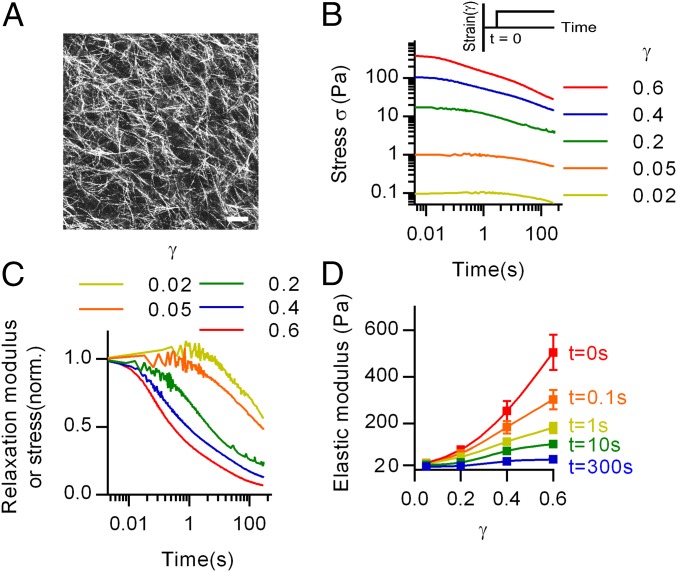
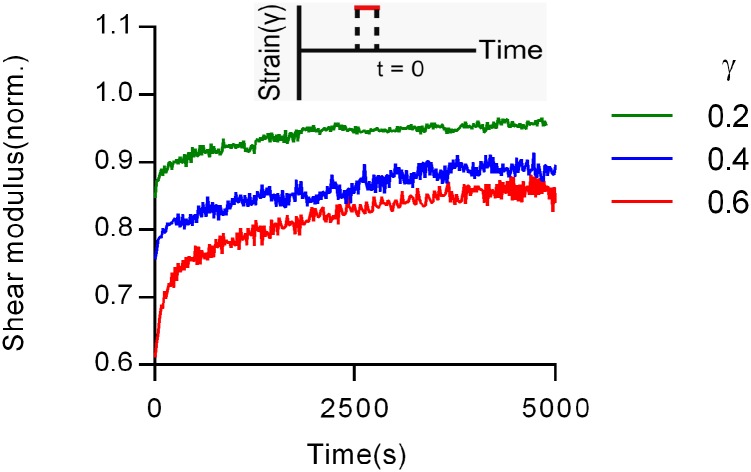
Since strain stiffening is induced from increasing strain (2), we first examined the stress relaxation of collagen gels as a function of increasing shear strain (Fig. 1A). In a stress relaxation test, a constant strain is applied to the gel, and the stress, directly proportional to the shear modulus in this test, is measured over time. Stress relaxation tests were conducted on collagen gels with various strains using a rheometer (Fig. 1B). Strikingly, normalization of the stress relaxation data with the initial values of stress for each strain revealed an enhancement in the rate of stress relaxation as strain was increased: higher strains led to faster relaxation (Fig. 1C). As the initial strain rate applied to establish a constant strain varied for these tests, stress relaxation tests with a constant strain rate were conducted and demonstrated the same behavior (Fig. S1 A and B). Similar results were found at a higher concentration of collagen (Fig. S1E). The stress relaxation behavior cannot be explained by poroelastic effects, as poroelastic stress relaxation, arising from water migration out of the gel, requires a volumetric deformation of the material, whereas shear rheology imposes a volume-preserving deformation on the gel (26). Consistent with the findings of the stress relaxation tests, creep tests, in which strain in response to a constant stress is measured, indicated that material flow was enhanced by increased stresses (Fig. S2). Additionally, frequency-dependent rheology tests demonstrate an increase in the loss modulus at higher strains (Fig. S3A), so that enhanced stress or strain generally induced increased viscous behaviors in the viscoelastic gels. To examine the implications of this strain-enhanced stress relaxation in collagen for nonlinear elasticity, the results were displayed isochronally (Fig. 1D). Immediately following the applied strain, the elastic modulus increased significantly over strain as consistent with previous reports (1–3). However, strain stiffening was substantially diminished within 1 s, and almost disappeared by 300 s, due to the strain-enhanced stress relaxation.
Fig. 1.
Strain-enhanced stress relaxation impacts nonlinear elasticity in collagen gels. (A) Confocal microscope image of a collagen gel using an overlay of images taken with confocal reflectance microscopy. (Scale bar: 25 µm.) (B) Stress relaxation tests on collagen with various strains. (Inset) A constant strain is applied during a stress relaxation test. (C) Normalized stress relaxation tests of collagen gels at different strains. In a stress relaxation test, the stress is directly proportional to the relaxation modulus. (D) Isochronal display of elastic modulus from the stress relaxation tests of different strains, showing the elastic modulus at each strain for the specific time points. Data are shown as mean ± SD; n = 5.
Fig. S1.
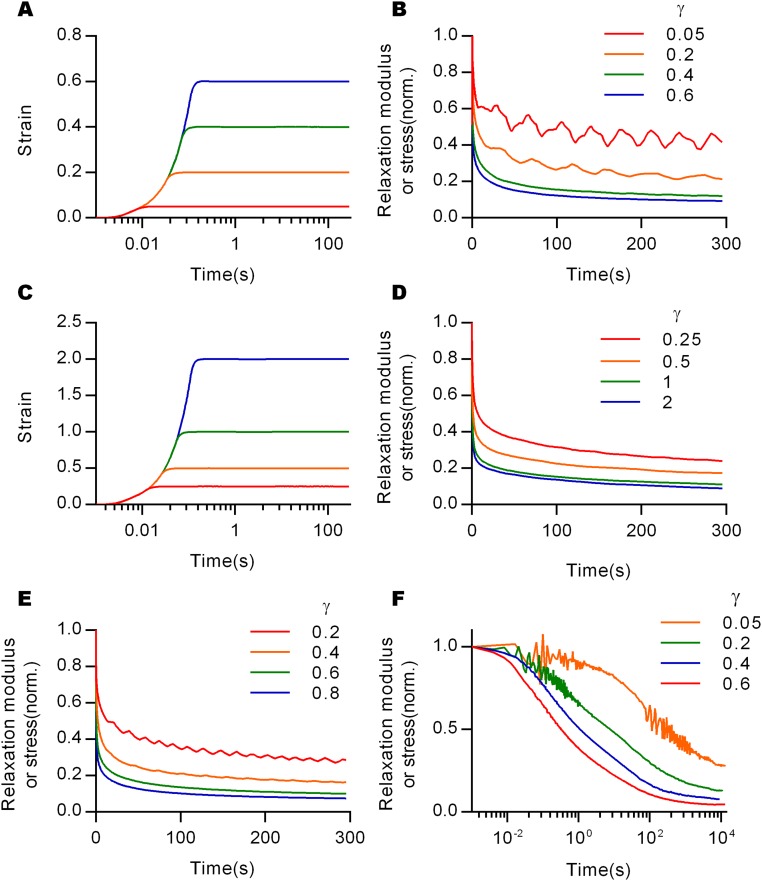
Stress relaxation tests with various conditions. The profiles of strains of stress relaxation test with constant strain rate and the corresponding results of stress relaxation with normalization (A and B) for collagen (5/s), and (C and D) for fibrin (16/s). (E) Stress relaxation tests with different strains were conducted for a collagen gel with a collagen concentration of 2.7 mg/mL. (F) Stress relaxation tests of collagen gels for the indicated strains at long timescales.
Fig. S2.
Creep tests on collagen gels with varying stress. A creep test was conducted by applying a constant stress to the gel and measuring the strain over time, as indicated by the schematic in the Inset. The flow of the matrix, indicated by the slope of the line, was enhanced at higher stresses. This finding can also be explained by the model of force-dependent unbinding of fibers proposed, with higher stresses leading to greater unbinding of fibers in the network and enhanced flow.
Fig. S3.
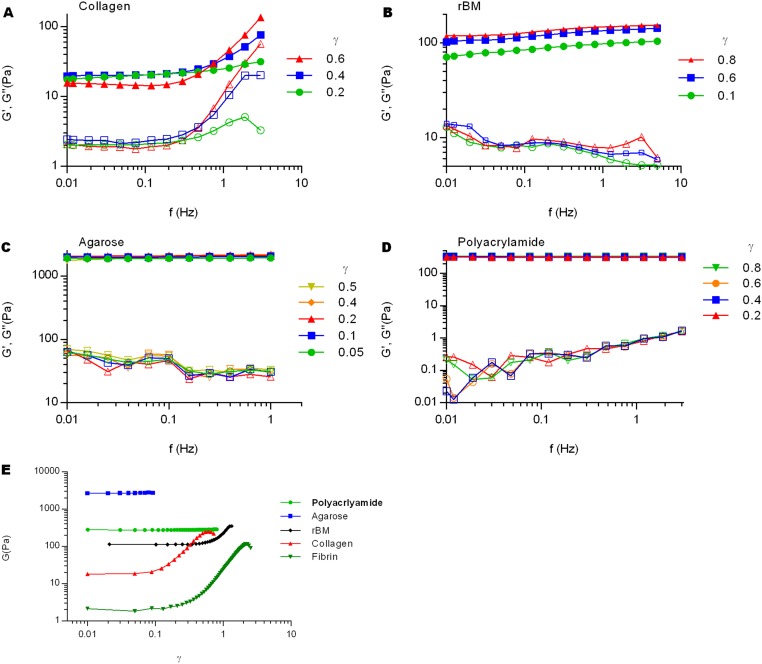
Frequency-dependent shear rheology of gels measured at different strains, and strain-dependent shear storage moduli of different gels. Frequency dependent shear storage (G′, filled symbols), and shear loss (G″, empty symbols) moduli of (A) collagen, (B) rBM, (C) agarose, and (D) polyacrylamide gels at various strains. (E) Oscillatory strains with increasing amplitudes were applied to the materials and shear storage moduli were measured. Collagen, fibrin, and rBM showed strain stiffening, but polyacrylamide and agarose were almost linearly elastic without significant change in modulus.
After finding strain-enhanced relaxation of collagen gels, we investigated whether strain-enhanced stress relaxation is a common behavior of other viscoelastic gels. First, the strain dependency of stress relaxation in fibrin gels, which form fiber networks similar to collagen, was examined. Fibrin gels also showed strain-enhanced stress relaxation, as well as a corresponding decline of strain stiffening over time, similar to collagen (Fig. 2 A and B and Fig. S1 C and D). Next, reconstituted basement membrane (rBM) matrix, a nonfibrillar matrix often used for 3D cell culture, was tested. Interestingly, although rBM matrix exhibited substantial stress relaxation, stress relaxation rates were similar for all strains, contrasting the behavior in collagen and fibrin gels (Fig. 2C). rBM matrix also displayed strain stiffening (Fig. S3E), demonstrating that strain stiffening is not necessarily associated with strain-enhanced stress relaxation. Finally, strain dependence of stress relaxation in agarose and polyacrylamide, which have been used for cancer spheroid assays and as substrates for 2D culture of cells (27), respectively, were assessed. Both nanoporous hydrogels are almost purely elastic, exhibiting very little stress relaxation across all strains below the fracture strain (Fig. 2 D and E). A comparison of the dependence of the time constant of stress relaxation, defined as the time over which the stress was relaxed halfway between its initial and equilibrium value (Fig. S4), on the strain highlighted the distinct classes of behavior (Fig. 2F). The time constants for relaxation of collagen and fibrin markedly decreased as strain increased, whereas other materials exhibited a strain-independent stress relaxation.
Fig. 2.
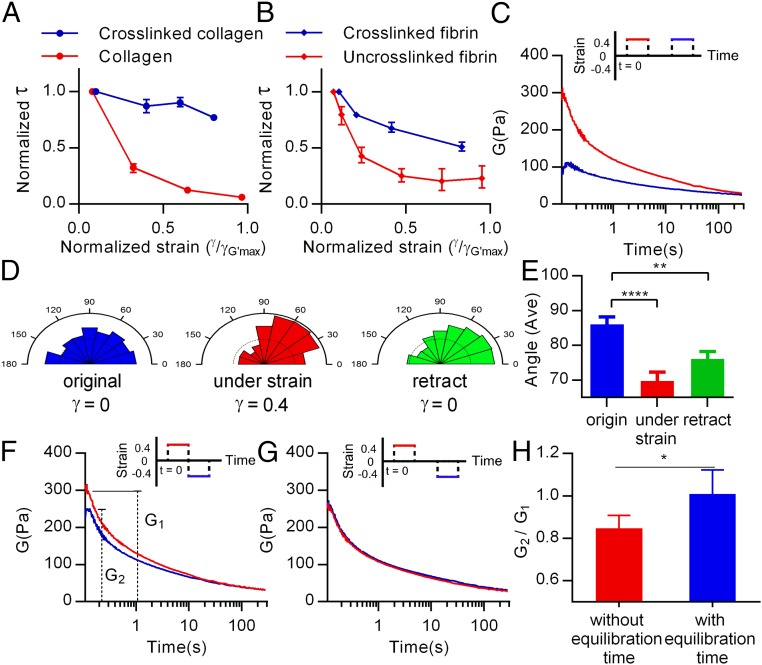
Stress relaxation tests with various materials commonly used for cell culture reveal that only fibrin and collagen gels exhibit strain-enhanced stress relaxation. (A) Stress relaxation tests at different strains for fibrin. (B) Isochronal display of elastic modulus for fibrin from stress relaxation tests of different strains. Data are shown as mean ± SD; n = 5. (C–E) Stress relaxation tests at different strains for polyacrylamide, agarose, and reconstituted basement membrane (rBM) matrix. Insets are all SEM images for each gel. (Scale bar: 1 µm.) (F) Normalized time constants of stress relaxation as a function of the normalized strain for the indicated materials. Strains were normalized by the strain at which the maximum of shear storage modulus (G′max) is measured in amplitude sweep, and time is normalized by the time constant for stress relaxation at low strains imposed for each material (Figs. S5 and S6).
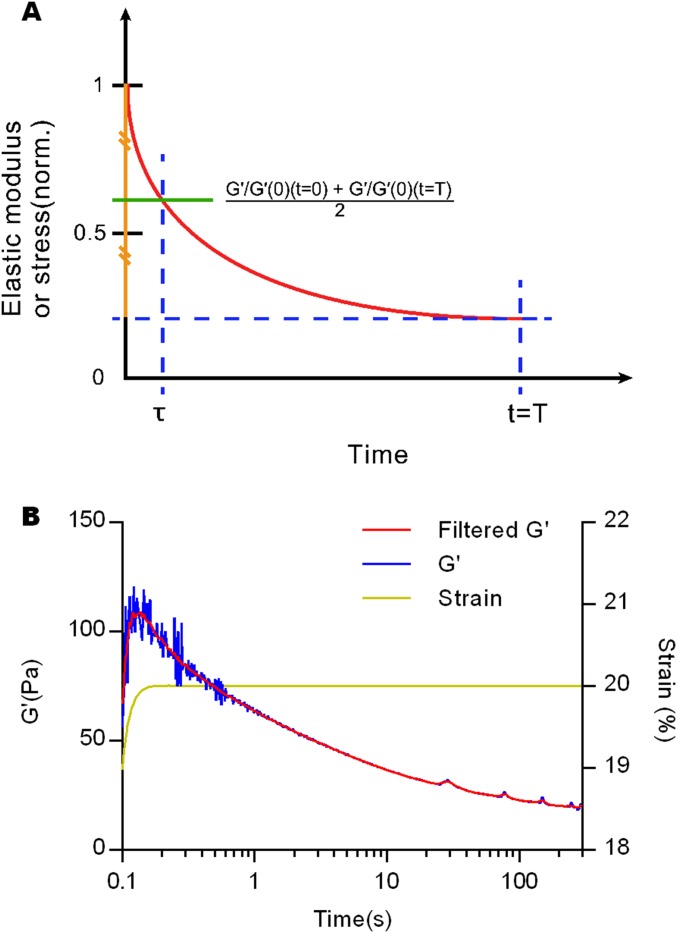
Fig. S4.
Analysis of stress relaxation tests. (A) Schematic describes how the time constant (τ) of a stress relaxation test was defined. τ was defined as the time when the initial modulus reaches the average of the initial modulus and equilibrium modulus at the end of stress relaxation. (B) A median filter was applied to noisy stress relaxation test to select the initial elastic modulus. This filter was only necessary for stress relaxation tests at very low strains. The initial elastic modulus for each strain was chosen on the filtered line at the time when strain reaches to desired value.
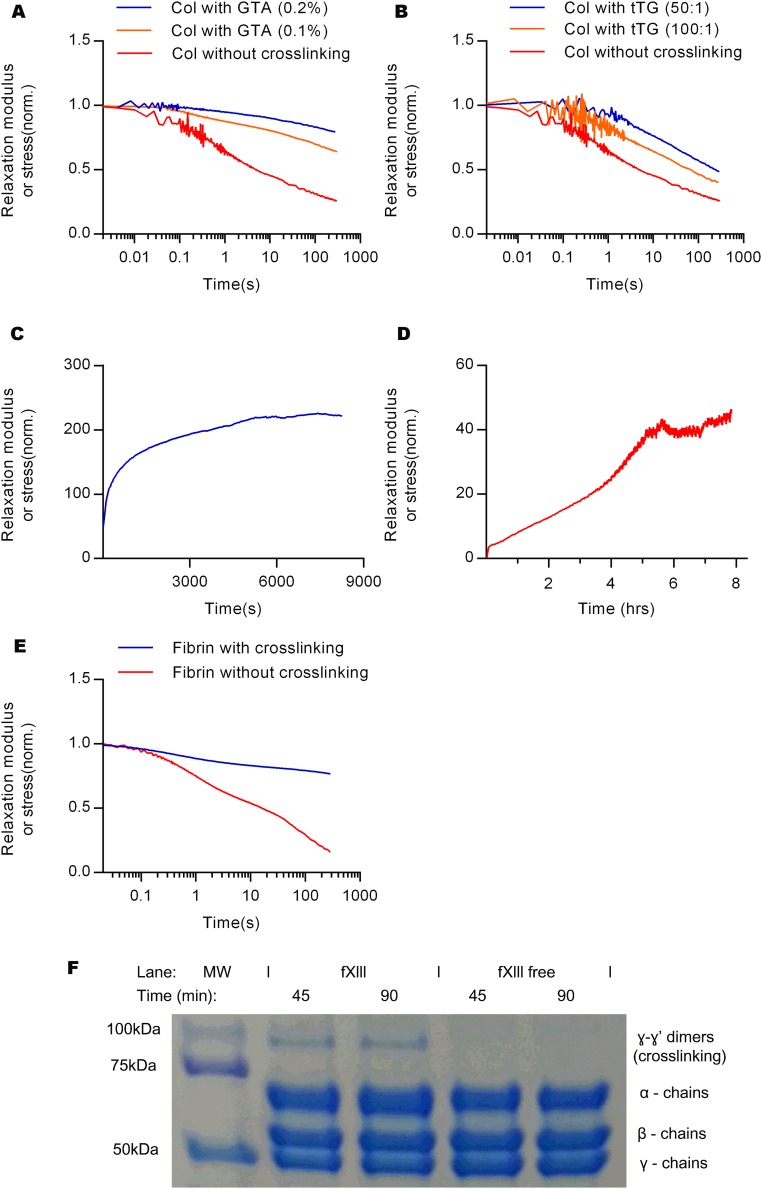
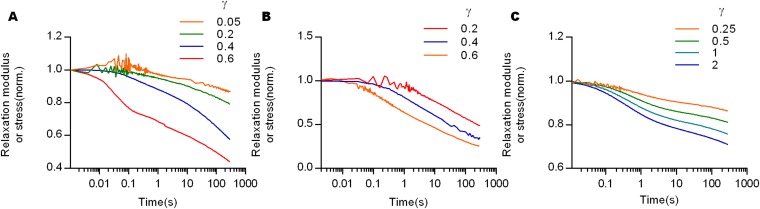
Next, we investigated the basis for strain-enhanced stress relaxation in collagen gels. The collagen gels are formed through weak cross-links between fibers, so we tested whether forming rigid covalent cross-links would impact stress relaxation. Collagen gels covalently cross-linked with glutaraldehyde (GTA) or transglutaminase (tTG) displayed a diminished degree of stress relaxation, although strain enhanced stress relaxation was still observed (Fig. 3A and Figs. S5 A and B and S6 A and B). Similar results were found from testing of fibrin gels cross-linked with factor XIII (Fig. 3B and Figs. S5E and S6C). These suggest that strain-enhanced stress relaxation in fibrin and collagen are associated with weak cross-linking.
Fig. 3.
Stress relaxation is associated with a weak cross-linking, axial dependent reorganization, and rebinding of fibers to the networks. Stress relaxation tests for (A) collagen, and (B) fibrin with and without covalent cross-linking. For cross-linking, collagen was treated by GTA and fibrin containing factor XIII was used. Data are shown as mean ± SD; n = 5. (C) Results for two sequential stress relaxation tests with identical positive strains. (D) The polar distribution of angles of collagen fibers in the network initially (Left), under shear (Center), and following removal of the imposed shear (Right). (E) A comparison of the averaged orientation of collagen fibers in the network, corresponding to the conditions in D. Data are shown as mean ± SEM; n = 387–439. (F) Multiple-stepwise stress relaxation test with a positive strain followed immediately by a test with a negative strain of the same magnitude, and (G) a stress relaxation test with a positive strain followed by a test with a negative strain of the same magnitude following an equilibration time. (H) A comparison of the recovery of the elastic modulus in a negative strain stress relaxation test following a positive stress relaxation test with or without an equilibration time. G1 and G2 represent the initial elastic modulus starting with stress relaxation. Data are shown as mean ± SD; n = 5. *P < 0.05; **P < 0.01; ****P < 0.0001 (Student’s t test). Insets are all schematics that describe the procedure for multiple stress relaxation tests. Red lines represent the first step of stress relaxation, and blue ones represent the successive stress relaxation.
Fig. S5.
The effect of cross-linking on the stress relaxation of fibrin and collagen gels. Comparison of stress relaxation of collagen gels at 0.2 strain with and without chemical cross-linking by (A) glutaraldehyde (GTA) (0.1% and 0.2%) and (B) transglutaminase (tTG) (wt/wt ratio, 50:1 and 100:1). The time course of storage modulus of collagen gel cross-linked with (C) GTA and (D) tTG. (E) Comparison of stress relaxation tests between fibrin network with and without cross-linking by factor XΙΙΙ. (F) Verification of purification of factor XIII from the fibrin gels without factor XIII cross-linking; SDS/PAGE gel of time evolution of fibrin gel with factor XΙΙΙ (fXΙΙΙ) and without it (fXΙΙΙ free).
Fig. S6.
Strain-enhanced stress relaxation in covalently cross-linked collagen and fibrin gels. Stress relaxation of collagen gel with cross-linking by (A) GTA (0.2%) and (B) transglutaminase (wt/wt, 50:1), and (C) fibrin gel with cross-linking for different strains.
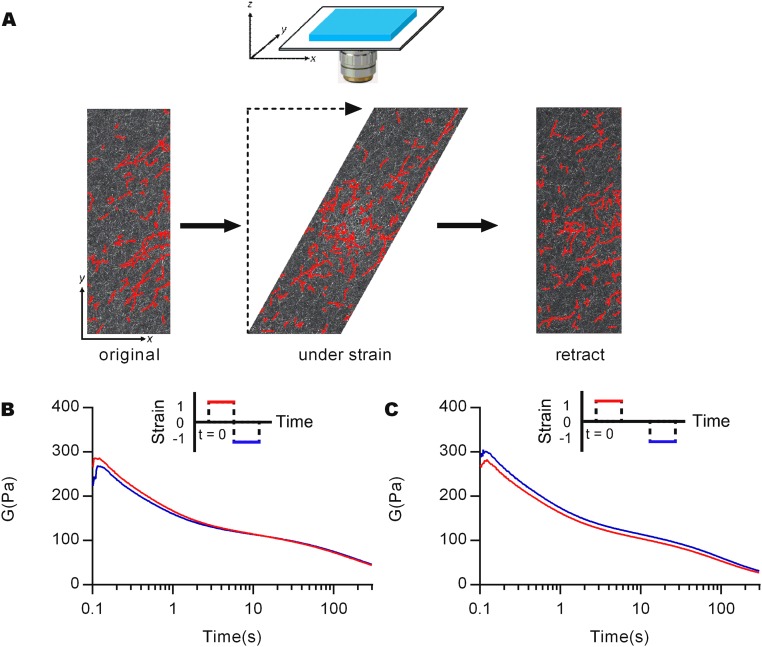
To reveal other important factors underlying strain-enhanced stress relaxation, stress relaxation tests were applied sequentially. After one stress relaxation test had been conducted on a collagen gel, an identical stress relaxation test was imposed again after the gel was allowed to equilibrate (Fig. 3C, Inset). The initial elastic modulus for the second step was dramatically reduced, indicating that plastic deformation, or permanent remodeling of gel architecture, had occurred (Fig. 3C). Plasticity was assessed by visualizing and quantifying fiber orientation initially, under shear, and following removal of the shear (Fig. 3D and Fig. S7A). A change in orientation of the fibers is induced by shear, and the change is sustained following removal of the imposed shear (Fig. 3 D and E), demonstrating plasticity. Next, a negative shear strain of the same magnitude was applied without any equilibration time following an initial stress relaxation test, and showed that the initial elastic modulus decreased slightly compared with the first step (Fig. 3F). When equilibration time was allowed between the stress relaxation tests, however, the gel recovered an initial modulus that was similar to the original value (Fig. 3 G and H). Although fiber lengthening may occur and lead to relaxation of the gels during the stress relaxation tests, self-assembly of the fibers is quenched by the time of the second test and the process of fiber lengthening is irreversible (19). Thus, the recovery of the modulus after an equilibration time indicates that the stress relaxation response cannot be fully explained by fiber lengthening. Instead, these results suggest a component of fiber–fiber unbinding during the first stress relaxation test, followed by rebinding of fibers during the equilibration time, leading to the recovery of the elastic modulus. Together, these results indicate axially dependent reorganization of the networks and unbinding of fibers due to a shear strain, followed by rebinding of fibers over time.
Fig. S7.
Structural change of collagen network under shear, and double stress relaxation tests for purified fibrin gels. (A) Images of a collagen gel taken by confocal reflectance on the x–y plane (schematic) before, during, and after shear deformation with fibers detected from the image processing overlaid in red. Double stress relaxation tests with positive and negative strains were conducted for purified fibrin (B) without equilibration time and (C) with containing equilibration time between steps.
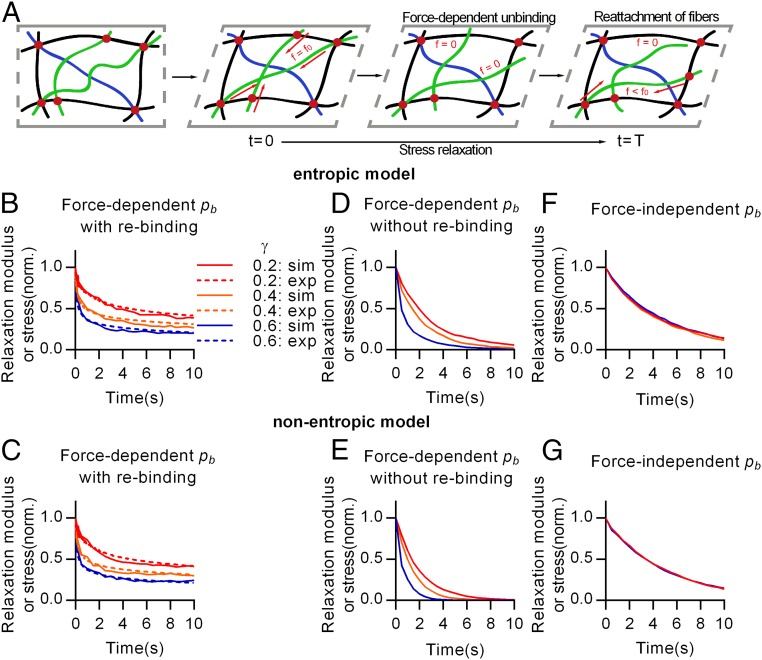
One plausible explanation for the strain-enhanced stress relaxation behavior of collagen gels is that it arises from force-dependent unbinding of bonds between fibers (Fig. 4A). When a strain is initially applied to the networks, individual fibers in the network are strained and exert a force opposing the strain based on their force–extension relation, leading to strain stiffening due to the nonlinear elasticity of single filaments (entropic model) or alignment of fibers in the direction of strain (nonentropic model) as has been proposed previously (2, 7). Forces on the fibers are carried through the bonds that link the fibers together in the network. Following the Bell model (28), we propose that unbinding of these links is force dependent, and that a greater force leads to a higher probability of unbinding. This force-dependent unbinding could lead to strain-enhanced stress relaxation: greater strains on the network lead to higher forces carried by the fibers and thus higher forces on the bonds linking the fibers, which in turn leads to faster unbinding of the fibers. Unbound fibers do not carry any force, so that unbinding of a fiber leads to a decrease in stress and network elasticity. Shorter timescales of unbinding translate to faster relaxation of stresses in the gel overall. Subsequently, we expect that unbound fibers can then rejoin to the network in a more relaxed state. We used computational modeling to investigate the feasibility of the proposed mechanism in both entropic and nonentropic models of nonlinear elasticity. Force-dependent unbinding and fiber rebinding were incorporated into previously established time-independent models (2, 7) for nonlinear elasticity in biological gels (SI Materials and Methods and Fig. S8). Force-dependent unbinding probability of fibers was incorporated through the following modification of the Bell model (28):
| [1] |
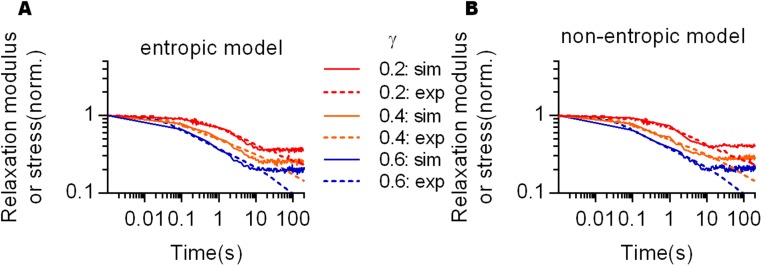
where is the probability of a given fiber in the network being bound and and are constants for binding and unbinding probability, is the force on a single fiber, and is a constant representing bond strength (SI Materials and Methods). Unbound fibers are assumed to have a constant probability of rebinding to the networks in a more relaxed state (SI Materials and Methods). With these inputs, the simulations of stress relaxation of fiber networks under different strains displayed the experimentally observed strain-enhanced stress relaxation behavior of collagen gels in both the entropic and nonentropic models (Fig. 4 B and C). When the force-dependent unbinding model was implemented without rebinding of fibers, the elastic moduli collapsed faster than those of experiments in both the entropic and nonentropic models (Fig. 4 D and E). This suggests that fiber rebinding may account for the nonzero equilibrium moduli that were experimentally observed (Fig. S1F). Alternatively, when both models were implemented with a probability of unbinding that is force independent, the simulations showed that stress relaxation became independent of strain, reminiscent of the behavior of rBM gels (Fig. 4 F and G). Taken together, these simulations indicate that force-dependent unbinding followed by rebinding of fibers can explain strain-enhanced stress relaxation in collagen networks.
Fig. 4.
Force-dependent unbinding of fibers leads to strain–enhanced stress relaxation in fiber networks. (A) Schematic of the proposed mechanism underlying strain-enhanced stress relaxation. Under strain imposed during a stress relaxation test, fibers in the network are strained and exert a force resisting the strain determined by the fiber’s force–extension relaxation. These forces are transmitted through cross-link points linking the fibers together. It is hypothesized that the probability of unbinding or cross-link disassociation is force dependent, or a higher force leads to a greater probability of unbinding for a fiber. This is predicted to lead to strain-enhanced stress relaxation. Unbound fibers can rebind to the networks, contributing the elastic modulus again. Comparison of stress relaxation data from experiments (exp, dotted line) and the corresponding results from the computational simulations (sim, solid line) of (B) the entropic model and (C) the nonentropic model for various strains. Simulation results given the assumptions that there is no rebinding of fibers to the networks for (D) the entropic model and (E) nonentropic model or that the probability of binding is independent of the force for (F) the entropic model and (G) nonentropic model.
Fig. S8.
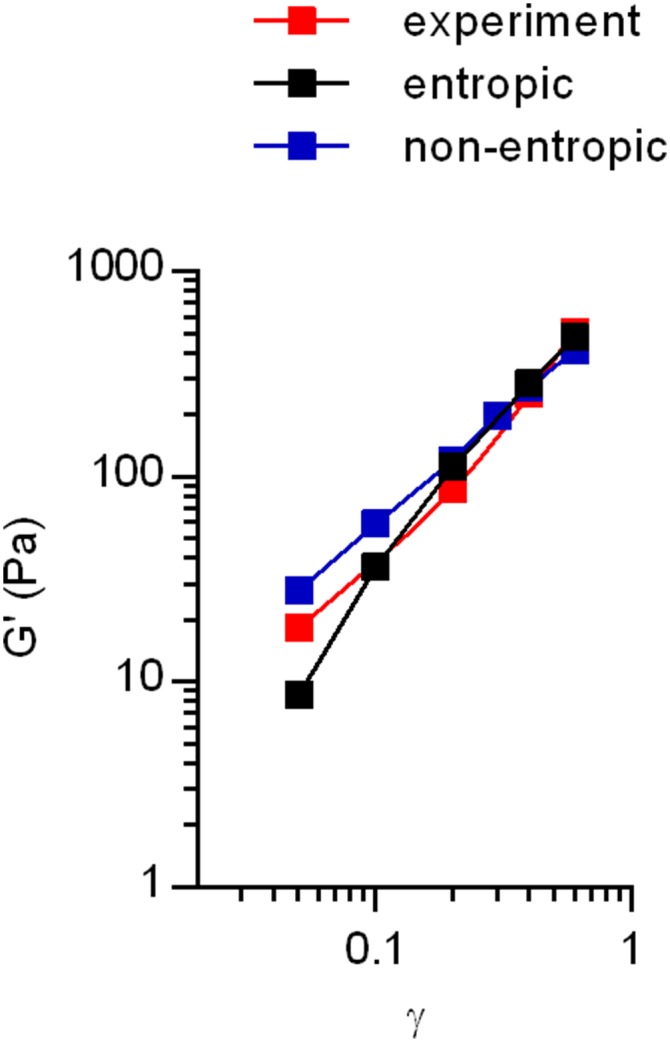
Computational model captures initial strain stiffening behavior of collagen gels. Experimental data of the initial strain stiffening was extracted from the stress relaxation tests of different strains at the initial time point. Implementation of the previous models (2, 7) of semiflexible biopolymer networks captured the experimental data.
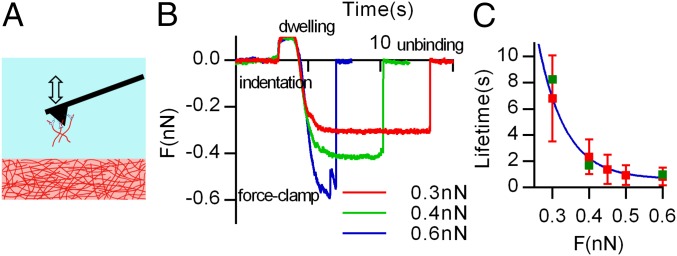
To directly verify the proposed molecular mechanism of force-dependent unbinding of fibers in collagen gels, the lifetimes of collagen fiber attachments under different forces were measured using atomic force microscopy (AFM) (Fig. 5A). First, collagen fibers were bound to AFM cantilever tips functionalized with a type I collagen antibody (SI Materials and Methods and Fig. S9A). Next, the collagen-coated AFM tips were indented into collagen gels, to initiate binding between collagen fibers on the tip and in the gel, and then constant tensile forces were exerted on these attachments until the attachments were ruptured. The lifetimes of the attachments were determined from these curves and found to decay exponentially with an increase in the clamping force (Fig. 5 B and C). Although the architecture of interactions between collagen fibers on the AFM cantilever and the surface of the collagen gel might not capture the interactions of collagen fibers that are polymerized together in the gel, the fundamental bonding mechanism between collagen fibers is expected to be similar. These results directly demonstrate the force dependence of unbinding of collagen fibers.
Fig. 5.
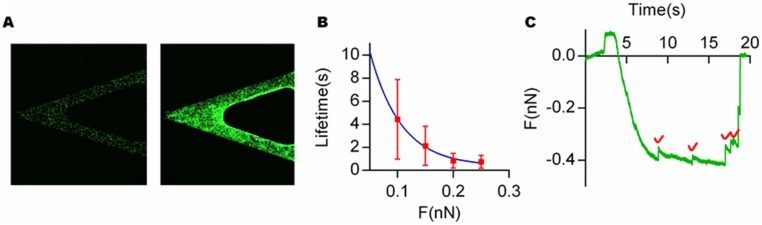
Force-clamp spectroscopy validates force-dependent unbinding on the collagen networks. (A) Schematic of the force-clamp spectroscopy: AFM cantilever tips (black) functionalized with collagen type Ι antibodies (blue) and collagen fibers (red) are indented and then retracted from a collagen gel (red). (B) Typical raw data obtained in AFM force-clamp experiments. After a small constant compressional force is applied, the AFM tip was retracted and held at different tensional forces on the attachment until the attachment was broken. (C) The averaged lifetimes of attachments between fibers as a function of tensional force. Blue line indicates the best-fit exponential function to the data. Green boxes indicate the lifetime measurements from the initial force-clamp experiments using an antibody-only coated cantilever, before the collagen fibers are attached to the cantilever. Data are shown as mean ± SD; n = 40.
Fig. S9.
A verification of antibody attachment and typical raw data of force-clamp experiments. (A) Fluorescence images of AFM cantilevers functionalized with a type I collagen antibody (Right) or uncoated cantilever (Left) incubated with a fluorescent secondary antibodies. These demonstrate successful functionalization of the AFM cantilevers. (B) The force-dependent unbinding curves obtained from the force-clamp experiments without functionalization of the AFM cantilever with a collagen type I antibody. These measurements represent the rupture of nonspecific attachments between the AFM cantilever and the collagen gel. Importantly, these are much lower than the force rupture measurements for the functionalized cantilevers (Fig. 5C). (C) Typical raw data of force-clamp experiments with the functionalized AFM cantilever tips show individual rupture events of on the order of 20 pN. Red checkpoints represent breaking individual fiber bonding.
SI Materials and Methods
Definition of Stress Relaxation Time Constant.
To quantify the rate of stress relaxation, a time constant (τ) was defined as the time at which the elastic modulus relaxes to the halfway between the initial modulus and the equilibrium modulus at the end of stress relaxation test (Fig. S4A). The time constants for each stress relaxation test were a measure of how fast stresses were relaxed in a material and were normalized by the time constant from the stress relaxation test with the lowest applied strain for that material.
Selecting the Initial Elastic Modulus in a Stress Relaxation Test.
For stress relaxation tests at very low strains, some noise of the measured stress during earlier time periods of stress relaxation was observed, likely due to the noise level of the instrument and possibly over damped feedback of the stress-controlled rheometer. To remove the noise and select appropriate value for the initial modulus, a median filter was used with a window size of 20 points (Fig. S4B). A median filter replaced each point with the median of neighboring points. Because stress relaxation tests were conducted at a constant strain, the initial elastic modulus for each strain was selected on the filtered line at the time when the applied strain first reached the designated value.
SDS/PAGE Analysis of Fibrin Cross-Linking.
The degree of covalent cross-linking in the fibrin networks without factor XIII was analyzed by electrophoresis with a polyacrylamide gel (SDS/PAGE), following a previously published method (19). At first, fibrinogen stocks containing factor XIII and depleted of factor XIII were polymerized at 37 °C by adding human thrombin. The polymerization was then stopped by adding Laemmli buffer (Bio-Rad) with 2-mercaptoethanol (βME) after 45 and 90 min, and the gel was decomposed by pipetting, followed by heating at 100 °C. Samples were analyzed by electrophoresis on a polyacrylamide gels along with a standard protein to confirm the size of protein within the samples. Coomassie blue staining was performed on the gel with destaining. The cross-linking of the fibrin with factor XIII was significantly enhanced over time in the unpurified fibrin as indicated by the band showing γ–γ dimers, which represent cross-linking of fibrin appear after polymerization. In contrast, a band of γ–γ dimers was not found in the purified fibrin gel, confirming that factor XIII has been depleted.
Image Analysis Network Structure Under Shear.
To demonstrate the structural deformation of collagen network during shearing, collagen gels were polymerized within a customized shearing device. This device consisted of a transparent shear cell in which controlled planar shear deformation could be applied, within a plane parallel to that of the microscope slide (x–y plane, Fig. S7A) so that shear deformation could be directly imaged. The device was placed on a laser-scanning confocal microscope (Leica SP8). Images of collagen gels were taken on the x–y plane (Fig. S7A) with confocal reflectance microscopy using a 25×/0.95 N.A. water-immersion objective and 488-nm wavelength light for excitation. Images were taken before, during, and after a shear deformation of γ = 0.4 (Fig. S7A). The images were analyzed using a previously described algorithm (46) to detect fibers in the network. Briefly, the image was first smoothed with a Gaussian filter and formed as a binary image with a threshold so that foreground pixels represent fibers. Next, the distance from each foreground pixel to the nearest background pixel was calculated. Nucleation points were formed based on the local maximal ridge of the calculated distances. The trajectory of the fibers was defined by connecting nucleation points. The orientation of each fiber was calculated as the angle of the line connecting the end points of each fiber.
Development of Computational Simulations of Stress Relaxation Tests.
Entropic model.
To verify the proposed mechanism in the present work, we first implemented a previously published isotropic entropic model (2) to capture the nonlinear strain stiffening of collagen. According to the model, the force–extension relation of single semiflexible polymers or fibers is given by the following:
| [S1] |
where and are the extension and the force exerted by a fiber, and and are contour and persistent length, respectively. In our computational simulation, the persistence length and the contour length of collagen are 20 and 2 µm, respectively, similar to previous reports (1). The force–extension relation is further modified by introducing a stretch modulus to account for filament or fiber extensibility, and the result (2) is as follows:
| [S2] |
The physical meaning of is a longitudinal compliance of fibers. So, would indicate inextensible fibers. The best-fit value for the stretch modulus of collagen to describe the experimental data was found to be ∼22 nN. As in the previous model, our model considered the elastic behavior of random isotropic networks of single fibers linked together at nodes, with the assumption that fibers can freely rotate around nodes. For the distribution of the initial length of fibers in the unstrained network, we used the previously suggested equilibrium distribution function of lengths of semiflexible inextensible fibers (2, 47) as below:
| [S3] |
where is the length of fibers. A shear strain is applied to the networks and the original position of each fiber is transformed into with an assumption of affine-deformation on the matrix. The deformation matrix is defined as follows:
where is the applied strain. Under strain, each fiber exerts a force based on its length that is derived from the modified force–extension relationship. The shear modulus of the networks can be calculated as follows:
| [S4] |
where is the number of fibers per unit volume, is the probability distribution for end-to-end vectors of fibers in the unstrained configuration. The number of fibers per unit volume is dependent on mesh size () of networks and can be calculated as as done previously.
Nonentropic model.
Besides the evaluating the impact of force-dependent unbinding of bonds between collagen fibers in the entropic model developed by Storm et al. (2), we also incorporated force-dependent unbinding of collagen fibers into the nonentropic model from Brown and colleagues (7). In this model, thermal fluctuations are not considered important and the nonlinear elasticity arises from the alignment of fibers along the direction of strain. The nonentropic model that we implemented is the three-chain model, a simple and traditional model to describe the networks using n/3 single chains in three orthogonal directions. As the model developed by Brown et al. was derived for uniaxial tensile tests, we modified the model for the context of shear deformation, relevant to our experiments.
In the three-chain model, fibers along with the vertical direction are extended due to shear deformation. The length of undeformed fiber and each side of cube are L. In the shear deformation, the length of the deformed fibers is calculated by L, where and is shear strain. The deformation gradient tensor can be obtained as above, and then the right Cauchy–Green strain tensor is given by . Generally, there are two different contributions to the strain energy of the network under deformation; the deformation of fibers and the change of volume. However, under shear deformation, we can assume that there is no volume change and that strain energy results only due to the deformation of fibers. Thus, the strain energy per unit reference volume due to the deformation of the fibers is given by , where is the number of fibers per unit reference volume and is the strain energy per unit reference length of the fiber. The force–extension relation for each fiber can be calculated by . As the force–extension relation of a collagen fiber is considered as nonentropic in this model, we assume a linear relation of , where E is the Young’s modulus and A is cross-sectional area. The second Piola–Kirchhoff stress tensor is obtained by . The Cauchy stress is given by . The shear stress can be calculated by , where , and . By the use of chain rule, we derive that , and . Finally, the shear modulus of the network for three-chain model can be calculated as follows:
Force-Dependent Unbinding.
Next, we incorporated time dependence into the models by using a modified version of the Bell model. The Bell model (28) was originally proposed to describe force-dependent reaction rate of the number of bonds between two cells. The Bell model was originally posited as follows:
| [S5] |
where is the number of bound receptors between cell A and cell B, and are the total number of receptors for cell A and cell B, respectively, and is a total force exerted on the cell–cell interactions. The Bell model shows that the number of bound receptors is dependent on the force exerted on the bonds. Similarly, we also assumed that the bonding of fibers in the networks is dependent on the force exerted by the fibers on the bonds linking the fibers together. Because we needed the binding probability of fibers, instead of the number of bonds itself, the Bell model equation was divided by the total number of fibers (), equivalent to receptors of the Bell model, and was relabeled , or a probability of a single fiber being bound. In addition, we can substitute to as a force exerted by a single fiber on the bond, which can be determined by the force–extension relation of the single fiber, and to as a new constant, because and are both constants. This resulted in what is shown as Eq. 1. During each time step of the simulation, each fiber was tested as to whether it unbinds or not. To determine whether a fiber under strain was unbound from the network, a number randomly generated from uniform distribution between 0 and 1 was compared with for each fiber. When the random number was greater than the , the fiber was unbound from the networks, leading to a decrease in the elastic modulus, as the fiber cannot contribute to the elastic modulus when not bound to the network. The probability of binding of fibers started with 1 at the initial time point for stress relaxation. During a stress relaxation test, the probability of binding decreased due to the forces exerted by fibers resulting from strain on the fibers, leading to fiber unbinding. Unbound fibers were allowed to rebind to the network with a constant probability at each time step. For the entropic model, the rebinding nodes can be anywhere around the unbound fiber due to the isotropic configuration. Furthermore, it is assumed that the rebound fiber may still carry a force, because the force may not have been relaxed completely and due to thermal fluctuations, so its value was randomly selected from a uniform distribution between zero and its original force before unbinding. In contrast, for the nonentropic model, the rebound fiber is assumed to carry the original force, because the rebinding nodes, where unbound fibers rejoin to the network, are restricted as cubical vertices when undeformed. The best fit for the value of the probability of rebinding to the experimental data was found to be ∼0.5. Although there was little existing experimental data that could guide selection of the constants , , and , it was found that stress relaxation is enhanced with increasing strain over a wide range of values for each parameter. At longer timescales, force-dependent unbinding due to Bell kinetics is balanced by rebinding of unbound filaments, leading to an equilibration of stress, deviating from the experimental results (Fig. S10). However, the model results demonstrate the key point that force-dependent unbinding leads to strain-enhanced stress relaxation.
Fig. S10.
Incorporation of Bell kinetics into the entropic or nonentropic model leads to strain-enhanced stress relaxation. Comparison of stress relaxation from experimental data of collagen (exp, dotted line) and the corresponding results from the computational simulations (sim, solid line) of (A) entropic model from Storm et al. (2) and (B) nonentropic model from Brown et al. (7).
Force-Clamp Spectroscopy with AFM.
Force-clamp spectroscopy was conducted using an Asylum Research MFP3D-Bio system combined with a Nikon Ti-E base. AFM cantilevers (MLCT; Bruker) were functionalized with an collagen type I antibody (Fig. S9A), using a previously established method (48). Briefly, the cantilevers were cleaned with chloroform for 30 s three times, and then immersed overnight in 5 M ethanolamine-HCl in dimethyl sulfoxide at room temperature. After washing in PBS, the cantilevers were immersed in 25 mM bis[sulfosuccinimidyl] suberate (BS3; Pierce) for 30 min. After washing in PBS, the cantilevers were incubated in 200 µg/mL collagen type I antibody (C2456; Sigma) for 30 min to conjugate the protein to the tips. The functionalized cantilevers were rinsed and kept in 4 °C before use. The binding of collagen type I antibody to the cantilevers was verified by incubating the antibody-functionalized cantilevers and uncoated cantilevers with a fluorescently labeled secondary antibody to the primary antibody, and then imaging the cantilevers (Fig. S1A). For preparation of sample, collagen gels were formed on poly-l-lysine coverslips to promote the attachment of collagen to the surface. The sample was placed in PBS and force-clamp experiments were conducted. Before force-clamp experiments, the tip was approached to the gel to bind to collagen fibers, and then retracted. Lifetime measurements for this initial attachment between the antibody-coated cantilever tip and the collagen gel are reported at different forces (green dots, Fig. 5C). Then the collagen-coated cantilever tips were indented into the gel until a trigger force (100 pN) was reached and retracted (1,000 pN/s) to a predetermined force. To promote binding of collagen fibers on the tip to collagen fibers on the gel, the indentations were held for a dwell time of 1 s. The time evolution of force curves was obtained and analyzed for quantifying the lifetimes of bonds. To demonstrate that the observed measurements were specific to collagen–collagen interactions, force-clamp experiments with the AFM tips without functionalization of the collagen type I antibody were performed, and showed that the range of attachment forces is significantly reduced due to the absence of the antibody (Fig. S9B). As there are many antibodies on the cantilever that can bind to fibers, the unbinding force likely represents the detachment of multiple bonds between multiple fibers. Single-bond detachment events are observed during the constant force regime and suggest single bonds between collagen fibers to be on the order of 20 pN (Fig. S9C). As single antibody–antigen bonds between an antigen and an antibody are known to be on the order of hundreds of piconewtons (49), the observed unbinding events represent the rupturing of multiple weak bonds between collagen fibers.
Discussion and Conclusion
In summary, collagen and fibrin gels stiffen as strained, but the strain stiffening is diminished over time due to strain-enhanced stress relaxation. Both entropic and nonentropic models of collagen network mechanics reveal that force-dependent unbinding between fibers leads to strain-enhanced stress relaxation, and AFM experiments confirm the presence of force-dependent unbinding between collagen fibers. We note that previous results have implicated the role of intrafibrillar lengthening in stress relaxation (19, 29, 30). However, intrafibrillar stress relaxation cannot explain the recovery of elastic modulus in double stress relaxation tests because the process of fiber lengthening is irreversible (Fig. 3 F and G). Furthermore, fiber lengthening cannot account for the permanent change in orientation of the fibers when the strain is removed while unbinding of fibers from one another, followed by reorientation of the fiber, and rebinding can (Fig. 3 D and E). Together, these indicate the force-dependent unbinding of fibers as the molecular mechanism underlying the observed behavior of strain-enhanced stress relaxation. However, it is likely that intrafibrillar lengthening, arising from sliding of fibrils relative to one another within a fiber, plays a role in the bulk stress relaxation tests reported here. It is possible that intrafibrillar lengthening may dominate the stress relaxation response at longer timescales over which the predictions from models based on force-dependent unbinding of fibers deviates from the experimental results (Fig. S10).
The viscoelastic behavior of collagen networks observed in this study contrasts with that of cross-linked actin networks. Actin is an intracellular semiflexible biopolymer, and cross-linked actin networks exhibit strain stiffening as does collagen (2, 5). A recent study examined the viscoelasticity of actin networks cross-linked by heavy meromyosin both experimentally and computationally (31). In response to a strain impulse, actin networks undergo fluidization, or a decrease in the elastic modulus and increase in the viscous modulus, followed by a full recovery of the initial properties. These results were modeled using a glassy worm-like chain model of actin, which accounts for the caging and enthalpic trapping of a worm-like chain polymer in a network by expanding the relaxation time modes of the worm-like chain (32), combined with reversible force-dependent bonds between the filaments. This model captured the experimentally observed behavior of fluidization and recovery in the actin networks. In contrast to the actin networks, collagen gels do not fully recover following fluidization and exhibit substantial plasticity (Fig. 3 D and E), highlighting the distinct behaviors between cross-linked actin networks and collagen gels (Fig. S11). However, we expect that incorporation of the glassy worm-like chain model into our entropic model of collagen network viscoelasticity that includes irreversible force-dependent bonds would result in a prediction of strain-enhanced stress relaxation, as fiber bonds in this model would also carry increased force at higher strains.
Fig. S11.
Shear fluidization test of collagen gels with different strain impulses. The recovery of elastic modulus after a transient strain impulse, followed by removal of strain. The response for each impulse was normalized to its preimpulse value.
For 3D cell culture experiments using collagen gels as ECM, these results suggest that the effect of mechanical properties of the ECM on cells may be highly dependent on the strain that cells exert, timescales over which cells sense mechanical cues, and the cross-linking state of the matrix. Although the higher the strain that cells exert on these matrices the higher the resistance cells encounter, the resistance of the ECM is relaxed rapidly due to strain-enhanced stress relaxation. The timescale for the cell–extracellular matrix interactions underlying mechanotransduction spans several orders of magnitude of time. Cells are able to bind to ECM over a timescale of ∼1 s (12), exert forces, and form stable adhesions on a timescale of minutes (23), and undergo cell spreading on a timescale of hours (33). These timescales fall within the range of time over which strain-enhanced stress relaxation is observed. Furthermore, cells on 2D substrates (34) and in 3D collagen gels (35) can exert strains of up to 0.5 and stresses on the order of 100–1,000 Pa (36), which are within the range of strains and stresses imposed and measured in our stress relaxation tests (Fig. 1B). Therefore, due to the overlap in timescales, levels of stress, and levels of strain between the regime over which strain-enhanced stress relaxation is observed with those relevant to cell–ECM interactions, it is expected that strain-enhanced stress relaxation impacts cell–ECM mechanotransduction. It was found that a greater degree of covalent cross-linking reduced the degree of stress relaxation in matrices. Interestingly, strain-enhanced stress relaxation is still observed in the presence of covalent cross-links, although the degree of stress relaxation is reduced (Fig. S6). Even in the case of fully cross-linked networks, cells secrete proteases to degrade collagen networks, possibly enhancing stress relaxation of the matrix adjacent to the cell (37).
There is some evidence that strain-enhanced stress relaxation behavior in collagen networks may be relevant to bulk tissue mechanics. Collagen fiber networks in skin exhibit plastic deformation under tensile loading due to slipping of collagen fibers (38), and sliding of collagen is observed in developing tendon (39), indicating the physiological relevance of weak bonds in collagen. However, one commonly used model of tissue biomechanics is the quasilinear viscoelastic model introduced by Fung (40), which decouples the contribution of the strain-dependent and time-dependent components of the stress relaxation response. In contrast, we have found that there is coupling between the strain- and time-dependent components of the response in in vitro collagen gels, as the timescale for relaxation is strain dependent. It is possible that this difference could be explained by the different structural composition of in vivo tissues, as tissues consist of various other structural components including elastin (38), and exhibit different levels of covalent cross-linking (41). Alternatively, another explanation could be in the standard practice of preconditioning biological tissues, or exerting stress–strain cycles on the tissue until the observed stress–strain curve is repeatable, before measurements are recorded and analyzed. The process of preconditioning may break the weak bonds in the collagen networks. Indeed, a study of preconditioning found it to be associated with enhanced collagen fiber alignment (42). There are some studies that have reported strain-enhanced stress relaxation in tissues such as ligaments and tendon (43, 44), although the mechanism of strain-enhanced relaxation underlying this tissue-scale behavior was not established.
Although the stiffness of ECM has been characterized in various contexts, these results highlight the complex viscoelastic properties of ECM at the microscale. Collagen networks strain stiffen, but the degree of strain stiffening is diminished over time due to strain-enhanced stress relaxation. Elucidating the complex mechanical behaviors in the ECM may be critical to understanding the how the mechanics of the ECM regulates cell behaviors.
Materials and Methods
Materials Preparation.
All gels were formed between the rheometer plates. Collagen type Ι (Corning) was diluted at 4 °C by 10× and 1× DMEM to reach a final concentration of 1 mg/mL, and pH was adjusted to 8.5 by adding 1 M NaOH, and immediately deposited on the rheometer plates. Polymerization of collagen was initiated by heating the solution to 37 °C. Matrigel (Corning) was used as rBM matrix at a concentration of 9.2 mg/mL The gelation of rBM was also initiated by heating to 37 °C. Low gelling temperature Agarose (Sigma) was dissolved into 1× DMEM to a concentration of 1% (wt/vol) at a pH of 7.4. The solid agarose was heated before use so that it forms a liquid and then cooled to 25 °C to solidify. The polyacrylamide gel was prepared by mixing acrylamide [3% (vol/vol)] and bis-acrylamide (0.15%) with tetramethylethylenediamine and ammonia persulfate following standard methods (45). For preparation of fibrin gel with cross-linking, 2 mg/mL human fibrinogen with factor XΙΙΙ diluted by 50 mM Tris⋅HCl buffer (7) at pH 7.4, containing 150 mM NaCl and 10 mM CaCl2, was mixed with human thrombin to a final concentration of 0.6 U/mL. To purify the fibrinogen of factor XΙΙΙ, human fibrinogen depleted of plasminogen, von Willebrand factor, and fibronectin (Enzyme Research Laboratories) was passed through an affinity column containing an antibody to factor XΙΙΙ (Affinity Biologicals) coupled to the CNBr Sepharose (Sigma) following a previously published method (19). To cross-link collagen networks covalently, a solution of 0.2% GTA (Sigma) in 1× DMEM was deposited around the collagen gel between the rheometer plates, after collagen have polymerized for at least 20 min. The GTA was allowed to diffuse into the collagen gel and cross-link it for 2 h before mechanical testing. After 2 h, the storage modulus of the collagen gels cross-linked by GTA was equilibrated. Collagen gels were also cross-linked with tTG (Sigma). The tTG was pretreated in 2 mM DTT in 50 mM Tris buffer (pH 7.4) for 10 min at room temperature before adding to a final buffer containing 5 mM CaCl2. Collagen stock solution was mixed with 2 mM DTT and 5 mM CaCl2 in 50 mM Tris buffer to a final weight ratio between collagen and tTG of 50:1 (wt/wt). The storage modulus did not reach an equilibrium value for collagen gels cross-linked with tTG, so stress relaxation tests were all conducted after 5 h of cross-linking.
Measurement of Stress Relaxation.
Rheology measurements of stress relaxation were performed using an AR-G2 stress-controlled rheometer (TA Instruments) equipped with 25-mm top- and bottom-plate geometry. Plates with stainless-steel surfaces were used for all of the materials except for collagen, as collagen gels were found to slip on the stainless-steel surface. To enhance the attachment of collagen to the surface, 25-mm poly-l-lysine–coated coverslips (Neuvitro Corporation) were glued to the surface. With this attachment, slipping of collagen against the surface was prevented. All materials were deposited onto the bottom plate of the rheometer immediately before gelation, and the top plate was lowered rapidly so that the gel formed a uniform disk between the two plates. To prevent dehydration of samples, the exposed gel surfaces within the rheometer geometry were coated with mineral oil (Sigma), except for the cross-linked collagen. Gelation was monitored with continuous oscillations at a strain of 0.01 and frequency of 1 rad/s, and mechanical tests were conducted once the storage modulus reached an equilibrium value; for stress relaxation tests, strains were applied with a rise time of 0.1 s, except for experiments with a constant strain rate. For the stress relaxation tests at different strain values, only one stress relaxation test is conducted on any given sample. For the double stress relaxation tests, the first strain is applied for 5 min on a fresh, previously unstrained sample, followed by a recovery time of 0–5 min, and subsequently the second strain is applied for another 5 min.
Acknowledgments
We acknowledge the help of Joanna Lee and Katrina Wisdom for discussions and technical assistance, Marc Levenston for discussions and use of rheometer, Stephan Munster for guidance on collagen gel attachment, and David Mooney (Harvard University) for review of the manuscript. This work was supported by the Jeongsong Cultural Foundation and Samsung Scholarship (to S.N.); NIH/NIGMS Grant R01 GM110482, NSF Grant CBET 1264833, and Stanford Child Health Research Institute grants (to M.J.B.); and DARPA Grant D14AP00044 (to O.C.).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1523906113/-/DCSupplemental.
References
- 1.Stein AM, Vader DA, Weitz DA, Sander LM. The micromechanics of three-dimensional collagen-I gels. Complexity. 2011;16(4):22–28. [Google Scholar]
- 2.Storm C, Pastore JJ, MacKintosh FC, Lubensky TC, Janmey PA. Nonlinear elasticity in biological gels. Nature. 2005;435(7039):191–194. doi: 10.1038/nature03521. [DOI] [PubMed] [Google Scholar]
- 3.Fratzl P, et al. Fibrillar structure and mechanical properties of collagen. J Struct Biol. 1998;122(1-2):119–122. doi: 10.1006/jsbi.1998.3966. [DOI] [PubMed] [Google Scholar]
- 4.Xu J, Tseng Y, Wirtz D. Strain hardening of actin filament networks. Regulation by the dynamic cross-linking protein alpha-actinin. J Biol Chem. 2000;275(46):35886–35892. doi: 10.1074/jbc.M002377200. [DOI] [PubMed] [Google Scholar]
- 5.Gardel ML, et al. Elastic behavior of cross-linked and bundled actin networks. Science. 2004;304(5675):1301–1305. doi: 10.1126/science.1095087. [DOI] [PubMed] [Google Scholar]
- 6.Chaudhuri O, Parekh SH, Fletcher DA. Reversible stress softening of actin networks. Nature. 2007;445(7125):295–298. doi: 10.1038/nature05459. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Brown AE, Litvinov RI, Discher DE, Purohit PK, Weisel JW. Multiscale mechanics of fibrin polymer: Gel stretching with protein unfolding and loss of water. Science. 2009;325(5941):741–744. doi: 10.1126/science.1172484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.MacKintosh FC, Käs J, Janmey PA. Elasticity of semiflexible biopolymer networks. Phys Rev Lett. 1995;75(24):4425–4428. doi: 10.1103/PhysRevLett.75.4425. [DOI] [PubMed] [Google Scholar]
- 9.Onck PR, Koeman T, van Dillen T, van der Giessen E. Alternative explanation of stiffening in cross-linked semiflexible networks. Phys Rev Lett. 2005;95(17):178102. doi: 10.1103/PhysRevLett.95.178102. [DOI] [PubMed] [Google Scholar]
- 10.Licup AJ, et al. Stress controls the mechanics of collagen networks. Proc Natl Acad Sci USA. 2015;112(31):9573–9578. doi: 10.1073/pnas.1504258112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Discher DE, Janmey P, Wang YL. Tissue cells feel and respond to the stiffness of their substrate. Science. 2005;310(5751):1139–1143. doi: 10.1126/science.1116995. [DOI] [PubMed] [Google Scholar]
- 12.Vogel V, Sheetz M. Local force and geometry sensing regulate cell functions. Nat Rev Mol Cell Biol. 2006;7(4):265–275. doi: 10.1038/nrm1890. [DOI] [PubMed] [Google Scholar]
- 13.Chaudhuri O, et al. Extracellular matrix stiffness and composition jointly regulate the induction of malignant phenotypes in mammary epithelium. Nat Mater. 2014;13(10):970–978. doi: 10.1038/nmat4009. [DOI] [PubMed] [Google Scholar]
- 14.DuFort CC, Paszek MJ, Weaver VM. Balancing forces: Architectural control of mechanotransduction. Nat Rev Mol Cell Biol. 2011;12(5):308–319. doi: 10.1038/nrm3112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Petrie RJ, Gavara N, Chadwick RS, Yamada KM. Nonpolarized signaling reveals two distinct modes of 3D cell migration. J Cell Biol. 2012;197(3):439–455. doi: 10.1083/jcb.201201124. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Das RK, Gocheva V, Hammink R, Zouani OF, Rowan AE. Stress-stiffening-mediated stem-cell commitment switch in soft responsive hydrogels. Nat Mater. 2016;15(3):318–325. doi: 10.1038/nmat4483. [DOI] [PubMed] [Google Scholar]
- 17.Winer JP, Oake S, Janmey PA. Non-linear elasticity of extracellular matrices enables contractile cells to communicate local position and orientation. PLoS One. 2009;4(7):e6382. doi: 10.1371/journal.pone.0006382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Wen Q, Janmey PA. Effects of non-linearity on cell-ECM interactions. Exp Cell Res. 2013;319(16):2481–2489. doi: 10.1016/j.yexcr.2013.05.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Münster S, et al. Strain history dependence of the nonlinear stress response of fibrin and collagen networks. Proc Natl Acad Sci USA. 2013;110(30):12197–12202. doi: 10.1073/pnas.1222787110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Guidry C, Grinnell F. Contraction of hydrated collagen gels by fibroblasts: Evidence for two mechanisms by which collagen fibrils are stabilized. Coll Relat Res. 1987;6(6):515–529. doi: 10.1016/s0174-173x(87)80050-x. [DOI] [PubMed] [Google Scholar]
- 21.Kurniawan NA, Wong LH, Rajagopalan R. Early stiffening and softening of collagen: Interplay of deformation mechanisms in biopolymer networks. Biomacromolecules. 2012;13(3):691–698. doi: 10.1021/bm2015812. [DOI] [PubMed] [Google Scholar]
- 22.McKinnon DD, Domaille DW, Cha JN, Anseth KS. Biophysically defined and cytocompatible covalently adaptable networks as viscoelastic 3D cell culture systems. Adv Mater. 2014;26(6):865–872. doi: 10.1002/adma.201303680. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Cameron AR, Frith JE, Cooper-White JJ. The influence of substrate creep on mesenchymal stem cell behaviour and phenotype. Biomaterials. 2011;32(26):5979–5993. doi: 10.1016/j.biomaterials.2011.04.003. [DOI] [PubMed] [Google Scholar]
- 24.Chaudhuri O, et al. Substrate stress relaxation regulates cell spreading. Nat Commun. 2015;6:6364. doi: 10.1038/ncomms7365. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Chaudhuri O, et al. Hydrogels with tunable stress relaxation regulate stem cell fate and activity. Nat Mater. 2016;15(3):326–334. doi: 10.1038/nmat4489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhao X, Huebsch N, Mooney DJ, Suo Z. Stress-relaxation behavior in gels with ionic and covalent crosslinks. J Appl Phys. 2010;107(6):63509. doi: 10.1063/1.3343265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Engler AJ, Sen S, Sweeney HL, Discher DE. Matrix elasticity directs stem cell lineage specification. Cell. 2006;126(4):677–689. doi: 10.1016/j.cell.2006.06.044. [DOI] [PubMed] [Google Scholar]
- 28.Bell GI. Models for the specific adhesion of cells to cells. Science. 1978;200(4342):618–627. doi: 10.1126/science.347575. [DOI] [PubMed] [Google Scholar]
- 29.Shen ZL, Kahn H, Ballarini R, Eppell SJ. Viscoelastic properties of isolated collagen fibrils. Biophys J. 2011;100(12):3008–3015. doi: 10.1016/j.bpj.2011.04.052. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Liu W, Carlisle CR, Sparks EA, Guthold M. The mechanical properties of single fibrin fibers. J Thromb Haemost. 2010;8(5):1030–1036. doi: 10.1111/j.1538-7836.2010.03745.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Wolff L, Fernández P, Kroy K. Resolving the stiffening-softening paradox in cell mechanics. PLoS One. 2012;7(7):e40063. doi: 10.1371/journal.pone.0040063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Semmrich C, et al. Glass transition and rheological redundancy in F-actin solutions. Proc Natl Acad Sci USA. 2007;104(51):20199–20203. doi: 10.1073/pnas.0705513104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Mooney DJ, Langer R, Ingber DE. Cytoskeletal filament assembly and the control of cell spreading and function by extracellular matrix. J Cell Sci. 1995;108(Pt 6):2311–2320. doi: 10.1242/jcs.108.6.2311. [DOI] [PubMed] [Google Scholar]
- 34.Lo C-M, Wang H-B, Dembo M, Wang YL. Cell movement is guided by the rigidity of the substrate. Biophys J. 2000;79(1):144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Legant WR, et al. Microfabricated tissue gauges to measure and manipulate forces from 3D microtissues. Proc Natl Acad Sci USA. 2009;106(25):10097–10102. doi: 10.1073/pnas.0900174106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Legant WR, et al. Measurement of mechanical tractions exerted by cells in three-dimensional matrices. Nat Methods. 2010;7(12):969–971. doi: 10.1038/nmeth.1531. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Sabeh F, Shimizu-Hirota R, Weiss SJ. Protease-dependent versus -independent cancer cell invasion programs: Three-dimensional amoeboid movement revisited. J Cell Biol. 2009;185(1):11–19. doi: 10.1083/jcb.200807195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Yang W, et al. On the tear resistance of skin. Nat Commun. 2015;6:6649. doi: 10.1038/ncomms7649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Silver FH, Freeman JW, Seehra GP. Collagen self-assembly and the development of tendon mechanical properties. J Biomech. 2003;36(10):1529–1553. doi: 10.1016/s0021-9290(03)00135-0. [DOI] [PubMed] [Google Scholar]
- 40.Fung YC. Biomechanics: Mechanical Properties of Living Tissues. Springer; New York: 1993. [Google Scholar]
- 41.Fratzl P, editor. Collagen: Structure and Mechanics. Springer; New York: 2008. [Google Scholar]
- 42.Quinn KP, Winkelstein BA. Preconditioning is correlated with altered collagen fiber alignment in ligament. J Biomech Eng. 2011;133(6):064506. doi: 10.1115/1.4004205. [DOI] [PubMed] [Google Scholar]
- 43.Pioletti DP, Rakotomanana LR. On the independence of time and strain effects in the stress relaxation of ligaments and tendons. J Biomech. 2000;33(12):1729–1732. doi: 10.1016/s0021-9290(00)00128-7. [DOI] [PubMed] [Google Scholar]
- 44.Duenwald SE, Vanderby R, Jr, Lakes RS. Viscoelastic relaxation and recovery of tendon. Ann Biomed Eng. 2009;37(6):1131–1140. doi: 10.1007/s10439-009-9687-0. [DOI] [PubMed] [Google Scholar]
- 45.Tse JR, Engler AJ. 2010. Preparation of hydrogel substrates with tunable mechanical properties. Curr Protoc Cell Biol Chapter 10:Unit 10.16.
- 46.Stein AM, Vader DA, Jawerth LM, Weitz DA, Sander LM. An algorithm for extracting the network geometry of three-dimensional collagen gels. J Microsc. 2008;232(3):463–475. doi: 10.1111/j.1365-2818.2008.02141.x. [DOI] [PubMed] [Google Scholar]
- 47.Wilhelm J, Frey E. Radial distribution function of semiflexible polymers. Phys Rev Lett. 1996;77(12):2581–2584. doi: 10.1103/PhysRevLett.77.2581. [DOI] [PubMed] [Google Scholar]
- 48.Wen JH, et al. Interplay of matrix stiffness and protein tethering in stem cell differentiation. Nat Mater. 2014;13(10):979–987. doi: 10.1038/nmat4051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Zlatanova J, Lindsay SM, Leuba SH. Single molecule force spectroscopy in biology using the atomic force microscope. Prog Biophys Mol Biol. 2000;74(1-2):37–61. doi: 10.1016/s0079-6107(00)00014-6. [DOI] [PubMed] [Google Scholar]