Spontaneous recovery of superhydrophobicity on nanotextured surfaces

Significance

Due to its aversion to the hydrophobic surface texture, a water droplet makes minimal contact with, and readily rolls off of, a superhydrophobic surface, conferring it with beneficial properties such as water repellency and self-cleaning. However, the surface texture can readily wet in response to conditions such as elevated pressures, leading to a breakdown of superhydrophobicity that is widely believed to be irreversible. By using specialized molecular simulations to study surfaces with nanoscale texture, here we find that the dewetting of the surface texture is strongly influenced by water density fluctuations. Furthermore, an understanding of the dewetting pathways allows us to design novel surface textures on which fluctuations can facilitate a spontaneous recovery of superhydrophobicity.

Abstract

Rough or textured hydrophobic surfaces are dubbed “superhydrophobic” due to their numerous desirable properties, such as water repellency and interfacial slip. Superhydrophobicity stems from an aversion of water for the hydrophobic surface texture, so that a water droplet in the superhydrophobic “Cassie state” contacts only the tips of the rough surface. However, superhydrophobicity is remarkably fragile and can break down due to the wetting of the surface texture to yield the “Wenzel state” under various conditions, such as elevated pressures or droplet impact. Moreover, due to large energetic barriers that impede the reverse transition (dewetting), this breakdown in superhydrophobicity is widely believed to be irreversible. Using molecular simulations in conjunction with enhanced sampling techniques, here we show that on surfaces with nanoscale texture, water density fluctuations can lead to a reduction in the free energetic barriers to dewetting by circumventing the classical dewetting pathways. In particular, the fluctuation-mediated dewetting pathway involves a number of transitions between distinct dewetted morphologies, with each transition lowering the resistance to dewetting. Importantly, an understanding of the mechanistic pathways to dewetting and their dependence on pressure allows us to augment the surface texture design, so that the barriers to dewetting are eliminated altogether and the Wenzel state becomes unstable at ambient conditions. Such robust surfaces, which defy classical expectations and can spontaneously recover their superhydrophobicity, could have widespread importance, from underwater operation to phase-change heat transfer applications.

Surface roughness or texture can transform hydrophobic surfaces into “superhydrophobic” surfaces and endow them with properties such as water repellency, self-cleaning, interfacial slip, and fouling resistance (1, 2). Each of these remarkable properties stems from the reluctance of water to penetrate the hydrophobic surface texture, so that a drop of water sits atop an air cushion in the so-called Cassie state, contacting only the top of the surface asperities. However, water can readily penetrate the surface texture, yielding the Wenzel state (3, 4) at elevated pressures (4, 5) or temperatures (6), upon droplet impact (7, 8), as well as due to surface vibration (9), localized defects (10), or proximity to an electric field (11); superhydrophobicity is thus remarkably fragile and can break down due to the wetting of the surface texture under a wide variety of conditions. To facilitate the recovery of superhydrophobicity and to afford reversible control over surface properties, significant efforts have focused on inducing the reverse Wenzel-to-Cassie dewetting transition. However, a true Wenzel-to-Cassie transition has been elusive (12), with most reported instances making use of trapped air (11, 13–15) or generating a gas film using an external energy source (16, 17) to jump-start the dewetting process. Insights into why achieving a Wenzel-to-Cassie transition remains challenging are provided by macroscopic interfacial thermodynamics (18), which suggests that the dewetting transition is impeded by a large free energetic barrier. This “classical” barrier is attributed to the work of adhesion for nucleating a vapor–liquid interface at the base of the textured surface. Consequently, the breakdown of superhydrophobicity upon wetting of the surface texture is widely believed to be irreversible (5, 12, 18), so that once the texture wets it remains in the wet state, even when the pressure is subsequently lowered or the electric field is switched off.

By using atomistic simulations in conjunction with specialized sampling techniques, here we challenge this conventional wisdom and uncover principles for the design of nanotextured surfaces that can spontaneously recover their superhydrophobicity by dewetting their surface texture at ambient conditions. Our work builds upon recent theoretical and simulation studies that have shown that water density fluctuations, which are not captured in macroscopic mean-field models, are enhanced at hydrophobic surfaces (19–24) and situate the interfacial waters at the edge of a dewetting transition (25). Such enhanced fluctuations have also been shown to modulate the pathways to dewetting and lead to reduced dewetting barriers in several confinement contexts (26–34). To investigate how fluctuations influence Cassie–Wenzel transitions on nanotextured surfaces, here we perform atomistic simulations of water adjacent to pillared surfaces, and use the indirect umbrella sampling (INDUS) method (35) to characterize the free energetics of the transitions and the corresponding pathways, as well as their dependence on pressure. By comparing our results to macroscopic theory, we find that although water density fluctuations do not influence the pressure at which the Cassie-to-Wenzel wetting transition occurs, they are nevertheless crucial in the Wenzel-to-Cassie dewetting transition, that is, in the process of recovering superhydrophobicity when it breaks down. In particular, fluctuations stabilize a nonclassical dewetting pathway, which features cross-overs between a number of distinct dewetted morphologies that precede the formation of the classical vapor–liquid interface at the basal surface; the nonclassical pathway offers a lower resistance to dewetting, leading to reduced dewetting barriers. Importantly, by uncovering the nanoscale dewetting pathways, and in particular by finding regions of the surface texture that are hardest to dewet, our results provide strategies for augmenting the surface texture to further destabilize the Wenzel state and reduce the barriers to dewetting. On such rationally designed surfaces the barriers to dewetting the texture can be eliminated altogether, so that the Wenzel state is no longer metastable but has been rendered unstable at ambient conditions, and the superhydrophobic Cassie state can be spontaneously recovered from the wet Wenzel state.

Free Energetics of Cassie–Wenzel Transitions

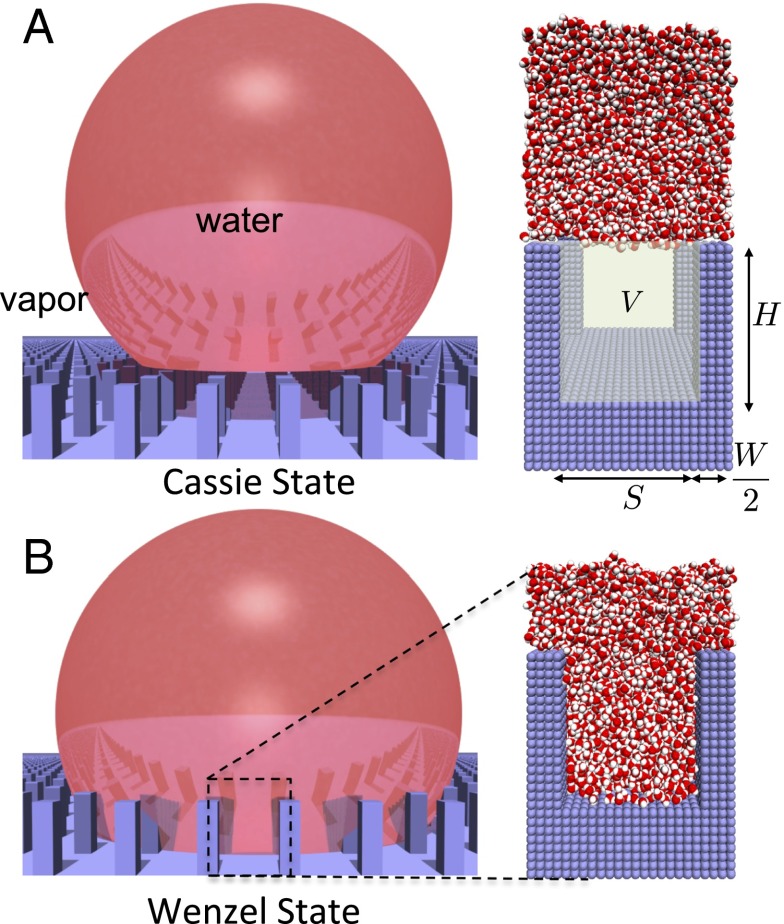
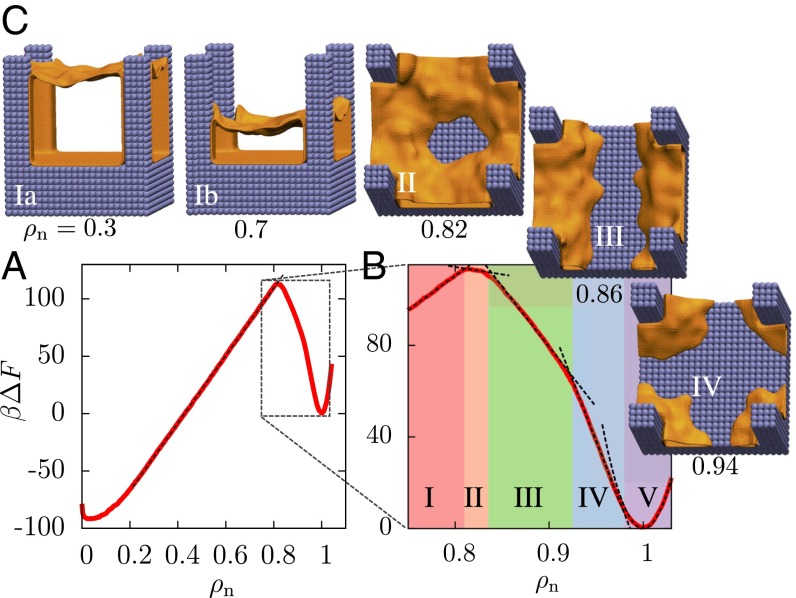
Fig. 1 contrasts the behavior of water on textured surfaces in the Cassie and Wenzel states; water does not penetrate the surface texture in the Cassie state but does so in the Wenzel state. In Fig. 1A, Right, the particular textured surface morphology that we study here is shown and consists of square pillars of height H and width W, arranged on a square lattice, and separated by a distance S. Also highlighted is the textured volume, V, which is devoid of water molecules in the Cassie state but is filled with water in the Wenzel state. The normalized water density, ${\rho }_{\text{n}}$ in V, thus serves as a reliable order parameter to distinguish the Cassie and the Wenzel states. In Fig. 2A, we show the free energy, $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$, of a system in the partially wet state relative to that in the Wenzel state, obtained using molecular dynamics simulations in conjunction with INDUS (35). Here, ${\rho }_{\text{n}}\equiv N/N_{\text{liq}}$, with N and $N_{\text{liq}}$ being the number of water molecules in V in the partially and fully wet states, respectively. Details pertaining to our simulation setups, the force-field parameters, and the algorithms used are included in Materials and Methods. The simulated free energy profile, $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$, clearly shows two basins, Cassie at ${\rho }_{\text{n}}\approx 0$ and Wenzel at ${\rho }_{\text{n}}\approx 1$, separated by a large barrier. To uncover the importance of water density fluctuations on the free energetics of Cassie–Wenzel transitions, we first compare the simulated $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$ with classical expectations based on macroscopic interfacial thermodynamics, which does not account for fluctuations.

Fig. 1.

Water on textured hydrophobic surfaces can exist in either the Cassie or the Wenzel state. (A) In the Cassie state, water is unable to penetrate the surface texture (blue) so that a water droplet (red) sits on a cushion of air, contacting only the top of the pillars. As a result, there is minimal contact between water and the solid surface, leading to a small contact angle hysteresis and a large contact angle, which are critical in conferring superhydrophobicity to the surface. Also shown is a simulation snapshot of the pillared surface that we study here (Right), which consists of square pillars arranged on a square lattice and is made of atoms (blue spheres) arranged on a cubic lattice. The textured volume, V, as well as the dimensions that characterize the pillared nanotextured surface are highlighted; the width of the pillars is W = 2 nm, their height is H = 4.5 nm, and the interpillar spacing is S = 4 nm. (B) In the Wenzel state, water wets the texture, so that there is extensive contact between water and the solid surface, leading to a large contact angle hysteresis and a smaller contact angle; in this state, the surface is no longer superhydrophobic. We define the normalized density, ${\rho }_{\text{n}}$, in the textured volume to be the number of waters in V, normalized by the corresponding number of waters in the Wenzel state.

Fig. 2.

Free energetics and pathways of wetting–dewetting transitions on a pillared surface. (A) The simulated free energy, $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$ (in units of the thermal energy, $k_{\text{B}}T\equiv {\beta }^{-1}$, with $k_{\text{B}}$ being the Boltzmann constant and T the temperature), features two basins that are separated by a large barrier. For $0.2<{\rho }_{\text{n}}<0.8$, $\mathrm{\Delta }F$ varies linearly with ${\rho }_{\text{n}}$, in agreement with macroscopic theory. However, the simulated barrier for dewetting (118 $k_{\text{B}}T$) is found to be smaller than the classical barrier (270 $k_{\text{B}}T$). (B) Between the Wenzel state and the barrier ($0.82<{\rho }_{\text{n}}<1$), $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$ is marked by several kinks, which demarcate five regions with distinct dewetted morphologies (dashed lines are a guide to the eye). (C) Representative configurations corresponding to these regions are shown as interfaces encompassing the dewetted volumes (shown in orange, waters omitted for clarity). Region V (${\rho }_{\text{n}}\approx 1$) displays Gaussian fluctuations resulting in a parabolic basin. Region IV ($0.93<{\rho }_{\text{n}}<0.98$) is characterized by vapor pockets at the base of the pillars. As ${\rho }_{\text{n}}$ is reduced, vapor pockets grow, break symmetry, and merge to form a striped vapor layer between the pillars. The stripe expands laterally in region III ($0.83<{\rho }_{\text{n}}<0.93$) until a nearly intact vapor–liquid interface is formed. Region II ($0.81<{\rho }_{\text{n}}<0.83$) is characterized by water molecules sticking to the center of the cell and also contains the nonclassical barrier, which eventually gives way to the classical region I at ${\rho }_{\text{n}}\approx 0.8$.

Macroscopic theory envisions dewetting being initiated with the nucleation of a vapor–liquid interface at the base of, and perpendicular to, the pillars; dewetting then proceeds through the ascent of this interface along the pillars (18). The height of the interface above the base of the pillars is thus given by $h\left({\rho }_{\text{n}}\right)=H\left(1-{\rho }_{\text{n}}\right)$, and the theoretical free energy profile, $\mathrm{\Delta }{F}_{\text{th}}\left({\rho }_{\text{n}}\right)$, is given by

$$\mathrm{\Delta }{F}_{\text{th}}\left({\rho }_{\text{n}}\right)=\mathrm{\Delta }{F}_{\text{adh}}+\left[\gamma \cos \theta A_{\text{side}}+\mathrm{\Delta }PV\right]\left(1-{\rho }_{\text{n}}\right),$$ [1]

where γ is the vapor–liquid surface tension, θ is the water droplet contact angle on a flat surface, and $\mathrm{\Delta }P$ is the difference between the system pressure and the coexistence pressure at the system temperature, T. In addition, $\mathrm{\Delta }{F}_{\text{adh}}\equiv \gamma A_{\text{base}}\left(1+\cos \theta \right)$ is always unfavorable (positive) and corresponds to the work of adhesion for creating the vapor–liquid interface, with $A_{\text{base}}=S\left(S+2W\right)$ being the basal area and $A_{\text{side}}=4WH$ being the area of the vertical faces of the pillars. Because $\cos \theta <0$ for hydrophobic surfaces, the second term could be favorable (negative) if $\mathrm{\Delta }P$ is sufficiently small, that is, if $\mathrm{\Delta }P\le \mathrm{\Delta }{P}_{\text{int}}\equiv -\gamma \cos \theta A_{\text{side}}/V$. Thus, the two key features of $\mathrm{\Delta }{F}_{\text{th}}\left({\rho }_{\text{n}}\right)$ are (i) a large adhesion barrier at ${\rho }_{\text{n}}\approx 1$, which must be overcome to nucleate the vapor–liquid interface, and (ii) a linear portion of $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$ corresponding to the vapor–liquid interface rising along the pillars as ${\rho }_{\text{n}}$ decreases. A derivation of Eq. 1 and details of the comparison between simulation and theory are included in SI Appendix.

Simulated configurations with $0.2<{\rho }_{\text{n}}<0.8$ (Fig. 2 C, Ia and Ib) are consistent with the macroscopic expectation and display dewetted regions with the vapor–liquid interface being perpendicular to the pillars, and at heights that are consistent with $h\left({\rho }_{\text{n}}\right)=H\left(1-{\rho }_{\text{n}}\right)$; see SI Appendix. Theory also predicts that $\mathrm{\Delta }F$ ought to vary linearly with ${\rho }_{\text{n}}$. At $\mathrm{\Delta }P=0$, the pressure at which our simulations are performed, the corresponding slope is expected to be $\left(-\gamma \cos \theta \right)A_{\text{side}}$. As seen in Fig. 2A, the simulated $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$ is indeed linear for $0.2<{\rho }_{\text{n}}<0.8$ (dashed line). The fitted slope yields a surface tension, ${\gamma }_{\text{fit}}=67$ mJ/m², which agrees well with that of our water model, ${\gamma }_{\text{SPC}/\text{E}}=63.6$ mJ/m² (36). The behavior of the system for $0.2<{\rho }_{\text{n}}<0.8$ is thus classical. Macroscopic theory also associates the barrier to dewetting with the work of adhesion to nucleate the vapor–liquid interface, which can be estimated as ${\gamma }_{\text{fit}}\left(1+\cos \theta \right)A_{\text{base}}\approx 270$ $k_{\text{B}}T$. In contrast, the corresponding simulated barrier is only 118 $k_{\text{B}}T$ (Fig. 2A). Thus, even though the ascent of the vapor–liquid interface along the pillars is classical, the nucleation of that vapor–liquid interface and the associated dewetting barriers, which are central to the recovery of superhydrophobicity, appear to be nonclassical.

Fluctuations Facilitate Nonclassical Dewetting Pathways with Reduced Barriers

To understand why the dewetting barrier is smaller than the classical expectation, we take a closer look at $\mathrm{\Delta }F\left({\rho }_{\text{n}}>0.8\right)$ (Fig. 2B) as well as the corresponding representative configurations (Fig. 2 C, II–IV), which are shown as instantaneous interfaces encompassing the dewetted regions (orange). A description of the algorithm used to compute the instantaneous interfaces and the corresponding averaged interfaces are included in SI Appendix. Interestingly, we observe a host of nonclassical partially wet configurations preceding the formation of the classical vapor–liquid interface. As ${\rho }_{\text{n}}$ is decreased from 1, vapor pockets first form at the base of the pillars, then grow to round the corners around the pillars (Fig. 2 C, IV). On further reducing ${\rho }_{\text{n}}$, symmetry is broken as vapor pockets from opposite pillars merge to form stripes of vapor spanning the interpillar region (Fig. 2 C, III). This change in the dewetted morphology coincides with a kink in $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$, suggesting that the system adopts a lower free energy path by transitioning from the vapor pocket to the stripe morphology. Subsequent decrease in ${\rho }_{\text{n}}$ results in another transition to a donut-shaped vapor layer (Fig. 2 C, II). $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$ displays a maximum in the donut morphology; the barrier thus corresponds to a configuration with water molecules sticking to the central region of the basal surface that is farthest from the pillars, rather than an intact vapor layer. Expelling the remaining water molecules to form an intact vapor layer is energetically favorable, as is the subsequent (classical) rise of the vapor–liquid interface along the pillars. This novel and clearly nonclassical pathway preceding the formation of a vapor–liquid interface, which is facilitated by nanoscopic water density fluctuations and involves transitions between various dewetted configurations (30, 34), results in a smaller barrier for the Wenzel-to-Cassie transition than anticipated by macroscopic theory (Eq. 1).

We note that the kinks in $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$ are a consequence of the high-dimensional free energy landscape being projected onto the scalar order parameter, ${\rho }_{\text{n}}$. Consequently, while we expect ${\rho }_{\text{n}}$ to suitably describe the transition pathway within the different regions (I–V), capturing transitions between regions with different dewetted morphologies would require consideration of additional order parameters (37). We further note that the use of periodic boundary conditions in our simulations leads to the correlated dewetting of adjacent cells. We have ensured that the nonclassical dewetting pathway discussed above is also observed in the absence of such correlations by additionally studying the dewetting of the first unit cell in a simulation setup containing four unit cells; see SI Appendix, Fig. S11.

How Pressure Influences Barriers to Wetting and Dewetting

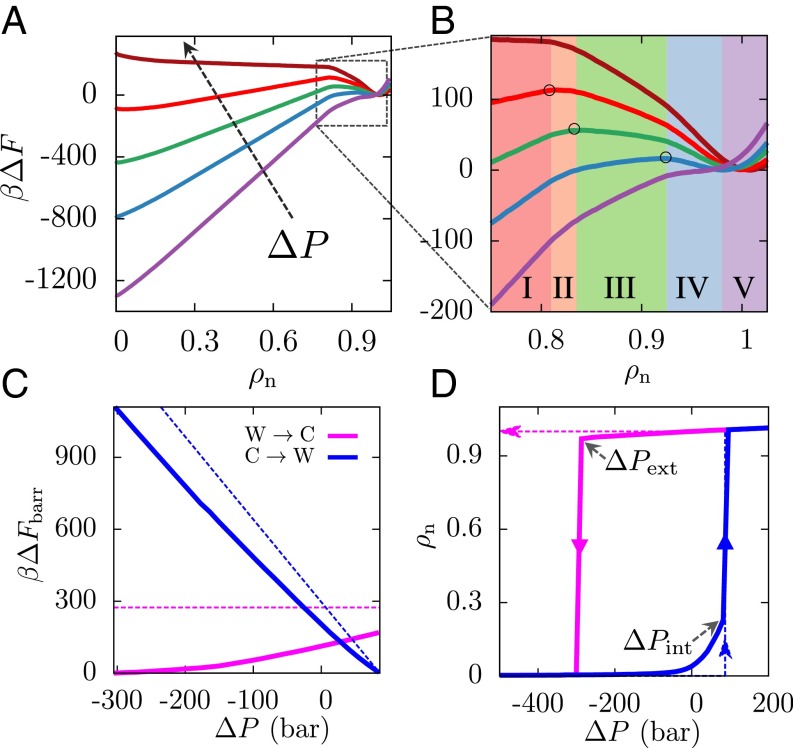
The implications of this nonclassical pathway on the pressure dependence of the dewetting transition are even more interesting. Because pressure favors configurations with higher densities in a well-defined manner, its effect on $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$ can be readily estimated, as shown in SI Appendix. As shown in Fig. 3A, the most striking effect of changing pressure is seen in the slope of region I; as pressure is increased, the slope decreases and the Cassie state is destabilized. The increase in pressure also leads to a decrease in the barrier to transition from the Cassie to the Wenzel state, as shown in Fig. 3C. The pressure at which this barrier for wetting disappears, $\mathrm{\Delta }{P}_{\text{int}}$, corresponds to the limit of stability (or spinodal) of the Cassie state; at $\mathrm{\Delta }P=\mathrm{\Delta }{P}_{\text{int}}$, a system in the Cassie state will spontaneously descend into the Wenzel state, as shown in the Cassie-to-Wenzel hysteresis curve (blue) in Fig. 3D. The exact agreement between the theoretical and simulated $\mathrm{\Delta }{P}_{\text{int}}$ values seen in Fig. 3 C and D is not coincidental, but a consequence of the fact that the value of vapor–liquid surface tension, ${\gamma }_{\text{fit}}$, used in the macroscopic theory, was obtained by fitting the simulated free energy profile in region I; see SI Appendix. The agreement between ${\gamma }_{\text{fit}}$ and ${\gamma }_{\text{SPC}/\text{E}}$ nevertheless suggests that the macroscopic theory prediction of intrusion pressure, $\mathrm{\Delta }{P}_{\text{int}}=-\gamma \cos \theta A_{\text{side}}/V$ (38, 39), should be reasonably accurate even for surfaces with nanoscale texture, a finding that is in harmony with recent experiments (15). This success of macroscopic theory in describing $\mathrm{\Delta }{P}_{\text{int}}$, the pressure at which superhydrophobicity fails, is a direct consequence of its ability to capture region I of $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$ accurately.

Fig. 3.

Effect of pressure on Cassie–Wenzel transitions. (A) $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$ is shown for pressures ranging from −350 to 100 bar, with the arrow pointing in the direction of increasing pressure (purple, −350 bar; blue, −200 bar; green, −100 bar; red, 0 bar; brown, 100 bar). As pressure is increased, the slope of the classical region I decreases, destabilizing the Cassie state; conversely, as pressure is decreased, the Wenzel state is destabilized. (B) This destabilization of the Wenzel state is manifested not only in an increase in the slope of region I but also in a corresponding increase in the slopes of the nonclassical regions II–IV, from negative toward zero to eventually being positive. As a result, a decrease in pressure shifts the location of the barrier (○) to higher ${\rho }_{\text{n}}$ and leads to a concomitant decrease in the height of the barrier. (C) The barriers for the wetting and dewetting transitions are shown here as a function of $\mathrm{\Delta }P$ (simulation, solid lines; theory, dashed lines). Both the simulated and the classical Cassie-to-Wenzel barriers (blue) decrease on increasing pressure, eventually disappearing at the intrusion pressure, $\mathrm{\Delta }{P}_{\text{int}}$. On the other hand, although the classical Wenzel-to-Cassie barrier (magenta) is predicted to be independent of pressure, simulations suggest that the barrier to dewetting disappears at a sufficiently small extrusion pressure, $\mathrm{\Delta }{P}_{\text{ext}}$. (D) Pressure-dependent hysteresis curves for ${\rho }_{\text{n}}$, assuming the system remains in its metastable basin and is unable to surmount barriers larger than 1 $k_{\text{B}}T$.

Although regions II to IV play no role in determining $\mathrm{\Delta }{P}_{\text{int}}$, their role is profoundly important in the reverse process, that is, the Wenzel-to-Cassie (dewetting) transition. As pressure is decreased, not only does the slope of region I increase (Fig. 3A), but the slopes of regions II–IV that are negative at $\mathrm{\Delta }P=0$ also increase, approaching zero at sufficiently negative pressures. Fig. 3B zooms in on the liquid basin of $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$ and highlights that as pressure is decreased the location of the peak in the free energy shifts to higher ${\rho }_{\text{n}}$ and is accompanied by a gradual decrease in the height of the dewetting barrier (Fig. 3C). This decrease in the dewetting barrier with decreasing pressure is in stark contrast with the classical expectation that a constant adhesion barrier must be overcome to go from the Wenzel to the Cassie state (18). Under sufficient tension (negative pressure), the barrier goes to zero as the Wenzel basin reaches the limit of its stability. Our simulations thus suggest that superhydrophobicity can be recovered, that is, a system in the Wenzel state can spontaneously and remarkably transition back into the Cassie state below a so-called extrusion pressure, $\mathrm{\Delta }{P}_{\text{ext}}$ (Fig. 3D).

Informing the Design of Robust Superhydrophobic Surfaces

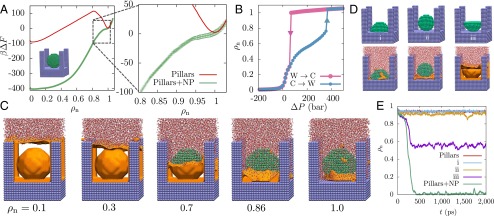
The term “robust” is used here to describe the superhydrophobic Cassie state (not the mechanical robustness of the surface texture), and in particular the ability of a surface to recover its superhydrophobicity once the surface texture is wet. For the surface studied here, the extrusion pressure, $\mathrm{\Delta }{P}_{\text{ext}}=-300$ bar, is quite small. Although water can sustain significant tension, and experiments have been able to access $\mathrm{\Delta }P\lesssim -\mathrm{1,200}$ bar before cavitation occurs (40), from a practical standpoint robust superhydrophobic surfaces with significantly larger $\mathrm{\Delta }{P}_{\text{ext}}$ values that exceed atmospheric pressure are desirable. Clues for designing such surfaces are contained within Fig. 2, which suggests that it is hardest to remove water molecules from the center of the simulation cell. To destabilize those waters and facilitate the formation of the vapor–liquid interface, we modify the pillared surface by adding a spherical nanoparticle at the center of the cell (Fig. 4A, Inset). A comparison of the free energy profile, $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$, of this novel surface with that of the pillared surface (Fig. 4A) highlights that the introduction of the nanoparticle has a dramatic influence on $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$; the Wenzel state is destabilized to such an extent that it is no longer metastable but has been rendered unstable at $\mathrm{\Delta }P=0$. In fact, as shown by the hysteresis curves in Fig. 4B, the Wenzel state remains unstable up to an extrusion pressure, $\mathrm{\Delta }{P}_{\text{ext}}=+68$ bar. The pressure dependence of $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$ for this surface as well as the corresponding barriers to wetting/dewetting are included in SI Appendix. Thus, a system prepared in the wet (Wenzel) state, by condensation or by starting at a high pressure, for example, should spontaneously dewet on decreasing the pressure below 68 bar, resulting in a recovery of the superhydrophobic Cassie state. To investigate this possibility and rule out the existence of any additional barriers to dewetting, we performed 26 equilibrium (unbiased) simulations starting with ${\rho }_{\text{n}}\approx 1$. In each case, the system spontaneously descends into the Cassie state within 700 ps, indicative of a barrierless transition from the Wenzel to the Cassie state. Details of these simulations are provided in SI Appendix and one of the dewetting trajectories is included as Movie S1.

Fig. 4.

Designing surface textures for the spontaneous recovery of superhydrophobicity. (A) The free energetics of a surface with a 3.5-nm diameter spherical nanoparticle at the center of the cell (Inset) are compared with the corresponding pillared surface; the surface modification stabilizes the superhydrophobic Cassie state and renders the Wenzel state unstable. (B) The modified surface features a positive extrusion pressure, $\mathrm{\Delta }{P}_{\text{ext}}=68$ bar, suggesting spontaneous recovery of superhydrophobicity at ambient conditions. (C) Representative instantaneous interface configurations highlight that dewetting commences at the center of the cell and spreads outward, facilitating the spontaneous formation of the vapor–liquid interface, which then rises along the pillars. Although waters stick to the top surface of the nanoparticle, the unfavorable gradient in water density between the edges and the center of the cell facilitates the depinning of the vapor–liquid interface. (D) We simulate three additional variants of the pillared surface, which displace waters from the center of the cell using (i) a 3.5-nm hemispherical particle, (ii) a 3-nm spherical nanoparticle, and (iii) an inverted 3.5-nm hemispherical particle. The three surfaces (top row) all violate one of the three criteria for spontaneous dewetting outlined in the text. When initialized in the Wenzel state, these surfaces are unable to undergo complete dewetting, as evidenced by the final configurations of 2-ns-long unbiased simulations (bottom row). (E) The time dependence of ${\rho }_{\text{n}}$ for such unbiased simulations highlights that the Wenzel state is unstable only for the pillared system with a 3.5-nm spherical nanoparticle.

The dewetting trajectory as well as characteristic configurations along the dewetting pathway (Fig. 4C) highlight that the strongly confined region between the nanoparticle and the basal surface nucleates a vapor bubble (${\rho }_{\text{n}}\approx 1$), which then grows to facilitate the spontaneous formation of an intact vapor–liquid interface (${\rho }_{\text{n}}=0.83$). Once formed, the vapor–liquid interface begins to rise, and although it adheres to the top of the nanoparticle, the interface continues to rise along the pillars; the unfavorable density gradient between the center and the edges of the cell then facilitates the barrierless depinning of the interface. This dewetting pathway suggests that the spontaneous recovery of superhydrophobicity requires (i) a confined (negative curvature) region of nanoscopic dimensions to nucleate a vapor bubble, which (ii) must grow to a large enough size to facilitate the formation of an intact vapor–liquid interface, which in turn (iii) must not be pinned by surface features as it rises along the pillars. To test the validity of these criteria, we study three additional surfaces that each destabilize the central waters but violate exactly one of the above criteria (Fig. 4D). By running unbiased simulations initialized in the Wenzel state, we show that none of the three surfaces is able to spontaneously transition to the Cassie state (Fig. 4E). In SI Appendix, Fig. S9 we also show $\mathrm{\Delta }F\left({\rho }_{\text{n}}\right)$ for these modified surfaces. In each case, the destabilization of the central waters by the nanoparticle leads to a substantial reduction in the dewetting barrier; however, this destabilization alone is insufficient to lead to the spontaneous recovery of the superhydrophobic Cassie state. Because augmenting the surface texture alters the stability of the barrier and the Wenzel states in different ways, and can also change the partially dewetted morphologies observed along the dewetting pathway, the relationship between the surface texture geometry and the height of the dewetting barrier is nontrivial. In particular, the extent to which a change in surface texture influences the dewetting barrier does not depend on its ability to (de)stabilize the barrier state or the Wenzel state alone; rather, how the surface texture modification influences the entire dewetting pathway is important. Indeed, by following the three design criteria outlined above, which pay attention to the dewetting pathway (Fig. 4C), we were able to design a second surface texture that displays an unstable Wenzel state at ambient conditions (see SI Appendix, Fig. S10). The fact that each of these complex criteria have to be satisfied for spontaneous dewetting could help explain why nanotextured surfaces that spontaneously recover superhydrophobicity have not been discovered serendipitously, despite the use of both nanoparticles and nanoscale pillars to texture surfaces (15, 41).

Outlook

The last decade has seen an explosion of studies pertaining to superhydrophobic surfaces, ranging from the development of novel techniques for their synthesis to those aimed at understanding the properties of these surfaces and their putative applications. Our work informs both fundamental and applied aspects of superhydrophobicity, not only uncovering nonclassical Cassie–Wenzel transition pathways, but also suggesting strategies for the rational design of robust superhydrophobic surfaces that can spontaneously recover their superhydrophobicity. In particular, we show that the free energetics of wetting–dewetting transitions on nanotextured surfaces, the corresponding mechanistic pathways, and their dependence on pressure are all strongly influenced by collective water density fluctuations. Although the importance of fluctuations at the nanoscale is clear, the extent to which fluctuations influence dewetting pathways for larger texture sizes remains an interesting open question. We note, however, that nonclassical effects stem from the stabilization of dewetted morphologies that precede the formation of an intact vapor–liquid interface at the basal surface; once a vapor–liquid interface is nucleated, the remainder of the dewetting process is classical. Because the width of this nascent vapor–liquid interface is not expected to depend on the texture size, and should always have nanoscale dimensions, fluctuations may continue to play an important role in the dewetting of surface textures with significantly larger feature sizes. Our results also clarify that even though certain aspects of dewetting on nanotextured surfaces are nonclassical, other aspects can be classical. In particular, because the intrusion pressure depends on the free energetics of the (classical) ascent of the vapor–liquid interface along the pillars, it is well described by macroscopic theory. Similarly, macroscopic models (42, 43) have also been shown to the capture apparent contact angle of a liquid droplet localized in the Cassie or the Wenzel basin (44–47).

An understanding of the Cassie–Wenzel transition pathway also facilitates the rational design of surfaces with superior superhydrophobicity. Although numerous methods have been suggested for texturing hydrophobic surfaces, from top-down fabrication to bottom-up self-assembly techniques (48–50), a key bottleneck in their widespread adoption has been the fragility of the superhydrophobic Cassie state and the associated irreversible breakdown of superhydrophobicity upon wetting (12). Our findings represent a major step in addressing this challenge, highlighting the importance of water density fluctuations in stabilizing nonclassical pathways on nanotextured surfaces, which reduce dewetting barriers and enable the spontaneous recovery of superhydrophobicity. Our results also suggest a general strategy for augmenting the design of existing nanotextured surfaces. By identifying the pathways to dewetting, and in particular the regions that are hardest to dewet, we were able to inform the location of sites where the introduction of additional texture would be optimal. The rational design of nanotextured surfaces with superior superhydrophobicity could be further bolstered by investigating the extent to which the dewetting of a unit cell is influenced by whether an adjacent cell is wet or dry. In particular, if a dry cell could facilitate the dewetting of adjacent cells, then not all cells would have to possess a nanoparticle for the spontaneous recovery of superhydrophobicity; once a nanoparticle-containing cell dewetted spontaneously, it could facilitate the dewetting of cells adjacent to it. Such cooperative effects would also have interesting implications on whether dewetting is nucleated at the edges or the center of a water droplet, and on the pinning of the three phase contact line and the associated contact angle hysteresis (51, 52). In conjunction with recent advances in introducing texture at the nanoscale (15, 53), our results thus promise to pave the way for robust superhydrophobic surfaces with widespread applicability under the most challenging conditions. One example of such an application involves sustained underwater operation (54), which would require the surface texture to not only remain dry under hydrostatic pressure but also be able to return to the dry state if the texture wets in response to a perturbation. Another example pertains to condensation heat transfer (55), wherein an unstable Wenzel state would facilitate the immediate roll-off of condensing water droplets and enable dropwise condensation to be sustained at higher fluxes.

Materials and Methods

Simulation Setup.

Each of the surfaces that we study is composed of atoms arranged on a cubic lattice with a lattice spacing of 0.25 nm; the surface atoms are constrained to remain in their initial positions throughout the simulations. The basal surface, which is situated at the bottom of the simulation box, is made of eight layers of atoms and is 2 nm thick. On the pillared surface, square pillars of height H = 4.5 nm and width W = 2 nm are used to introduce surface texture. The pillars are placed on a square lattice with interpillar spacing S = 4 nm. We also study surfaces that additionally contain spherical or hemispherical nanoparticles that are also made of atoms on a cubic lattice and are placed at the center of the simulation cell, touching the top of the basal surface. Each system is periodic in all three spatial directions and is initialized in the Wenzel state. The surfaces are hydrated with roughly 7,000 water molecules, so that even in the Wenzel state a 2-nm-thick water slab rests above the pillars. We also provide a buffering vapor layer at the top of the simulation box, which is roughly 6 nm thick in the Wenzel state. As waters leave the textured region the vapor layer shrinks to roughly 2 nm in the Cassie state. The vapor layer, which is thus present in our system at all times, ensures that water is in coexistence with its vapor, and $\mathrm{\Delta }P=0$ (29). To ensure that the vapor layer remains at the top of the 6 $\times$ 6 $\times$ 15 nm³ simulation box, we include a repulsive wall at z = 14.5 nm.

Simulation Details.

We have chosen the SPC/E model of water (56) because it adequately captures the experimentally known features of water, such as surface tension, isothermal compressibility, and the vapor–liquid equation of state near ambient conditions, all of which are important in the study of dewetting on hydrophobic surfaces (19, 20, 36, 57). The surface atoms interact with the water oxygens through the Lennard-Jones (LJ) potential (σ = 0.35 nm, ε = 0.40 kJ/mol). As shown in SI Appendix, this choice leads to a flat surface water droplet contact angle, θ = 116.2°, in accord with contact angles observed on typical hydrophobic surfaces, such as alkyl-terminated self-assembled monolayer surfaces (23). We use the GROMACS molecular dynamics simulation package (58), suitably modified to perform INDUS simulations in the canonical ensemble. A detailed description of the INDUS calculations (24, 35), which we use to characterize the free energetics of wetting–dewetting transitions on nanotextured surfaces, is included in SI Appendix. To maintain a constant temperature of T = 300 K (59), the canonical velocity-rescaling thermostat with a time constant of 0.5 ps is used. LJ interactions and the short-ranged part of the electrostatic interactions are truncated at 1 nm, and the particle mesh Ewald algorithm is used to treat the long-ranged part of electrostatic interactions (60). The SHAKE algorithm is used to constrain the bond lengths of the water molecules (61).