Receptor arrays optimized for natural odor statistics

Significance

Natural odors typically consist of many molecules at different concentrations, which together determine the odor identity. This information is collectively encoded by olfactory receptors and then forwarded to the brain. However, it is unclear how the receptor activity can encode both the composition of the odor and the concentrations of its constituents. We study a simple model of the olfactory receptors from which we derive design principles for optimally communicating odor information in a given natural environment. We use these results to discuss biological olfactory systems, and we propose how they can be used to improve artificial sensor arrays.

Abstract

Natural odors typically consist of many molecules at different concentrations. It is unclear how the numerous odorant molecules and their possible mixtures are discriminated by relatively few olfactory receptors. Using an information theoretic model, we show that a receptor array is optimal for this task if it achieves two possibly conflicting goals: (i) Each receptor should respond to half of all odors and (ii) the response of different receptors should be uncorrelated when averaged over odors presented with natural statistics. We use these design principles to predict statistics of the affinities between receptors and odorant molecules for a broad class of odor statistics. We also show that optimal receptor arrays can be tuned to either resolve concentrations well or distinguish mixtures reliably. Finally, we use our results to predict properties of experimentally measured receptor arrays. Our work can thus be used to better understand natural olfaction, and it also suggests ways to improve artificial sensor arrays.

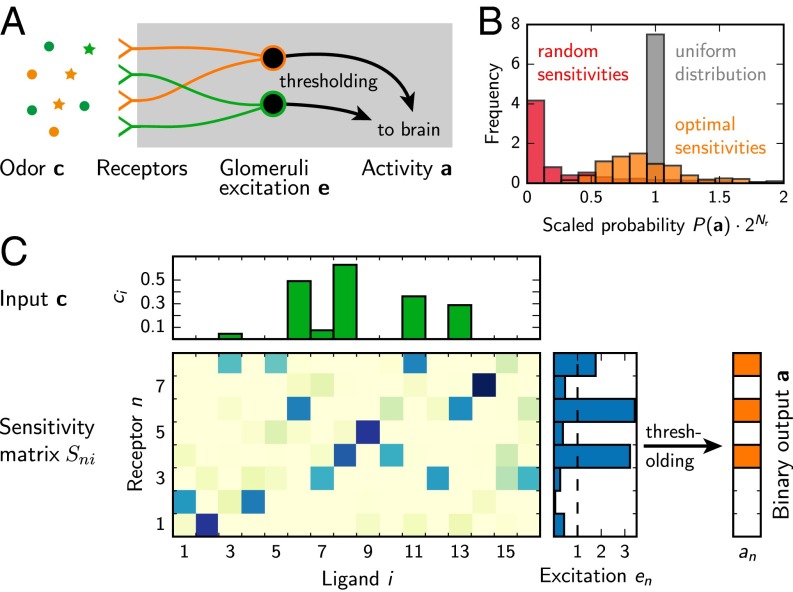
Discrimination of olfactory signals occurs in a high-dimensional space of odor stimuli in which a large number of distinct molecules and their mixtures can be distinguished by a much smaller number of receptors (1–3). For example, humans have about 300 distinct olfactory receptors (4), which can sense at least 2,100 odorant molecules (5), and the real number might be much larger (1). Moreover, humans can differentiate between mixtures of up to 30 odorants (6). Such remarkable molecular discrimination is thought to use a combinatorial code (7, 8), where typical odorant molecules bind to receptors of multiple types (1, 3). Each receptor type is expressed in many cells (9), and the information from all receptors of the same type is accumulated in corresponding glomeruli in the olfactory bulb (10, 11) (see Fig. 1A). The activity of a single glomerulus is thus the total signal of the associated receptor type, so the information about the odor is encoded in the activity pattern of the glomeruli (11, 12). This activity pattern is interpreted by the brain to learn about the composition and the concentration of the inhaled odor. We here study how receptor arrays can maximize the transmitted information.

Fig. 1.

(A) Schematic representation of the olfactory system, where ligands bind to receptors, whose excitation is accumulated in glomeruli, thresholded, and relayed to the brain. (B) Histogram of the probabilities $P\left(\mathit{a}\right)$ of the $2^{N_{\text{r}}}$ output patterns $\mathit{a}$ for a random receptor array (red, entropy $I=6.15\hspace{0.17em}\text{bits}$), a numerically optimized one (orange, $I=7.83\hspace{0.17em}\text{bits}$), and the theoretical optimum of a uniform distribution (gray, $I=8\hspace{0.17em}\text{bits}$). (C) Schematic representation of our physical model, where the input $\mathit{c}$ (green bars) is mapped to excitations (blue bars), which are turned into the output $\mathit{a}$ (orange) by thresholding. Parameters in B and C are: receptor count $N_{\text{r}}=8$, ligand count $N_{\text{l}}=16$, ligand frequency $p_i=1/4$, and mean ${\mathit{\mu }}_i=1$ and SD ${\mathit{\sigma }}_i=1$ of the ligand concentration.

It is known (13, 14) that the input−output characteristics of sensory apparatuses of many organisms are tailored to the statistics of the organism’s natural environment to maximize information transmission. For example, in the visual circuit of the fly, the input−output relationship of neurons is matched to the cumulative distribution of the input distribution (13). Similar observations have since been made in many sensory systems (14, 15) and even in transcriptional regulation (16). In all these cases, the distinguishable outputs of the sensory system must be dedicated to equal parts of the input distribution, which is known as Laughlin’s principle (13) or histogram equalization (17). Intuitively, more of the response range is dedicated to common stimuli, at the expense of less frequent stimuli (13).

Similarly, the binding affinities of olfactory receptors might reflect the natural statistics of odors in an organism’s environment. Odors vary across environments and differ in both their frequency and composition (18). For example, some molecules might frequently appear together because they originate from the same source, whereas others are rarely found in the same odor. Additionally, some odors are more important to recognize than others, which corresponds to considering an increased frequency for these odors. Together, the frequencies and correlations constitute the natural olfactory scene.

It is not clear how olfactory receptors can account for natural odor statistics. Merely dedicating more receptors to common odors is not optimal, given the small number of available receptors and the many-to-many relationship between receptors and odors. Further, the value of a receptor is strongly dependent on how it complements the other receptors in the array; many “good” receptors can still create a poor array. Finally, the concentrations of molecules composing an odor can vary widely. Odors need to be distinguished in both quality and quantity; hence receptors must vary in both what molecules they respond to and how strongly they do this. Given the statistics of an olfactory scene, what combination of odorants should different receptors in an array respond to?

We use an information theoretic approach to quantify how well a receptor array is matched to given odor statistics. We generalize Laughlin’s principle to the high-dimensional case and show that optimal receptor arrays should obey two general principles: (i) Each receptor should be active half the time when odors are presented with natural statistics. (ii) The activities of any pair of receptors should be uncorrelated when averaged over all odors presented with natural statistics. If both conditions are satisfied for an array of ${\mathit{N}}_{\text{r}}$ receptors with binary readouts, all $2^{N_{\text{r}}}$ activity patterns are equally likely when odors are presented with natural statistics (see Fig. 1B). The two basic principles may be obvious with some thought, but they usually cannot be satisfied simultaneously. We thus also determine the relative costs of violating the two conditions and use this to carry out numerical and analytical optimizations to determine conditions for optimal receptor arrays. Furthermore, our model implies relationships between the typical ligand concentrations and the ability to discriminate mixtures that have been missed before.

After introducing our general framework below, we first discuss general properties of optimal receptor arrays. We then consider two different classes of natural statistics, for which we find optimal receptors in terms of random matrices. Here, our information theoretic approach provides a combined measure of the array’s performance in multiple aspects—from the resolution of ligand concentrations to the discrimination of mixture composition. We thus finally discuss the trade-off between such potentially mutually exclusive goals and compare our results to experimentally measured receptor arrays.

Results

Odors are mixtures of odorant molecules that are ligands of olfactory receptors. Any odor can be described by a vector $\mathit{c}\mathrm{=}\left(c_1,c_2,\dots ,c_{N_{\text{l}}}\right)$ that specifies the concentrations $c_i$ of all $N_{\text{l}}$ possible ligands ($c_i\ge 0$). During a single sniff, the ligands in the odor $\mathit{c}$ come in contact with $N_{\text{r}}$ different odor receptors. In the simplest case, the sensitivity of receptor n to ligand i can be described by a single number $S_{ni}$, and the total excitation $e_n$ of receptor n is given by (19, 20)

$$e_n={\displaystyle \sum _i{S}_{ni}{c}_i}.$$ [1]

Typical receptors have a nonlinear dose–response curve (21), and the output $a_n$ is thus a nonlinear function of $e_n$. Moreover, receptors are subject to noise (22), e.g., from stochastic binding, which limits the number of distinguishable outputs. To capture both effects, we consider receptors with only two output states, which corresponds to large noise (23). In this case, the activity $a_n$ of receptor n is given by

$$a_n=\{\begin{array}{cc}0& e_n<1\\ 1& e_n\ge 1\end{array},$$ [2]

i.e., the receptor is active if its excitation $e_n$ exceeds a threshold. Eqs. 1 and 2 describe the mapping of the odor $\mathit{c}$ to the activity pattern $\mathit{a}=\left(a_1,a_2,\dots ,a_{N_{\text{r}}}\right)$, where the receptor array is characterized by the sensitivity matrix $S_{ni}$ (see Fig. 1C). This activity pattern is then analyzed by the brain to infer the odor $\mathit{c}$. Such a distributed representation of odors in activity patterns has been compared with compressed sensing (24); here we focus on how this representation can be tuned to match the structure of natural odors.

We assume that the structure of natural odors in a given environment can be captured by a probability distribution $P_{\text{env}}\left(\mathit{c}\right)$ from which odors are drawn. $P_{\text{env}}\left(\mathit{c}\right)$ can encode, for example, the fact that some ligands are more common than others or that some ligands are strongly correlated or anticorrelated in their occurrence. Because natural odor statistics are hard to measure (18), we work with a broad class of distributions $P_{\text{env}}\left(\mathit{c}\right)$ characterized by a few parameters. We define $p_i$ to be the probability with which ligand i occurs in a random odor. The correlations between the occurrences of ligands are captured by a covariance matrix $p_{ij}$. We expect $p_i$ to be small because any given natural odor typically contain tens to hundreds of ligands (20, 25), which is a small subset of all $N_{\text{l}}\mathrm{\gtrsim }\mathrm{2,100}$ ligands (18). When a ligand i is present, we assume its concentration $c_i$ has mean ${\mathit{\mu }}_i$ and standard deviation (SD) ${\mathit{\sigma }}_i$. Thus, the full natural odor statistics $P_{\text{env}}\left(\mathit{c}\right)$ are parameterized by $p_i$, ${\mathit{\mu }}_i$, and ${\mathit{\sigma }}_i$ for all ligands i and a covariance matrix $p_{ij}$ in our model.

Optimal Receptor Arrays.

An optimal receptor array must tailor receptor sensitivities $S_{ni}$ so that the odors-to-activity mapping given by Eqs. 1 and 2 dedicates more activity patterns to more frequent or more important odors as specified by $P_{\text{env}}\left(\mathit{c}\right)$. In information theoretic terms, the array must maximize the mutual information $I\left(\mathit{c},\mathit{a}\right)$ (26). In our model, the mapping from $\mathit{c}$ to $\mathit{a}$ is deterministic, and I can be written as the entropy of the output distribution $P\left(\mathit{a}\right)$,

$$I=-{\displaystyle \sum _{\mathit{a}}P\left(\mathit{a}\right){\log }_{2}P\left(\mathit{a}\right)},$$ [3]

where the sum is over all possible activity patterns $\mathit{a}$. Note that $P\left(\mathit{a}\right)={\displaystyle \int \text{d}\mathit{c}\hspace{0.17em}P\left(\mathit{a}|\mathit{c}\right)P_{\text{env}}\left(\mathit{c}\right)}$, where $P\left(\mathit{a}|\mathit{c}\right)$ describes the mapping from $\mathit{c}$ to $\mathit{a}$. Consequently, I depends on $S_{ni}$ and the odor environment $P_{\text{env}}\left(\mathit{c}\right)$. In fact, I is maximized by sensitivities $S_{ni}$ that are tailored to $P_{\text{env}}\left(\mathit{c}\right)$ such that all activity patterns $\mathit{a}$ are equally likely (13, 26).

The mutual information I can be approximated (27) in terms of the mean activities $\langle a_n\rangle$ and the covariance between receptors, $\text{cov}\left(a_n,a_m\right)\mathrm{=}\langle a_n{a}_m\rangle -\langle a_n\rangle \langle a_m\rangle$, encoded by $P\left(\mathit{a}\right)$,

$$\begin{array}{c}I\mathrm{\approx }-{\displaystyle \sum _n\left[\langle a_n\rangle {\log }_2\langle a_n\rangle +\left(1-\langle a_n\rangle \right){\log }_2\left(1-\langle a_n\rangle \right)\right]}\\ -\frac{8}{\text{ln}\hspace{1em}2}{\displaystyle \sum _{n<m}\text{cov}{\left(a_n,a_m\right)}^2},\end{array}$$ [4]

which is an expansion up to quadratic order in $\text{cov}\left(a_n,a_m\right)$. The first term gives the information gained through each receptor in isolation. The second term describes the reduction of information due to correlations between different receptors. For both Eqs. 3 and 4, the maximal mutual information of $N_{\text{r}}\hspace{0.17em}\text{bits}$ can only be obtained if

$$\begin{array}{c}{\langle a_n\rangle }^{\text{*}}=\frac{1}{2}\end{array}$$ [5a]

and

$$\begin{array}{c}\text{cov}{\left(a_n,a_m\right)}^{\text{*}}=0.\end{array}$$ [5b]

Consequently, in a receptor array optimized for its natural environment, each receptor responds to about half of all odors and any pair of receptors is uncorrelated in its response to odors, assuming odors are presented with frequency $P_{\text{env}}\left(\mathit{c}\right)$.

These design principles follow from very general considerations, but they may not always be simultaneously achievable. To understand such constraints, we study how microscopic properties of receptor arrays (the sensitivities $S_{ni}$) determine both $\langle a_n\rangle$ and $\text{cov}\left(a_n,a_m\right)$. The mean receptor activity $\langle a_n\rangle$ is given by the probability that the associated excitation $e_n$ exceeds 1, $\langle a_n\rangle =1-F_n\left(1\right)$, where $F_n\left(e_n\right)$ denotes the cumulative distribution function of $e_n$ (see Supporting Information). The covariance $\text{cov}\left(a_n,a_m\right)$ can be estimated in terms of ${\text{cov}}_c\left(e_n,e_m\right)$ using a normal approximation around the maximum of I (see Supporting Information). These statistics of $e_n$ can be calculated from Eq. 1 and read

$${\langle e_n\rangle }_c={\displaystyle \sum _i{S}_{ni}\langle c_i\rangle }$$ [6a]

$${\text{cov}}_c\left(e_n,e_m\right)={\displaystyle \sum _{i,j}{S}_{ni}{S}_{mj}\text{cov}\left(c_i,c_j\right)},$$ [6b]

where $\langle c_i\rangle$ and $\text{cov}\left(c_i,c_j\right)$ follow from $P_{\text{env}}\left(\mathit{c}\right)$.

Combining Eqs. 4 and 6 to estimate mutual information, we can quantify how well an array’s sensitivities $S_{ni}$ are matched to natural odor statistics $P_{\text{env}}\left(\mathit{c}\right)$. As a computational matter, these equations also allow a rapid calculation of mutual information without calculating the full distribution $P\left(\mathit{a}\right)$.

Random Sensitivity Matrices.

We next study which sensitivity matrices $S_{ni}$ obey the optimization goals given in Eq. 5 for given odor statistics. Here, we will show that random $S_{ni}$ with independent and identically distributed entries drawn from the right distribution can be close to optimal. This is because such matrices generically have low correlations, and the resulting activities $a_n$ are thus only weakly correlated. In this section, we study what distributions lead to $\langle a_n\rangle =\frac{1}{2}$ and under what conditions these matrices minimize $\text{cov}\left(a_n,a_m\right)$ for two different classes of odor distributions.

Narrow concentration distributions.

We begin with the simple case where the concentration distributions are narrow, ${\mathit{\sigma }}_i\ll {\mathit{\mu }}_i$. In this case, we can focus on determining which ligands appear in a mixture. Receptors that are optimal for this task must be highly sensitive to some ligands while they ignore the others, but the exact value of the sensitivity does not matter. This property can be encoded in a binary sensitivity matrix ${\widehat{S}}_{ni}$ where ${\widehat{S}}_{ni}=1$ if receptor n reacts to ligand i and ${\widehat{S}}_{ni}=0$ if it does not. We can then calculate activity statistics using Eqs. 2 and 6, as shown in Supporting Information. In the simple case of uncorrelated mixtures ($p_{ij}=0$ for $i\ne j$), $\langle a_n\rangle \approx {\displaystyle {\sum }_i{\widehat{S}}_{ni}\hspace{0.17em}{p}_i}$ and $\text{cov}\left(a_n,a_m\right)\approx {\displaystyle {\sum }_i{\widehat{S}}_{ni}{\widehat{S}}_{mi}\hspace{0.17em}{p}_i}$. In Supporting Information, we also calculate corrections due to the correlated appearance of ligands ($p_{ij}\ne 0$); e.g., $\langle a_n\rangle \approx {\langle a_n\rangle }_0+\frac{1}{2}\left(1-{\langle a_n\rangle }_0\right){\displaystyle {\sum }_{i,j}\left({\widehat{S}}_{ni}+{\widehat{S}}_{nj}-{\widehat{S}}_{ni}{\widehat{S}}_{nj}\right)p_{ij}}$, where ${\langle a_n\rangle }_0={\displaystyle {\sum }_i{\widehat{S}}_{ni}\hspace{0.17em}{p}_i}$ is the receptor activity in the uncorrelated case.

In the case of uncorrelated mixtures, we find, using Eq. 5, that ${\widehat{S}}_{ni}$ for optimal receptor arrays must satisfy

$$\begin{array}{c}{\displaystyle \sum _i{\widehat{S}}_{ni}^{\text{*}}\hspace{0.17em}{p}_i}=\frac{1}{2}\end{array}$$ [7a]

and

$$\begin{array}{c}{\displaystyle \sum _i{\widehat{S}}_{ni}^{\text{*}}{\widehat{S}}_{mi}^{\text{*}}\hspace{0.17em}{p}_i}=0.\end{array}$$ [7b]

Receptors are thus optimal if (i) the occurrence probabilities ${\mathit{p}}_i$ of the ligands they react to add up to 1/2 and (ii) no ligand activates multiple receptors. Because any given ligand is rare in natural odors, $p_i\ll 1/2$, such optimization is equivalent to a partition problem where the $N_{\text{l}}$ probabilities $\left\{p_i\right\}$ have to be put into $N_{\text{r}}$ groups (i.e., a group of ligands for each receptor), such that the sum of the elements is close to 1/2, while a minimal number of elements should appear in several groups. Eq. 4 gives the relative cost of violating these two possibly conflicting requirements.

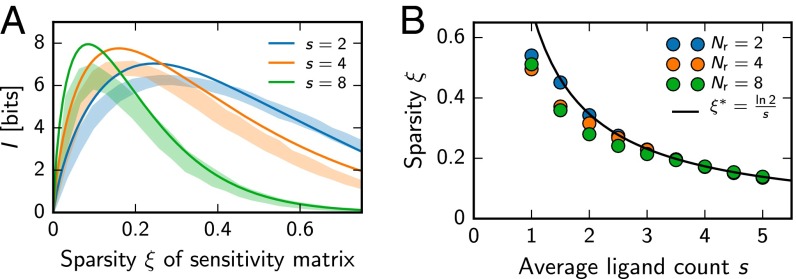
This partition problem can be solved approximately using random binary sensitivity matrices. The ensemble of such matrices is characterized by a single parameter, the fraction of nonzero entries or sparsity ξ. Fig. 2A shows that there is an optimal sparsity ${\mathit{\xi }}^{\text{∗}}$, at which I is maximized. It follows from $\langle a_n\rangle =1/2$ that

$${\mathit{\xi }}^{\text{*}}\approx \frac{\ln 2}{s},$$ [8]

where $s={\displaystyle {\sum }_i{p}_i}$ is the mean mixture size (see Supporting Information). This condition for random matrices agrees well with the sparsity found from numerical optimization over all binary matrices (see Fig. 2B). However, for small s, the sparsity ${\mathit{\xi }}^{\text{∗}}$ becomes large, which leads to significant correlations $\text{cov}\left(a_n,a_m\right)$ and thus reduced performance. Optimal matrices thus have a sparsity that is lower then predicted by Eq. 8 for small mixture sizes s (see Fig. 2B).

Fig. 2.

Receptor arrays with random sensitivity matrices whose sparsity ξ is tuned to match natural statistics achieve near-optimal information transmission of odor composition. (A) Information I gained by $N_{\text{r}}=8$ receptor as a function of the average sparsity ξ of random binary sensitivity matrices for mixtures made of s ligands drawn from a total of $N_{\text{l}}=32$ ligands. Numerical results (shaded areas; mean $\pm$ SD; 32 samples) and analytical results (lines) following from Eq. 4 are shown. (B) Sparsity ξ of general binary sensitivity matrices that were numerically optimized for maximal I (symbols) is compared with the prediction from random binary matrices (solid line, Eq. 8) for different s and $N_{\text{r}}$ at $N_{\text{l}}=128$.

Wide concentration distributions.

In reality, odor concentrations vary widely, and receptor arrays must thus measure both odor composition and concentrations. The concentration of a single ligand can be measured if many receptors react to it with different sensitivities (7). The receptor array is optimal for this task if all possible outputs occur with equal frequency. This is the case if the inverse of the sensitivities follows the same distribution as the ligand concentrations (13), which is known as Laughlin’s principle. However, it is not clear how this principle can be generalized for measuring the concentration of multiple ligands simultaneously.

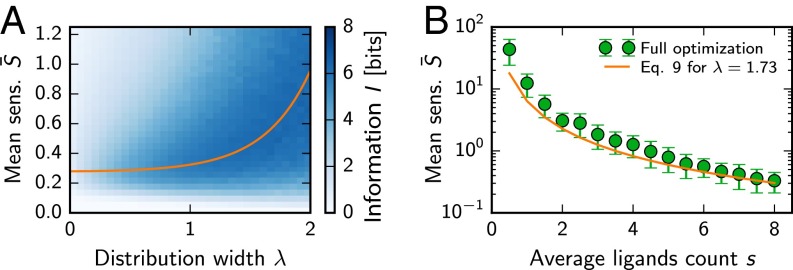
We study this problem by considering random sensitivities that are lognormally distributed. This choice is motivated by the complex interaction between receptors and ligands, which typically leads to normally distributed binding energies (28). We will show later that experimentally measured sensitivities indeed appear to be lognormally distributed. Lognormal distributions are characterized by two parameters, the mean $\overline{S}$ and the SD λ of the underlying normal distribution. We thus next ask how these parameters have to be chosen to maximize the mutual information I. To estimate I, we need to consider the excitations $e_n$, which approximately also follow a lognormal distribution (29). Their statistics are given by Eq. 6 and read ${\langle e_n\rangle }_{c,S}=\overline{S}\langle c_{\text{tot}}\rangle$ and ${\mathrm{cov}}_{c,S}\left(e_n,e_m\right)={\overline{S}}^2\mathrm{var}\left(c_{\text{tot}}\right)+{\mathit{\delta }}_{nm}\mathrm{var}\left(S\right){\displaystyle {\sum }_i\langle c_i^2\rangle }$, where $c_{\text{tot}}={\displaystyle {\sum }_i{c}_i}$ and $\text{var}\left(S\right)={\overline{S}}^2\left[\exp \left({\lambda }^2\right)-1\right]$. We use this to calculate $\langle a_n\rangle$ from Eq. 2 and find that the receptor array is optimal ($\langle a_n\rangle =1/2$) if (see Supporting Information)

$$\overline{S}=\frac{1}{\langle c_{\text{tot}}\rangle }{\left[1+\frac{\text{var}\left(c_{\text{tot}}\right)}{{\langle c_{\text{tot}}\rangle }^2}+\frac{{\displaystyle {\sum }_i\langle c_i^2\rangle }}{{\langle c_{\text{tot}}\rangle }^2}\left(e^{{\lambda }^2}-1\right)\right]}^{\frac{1}{2}}.$$ [9]

We test this equation by numerically calculating the mutual information I as a function of $\overline{S}$ and λ. Fig. 3A shows that Eq. 9 predicts the optimal parameters of lognormally distributed sensitivities very well. Fig. 3B shows that this result also predicts the mean $\overline{S}$ for numerical optimizations over general sensitivity matrices.

Fig. 3.

Random receptor arrays with a suitable mean sensitivity $\overline{S}$ and distribution width λ can transmit information about both odor concentration and composition. (A) Information I for lognormally distributed sensitivities as a function of the mean $\overline{S}$ and width λ of the distribution. The shown mean of I was calculated from Eqs. 1−3 using Monte Carlo sampling of 32 realizations per point. The orange line marks the optimum given by Eq. 9. (B) Mean sensitivity $\overline{S}$ for different average mixture sizes s. Numerical optimizations over general sensitivity matrices (symbols; mean $\pm$ SD; 64 samples) are compared with lognormally distributed matrices (solid line, Eq. 9) with $\mathit{\lambda }=1.73$, equal to the mean of the numerical data. Additional parameters in A and B are the same as in Fig. 1.

Log-normally distributed sensitivities perform badly if the distribution width λ is small (see Fig. 3A). This is expected because receptors with narrowly distributed $S_{ni}$ respond similarly to all ligands, leading to large correlations $\text{cov}\left(a_n,a_m\right)$ and thus reduced performance I. Interestingly, for large enough λ, the correlations are so small that the exact value of λ does not influence I significantly (see Fig. 3A). In fact, for very large λ, the $S_{ni}$ are likely very large or very small compared with $\overline{S}$. When $\overline{S}$ is chosen according to Eq. 9, receptors can thus only detect whether ligands are present or not, corresponding to the binary sensitivities discussed above, which cannot resolve the concentration of the ligands. Consequently, λ must influence how well such receptor arrays can resolve concentrations.

Trade-off between concentration resolution and mixture discriminability.

When the distribution width λ is large, the receptor arrays have similar performance I, so they are equally good at the combined problem of resolving concentrations and discriminating mixtures. However, the performance in the individual problems can vary widely. Because, in many contexts, we might wish to trade off performance, say, by sacrificing some ability to discriminate mixtures in favor of a better concentration resolution, we next investigate these properties in detail.

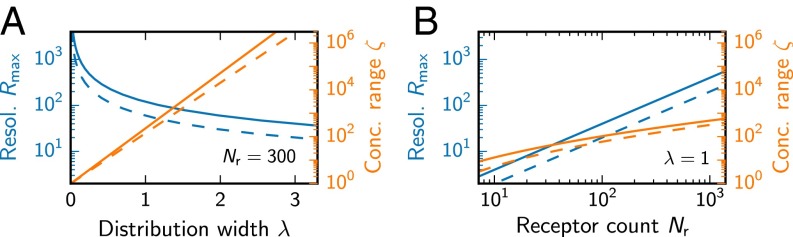
We define the concentration resolution R as the ratio of the concentration c at which a single ligand is presented and the concentration change $\mathit{\delta }c$ that is necessary to register a change, $R=c/\mathit{\delta }c$. Here, we consider the simple case where η additional receptors have to be excited to register a change in concentration. R is a function of the concentration c at which it is measured and its maximal value

$$R_{\text{max}}=\frac{N_{\text{r}}}{\sqrt{2\mathit{\pi }}\mathit{\eta \lambda }}$$ [10]

is obtained for $c\mathrm{=}{\overline{S}}^{\mathrm{-}1}\text{exp}\left[\left(1/2\right){\mathit{\lambda }}^2\right]$, which is the inverse of the median of the sensitivity distribution (see Supporting Information).

The range of concentrations that can be detected by the receptor array is given by the ratio of the largest concentration $c_{\text{max}}$ at which concentration differences can be detected to the lowest detectable concentration $c_{\text{min}}$, the odor detection threshold (30). In terms of η, the logarithm of the concentration range $\mathit{\zeta }=c_{\text{max}}/c_{\text{min}}$ reads (see Supporting Information)

$$\text{ln}\left(\mathit{\zeta }\right)=\sqrt{8}\mathit{\lambda }{\text{erf}}^{-1}\left(1-\frac{2\mathit{\eta }}{N_{\text{r}}}\right),$$ [11]

where ${\text{erf}}^{-1}\left(z\right)$ is the inverse error function. Eq. 11 shows that λ determines the number of concentration decades over which the receptor array is sensitive.

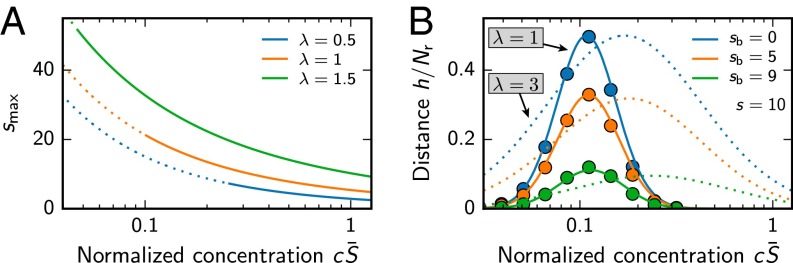
Taken together, λ has opposing effects on the resolution and the range of concentration measurements (see Fig. 4A). Consequently, λ can be tuned either for receptors that resolve concentrations well or cover a large concentration range. If only single ligands are measured, the optimal λ only depends on the concentration distribution $P_{\text{env}}\left(\mathit{c}\right)$. In this case, the mutual information I can be calculated from the resolution function $R\left(c\right)$, and optimizing $R\left(c\right)$ is equivalent to maximizing I (31). For odor mixtures, I accounts for a combination of the concentration resolution and the mixture discrimination, and maximizing I does not uniquely determine an optimal receptor array. We thus next study how the distribution width λ influences the ability to discriminate mixtures.

Fig. 4.

The width λ of the sensitivity distribution has opposing effects on concentration resolution $R_{\max }$ (blue, Eq. 10) and range ζ (orange, Eq. 11). (A) $R_{\max }$ and ζ as a function of the width λ for $N_{\text{r}}=300$ receptors. (B) $R_{\max }$ and ζ as a function of $N_{\text{r}}$ for $\mathit{\lambda }=1$. In A and B, $\mathit{\eta }=1$ (solid lines) and $\mathit{\eta }=2$ (dashed lines) changes in the output pattern are required to distinguish inputs.

We first consider mixtures of s ligands, each at concentration c, and determine the maximal size $s_{\text{max}}$ where adding an additional ligand does not significantly alter the activity pattern. Here $s_{\text{max}}$ is given by the largest s that obeys (see Supporting Information)

$$\frac{\text{d}{\langle a_n\rangle }_S}{\text{d}s}\ge \frac{\mathit{\eta }}{N_{\text{r}}},$$ [12]

where ${\langle a_n\rangle }_S\approx 1-F_{\text{LN}}\left[c^{-1};\overline{S}s,\text{var}\left(S\right)s\right]$ with $F_{\text{LN}}\left(x;\mathit{\mu },{\mathit{\sigma }}^2\right)$ being the cumulative distribution function of a lognormal distribution with mean μ and variance ${\mathit{\sigma }}^2$. Fig. 5A shows that $s_{\text{max}}$ increases with decreasing concentrations, but, if the concentration falls below the odor detection threshold, individual ligands cannot be detected (dotted lines).

Fig. 5.

The discriminability of mixtures strongly depends on the concentrations at which odors are presented. (A) Maximal mixture size $s_{\max }$ (from Eq. 12) as a function of the ligand concentration c for different widths λ of the sensitivity distribution at $N_{\text{r}}/\mathit{\eta }=300$. Dotted lines indicate where c is below the detection threshold for single ligands. (B) Mean difference h in the activation pattern of two mixtures of size $s=10$ as a function of c for different numbers $s_{\text{b}}$ of shared ligands and widths λ. Analytical results (lines) are compared with numerical simulations (symbols).

Not all mixtures with less then $s_{\text{max}}$ ligands can be distinguished from each other. We show this by calculating the Hamming distance h of the activity patterns $\mathit{a}$ of two mixtures, i.e., the number of differences in the output. For simplicity, we consider mixtures that contain s ligands, sharing $s_{\text{b}}$ of them. In this case, a given receptor is activated by one of the mixtures if $e_{\text{b}}+e_{\text{d}}>1$, where $e_{\text{b}}$ and $e_{\text{d}}$ are the excitations caused by the $s_{\text{b}}$ shared and the $s-s_{\text{b}}$ different ligands, respectively. Approximating the probability distribution of the excitations as a lognormal distribution, we can calculate the expected distance h (see Supporting Information). Fig. 5B shows that this approximation (solid lines) agrees well with numerical calculations (symbols). The figure also shows that mixtures can only be distinguished well if the concentration of the constituents is in the right range. This is because receptors are barely excited for too small concentrations, whereas they are saturated for large concentrations. The distance h also strongly depends on the number $s_{\text{b}}$ of shared ligands between the two mixtures, which has also been shown experimentally (32). The distance vanishes for $s_{\text{b}}=s$, but Fig. 5B shows that a single different ligand can be sufficient to distinguish mixtures in the right concentration range (green line). This range increases with the width λ of the sensitivity distribution, similar to the range over which concentrations can be measured (see Eq. 11). The suitable concentration range is also a function of the mean sensitivity $\overline{S}$, which, in turn, must be adjusted to the odor statistics (see Eq. 9). Consequently, our model predicts that only mixtures with total concentrations near the average concentration in natural mixtures can be distinguished well.

Experimentally Measured Receptor Arrays.

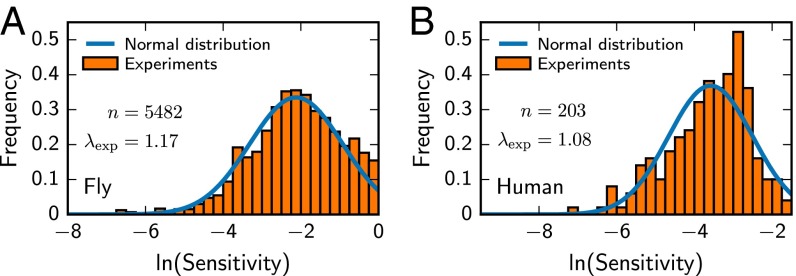
The response of receptors to individual ligands has been measured experimentally for flies (33) and humans (34). We use these published data to estimate the statistics of realistic sensitivity matrices as described in Supporting Information. Fig. 6 shows the histograms of the logarithms of the sensitivities for flies and humans. Both histograms are close to a normal distribution, with similar SDs ${\mathit{\lambda }}_{\exp }\approx 1.1$, which implies lognormally distributed sensitivities. Using a simple binding model between receptors and ligands, ${\mathit{\lambda }}_{\text{exp}}$ can also be interpreted as the SD of the interaction energies (see Supporting Information). Consequently, these interaction energies exhibit a similar variation on the order of 1 $k_{\text{B}}T$ for both organisms, which could be caused by the biophysical similarity of the receptors.

Fig. 6.

Sensitivities of olfactory receptors appear to be lognormally distributed for (A) flies (33) and (B) humans (34). The histograms of the logarithms of n entries of the sensitivity matrix (orange) are compared with a normal distribution (blue) with the same mean and SD ${\mathit{\lambda }}_{\exp }$.

We next use the measured lognormal distribution for the sensitivities to compare the concentration resolution R predicted by Eq. 10 to measured “just noticeable relative differences” $R^{-1}$ (23). For humans ($N_{\text{r}}=300$), the measured values are as low as 4% (35), which implies $\eta \mathit{\lambda }\approx 4.8$. Using $\mathit{\lambda }\approx 1.1$, this suggest that about four receptors have to be activated until a change in concentration can be registered. Additionally, our theory predicts that humans can sense concentrations over about 2.6 orders of magnitude, which follows from Eq. 11 for $\mathit{\lambda }=1.1$, $\mathit{\eta }=1$, and $N_{\text{r}}=300$. However, we are not aware of any measurements of the concentration range for humans.

Our theory also predicts the maximal number of ligands that can be distinguished as a function of the concentration c of the individual ligands. For $\mathit{\lambda }\approx 1.1$, we expect that the maximal number $s_{\text{max}}$ of ligands in a mixture is around 20 if individual ligands can be detected (see Fig. 5A). Experimental studies report similar numbers, e.g., $s_{\max }\approx 15$ (36) and $s_{\max }<30$ (6). However, Fig. 5A shows that $s_{\text{max}}$ strongly depends on the concentration of the individual ligands and thus on experimental details. Similarly, how well mixtures can be discriminated also depends strongly on the ligand concentration. Fig. 5B shows that the concentration range over which mixtures can be distinguished is less than an order of magnitude for $\mathit{\lambda }\approx 1.1$.

Discussion

We studied how arrays of olfactory receptors can be used to measure odor mixtures, focusing on the combinatorial code of olfaction, i.e., how the combined response of multiple receptors can encode the composition (quality) and the concentration (quantity) of odors. Such arrays are optimal if each receptor responds to half of the encountered odors and the receptors have distinct ligand binding profiles to minimize correlations.

Our simple model of binary receptors can, in principle, distinguish a huge number of odors, because there are $\sim {10}^{90}$ different output combinations for $N_{\text{r}}=300$. However, it is not clear whether all outputs are achievable and how they are used to distinguish odors. We showed that the mean receptor sensitivity must be tailored to the mean concentration to best use the large output space. Another important parameter of receptor arrays is the fraction of receptors that is activated by a single ligand, which is equivalent to the sparsity ξ in the simple case of binary sensitivities. If ξ is small, combining different ligands typically leads to unique output patterns that allow identification of the mixtures, but the concentration of isolated ligands cannot be measured reliably, because only a few receptors are involved. Conversely, if ξ is large, mixtures of multiple ligands will excite almost all receptors, such that neither the odor quality nor the odor quantity can be measured reliably. However, here, the concentration of an isolated ligand can be measured precisely. We discussed this property in detail for sensitivities that are lognormally distributed, where the width λ controls whether mixtures can be distinguished well or concentrations can be measured reliably. Interestingly, experiments find that individual ligands at moderate concentration only excite a few glomeruli (37), but natural odors at native concentrations can excite many (38). This could imply that the sensitivities are indeed adapted such that each receptor is excited about half the time for natural odors.

Our model implies that having more receptor types can improve all properties of the receptor array. In particular, both the concentration resolution R and the typical distance h between mixtures are proportional to $N_{\text{r}}$, a prediction that can be tested experimentally. For instance, mice, with $N_{\text{r}}\approx \mathrm{1,000}$ receptor types, are very good at identifying a single odor in a mixture (39), but flies, with $N_{\text{r}}=52$ (33), should perform much worse. However, quantitative comparisons might be difficult because the discrimination performance strongly depends on the normalized concentration $c\overline{S}$ at which odors are presented. In fact, we predict that mixtures can hardly be distinguished if the concentration of the individual ligands is changed by an order of magnitude (see Fig. 5B).

Our results also apply to artificial chemical sensor arrays known as “artificial noses” (40, 41). Having more sensors improves the general performance of the array, but it is also important to tune the sensitivity of individual sensors. Here, sensors should be as diverse as possible while still responding to about half the incoming mixtures. Unfortunately, building such chemical sensors is difficult, and their binding properties are hard to control (41). If the sensitivity matrix of the sensor array is known, our theory can be used to estimate the information $I_n$ that receptor n contributes as $I_n\approx H\left(\langle a_n\rangle \right)+H\left(1-\langle a_n\rangle \right)-\left(4/\ln 2\right){\displaystyle {\sum }_{m\ne n}\text{cov}{\left(a_n,a_m\right)}^2}$ where $H\left(p\right)=-p\hspace{0.17em}{\log }_2\hspace{0.17em}p$, such that $I={\displaystyle {\sum }_n{I}_n}$ (see Eq. 4). This can then be used for identifying poor receptors that contribute only a little information to the overall results.

Our focus on the combinatorial code of the olfactory system certainly neglects intricate details of the system. For instance, we do not consider the dynamics of sniffing and odor absorption, which are the first processing steps and influence the perception (42). Further, our simple model of the binding of odorants to receptors, described by sensitivity matrices with independent entries, neglects biophysical constraints that will cause chemically similar ligands to excite similar receptors (8, 43). This is important because it makes it difficult to distinguish similar ligands (44), and it might thus be worthwhile to dedicate more receptors to such a part of chemical space. Additionally, receptors or glomeruli might interact with each other, e.g., causing inhibition reducing the signal upon binding a ligand (45). We can, in principle, discuss inhibition in our model by allowing for negative sensitivities, but more complicated features cannot be captured by the linear relationship in Eq. 1. One important nonlinearity is the dose–response curve of individual receptor neurons (21), which we approximate by a step function (see Eq. 2). This simplification reduces the information capacity of a single glomerulus to 1 bit, whereas it is likely higher in reality. However, we expect that allowing for multiple output levels would only increase the concentration resolution and not change the discriminability of mixtures very much (23). Additionally, these perceptual quantities could be influenced by other processes, e.g., lateral inhibition between glomeruli (11, 46) and top-down modulation that adjusts the sensory system based on behavior (46). Besides such enhancements of olfactory sensing, further processing can only remove information, so our results provide an upper bound for the ability to recognize odors.

Receptor Sensitivities

Equilibrium Binding Model.

We consider a simple model where receptors $R_n$ get activated when they bind ligands $L_i$. This binding is described by the chemical reaction $R_n+L_i\rightleftharpoons R_n{L}_i$, where $R_n{L}_i$ is the receptor−ligand complex. The equilibrium of the reaction is characterized by a binding constant $K_{ni}$, which reads

$$K_{ni}=\exp \left(\frac{E_{ni}}{k_{\text{B}}T}\right),$$ [S1]

where $E_{ni}$ is the interaction energy between receptor n and ligand i. In equilibrium, the concentrations denoted by square brackets obey $\left[R_n{L}_i\right]=K_{ni}\cdot \left[R_n\right]\left[L_i\right]$. Hence,

$$\left[R_n{L}_i\right]=\frac{c_n^{\text{rec}}{K}_{ni}{c}_i}{1+{\displaystyle {\sum }_i{K}_{ni}{c}_i}},$$ [S2]

where we consider the case where multiple ligands compete for the same receptor. Here, $c_n^{\text{rec}}=\left[R_n\right]+{\displaystyle {\sum }_i\left[R_n{L}_i\right]}$ denotes the fixed concentration of receptors, and $c_i=\left[L_i\right]$ is the concentration of free ligands. We consider a simple receptor model in which the excitation $e_n^{\text{rec}}$ of a receptor of type n is proportional to the concentration of bound ligands,

$$e_n^{\text{rec}}=\frac{\alpha }{c_n^{\text{rec}}}{\displaystyle \sum _i\left[R_n{L}_i\right]},$$ [S3]

where ${\mathit{\alpha }}_n$ characterizes the excitability of receptor type n. As discussed in the Introduction, the excitations of all receptors of a given type are accumulated in the respective glomeruli, whose excitation $e_n^{\text{glo}}$ is thus given by $e_n^{\text{glo}}=N_n^{\text{rec}}{e}_n^{\text{rec}}$, where $N_n^{\text{rec}}$ is the number of receptors of type n. In the simple case of binary outputs, a glomerulus becomes active if its excitation exceeds a threshold $t_n$, $a_n=\mathrm{\Theta }\left(e_n^{\text{glo}}-t_n\right)$, where $\mathrm{\Theta }\left(z\right)$ denotes the Heaviside step function. We consider the case ${\alpha }_n\gg t_n$, where the glomerulus signals before the associated receptors become saturated. In this case, we can linearize Eq. S2 and introduce the rescaled quantities

$$\begin{array}{ccc}{e}_n=\frac{e_n^{\text{glo}}}{t_n}& \text{and}& S_{ni}=\frac{{\alpha }_n{N}_n^{\text{rec}}}{t_n}{K}_{ni}\end{array}$$ [S4]

to obtain Eqs. 1 and 2.

A simple theory (28) predicts that the interaction energies $E_{ni}$ between receptors and ligands are normal distributed. For the receptor model described above, this implies lognormal distributed binding constant $K_{ni}$ (see Eq. S1). In this case, the sensitivities $S_{ni}$ will also be lognormal distributed (see Eq. S4).

Measured Receptor Sensitivities.

Response matrices have been measured experimentally for flies (33) and humans (34). The fly database has been constructed by merging data from many studies that used various methods to measure receptor responses (33). It contains a nonzero response for 5,482 receptor−ligand pairs, covering all 52 receptors that are present in flies. Fig. 6A shows the histogram of the logarithm of the associated sensitivities together with a normal distribution with the same mean and variance as the data.

The only comprehensive study of human olfactory receptors used a luciferase assay to measure receptor responses in vitro (34). It reports the intensity of clones of 511 human olfactory receptors in response to various concentrations of 73 ligands. Typically, the intensity of a given receptor−ligand pair is monotonously increasing as a function of ligand concentration c. We normalize the intensity to lie between 0 and 1 and fit a hyperbolic tangent function to determine the concentration $c_{\text{*}}$ at which the normalized intensity reaches 0.5. Here, the only fit parameters are the concentration $c_{\text{*}}$ and the slope of the tangent function at this point. We exclude poor fits, where the relative error in either parameter is above $50\mathrm{\%}$. This leaves us with 203 of the 623 receptor−ligand combinations, for which we then define the sensitivity as $c_{\text{*}}^{-1}$. Fig. 6B shows the histogram of the logarithm of these sensitivities together with a normal distribution with the same mean and variance as the data.

Receptor Response

We next discuss the statistics of the receptor responses as a function of the odor statistics $P_{\text{env}}\left(\mathit{c}\right)$. We first analyze narrow concentration distributions, where only the presence of ligands needs to be detected and their concentration is of minor interest. Then, we consider the more complex case of wide concentration distributions, which require a distribution of sensitivities for sensing different concentrations.

Narrow Concentration Distribution.

In this case, we are only interested in measuring the composition of an odor $\mathit{c}$. Consequently, it is sufficient to consider binary vectors $\mathit{c}$, where $c_i\mathrm{\in }\left\{\mathrm{0,1}\right\}$. Instead of parameterizing the statistics $P_{\text{env}}\left(\mathit{c}\right)$ by the ligand frequency $p_i$ and the correlations $p_{ij}$, it will prove useful to write the odor statistics as

$$P_{\mathrm{env}}\left(\mathit{c}\right)=\frac{1}{Z_J\left[h\right]}\exp \left({\displaystyle \sum _{i,j}{J}_{ij}{c}_i{c}_j+{\displaystyle \sum _i{h}_i{c}_i}}\right).$$ [S5]

Here, $h_i$ denotes the commonness of ligand i (related to $p_i$) and $J_{ij}$ parameterizes correlations between ligands i and j (related to $p_{ij}$). Without loss of generality, $J_{ij}$ is symmetric with zeros on the diagonal. The associated partition function $Z_J$, which ensures that ${\displaystyle \int \text{d}\mathit{c}{P}_{\text{env}}\left(\mathit{c}\right)}=1$, reads

$$Z_J\left[h\right]={\displaystyle \int \text{d}\mathit{c}\hspace{0.17em}{e}^{J_{ij}{c}_i{c}_j+h_i{c}_i}},$$ [S6]

where the integral is over all binary vectors of length $N_{\text{l}}$. Note that in this section on narrow concentration distributions, we use the Einstein summation convention, i.e., we imply summation over repeated indices.

Uncorrelated mixtures.

For uncorrelated mixtures ($J_{ij}=0$), the partition function reads $Z_0\left[h\right]={\displaystyle \int \text{d}\mathit{c}{e}^{h_i{c}_i}}$. The probability $p_i^{\text{∗}}={\langle c_i\rangle }_h$ of finding a ligand then reads

$$p_i^{\text{*}}=\frac{1}{Z_0\left[h\right]}{\displaystyle \int \text{d}\mathit{c}\hspace{0.17em}{c}_i\hspace{0.17em}{e}^{h_j{c}_j}}=\frac{e^{h_i}}{1+e^{h_i}},$$ [S7]

where the notation ${\langle \cdot \rangle }_h$ and the index * denote the average with respect to uncorrelated mixtures. Eq. S7 provides the mapping between the commonness $h_i$ used in Eq. S5 and the ligand frequency $p_i=p_i^{\text{∗}}$ used in the main text. The covariance $p_{ij}^{\text{∗}}={\langle c_i{c}_j\rangle }_h-{\langle c_i\rangle }_h{\langle c_j\rangle }_h$ follows from

$${\langle c_i{c}_j\rangle }_h=\frac{1}{Z_0\left[h\right]}{\displaystyle \int \text{d}\mathit{c}\hspace{0.17em}{c}_i{c}_j\hspace{0.17em}{e}^{h_k{c}_k}}=p_i^{\text{*}}{p}_j^{\text{∗}}-{\delta }_{ij}{\left(p_i^{\text{*}}\right)}^2+{\delta }_{ij}{p}_i^{\text{*}}$$ [S8]

and reads

$$p_{ij}^{\text{∗}}={\delta }_{ij}{p}_i^{\text{*}}\left(1-p_i^{\text{*}}\right).$$ [S9]

The receptor activity $a_n$, given by Eq. 2, is a function of the excitation $e_n={\widehat{S}}_{ni}{c}_i$, which involves the binary sensitivities ${\widehat{S}}_{ni}\in \left\{\mathrm{0,1}\right\}$. Consequently, $e_n\in \mathrm{\mathbb{N}}$ and the step function in Eq. 2 can be approximated by

$$a_n\approx 1-e^{-\gamma e_n},$$ [S10]

which becomes exact in the limit $\gamma \to \infty$. We use this to calculate the moments of ${\overline{a}}_n=1-a_n$,

$$\begin{array}{c}{\langle {\overline{a}}_n\rangle }_h=\frac{Z_0\left[h^{\left(n\right)}\right]}{Z_0\left[h\right]}\end{array}$$ [S11a]

and

$$\begin{array}{c}{\langle {\overline{a}}_n{\overline{a}}_m\rangle }_h=\frac{Z_0\left[h^{\left(nm\right)}\right]}{Z_0\left[h\right]},\end{array}$$ [S11b]

where

$$h_i^{\left(n\right)}=h_i-\mathit{\gamma }{\widehat{S}}_{ni}$$ [S12a]

$$h_i^{\left(nm\right)}=h_i-\gamma \left({\widehat{S}}_{ni}+{\widehat{S}}_{mi}\right).$$ [S12b]

In particular, we have in the limit $\gamma \to \infty$,

$$Z_0\left[h\right]={\displaystyle \prod _i\left(1+e^{h_i}\right)}$$ [S13a]

$$Z_0\left[h^{\left(n\right)}\right]={\displaystyle \prod _i\left[1+e^{h_i}\left(1-{\widehat{S}}_{ni}\right)\right]}$$ [S13b]

$$Z_0\left[h^{\left(nm\right)}\right]={\displaystyle \prod _i\left[1+e^{h_i}\left(1-{\widehat{S}}_{ni}\right)\left(1-{\widehat{S}}_{mi}\right)\right]}.$$ [S13c]

Hence,

$${\langle a_n\rangle }_h=1-{\displaystyle \prod _i\left(1-{\widehat{S}}_{ni}{p}_i^{\text{*}}\right)}$$ [S14a]

$$\begin{array}{c}{\text{cov}}_h\left(a_n,a_m\right)={\displaystyle \prod _i\left[1-\left({\widehat{S}}_{ni}+{\widehat{S}}_{mi}-{\widehat{S}}_{ni}{\widehat{S}}_{mi}\right)p_i^{\text{*}}\right]}\\ -{\displaystyle \prod _i\left(1-{\widehat{S}}_{ni}{p}_i^{\text{*}}\right)\left(1-{\widehat{S}}_{mi}{p}_i^{\text{*}}\right)}\hspace{0.17em}.\end{array}$$ [S14b]

We develop these equations to linear order in $p_i^{\text{∗}}$ to obtain Eqs. 7.

The receptor activity for binary sensitivity matrices with independent and identically distributed entries is described by

$${\langle a_n\rangle }_h=1-{\displaystyle \prod _i\left(1-\xi p_i^{\text{*}}\right)}\approx \xi s,$$ [S15a]

$${\text{cov}}_h\left(a_n,a_m\right)\approx {\xi }^{2}s,$$ [S15b]

where $s={\displaystyle {\sum }_i{\langle c_i\rangle }_h}$ is the mean number of ligands in a mixture. Here, ξ denotes the sparsity of ${\widehat{S}}_{ni}$, which is the only parameter of the random ensemble. The optimal sparsity ${\mathit{\xi }}^{\text{∗}}$ at which I is maximized is given by the condition ${\langle a_n\rangle }_h=1/2$. Using Eq. S14a and solving for ξ, we obtain

$${\xi }^{\text{*}}\approx N_{\text{l}}\frac{1-2^{-\frac{1}{N_{\text{l}}}}}{s},$$ [S16]

which, for large $N_{\text{l}}$ at constant s, becomes ${\mathit{\xi }}^{\text{∗}}=s^{-1}\ln \hspace{0.17em}2$.

Correlated mixtures.

We consider weakly correlated mixtures, where we expand all results to linear order in $J_{ij}$. Hence,

$$Z_J\left[h\right]\approx Z_0\left[h\right]\cdot \left(1+J_{ij}{\langle c_i\rangle }_h{\langle c_j\rangle }_h\right).$$ [S17]

The probability $p_i={\langle c_i\rangle }_J$ with which ligand i appears reads

$$\begin{array}{c}{p}_i=\frac{1}{Z_J\left[h\right]}{\displaystyle \int \text{d}\mathit{c}\hspace{0.17em}{c}_i\hspace{0.17em}{e}^{J_{jk}{c}_j{c}_k+h_j{c}_j}}\\ \approx {\langle c_i\rangle }_h\left[1-J_{jk}{\langle c_j\rangle }_h{\langle c_k\rangle }_h\right]+J_{jk}{\langle c_i{c}_j{c}_k\rangle }_h,\end{array}$$ [S18]

where

$$\begin{array}{c}{\langle c_i{c}_j{c}_k\rangle }_h=p_i^{\text{∗}}{p}_j^{\text{∗}}{p}_k^{\text{∗}}+{\delta }_{ij}{\overline{p}}_i^{\text{∗}}{p}_i^{\text{∗}}{p}_k^{\text{∗}}+{\delta }_{ik}{p}_i^{\text{∗}}{\overline{p}}_i^{\text{∗}}{p}_j^{\text{∗}}\\ +{\delta }_{jk}{p}_i^{\text{∗}}{p}_j^{\text{∗}}{\overline{p}}_j^{\text{∗}}+{\delta }_{ij}{\delta }_{jk}{p}_i^{\text{∗}}{\overline{p}}_i^{\text{∗}}\left(1-2p_i^{\text{∗}}\right)\end{array}$$ [S19]

with ${\overline{p}}_i^{\text{∗}}=1-p_i^{\text{∗}}$. Hence,

$$p_i\approx p_i^{\text{∗}}\left[1+2J_{ij}{\overline{p}}_i^{\text{∗}}{p}_j^{\text{∗}}\right],$$ [S20]

where we used $J_{ij}=J_{ji}$ and $\text{diag}\left(J\right)=\mathbf{0}$. Similarly, the covariance $p_{ij}={\langle c_i{c}_j\rangle }_J-{\langle c_i\rangle }_J{\langle c_j\rangle }_J$ between ligands can be calculated from ${\langle c_i{c}_j\rangle }_J$, which involves

$$J_{kl}\langle c_i{c}_j{c}_k{c}_l\rangle ={\delta }_{ij}{p}_i^{\text{∗}}{\overline{p}}_i^{\text{∗}}\left[2J_{ki}{p}_k^{\text{∗}}\left(1-2p_i^{\text{∗}}\right)+J_{kl}{p}_l^{\text{∗}}{p}_k^{\text{∗}}\right]+p_i^{\text{∗}}{p}_j^{\text{∗}}\left[2J_{ij}{\overline{p}}_i^{\text{∗}}{\overline{p}}_j^{\text{∗}}+2J_{il}{\overline{p}}_i^{\text{∗}}{p}_l^{\text{∗}}+2J_{jl}{\overline{p}}_j^{\text{∗}}{p}_l^{\text{∗}}+J_{kl}{p}_l^{\text{∗}}{p}_k^{\text{∗}}\right]$$ [S21]

and thus reads

$$\begin{array}{c}{\langle c_i{c}_j\rangle }_J\approx {\langle c_i{c}_j\rangle }_h\left[1-J_{kl}{\langle c_k\rangle }_h{\langle c_l\rangle }_h\right]+J_{kl}{\langle c_i{c}_j{c}_k{c}_l\rangle }_h\\ =p_i^{\text{∗}}{p}_j^{\text{∗}}\left[1+2J_{ij}{\overline{p}}_i^{\text{∗}}{\overline{p}}_j^{\text{∗}}+2J_{il}{\overline{p}}_i^{\text{∗}}{p}_l^{\text{∗}}+2J_{jl}{\overline{p}}_j^{\text{∗}}{p}_l^{\text{∗}}\right]\\ +{\delta }_{ij}{p}_i^{\text{∗}}{\overline{p}}_i^{\text{∗}}\left[1+2J_{il}{p}_l^{\text{∗}}\left(1-2p_i^{\text{∗}}\right)\right],\end{array}$$ [S22]

where we used Eq. S8. Hence,

$$p_{ij}={\langle c_i{c}_j\rangle }_J-{\langle c_i\rangle }_J{\langle c_j\rangle }_J\approx {\delta }_{ij}{p}_i{\overline{p}}_i+2J_{ij}{p}_{ii}^{\text{∗}}{p}_{jj}^{\text{∗}},$$ [S23]

where ${\overline{p}}_i=1-p_i$. Taken together, Eqs. S20 and S23 provide the mapping between $\left\{p_i,p_{ij}\right\}$ used in the main text and $\left\{h_i,J_{ij}\right\}$ used in the definition of $P_{\text{env}}\left(\mathit{c}\right)$ in Eq. S5.

The statistics of the receptor activity $a_n=1-{\overline{a}}_n$ follow from

$$\begin{array}{c}{\langle {\overline{a}}_n\rangle }_J=\frac{Z_J\left[h^{\left(n\right)}\right]}{Z_J\left[h\right]}\end{array}$$ [S24a]

and

$$\begin{array}{c}{\langle {\overline{a}}_n{\overline{a}}_m\rangle }_J=\frac{Z_J\left[h^{\left(nm\right)}\right]}{Z_J\left[h\right]},\end{array}$$ [S24b]

which can be expressed as

$${\langle {\overline{a}}_n\rangle }_J\approx {\langle {\overline{a}}_n\rangle }_h\cdot \frac{1+J_{ij}{p}_i^{\left(n\right)}{p}_j^{\left(n\right)}}{1+J_{ij}{p}_i^{\text{∗}}{p}_j^{\text{∗}}}$$ [S25a]

$${\langle {\overline{a}}_n{\overline{a}}_m\rangle }_J\approx {\langle {\overline{a}}_n{\overline{a}}_m\rangle }_h\cdot \frac{1+J_{ij}{p}_i^{\left(nm\right)}{p}_j^{\left(nm\right)}}{1+J_{ij}{p}_i^{\text{∗}}{p}_j^{\text{∗}}},$$ [S25b]

where

$$p_i^{\left(n\right)}\equiv {\langle c_i\rangle }_{h^{\left(n\right)}}=p_i^{\text{∗}}\left(1-{\widehat{S}}_{ni}\right)$$ [S26a]

$$p_i^{\left(nm\right)}\equiv {\langle c_i\rangle }_{h^{\left(nm\right)}}=p_i^{\text{∗}}\left(1-{\widehat{S}}_{ni}\right)\left(1-{\widehat{S}}_{mi}\right).$$ [S26b]

Expanding the fractions in Eq. S25, we obtain

$${\langle {\overline{a}}_n\rangle }_J\approx {\langle {\overline{a}}_n\rangle }_h\left(1+J_{ij}{p}_i^{\left(n\right)}{p}_j^{\left(n\right)}-J_{ij}{p}_i^{\text{∗}}{p}_j^{\text{∗}}\right)$$ [S27a]

$${\langle {\overline{a}}_n{\overline{a}}_m\rangle }_J\approx {\langle {\overline{a}}_n{\overline{a}}_m\rangle }_h\left(1+J_{ij}{p}_i^{\left(nm\right)}{p}_j^{\left(nm\right)}-J_{ij}{p}_i^{\text{∗}}{p}_j^{\text{∗}}\right).$$ [S27b]

Substituting Eq. S26, this becomes

$$\begin{array}{c}{\langle a_n\rangle }_J\approx {\langle a_n\rangle }_h+\left(1-{\langle {\overline{a}}_n\rangle }_h\right)\left({\widehat{S}}_{ni}+{\widehat{S}}_{nj}-{\widehat{S}}_{ni}{\widehat{S}}_{nj}\right)J_{ij}{p}_i^{\text{∗}}{p}_j^{\text{∗}}\\ ={\langle a_n\rangle }_h+\left(1-{\langle a_n\rangle }_h\right)\left({\widehat{S}}_{ni}+{\widehat{S}}_{nj}-{\widehat{S}}_{ni}{\widehat{S}}_{nj}\right)\frac{p_{ij}}{2{\overline{p}}_i^{\text{∗}}{\overline{p}}_j^{\text{∗}}},\end{array}$$ [S28]

where, in the last expression, the ${\overline{p}}_i^{\text{∗}}$ can also be replaced by ${\overline{p}}_i$ to first order in $J_{ij}$. For the simple case of a random, binary sensitivity matrix with sparsity ξ, we obtain

$${\langle a_n\rangle }_J\approx {\langle a_n\rangle }_h+p_{ij}\left(1-{\langle a_n\rangle }_h\right)\left(\xi -\frac{{\xi }^2}{2}\right).$$ [S29]

In the case where the correlations are predominately positive ($p_{ij}>0$), the frequency of individual ligands and the receptor response are increased, $p_i>p_i^{\text{∗}}$ and ${\langle a_n\rangle }_J>{\langle a_n\rangle }_h$, respectively. Consequently, the optimal sparsity must be smaller than in the uncorrelated case to have ${\langle a_n\rangle }_J=1/2$.

Wide Concentration Distribution.

We next consider mixtures where the concentrations of the individual ligands are drawn from a continuous distribution ($c_i\ge 0$). For simplicity, we consider uncorrelated mixtures ($J_{ij}=0$, $p_{ij}=0$ for $i\ne j$), which are characterized by the ligand frequencies $p_i$, their mean concentrations μ_i, and their SD σ_i. In the case where a receptor is excited by many ligands, its excitation $e_n$ can be described by a lognormal distribution (29), which is parameterized by the mean and variance given in Eq. 6. The associated mean receptor activity $\langle a_n\rangle$ is then given by the probability that $e_n\ge 1$. Using the survival function of a lognormal distribution that is parameterized by its mean and variance we obtain

$$\langle a_n\rangle \approx \frac{1}{2}\hspace{0.17em}\text{erfc}\left[\frac{\ln \left(\frac{\sqrt{{\langle e_n\rangle }_c^2+{\text{var}}_c\left(e_n\right)}}{{\langle e_n\rangle }_c^2}\right)}{\sqrt{2\hspace{0.17em}\ln \left(\frac{{\mathrm{var}}_c\left(e_n\right)}{{\langle e_n\rangle }_c^2}+1\right)}}\right].$$ [S30]

Because $a_n^2=a_n$, the associated variance reads

$$\text{var}\left(a_n\right)=\langle a_n\rangle \left(1-\langle a_n\rangle \right),$$ [S31]

which also determines the diagonal values of the covariance matrix $\text{cov}\left(a_n,a_m\right)$. For $n\ne m$, we have

$$\langle a_n{a}_m\rangle ={\displaystyle {\int }_1^{\infty }{\displaystyle {\int }_1^{\infty }{P}_{\text{e}}\left(e_n,e_m\right)\text{d}{e}_n\text{d}{e}_m}},$$ [S32]

where $P_{\text{e}}\left(e_n,e_m\right)$ is the multivariate distribution of the two excitations $e_n$ and $e_m$. We approximate $P_{\text{e}}\left(e_n,e_m\right)$ by a normal distribution, which describes the excitations $e_n$ and $e_m$ in the vicinity of $\langle a_n\rangle =\langle a_m\rangle =1/2$. This distribution is characterized by the means $\langle e_n\rangle$ together with the covariances $\mathrm{cov}\left(e_n,e_m\right)$, which comprise five parameters in total. Hence,

$$\begin{array}{c}\langle a_n{a}_m\rangle \approx \frac{1}{4}+\frac{1}{\sqrt{8\pi }}\left(\frac{\langle e_n\rangle -1}{\sqrt{\text{var}\left(e_n\right)}}+\frac{\langle e_m\rangle -1}{\sqrt{\mathrm{var}\left(e_m\right)}}\right)\\ +\frac{\left(\langle e_n\rangle -1\right)\left(\langle e_m\rangle -1\right)+\mathrm{cov}\left(e_n,e_m\right)}{2\pi \sqrt{\mathrm{var}\left(e_n\right)\mathrm{var}\left(e_m\right)}}\end{array}$$ [S33]

for $n\ne m$. The associated covariance $\mathrm{cov}\left(a_n,a_m\right)$ follows from the definition $\mathrm{cov}\left(a_n,a_m\right)=\langle a_n{a}_m\rangle -\langle a_n\rangle \langle a_m\rangle$, where we obtain the mean $\langle a_n\rangle$ by expanding Eq. S30 around the optimal point $\langle e_n\rangle =1$ for small $\text{var}\left(e_n\right)$,

$$\langle a_n\rangle \approx \frac{1}{2}+\frac{\langle e_n\rangle -1}{\sqrt{2\pi \mathrm{var}\left(e_n\right)}},$$ [S34]

which is the same approximation that also led to Eq. S33. Consequently, we have

$$\text{cov}\left(a_n,a_m\right)\approx \{\begin{array}{ll}\frac{1}{4}-\frac{{\left(\langle e_n\rangle -1\right)}^2}{2\pi \text{var}\left(e_n\right)}\hfill & n=m\hfill \\ \frac{\text{cov}\left(e_n,e_m\right)}{2\pi \sqrt{\text{var}\left(e_n\right)\text{var}\left(e_m\right)}}\hfill & n\ne m\hfill \end{array}.$$ [S35]

The conditions for optimal sensitivity matrices, $\langle a_n\rangle =1/2$ and $\mathrm{cov}\left(a_n,a_m\right)=0$, can thus be expressed as (see Eqs. S30 and S35)

$${\langle e_n\rangle }^4={\langle e_n\rangle }^2+\text{var}\left(e_n\right)$$ [S36a]

$$\mathrm{cov}\left(e_n,e_m\right)=0.$$ [S36b]

For small $\mathrm{var}\left(e_n\right)$, this reduces to $\langle e_n\rangle \approx 1$, which indeed leads to $\langle a_n\rangle =1/2$ in the approximation given in Eq. S34.

Numerical Simulations.

We use a simple two-step procedure to draw odors $\mathit{c}$ from the statistics $P_{\text{env}}\left(\mathit{c}\right)$. First, we determine the ligands that appear in a given mixture by drawing a random binary vector $\mathit{b}=\left(b_1,b_2,\dots ,b_{N_{\text{l}}}\right)$ with $b_i\in \left\{\mathrm{0,1}\right\}$ from

$$P_{\text{cor}}\left(\mathit{b}\right)\propto \text{exp}\left(J_{ij}{b}_i{b}_j+h_i{b}_i\right),$$ [S37]

analogously to Eq. S5. Here, $h_i$ and $J_{ij}$ determine $p_i$ and $p_{ij}$ according to Eqs. S20 and S22, respectively. In the case of narrow concentration distributions, the odor $\mathit{c}$ is given by $\mathit{b}$. For wide concentration distributions, we draw the concentration $c_i$ for each ligand i that appears in a mixture ($b_i=1$) from a lognormal distribution with mean ${\mu }_i$ and SD ${\sigma }_i$, which is described by the probability density function

$$P\left(c_i|b_i\right)=\frac{b_i}{c_i\sqrt{\pi {\chi }_i}}\cdot \exp \left[-\frac{1}{{\chi }_i}{\left(\text{ln}\left(\frac{c_i}{\mu }\right)+\frac{{\chi }_i}{4}\right)}^2\right],$$ [S38]

where ${\chi }_i=2\ln \left(1+{\sigma }_i^2{\mu }_i^{-2}\right)$. Taken together, this describes the odor statistics $P_{\text{env}}\left(\mathit{c}\right)={\displaystyle {\sum }_{\mathit{b}}{P}_{\text{cor}}\left(\mathit{b}\right)}{\displaystyle {\prod }_{i}P\left(c_i|b_i\right)}$.

Given this odor statistics $P_{\text{env}}\left(\mathit{c}\right)$ and a sensitivity matrix $S_{ni}$, the mutual information I can, in principle, be calculated from Eqs. 1−3. Calculating $P\left(\mathit{a}\right)$ to evaluate Eq. 3 involves an integral over $P_{\text{env}}\left(\mathit{c}\right)$ over the nonlinear function given in Eq. 2. We approximate this integral using Monte Carlo sampling of the odor statistics $P_{\text{env}}\left(\mathit{c}\right)$. Because of the stochastic nature of Monte Carlo sampling, the calculated I is not exact. Consequently, we use the stochastic, derivative-free numerical optimization method covariance matrix adaptation evolution strategy (CMA-ES) (47) to optimize the sensitivity matrix $S_{ni}$ with respect to I to produce Fig. 3B.

Properties of Arrays with Random Sensitivities

We study properties of receptor arrays characterized by random sensitivity matrices $S_{ni}$ whose entries are independent and identically distributed. Here, we consider a lognormal distribution for the sensitivities, whose probability density function $f_{\text{S}}\left(S\right)$ and cumulative distribution function $F_{\text{S}}\left(S\right)$ read

$$f_{\text{S}}\left(S\right)=\frac{1}{\sqrt{2\pi }S\mathit{\lambda }}\exp \left[-\frac{1}{2{\lambda }^2}{\left(\ln \frac{S}{\overline{S}}+\frac{{\lambda }^2}{2}\right)}^2\right]$$ [S39a]

$$F_{\text{S}}\left(S\right)=\frac{1}{2}\mathrm{erfc}\left[-\frac{1}{\sqrt{2}\lambda }\left(\ln \frac{S}{\overline{S}}+\frac{{\lambda }^2}{2}\right)\right]$$ [S39b]

and are parameterized by the mean $\overline{S}$ and the width λ, which is the SD of the underlying normal distribution. Note that all following calculations could also be performed for other sensitivity distributions.

Concentration Resolution.

The fraction ${\mathrm{\Phi }}_1\left(c\right)$ of receptors that are activated by a single ligand at concentration c reads

$${\mathrm{\Phi }}_1\left(c\right)=1-F_{\text{S}}\left(c^{-1}\right).$$ [S40]

The typical concentration change $\delta c$ that is necessary to excite η additional receptor is then defined by the condition ${\mathrm{\Phi }}_1\left(c+\delta c\right)-{\mathrm{\Phi }}_1\left(c\right)=\eta N_{\text{r}}^{-1}$. Expanding ${\mathrm{\Phi }}_1$ around c, the solution for $\delta c$ reads

$$\delta c\left(c\right)=\frac{\eta }{N_{\text{r}}{\mathrm{\Phi }}_1^{\prime }\left(c\right)}=\frac{\eta c^2}{N_{\text{r}}{F}_{\text{S}}^{\prime }\left(c^{-1}\right)}.$$ [S41]

For lognormal distributed sensitivities, the maximum of the associated resolution $R=c/\delta c$ is given in Eq. 10.

Concentration Range.

The minimal concentration $c_{\text{min}}$ that can be sensed is defined by the condition ${\mathrm{\Phi }}_1\left(c_{\text{min}}\right)=\eta /N_{\text{r}}$, whereas $c_{\text{max}}$ is given by ${\mathrm{\Phi }}_1\left(c_{\text{max}}\right)=1-\eta /N_{\text{r}}$. Solving these equations, the concentration range $\zeta =c_{\text{max}}/c_{\text{min}}$ becomes

$$\zeta =\frac{G_{\text{S}}\left(1-\frac{\eta }{N_{\text{r}}}\right)}{G_{\text{S}}\left(\frac{\eta }{N_{\text{r}}}\right)},$$ [S42]

where $G_{\text{S}}\left(y\right)$ is the inverse function of the cumulative distribution function $F_{\text{S}}\left(x\right)$. For lognormal distributed sensitivities, we obtain Eq. 11.

Maximal Number of Distinguishable Ligands.

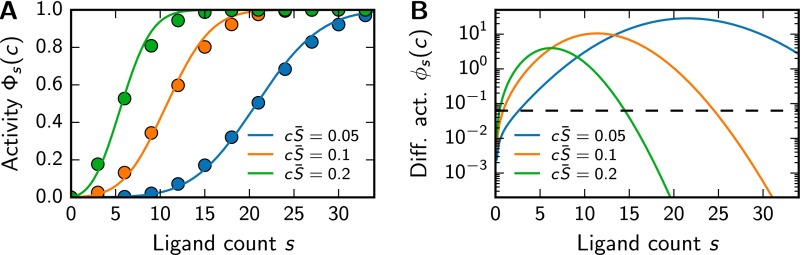
In the simple case of a mixture with s ligands, all at concentration c, the fraction ${\mathrm{\Phi }}_s\left(c\right)$ of excited receptors is given by

$${\mathrm{\Phi }}_s\left(c\right)=1-{\widehat{F}}_{\text{S}}\left(c^{-1};s\right),$$ [S43]

where ${\widehat{F}}_{\text{S}}\left(z_n;s\right)$ is the cumulative probability function of the sum $z_n={\displaystyle {\sum }_{i=1}^s{S}_{ni}}$. If the $S_{ni}$ are lognormal distributed, the distribution for $z_n$ can also be approximated by a lognormal distribution (29), which has mean $s\langle S_{ni}\rangle$ and variance $s\mathrm{var}\left(S_{ni}\right)$. In this case,

$${\mathrm{\Phi }}_s\left(c\right)=1-\frac{1}{2}\text{erfc}\left[\frac{\text{ln}\left(\frac{c\overline{S}{s}^2}{\sqrt{s\left(r+s\right)}}\right)}{\sqrt{2\hspace{0.17em}\ln \left(\frac{r+s}{s}\right)}}\right]$$ [S44]

where $r={\overline{S}}^{-2}\mathrm{var}\left(S\right)=\exp \left({\lambda }^2\right)-1$ is the squared coefficient of variation. Fig. S2A shows that Eq. S44 approximates the numerically determined ${\mathrm{\Phi }}_s\left(c\right)$ well.

Fig. S2.

Receptors are most sensitive to mixtures of medium size. (A) ${\mathrm{\Phi }}_s\left(c\right)$ as a function of s for various c at $\lambda =1$. Eq. S44 (solid lines) is compared with numerical simulations (symbols, 10⁴ samples per point). (B) ${\varphi }_s=\text{d}{\mathrm{\Phi }}_s/\text{d}s$ as a function of s for various c at $\lambda =1$. The dashed line marks the threshold $N_{\text{r}}^{-1}$ below which mixtures are not distinguishable for $N_{\text{r}}=16$.

We next consider the maximal number of ligands that can be distinguished. Here, we, for simplicity, consider the case where mixtures can be distinguished when they excite activity patterns that differ for at least η receptors. Because a mixture with s components on average excites $N_{\text{r}}{\mathrm{\Phi }}_s$ receptors, this condition reads

$$N_{\text{r}}{\mathrm{\Phi }}_{s+1}\left(c\right)\ge N_{\text{r}}{\mathrm{\Phi }}_s\left(c\right)+\eta .$$ [S45]

Expanding ${\mathrm{\Phi }}_s\left(c\right)$ as a function of s, this condition can be approximated by

$${\varphi }_s\left(c\right)\ge \frac{\eta }{N_{\text{r}}},$$ [S46]

where ${\varphi }_s\left(c\right)=\text{d}{\mathrm{\Phi }}_s\left(c\right)/\text{d}s$. Fig. S2B shows that this function has a single peak. Mixtures with $s=0,\dots ,s_{\text{*}}$ ligands can thus all be distinguished from each other if

$$\begin{array}{ccc}{\varphi }_1\left(c\right)\ge \frac{\eta }{N_{\text{r}}}& \text{and}& {\varphi }_{s^{\text{∗}}}\left(c\right)\ge \frac{\eta }{N_{\text{r}}}.\end{array}$$ [S47]

Here, the first condition ensures that c is above the odor detection threshold, and the second condition ensures that the two largest mixtures excite sufficiently different activity patterns.

Discriminability of Two Mixtures of Equal Size.

We next consider how well two mixtures can be discriminated. For simplicity, we consider two mixtures, each with s ligands of which $s_{\text{b}}$ are shared. We call these two mixtures plus ($+$) and minus ($-$) to distinguish them. To determine the Hamming distance between the activation patterns, we first consider the excitations $e_{\pm }$ of a single receptor caused by the two mixtures,

$$e_{\pm }={\displaystyle \sum _{i\in {\mathcal{C}}_{\text{b}}}{S}_{ni}c}+{\displaystyle \sum _{i\in {\mathcal{C}}_{\pm }}{S}_{ni}c}.$$ [S48a]

Here, ${\mathcal{C}}_{\text{b}}$ denotes the set of ligands appearing in both mixtures, and ${\mathcal{C}}_{\pm }$ denote those only appearing in one of the mixtures. Note that we only consider the case where the ligands appear with the same concentration c. The excitations can be rewritten as

$$e_{\pm }=\left(z_{\text{b}}+z_{\pm }\right)c$$ [S49]

where the $z_x$ are random variables. Here, $z_{\text{b}}$ is distributed according to ${\widehat{F}}_{\text{S}}\left(z;s_{\text{b}}\right)$, and $z_{\pm }$ are distributed according to ${\widehat{F}}_{\text{S}}\left(z;s-s_{\text{b}}\right)$. The probability $p_{\text{s}}$ that the receptor activity is the same for both mixtures is given by

$$p_{\text{s}}=P\left(e_{+}<1\wedge e_{-}<1\right)+P\left(e_{+}>1\wedge e_{-}>1\right).$$ [S50]

The first term can be expressed as

$$P\left(e_{+}<1\wedge e_{-}<1\right)={\displaystyle {\int }_0^{\frac{1}{c}}\text{d}{z}_{\text{b}}{\widehat{f}}_{\text{S}}\left(z_{\text{b}};s_{\text{b}}\right)}\cdot {\displaystyle {\int }_0^{\frac{1}{c}-z_{\text{b}}}\text{d}{z}_{+}{\widehat{f}}_{\text{S}}\left(z_{+};s_{\text{d}}\right){\displaystyle {\int }_0^{\frac{1}{c}-z_{\text{b}}}\text{d}{z}_{-}{\widehat{f}}_{\text{S}}\left(z_{-};s_{\text{d}}\right)}},$$ [S51]

where $s_{\text{d}}=s-s_{\text{b}}$ is the number of ligands that differ between the two mixtures. Here, ${\widehat{f}}_{\text{S}}\left(z;s\right)$ denotes the probability density functions of ${\widehat{F}}_{\text{S}}\left(z;s\right)$. Eq. S51 can also be written as

$$P\left(e_{+}<1\wedge e_{-}<1\right)={\displaystyle {\int }_0^{\frac{1}{c}}\text{d}{z}_{\text{b}}{\widehat{f}}_{\text{S}}\left(z_{\text{b}};s_{\text{b}}\right){\left[{\widehat{F}}_{\text{S}}\left(\frac{1}{c}-z_{\text{b}};s_{\text{d}}\right)\right]}^2}.$$ [S52]

Similarly, the second term in Eq. S50 can be expressed as

$$P\left(e_{+}>1\wedge e_{-}>1\right)=1-{\widehat{F}}_{\text{S}}\left(\frac{1}{c};s_{\text{b}}\right)+{\displaystyle {\int }_0^{\frac{1}{c}}\text{d}{z}_{\text{b}}{\widehat{f}}_{\text{S}}\left(z_{\text{b}};s_{\text{b}}\right){\left[1-{\widehat{F}}_{\text{S}}\left(\frac{1}{c}-z_{\text{b}};s_{\text{d}}\right)\right]}^2},$$ [S53]

where the first term is the probability that the ligands appearing in both mixtures excite the receptor alone. The second term denotes the probability that although $z_{\text{b}}$ is not large enough, both $z_{+}$ and $z_{-}$ are sufficient to bring the excitation above threshold. The mean Hamming distance $h=N_{\text{r}}\left(1-p_{\text{s}}\right)$ between the activation patterns of the two mixtures then reads

$$h=2N_{\text{r}}{\displaystyle {\int }_0^{\frac{1}{c}}{\widehat{f}}_{\text{S}}\left(\frac{1}{c}-z;s_{\text{b}}\right){\widehat{F}}_{\text{S}}\left(z;s_{\text{d}}\right)\left[1-{\widehat{F}}_{\text{S}}\left(z;s_{\text{d}}\right)\right]\text{d}z}.$$ [S54]

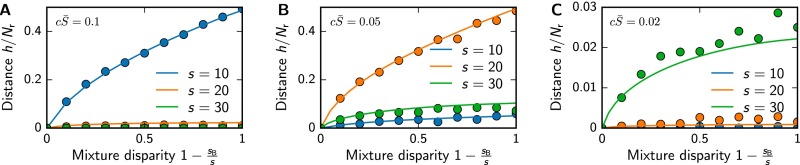
To test this equation, we randomly draw mixtures at given s and $s_{\text{b}}$, determine their activation pattern according to Eqs. 1 and 2, and determine the associated difference. Fig. S1 shows that Eq. S54 agrees well with these numerical results. Although h is a function of s, $s_{\text{b}}$, c, $\overline{S}$, λ, and $N_{\text{r}}$, the only important parameters are s, $s_{\text{b}}$, $c\overline{S}$, and λ, because $N_{\text{r}}$ is just a prefactor and $\overline{S}$ only sets the scale of typical concentrations. We can thus explore the behavior by plotting h as a function of s and $c\overline{S}$ for different $s_{\text{b}}$ (see Fig. S3). This plot shows that mixtures can be distinguished well when the concentration is in the right interval. Fig. S3 can be used to determine the parameter region in which a receptor array is likely able to distinguish two mixtures. In the simple case where the activity patterns must be different in at least η receptors, mixtures can typically be distinguished if $h>\eta$.

Fig. S1.

Mean normalized mixture distance $h/N_{\text{r}}$ as a function of the mixture disparity $1-s_{\text{b}}/s$ for $\lambda =1$, various mixture sizes s, and (A) $c\overline{S}=0.1$, (B) $c\overline{S}=0.05$, or (C) $c\overline{S}=0.02$. The analytical result given in Eq. S54 (solid lines) is compared with numerical simulations (symbols, 10⁴ samples per point).

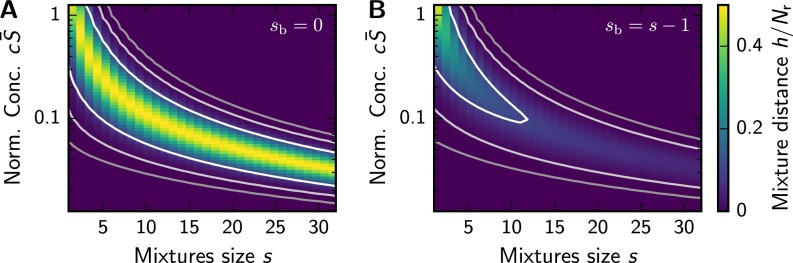
Fig. S3.

Mean normalized mixture distance $h/N_{\text{r}}$ from Eq. S54 as a function of mixture size s and concentration c of the ligands for $\lambda =1$ and (A) $s_{\text{b}}=0$ or (B) $s_{\text{b}}=s-1$. The lines indicate isocontours at $h/N_{\text{r}}=0.1,0.01,0.001$ (white to gray).