Quantitative Assessment of Commutability for Clinical Viral Load Testing Using a Digital PCR-Based Reference Standard

Abstract

Given recent advances in the development of quantitative standards, particularly WHO international standards, efforts to better understand the commutability of reference materials have been made. Existing approaches in evaluating commutability include prediction intervals and correspondence analysis; however, the results obtained from existing approaches may be ambiguous. We have developed a “deviation-from-ideal” (DFI) approach to evaluate commutability of standards and applied it to the assessment of Epstein-Bar virus (EBV) load testing in four quantitative PCR assays, treating digital PCR as a reference assay. We then discuss advantages and limitations of the DFI approach as well as experimental design to best evaluate the commutability of an assay in practice.

INTRODUCTION

Quantification of viral load is integral to clinical care, particularly among immunocompromised patients (1–4). Increases in viral load may trigger preemptive therapy to prevent or treat systemic viral disease. It may also be used to monitor therapeutic response and to determine treatment endpoints. A wide variety of assays are used for these determinations (few FDA approved), and the field continues to be hindered by a lack of agreement among the results of these tests (5–8). In turn, this lack of agreement (particularly between laboratories) prevents both the development of standardized therapeutic breakpoints and the portability of patient results among institutions. Numerous factors have been shown to contribute to the variability of results (9), one of which is a lack of standardized calibration standards. The availability of WHO international quantitative standards for cytomegalovirus (CMV) and, more recently, Epstein-Barr virus (EBV) should help the process of developing such standardization; however, numerous issues remain. These issues include the development of reliable secondary standards, which are traceable to and accurately representative of the WHO standard material. As has been shown for CMV secondary standards, such trueness cannot be assumed (10).

Another issue of concern is the commutability of reference materials, which focuses on whether standards behave like patient samples and are consistent across different assays. Commutability has been defined as “the equivalence of the mathematical relationships among the results of different measurement procedures for a reference material and for representative samples of the type intended to be measured” (11). First defined and accepted in the field of clinical chemistry, more recent work in clinical molecular virology demonstrated its importance to interassay agreement, with commutable standards improving and noncommutable standards diminishing quantitative agreement (12–15). Currently, commutability is typically assessed via prediction interval approaches (14) or by multivariate techniques such as correspondence analysis (16), both based on evaluating whether a reference material belongs to the same distribution obtained from measures of human specimens using two or more assays. Prediction interval approaches are intuitive and simple to apply; however, they are often restricted to a two-assay setting. If there are more assays of interest, advanced multivariate techniques are often used. A drawback of the current approaches is that when a series of dilutions of a reference material is under examination, conclusions can be difficult to interpret. The “commutability” conclusion drawn from existing approaches is a relative concept, referring to the behavior of a reference material between two or more assays compared to that of human specimens. It cannot address whether a reference material is commutable to human specimens in a single assay of interest (AI). This can lead to differing determinations of commutability depending on which assays are included in a given evaluation. In addition, both prediction interval approaches and multivariate approaches do not take data variability into account; thus, a conclusion of commutability may be drawn only because the data are too variable. Furthermore, both primary methods in use today often produce only a “yes” or “no” determination of commutability, failing to make a straightforward connection between interassay discrepancies in clinical values and commutability inference. Moreover, this limitation of existing approaches arises from the definition of commutability that does not reflect result accuracy, hindering direct comparisons of commutability results across assays.

Here, we seek to evaluate commutability by using traditional approaches that produce relative commutability between assays but also by producing absolute measures of commutability in a single assay by normalizing both patient and reference material results against the reference standard of digital PCR. The latter depends on the concept of limiting dilution, using large-scale partitioning of each master mix, followed by endpoint PCR. Quantitation is then determined by counting the number of positive nanoscale reactions and using Poisson statistics to produce a result that no longer depends on relation to a standard curve. Digital PCR has increasingly been thought to represent a reference standard for quantitation, particularly of DNA viruses (17–19). In addition to generating single-assay commutability determinations, we introduce a novel statistical term that directly relates the concept of commutability with clinical scales, asking whether degree of commutability is a useful concept in establishing clinical significance. This approach is presented together with methods that have been widely applied in evaluating commutability. All methods are applied here to four quantitative real-time EBV PCR assays using commercial secondary standard material and the WHO standard as proof-of-concept examples for this approach.

MATERIALS AND METHODS

Patient samples and quantitative standards.

Reference materials utilized in the study included the EBV B95-8 WHO international standard (NIBC, Potters Barr, United Kingdom) and purified B95-8 virus stock (EBV type 1) inactivated cell extract (Advanced Biotechnologies [ABI], Columbia, MD). External positive-control material was prepared by using the AcroMetrix EBV plasma panel (Thermo Fisher Scientific, Inc., Waltham, MA). WHO standard material was reconstituted, according to the manufacturer's recommendations, to a final concentration of 6.7 log₁₀ IU/ml, with subsequent 10-fold serial dilutions in human whole blood (Biological Specialty Corporation, Colmar, PA) to concentrations of 5.7 to 1.7 log₁₀ IU/ml. Material from ABI was diluted in phosphate-buffered saline (PBS) to ∼8 log₁₀ copies/ml and then further diluted in whole blood in 10-fold increments from ∼7 to 1 log₁₀ copies/ml. The 7-log₁₀ member of the AcroMetrix panel was diluted in whole blood to produce high and low controls of 5 log₁₀ copies/ml and 3 log₁₀ copies/ml, respectively.

Clinical patient samples included for evaluation included frozen whole blood remaining from clinical testing performed at St. Jude Children's Research Hospital (SJCRH) from November 2008 to February 2013. Subsequent to clinical testing, samples were aliquoted and frozen at −80°C prior to use. A total of 194 samples were selected for inclusion, based on the results of routine clinical EBV load testing (using a laboratory-developed test [LDT]). These samples were thawed and anonymized prior to nucleic acid extraction. Each sample was tested in duplicate by each PCR methodology (see below). This study was classified as “exempt” by the SJCRH Institutional Review Board (IRB), thereby allowing informed consent requirements to be waived.

Nucleic acid extraction of 200-μl aliquots of all calibrators, controls, and patient samples was carried out on the QiaSymphony SP instrument (Qiagen, Valencia, CA) using the Qiagen QiaSymphony DNA minikit 200v6_Blood protocol, producing 200 μl of eluate in ATE buffer.

Quantitative testing by real-time and digital PCR.

The reader is referred elsewhere for details regarding PCR methodologies, together with comparisons of the performance characteristics of these methods (20). In brief, four LDT methods were used here, three utilizing analyte-specific reagents (ASRs), produced by Luminex Corporation (Austin, TX), Focus Diagnostics (Cypress, CA), and ELITech Group (Bothell, WA), and the fourth using in-house-developed reagents. Information regarding instrumentation, cycling parameters, and master mix composition is shown in Table 1. Digital PCR (dPCR) was performed on a QX100 droplet dPCR (ddPCR) system (Bio-Rad, Hercules, CA) for ddPCR amplification, using reagents from the in-house-developed LDT. While it is ideal if the reference assay (RA) is completely independent of the methods under evaluation, the same primers and probes were used for the digital PCR and for the LDT real-time PCR methods. This lack of independence is not desirable but was tolerated for this teaching example.

TABLE 1.

Key assay characteristics^a

Assay	Reagent manufacturer (location)	Chemistry	Instrumentation (manufacturer)	Total reaction mixture vol (μl)	Sample vol (μl)
ELITech	ELITech Group (Bothell, WA)	TaqMan, MGB Alert probe/primer mixture	7500 real-time PCR instrument (Life Technologies, Grand Rapids, NY)	25	5
Focus	Focus Diagnostics (Cypress, CA),	Scorpion-labeled primers	3 M integrated cycler (Focus Diagnostics)	10	5
Luminex	Luminex Corporation (Austin, TX)	MultiCode-labeled primers	7500 real-time PCR instrument	25	5
LDT	In-house developed	TaqMan	7500 real-time PCR instrument	25	5

^aSee reference 20.

Commutability assessment. (i) Prediction interval analysis.

Simple linear regression (SLR) was applied to log₁₀-transformed EBV load measures of patient samples between the Luminex, LDT, Focus, and ELITech methods with dPCR. Ninety percent, 95%, and 99% prediction intervals were then plotted. Measures of dilution series of reference materials were overlaid and checked for whether they all fell within the prediction intervals. Commutability of a reference material in an assay was concluded only if all measures of a reference material fell within the designated prediction interval.

(ii) Correspondence analysis.

Technical details of correspondence analysis were reported previously (10, 16). In short, log₁₀-transformed measures of patient samples using all assays of interest and reference materials were considered active elements and projected onto a factorial plane, with the two axes representing the first two factors explaining most of the information in data. A 95% confidence eclipse was plotted. Measures of reference materials were then treated as supplemental or inactive elements to avoid distortion of the pattern derived from clinical samples. Reference material was determined to be commutable if its measures all fell within the confidence region, indicating close proximity of the behavior of that reference material to patient samples.

(iii) Deviation-from-ideal approach.

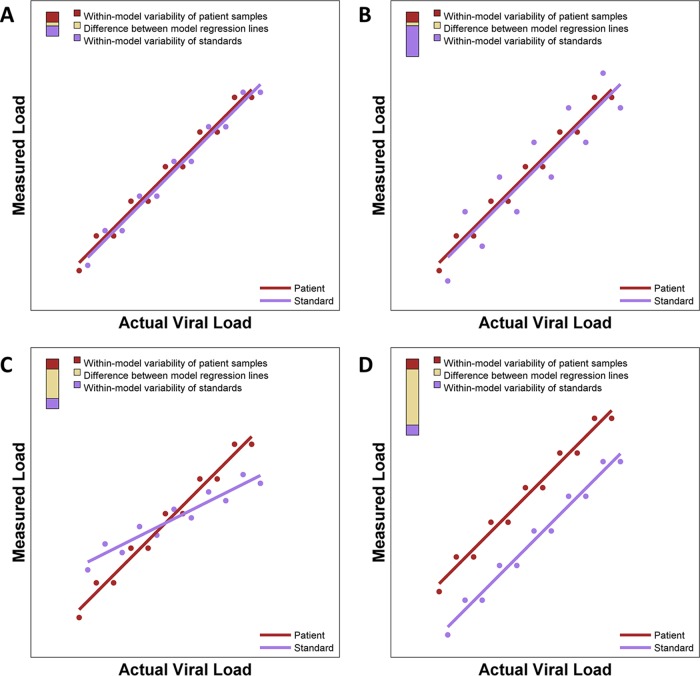
For an ideal assay, the quantitative relationship between the actual and measured viral loads of quantitative standards (often modeled by simple linear regression) is identical to that of patient samples, and both patient samples and standard samples should show minimal variability (Fig. 1A). We propose that commutability be quantitatively evaluated by computing a statistical metric of an assay's deviation from the ideal (DFI), which is partitioned into components that are directly attributable to certain forms of deviation from the ideal.

FIG 1.

Idealized illustration of DFI plots showing differing types of assay performance. Each panel shows regression models of both patient samples and standards. To the right of each regression model, a three-color bar graphically depicts contributions to the deviation from the ideal. The total height of the bar is the DFI. The proportions of the DFI attributable to within-model variability of patient samples, within-model variability of standards, and the difference between model regression lines are shown. (A) Nearly ideal case with almost identical regression lines that each have minimal variability, giving a small DFI. (B) Two nearly identical regression lines but with one line having extensive variability and the other having minimal variability. (C) Two very skewed regression lines. (D) Two parallel regression lines with distinct intercepts.

There are several ways in which the actual performance of an assay may deviate from the ideal (Fig. 1B to D), with similar quantitative relationships but with one set of samples having much larger variability or even different regression relationships between actual and measured viral loads. It can be advantageous for DFI to capture specific forms of departure. For example, in a setting like that shown in Fig. 1B, the variability of the standards is the greatest contribution to the overall DFI. In such a setting, improvements in the processing of standards that reduce variability may greatly reduce the overall DFI.

DFI metrics are developed for studies that collect viral load measurements for both patient samples and quantitative standards and with both the assay under evaluation (AUE) and an RA. The DFI metric is computed from the regression of AUE viral loads on RA viral loads for the patient samples and the regression of AUE viral loads on RA loads for the quantitative standards. In the appendix, we mathematically define the DFI as a metric of the average deviation between the AUE measurements of a patient sample and a quantitative standard that have the same actual viral load according to the RA. The interpretative implications of this definition of DFI are elaborated below.

The DFI is partitioned into three distinct components: (i) precision of measurements for patient samples, (ii) precision of measurements for standards, and (iii) accuracy of standards as a representation of patient samples.

The DFI and the relative contributions of its three components may be reported numerically and graphically. Figure 1 illustrates a graphical representation of the DFI and its three components with a tricolored bar in the top left corner of each panel. The height of the bar is the DFI, and the proportions of the bar in red, violet, and gold represent the contributions of patient sample variability, standard sample variability, and difference between regression lines to the DFI, respectively. Thus, the short bar in Fig. 1A indicates that the DFI is small (suggesting very good performance of the AUE), and the very tall bar in Fig. 1D indicates that the DFI is large (suggesting poor performance of the AUE). The long violet segment of the bar shown in Fig. 1B indicates that most of the deviation from the ideal is attributable to variability of standards, and the long gold segments in Fig. 1C and D indicate that most of the deviation from the ideal is attributable to differences between the regression line of patient samples and that of standard samples. The relative contributions of these three components to the DFI may provide some guidance to help determine which elements of a particular assay should be improved to enhance its performance. For instance, one may consider revising laboratory procedures for preparation and processing of standards if 90% of the DFI is attributable to variability among standard samples.

A major advantage of DFI is that it measures deviation from the ideal in the same units that the AUE measures viral load, which makes it possible to perform meaningful comparisons of DFI values among a set of assays that measure viral load in the same units. Furthermore, with consensus among a range of stakeholders and the relationship between DFI and meaningful consensus, a “clinically acceptable threshold of variability” could be established. For example, one may consider cutoffs to interpret the DFI value as showing “good” (i.e., 0.0 to 0.40 log₁₀ copies/ml), “intermediate” (i.e., 0.41 to 0.60 log₁₀ copies/ml), or “poor” (i.e., >0.60 log₁₀ copies/ml) commutability.

By definition, the DFI is an absolute measure of deviation from the ideal only in settings in which the RA can legitimately be considered a “gold standard.” Otherwise, the DFI can be interpreted in the more limited sense that it measures deviation relative to the particular assay.

For this study, we computed the DFI metrics of the LDT, Luminex, Focus, and ELITech methods using WHO material and ABI standards as assay systems under evaluation, with digital PCR as the reference assay.

All statistical analyses were performed on measures no lower than the lower limit of quantification of all assays, as reported previously (20), on 194 samples and with SAS 9.3 unless otherwise specified. The SAS macro and R function for generating DFI results are available as Files S1 and S2 in the supplemental material.

RESULTS

WHO standards.

Results of the prediction interval analysis for WHO standards are shown in Fig. S1 in the supplemental material. This analysis fits a linear regression to the clinical samples for each pair of assay systems to determine prediction intervals. The results for the standards are then plotted to determine whether standards fall within these intervals. At least one standard value fell outside the 90% prediction intervals in the evaluations of the LDT and Luminex (see Fig. S1A in the supplemental material), LDT and Focus (see Fig. S1D in the supplemental material), Focus and ELITech (see Fig. S1E in the supplemental material), and LDT and ELITech (see Fig. S1F in the supplemental material) methods. All standards fell within the 90% prediction intervals in evaluations of the Focus and Luminex (see Fig. S1B in the supplemental material) and ELITech and Luminex (see Fig. S1C in the supplemental material) methods. For some comparisons, the number of points falling within or outside the prediction intervals depends on the arbitrary selection of 90%, 95%, or 99% prediction intervals (see Fig. S1A, S1D, and S1E in the supplemental material). This analysis shows that the performance of the LDT differs from that of the other three assay systems. However, without a gold standard assay system, this analysis does not clearly indicate which, if any, of these assay systems is actually the best performer in terms of commutability.

Correspondence analysis results are shown in Fig. S2 in the supplemental material. One standard sample falls outside the 95% prediction ellipse, suggesting that the standard samples do not have a behavior similar to that of patient samples across all four assays.

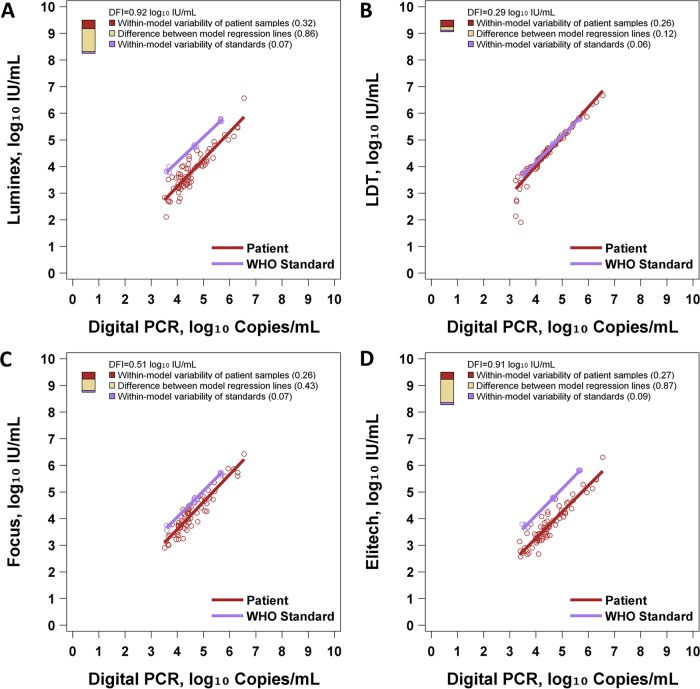
Figure 2 and Table 2 show the results of DFI analysis. The Luminex, LDT, Focus, and ELITech methods had DFI values of 0.92, 0.29, 0.51, and 0.91 log₁₀ IU/ml, respectively. Thus, in terms of DFI, the LDT showed the best performance in this study, because it performed well in each of the three components of DFI. With the LDT method, patient samples and standards had almost identical regression lines, patient samples showed little variability across most of the range, and standards showed little variability (Fig. 2B). Conversely, Luminex and ELITech had poor DFI due to large differences between the regression lines of patient samples and standards (Fig. 2A and D). The Focus assay had an intermediate DFI of 0.51 log₁₀ IU/ml, attributable mostly to variability of patient samples, with a moderate gap between the regression lines of patient samples and standard samples (Fig. 2C). This analysis also shows that the LDT differs from the other three assay systems: the LDT shows much better commutability than the other three systems. While the other three assay systems show a considerable shift between the regression lines of standards and patient samples, these lines are almost identical for the LDT system. This is also observed in the numerical values for the deviation from the ideal due to a difference between the regression lines (0.12 for the LDT versus 0.43 for Focus, 0.86 for Luminex, and 0.87 for ELITech). The other components of DFI did not vary so dramatically across the four assay systems. The variability of standards ranged from 0.06 to 0.09 across assay systems, and the variability of patient samples ranged from 0.26 to 0.32 across assay systems.

FIG 2.

DFI assessment of WHO EBV standards. Each panel illustrates regression models for patient samples and standards. Digital PCR is regarded as the reference standard assay. To the right of each regression model, a three-color bar graphically depicts the DFI. The total height of the bar is the DFI. The proportions of the DFI attributable to within-model variability of patient samples, within-model variability of standards, and differences between model regression lines are shown. (A) Performance of the WHO standard with Luminex. (B) Performance of the WHO standard with the LDT. (C) Performance of the WHO standard with Focus. (D) Performance of the WHO standard with ELITech.

TABLE 2.

DFI commutability assessment of the WHO standard

Assay	Root variability of patient sample regression line (log10 IU/ml) (%)	Root variability of WHO material regression line (log10 IU/ml) (%)	Avg difference between 2 regression lines (log10 IU/ml) (%)	DFI (log10 IU/ml)
ELITech	0.27 (9)	0.09 (1)	0.87 (90)	0.91
Focus	0.26 (27)	0.07 (2)	0.43 (71)	0.51
LDT	0.26 (79)	0.06 (5)	0.12 (16)	0.29
Luminex	0.32 (12)	0.07 (1)	0.86 (87)	0.92

ABI standards.

Results of the prediction interval analysis for ABI standards are shown in Fig. S3 in the supplemental material. All standards fell within the 90% prediction intervals in the evaluation of the LDT and Luminex (see Fig. S3A in the supplemental material) and in the evaluation of the LDT and Focus (see Fig. S3D in the supplemental material) methods. At least one standard fell outside the 90% prediction intervals for each of the other pairwise evaluations (see Fig. S3B, S3C, S3E, and S3F in the supplemental material). Again, the number of standards falling outside the prediction interval varied across pairwise evaluations and according to the arbitrary choice of using 90%, 95%, or 99% prediction intervals.

Correspondence analysis results are shown in Fig. S4 in the supplemental material. Overall, ABI standards behaved similarly to patients samples in the four assays under investigation when a 95% confidence region was applied as the threshold.

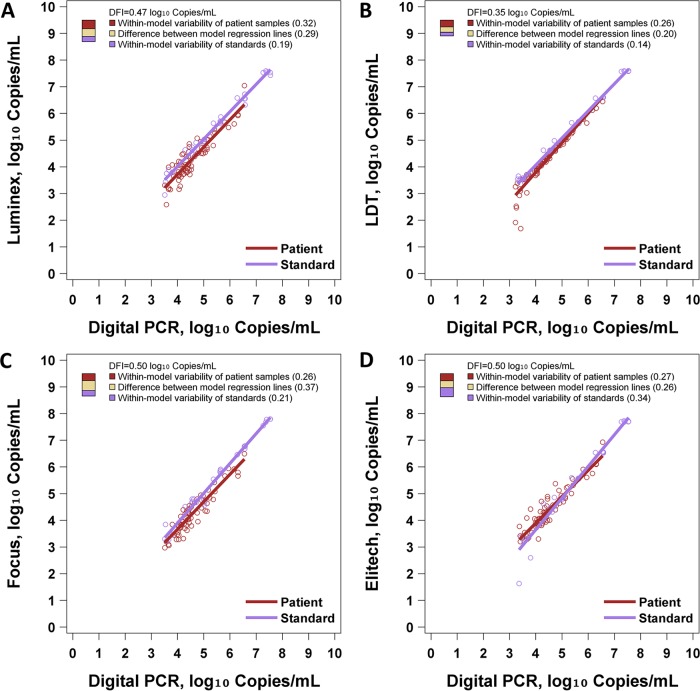
Figure 3 and Table S1 in the supplemental material show the results of DFI analysis. The Luminex, LDT, Focus, and ELITech methods had DFI values of 0.47, 0.35, 0.50, and 0.50 log₁₀ IU/ml, respectively, when using the ABI standards. Notably, all assays showed a DFI of ≤0.5 log₁₀ IU/ml. Comparatively, assay systems including the ABI standards generally showed better commutability than did those using the WHO standards. Among the latter, the LDT-WHO assay system showed the best commutability by DFI. The LDT-ABI system showed the lowest DFI, and the ABI system showed a DFI of less than half a log unit with all four reagent sets. The partitioning of the DFI into its three sources is illuminating in this case. The four assay systems did not differ greatly in terms of variability of patient samples (range of 0.26 to 0.32). ELITech showed considerably greater variability of standards (0.34 versus 0.14 to 0.21 for others), and the LDT showed considerably less difference between the patient sample regression line and the standard sample regression line (0.20 versus 0.26 to 0.37 for others).

FIG 3.

DFI assessment of ABI EBV standards. Each panel illustrates regression models for patient samples and standards. Digital PCR is regarded as the reference assay. To the right of each regression model, a three-color bar graphically depicts the DFI. The total height of the bar is the DFI. The proportions of the DFI attributable to within-model variability of patient samples, within-model variability of standards, and the difference between model regression lines are shown. (A) Performance of ABI standards with Luminex. (B) Performance of ABI standards with the LDT. (C) Performance of ABI standards with Focus. (D) Performance of ABI standards with ELITech.

DISCUSSION

Evaluation of commutability with any given quantitative standards can be viewed as fundamental to the performance of viral load assays. Commutability may directly affect quantitative accuracy and comparability of results among assays and therefore may be a determinant of clinical utility. Much of the literature has discussed commutability as a property of standards. While it is certainly true that properties and processing of standards may profoundly impact commutability, it is also important to recognize that commutability is a property of an entire assay system. All procedures and materials of an assay impact the data that should be ultimately evaluated statistically. Many studies that formally evaluate commutability are not designed to isolate the contributions of particular components of an assay due to the excessive cost and effort required. Thus, the conclusions of a statistical evaluation of commutability apply to an entire assay procedure and not just the standards themselves.

Currently, linear regression prediction intervals and correspondence analysis prediction ellipses are two statistical methods that are commonly used to evaluate commutability in the literature. These methods have provided useful insights regarding the commutability of several assays. However, the results of these methods should be interpreted with caution due to a number of technical considerations involving variability and sample size. The sizes of prediction intervals and ellipses increase with variability of the data. Conceptually, it is possible that an assay may produce extremely noisy viral load measurements for patient samples so that the prediction intervals or ellipses are very large. In such a setting, it is essentially guaranteed that the standard samples will fall within the 95% prediction bounds. In such a setting, this observation is not scientifically meaningful. Also, sample size must be considered when interpreting the number of points that fall within or outside prediction bounds. If a large number of data points are collected, then by definition, 5% of such points are expected to fall outside the prediction bounds when statistical modeling assumptions are satisfied. Therefore, simply counting the number of data points falling outside linear regression prediction intervals or correspondence analysis prediction ellipses does not always yield a scientifically, practically, or statistically meaningful interpretation. Finally, as seen in our analysis of the WHO samples, pairwise comparison of two assay systems with prediction intervals can show only that the assay systems perform differently but does not indicate whether either is truly commutable.

Here, we provide a formal statistical definition of the DFI and describe how to compute it. The DFI is developed for studies that collect viral load measures for both patient samples and standards from an assay under evaluation and a reference assay. The DFI is a function of the data values and the results of linear regression of AUE viral loads on RA viral loads for patient samples and for standards. The DFI reports deviation of the viral load measurements of the assay under evaluation from the ideal performance and measures deviation from the ideal in the units of the assay under evaluation. This greatly facilitates the interpretation and practical utility of the DFI. This property makes it easier to characterize the relationship between DFI and other metrics of accuracy and agreement to guide the subsequent development of guidelines regarding clinically acceptable limits for the DFI. Also, the DFI can be partitioned into relative contributions from three distinct sources: precision of measurements for patient samples, precision of measurements for standards, and accuracy of standards as a representation of patient samples. In some cases, this partition may help focus attention on improving specific elements of an assay to improve its performance.

Clearly, the appropriate interpretation of DFI is determined largely by the reliability of the reference assay. This may be considered a limitation of DFI. All three of the presented methods implicitly have the limitation that at least two assays must be used to obtain statistical results. For linear regression prediction intervals, the assay used to obtain data for the “x” axis could be implicitly used as a reference assay, although the usage of a reference assay in this approach was barely touched upon in the literature. Also, from a technical perspective, correspondence analysis evaluates the agreement of a set of assays. As such, the assays that are most influential in defining the prediction ellipse in a particular data set are implicitly serving as references. Thus, we feel that it is appropriate to explicitly state that evaluation of commutability is uniformly subject to the intrinsic limitation that some assay is essentially serving as a reference, and the reliability of the final result depends on the reliability of the reference assay. Likewise, it is ideal if the reference assay is completely independent of the methods under evaluation. In the work presented here, the same primers and probes were used for the digital PCR and for the LDT real-time PCR methods, which is a major limitation of this study. This likely was an important factor in the lower DFI value of the LDT assay.

The apparent advantage of the LDT in commutability was more marked when using the WHO standard, where the DFI using the other three assay systems was more clearly elevated. When using the ABI standard, all DFIs were within a range of 0.15 log₁₀ copies/ml. Examination of the DFI regressions showed little difference among the four assay systems, suggesting that commutability would not significantly impact interassay agreement. The reason for the differing commutability between the WHO and ABI material is uncertain. Previous work has shown limitations in commutability utilizing WHO standards (21). Here, both standards were whole-virus preparations, but one still showed behavior more like clinical samples. However, in the absence of DFIs for all of the assays in the previous study, the results here are not directly comparable. Numerous factors can affect viral load accuracy, and it is likely that any of these factors can also affect commutability, reflected by a change in any or all components of the DFI. Possibilities might include differing sample matrices or differences in virus strains used for each standard.

Work here highlights the limitations of methodologies that do not evaluate commutability based on a reference assay (here digital PCR). The analyses performed using only regression prediction intervals and correspondence analysis can show only that assay systems differ from one another but cannot indicate which is best. In some cases, the apparent outlier assay by such methods may in fact show the best commutability compared to a reference standard assay. This is seen in the present study, where the LDT would be called least commutable by prediction intervals and correspondence analysis but turns out to be the most commutable compared to a reference assay using DFI.

Like existing approaches based on regressions, there are several other limitations of the DFI approach. If the underlying mathematical relationship is not linear, or if the relationship does not have constant variability, any approach based on simple linear regression is questionable. Furthermore, investigation can be performed only within the quantitative patient sample range. Finally, all approaches require a well-established commutability acceptance criterion, which is largely missing in the field. Potential remedies to the violation of linear regression assumptions could take advantage of weighted Deming regression (22) or nonparametric regressions (23). Commutability acceptance criteria may depend on the intent of the investigator, but when used to determine impact on interassay system agreement, one approach would be to develop an agreement statistic (data not shown) using principles introduced in this work. Empirically, an achievable upper bound for acceptable DFI might be set, based on the data presented above.

The DFI statistic measures how closely the behavior of the standard material resembles that of human specimens. To establish an acceptable limit of agreement using the DFI, one can combine the knowledge of the uncertainty budget and the clinical deviation allowance (24). However, in practice, it is always optimal to assess commutability or agreement of an assay(s) using DFI together with descriptive plots, as presented in this study. DFI describes the average deviation from the ideal defined above; thus, the magnitude of the DFI alone may hide the fact that standard material samples behave differently from human specimens. For example, in Fig. 1C, the two regression lines clearly cross, and it would be questionable to conclude commutability, while the overall DFI value could still be small, since in the middle range, the deviation is close to zero. In this case, the plot will clearly complement the numerical inference. Thus, we recommend that a complete analysis of commutability include the generation and visualization of regression plots to complement the computation of the DFI statistic and its three components.

Although commutability is not a new concept, more in-depth work is needed to reliably assess the performance of standard materials together with various assays and to set clinically meaningful thresholds for acceptable commutability. Our proposal could be regarded as a first exploratory step toward this goal. Work is under way to develop formal statistical metrics for the evaluation of DFI in two or more assays, allowing DFI-based prediction of interassay result comparability, and to assess how the choices of DFI component weighting would impact the result. The latter will help to understand the performance of the DFI metric if, in practice, one component is of most interest. Another future extension of the current DFI approach includes the generalization of the definition when Deming regression (weighted or unweighted) is applied.

APPENDIX

Here, we describe the calculation of the deviation-from-ideal (DFI) metric. Suppose we have obtained measurements for i = 1,…,n patient samples and j = 1,…,m reference material samples from both the reference assay (RA) and the assay of interest (AI). For the i = 1,…,n patient samples, let x_i and y_i represent the measurements obtained from the RA and AI, respectively. For the j = 1,…,m reference material samples, let u_j and w_j represent the measurements obtained from the RA and AI, respectively. A simple linear regression is fitted on the patient measurements (x_i and y_i) to obtain the estimated line y = β₀ + β₁x, and a simple linear regression is fitted on the reference material measurements (u_j and w_j) to obtain the estimated line w = γ₀ + γ₁u. Using these estimated lines, we compute $\widehat{y_1}={\hat{\beta }}_0+{\hat{\beta }}_i{x}_i$ for each patient sample i = 1,…,n and ${\hat{w}}_j={\hat{\gamma }}_0+{\hat{\gamma }}_1{u}_i$ for each reference material sample j = 1,…,m. Here, the notation ^ represents estimates from a fitted linear regression. Now, the mean square error of the patient samples (MSPS) is defined as $MSPS=\frac{1}{n}\sum _{i=1}^n{({\hat{\text{Y}}}_i-Y_i)}^2$, the mean square error of the reference samples (MSRS) is defined as $MSRS=\frac{1}{m}\sum _{j=1}^m{({\hat{\text{W}}}_j-{\text{W}}_j)}^2$, and the mean square difference between the lines (MSBL) is defined as $MSBL=\frac{1}{n}\sum _{i=1}^n{({\hat{\text{Y}}}_i-{\hat{\text{W}}}_i)}^2$. MSPS is a metric of the precision of patient sample measurements, MSRS is a metric of the precision of the reference material measurements, and MSBL is a metric of the accuracy of the standards as a representation of the patient samples. The total value of MSPS + MSRS + MSBL is a metric of deviation from the ideal scenario in which the regression lines for patient samples and reference material are identical and both sets of samples show no deviation from that line. The proportional contributions of these three terms to the total can also be reported. Finally, the DFI statistic is the square root of the sum of these three components.