Assessing Predictive Performance of Published Population Pharmacokinetic Models of Intravenous Tobramycin in Pediatric Patients

Abstract

Several population pharmacokinetic models describe the dose-exposure relationship of tobramycin in pediatric patients. Before the implementation of these models in clinical practice for dosage adjustment, their predictive performance should be externally evaluated. This study tested the predictive performance of all published population pharmacokinetic models of tobramycin developed for pediatric patients with an independent patient cohort. A literature search was conducted to identify suitable models for testing. Demographic and pharmacokinetic data were collected retrospectively from the medical records of pediatric patients who had received intravenous tobramycin. Tobramycin exposure was predicted from each model. Predictive performance was assessed by visual comparison of predictions to observations, by calculation of bias and imprecision, and through the use of simulation-based diagnostics. Eight population pharmacokinetic models were identified. A total of 269 concentration-time points from 41 pediatric patients with cystic fibrosis were collected for external evaluation. Three models consistently performed best in all evaluations and had mean errors ranging from −0.4 to 1.8 mg/liter, relative mean errors ranging from 4.9 to 29.4%, and root mean square errors ranging from 47.8 to 66.9%. Simulation-based diagnostics supported these findings. Models that allowed a two-compartment disposition generally had better predictive performance than those that used a one-compartment disposition model. Several published models of the pharmacokinetics of tobramycin showed reasonable low levels of bias, although all models seemed to have some problems with imprecision. This suggests that knowledge of typical pharmacokinetic behavior and patient covariate values alone without feedback concentration measurements from individual patients is not sufficient to make precise predictions.

INTRODUCTION

Tobramycin is an aminoglycoside antibiotic and one of the most effective antibiotics for the treatment of severe Gram-negative bacterial infections (1). Tobramycin is particularly effective against Pseudomonas aeruginosa and is commonly used in patients with cystic fibrosis (2). Tobramycin exhibits concentration-dependent bactericidal action, whereby higher drug concentrations are correlated with a greater magnitude and a higher speed of bacterial eradication (3, 4). Treatment success and a decreased incidence of antibiotic resistance have been correlated with a ratio of the peak (maximum) tobramycin concentration (C_max) to the MIC of >7 to 10 (5, 6) and a ratio of the area under the concentration-time curve (AUC) to the MIC of >80 (7, 8). A prolonged high level of exposure to tobramycin and, in particular, sustained, elevated trough (minimum) serum concentrations (C_min) have been associated with significant adverse effects (9, 10), such as nephrotoxicity, which is typically reversible, and ototoxicity, which can be permanent and result in hearing loss (4). Consequently, tobramycin dosing aims to achieve a sufficiently high C_max and AUC for effective bactericidal activity while producing a sufficiently low C_min to minimize the potential for toxicity (11) and the emergence of resistant microorganisms (12).

Furthermore, tobramycin has a narrow therapeutic window and displays a high level of pharmacokinetic variability (11). This variability is particularly increased in pediatric patients, if great changes in maturation, body size, and renal function over a short time frame are not accounted for (13). As a result, if treatment for more than 48 h is required (14), some guidelines recommend computerized therapeutic drug monitoring with Bayesian forecasting software programs (15, 16). Such methods are increasingly being used in practice (17). Bayesian forecasting methods use a priori pharmacokinetic parameters from a suitable population model and current concentration observations to estimate each patient's exposure (15, 18, 19). A suitable population model that characterizes average exposure after drug administration, along with pharmacokinetic variability and the influence of patient covariate factors, such as the patient's age, weight, and creatinine clearance (CL_CR), on pharmacokinetic parameters, is required (20–22). Before a population pharmacokinetic model can be confidently used in clinical practice in a Bayesian forecasting computer program, it must be adequately validated (23). Model validation seeks to quantify the reproducibility and accuracy of a model (24). The most robust form of validation is external validation, which involves the collection of data from a new patient cohort receiving the drug and assessment of the predictive performance of the model (23, 24).

This study aimed to identify and compare population pharmacokinetic models of intravenous tobramycin previously published in the literature and externally validate these models by applying them to a new patient cohort to assess their predictive performance. The overarching goal of the study was to find suitable models to aid computerized therapeutic drug monitoring.

MATERIALS AND METHODS

Literature search.

A search of the literature in the databases PubMed, Medline, and EMBASE was performed, and published models of the population pharmacokinetics of tobramycin were identified. The search was conducted from February to March 2016 using the terminology “tobramycin,” “pharmacokinetics,” and “intravenous” and/or “population pharmacokinetics,” “nonlinear mixed effects modeling,” and “NONMEM.” A manual search for population models was also conducted by inspecting the bibliographies of relevant journal articles. No restriction was placed on the study publication date; the study language was limited to English. Population models were included in this study if they had been developed with data from humans and included data from pediatric patients, the pharmacokinetic analyses had involved a compartmental approach, and the majority of concentration-time points modeled (>50%) were based on measurements for tobramycin, as opposed to other aminoglycosides. Population models were excluded from the external validation if not enough information was provided for the model to be fully reproducible in terms of typical parameter values or covariate relationships or the residual unexplained variability (RUV) reported was above 50%.

Patients and validation data collected.

Pharmacokinetic and demographic data were collected retrospectively from the medical records of pediatric patients with cystic fibrosis who received treatment with intravenous tobramycin at the Lady Cilento Children's Hospital in Brisbane, Australia. This study was approved by the Ethics Committees of the University of Queensland (approval number 2012001415) and Lady Cilento Children's Hospital (approval number HREC/12/QHC75). No patient data in the external validation data set had previously been included in the development of any of the models. The pharmacokinetic data recorded included the tobramycin dose administered, the time of dosing, the infusion time and rate, tobramycin plasma concentrations, and the times at which serum samples were taken for measurement of the tobramycin concentration. Data were included if at least one intravenous dose of tobramycin and the respective concentration-time measurement were available. The demographic data recorded included the following: patient age, sex, weight, and height; the indication for tobramycin treatment; and serum creatinine (SCR) concentrations. Missing SCR measurements were replaced by an expected mean SCR concentration, based on the age and gender of the patient, as described by Ceriotti et al. (25). SCR measurements recorded as <30 μmol/liter, which is below the limit of quantification (LOQ), were replaced by a value of 29 μmol/liter. Data were excluded from the analysis if there was uncertainty about the time of dosing or the time of drug concentration measurement and if dosing information was absent. An occasion was defined as a single tobramycin dosing interval. Tobramycin concentrations were measured using fluorescence polarization immunoassays, which had a lower LOQ of 0.2 mg/liter. The within- and between-assay coefficients of variation were below 10%.

Assessment of predictive performance.

Each selected population pharmacokinetic model was separately implemented in NONMEM (version 7.3) (26) as described in the original article, and the output was visually explored by the use of graphics produced by the Rstudio program (version 0.99.484). Parameter values and covariate relationships for each model were set to those determined in the publications, and predictions were generated on the basis of the doses, sampling times, and covariate values recorded in the validation data set. If the models did not report between-subject variability (BSV) for the pharmacokinetic parameters or RUV in the model, a BSV value of 30% for clearance was supplemented and an additive error of 0.05 mg/liter and a proportional error of 20% were supplemented for RUV. For models that included renal function as a covariate, creatinine clearance (CL_CR) was estimated from patient demographics in the validation data set according to the exact method described in each published study.

The predictive performance of each model was assessed visually by comparing plots of the population predicted concentration (C_pred) and the observed concentration (C_obs) to look for bias (a systematic upward or downward deviation from the line of unity in these plots) and imprecision (a high degree of scatter of data points around the line of unity) and numerically through calculation of the mean error (ME; in milligrams per hour; equation 1), the mean relative error (MRE; in percent; equation 2), and the relative root mean squared error (RMSE; in percent; equation 3) (27).

$$\text{ME}=\frac{1}{n}\sum _{i=1}^n(C_{\text{pred}}-C_{\text{obs}})$$ (1)

$$\text{MRE}=\frac{1}{n}\sum _{i=1}^n\left(\frac{C_{\text{pred}}-C_{\text{obs}}}{C_{\text{obs}}}\right)$$ (2)

$$\text{RMSE}=\sqrt{\frac{1}{n}\sum _{i=1}^n{\left(\frac{C_{\text{pred}}-C_{\text{obs}}}{C_{\text{obs}}}\right)}^2}$$ (3)

Predicted performance was also assessed by the use of simulation-based diagnostics. Visual predictive check (VPC) (28) plots were generated on the basis of 1,000 Monte Carlo simulations by applying the literature models and by using the validation data set design. The 10th and 90th percentiles of the simulated and validation data were plotted versus time after dosing, and the plots were compared visually for model deviations from the validation data. Plots of the normalized prediction distribution error (npde) versus time after dosing were also generated on the basis of 1,000 Monte Carlo simulations of the validation data set's patient dosage history and covariate values. The mean, variance, skewness, and kurtosis of the npde values were calculated and examined statistically (29, 30).

RESULTS

Literature search.

Figure S1 in the supplemental material shows the steps involved in the literature search. Seven studies describing a total of eight population pharmacokinetic models of tobramycin were deemed appropriate for external validation. The models were numbered from 1 to 8 and are referred to as M1 to M8. Table 1 provides a summary of the key information about the published population pharmacokinetic models of tobramycin that were examined. Two models were developed with data from both adults and pediatric patients (age, ≤18 years), and six models were developed only with data from pediatric populations. The largest model was developed with data from 732 adults and pediatric patients with and without cystic fibrosis and 5,605 samples in which the tobramycin concentration was determined, while the smallest model was developed with data from 35 cystic fibrosis patients providing 318 concentration samples in a mainly pediatric population (0.5 to 17.9 years). All models were based on intravenous administration of tobramycin with first-order linear elimination. Five models were developed solely with data from cystic fibrosis patients, one was developed with data from patients with and without cystic fibrosis, and the remaining model was developed with data from general population patients, neonates, and patients with severe infections or in an intensive care unit (ICU). While some models included data from patients with moderate renal impairment, the average renal function in each study population was normal to mildly reduced.

TABLE 1.

Summary of published models of the population pharmacokinetics of tobramycin for external validation^a

Model no. (reference)	No. of patients (total no. of samples)	Age (yr)	Wt (kg)	CLCR	Structural model	Parameter values and covariate relationships included	BSV (%) (BOV [%])	RUV
Adults and pediatric patients
M1 (32)	136 CF patients (NR)	5–50b	15–82b	30–148 ml/minb	1 CMT	kel (h−1) = 0.01 + 0.00294 × CLCR	NR	NR
						CL (liters/h) = V × kel
						V (liters) = 0.335 × wt
M2 (36)	732 CF and general patients (5,605)	0.01–85.0b	3.3–120.0b	34–145 ml/minb	2 CMT	CL (female) (liters/h/70 kg) = 8.08 × (LBW/70)0.952 × (1 + [−0.021 × (age − 18)]) × (mean SCR/SCR)0.222	CL = 25.9 (12.7)	Prop = 20.4%
						CL (male) (liters/h/70 kg) = 9.39 × (LBW/70)0.952 × (1 + [−0.021 × (age − 18)]) × (mean SCR/SCR)0.222	V1 = 15.2
						V1 (female) (liters/70 kg) = 20.1 × (LBW/70)	Q = 41.8
						V1 (male) (liters/70 kg) = 25.1 × (LBW/70)	V2 = 58.5
						V2 (liters/70 kg) = 9.98 × (LBW/70)
						Q (liters/h/70 kg) = 1.5 × (LBW/70)0.952
M3 (33)	44 CF patients (329)	13.4 (0.75–20)c	39 ± 14.6	NR	1 CMT	CL (liters/h) = 0.103 × wt0.75	NR	NR
						V (liters) = 0.267 × wt
Pediatric patients
M4 (32)	85 CF patients (NR)	10.0 (5–15)c	34.0 (15–78)c	80 ml/min (30–128 ml/min)c	1 CMT	kel (h−1) = 0.01 + 0.00281 × CLCR	NR	NR
						CL (liters/h) = V × kel
						V (liters) = 0.363 × wt
M5 (31)	140 neonates with severe infections (365)	0.012 ± 0.008 (0.003–0.044)d	2.75 ± 0.76 (0.8–4.25)d	0.76 ± 0.19 mg/dl (0.04–1.20 mg/dl)e	1 CMT	CL (liters/h) = 0.0508 × wtf	CL = 25.8	Prop = 19.2%
						V (liters) = 0.533 × wt	V = 21.9
M6 (11)	35 CF patients (318)	9.5 (0.5–17.9)c	34 (6.0–72.6)c	106 ml/min (23–195 ml/min)c	2 CMT	CL (liters/h/70 kg) = 6.37 × (wt/70)0.75	CL = 11.7 (6.5)	Prop = 19.0%
						V1 (liters/70 kg) = 18.7 × (wt/70)	V1 = 11.7
						Q (liters/h) = 0.39	V2 = 42.0
						V2 (liters) = 1.32
M7 (3)	257 CF patients (2,015)	8.1 (4.6–13.9)g	23.9 (16.3–42.6)g	0.5 mg/dl (0.4–0.6 mg/dl)h	1 CMT	CL (liters/h) = 5.59 × (wt/70)0.75	CL = 22.8	Prop = 19.1%
						V (liters) = 18.90 × (wt/70)	V = 11.2	Add = 1.4 mg/liter
M8 (41)	614 ICU patients (1,273)	0.008 (0–18)c	2.01 (0.485–85)c	0.81 mg/dl (0.13–1.17 mg/dl)i	2 CMT	CL (liters/h) = 0.28 × (wt/4)BDE	CL = 39.7	Prop = 29.8%
						BDE = 2.23 × wt−0.065		Add = 0.05 mg/liter
						V1 (liters) = 1.9 × (wt/4)0.735
						Q (liters/h) = CL
						V2 (liters) = V1

^aAdd, additive residual unexplained error; BDE, body weight-dependent exponent; BOV, between-occasion variability; BSA, body surface area; BSV, between-subject variability; CF, cystic fibrosis; CL, total body clearance; CL_CR, creatinine clearance (milliliters per minute); CMT, distribution compartment; CV, coefficient of variation; GFR, glomerular filtration rate calculated, as described by Manjunath et al. (44); ICU, intensive care unit; k_el, elimination rate constant; LBW, lean body weight (in kilograms); NR, not reported; Prop, proportional residual unexplained error; Q, typical intercompartmental clearance; RUV, residual unexplained variability; V, apparent volume of distribution; V₁, typical volume of the central compartment; V₂, typical volume of the peripheral compartment.

^bThe median or mean only was reported separately for pediatric patients and adults and was not reported for the data combined. Values represent the range of values obtained.

^cData represent the mean (range).

^dData represent the mean ± standard deviation (range).

^eData represent the mean ± standard deviation (range) serum creatinine concentration.

^fCL (liters per hour) = 0.0508 × 0.843 if the birth weight is ≤2.5 kg.

^gData represent the mean (interquartile range).

^hData represent the mean (interquartile range) serum creatinine concentration.

ⁱData represent the mean (range) serum creatinine concentration.

The disposition of tobramycin was described by a one-compartment distribution in five models (62.5%) and a two-compartment distribution in three models. However, a trend toward the reporting of two-compartment models in more recent publications was noted. As a significant predictor of variability in tobramycin clearance, 75% of the models included a measure of body size (total body weight or lean body weight) and 37.5% of the models included a measure of renal function (CL_CR or SCR). All models included a measure of patient size as a significant predictor of variability in the tobramycin volume of distribution (V), with 12.5% using lean body weight and all others using total body weight. Other covariates reported to be significant in some studies included the patient's sex and age and low birth weight. Typical values for tobramycin clearance in the studies ranged from 0.06 to 4.42 liters/h, with the lowest value being reported in studies performed with neonates. In studies based on a one-compartment model, the typical volume of distribution varied across different subpopulations, ranging from 1.47 to 12.34 liters, with the lowest values being reported in studies performed with neonates. In models based on a two-compartment model, the typical volume of the central compartment ranged from 1.15 to 2.83 liters, with lower values being reported for neonates. Most models (62.5%) estimated the BSV (coefficient of variation [CV], in percent) associated with tobramycin clearance, with values ranging from 11.7 to 39.7%. The highest BSV in clearance was reported in a study conducted with ICU patients. The between-occasion variability (BOV) (CV) in clearance was reported in only two studies and ranged from 6.5 to 12.7%. RUV (CV) was modeled using a proportional or combined proportional/additive error model in 37.5% and 25% of models, respectively, with the values ranging from 19.0 to 29.8% for the proportional component and 0.05 to 1.4 mg/liter for the additive component. Further information can be found in Table 1. The majority (87.5%) of the models were internally validated, most commonly using a log-likelihood ratio test, goodness-of-fit plots, visual predictive checks, and/or a nonparametric bootstrap. One study employed external validation by using data from a new patient population (31). Six of the eight models were developed using NONMEM software; the others used MW/Pharm (32) and WinNonMix (33) software to develop the population pharmacokinetic model.

Patient and validation data collected.

The data used for external evaluation were collected from 41 patients. A summary of the key demographic and pharmacokinetic features of the patients providing data for this data set is provided in Table 2. All children in this population had cystic fibrosis. The median age, weight, and height of the population were 2.2 years (interquartile range [IQR], 1.1, 4.9 years), 12.4 kg (IQR, 8.6, 21.0 kg), and 89.0 cm (IQR, 71.0, 112.0 cm), respectively. The majority of patients for whom data were collected had normal renal function with a median CL_CR of 90.6 ml/min/1.73 m² (IQR, 71.7, 112.0 ml/min/1.73 m²), calculated using the modified Schwartz formula (34). Heights were not recorded for two children, and their height was estimated using average age-associated values from WHO growth charts (35). For five patients, SCR was measured greater than 3 months before or after tobramycin administration, and in these instances, the expected mean SCR was used (25). In total, data from 269 concentration-time points were available for external validation. No concentration measurements were below the assay LOQ for tobramycin. Figure 1 displays these concentration measurements versus time after dosing. Ninety-eight percent of the tobramycin doses were administered as an intravenous infusion over 30 min, with the other 2% of the doses being given over 45 to 60 min. In general, concentration measurements were obtained at about 2 and 6 h after the dose was administered.

TABLE 2.

Key demographic and pharmacokinetic features of the patients providing data for the external validation data set^a

Characteristic	Value(s)
Median (IQR) age (yr)	2.2 (1.1, 4.9)
No. of patients aged (yr):
<2	20
2–12	19
>12	2
No. of males/no. of females	24/17
Median (IQR) total body wt (kg)	12.4 (8.6, 21.0)
Median (IQR) ht (cm)	89.0 (71.0, 112.0)
Median (IQR) serum creatinine concn (μmol/liter)	29 (<30, 51)
Median (IQR) creatinine clearance (ml/min/1.73 m2)b	90.6 (71.7, 112.0)
No. of observations	269
Median (IQR) no. of sampling occasions/patient	6.6 (3, 11)
Median (IQR) dose (mg/kg)	11.3 (9.9, 12.5)
Median (IQR) time of sampling after dosing (h)	5.1 (2.1, 6)
Median (IQR) tobramycin concn (mg/liter)	6.1 (2.8, 15.2)

^aData are for 41 patients.

^bCalculated using the modified Schwartz formula (34).

FIG 1.

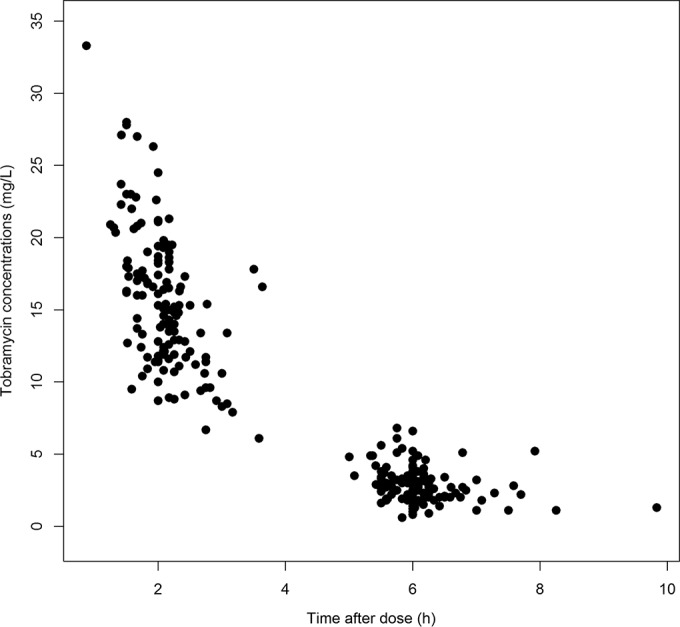
Tobramycin concentration versus time after dosing obtained with data available for external validation of the identified models.

Assessment of predictive performance.

Figure 2 displays the observed versus the population predicted concentrations when each selected population pharmacokinetic model was implemented in NONMEM. Models 2, 6, and 7 exhibited the smallest bias and imprecision in graphic comparisons of the predicted versus the observed concentrations. Graphical results were closely mirrored in numerical estimates of the model predictive performance presented in Table 3. Models 2, 6, and 7 were consistently ranked as the top three models with the lowest values of ME, MRE, and RMSE. Models 3 and 5 consistently obtained the highest values for these metrics. ME was found to be similar among the models ranked as the top three, with the smallest ME, which was for model 3, being −0.4 mg/liter (95% confidence interval [CI], −0.7, 0.01 mg/liter) for model 6. The overall highest ME was 12.1 mg/liter (95% CI, 11.4, 12.7 mg/liter). MREs were 4.9%, 19.2%, and 29.4% for the models ranked as the top three. Overall, the lowest MRE was 4.9% (95% CI, −0.8, 10.6%), which was for model 6, and the highest MRE was 274.1% (95% CI, 240.4, 307.7%), which was for model 3. Overall RMSE values ranged from 47.8% for model 6 to 392.4% for model 3.

FIG 2.

Observed drug concentrations versus population predicted concentrations for eight models of the population pharmacokinetics models of tobramycin. The M numbers represent the models described in Table 1.

TABLE 3.

Predictive performance of published pharmacokinetic models of tobramycin, including ME, MRE, and RMSE, and results of simulation-based npde diagnostics^a

Model no. (reference)	Bias and imprecision			npde diagnostics
	ME (mg/liter)b	MRE (%)b	RMSE (%)	Mean	Variance	Skewness	Kurtosis	P value
								Wilcoxon signed-rank test	Fisher test for variance	Shapiro-Wilks test
Adult and pediatric patients
M1 (32)	3.0 (2.5,3.5)	75.3 (62.5, 88.2)	131.1	−0.3	1.5	0.5	−0.1	0.0	0.0	0.0
M2 (36)	1.0 (0.5,1.4)	19.2 (12.7, 25.7)	57.6	−0.1	0.7	−0.1	1.2	0.2	0.0	0.0
Pediatric patients
M3 (33)	12.1 (11.4, 12.7)	274.1 (240.4, 307.7)	392.4	−1.1	1.1	−0.2	−0.6	0.0	0.5	0.0
M4 (32)	2.4 (2.0, 2.9)	71.5 (58.6, 84.4)	129.1	−0.3	1.6	0.4	−0.3	0.0	0.0	0.0
M5 (31)	6.0 (5.3, 6.6)	222.0 (187.2, 256.8)	365.9	−0.9	2.3	0.2	−0.7	0.0	0.0	0.0
M6 (11)	−0.4 (−0.7, 0.01)	4.9 (−0.8, 10.6)	47.8	0.0	0.8	0.0	1.6	0.5	0.0	0.0
M7 (3)	1.8 (1.4, 2.3)	29.4 (22.2, 36.6)	66.9	−0.1	0.7	−0.1	1.2	0.2	0.0	0.0
M8 (41)	−4.0 (−4.6, −3.4)	−20.2 (−27.9, −12.5)	67.4	0.2	2.7	0.0	−1.3	0.0	0.0	0.0

^aPresented are summary statistics for the distribution of the npde’s: mean, variance, skewness, and kurtosis. The expected value of these four variables for N(0, 1) are, respectively, 0, 1, 0, and 0. Further results for (i) a Wilcoxon signed-rank test, to test whether the mean is significantly different from 0, (ii) a Fisher test for variance, to test whether the variance is significantly different from 1, and (iii) a Shapiro-Wilks test, to test whether the distribution is significantly different from a normal distribution, are presented (30).

^bData in parentheses are 95% confidence intervals.

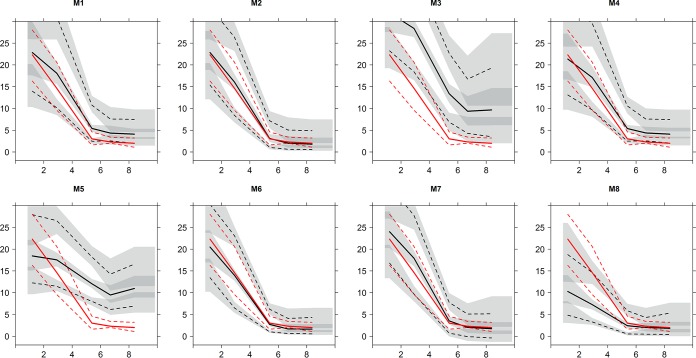
Table 3, Fig. S2 in the supplemental material, and Fig. 3 illustrate the results from the simulation-based diagnostics. Models 2, 6, and 7 showed visually better VPC graphics than the other models and an improved npde-versus-time after dosing statistics compared to those of the other models. Several models, in particular, models with a one-compartment distribution (four out of five models), showed weaknesses in model fit when the simulation was examined.

FIG 3.

Visual predictive checks performed using the identified models (M1 to M8; Table 1) and the validation data set. Here, the 95th and the 5th percentiles (broken lines) and the 50th percentile (continuous lines) of the validation data concentrations (red) and the model-predicted concentrations (black) on the x axis are plotted versus time after dosing (hours) on the y axis. The shaded areas present the binning and the 95% prediction interval.

DISCUSSION

This study is the first to review models of the population pharmacokinetics of tobramycin in pediatric patients currently published in the literature and to systemically externally evaluate the predictive performance of these models. Population pharmacokinetic models 2, 6, and 7 stood out as having the best predictive performance across all the different tests. These models displayed visually favorable observed concentration-versus-population predicted concentration plots, with model 6 appearing to be the best. The same models were distinguished in the numerical predictive performance assessment, ranking in the top three for at least two of the three criteria: ME, MRE, and RMSE. They also stood out as being the best using simulation-based diagnostics.

Model 2 (36), which was developed using the largest data set and which included the greatest number of covariate influences on pharmacokinetic parameters, was consistently among the top three models for all assessments. This model's distinguished performance likely suggests that large population studies which include a number of covariate influences will likely have a better predictive ability with future patients. A trend toward an improved predictive performance was noted for models with a two-compartment disposition rather than a one-compartment disposition, with the two best models (M2 and M6) being two-compartment models and the two least favorable models (M3 and M5) being one-compartment models. A multiple-compartment distribution likely better characterizes the tissue accumulation reported for tobramycin (37). Distinguishing between distribution and elimination processes is, however, highly dependent on the sampling scheme (6, 38). It can be seen that model 3, a one-compartment model developed with data from a pediatric cystic fibrosis population, struggles to predict peak concentrations (Fig. 3; see also Fig. S2 in the supplemental material). All models incorporated the influence of body size on either CL or V; this makes sense, as tobramycin distributes into extracellular fluid, which tends to increase with increasing patient size (39). Models 2, 3, 6, 7, and 8 used a nonlinear function to describe the relationship between drug clearance and patient size; while three of these were the best-performing models, the others were the worst-performing models. Only one of the top three models included the influence of a renal function descriptor on tobramycin clearance, which is surprising, as tobramycin is largely renally eliminated (40). However, most studies were based on patients with normal to moderately impaired renal function, and hence, the influence of renal function on drug clearance may not be significant enough to be detected in this circumstance. Similarly, most patients in the validation data set had normal to only moderately impaired renal function, so the inclusion or the lack of inclusion of renal function in the population model may be of little importance in this circumstance.

Some models may have performed poorly, as they were not externally validated with data from a population similar to that with which they were developed. The validation data set did not include any ICU patients and included only 3 infants between the ages of 5 and 15 weeks. Model 8 (41) was developed with data from ICU patients who were predominately less than 1 month old and reported the large pharmacokinetic variability commonly seen in this population (39, 42). Similarly, model 5 (31) was developed using data from neonates, which may exhibit pharmacokinetics different from those exhibited by older pediatric patients (31, 41). This model was the only one originally externally validated with data from a patient population very similar to the population with which it was developed, but it did not perform so well in this study. The underprediction of particular peak tobramycin concentrations (Fig. 3; see also Fig. S2 in the supplemental material) seen with these models might be due to the larger volume of distribution (on a per-kilogram basis) often seen in individuals and neonates in ICUs than in other populations.

For all models tested, RMSE was >30%. This suggests that knowledge of typical pharmacokinetic behavior and patient covariate values alone without feedback concentration measurements from individual patients is not sufficient to make precise predictions. This could improve by incorporation of the model in Bayesian forecasting software, which would allow feedback from subsequent measurements and the further individualization of the parameters (43).

There were limitations associated with this study. One weakness of the analysis is the limited size and heterogeneity of the external data set used for validation. Data came only from cystic fibrosis patients, and few patients were neonates or had renal impairment. As with any study involving retrospective data collection, uncertainty is associated with data records (21). Interpretation of the published models was complicated in some instances where exact methodologies were not clearly described and details were absent. Three of the eight models did not report any RUV or BSV values. Substitute values were added for application of the models, but this may have altered the ability of models 1, 3, and 4 to accurately predict tobramycin concentrations. Furthermore, some patients contributed more data to the validation data set than others, and all observations were treated independently in the analysis, which can result in bias toward results for patients that contributed larger amounts of data. Of note, for 56% of patients, at least one SCR measurement was recorded as <30 μmol/liter, which is below the LOQ of the assay used to measure this compound. In order to be able to partly utilize this information, these measurements were fixed to 29 μmol/liter, as no other data were available. This, however, may have influenced the predictive performance of the models that included renal function as a covariate.

This study externally evaluated eight published models of the population pharmacokinetics of tobramycin with newly collected clinical data. Several of the published models were found to have reasonably low levels of bias but a greater degree of imprecision. This suggests that knowledge of typical pharmacokinetic behavior and patient covariate values alone without feedback concentration measurements from individual patients is not sufficient to make precise predictions.