Skip to main content
PMC home page
Journal of Sports Science & Medicine logoLink to Journal of Sports Science & Medicine
. 2016 May 23;15(2):239–246.

Comparison of Level and Graded Treadmill Tests to Evaluate Endurance Mountain Runners

Pascal Balducci 1,✉, Michel Clémençon 1, Baptiste Morel 1, Géraud Quiniou 1, Damien Saboul 1,2, Christophe A Hautier 1
PMCID: PMC4879436  PMID: 27274660

Abstract

Mountain endurance running has increased in popularity in recent years. Thus the aim of the present study was to determine if maximal oxygen uptake (VO2max) and energy cost of running (Cr) measured during level and uphill running are associated. Ten high level male endurance mountain runners performed three maximal oxygen uptake tests at three slope conditions (0, 12.5 and 25%). Metabolic data, step frequency (SF) and step length (SL) were recorded. No significant differences were found in VO2max (63.29 (±3.84), 63.97 (±3.54) and 63.70 (±3.58) mlO2/kg-1/min-1) or associated metabolic data at 0, 12.5 and 25% slope respectively. High intra-individual correlations were found between metabolic data measured in the three conditions. The energy cost of running was significantly different between slopes (0.192 (±0.01), 0.350 (±0.029) and 0.516 (±0.035) mlO2/kg-1/min-1, p < 0.01), 0, 12.5 and 25% respectively. However, Cr0% was not correlated with either Cr25% or Cr12.5% (rs = 0.09 and rs = 0.10), in contrast, Cr25% and Cr12.5% were correlated (rs = 0.78). Step length was positively correlated with speed under the three slope conditions. Step frequency was significantly lower at 25 compared to 12.5 and 0% slope. We found that the maximum aerobic power did not differ between level and graded treadmill tests. However, the increase in Cr on the inclined versus level conditions varied between subjects. None of the measured anthropometric or kinematic variables could explain the higher increase in Cr of some subjects when running uphill. Thus, a short graded (5min at 12.5%) running test should be performed at a submaximal velocity (around 40% of level vVO2max) to enhance understanding of an endurance runner’s uphill capability.

Key points.

  • In elite endurance mountain runners, there is no difference in VO2max values between level and uphill running.

  • In a homogeneous group of mountain runners, uphill Cr is not associated with level Cr.

  • To assess performance potential of endurance mountain runners, a standardized uphill running protocol should be performed.

Key words: uphill running, VO2max, energy cost of running, step frequency

Introduction

The recent popularity of mountain endurance running has led to the growth of a new field of experimentation in the sports sciences. Many studies (Hoffman et al., 2012; Millet et al., 2011; Millet and Millet, 2012; Saugy et al., 2013) have focused on neuromuscular fatigue during extreme trail running races. As previously reported (e.g. di Prampero et al., 1986), long-distance running performance depends on several factors: maximal oxygen uptake (VO2max), the energy cost of running (Cr) and the fraction of VO2max that can be sustained throughout a race. These parameters are usually measured during level and/or shallow slope uphill running. However, little is known about how parameters measured during level running are related to uphill running performance in a homogeneous group of well-trained mountain runners. Many studies (Margaria et al., 1963; Minetti et al., 1994; 2002, Padulo et al., 2012; 2013; Snyder and Farley, 2011) have investigated the bioenergetics and mechanics of running on level and sloped surfaces. Inclined protocols seem to elicit higher VO2max values in untrained subjects (Åstrand and Saltin, 1961; Taylor et al., 1955) in comparison to horizontal protocols but the results reported for trained subjects differ among studies. Some studies reported a higher VO2max with an inclined treadmill protocol compared to a horizontal treadmill protocol (Paavolainen et al., 2000) whereas other studies (Davies et al., 1974; Kasch et al., 1976) found no significant differences in VO2max values. Wilson et al. (1979) reported a higher VO2max during a horizontal compared to an inclined protocol. It may be that specifically trained subjects exhibit smaller differences in VO2max between level and uphill running since their muscles are well adapted to uphill locomotion.

The energy cost of running on level and on positive gradients has been extensively investigated (di Prampero et al., 1986; 2009; Hoogkamer et al., 2014; Lussiana et al., 2013; Margaria et al., 1963; Minetti et al., 1994), even on extreme slopes (>20%) (Minetti et al., 2002). Generally, Cr is independent of speed (Dill, 1965, Margaria et al., 1963) and depends on the incline and on the characteristics of the terrain (Minetti et al., 1994; Soule and Goldman, 1972; Zamparo et al., 1992). According to Minetti et al. (2002), uphill Cr can be calculated from level Cr, but individual differences cannot be determined. Considering that many factors are influencing Cr (Lacour and Bourdin, 2015; Saunders et al., 2004) and that individual characteristics may generate different adaptative strategies to uphill running, it can be hypothesized that some runners may have an inferior (greater) Cr in level running and a superior (lower) Cr in uphill running, and vice versa. Thus, it is not yet possible to ascertain whether uphill Cr is associated with level Cr in a homogenous group of high level mountain endurance runners.

The aim of the present study was to determine if uphill running performance can be predicted, based on level treadmill tests or if uphill testing is required to predict performance in a homogenous group of high level mountain endurance runners. Maximal oxygen uptake and the energy cost of running measured during level treadmill tests were compared to data obtained during moderate (12.5%) and extreme (25%) slope running tests. It was hypothesized that there would be no difference in the maximum aerobic power between slope condition and participants would maintain the same rank for VO2max. . It was expected that Cr would increase with slope and it was hypothesized that the ratio between Cr level and Cr uphill would vary between individuals depending on morphological parameters namely: differences in knee extensor force, stride length and stride frequency.

Methods

Participants

Ten high-level male endurance mountain runners participated in the present study (age 38.5 ± 6.4 [mean ±SD] years, height 1.77 ± 0.08 m, mass 69.8 ± 8.6 kg, Body Mass Index 22.3 ± 1.9 kg/m2). Subjects were chosen for their high level of performance in trail running. They all ranked in the top 25 best runners of the French TTN (National Trail Tour). Moreover, their velocity at VO2max (vVO2max), between 5.00 and 5.56 m/s-1 (18 and 20 km/h-1)) and their training load (between 8 and 12 hours running per week) were consistent during the course of the study. Subjects trained on the level and on different slopes. The subjects were healthy, without injuries, and were not taking any medication. The participants did not undergo any strenuous training in the three days before each test. Written informed consent was obtained from the subjects, and the study was conducted according to the principles laid down in the Declaration of Helsinki. Approval for the project was obtained from the Lyon 1 University Ethics Committee on human experimentation.

Procedure

The present study was conducted in a three week period with one test-protocol per week per subject. Each test took place in the morning, at least two hours post-absorptive. All participants wore their same competition shoes for the three sessions. Each protocol was conducted in a randomized order. After a ten minute standardized treadmill warm-up (60% of vVO2max), knee extensor force was measured using an isokinetic dynamometer (Biodex 3, Biodex, Shirley, NY). Then, subjects were equipped with a breath-by-breath metabolic measurement system (Metamax 3B Cortex, Leipzig, Deutschland). A resting blood lactate concentration ([La]r) was measured one minute before each maximal oxygen uptake test at 0,12.5, or 25% slope. All tests were performed on a motorized treadmill (h/p/cosmos quasar med, 3.3 kW). During the test, metabolic data, step frequency (SF) and step length (SL) were recorded. A final blood lactate concentration ([La]f) was measured three minutes after the end of the test, in order to calculate the blood lactate accumulation ([BLA] = [La]f – [La]r).

Incremental tests

Attaining VO2max depends on test duration (Astorino et al., 2004, Midgley et al., 2007), here the stage duration was the same (2min) whatever the slope, but running velocity of the first stage and velocity increments (0.28 m/s-1 (1 km/h-1) at 0%, 0.14 m/s-1 (0.5 km/h-1) at 12.5% and 0.08 m/s-1 (0.3 km/h-1) at 25%) were calculated in accordance with Margaria et al. (1963) and Minetti et al. (2002) on the basis of the individual vVO2max, which was measured one week beforehand with a continuous multi-stage track test (Léger and Boucher, 1980).

The treadmill velocity and incline settings were calibrated before and after each test. Percent grade was expressed as being equal to the tangent x 100.

Peak torque

Maximal voluntary isometric strength (IMVC) of the right knee extensors was assessed at 90° (full knee extension = 0°). The force was recorded by a force sensor (Ergometer ® – Globus Italia S.r.l., Codogne, Italia) using a custom-built chair. The IMVC force plateau was determined over a 500-ms period.The subjects sat with their hips at 80° and were tightly strapped across the chest, hips, and the working leg to avoid lateral and frontal displacement. They were also asked to cross their arms over the chest during the voluntary contractions to limit the involvement of peripheral muscles. The participants performed an IMVC of three seconds (twice), with thirty seconds between each contraction. Peak torque was identified for each contraction by the dynamometer software. The value retained was that of the average of the two peak contractions.

Oxygen uptake, energy cost of running, ventilatory flow rate, ventilatory threshold, velocity at VO2max

Gas exchange was measured during each treadmill protocol. O2 consumption (VO2) and CO2 production VCO2) were then calculated and expressed as STPD. VO2max was determined as the maximal value of VO2 over a thirty seconds sliding window. The VO2max was reached when criteria described by Bertuzzi et al. (2012) were met. The velocity at VO2max was established as the minimal speed that elicited VO2max. If a runner achieved VO2max during a stage that could not be maintained for one minute, the speed in the previous stage was defined as vVO2max (Bertuzzi et al. (2012).

Ventilatory flow rates were expressed in l/min-1 (BTPS). Energy cost of running, expressed in mlO2/kg-1/m-1 at a given speed was calculated during the last thirty seconds of each stage as in equation 1:

graphic file with name jssm-15-239-e001.jpg (equation 1)

with VO2 (mlO2/s-1), v (m/s-1), m (kg) and the constant 0.083 (mlO2/s-1) is the 2 value when v = 0, extrapolated from the relation VO2 – v, established by Medbø et al. (1988) in young men. Only the energy cost below an individual’s ventilatory threshold (VT) was calculated. VTs were determined by the visual method of Wasserman et al. (1973) and verified by three independent experimenters (Vallier et al., 2000). They are reported as percentages of VO2max (Table 1).

Table 1.

Mean values for physiological and metabolic data measured at three conditions of slope: 0, 12.5 and 25%. Data are means (±SD).

Parameter / Condition 0% 12.5% 25%
VO2 max (ml/min-1/kg-1) 63.3 (3.9) 64 (3.5) 63.7 (3.6
HRmax (b/min-1) 182(6) 181.9 (4.9) 182(8)
VE (l/min-1) 152.2 (23.8) 159.0 (23.0) 159.0 (22.6)
VT (%VO2max) 90.4 (2.4) 90.6 (2.6) 91.3 (2.3)
Cr (mlO2/.kg-1/m-1) .192 (.007) .350 (.029) ** .516 (.035) ** ##
[La]r / [La]f (mmol/l-1) 2.8 (2.2) / 13.1 (2.7) 2.0 (.8) / 12.3 (3.3) 3.7 (2.7) / 12.7 (2.4)
Test duration (s) 920(78) 960(116) 908(100)
Rating of Perceived Exertion 8.6 (1.1) 8.25 (.9) 8.6 (1.0)
Open in a new tab

*= significant difference between 25% or 12.5 % and 0%; *: p < 0.05 **: p < 0.01.

# = significant difference between 25% and 12.5%; #: p < 0.05, ##: p < 0.01.

Heart rate, blood lactate, rating of perceived exertion

Heart Rate (HR) was continuously measured by a heart rate monitor (Polar RS800) in beats per minute (b/min-1). Blood lactate (mmol/l-1) was taken by fingerstick and immediately analyzed (Lactate Pro (LT-1710), Arkray, Japan). The subjective difficulty was assessed by a Rating of Perceived Exertion (RPE) scale (0-10), one minute after the end of each test.

Gait analysis

Step length (SL) and step frequency (SF) were recorded for each protocol and at each speed, using an Optojump Next, a floor-based photocell system (Optogait, Microgate, Bolzano, Italy) validated by Lienhard et al. (2013), fixed on the treadmill. A camera (30 frames/second) is integrated into the system. As the Optogait device could not register reliable data at 25% of slope (most likely due to the shuffling gait), video recordings were used to calculate SF (SF = number of strides divided by time). SL was derived using the following formula: Stride length = speed of the treadmill (m/s-1) / stride frequency.

Statistical analysis

Descriptive statistics are presented as means (± SD). Statistical analysis was performed using Statistica (Statsoft.com, 2011). The effect of slope and velocity on dependent variables was assessed using Friedman’s Rank Sum Test (Friedman’s ANOVA), and the Wilcoxon test for post-hoc testing. A P-value < 0.05 was considered statistically significant. Linear regression analysis, using the nonparametric Spearman correlation coefficient (rs), was used to indicate the strength of the association between measured and estimated vVO2max, and between physiological parameters measured during level and inclined protocols.

Results

vVO2max achieved during uphill tests 2.92 ± 0.17 m/s-1 (10.50 ± 0.62 km/h-1) at 12.5%, and 1.90 ± 0.09 m/s-1 (6.85 ± 0.33 km/h-1) at 25%) were strongly associated (rs = 0.88, p < 0.01 and rs = 0.71, p < 0.05 respectively) with vVO2max obtained from level tests (5.22 ± 0.26 m/s-1 (18.8 ± 0.92 km.h-1)). There was no difference in VO2max values due to slope (Table 1 and 2). VO2max values measured under the three conditions were significantly correlated (Table 3).

Table 2.

Individual, physical and physiological data vVO2max (velocity at VO2max), BMI (Body Mass Index), and Cr (Energy cost of running). In the last three columns, inter-athlete ranking for Cr is provided in brackets. For example, athlete number 8 with the 9th Cr at 0% of slope, had the lowest Cr at 12.5 and 25% of slope.

Subjects Age
(yrs)		 Height
(m)		 Mass
(kg)		 BMI
(kg/m-2)		 Peak
torque
(N/m)		 Level
vVO2max
m/s-1 (km/h-1)		 VO2max (ml/min-1/kg-1) Cr (mlO2/kg-1/m-1)
0% 12,5% 25% 0% 12.5% 25%
1 42 1.70 59.0 20.4 110.1 5.28(19) 64.5 62.0 60.3 .189(4) .335(3) .487(3)
2 36 1.69 69.0 24.2 121.3 5.56(20) 68.1 70.7 68.6 .189(4) .352(6) .512(5)
3 40 1.77 81.6 26.0 143.2 5(18) 58.6 62.8 60.6 .186(2) .353(7) .503(4)
4 38 1.69 62.5 21.9 105.1 5.56(20) 65.2 66.6 67.0 .181(1) .347(5) .517(6)
5 29 1.90 86.0 23.8 133.0 5.28(19) 62.5 63.8 63.1 .186(2) .358(8) .545(8)
6 47 1.82 73.0 22.0 96.8 5(18) 60.0 60.1 59.3 .189(4) .324(2) .468(2)
7 49 1.75 65.2 21.3 100.6 5(18) 59.5 58.3 61.3 .195(7) .343(4) .560(10)
8 32 1.72 62.0 21.0 102.6 5.56(20) 70.7 66.9 70.5 .202(9) .302(1) .467(1)
9 33 1.89 71.0 19.9 187.1 5(18) 61.5 64.5 62.5 .195(7) .397(10) .557(9)
10 39 1.74 69.0 22.8 144.7 5(18) 62.3 63.9 63.9 .203(10) .392(9) .543(7)
Mean 38.5 1.77 69.8 22.3 124.4 5.22 (18.8) 63.3 64.0 63.7 .192 .350 .516
± SD 6.4 .08 8.6 1.9 28.2 .26 (.92) 3.9 3.5 3.6 .007 .029 .035
Open in a new tab

Table 3.

Correlation matrix between two conditions of slope for VO2 max (mlO2/kg-1/min-1), Heart Rate Max (HRMax, b/min-1), Ventilatory Flow Rate (VE, l/min-1), Energy Cost of running (Cr, mlO2/kg-1/m-1), Blood Lactate Accumulation (BLA, mmol/l-1), Step frequency (SF, Hz), Step Length (SL, m) and velocity at VO2max (vVO2max, km/h-1).

Cor. Coef. VO2max HRmax VE Cr BLA SF SL vVO2max
0% / 12.5% .77** .70* .94*** .10 .78** .73* .62 .88***
0% / 25% .88*** .64* .90*** .09 .74* .78* .72* .71*
12.5% / 25% .84** .79** .85** .78** .52 .93*** .91*** .89***
Open in a new tab

*: p < 0.05

**: p < 0.01

***: p < 0.001

There was no difference in maximal heart rate. There was no statistical difference between values for VEmax, between level and graded conditions, and this parameter was also correlated between tests (Table 3). There was no difference in blood lactate accumulation between 0, 12.5 and 25% protocols; this parameter was strongly correlated between tests except between 12.5 and 25% (rs = 0.52) (Table 3). Lastly, no difference was found between 0, 12.5 and 25% slope for test duration, RPE and VT.

There was a significant difference for Cr between slope conditions (Figure 1A). Energy cost was independent of speed at 0 and 12.5 but not at 25% (p = 0.02). Only Cr25% and Cr12.5% were associated (rs = 0.78) whereas Cr0% was not associated with either Cr25% or Cr12.5% (rs = 0.09 and rs = 0.10), (Table 3).

Figure 1.

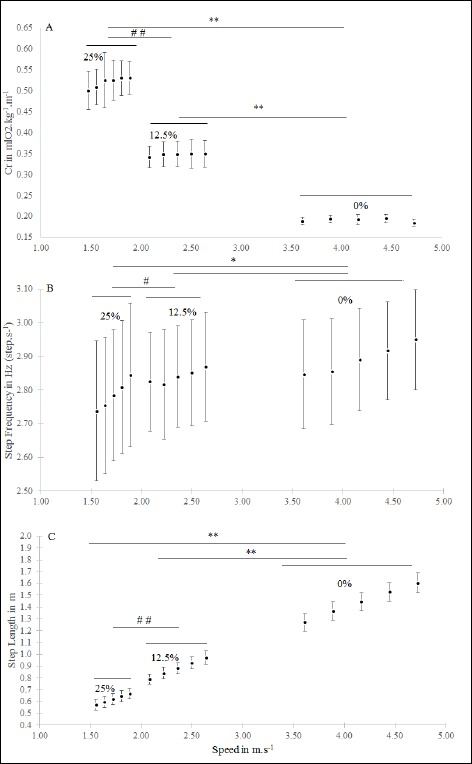
Figure 1.

Open in a new tab

A. Energy cost of running (Cr, mlO2 .kg-1.m-1) measured at five velocities at the Ventilatory Threshold at the three conditions of slope. Significant differences, p < 0.01, have been observed between 0, 12.5 and 25%. There was a speed effect only at 25%, p < 0.05 and no differences observed between the five speeds at 0 and 12.5%. B. Step Frequency (SF, Hz, step.s-1) measured at five velocities at the Ventilatory Threshold at three conditions of slope. SF increased with speed at 0 and 25% grade and SF at 25% was significantly lower than that observed at 12.5% and 0%, p < 0.05. C. Step length (SL, m) measured at five velocities at the Ventilatory Threshold at the three conditions of slope. (SL significantly increased with speed in each condition and SL at 25% was significantly lower compared to SL at 12.5% (p < 0.01) and SL at 0% (p < 0.01) in the same way, SL at 12.5% was significantly lower than SL at 0% (p < 0.05)). Energy Cost of Running, Step Frequency and Step Length measured at five velocities at the Ventilatory Threshold under the three slopes conditions.

Step Frequency was calculated at each stage of each slope (Figure 1B). SF at 25% was significantly lower compared with 12.5 and 0%, but there was no difference between SF at 12.5 versus 0%.

Concerning Step Length (Figure 1C), statistical differences were observed between 0, 12.5 and 25% of slope. SL at 25% was significantly shorter versus 12.5 and 0% (p < 0.01). SL at 12.5% was significantly shorter compared with 0%.

The increase in Cr between level and graded conditions expressed in absolute (ml/m-1/kg-1) or relative (% of level Cr) units was not related to anthropometric characteristics (body mass, height and body mass index) or knee extensor force. In the same way, the absolute and relative increases in Cr were not related to changes in SF or SL.

Discussion

The purpose of the present study was to determine if individual factors related to performance, determined during level running could be accurate predictors of uphill running performance in mountain runners. The present study demonstrated that VO2max and physiological parameters (HRmax, VEmax, VT) measured during incremental running tests are not significantly influenced by slope in a homogeneous group of well-trained mountain endurance runners. Contrastingly the energy cost of running was significantly different between 0, 12.5 and 25% slope running. Moreover, the present study shows that the increase in the energy cost of running between level and uphill conditions differed between trained subjects. Individual differences may partly explain why uphill running performance cannot be predicted from level running tests and justifies the measurement of Cr in uphill running tests.

Heart rate, blood lactate accumulation and test duration during the three tests were in accordance with the guidelines of a maximal aerobic test (e.g. Bertuzzi et al., 2012). Running velocity of the first stage and velocity increments calculated from previous studies (Minetti et al., 1994; 2002) allowed all subjects to achieve VO2max in approximately the same duration. Moreover VO2max measured during uphill running was not significantly different to that measured during level running. This is in accordance with the studies of Kasch et al. (1976) and Davies et al. (1984) but differs from the results reported by (Åstrand and Saltin, 1961, Taylor et al., 1955). These different results may be explained by factors that limit VO2max among runners of different ability. Untrained subjects may stop exercise prior to attaining VO2max because of severe functional alterations at the local muscle level (Levine, 2008). In the present study, it can be hypothesised that the highly trained subjects reached their maximal oxygen transport capacity during level running. In the present study there was no significant difference in VO2max values, regardless of slope. This means that VO2max can be measured during level running even for subjects engaged predominantly in mountain running. The present results failed to demonstrate any difference in VT among the different conditions. Additionally, BLA was not different. This tends to indicate that the anaerobic contribution to energy supply is comparable during level and uphill running in highly trained mountain runners. Therefore, data from the present study suggests that neither VO2max nor VT, expressed in percentages of vVO2max, are influenced by slope in well trained subjects. It demonstrates that these parameters can be accurately measured during level tests and that the results are directly transferable to uphill running.

In accordance with previous studies, energy cost of running increased between level, 12.5 and 25% slope (Margaria et al., 1963; Minetti et al., 1994). Despite stages of shorter duration (2 versus 4 min), the mean net Cr values calculated during the present study were very similar to those reported or calculated by (Hoogkamer et al., 2014; Vernillo et al., 2014), and the gross Cr calculated in the present study are slightly higher than those reported by (di Prampero et al., 1986; 2009; Minetti et al., 2002). Cr at a given grade was not influenced by speed, except at 25% (p < 0.05) (Figure 1A) which seemed to be related to running with the Cortex mask which obscured a view of the feet. The present study showed for the first time, that Cr varied individually with slope. For example, a 50% Cr increase was observed for some subjects from 0 to 12.5% whereas other subjects experienced a 104% increase under the same conditions (Table 2). The importance of energy cost in mountain ultra-marathon performance is still debated (Millet, 2012; Millet et al., 2012; Vernillo et al., 2014; 2015), nevertheless it is interesting to observe that individuals vary widely in their uphill Cr. For example, two subjects (subjects 6 and 7, Table 2) have similar VO2max values, and the same vVO2max during level running; one of them would theoretically lose almost ten minutes during a 5km race run at 75% of VO2max on a 25% slope (52min vs. 61min 53s), due to a higher energy cost of running. However, it should be kept in mind that the present results were measured on a treadmill, and that individual differences in Cr from level to uphill running may be sensitive to differences in running technique. Considering that Cr can be improved by appropriate training (Barnes et al., 2013), it can be hypothesized that Cr during uphill running could be improved in runners showing a large difference between Cr of level and uphill running.

The fact that some subjects increased Cr less than others may be explained by different parameters like anthropometric characteristics, maximal muscle force, rate of force development (Vernillo et al., 2014), muscle recruitment, internal and external mechanical work and the negative/positive work ratio related to the storage of elastic energy. Considering the last parameter, some subjects may retain a better use of elastic energy during uphill running by optimizing their centre of mass displacement (Margaria, 1938). Minetti et al. (1994) found that at inclines of 15% and steeper, purely positive mechanical work was generated. Thus, with a 25% uphill slope, differences in Cr between subjects cannot be explained by differences in the capacity to store and or return elastic energy. Muscle recruitment and mechanical work were not directly measured in the present study although SF and SL may be considered as indirect indicators of running technique (Chen et al., 2009). However, SF was strongly associated among subjects between 0, 12.5 and 25% uphill running and no association was found between changes in Cr and changes in SF between level and graded running. This suggests that individual differences in SF cannot explain differences in Cr between level and graded running. In the same way, SL changes were strongly related to running velocity regardless of slope and not related to differences in Cr. Therefore, simple kinematic parameters cannot explain individual differences in Cr increase between level and graded running and further studies are needed to elucidate more precisely these data. Additionally, the present results demonstrated that body mass, height and body mass index were not related to the increase in Cr between conditions. The maximal isometric force of the knee extensors (peak torque in N.m) was not related to SL and changes in SL between conditions, and we found no association between force and the Cr of each participant, nor between force and the individual increase in Cr from level to graded running. This is surprising since it could be hypothesised that physically stronger subjects may be less affected by the slope, inducing fewer changes in running kinematics and thus a smaller increase in Cr when running uphill. However, it should be kept in mind that only the isometric force was measured which does not correspond to the predominant muscle contraction mode used in running. Further studies are needed to determine why some subjects are more affected by slope from a biomechanical point of view. This would make it possible to prescribe strength and or technical training for high level mountain runners to improve Cr during uphill running.

Conclusion

In conclusion, the results of the present investigation demonstrated that level VO2max and VT are not significantly different compared with the same measures during uphill running among highly trained endurance mountain runners, indicating that these parameters can be reliably measured during a level treadmill test. On the contrary, level Cr is not a predictor of uphill Cr in a homogenous group. Therefore, as Cr is crucial for endurance performance (Lacour and Bourdin, 2015; di Prampero et al., 1986; 2009) and because the time spent running uphill is characteristic of mountain and trail racing, uphill running Cr should be measured during an additional uphill running test. Considering the fact that Cr at 12.5 and 25% grades were strongly associated (rs = 0.78) and the fact that Cr was not influenced by speed, a short graded (5min at 12.5%) test should be performed at one submaximal velocity (around 40% of level vVO2max) to evaluate a runner’s uphill “efficiency”. This uphill Cr may be compared to the theoretical one that can be calculated from level Cr and the equation reported by di Prampero et al. (2009) to assess uphill running ability. Considering that no variables measured so far can explain intra-individual differences in energy cost, further studies may be conducted to evaluate the influence of anthropometric, muscular and coordination variables that determine an increase in uphill Cr (Williams and Cavanagh, 1987).

Biographies

graphic file with name jssm-15-239-g002.gif

Pascal BALDUCCI

Employment

Athletic coach, PhD student, Univ Lyon, Univ. Claude Bernard Lyon 1, LIBM, F-69622, Villeurbanne, France.

Degree

MSc

Research interests

Exercise physiology, Energetics and biomechanics of long distance and mountain running, Performance.

E-mail: balduccip@wanadoo.fr

graphic file with name jssm-15-239-g003.gif

Michel CLÉMENÇON

Employment

Research and teaching assistant, Univ Lyon, Univ. Claude Bernard Lyon 1, LIBM, F-69622, Villeurbanne, France

Degree

PhD

Research interests

Sport science, aging, muscle contraction, performance

E-mail: michel.clemencon@univ-lyon1.fr

graphic file with name jssm-15-239-g004.gif

Baptiste MOREL

Employment

Research and teaching assistant, “Motion Interaction Performance” Laboratory, University of Maine, France

Degree

PhD

Research interests

Neuromuscular fatigue, Muscle biomechanics, Sport performance

E-mail: baptiste.morel@gmail.com

Géraud QUINIOU

Employment

PhD student, Univ Lyon, Université Claude Bernard Lyon 1, LIBM, F-69622, Villeurbanne, France

Degree

MSc

Research interests

Sport science, physiology, and biomechanics.

E-mail: quiniou_geraud@yahoo.fr

graphic file with name jssm-15-239-g005.gif

Damien SABOUL

Employment

Head of Research Project, Almerys, France, Univ Lyon, Université Claude Bernard Lyon 1, LIBM, F-69622, Villeurbanne, France

Degree

PhD

Research interests

Heart rate variability, exercise physiology, performance monitoring

E-mail: dsaboul@free.fr

graphic file with name jssm-15-239-g006.gif

Christophe A HAUTIER

Employment

Lecturer, Univ Lyon, Université Claude Bernard Lyon 1, LIBM, F-69622, Villeurbanne, France

Degree

PhD

Research interests

Sport and exercise biology, neuromuscular fatigue.

E-mail: christophe.hautier@univ-lyon1.fr

References

  1. Astorino T.A., Rietschel J.C., Tam P.A., Taylor K., Johnson S.M., Freedman T.P., Sakarya C.E. (2004) Reinvestigation of optimal duration of VO2max testing. Journal of Exercise Physiology 7(6), 1-8. [Google Scholar]
  2. Åstrand P.O., Saltin B. (1961) Maximal oxygen uptake and heart rate in various types of muscular activity. Journal of Applied Physiology 16, 977-981. [DOI] [PubMed] [Google Scholar]
  3. Barnes K.R., Hopkins W.G., Mcguigan M.R., Northuis M.E., Kilding A.E. (2013) Effects of resistance training on running economy and cross-country performance. Medicine and Science in Sports & Exercise 45(12), 2322–2331. [DOI] [PubMed] [Google Scholar]
  4. Bertuzzi R., Bueno S., Pasqua L.A., Acquesta F.M., Batista M.B., Roschel H., Kiss M.A., Serrao J.C., Tricoli V., Ugrinowitsch C. (2012) Bioenergetics and neuromuscular determinants of the time to exhaustion at velocity corresponding to VO2max in recreational long-distance runners. The Journal of Strength and Conditioning Research 26(8), 2096-2102. [DOI] [PubMed] [Google Scholar]
  5. Chen T.C., Nosaka K., Lin M.J., Chen H.L., Wu C.J. (2009) Changes in running economy at different intensities following downhill running. Journal of Sports Sciences 27(11), 1137-1144. [DOI] [PubMed] [Google Scholar]
  6. Davies B., Daggett A., Jakeman P., Mulhall J. (1984) Maximum oxygen uptake utilising different treadmill protocols. British Journal of Sports Medicine 18(2), 74-79. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Davies C.T., Sargeant A.J., Smith B. (1974) The physiological responses to running downhill. European Journal of Applied Physiology and Occupational Physiology 32(3), 187-194. [DOI] [PubMed] [Google Scholar]
  8. di Prampero P.E., Atchou G., Bruckner J.C., Moia C. (1986) The energetics of endurance running. European Journal of Applied Physiology and Occupational Physiology 55(3), 259-266. [DOI] [PubMed] [Google Scholar]
  9. di Prampero P.E., Ferretti G. (1990) Factors limiting maximal oxygen consumption in humans. Respiration Physiology 80(2-3), 113-127. [DOI] [PubMed] [Google Scholar]
  10. di Prampero P.E., Salvadego D., Fusi S., Grassi B. (2009) A simple method for assessing the energy cost of running during incremental tests. Journal of Applied Physiology 107(4), 1068-1075. [DOI] [PubMed] [Google Scholar]
  11. Dill D. (1965) Oxygen used in horizontal and grade walking and running on the treadmill. Journal of Applied Physiology 20, 19-22. [DOI] [PubMed] [Google Scholar]
  12. Ferley D.D., Osborn R.W., Vukovich M.D. (2014) The effects of incline and level-grade high-intensity interval treadmill training on running economy and muscle power in well-trained distance runners. The Journal of Strength and Conditioning Research 28(5), 1298-1309. [DOI] [PubMed] [Google Scholar]
  13. Hoffman M.D., Ingwerson J.L., Rogers I.R., Hew-Butler T., Stuempfle K.J. (2012) Increasing creatine kinase concentrations at the 161-km Western States Endurance Run. Wilderness and Environmental Medicine 23(1), 56-60. [DOI] [PubMed] [Google Scholar]
  14. Hoogkamer W., Taboga P., Kram R. (2014) Applying the cost of generating force hypothesis to uphill running. PeerJ 2, e482. [DOI] [PMC free article] [PubMed] [Google Scholar]
  15. Kasch F., Wallace J., Huhn R., Krogh L., Hurl P. (1976) VO2 max during horizontal and inclined treadmill running. Journal of Applied Physiology 40, 982-983. [DOI] [PubMed] [Google Scholar]
  16. Lacour J.R., Bourdin M. (2015) Factors affecting the energy cost of level running at submaximal speed. European Journal of Applied Physiology 115(4), 651-673. [DOI] [PubMed] [Google Scholar]
  17. Léger L., Boucher R. (1980) An indirect continuous running multistage field test: the Universite de Montreal track test. Canadian Journal of Applied Sport Sciences 5(2), 77-84. [PubMed] [Google Scholar]
  18. Levine B.D. (2008) VO2,max: what do we know, and what do we still need to know. Journal of Physiology 586(1), 25-34. [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Lienhard K., Schneider D., Maffiuletti N.A. (2013) Validity of the Optogait photoelectric system for the assessment of spatiotemporal gait parameters. Medical Engineering and Physics 35(4), 500-504. [DOI] [PubMed] [Google Scholar]
  20. Lussiana T., Fabre N., Hébert-Losier K., Mourot L. (2013) Effect of slope and footwear on running economy and kinematics. Scandinavian Journal of Medicine & Science in Sports 23(4), e246-e253. [DOI] [PubMed] [Google Scholar]
  21. Margaria R. (1938) Sulla fisiologia e specialmente sul consumo energetico della marcia e della corsa a varie velocita ed inclinazioni del terreno. Atti della Accademia Nazionale dei Lincei 7, 299- [Google Scholar]
  22. Margaria R., Cerretelli P., Aghemo P., Sassi G. (1963) Energy cost of running. Journal of Applied Physiology 18, 367-370. [DOI] [PubMed] [Google Scholar]
  23. Medbø J.I., Mohn A.C., Tabata I., Bahr R., Vaage O., Sejersted O.M. (1988) Anaerobic capacity determined by maximal accumulated O2 deficit. Journal of Applied Physiology 64(1), 50-60. [DOI] [PubMed] [Google Scholar]
  24. Midgley A.W., McNaughton L.R., Polman R., Marchant D. (2007) Criteria for determination of maximal oxygen uptake. Sports Medicine 37(12), 1019-1028. [DOI] [PubMed] [Google Scholar]
  25. Millet G.P. (2012) Economy is not sacrificed in ultramarathon runners. Journal of Applied Physiology 113(4), 686-686. [DOI] [PubMed] [Google Scholar]
  26. Millet G.P., Millet G.Y. (2012) Ultramarathon is an outstanding model for the study of adaptive responses to extreme load and stress. BMC Medicine 10, 77. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Millet G.Y., Hoffman M.D., Morin J.-B. (2012) Sacrificing economy to improve running performance—a reality in the ultramarathon? Journal of Applied Physiology 113(3), 507-509. [DOI] [PubMed] [Google Scholar]
  28. Millet G.Y., Tomazin K., Verges S., Vincent C., Bonnefoy R., Boisson R.C., Gergele L., Feasson L., Martin V. (2011) Neuromuscular consequences of an extreme mountain ultra-marathon. PLoS One 6(2), e17059. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Minetti A.E., Ardigo L.P., Saibene F. (1994) Mechanical determinants of the minimum energy cost of gradient running in humans. Journal of Experimental Biology 195, 211-225. [DOI] [PubMed] [Google Scholar]
  30. Minetti A.E., Moia C., Roi G.S., Susta D., Ferretti G. (2002) Energy cost of walking and running at extreme uphill and downhill slopes. Journal of Applied Physiology 93(3), 1039-1046. [DOI] [PubMed] [Google Scholar]
  31. Paavolainen L., Nummela A., Rusko H. (2000) Muscle power factors and VO2max as determinants of horizontal and uphill running performance. Scandinavian Journal of Medicine and Science in Sports 10(5), 286-291. [DOI] [PubMed] [Google Scholar]
  32. Padulo J., Annino G., Migliaccio G.M., D’Ottavio S., Tihanyi J. (2012) Kinematics of running at different slopes and speeds. The Journal of Strength and Conditioning Research 26(5), 1331-1339. [DOI] [PubMed] [Google Scholar]
  33. Padulo J., Powell D., Milia R., Ardigo L.P. (2013) A paradigm of uphill running. PLoS One 8(7), e69006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Saugy J., Place N., Millet G.Y., Degache F., Schena F., Millet G.P. (2013) Alterations of neuromuscular function after the world’s most challenging mountain ultra-marathon. PLoS One 8(6), e65596. [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Saunders P.U., Pyne D.B., Telford R.D., Hawley J.A. (2004) Factors affecting running economy in trained distance runners. Sports Medicine 34(7), 465-485. [DOI] [PubMed] [Google Scholar]
  36. Snyder K.L., Farley C.T. (2011) Energetically optimal stride frequency in running: the effects of incline and decline. Journal of Experimental Biology 214(Pt 12), 2089-2095. [DOI] [PubMed] [Google Scholar]
  37. Soule R.G., Goldman R.F. (1972) Terrain coefficients for energy cost prediction. Journal of Applied Physiology 32(5), 706-708. [DOI] [PubMed] [Google Scholar]
  38. Taylor H.L., Buskirk E., Henschel A. (1955) Maximal oxygen intake as an objective measure of cardio-respiratory performance. Journal of Applied Physiology 8(1), 73-80. [DOI] [PubMed] [Google Scholar]
  39. Vallier J., Bigard A., Carré F., Eclache J., Mercier J. (2000) Détermination des seuils lactiques et ventilatoires. Position de la Société française de médecine du sport. Science & Sports 15(3), 133-140. [Google Scholar]
  40. Vernillo G., Savoldelli A., Zignoli A., Skafidas S., Fornasiero A., La Torre A., Schena F. (2015). Energy cost and kinematics of level, uphill and downhill running: fatigue-induced changes after a mountain ultramarathon. Journal of sports sciences (ahead-of-print), 1-8. [DOI] [PubMed] [Google Scholar]
  41. Vernillo G., Savoldelli A., Zignoli A., Trabucchi P., Pellegrini B., Millet G.P., Schena F. (2014) Influence of the world’s most challenging mountain ultra-marathon on energy cost and running mechanics. European Journal of Applied Physiology 114(5), 929-939. [DOI] [PubMed] [Google Scholar]
  42. Wasserman K., Whipp B.J., Koyl S.N., Beaver W.L. (1973) Anaerobic threshold and respiratory gas exchange during exercise. Journal of Applied Physiology 35(2), 236-243. [DOI] [PubMed] [Google Scholar]
  43. Williams K.R., Cavanagh P.R. (1987) Relationship between distance running mechanics, running economy, and performance. Journal of Applied Physiology 63(3), 1236-1245. [DOI] [PubMed] [Google Scholar]
  44. Zamparo P., Perini R., Orizio C., Sacher M., Ferretti G. (1992) The energy cost of walking or running on sand. European Journal of Applied Physiology and Occupational Physiology, 65(2), 183-187. [DOI] [PubMed] [Google Scholar]

Articles from Journal of Sports Science & Medicine are provided here courtesy of Dept. of Sports Medicine, Medical Faculty of Uludag University

RESOURCES