A Six‐Stage Workflow for Robust Application of Systems Pharmacology

Abstract

Quantitative and systems pharmacology (QSP) is increasingly being applied in pharmaceutical research and development. One factor critical to the ultimate success of QSP is the establishment of commonly accepted language, technical criteria, and workflows. We propose an integrated workflow that bridges conceptual objectives with underlying technical detail to support the execution, communication, and evaluation of QSP projects.

Mathematical modeling of systems dynamics has a long history in the mathematics and engineering disciplines, from basic research in nonlinear dynamical systems to application in chemical, mechanical, and electrical process control. These methodologies were subsequently applied to study how biological systems respond to input conditions and perturbations, including pharmaceutical agents, and even to optimize treatment approaches.1 As efforts converged with developments in pharmaceutical sciences and systems biology and with advances in analytical and computational capabilities, the discipline of quantitative systems pharmacology (QSP) emerged at the intersection of these fields. QSP has been described as the “quantitative analysis of the dynamic interactions between drug(s) and a biological system that aims to understand the behavior of the system as a whole.” 2 QSP approaches typically share several attributes that, taken together, highlight how the discipline integrates the drug and treatment outcome considerations of pharmaceutical sciences; the first‐principles mechanistic modeling and dynamical analysis of engineering and applied mathematics; and the complex biological network science of systems biology (adapted from ref. 3).

Common features of QSP approaches

• A coherent mathematical representation of key biological connections in the system of interest, consistent with the current state of knowledge.

• A general prioritization of necessary biological detail over parsimony, potentially including detail at various physiological scales.

• Consideration of complex systems dynamics resulting from biological feedbacks, cross‐talk, and redundancies.

• Integration of diverse data, biological knowledge, and hypotheses.

• A representation of the pharmacology of therapeutic interventions or strategies.

• The ability to quantitatively explore and test hypotheses and alternate scenarios via biology‐based simulation.

The increasing interest in QSP in pharmaceutical research and development is evidenced by the convening of an National Institutes of Health (NIH) working group on QSP and its issuance of a whitepaper4, 5 and the recent use by the US Food and Drug Administration (FDA) in review of a biological license application.6 Yet, as an emerging field, QSP faces challenges to its ultimate broader success.7, 8, 9

One need is adoption of commonly understood language, technical criteria, and workflows to allow communication and assessment by peers, collaborators, and reviewers. This is a challenge given the variety of QSP approaches and applications, including gene/protein/metabolomics regulation networks, metabolic flux analysis, signal transduction, cellular interactions, tissue dynamics, disease platforms, and more. Different conceptual workflows have been proposed in the literature for model development or qualification in QSP7, 10 and are similar to those in systems biology.11, 12 Other efforts have focused on particular technical methodologies (e.g., ref. 13). In this study, we present a conceptual workflow, consistent with those previously proposed, integrated with underlying technical detail in order to support robust application of QSP (Figure 1). Illustrative examples are provided, although these are by no means exhaustive and do not encompass all areas of the QSP field. The workflow is presented as a staged progression, although there is invariably iteration and interaction between stages. The following sections describe the workflow and address efforts, insights, and caveats at each stage. The workflow offers a framework that can be tailored to a broad variety of projects and also addresses common questions and criticisms facing QSP efforts, discussed in the Summary. Illustration of the application of the overall workflow in two published examples is provided in the Supplementary Table S1.

Figure 1.

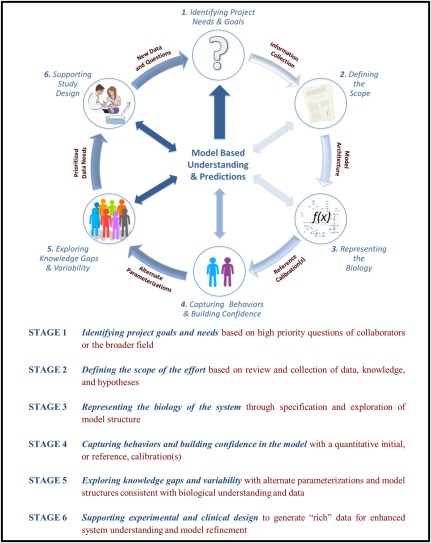
A six‐stage iterative workflow for quantitative systems pharmacology (QSP) project execution, including the conceptual objective of each stage (blue text) and the corresponding technical objective (red text). The workflow is iterative and model‐based insights of different nature and degrees of robustness can be obtained at each stage.

STAGE 1. PROJECT NEEDS AND GOALS

The first step of any project is consideration of problem context and goals. We briefly comment on high priority considerations in QSP.

Interaction with collaborators

The success of any modeling and simulation effort depends on clear identification of high priority questions for which results are likely to have valuable contributions. It is also important to identify time constraints on when answers are needed (e.g., drug development decision points). Regular interaction is important in all collaborative work, and especially so in QSP in which the models themselves are multidisciplinary, predicated on a mathematical representation of complex biology, and thus requiring cross‐education on the biology and the modeling. These interactions also foster a “co‐ownership” of the model goals, assumptions, hypotheses, implementation, and results. The first stage of the project must establish these collaborations and achieve agreement on feasible modeling goals, as well as identify individual responsibilities for data generation and sharing, modeling, discussion, and review should be established at project initiation.

Technical considerations

Pragmatic considerations on whether to initiate a QSP effort include: sufficient data/knowledge available to inform the modeling; the question best addressed by QSP vs. other experimental or modeling approaches; sufficient resources to allow timely execution; and how robust do predictions need to be to provide value? Even a limited analysis of data and project feasibility at this stage can set expectations for reasonable project goals and rough resource requirements subject to revision during more extensive scoping in Stage 2.

OUTCOMES

The desired outcomes of Stage 1 are:

• Specification of and agreement with any collaborators on questions of interest

• Identification of potential project goals, including any timeline and resource pressures

• Definitions of roles and responsibilities of collaborators

STAGE 2. REVIEWING THE BIOLOGY: DETERMINING THE PROJECT SCOPE

A necessary step in planning a QSP effort is the identification of the biological scope a model must encompass and behaviors it must recapitulate in order to make predictions to support the specific project goals. Scope decisions are guided by the project goals and available data, knowledge, and hypotheses of interest.

Model scale

One consideration in scoping is the breadth and depth of detail and the biological scales to include (intracellular, multicellular, tissue, organ, and whole body). Disease or biology platforms and multiscale models are models that span multiple subsystems, pathways, and biological scales; these models are typically larger in scope and can be used to address multiple questions and the interaction of the subsystems. Platform models have been used to compare and evaluate diverse targets or across a wide range of contexts involving common biology.14, 15 However, the development of these models tends to be resource intensive. Focusing on specific targets, compounds, or signaling or biological‐interaction pathways, possibly in greater depth (e.g., refs. 16, 17, 18), can limit scope while allowing for later expansion to other applications. Another aspect of scale is the importance of spatial and temporal effects (i.e., time‐scales of interest and the importance of spatial heterogeneity). These considerations help determine a suitable modeling approach.

Information and data collection

One must also consider what features and components to address (or exclude) in the model, namely:

• Species: what molecular, cellular, or physiological entities to consider

• Relationships: how do the species interact (chemical transformations, regulatory mechanisms, etc.)

• Inputs and outputs: what are the conditions and phenotypic responses of interest

• Data types: what data will be used in the modeling

This involves aggregation and analysis of information from disparate sources, as outlined in Table 1.

Table 1.

Data types and sources for QSP model‐based development and research

	KOLs & area experts	Literature & abstracts	Databases	“In‐house” data
General understanding	Disease, biology, & clinical experts	Review articles		Summary material (presentations, etc.)
Mechanistic understanding and data	Disease, biology, & target experts	In vitro and in vivo studies	Pathway DBs	In vitro, in vivo, & clinical studies
Pharmacology understanding and data	Pharmacology & drug development experts	In vitro, in vivo, & clinical studies		In vitro, in vivo, & clinical studies
Clinical understanding and data	Clinical experts	Clinical reports & experience, study results	Molecular DBs, aggregated trial DBs,& deidentified patient data DBs	Summary data & patient‐level data
Modeling approaches	QSP, PK‐PD & pharmacometric, bioinformatics, and statistics experts	Prior art	Model repositories	Parallel or prior PK‐PD & statistical models

DBs, Databases; KOLs, key opinion leaders; PK‐PD, pharmacokinetic‐pharmacodynamic; QSP, quantitative systems pharmacology.

Expert knowledge

Discussion with biology, drug development, and clinical experts provides a valuable source of knowledge. In these discussions, it is important to clearly identify what aspects of the biology are robustly established in the field, what is contentious, and what are the open questions and working hypotheses in the field. Continued partnership with subject matter experts helps ensure that the model maintains relevance throughout the effort.

Public literature

Numerous publicly available sources provide information on the underlying biology, key biological components, experimental systems, knowledge gaps, and prior art. Review articles on the disease or biology are a good starting point. Clinical literature and updates on ongoing studies from sources, such as clinicaltrials.gov, conferences, and abstracts, provide information on patient phenotypes, drug response patterns, the competitive landscape, and unmet medical needs and open problems. Information on direct mechanistic cellular or molecular pathways and interactions are most commonly described in preclinical studies (e.g., direct effects of mediators on specific cell types). Public literature is often also a valuable source of datasets useful for model development, calibration, and testing.

Identifying and reviewing these resources can be a momentous undertaking. Natural language processing and text mining algorithms and tools are available to parse biomedical literature to read context, compile specific measurements, and construct molecular interaction networks.19 These capabilities are progressing rapidly, but application to mechanistic interpretation still requires significant user curation. Efforts, such as DARPA's “Big Mechanism” program (DARPA‐BAA‐14‐14, http://www.ncbi.nlm.nih.gov/pubmed/26178259), are underway to advance this field. Until such tools become efficient, literature review remains a bottleneck in the scoping process and focusing on key aspects becomes critical.

The review of public domain material for relevant mathematical models and prior work is also important. Some journals, such as CPT:PSP, publish core models associated with the research articles. Systematic reviews of existing models in a given disease or biological area also support the reuse, repurposing, and extension of prior work (e.g., ref. 20). Although one may not find a model or set of equations that can be used directly, prior work can provide ideas or a starting place for subsequent efforts.

Databases and repositories

Different kinds of databases can provide information for the construction of a QSP model (Supplementary Table S2). Pathway databases codify signal transduction, metabolic, gene regulatory, or even disease pathway interactions. However, these curated representations of even well‐established pathways, such as “epidermal growth factor receptor (EGFR) signaling”21 can differ greatly, in part because of the different scope and granularity used in defining the pathway and other biomolecular interactions.22 Molecular databases contain cellular/molecular data from in vitro, in vivo, and/or clinical settings. For example, full molecular profiles are now publicly available for 1,000+ immortalized cancer cell lines with in vitro proliferative responses to 100+ anticancer agents,23, 24 and The Cancer Genome Atlas (TCGA) project hosts molecular profile data on thousands of primary tumor samples from many cancer indications.25 Such data can be used to help quantify model species and assess frequencies of molecular events (mutations or gene expression patterns) within and between populations of interest. Pharmacological (e.g., ChEMBL, DrugBank) and pharmacogenomic databases (e.g., PharmGKB) include data on compound bioactivity and how individual genetic profiles influence drug pharmacokinetic (PK) and downstream effects, and can help elucidate mechanism and identify different patient profiles. Clinical databases from individual or multiple clinical trials are available from public consortia or private sources. Finally, repositories that include published models in standardized formats (CellML and SBML) also exist. Widespread use of such repositories has been hindered26 by the nonuniformity of QSP model formats and software packages, as compared to PK/pharmacodynamic (PD) models, which typically use standard packages (e.g., NONMEM, Phoenix, ADAPT, SIMCYP, or PKSim). However, provided adequate specifications, the models can be recreated in the software of choice.

Data management

Data aggregation

Collecting, extracting, analyzing, and documenting available data is a complex task. Once in hand, spreadsheets and databases are useful for organizing the extracted information and enabling subsequent analysis. For example, while developing a QSP model of type 1 diabetes in the nonobese diabetic (NOD) mouse,27 Shoda et al.28 performed a comprehensive review and analysis of response to interventions tested in the animal model, ultimately providing broader insight on timing, dose, and mechanism related patterns for researchers in the field. In aggregating information, it is important to document any debate about the data, concerns about its relevance, or inconsistencies between datasets that must be considered in selecting “reliable” data or testing alternate hypotheses (e.g., upregulation vs. downregulation of gene X by protein Y). Recording statistical variation within and among datasets supports later exploration of variability. Formal meta‐analyses or simpler approaches, such as weighted averaging by sample size, can be used for cross‐study data aggregation.29

Data generation

Any additional data acquisition is dictated by gaps in current knowledge and available data. Generally, parameter estimation for dynamical systems requires “cue‐signal‐response” experiments30; that is, perturbation of the system with relevant environmental “cues” (e.g., biological stimuli, mutations, and drugs) and measurement of resulting “signals” (e.g., protein or gene expression, and cellular processes) and phenotypic “responses” (e.g., in vitro proliferation, in vivo, or clinical response). To enable parameter estimation, conditions should be selected that induce orthogonal, or at least diverse, changes.

Data analysis

Preliminary analysis of the available data can be highly informative. For large datasets, hierarchical clustering and Principal Components Analysis (PCA) can reveal patterns that are not obvious in raw data. Analysis based on measurement covariation or statistical interaction networks (i.e., Bayesian or Mutual Information) can be compared against canonical knowledge of the system to assess consistency or novelty. Multivariate regression methods, such as partial least squares (PLS), can help identify input‐output relationships and reveal underlying mechanisms or variables that are/not strongly predictive of clinical behavior.31, 32 For aggregated clinical data, meta‐analyses can be used to compare responses to different interventions or understand interstudy variability (e.g., refs. 29, 33). Ultimately, these analyses enable structural model development.

Visual note‐taking

Visual mapping of the biology is useful for recording interactions identified during scoping efforts. Diagrams enable easy representation, interpretation, and revision of the biological understanding associated with a mathematical model. Furthermore, they support cross‐disciplinary communication with collaborators. A visual diagram can also serve as a starting point for technical specification of model topology.

In simple cases, one can use nontechnical software with drawing capability (e.g., Microsoft PowerPoint) to generate these diagrams. User‐friendly software designed to encode, visualize, and analyze networks allow efficient generation and modification of diagrams of greater complexity.³⁴ Figure 2 shows one example of a signaling network diagram in Cytoscape, a freely available network construction and analysis platform. This and other software are also compatible with standardized graphical and computational notations for representing, importing, and exporting biological pathways.36, 37, 38 One consideration in selecting a tool is the ease of transition from the scoping effort to later model implementation. Network analysis software designed for systems biology/omics data does not usually enable dynamic modeling and simulation; however, they can be integrated with modeling software via user‐developed scripts or “apps.” For example, in their work on intracellular signaling, Saez–Rodriguez et al.35 developed apps to link Cytoscape with mathematical capability in R.39 Other graphical user interface (GUI) based diagramming software, including JDesigner, CellDesigner, and SBML's Qualitative Models Package,40 can be integrated with mathematical tools, such as the Systems Biology Workbench or SBML‐compatible modeling software. Some biological systems modeling software, such as the MATLAB SimBiology package, integrate the diagrammatic and mathematical aspects through a GUI‐based interface to an underlying simulation engine, although with less flexible and more technical network visualization. Many more system's visualization and modeling tools exist or are in development.

Figure 2.

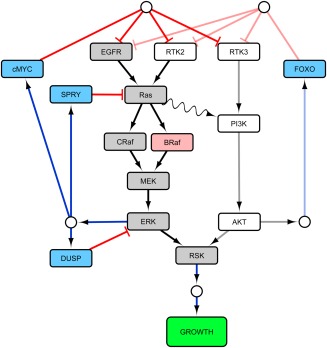
Signaling pathway diagram generated in Cytoscape software. Visual properties of nodes and edges are user‐specified. Diagrams can be generated for any network directly in GUI or through text/tabular file specification of nodes and connectivity.

Model development, qualification, and research plan

The literature review, expert consultation, data assessment, and biological network diagramming are used to develop a plan for execution of the project. Friedrich10 has presented an approach to documenting this and supporting the project moving forward. A comprehensive plan includes details of what biology will be modeled and what will be excluded, assumptions, behaviors of interest, questions to be addressed, and hypotheses to be explored. It also includes documentation of the information reviewed and how available data will be used to develop the model. It is important to identify in advance which data will be used to inform model generation and calibration (e.g., in vitro and clinical data), which data will be reserved to test model predictivity (e.g., additional therapeutic responses), and which data will be used to support subsequent exploration (e.g., novel compound PK or biomarker data). This ensures proper use of data and clear communication of what will qualify the model as “fit for purpose.”

Specification of calibration and testing datasets and success criteria requires careful consideration. Calibration must constrain the relevant biological mechanisms sufficiently to have confidence in subsequent predictions. Testing datasets must probe biology that was already constrained in calibration and that is relevant to future prediction. Educating collaborators on the proposed approach and gaining agreement on chosen qualification criteria is essential, or later results may be discounted. Explanation of the strategy is also important as these procedures often differ between QSP and traditional data‐driven pharmacometrics.35, 40

OUTCOMES AND INSIGHTS

The primary outcome of this stage is identification and documentation of intended model scope and project plan, including:

• Visual mapping of biology

• Organized summaries or repositories of data collected and reviewed

• Documentation of key opinion leader input, data, analyses, hypotheses, assumptions

• Specified qualification criteria and project execution plan (including data use)

Integrated analysis of aggregated data often provide fundamental insight, identifying potential unanticipated topological connections, or areas of poor data availability and knowledge gaps in the field. These insights can provide both qualitative and quantitative value to collaborators and the broader community. Whereas results of data analysis can be quantitatively robust, proposed novel topology should be quantitatively explored in subsequent stages for confidence in its consistency with all data and its relevance to predictions.

STAGE 3. REPRESENTING THE BIOLOGY: DEVELOPING THE MODEL STRUCTURE

Capturing system behaviors requires specification of model topology and mathematical formulation in a manner consistent with biological understanding and capable of capturing salient features of the relevant data.

Model topology

“Model topology” is defined here as the set of species and their connections as represented in the quantitative model, although the nature of specifying the topology will differ among different mathematical approaches. A visual map of the topology plays an important role in development, revision, and communication of the model. Visual note‐taking diagrams generated in the scoping phase can serve as the starting point for topological specification of the mathematical model.

Specification of model topology

Different technical approaches exist for specification of the model topology. Fully supervised approaches have been widely used in QSP efforts ranging from signaling models42 to disease platforms.14, 15 In these efforts, model topology is based on prior understanding and includes representation of: biological connections based on current or expert understanding; competing hypotheses that have been proposed; and additional mechanisms needed to qualitatively capture observations and data. Supervised approaches are well suited to the integration of disparate, diverse, and/or sparse datasets and to relatively well understood (or hypothesis‐driven) biology. However, alternate a priori unappreciated topologies or hypotheses consistent with available data are likely to be missed. In contrast, unsupervised approaches reconstruct model topology from qualitative network analysis or quantitative data analysis. Larger datasets with coordinated measurements of numerous modeled species under different conditions enable network reconstruction. These “network inference” and “reverse engineering” methods rely on statistical analyses to elucidate model topology. Several techniques, including correlation‐based methods, Boolean networks, Bayesian networks, and model‐based methods have been utilized for inference of metabolic networks from metabolomics data,43 signaling networks from proteomic data (e.g., refs. 44, 45) and gene regulatory networks from expression data,46 and in deducing connectivity between gene expression and clinical measurements in disease.47 Unsupervised approaches are largely drawn from prior art in systems biology. Combinations of supervised and unsupervised strategies can also be used to leverage the benefits of each approach.48, 49 The choice of approach depends on the data and prior mechanistic understanding; regardless, the resulting topology should be reviewed to verify biological plausibility.

Alternate model topologies

Alternate model topologies address qualitative mechanistic uncertainty. Automated approaches, such as those developed by Saez–Rodriguez et al.,35 can be used to generate and test alternate topologies. In cases in which the mechanisms are believed to be well understood, one can focus instead on topologies reflecting preidentified alternate hypotheses. Even so, the possibility of alternate structures should be considered and documented as a potential uncertainty with associated caveats for predictions.

Graphical network analysis

Proposed topologies can be analyzed using graph theory to identify degree of connectivity of nodes (states/entities), node‐node interactions (number of paths, path length, direction of connectivity; positive vs. negative relationships), and more. This information can be used to identify critical sensor nodes, network hubs, submodules, feedback loops, redundancies, and the “proximity” of different biological entities, all of which can shed light on the biology and suggest potential quantitative model behaviors and experimental data needs.50, 51, 52 Various algorithms and software, including Cytoscape, enable graphical analysis.

Mathematical modeling formalisms

Representation of the biology includes formulation of mathematical equations describing the interactions in the topological network. Application‐specific considerations guide the selection of a modeling formalism appropriately as follows:

• Kinetic data availability: Are rich time‐course data or biological understanding of mechanistic kinetics available?

• Data types: Are experimental measurements derived from unified larger datasets or from smaller disparate datasets?

• Time‐scales: Will the model include dynamics on widely different time‐scales? Can faster processes be assumed as steady state?

• Spatial heterogeneity: Is there a need to capture spatial heterogeneity, or will a coarse or lumped representation of spatial effects suffice?

• Deterministic vs. probabilistic: How important are random/stochastic effects?

Here, we highlight some of the more commonly used approaches (Table 2 32, 53, 54, 55, 56), which have been discussed in greater detail in prior reviews,57, 58, 59 although various other formalisms exist. These include data‐driven approaches (common in systems biology), ordinary differential equations (common in PK and PD and engineering), and approaches that include spatial effects (derived from engineering).

Table 2.

Common modeling formalisms in QSP

Modeling approach	Mathematical form	Strengths	Potential drawbacks	Example & software/language
Statistical data‐driven	Algebraic + probabilistic equations	• Data‐driven biology	• Less mechanistic • Best for coordinated measurement of numerous variables	Apoptosis signaling32
Logic‐based	Rule‐based interactions	• Intuitive rules	• Less kinetic richness • Best for coordinated measurement of numerous variables	Kinase pathway crosstalk56 (MATLAB Fuzzy Logic toolboxa); Myeloma cell‐line pharmacodynamics53 (MATLAB ODEfy54)
Differential equations	Temporal ODEs or SDEs	• Continuous temporal dynamics • Random effects, if SDEs	• Potential stiffness • Requires rich kinetic data	NGF signaling pathway and targets16 (MATLAB Simbiologya)
	Spatiotemporal PDEs or SDEs	• Continuous spatial and temporal dynamics • Random effects, if stochastic SDEs	• Computational expense • Spatial information needed	Ocular drug dissolution and distribution55 (ANSYSb)
Cellular automata & agent‐based models	Interaction and evolution rules for collection of “agents”	• Intuitive rules • Spatial and temporal dynamics • Random effects & emergent behaviors	• Computational expense • Spatial information needed • Link to higher level behaviors	TB granuloma & inhaled treatment response56 (C++)

ODEs, ordinary differential equations; PDEs, partial differential equations; QSP, quantitative systems pharmacology; SDEs, stochastic differential equations.

^aMathworks, Natick, MA. ^bANSYS, Canonsburg, PA.

Statistical and data‐driven systems models

For rich measurement sets obtained with multiple perturbations, data‐driven approaches, such as PCA, PLS, discriminant analysis, and Bayesian inference, are not only useful in analyzing data and identifying topology, but also to quantitatively specify the connections. These systems biology approaches are often used in QSP models of gene and protein networks.61, 62 They are also useful in linking clinical biomarkers with outcomes in disease as in the Archimedes Model of clinical outcomes in diabetes and cardiovascular disease.63, 64

Logic‐based models

Logic models are useful when the detailed kinetics of the system are not well‐characterized or less important for the questions at hand, or where the relationships between inputs to a state and the state itself are only qualitatively understood. These approaches use logic rules (“and,” “or,” “not” statements, for example) to relate entities and have been applied especially to models of cell signaling or fate.65 In Boolean or discrete logic, nodes assume one of two or more discrete values; this approach is useful for analyzing system states or state transitions, but does not address continuous dynamics. In fuzzy logic approaches,60 states including time can take on a continuous range of values to enable simulation of continuous behaviors and dynamics. Logic models can also be converted to differential equation models to address dynamics.53

Temporal differential equations

Models based on deterministic ordinary differential equations (ODEs) are common in QSP. The equations simulate continuous time‐course behaviors by explicitly accounting for kinetic processes. However, appropriate parameterization of these models requires rich kinetic understanding or data, or rate parameters must be assigned or tuned based on physiological assumptions. Additionally, explicit inclusion of both comparatively rapid and slow kinetics can lead to numerical stiffness and slower simulation times even with stiff‐solver algorithms. Random effects can be addressed in QSP models with stochastic differential equations (SDEs; e.g., ref. 66). In their simplest form, these can be random or probabilistic effects incorporated into ODEs, although numerous other SDE forms exist.

Spatiotemporal differential equations

Describing continuous spatial effects requires alternate approaches. Partial differential equation (PDE) models address both temporal and spatial dynamics and can be solved using numeric methods, such as finite differences or finite elements. These approaches have been used to investigate pharmacological effects on bone structure and fracture risk7 and fluid dynamic effects on drug distribution in the eye.55 Again, stochastic PDEs can be used to account for random effects.

Agent‐based and cellular automata models

Agent‐based models (ABMs) and cellular automata (CA) capture interactive and emergent behaviors of discrete agents (molecules, cells, virions, and individuals) and address spatial effects in a nondeterministic manner.67 These techniques represent interactions and fates of numerous discrete entities that drive the evolution of the system. The behavior of each agent depends on rules for decision‐making that can include stochastic or statistically driven effects. Spatial effects can be treated continuously or using lattices. Monte Carlo approaches are used for simulation of system evolution, including statistical predictions of variability. Both approaches have been used to study cell or organism interaction and spatial or morphological pattern behavior, especially for tumor growth, immune cell interactions, and infectious agent dynamics.60, 68, 69, 70

Hybrid and integrated models

Models in which different formalisms are integrated are valuable when the requirements for capturing spatial and dynamic behaviors differ among submodules. This is often the case in multiscale models, especially when dealing with spatial heterogeneity. In modeling tumor immunology, Mallet and De Pillis71 superimposed a CA model of cellular interactions with a PDE reaction‐diffusion model of soluble mediator distribution to reproduce different patterns of tumor growth; Kim and Lee72 integrated ABM for tumor dynamics with delay differential equation representation of lymph node dynamics to explore questions related to cancer vaccines. PK models (including physiologically based PK (PBPK) and population PK) can serve as inputs into models of downstream biology (e.g., refs. 60, 73, 74). PBPK approaches can themselves be considered QSP given the mechanistic detail included. The core structure of such a model is generally preserved and extension is typically needed to represent downstream biology and drug effects. QSP models that predict PD biomarkers can also be integrated with statistical models that link these biomarkers to clinical outcomes. The specific combination of approaches must be tailored to the subsystems and questions of interest.

OUTCOMES AND INSIGHTS

The desired outcomes of this stage are:

• Diagram of biology including one or more topologies

• Mathematical formulation of the model

• Results of any topological analyses

• Description of any model‐based insights or changes

In a collaborative setting, an important goal of this stage is to foster understanding, agreement, and buy‐in with collaborators on the technical implementation and assumptions.

Construction of a model can help identify novel biological connections and mechanistic behaviors, including insights such as connections that could result in biphasic kinetics or redundancies and feedback. However, because at this point the model is generally not calibrated or tested, these findings are at best semiquantitative and must be subsequently tested for consistency with parameter ranges and data.

STAGE 4: CAPTURING BEHAVIORS & BUILDING CONFIDENCE: CALIBRATING “REFERENCE” SUBJECTS

To verify that the specified model structure can capture behaviors of interest, it is important to develop initial calibrations for representative scenarios and build confidence in the model “functionality.” After initial specification of reasonable parameter ranges for exploration, model analyses, including parametric sensitivity analysis, dynamical analysis, and model reduction, can be used along with formal parameter estimation to identify “reference” calibrations. The order of these efforts is not critical and they can be conducted iteratively depending on project needs.

Parametric and structural model analysis

Identification of feasible parameter ranges is an initial step in the quantitative exploration and calibration process. This typically involves review of the experimental variability around given data and mechanisms and any physiology‐based insight into feasible ranges.

For a given model structure and associated parameter ranges, different analyses can be used to gain greater understanding of the model prior to or iteratively with calibration and parameter estimation efforts. These analyses also enable correction of structural or parametric limitations of the model in reproducing desired behaviors and outcomes.

Sensitivity analysis

One analysis of 17 models revealed that systems models often include many “sloppy” parameters whose values do not strongly influence the system behaviors of interest.75 Performing a sensitivity analysis (SA) prior to parameter estimation enables the identification of parameters in the model that most influence the outputs and thus require more careful consideration, especially in large models in which simultaneous optimization of all parameters is challenging. Local sensitivity analysis evaluates changes in model outputs in response to parameter variations around a particular point in the parametric space; the results are relevant only in the local space around that point. Local SA is thus most commonly used as a means of evaluating relative importance after model parameters have already been estimated; for example, local SA was used to evaluate the impact of alternate targets in ErbB‐driven PI3K signaling.18 In contrast, global SA methods consider the entire range of the parametric space, giving a composite measure of changes in the output over the space. In addition to identifying key parameters that influence outputs of interest, global SA also reveals whether the desired range of output values is achievable for the specified parametric space or whether model revision is needed. Parameter optimization can also be used for to verify this, but requires optimization for each desired output profile; furthermore, failed optimization might reflect an inadequate optimization approach rather than a model liability. Zhang et al.13 and Marino et al.76 reviewed common global SA methods, highlighting their relative advantages and disadvantages. Zhang et al.13 favored the Sobol SA method, illustrating its application to their model of vascular endothelial growth factor receptor (VEGFR)‐mediated endothelial biology. Sobie77 used an approach in which multivariate regression coefficients for outputs vs. parameters provided global sensitivities of the outputs to the parameters. For the cardiac electrophysiology models used in this work, the regression models were quite accurate despite the nonlinearities in the model.

Dynamical analysis

Based on the model topology and the mathematical formulation, dynamical analysis can be used to evaluate potential system behaviors for specified ranges of parameter values. Although not frequently considered, this is a valuable approach to identify dynamical features of the system, such as the stability of steady states, the existence of bifurcations and alternate steady‐states, hysteresis, oscillations, and instabilities. Dynamical analysis of the multistep mitogen‐activated protein kinase (MAPK) phosphorylation cascade correctly predicted ultrasensitivity of MAPK phosphorylation to stimuli and identified situations in which it can exhibit bistability/hysteresis or oscillatory behavior.78, 79, 80 A list of tools that support dynamical systems analysis is currently available through the Dynamical Systems website (http://www.dynamicalsystems.org/sw/sw/).

Model reduction

Model reduction can improve the efficiency of QSP efforts by simplifying the model without sacrificing its ability to recapitulate specific emergent properties and address the prioritized question(s). Model reduction techniques have been efficiently used in the engineering disciplines81 and can broadly be classified as lumping methods, SA‐based techniques, and time‐scale‐based techniques. In the lumping methods, model components are aggregated or eliminated based on expert supervision or systematic analyses, such as correlation between variables and simplification of mathematical forms to maintain original model behaviors. For example, Schmidt et al.82 developed a method whereby rate expressions repeatedly used in metabolic network models are lumped into a simplified form, reducing the number of model parameters. However, lumped parameters can be difficult to interpret biologically. In SA‐based approaches, subsections of the model that do not influence the outputs of interest are eliminated. Time‐scale‐based approaches are useful if the processes in the model vary over multiple time scales, such that faster processes can be assumed to be quasisteady. Schmidt et al.83 demonstrated a time‐scale‐based model reduction of a published bone metabolism model. Reduction can render models identifiable and eliminate the impact of parameter uncertainty, accelerate simulations, reduce the parameter space for exploration and optimization, reduce combinatorics of parameter or pathway exploration, and focus interpretation and communication of results on the most relevant aspects.

Parameter estimation

Once the parameter space for exploration is specified, parameter estimation is typically used to calibrate the model to data on responses to specified stimuli or conditions and build confidence that the model structure and the parameter space are suitable for describing the data. Initial calibration of simple model subsystems can be performed as a first step, either informally (hand‐tuning) or using parameter estimation. For example, a cell turnover subsystem of a larger disease model can be calibrated to biomarker data on cell numbers and proliferative and apoptotic markers. Subsystem calibration can verify that the structure can capture the relevant data, provide good initial parameter estimates, and make subsequent integrated model calibration more tractable.

Specification of major phenotypes

As a first step, one can define a limited number of representative profiles corresponding to mean results for phenotypes of interest (e.g., different cell lines or clinical disease severities). Different model parameterizations can then be estimated to capture each of these profiles. At this stage, we focus on an initial parameterization for each phenotypic profile, which we term a reference virtual subject (VS). For either underspecified systems or alternate biological hypotheses, alternate reasonable parameterizations and structures must also be explored via alternate VSs. We defer discussion of this process until Stage 5 (Figure 3), although these alternate solutions can be explored in parallel rather than starting with a reference VS.

Figure 3.

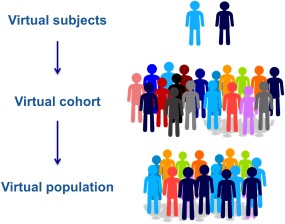
Schematic for use of virtual subjects in quantitative systems pharmacology (QSP) research. Reference subjects are developed to represent major phenotypes of interest (here, responder vs. nonresponder patients to a specified therapy). For each phenotype, starting with the reference subject, numerous alternate virtual subjects are generated to address parametric uncertainty and variability. Finally, a virtual cohort represents the combination of numerous virtual subjects of interest, potentially including prevalence weighting to capture statistical measures of population outcomes to create a virtual population.

The objective function

Parameter estimation involves optimization of model predictions relative to data selected for calibration. This is achieved by minimizing an objective function that quantifies the divergence between simulation results and calibration data. Log or linear normalization of output values between 0 and 1 in the objective function helps ensure equal weighting of each output in the optimization. The objective function can then be represented as a sum of square errors across all the data, or different weightings can be applied to outputs of greater priority. Other metrics, such as time to peak measurement, can also be used in the objective function. Specifying an appropriate objective function is nontrivial and may require iteration. The objective function may also include a component that is utilized for model selection criteria where, essentially, a penalty is imposed for increasing model complexity and/or deviations of parameter values from prior values. Kearns et al.84 and Sébastien85 have reviewed different algorithms utilized for model selection.

Optimization algorithms

Optimization methods can broadly be classified into local and global methods. Local approaches search for minima of the objective function in the vicinity of initial parameter estimates. These methods are recommended when one is confident that the optimal solution is “close” to the initial guess and that the objective function is smooth and convex over the parameter range explored. Global optimization methods search for minima over the entire parameter space. Deterministic global optimization methods guarantee that the global minimum is achieved, but are computationally expensive and might sometimes be unfeasible. In contrast, stochastic global optimization methods can reach the global or near‐global minima and are typically more computationally efficient. Repeated execution of stochastic approaches can yield alternate parameter sets with similar objective function values, which can be considered alternate VSs. In most cases, these algorithms can currently be executed in hours on standard multiprocessor laptops, although parallelization or computer clusters/servers can accelerate the process. Various review articles have discussed optimization methods suitable for QSP models,86, 87, 88 including those listed in Table 3.89, 90 Hybrid approaches that apply global optimization along with deterministic local optimization methods are also frequently used; for example, Rodriguez–Fernandez et al.89 proposed an approach that combines the Scatter Search algorithm with local search methods, applying it to three smaller nonlinear biochemical systems models. Finally, comparison of optimized parameter values to literature‐based prior estimates can provide a useful consistency check with the literature, and a large divergence can suggest a biologically implausible solution. Divergence of optimized parameter values from prior estimates can even be incorporated as a penalty in the objective function, as done by Lu et al.90 in their work on lipid metabolism and kinetics. Many algorithms have been successfully applied in QSP research; the “best” choice and relative performance will depend on the specific application, and modified or new approaches may be required for challenging problems.

Table 3.

Parameter optimization approaches

Optimization approach	Example algorithms	Strengths	Caveats	Example applications
Local	Levenberg–Marquardt	Simplicity, computational efficiency	Local minimum only; requires convex, smooth objective function	Glycolysis pathway model91
Deterministic global	Branch and Bound	Guaranteed global minimum	Computationally expensive	Metabolic systems92
Stochastic global	Simulated Annealing, genetic algorithms, evolutionary programming, evolutionary strategies, particle swarm, scatter search	Computational efficiency; near global minimum	Global minimum not guaranteed	Blood coagulation93; signal transduction94; signaling95
Hybrid	Combinations of the above	Leverages strengths of local and global approaches	Fewer and less widely tested algorithms available	Dynamic biological systems89 and lipid metabolism90

Reference calibration testing and exploration

Reference VSs that capture representative behaviors of phenotypes of interest can be used for initial testing. If simulations recapitulate critical features of data not used for calibration, it increases confidence in the model development. Note that this need not be formal validation, but rather the degree of “testing” judged sufficient to build confidence in the reference VSs as a reasonable starting point for future exploration. Because only a few among many possible VS parameterizations are tested here, close quantitative agreement might be an unrealistically high bar. Instead, critical features of the data to be reproduced should be prespecified, and could include for example: behavior within specified deviation from mean or median data; correct relative ranking of impact of different perturbations; or appropriate parameter/mechanism sensitivity.

Simulation with the reference VSs can also be used for preliminary exploration of questions of interest. However, this should be accompanied with caution as the reference parameterizations may not be the most “biologically relevant” solutions and may provide misleading predictions. Even so, if sensitivity analysis is used to highlight potential uncertainty in the predictions, an initial exploration can support understanding of the subject phenotypes and provide insight into project questions.

OUTCOMES AND INSIGHTS

The following primary outcomes of Stage 4 should be reviewed with all collaborators:

• Output sensitivity to different parameters; identification of associated “sensitive” parameters

• Initial calibration(s) of reference subjects corresponding to major phenotype(s) of interest

• Results of any dynamical analyses

• Reduced model if appropriate

• Successful testing and, as needed, revision of reference subject(s)

The successful completion of this stage builds confidence in the ability of the model to reproduce a multiplicity of critical behaviors using a single biologically reasonable parameterization for each reference VS. Structural changes needed to capture known behaviors can highlight gaps in biological understanding. Results of global sensitivity and dynamical systems analysis can elucidate fundamental system behaviors and factors that govern them. The reference calibrations begin to give quantitative insight into the biology, such as what mechanistic activities are consistent with outcomes and what mechanistic differences could drive different phenotypes. However, quantitative insights are subject to the caveats that reference VSs represent few among many potential parameterizations, and predictions are limited to identification of “possible” outcomes.

STAGE 5. EXPLORING KNOWLEDGE GAPS AND VARIABILITY: ALTERNATE PARAMETERIZATIONS

QSP models can enable hypothesis exploration and prediction in broader contexts than empirical models (i.e., novel targets, combinations, and biomarkers) and with consideration of complex dynamics not usually addressed in other mechanistic PK‐PD models or systems biology models. However, the biological understanding central to these models is often imperfect and underconstrained, such that model structures and parameterizations cannot be uniquely identified. This might in fact reflect the robustness of a biological system, in which behavior must be maintained over a broad range of physiological perturbation and variability. Thus, exploration of variability and knowledge gaps through the use of alternate parameterizations is an extremely important aspect of QSP‐based work. Alternate parameterizations that produce comparable high‐level behaviors under some contexts, may yield different predictions in new contexts, and thus must be considered for robust predictions. Gutenkunst et al.75 proposed that, because of the extent of parameter “sloppiness” in systems models, the focus should not be the uncertainty around individual parameters, but rather the range of possible model predictions. Exploration of knowledge gaps and variability can be used to identify different predictions that result from alternate reasonable model structures and/or parameterizations. This approach outlined to relating variability in predictions to underlying model parameters is very different than data‐driven pharmacometric strategies for identifying causes of variability, in which covariance among parameters is a serious challenge.

Virtual subjects and populations

Here, we refer to each different model instance (structure + parameterization) as an alternate VS, which can correspond to a virtual cell, organ, patient, pathway, or other biological system. As discussed above, a reference VS is a single VS representative of a given phenotype, a virtual cohort is a collection of VSs that match data for the phenotypic population of interest, and a virtual population (Vpop) is a virtual cohort in which each VS's contribution is weighted such that the Vpop reproduces statistical features of the data. These concepts are further described below and in Figure 3.

Virtual subjects

Each VS corresponds to one point in parameter space for a given model structure. For a VS to be “acceptable,” all model outputs for that VS, simulated under the appropriate conditions (e.g., untreated and treated), should be within the limits seen in real world data. A collection of acceptable ranges across all outputs defines VS acceptance criteria. The criteria can include higher‐level properties of the phenotype (e.g., diabetic patient criteria of fasting glucose >126 mg/dL) but would ideally include plausible values of any relevant subsystem or biomarker measures (e.g., hormone concentrations and tissue properties). Monte Carlo based exploration of the parameter space and VS selection against the established acceptance criteria will generate a pool of virtual patients. Gomez–Cabrero et al.96 developed a workflow for generating alternate hypothesis from models with parameter uncertainty: a collection of feasible parameter sets is identified using parameter estimation techniques, and corresponding model predictions are clustered to identify “key” behaviors and the corresponding parameters that produce them.

Virtual cohorts

A collection of VSs forms a virtual cohort. Virtual cohorts are used to predict the possible range of outcomes in simulated experiments. “Inclusion” criteria are highly dependent on the application. For example, for clinical trial simulation, the criteria could be the inclusion/exclusion criteria of the corresponding clinical study, and/or behavior within the variability of results from previous trials.

Virtual population

When statistical data are available on variability in the real‐world measurements relating to model outcomes (e.g., tumor cell/mass growth, disease activity, and biomarker correlations), Vpops can be used to refine predictions associated with a virtual cohort. We define a Vpop as a collection (cohort) of VSs that are selected or weighted to reproduce statistical features of experimental measurements. In a Vpop, individual VSs are assigned weights corresponding to their relative contribution to the population measurements and statistics. These statistical (or “prevalence”) weights reflect the potential probability of occurrence of each VS in the corresponding real‐world studies. A binary 0 vs. 1 weighting can be used to “select” VSs that together constitute a Vpop with the desired statistical features.17 More complex schemes that try to maximize the mechanistic or parametric diversity of the Vpop have also been used.97 Once developed, Vpops can be used for predictions of means and ranges of responses to interventions of interest (discussed below) and to analyze correlations among parameters and variables.

Qualification and predictive capability

Qualification and testing of QSP models is fundamentally different than validation and testing of PK‐PD, pharmacometric, and statistical models, as discussed by Agoram.41 The biological understanding central to QSP models is often imperfect and underconstrained. Modeling can reduce or highlight critical unknowns, but predictions are still subject to uncertainty. Thus, prior discussions of QSP qualification10, 41 have focused on ensuring that the model addresses uncertainties in the critical biology and that simulation results are consistent with (but not necessarily predictive of) specified data. Even so, it is valuable to test the predictive capability of a QSP model to set expectations for and enable interpretation of prospective predictions.

Once VSs have been developed to capture relevant data, the model predictive performance is tested by assessing agreement between simulated predictions and selects experimental or clinical outcomes data reserved for this effort. Admittedly, reserving data for predictive verification in an underconstrained setting in which data are already insufficient can be challenging, and this step is sometimes omitted. However, when reserving valuable data is problematic, even limited verification is useful. For example, Gadkar et al.17 used data from a single dose monotherapy arm of a trial for calibration and multidose monotherapy and combination therapy data from the same trial for prediction.

As VSs represent a range of hypotheses and parameterizations, only some of which might prove valid, only a subset of VSs might match the testing criteria. VSs with unrealistic or inconsistent behaviors can then be eliminated from the population. If few (or no) VSs generate predictions consistent with test data, iterative generation and testing of VSs, possibly including model revision, should be performed. Regardless, interpretation of model predictions depends on the robustness and extent of predictive verification.

Finally, unlike the case with empirical PK‐PD models, mismatches between data and QSP‐based predictions can offer valuable insight by highlighting inconsistencies between biological hypotheses and real‐world observations: What behaviors do not fit our mechanistic understanding? Are specific qualitative or quantitative hypotheses invalidated? What new hypotheses could resolve the mismatch? Thus, mismatches are not solely an issue with the model, but can reflect the state of understanding in the field.

Predictive simulation

A virtual cohort or Vpop whose behavior has been verified against appropriate data can be used to make predictions relevant to project questions. For an unweighted virtual cohort, the variability in predictions offers a range of possible quantitative outcomes. These results can also be used to assess relationships between biomarkers or parameters and responses or phenotypes, for example by hierarchical clustering. A weighted Vpop can provide statistical predictions, such as mean outcomes, variability, and correlations. The more data used in the weighting, the more confidence one can have in the statistical aspects of the predictions. Robustness of predictions, however, is dependent on the robustness of the total set of data (quantity, quality, and nature) used to develop and constrain the model and the VSs. Thus, the degree of confidence in predictions must be carefully assessed and communicated on a case‐by‐case basis.

OUTCOMES AND INSIGHTS

The outcomes of this stage are the final QSP‐based findings on questions identified in scoping before any expansion or revision of the model, for example as new data emerge, and include:

• Robust quantitative simulation‐based predictions and understanding

• Influence of variability or uncertainty on predictions and the responsible parameters/biology

• Explanation of how the results follow from biological understanding and data

The final point, in particular, is invaluable for collaborator understanding and acceptance and should be the focus of discussions and recommendations. However, as every stage of the workflow helps support acceptance and interpretation of the final predictions, clear communication of the workflow and results along the way are also important to the ultimate project success. For less technical interactions or for senior managers in industry, concise description of the biological mechanisms leading to the prediction, any uncertainties/risks in the predictions, and the modeling‐guided recommendation or decision promote adoption.

STAGE 6. SUPPORTING EXPERIMENTAL AND CLINICAL DESIGN: REFINING KNOWLEDGE

In addition to directly providing insight into the originally defined project questions and goals, model‐based understanding can be used to guide collection of important data to enhance biological understanding or to verify “testable” predictions.

Data gaps and sensitivities identified throughout the workflow can be used to propose critical experiments or measurements that will clarify important biology of the system. The identification and prioritization of data and knowledge gaps highlight what experiments are needed or what biomarkers should be measured. Experimentalists and modelers can then collaborate to propose preclinical experiments or clinical trial design to resolve these uncertainties. In some cases, model results are predicated on or lead to testable hypotheses and predictions, and subsequent experiments can be used to verify these and guide revision of the model and the related biological understanding.

Experiments can also be designed to improve parameter estimation or for model discrimination. Optimal experiment design, including selection of species to measure, timing of measurement, and choice of perturbations, is based on maximizing the information content contained in the Fisher Information Matrix. Iterative modeling and experimental approaches have also been described.98, 99, 100

OUTCOMES AND INSIGHTS

The primary outcomes of this stage of the workflow are:

• Recommended experiments and experimental design to support refinement of understanding and predictions

• Refinement of previous predictions based on incorporation of the experimental results into the model

The efforts in this stage provide insight into missing information in the field and support efficient experiment design. Results of model‐informed experiments can be used to constrain parameters and test alternate hypotheses. Once these results are incorporated into the model, updated simulations can be performed to refine predictions made in the previous stage(s) of the workflow.

Of course, the exploration of one set of questions invariably leads to new ones. As such, the workflow is not linear but cyclic, allowing for continued refinement or expansion of QSP models based on emerging experimental or clinical data and new questions and goals.

SUMMARY

We have presented a staged workflow for the application of QSP. Notably, this workflow helps address several questions and criticisms commonly facing QSP projects, as outlined in Table 4. By providing a common, organized strategy along with guidance on technical approaches to address these and other considerations, we believe this workflow and subsequent evolution thereof can offer a useful framework for the execution, communication, and acceptance of QSP endeavors.

Table 4.

Approaches to answering frequently asked questions in QSP

Frequently asked questions/criticisms and responses
How can you build a model of biology we do not quite understand? What about competing hypotheses? Conflicting data? The model is an integrated, quantitative formalization of our current understanding of the biology and data. It allows evaluation of the hypothesized biology, including competing hypotheses and data, which can be implemented via alternate structures and parameterizations. The model can be used to identify inconsistencies between hypotheses and data to support evaluation of the hypotheses and even propose new hypotheses.
With enough parameters you can fit an elephant. The model is underspecified and the parameters are not identifiable. The first assertion is not true, because the model structure is not empirical but based on biological mechanism. Thus, the ability to “fit” the data is not guaranteed, regardless of the numbers of parameters. QSP models often contain many so‐called “sloppy” parameters, which do not influence behaviors of interest. Sensitivity analysis identifies influential parameters to vary in alternate parameterizations. Numerous alternate parameterizations consistent with the data are explored. Model reduction can be used to make parameters identifiable if needed.
How do we evaluate and interpret this work? To what extent should we trust the predictions?
• Interpretation of results is based on the following criteria (corresponding to the workflow stages): Application to questions for which it is qualified Quantity/quality of biological knowledge and data Reasonable representation of the biology Consistency with all relevant behaviors Adequate exploration of variability and uncertainty and testing of predictive capability Articulation of important data gaps for experimental evaluation, and proposal/verification of “testable” hypotheses The robustness of the predictions depends on the extent of exploration of the above
The models are too complex to explain to collaborators. Regular discussion with collaborators and advisors promotes shared understanding and ownership of the model Emphasis on the biological explanation/justification of decisions and findings fosters acceptance and adoption
Model predictions were wrong. Therefore the model is not useful. Incorrect predictions can offer valuable insight by identifying inadequacies in the understanding of the biology, as formalized in the model. Proposing mechanisms that could resolve the mismatches provides novel biological hypotheses and highlights areas for further experimental exploration to advance the understanding in the field.

QSP, quantitative systems pharmacology.

Conflict of Interest

The authors declared no conflict of interest.

Supporting information

Supporting Information