Automatic Craniomaxillofacial Landmark Digitization via Segmentation-guided Partially-joint Regression Forest Model and Multi-scale Statistical Features

Abstract

Objective

The goal of this paper is to automatically digitize craniomaxillofacial (CMF) landmarks efficiently and accurately from cone-beam computed tomography (CBCT) images, by addressing the challenge caused by large morphological variations across patients and image artifacts of CBCT images.

Methods

We propose a Segmentation-guided Partially-joint Regression Forest (S-PRF) model to automatically digitize CMF landmarks. In this model, a regression voting strategy is first adopted to localize each landmark by aggregating evidences from context locations, thus potentially relieving the problem caused by image artifacts near the landmark. Second, CBCT image segmentation is utilized to remove uninformative voxels caused by morphological variations across patients. Third, a partially-joint model is further proposed to separately localize landmarks based on the coherence of landmark positions to improve the digitization reliability. In addition, we propose a fast vector quantization (VQ) method to extract high-level multi-scale statistical features to describe a voxel's appearance, which has low dimensionality, high efficiency, and is also invariant to the local inhomogeneity caused by artifacts.

Results

Mean digitization errors for 15 landmarks, in comparison to the ground truth, are all less than 2mm.

Conclusion

Our model has addressed challenges of both inter-patient morphological variations and imaging artifacts. Experiments on a CBCT dataset show that our approach achieves clinically acceptable accuracy for landmark digitalization.

Significance

Our automatic landmark digitization method can be used clinically to reduce the labor cost and also improve digitalization consistency.

I. Introduction

Craniomaxillofacial (CMF) deformities involve congenital and acquired deformities of the head and face. It is estimated that 16.8 million Americans require surgical or orthodontic treatment to correct the deformities [1]. Jaw deformity is the most common type in CMF deformities, and orthognathic surgery is the procedure to correct the jaw deformity. Jaw deformity can mainly be classified into three types: Class I (normal relationship between the upper and lower jaws), Class II (lower jaw retrusion, upper jaw protrusion, or the combination), and Class III (lower jaw protrusion, upper jaw retrusion, or the combination).

During the diagnosis and treatment planning of jaw deformities, a multi-slice computed tomography (MSCT) or a cone-beam CT (CBCT) scan is often acquired, and the bones are segmented, in order to reconstruct three-dimensional (3D) models of CMF structures. Since CBCT has significant advantages of low radiation dosage and cost in comparison to the MSCT and is also readily available in most physician's offices, CBCTs are more often used. The deformities are then quantified on the 3D skull models by 1) placing a set of anatomical landmarks (called: digitized) onto the 3D models and 2) subsequently performing quantitative measurements (called: cephalometry).

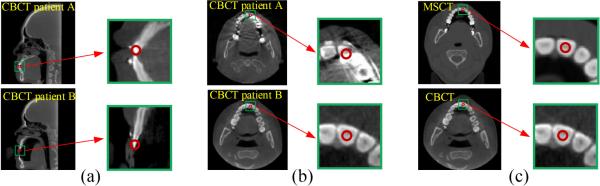
Accurate landmark digitization is a critical step in the jaw deformity quantification. In our current routine clinical practice, all anatomical CMF landmarks are manually digitized on the 3D models. However, this is a time-consuming process. In addition, inter- and intra-examiner reliability and repeatability of manual landmark digitization are also limited. To date, there is no effective method available that allows automatic landmark digitization for clinical purpose due to two major challenges. The first challenge is related to the morphological variations among different patients, which causes significant appearance variations of anatomical landmarks across patients. As shown in Fig. 1 (a), local morphological appearance around the same tooth landmark can be significantly different across patients A and B. The second challenge is related to the image artifacts of CBCT that are caused by amalgam dental fillings, orthodontic wires, bands and braces. For example, the top image in Fig. 1 (b) shows the streak artifacts on the CBCT image of patient A. They are caused by orthodontic braces, which deteriorate CBCT image quality and result in inconsistent local appearances of teeth landmarks across patients. The bottom image in Fig. 1 (b) shows a regular CBCT image of patient B without such artifacts.

Fig. 1.

Inconsistent appearances of anatomical landmarks across different patients caused by (a) CMF deformity, and (b) metal effect. (c) Similar appearances in both MSCT and CBCT images.

A number of research works have been reported on localizing landmarks or anatomical structures in medical applications. To summarize, there are three mainstreams: 1) Interest point detection [2], [3], 2) Atlas-based landmark detection [4], [5], [6], [7], and 3) Machine-learning-based landmark detection.

Among of them, machine-learning-based methods have become more and more popular in landmark localization. Previous learning-based works focus on using voxel-wise classification to localize anatomical landmarks. Here, the localization is formulated as a binary classification problem, where the voxels near the landmark are regarded as positives and the rest as negatives. Then, a classifier is typically trained to distinguish landmark voxels from others. For example, Zhan et al. [8] detected anatomical landmarks of multiple organs via confidence maximizing sequential scheduling. Criminisi et al. [9] used a classification forest to automatically localize the bounding boxes of multiple organs in CT images. Cheng et al. [10] used random forest classifier to localize a dent-landmark. Zhan et al. [11] used cascade Ada-boost classifier for MR knee landmark detection. As classification-based methods rely on only the local appearance for landmark localization, their performances are jeopardized if landmark appearances are inconsistent across patients, such as the teeth landmarks shown in Fig. 1 (a-b).

On the other hand, regression-based methods are another type of machine-learning-based methods in landmark localization. Different from the classification-based methods, regression-based methods aim to learn a mapping from a voxel's appearance to its 3D displacement towards a landmark. When provided with a testing image, the 3D displacement from every voxel to the target landmark can be estimated with the learned mapping. Hence, every voxel can cast one vote to the potential landmark position, pointed by the estimated displacement. By aggregating all votes, the landmark position can be localized at the voxel that receives the maximum votes. The regression-based methods can potentially overcome the limitations of classification-based methods by borrowing the context information from nearby voxels with consistent local appearances. Recently, regression-forest-based methods have demonstrated their superiority in different related computer vision and medical tasks [12], [13], [14], [15], [16], [17]. For example, Criminisi et al. [12] proposed to use regression forest to estimate the 3D displacement from each voxel to the bounding box of target organ. Their experimental results demonstrate that regression-based methods are more accurate than classification-based methods in bounding box detection. With the similar regression voting idea, Cootes et al. [13] extends Criminisi et al. [12] for facial landmark localization. To further enforce spatial consistency of localized landmarks, Gao et al. [17] proposed a two-layer context-aware regression forest for prostate landmark detection. The problem in these methods is that they treat the vote from every voxel equally. As a result, the final localization result can be impacted by noisy votes from informative votes. To address this issue, Donner et al. [18] proposed to use classifier to pre-filter the voting voxels, by allowing only the voxels nearby the landmark to vote. Besides using regression forest for estimating the displacement to the target landmark, Chen et al. [19], [20] developed a data-driven method to jointly estimate displacements from all patches to landmarks together, thus achieving remarkable accuracy on X-ray landmark detection and also intervertebral discs localization from MR Images.

The limitations of most existing regression-based methods come from two folds: 1) They did not consider effects of uninformative voxels caused by morphological changes across patients. For example, voxels beneath the tooth landmark of Fig. 1 (a) are uninformative in terms of the precise localization of this landmark due to morphological variations caused by CMF deformities, even though they are close. 2) They did not consider the spatial incoherence among landmarks, and thus simply just jointly detected all landmarks together. Actually, the relative position of one landmark to other landmarks may dramatically change due to morphological changes. Fully-joint detection may be an over-strong spatial constraint for certain applications, since the relative positions of landmarks may be incoherent.

In this paper, to address these two limitations and correctly use semantics among landmarks, we present a Segmentation-guided Partially-joint Regression Forest (S-PRF) model for automatic landmark digitization in CBCT images. First, CBCT segmentation is utilized to remove uninformative voxels. Second, a partially-joint model is further proposed to separately localize landmarks, based on the coherence of related landmark positions, to improve the digitization reliability. In addition, we propose a fast vector quantization (VQ) method to extract high-level multi-scale statistical features with high efficiency and low dimensionality. The features are invariant to local inhomogeneity, which can also relieve the problem caused by image artifacts. Moreover, we enhance the performance by including MSCT scans into the training dataset, since MSCT shares many similar local patch appearances with CBCT as shown in Fig. 1 (c), thus helpful to improve the digitization performance. All proposed methods have been validated, with the results presented in the experimental section. Finally, although our approach is mainly developed for CBCT, it can also be applied to MSCT, using the data-driven property of our method.

Our paper is organized as follows. Section II details the proposed S-SRF method for CMF landmark digitization and the proposed fast VQ method for feature extraction. In Section III, we first evaluate our method on CBCT dataset and then conduct experiments to analyze each component of our method. Finally, a conclusion is presented in Section IV.

II. Method: Segmentation-guided Partially-joint Regression Forest (S-PRF) Model

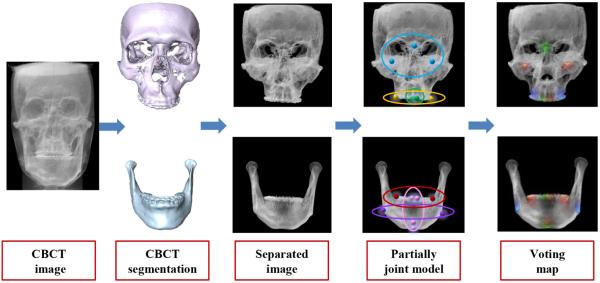
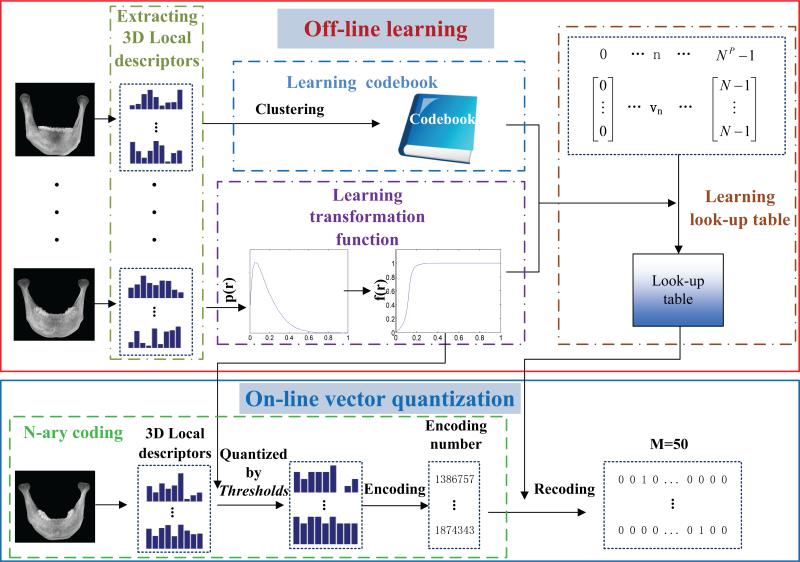
In this section, we propose an S-PRF model for automatic landmark digitization in CBCT images. Fig. 2 shows the flowchart of our method, which consists of three steps: 1) using an automatic 3D segmentation method to separate mandible from maxilla, which obtains two segmentation masks; 2) utilizing the obtained 3D segmented maxilla and mandible to mask the respective regions in CBCT image; and 3) detecting landmarks on mandible and maxilla separately by our partially-joint random forest model on the respective masked CBCT images.

Fig. 2.

Flow chart of proposed landmark digitization method.

A. Segmentation-guided strategy

As stated above, one limitation of the traditional regression-forest-based methods is the failure to consider the voting confidence of each voxel and to equally treat their votes in landmark digitalization. Since different voxels have different voting confidences, it is reasonable to associate voting weight for each voxel. To address this issue, we consider two types of uninformative voxels, as detailed below.

The first type of uninformative voxels is the faraway voxels. An intuitive way to consider those voxels is to assign large voting weights only for the voxels near the landmark, while assigning small voting weights for the faraway voxels since they are not informative to precise landmark location. In this paper, we use $w=e^{-\frac{\Vert \tilde{\mathbf{d}}\Vert }{\alpha }}$ to define the voting weight of a voxel, where d̃ is the estimated 3D displacement from this voxel to the target landmark, and α is a scaling coefficient.

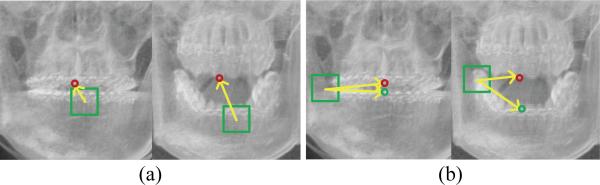
The second type of uninformative voxels is the voxels with ambiguous displacements. For example, voxels in mandible often have consistent 3D displacements to the lower teeth landmarks, but can also have ambiguous 3D displacements to the upper teeth landmarks. Fig. 3 (a) gives one typical example, where the left patient can closely bite their teeth, while the right patient cannot because of CMF deformities. This difference between the two patients makes the votes from the voxels in the lower teeth region unreliable for localizing the positions of upper teeth landmarks. However, with the distance-based voting weight designed above, it is impossible to filter out uninformative voxels caused by this inter-patient morphological variations.

Fig. 3.

Problems for the regression-forest-based landmark digitization. (a) Uninformative voxel in the mandible for localizing a landmark on upper tooth. (b) Incoherent displacements to the two same landmarks from two different patients.

In our specific application, we found that the voxels from mandible are informative for the landmarks from maxilla, and vice versa. Therefore, image segmentation, a process of partitioning an original image into multiple sets of voxels, is performed and used as guidance to remove those uninformative voxels. As shown in Fig. 2, the original CBCT image is first segmented into mandible and maxilla using a robust and accurate segmentation method [21], [22], [23]. Specifically, deformable registration method is first used to warp all atlases to the current testing image. Then, a sparse representation based label propagation strategy is employed to estimate a patient-specific atlas from all aligned atlases. Finally, the patient-specific atlas is integrated into a Bayesian framework for accurate segmentation. By using the segmented mandible and maxilla as masks, we can separate mandible from maxilla in the original CBCT image. Hence, landmarks on mandible and maxilla can now be separately digitized using the regression forest models trained on the respective masked CBCT images. In this way, those uninformative voxels, caused by inter-patient morphological variations, can be removed in the landmark digitalization.

B. Partially-joint strategy

A fully-joint model simultaneously predicts the 3D displacements of a voxel to multiple landmarks, based on the local appearance of this voxel. It assumes that similar local appearance corresponds to coherent displacements to multiple landmarks. Actually, this is not the case. For example, for voxels with similar local appearances across different patients, their 3D displacements to all landmarks could be dramatically incoherent. Those incoherent displacements make the above assumption invalid, which brings ambiguity to the training of the conventional regression forest. For example, Fig. 3 (b) shows CBCT images of two patients, where the displacements to lower and upper teeth landmarks are not coherent. Since regression forest predicts the 3D displacements solely based on the local appearance features, the ambiguous 3D displacements, associated with voxels of same appearance, can mislead the training procedure, which could decrease the accuracy of landmark digitization.

To address this issue, we exploit the coherence of related landmarks and separately detect them with the partially-joint regression forest models. Specifically, we propose a simple but effective way to divide all CMF landmarks into several groups based on their spatial coherence. Afterwards, landmarks within the same group can be jointly detected without the issue of displacement ambiguity suffered by fully-joint model.

Landmark partition with spatial coherence

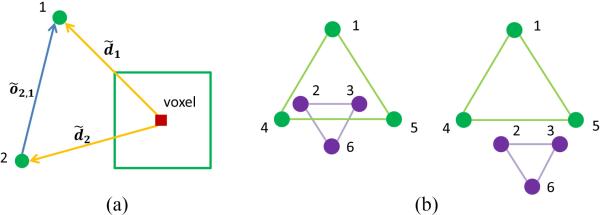
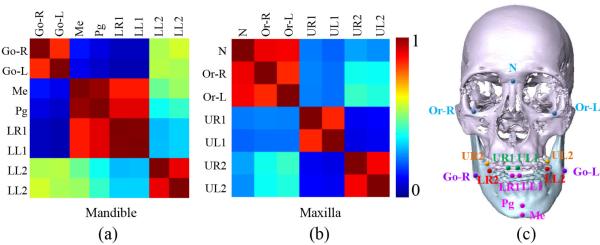
The global spatial structure formed by all landmarks is not stable, but its sub-structures could be spatially stable. Fig. 4 (b) provides a schematic illustration. In this paper, we intend to exploit those stable sub-structures and then jointly digitize landmarks within the same sub-structure, instead of jointly digitizing all landmarks together. Here, affinity propagation [24] is used to cluster all landmarks into several groups with spatial coherence.

Fig. 4.

Schematic view of coherence of landmarks and multi-scale 3D patches for one voxel. (a) Definition of offset. (b) Stable substructures, where the substructure of Landmarks 1, 4, 5 and the substructure of landmarks 2, 3, 6 are relatively stable across different patients.

To construct the affinity matrix A, the pair-wise similarity between two landmarks is defined based on the variance of vector distances between two landmarks across patients. The variance of inter-landmark distance across patients is defined below:

$$v_{i,j}=\frac{1}{3}\sum _{s=1}^S{\Vert {\tilde{o}}_{i,j}^s-\frac{1}{S}\sum _{a=1}^S{\tilde{o}}_{i,j}^a\Vert }_2^2$$ (1)

where õ_i,j is the 3D offset from landmark i to landmark j and S is the total number of patients. As shown in Fig. 4 (a), õ_i,j = d̃_i − d̃_j, where d̃_i and d̃_j are 3D displacements from a specific voxel to landmarks i and j, respectively. Clearly, the coherence of displacements from one specific voxel to two landmarks could be measured by the offset between two landmarks (note here, we use offset to define the vector distance between landmarks to avoid the confusion with 3D displacement from voxel to landmark).

Therefore, the pair-wise similarity is defined below:

$$a_{i,j}=e^{-\frac{v_{i,j}}{Mean\left(v_{i,j}\right)}},$$ (2)

where Mean(v_i,j) is the mean value of all pair-wise similarity between landmarks. Finally, the affinity matrix A can be defined below:

$$\mathbf{A}=\left[\begin{array}{ccc}\hfill a_{1,1}\hfill & \hfill \cdots \hfill & \hfill a_{1,L}\hfill \\ \hfill ⋮\hfill & \hfill \ddots \hfill & \hfill ⋮\hfill \\ \hfill a_{L,1}\hfill & \hfill \cdots \hfill & \hfill a_{L,L}\hfill \end{array}\right],$$ (3)

where L is the total number of landmarks.

By using the affinity propagation [24], all landmarks can be partitioned into different groups. For example, Fig. 8 (e) shows the landmark partition results in our experiment. A fully-joint regression forest model will be then learned for each group. All these fully-joint regression forest models build up our partially-joint regression forest model. With this approach, the ambiguous displacement problem caused by morphological variations can be largely alleviated. In our application, all landmarks are first separated into two groups: 1) Maxilla landmarks and 2) Mandible landmarks. Then, each group of landmarks is further partitioned based on the spatial coherence with the affinity propagation technique as discussed above. In the following, we will detail on how to train the fully-joint regression forest model for each group.

Fig. 8.

Landmark partition based on the landmark coherence. (a-b) Affinity matrices of landmarks from mandible and maxilla. (c) Partition result of landmarks. Note that the landmarks in the same group are shown in the same color.

C. Regression forest model

In the training stage, for each landmark group, a multi-target regression forest is trained to learn a nonlinear mapping between a voxel's local appearance and its 3D displacements to all target landmarks in that group. Generally, the local appearance can be described by the appearance features such as Haar-like features [25], scale invariant feature transform (SIFT) features [26], histogram of oriented gradient (HOG) features [27], and local binary pattern (LBP) features [28]. However, in this application, the low-level features can be easily affected by the local inhomogeneity caused by artifacts. Therefore, we propose to use high-level multi-scale statistical features, which show better robustness to local inhomogeneity and image artifacts than Haar-like features in our experiment.

In the testing stage, the learned regression forest can be used to estimate 3D displacements from every voxel in the image to the potential positions of landmarks, based on local appearance features extracted from each voxel. Using the estimated 3D displacements, each voxel can cast one vote to the potential positions of landmarks. By aggregating all votes from all voxels, a voting map can then be obtained (Fig. 2), from which the positions of these landmarks can be easily identified as the location with the maximum vote. By voting the positions from context locations, the regression-forest-based methods are able to improve the robustness of landmark digitization in case that the local appearances of landmarks are indistinct, which usually happens in the presence of artifacts in CBCT image as shown in Fig. 1 (b). In the following, we will detail on how to effectively and efficiently extract features during the training and testing stage.

D. Feature extraction

Features are important in training a robust and accurate regression forest model. A good set of features should include: 1) Low feature dimensionality and high extraction efficiency. This is because large 3D image size not only challenges the efficiency of feature extraction, but also requires massive sampling voxels to build accurate regression forest model, which limits feature dimensionality. 2) Good discriminative ability. That is, features should also be discriminative enough to clearly separate different anatomical regions.

To fulfill these requirements, we propose high-level multi-scale statistical features for landmark digitization, instead of using the traditional low-level features. The proposed features possess low dimensionality, high efficiency, and good discriminative ability simultaneously. Specifically, a voxel's local appearance is first described by low-level local descriptors. Then, the coding strategy is conducted to encode local descriptors, therein, we propose a fast vector quantization (VQ) method to code local descriptors with high efficiency. Finally, the statistical histogram of the encoded local descriptors, within a patch centered in the target voxel, is used as the feature vector to describe the local appearance of the target voxel. Fig. 5 shows the entire flowchart of our feature extraction based on fast VQ method. In the following, we describe each step of feature extraction in detail.

Fig. 5.

Diagram of our fast VQ for the feature extraction.

1) Local descriptor

A voxel's appearance is first described by a low-level local descriptor, called oriented energies [29]. Specifically, the local descriptor of each voxel is obtained by using a set of oriented second derivatives of Gaussian-like filters. The steerable filters are x-y-z separable, and can be rotated to any arbitrary orientations through linear combination of basis filters, which helps to obtain filter responses with a very high efficiency [30]. To make local descriptors more robust to intensity variations, a series of rectifications including filtering, nonlinearity, smoothing and normalization are conducted. For feature extraction in this paper, we focus on speeding up the encoding efficiency of codebook, thus we simply use oriented energies as low-level local descriptors. Other low-level discriminative descriptors may also be used for our purpose.

2) Fast vector quantization (VQ)

The general traditional codebook-based VQ has three steps. 1) Codebook construction. All local descriptors in the training set are clustered to form a codebook, where each element in the codebook is a clustering center. 2) Local descriptor encoding. Each local descriptor could be encoded into a binary vector with the codebook, where an entry is 1 if the corresponding element in the codebook is the nearest neighbor to the given local descriptor, and otherwise 0. Generally, the computational cost of finding nearest neighbors in the codebook is high. Although many published works can be used to accelerate this step [31], [32], [33], [34], [35], [36], [37], the speed of encoding step is still limited, due to the inevitable calculations of Euclidean distances between local descriptors and elements in the codebook. Since a 3D medical image often consists of millions of voxels, the efficiency related issue of the conventional encoding step becomes a bottleneck when applied to feature extraction in medical images.

In order to enhance the efficiency of VQ, we propose a fast VQ method based on codebook. The idea is motivated by the N-ray coding strategy [29]. Specifically, we pre-partition the vector space of local descriptors by N-ray codes, and then construct a look-up table from N-ray code to codebook-based binary code (off-line). In order to attain the code of a new descriptor, we first encode it into N-ray codes and then convert it to codebook-based binary code with the look-up table. As a result, local descriptors can be efficiently encoded into codebook-based binary codes, without having to calculate Euclidean distances between elements in the codebook and local descriptors. Our fast VQ method is detailed in the following steps.

N-ray coding [29]

During N-ray coding, each entry of local descriptor is first quantized into N states. Then, the state indexes of entries are converted into a decimal number by N-ray coding to form the code. Generally, the distribution of local descriptor entries is not uniform, making it unreasonable to quantize them into N states uniformly. Therefore, we need to learn N − 1 quantization thresholds to ensure that the quantized local descriptors are distinct and preserve enough information. When the appearing frequencies of N states (for all the local descriptor after thresholding) are roughly equal to each other, the N states could be fully used. Therefore, based on the theory of histogram specification [38], the distribution of local descriptor entries can be transformed into a uniform distribution by a monotonous transformation function f(·) which is defined as follows.

Let r denote the possible values of entries in the vector of the local descriptor (with the range of r in [0, 1), after normalization). The transformation function f(r) is defined as:

$$f\left(r\right)={\int }_0^{r}p\left(\omega \right)d\omega ,$$ (4)

where p(ω) is the PDF of ω. It should be noted that when the argument for f(·) is a vector, the function acts on each entry of the vector.

Accordingly, N − 1 self-adaptive thresholds are learned as:

$$T=\{f^{-1}\left(\frac{1}{N}\right),f^{-1}\left(\frac{2}{N}\right),\dots ,f^{-1}\left(\frac{N-1}{N}\right)\}.$$ (5)

Hence, the entries of each local descriptor could be quantized to N states by T. Then, the state indexes of entries replace the original entries and we denote the quantized local descriptor as v′, thus the N-ray coding number is:

$$n={\mathbf{v}}^{\prime }\cdot {\mathbf{w}}^{\mathbf{T}},$$ (6)

where w = [N^P−1, . . . , N⁰] is the weighting vector to transform v′ to a decimal number, and P is the dimensionality of local descriptor.

Learning a look-up table

First, K-means clustering is used to aggregate local descriptors to construct a codebook C = {c₁, . . . , c_i, . . . , c_M}, where c_i is the i-th clustering center, and M is the total number of clustering centers. Then, we construct a look-up table off-line for converting N-ary code to codebook-based binary code. Let's denote v_n, n = 0, . . . , N^P − 1} be the entire set of N-ary code vectors for local descriptor. The look-up table can be constructed with the following equations:

$$R\left(n\right)=\underset{i\in \{1,\dots ,M\}}{\mathrm{argmin}}{\Vert {\mathbf{v}}_n-Nf\left({\mathbf{c}}_i\right)\Vert }_2^2.$$ (7)

We perform f(·) on codebook to make the codebook and N-ary vector lie in the same manifold. With equation (7), each N-ary code n ∈ {N⁰, . . . ,N^P − 1} can be associated with a codebook-based binary code where R(n)-th entry is 1, and otherwise 0.

Encoding a new local descriptor

Given a new local descriptor, we first encode it into N-ary code [29], which is then converted into codebook-based binary code with the look-up table. Since the look-up time is instant, the efficiency of our VQ method is the same as N-ary code.

3) Statistical histogram

For a target voxel, we compute codebook-based binary codes for all neighboring voxels within its local patch. Then, a statistical histogram within that local patch is built for all binary codes (summation of all the binary codes) and used as final feature representation for this voxel.

Since local appearances are repeatable in 3D medical images, we adopt multi-scale feature representations to further increase the feature discrimination by capturing both coarse and fine structural information. In this paper, we use different sizes of Gaussian kernels to compute local descriptors. For each Gaussian kernel local descriptor, we select specific patch size to calculate its statistical histogram. The final feature representation is the concatenated histograms from all scales.

It should be emphasized that the step of learning the lookup table is an off-line operation and is calculated only once for each training dataset, thus not affecting the on-line landmark digitalization. The features of the proposed fast VQ can be described from two different points of view. First, compared with the codebook-based approach, our method has a much higher efficiency, as our method can avoid the computationally expensive step of searching for the nearest neighbor in the codebook. Second, compared with the N-ary coding, our method obtains much lower feature dimensionality. It could also be treated as one step of dimensionality reduction idea for N-ary coding. In other words, our method bridges the approaches of codebook and N-ary coding. In the following paragraphs, we provide more analysis on computational cost, and representation dimensionality.

Computational cost of the VQ

As for this part, we compare the computational cost of the proposed fast VQ with the methods of codebook and N-ary coding. The learning of codebook and look-up table are done once, and also as an off-line step, thus their computational cost is not important for the final application. The computational cost is summarized in Table I. C1 is the computation complexity in theory, where X × Y × Z are the image size, P is the dimensionality of local descriptor for each voxel, and M is the total number of elements in the codebook. C2 is the runtime of quantizing all voxels in an image with size of 256×256×256 using Matlab software. The computer used is with a processor Intel(R) Core(TM)2 i7-4700HQ 2.40GHz. The dimensionality of our local descriptor is 9, and M = 50. From Table I, we can see that the efficiency of our method is almost the same as N-ary coding, but much faster than codebook.

TABLE I.

Comparison of computational cost among codebook, N-nary coding, and our proposed method.

	N-ary coding	Codebook	Proposed method
C1	O(XYZP)	O(XYZMP)	O(XYZP)
C2	1.54s	47.43s	1.56s

Dimensionality of features

For statistical representation, the number of elements in the codebook determines the representation dimensionality. Table II shows the quantized results of different methods (single scale). D1 shows the theoretical values of these methods, and D2 shows a real dimensionality when N = 3, P = 9 and M = 50. We can see that the dimensionality of our fast VQ is much lower than that of N-ary coding. For N-ary coding, due to the dimensionality problem, both N and P should be relatively small numbers, which restricts the application of N-ary coding to our interested problem.

TABLE II.

Dimensionality of the representation for codebook, N-ary coding, and our proposed method.

	N-ary coding	Codebook	Proposed method
D1	NP	M	M
D2	19683	50	50

III. Experiments

A. Data description

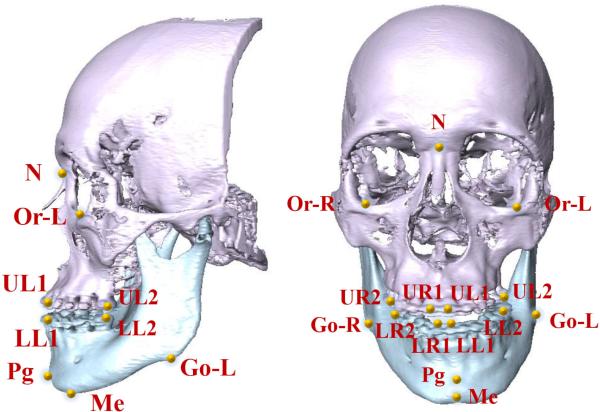
41 CBCTs (0.4×0.4×0.4mm³) from 41 patients with non-syndromic dentofacial deformity were used (IRB# IRB0413-0045) in our experiments. Twenty patients were Class II jaw deformity while 21 patients were Class III. In addition, 30 MSCTs (0.488×0.488×1.25mm³) of normal subject (Class I) were used as additional training dataset. To validate our landmark digitalization method, we used 15 anatomical landmarks most relevant to clinical practice. They were manually digitized by an experienced CMF surgeons serving as ground-truth landmarks (Fig. 6).

Fig. 6.

CMF landmarks annotated on a 3D skull model.

B. Parameters optimization

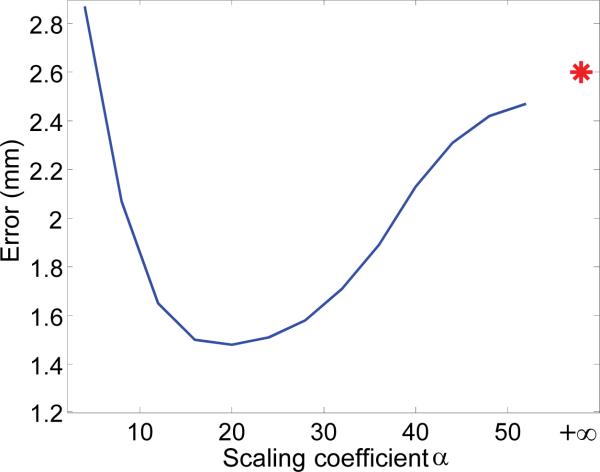
The parameters in this paper were determined based on 30 MSCT subjects via leave-one-out cross validation. Specifically, at each leave-one-out case, we used 29 MSCTs for training, and validated the performance on the remaining one MSCT. By averaging the performance of different leave-one-out cases, we obtained the final performance for each parameter combination. Finally, the one with the best performance was selected as our parameter setting. For example, to determine the scaling coefficient α for our weighted voting strategy, we calculated the distance errors in terms of different values of α, as shown in Fig. 7. It can be seen that the optimal values of scaling coefficient span in a wide range (i.e., from 10 to 30), which shows that our weighting strategy is not sensitive to the choice of α. It is also worth noting that, compared with the result without the weighted voting (indicated by a red star), the proposed weighted voting strategy significantly increases the digitization performance. In following experiments, the scaling coefficient α for voxel weighting is set to 20. Similarly, other parameters are also optimized. Specifically, in the feature extraction, the local patch sizes are set isotopically as 7.5mm,15mm and 30mm, respectively. The dimensionality of each local descriptor is P = 9. For each scale, the codebook consists of 50 elements, which results in the length of histogram features as 150. Quantization level is N = 5, thus, the length of the look-up table is 5⁹ = 1953125. In the regression forest, the number of trees is set to 10 and the tree depth is set to 20.

Fig. 7.

Effect of weighted voting. The star is the digitization error without weighted voting.

C. Experimental results

We conducted five-fold cross validations for 41 patient's CBCTs to evaluate the performance of our S-PRF model. Note that the 30 MSCTs were added into the training dataset for each cross validation in order to enlarge the sample size of training data.

As stated in SectionII, all landmarks were separated into different groups by their pair-wise spatial coherences. The landmark partition results depend only on the training subjects, which may influence them to differ in each fold of cross validation. In the five-fold experiment, the partition results happened to be the same given the fact that affinity matrices from five folds are very similar. The exemplary affinity matrices of one fold are shown in Fig. 8 (a-b). In our experiment, landmarks in maxilla and mandible regions were automatically clustered into 3 groups, respectively. Fig. 8 (c) gives the partition results, where landmarks with same color belong to the same group.

Table III shows the mean errors of all 15 landmarks automatically detected by our approach, in comparison to the ground truth. Note that the intra- and inter-examiner variations of manual CMF landmark digitization from 3D CT/CBCT image are mostly from 1.5 ~ 2mm [39], [40]. In our experiment, all the errors are less than 2mm, thus results are clinically acceptable. In addition, we also conducted experiments to evaluate the contribution of each strategy used in our approach. They are detailed below.

TABLE III.

Digitization errors of five-fold cross validation for 41 CBCT images with additional 30 MSCT images for training.

Landmark	Go-R	Go-L	Me	Pg	LR1	LL1	LR2	LL2	N	Or-R	Or-L	UR1	UL1	UR2	UL2
Error (mm)	1.61	1.59	1.02	1.03	1.40	1.49	1.63	1.24	1.62	1.58	1.55	1.10	1.30	1.59	1.81

1) Partially-joint versus fully-joint models

In order to evaluate the effect of morphological variations to the joint landmark digitization, we compared the performance of automatic landmark digitization using a partially-joint model or a fully-joint model. In this experiment, both models did not utilize the CBCT segmentation as guidance. In order to solely compare the fully-joint and partially-joint models, we did not separate landmarks in mandible and maxilla at the beginning. Instead, we constructed the affinity matrix for all 15 landmarks and partition them into four groups.

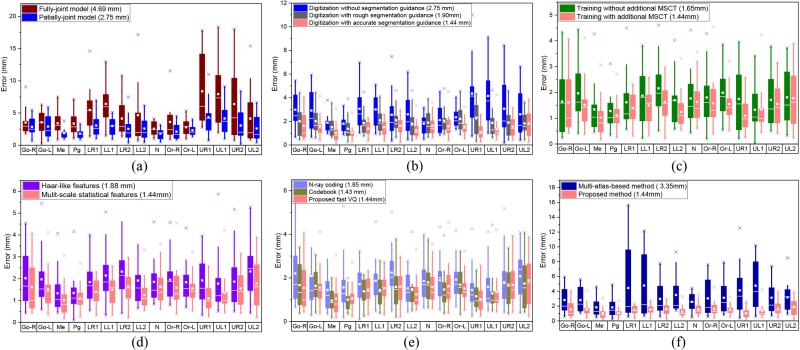
As shown in Fig. 9 (a), our partially-joint model achieves much better performance than the fully-joint model. These results confirm our observation that the global spatial structure of all landmarks is not stable, due to morphological variations across patients with CMF deformities. Hence, it is necessary to exploit stable sub-structure for robust and accurate digitalization.

Fig. 9.

Quantitative comparisons. Note that the results of the same color across different subfigures are the same, and the number inside the parenthesis is the mean error for all the landmarks and patients. (a) Digitization errors with different segmentation accuracies. (b) Digitization errors of using partially-joint model or fully-joint model. (c) Digitization errors with and without MSCT for training. (d) Digitization errors of using Haar-like features or multi-scale statistical features. (e) Digitization errors of using different VQ methods. (f) Comparison with multi-atlas-based method.

2) Segmentation-guided strategy

We compared the accuracy of automatic landmark digitization in three situations: 1) using rough CBCT segmentation, 2) using accurate CBCT segmentation, and 3) using no segmentation for guidance. A rough CBCT segmentation was obtained by simple majority voting after non-rigidly registering multiple atlases onto the target image space, which offered the average Dice ratio of 0.78. An accurate CBCT segmentation was obtained by using the patch-based sparse representation method [21], which offered the average Dice ratio of 0.89.

The results in Fig. 9 (b) show that the performance of automatic landmark digitization is significantly improved even using rough segmentation, by roughly separating the mandible from the maxilla. It also demonstrates that most of uninformative voxels can be removed by rough CBCT segmentation. With more accurate CBCT segmentation, we see that the accuracy of landmark digitalization can be further improved. Since the CBCT segmentation is an inevitable step in CMF surgery, it is reasonable to use segmentation as prior to enhance the landmark digitization performance.

3) Adding additional MSCT images into the training dataset

We also compared the performance of our method with and without adding additional 30 MSCTs into the training dataset. Although CBCT and MSCT are different modalities, they share very similar morphology as shown in Fig. 1 (c). The results in Fig. 9 (c) show that the performance of automatic landmark digitization can be significantly improved by using the additional MSCTs to help training.

4) Multi-scale statistical features versus Haar-like features

We also compared Haar-like features and our multi-scale statistical features in our framework. The results in Fig. 9 (d) show that our framework, with multi-scale statistical features, achieves better digitization accuracy than that of Haar-like features. This explains the effectiveness of our features in CBCT landmark digitalization. On the other hand, since the features in our landmark digitization framework can act differently, the use of prevalent deep neural networks [41] features might be another option to improve our method.

5) Effects of different VQ methods

We also compared the landmark digitization performances using different VQ methods. As shown in Fig. 9 (e), our method has similar results with that of the codebook approach, which is expected, since we have little sacrifice in digitization accuracy although we significantly increase the encoding efficiency. The N-ary coding method obtains somewhat worse results, as we had to use N = 2 to extract features with proper dimensionality (512 × 3), which led to the significant loss of structural information during the VQ process. If we choose N = 3, the dimensionality of representation should be 19683 × 3, which is impossible to train a regression model with the limited computer memory.

6) Comparison with other methods

Finally, we qualitatively compared our results with CBCT landmark digitization methods published in [10], [42] and [7]. The mean error of our approach is 1.44mm, which is significantly better than the mean errors of 3.15mm, 2.41mm and 3.40mm in [10], [42] and [7], respectively. Although the datasets were different, the significantly reduced error implies the effectiveness of our method, compared with the state-of-the-art. In order to provide quantitative comparison with other methods, we implemented a multi-atlas-based landmark digitization approach which is similar to reference [7], where the landmarks are mapped from the corresponding positions in the non-linearly aligned atlases with the averaging strategy. As shown in Fig. 9 (f), the digitization error, obtained by the multi-atlas-based method, is large (3.35mm) due to registration errors. Our method specifically considers those large morphological variations across patients during the landmark detection, thus achieving superior landmark digitization performance.

IV. Conclusion

We proposed a new S-PRF model to automatically digitize CMF landmarks. Our model has addressed challenges of both inter-patient morphological variations and imaging artifacts. Specifically, by using regression based voting, our model can potentially resolve the issue of imaging artifacts near the landmark. Also, by using image segmentation as guidance, our model can address the issue of uninformative voxels caused by inter-patient morphological variations, especially for teeth. Moreover, by using a partially-joint model, the digitization reliability can be further improved through the best utilization of spatial coherence of landmark positions. Besides, we proposed a new fast VQ method to extract high-level multi-scale statistical discriminative features with high efficiency and low feature dimensionality. Experimental results showed that the accuracy of our automatically digitized landmarks was clinically acceptable and also performed better than the state-of-the-art methods.

However, there are still two potential issues with our proposed method. 1) We used the segmentations of maxilla and mandible to remove the uninformative voxels. This prior knowledge might be different in different applications, such as other forms of deformities. In the future, we will generalize our approach to other forms of CMF deformities. 2) We clustered the landmarks into several groups and detected them separately in groups. It is a data-driven strategy and depends solely on the training data. However, for some special cases or applications, if the deformities of the testing images have little correlation to the training samples (i.e., the shape constraint learned from training is invalid), the model may not be accurate. In this case, detecting each landmark individually (i.e., removing the shape constraint) may yield more reasonable results.

Besides, since the number of samples used in this paper is limited, it is challenging for many statistical methods. So, we used prior knowledge, i.e., large variations between maxilla and mandible across subjects, to remove informative voxels with the guidance from segmentation results. In the future, we can also either construct representative database with more typical subjects, or even add the synthetic images (i.e., generated with different degrees of occlusion between upper and lower teeth from typical subjects) to increase the size of training dataset.