Abstract
Distinguishing progressive mild cognitive impairment (pMCI) from stable mild cognitive impairment (sMCI) is critical for identification of patients who are at-risk for Alzheimer’s disease (AD), so that early treatment can be administered. In this paper, we propose a pMCI/sMCI classification framework that harnesses information available in longitudinal magnetic resonance imaging (MRI) data, which could be incomplete, to improve diagnostic accuracy. Volumetric features were first extracted from the baseline MRI scan and subsequent scans acquired after 6, 12, and 18 months. Dynamic features were then obtained by using the 18th-month scan as the reference and computing the ratios of feature differences for the earlier scans. Features that are linearly or non-linearly correlated with diagnostic labels are then selected using two elastic net sparse learning algorithms. Missing feature values due to the incomplete longitudinal data are imputed using a low-rank matrix completion method. Finally, based on the completed feature matrix, we build a multi-kernel support vector machine (mkSVM) to predict the diagnostic label of samples with unknown diagnostic statuses. Our evaluation indicates that a diagnosis accuracy as high as 78.2% can be achieved when information from the longitudinal scans is used – 6.6% higher than the case using only the reference time point image. In other words, information provided by the longitudinal history of the disease improves diagnosis accuracy.
Keywords: Longitudinal MRI, progressive mild cognitive impairment (pMCI), elastic net, low rank matrix completion, multi-kernel learning, missing data
1. Introduction
Mild cognitive impairment (MCI) is a brain disorder characterized by noticeable impairment of cognitive functions, such as memory loss, beyond the decline due to normal aging, but not to the extent of significantly affecting activities of daily life. MCI is caused by neurodegeneration (loss or death of brain neuron cell), and is generally known as a transitional stage between normal aging and Alzheimer’s disease (AD). Studies suggest that 3% to 19% of adults older than 65 years may be affected by MCI (Gauthier et al., 2006). Although some MCI patients recover over time, more than half will progress to dementia within 5 years (Gauthier et al., 2006). To identify patients who need to receive early treatment, it is vital to distinguish between progressive MCI (pMCI) patients, who will eventually progress to AD, from stable MCI (sMCI) patients, whose conditions will cease to deteriorate.
In the past few decades, a lot of studies have been focused on identifying possible biomarkers for AD/MCI diagnosis using neuroimaging data acquired with magnetic resonance imaging (MRI) (Weiner et al., 2013). MRI is a noninvasive technology that can be used to quantify gray and white matter integrity of the brain with high reproducibility (Haacke et al., 1999; Jack et al., 2008). MRI-based studies indicate that AD/MCI subjects are normally associated with cortical thinning and brain atrophy in the temporal lobe, parietal lobe, frontal cortex, and other brain regions (Jack et al., 2002; Stefan J et al., 2006; Whitwell et al., 2008). Based on these findings, different types of MRI-based measures, e.g., region-of-interest (ROI) based volumetric measures (Jack et al., 1999; Zhou et al., 2011; Li et al., 2015), cortical thickness measures (Querbes et al., 2009; Wee et al., 2013), morphometric measures (Ashburner and Friston, 2000; Hua et al., 2008), functional measures Wee et al. (2012a, 2014); ?); ?, and diffusion measures Wee et al. (2011, 2012b) have been proposed for AD/MCI diagnosis. In addition to MRI, other modalities such as positron emission topography (PET), cerebrospinal fluid (CSF), and genetic data have also been used (Kohannim et al., 2010; Hinrichs et al., 2009; Huang et al., 2011; Wang et al., 2012; Zhang and Shen, 2012a). Compared with other modalities, structural MRI offers important advantages such as non-invasiveness, rapid acquisition, lower acquisition cost, and greater data availability. In this study, we focus our analysis on MRI data, even though our framework can be generalized and extended to include other modalities.
There are two broad categories of AD studies: cross-sectional and longitudinal. In cross-sectional studies, only data from one time point are involved. Most studies using the Alzheimer’s Disease Neuroimaging Initiative (ADNI)1 dataset employ only the baseline data (i.e., the first screening data) and therefore belong to this category (Davatzikos et al., 2011; Hinrichs et al., 2011; Weiner et al., 2013). The preference for cross-sectional studies is partly due to the completeness of the baseline data, both in terms of the number of subjects in different cohorts (i.e., AD, MCI and NC) and the number of modalities (i.e., MRI, PET and CSF) when compared with the data collected at subsequent time points. Due to greater data availability in the baseline, cross-sectional studies using the baseline data might benefit from greater statistical power. Moreover, complementary data from multiple modalities, which are most complete at the baseline, can be employed for more accurate AD/MCI analysis (Wang et al., 2012; Zhang and Shen, 2012a; Thung et al., 2014; Liu et al., 2014; ?; Huang et al., 2015; Zhu et al., 2015; Thung et al., 2015; Adeli-Mosabbeb et al., 2015). However, cross-sectional studies can only provide information on a single biological and neuropsychological state of the disease and is hence insufficient for characterizing the temporal evolution of the disease.
In longitudinal studies, data collected at multiple time points are involved (Zhang and Shen, 2012b; Liu et al., 2013; Weiner et al., 2013). In contrast to data from a single time point, longitudinal data capture temporal dynamics, such as the rate of deterioration, of disease progression. For example, we can quantify pathological changes using MRI-based measurements from multiple time points to determine whether an MCI patient is progressing toward AD. However, due to various practical issues (e.g., subject drop-outs, image quality issues, etc.), longitudinal data are quite often incomplete. The easiest way to deal with this problem, as done in most studies, is by discarding samples with missing data (Liu et al., 2013; Weiner et al., 2013) and performing analysis only using data that are complete. By doing so, sample size is inevitably reduced and hence statistical power is sacrificed (van der Heijden et al., 2006; MacCallum et al., 1996). An alternative to dealing with missing data is to perform data imputation, using methods such as k-nearest neighbor (KNN) (Speed, 2003; Troyanskaya et al., 2001), expectation maximization (EM) (Schneider, 2001), and low rank matrix completion (Candès and Recht, 2009; Goldberg et al., 2010; Sanroma et al., 2014).
In this study, we utilize longitudinal MRI data, with explicit consideration of missing data, for pMCI/sMCI classification. We hypothesize that pMCI patients undergo a trajectory of brain structural changes that is different from sMCI patients. This trajectory, which is reflected by the longitudinal MRI data, can be used to improve pMCI/sMCI classification. Our main contributions and findings are as follows:
We developed a pMCI identification framework using longitudinal incomplete data. Unlike longitudinal studies that discard incomplete data, we impute missing feature values and diagnostic labels of a testing sample simultaneously by utilizing all available samples.
We developed a feature selection method for incomplete longitudinal data, extracting, at each time point, features that are correlated linearly and nonlinearly with the class labels.
We found that dense temporal sampling is not always necessary for improving pMCI identification. Our investigation shows that scans that are appropriately spaced out in time is often sufficient.
Our framework uses both static and dynamic features to predict the diagnostic label of a sample. The static features are the gray matter volumes of 93 ROIs extracted from each MR image in the longitudinal series. The dynamic features are the volumetric change ratios computed between the image at a reference time point and images at other time points. By concatenating the static and dynamic features, each sample can be represented as a feature vector. All the feature vectors are stacked to form a feature matrix. Instead of performing imputation based on the whole matrix, we apply feature selection to reduce the matrix to contain only discriminative features so that imputation can be carried out more effectively. More specifically, features that show linear and nonlinear relationships with clinical diagnostic labels are selected via least-squares and logistic elastic net regressions (Liu et al., 2009). Missing feature values in the reduced feature matrix are then imputed using a label guided low rank matrix completion method (Goldberg et al., 2010). Lastly, we will build a classifier by using multiple kernel SVM (Rakotomamonjy et al., 2008), which combines a set of linear, Gaussian, and polynomial kernels. Experimental results show that our framework improves identification accuracy when longitudinal MRI data with dynamic features are used.
2. Materials and Data Processing
2.1. ADNI Background
Data used in the preparation of this article were obtained from the ADNI database (adni.loni.ucla.edu). The ADNI was launched in 2003 by the National Institute on Aging (NIA), the National Institute of Biomedical Imaging and Bioengineering (NIBIB), the Food and Drug Administration (FDA), private pharmaceutical companies and non-profit organizations, as a $60 million, 5-year public-private partnership. The primary goal of ADNI has been to test whether serial MRI, PET, other biological markers, and clinical and neuropsychological assessment can be combined to measure the progression of MCI and early AD. Determination of sensitive and specific markers of very early AD progression is intended to aid researchers and clinicians to develop new treatments and monitor their effectiveness, as well as lessen the time and cost of clinical trials.
The Principal Investigator of this initiative is Michael W. Weiner, MD, VA Medical Center and University of California - San Francisco. ADNI is the result of efforts of many co-investigators from a broad range of academic institutions and private corporations, and subjects have been recruited from over 50 sites across the U.S. and Canada. The initial goal of ADNI was to recruit 800 subjects but ADNI has been followed by ADNI-GO and ADNI-2. To date, these three protocols have recruited over 1500 adults, ages 55 to 90, to participate in the research, consisting of cognitively normal older individuals, people with early or late MCI, and people with early AD. The follow up duration of each group is specified in the protocols for ADNI-1, ADNI-2 and ADNI-GO. Subjects originally recruited for ADNI-1 and ADNI-GO had the option to be followed in ADNI-2. For up-to-date information, see www.adni-info.org.
2.2. Materials
In the ADNI dataset, there are about 400 MCI subjects scanned at screening time (i.e., the baseline). After the baseline scan, follow-up scans were acquired every 6 or 12 months for up to 84 months. MCI subjects who progressed to AD after some period of time were retrospectively labelled as pMCI subjects. Following this convention, the labelling of pMCI/sMCI is affected by the reference time point and the time period in which the patients are monitored for conversion to AD. We chose the 18th month as the reference and 30 months as the time period to monitor for conversion, so that there is a sufficient number of earlier scans (i.e., baseline, 6th, and 12th month) in each cohort (i.e., pMCI and sMCI). Thus, patients who converted to AD within the 18th to 48th month (a duration of 30 months) are labelled as pMCI patients, and those whose conditions do not deteriorate are labelled as sMCI patients. Patients who converted to AD prior to the 18th month were excluded from the study because they were no longer MCI patients at the reference time point. Patients who converted to AD after the 48th month were also excluded to avoid labelling uncertainty. Based on the criteria mentioned above, a total of 60 pMCI and 53 sMCI subjects were available for this study. The associated demographic information is shown in Table 1. Using the data at and before the 18th month, we investigated whether longitudinal MRI scans are conducive to improving pMCI/sMCI classification.
Table 1.
Demographic information of pMCI/sMCI subjects. (Edu.: Education, SD: standard deviation)
| Number of subjects | Gender | Age (years) | Edu. (years) | |
|---|---|---|---|---|
|
| ||||
| male/female | mean ± SD | mean ± SD | ||
|
| ||||
| pMCI | 60 | 36/24 | 75.2 ± 6.1 | 15.2 ± 3.4 |
| sMCI | 53 | 30/23 | 75.7 ± 5.8 | 15.9 ± 3.2 |
| Total | 113 | 66/47 | 75.4 ± 5.9 | 15.5 ± 3.3 |
2.3. MR Image Processing
A maximum of 4 time points were used – baseline, 6th month, 12th month, and 18th month. The processing steps involved are described as follows. Each MRI T1-weighted image was first anterior commissure (AC) – posterior commissure (PC) corrected using MIPAV2, intensity inhomogeneity corrected using the N3 algorithm (Sled et al., 1998), skull stripped (Wang et al., 2011) with manual editing, and cerebellum-removed (Wang et al., 2014). We then used FAST (Zhang et al., 2001) in the FSL package3 to segment the image into gray matter (GM), white matter (WM), and cerebrospinal fluid (CSF), and used HAMMER (Shen and Davatzikos, 2002) to register the images to a common space. GM volumes obtained from 93 ROIs defined in (Kabani, 1998), normalized by the total intracranial volume, were extracted as features.
3. pMCI/sMCI Classification Framework
3.1. Image Features
Let {Tt ∈ ℝn×r, t = 1, …, 4} denote the matrices containing the r = 93 ROI volumetric features of n subject samples at baseline (t = 1), 6th month, 12th month, and 18th month (t = 4), respectively. Additional dynamic features are computed as the volumetric change ratios between 18th month (reference time point) and earlier time points, i.e., {Dt = (Tt − T4) · /(T4 + c), t = 1, …, 3}, where ·/ denotes element-wise division, and c is a small constant to avoid division by zero. Since the ADNI longitudinal data were not acquired exactly at the design time points, we normalize the dynamic features using the following method. The normalizer for the j-th row (i.e., j-th subject) of Dt is denoted as
| (1) |
The corrected dynamic features is given by
| (2) |
where Wt = diag(wt,1, wt,2, ···, wt,j, ···, wt,n).
For simplicity, we concatenate all the volumetric and dynamic features into a matrix X = [X(1) ··· X(i) ··· X(m)] ∈ ℝn×d, where d = r × m is the total number of features for one subject sample, and m is the total number of feature submatrices. Depending on the number of time points and the feature combination used in the experiments, each feature submatrix X(i) represents either Tt or Dt. For example, if all volumetric and dynamic features from all 4 time points are used, there are m = 7 submatrices: X(i) = T5–i for i = {1, 2, 3, 4}, X(i) = D8–i for i = {5, 6, 7}, and X = [X(1) ··· X(i) ··· X(m)] = [T4 T3 T2 T1 D3 D2 D1]. Denoting y ∈ ℝn×1 as the target label vector (1 for pMCI, −1 for sMCI), our objective is to predict Y given X.
3.2. Framework Overview
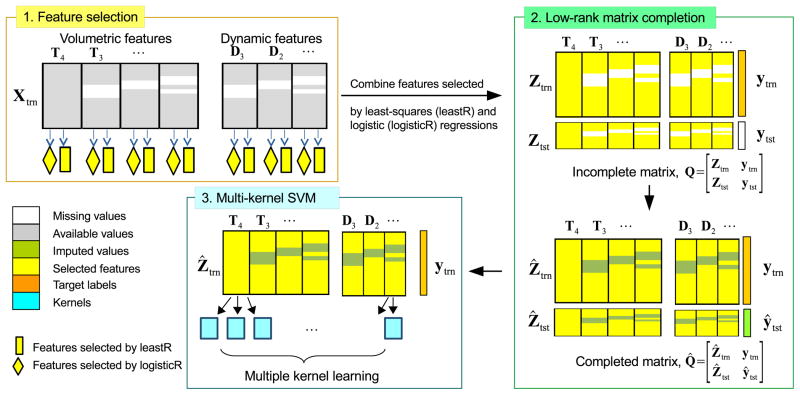
The proposed framework (see Figure 1) consists of three components: feature selection, data imputation using matrix completion, and classification using multi-kernel support vector machine (mkSVM). We partitioned the feature matrix into training and testing samples: . Our model was trained with Xtrn ∈ ℝntrn×d, and was tested with Xtst ∈ ℝntst×d. The corresponding target label vectors for the training and testing data are denoted as Ytrn ∈ ℝntrn×1 and Ytst ∈ ℝntst×1, respectively. Since some feature values are possibly missing in X due to the incomplete dataset, data imputation is needed before it can be used to train a classifier. To reduce the number of values that need to be imputed and also to restrict imputation to only discriminative features, we first reduce the size of Xtrn via feature selection.
Figure 1.
Overview of the proposed pMCI/sMCI classification framework.
3.3. Feature Selection
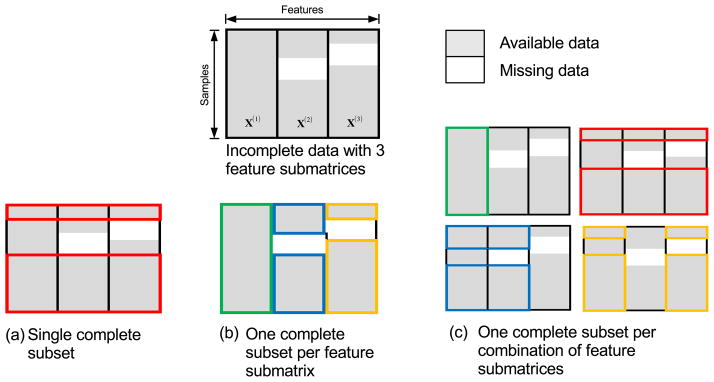
Sparse feature selection methods such as least absolute shrinkage and selection operator (Lasso) (Tibshirani, 1996) and its variants (Zou and Hastie, 2005; Friedman et al., 2010; Simon et al., 2013; Zhou et al., 2012; Zhang et al., 2012) have been shown to be effective in dealing with high-dimensional data. However, these feature selection methods can only be applied to complete data with no missing values. One workaround for this problem is to apply feature selection on complete subset(s) of the data. Three methods can be used to extract such subsets, as shown in Figure 2. Each feature submatrix in the figure represents data from one time point (volumetric or dynamic features), and each color box in the figure represents the subset of data. For simplicity, we use an example of incomplete data with only three feature submatrices. The first method (Figure 2(a)), which is widely used, discards samples with missing values and retains only complete samples, thus throwing away a significant amount of useful information. The second and third methods (Figure 2(b) and (c)) avoid this problem by using multiple complete subsets. Specifically, the second method defines subsets according to feature submatrices, while the third method defines subsets according to combinations of features. To maximize the number of samples for each subset, the third method allows overlaps among subsets. In this study, the second method was used.
Figure 2.
Three ways of handling incomplete data: (a) One subset of complete samples, (b) One complete subset for each feature submatrix, and (c) One complete subset for each combination of feature submatrices.
In longitudinal data, the volumetric features vary gradually over time and are highly correlated. Based on our experience, if sparse method such as Lasso is used for feature selection on data from two or more time points, similar but not necessarily redundant features will be removed. We avoid this problem by performing elastic net feature selection for each submatrix , i.e., second method in Figure 2(b). In addition, we use two types of elastic net regressions, least-squares and logistic regressions both with elastic net regularizer (Liu et al., 2009), to select features that are linearly and non-linearly correlated with the target labels (see feature selection component in Figure 1). The problems associated with the two sparse regressions are given as
| (3) |
| (4) |
where is the j-th samples in , yj is the corresponding j-th output label, ||·||1 is the l1-norm, ||·||2 is the l2-norm, and λ1 to λ4 are the regularization parameters. Elastic net enforces l1-norm and l2-norm penalization on the weight vector β(i) ∈ ℝr×1, combining the advantages of both Lasso and ridge regressions. In particular, the l1-norm in the above equations causes weight vectors and to be sparse, while the l2-norm helps to retain highly correlated features. Features corresponding to the rows with non-zero values in matrix were selected from { , i = 1, 2, …}. This implies that the same set of features will be selected for all feature submatrices in Xtrn. Features found discriminant at one time point will also be selected at other time points.
3.4. Matrix Completion
After feature selection, we obtain feature-reduced matrices Ztrn and Ztst, which are possibly incomplete due to missing data. While there are a number of existing data imputation methods (Schneider, 2001; Goldberg et al., 2010; Ma et al., 2011; Troyanskaya et al., 2001), we chose to use a label guided low rank matrix completion algorithm (Goldberg et al., 2010; Thung et al., 2014). This is because the longitudinal data are highly correlated and each column of could potentially be represented by a linear combination of other columns in Z, satisfying the low rank assumption of low rank matrix completion algorithm. Following (Goldberg et al., 2010), we augmented Z with the target label vector before performing matrix completion. More specifically, matrix completion is performed on an augmented matrix , where Ytst is unknown and will be imputed (Thung et al., 2014). The imputed or completed matrix is denoted as , where Ŷtrn is same as Ytrn as there is no missing label in the training set. The imputation optimization problem is given as:
| (5) |
where ΩZ and ΩY denote the set of indices of the observed non-missing values in Z and the label vector Y, respectively, |.| denotes the cardinality of a set, ||.||* denotes the trace norm, qij and q̂ij denote the original and the predicted values, respectively. The first term in the above equation is to ensure that the predicted matrix Q̂ is low rank. The second term is the squared loss term L1(u, v) = 1/2(u − v)2, which accounts for errors in feature imputation. The final term is a logistic loss term L2(u, v) = log(1+exp(−uv)), which accounts for errors in label imputation. λm and μ are the positive-valued tuning parameters. The imputed label vector Ytst can be taken as the predicted labels without explicitly building a classifier. To improve the prediction accuracy, we detail in the following how classifiers can be constructed based on the completed feature matrix.
3.5. Classification
Various classifiers can be constructed based on the completed feature matrix Ẑtrn to predict the class label vector Y. First, we applied least-squares elastic nets, logistic elastic net, linear kernel SVM, and Gaussian kernel SVM on Ẑtrn as a whole for prediction. Second, we used the kernel trick to combine different feature submatrices into a single matrix for prediction. Specifically, we built one or more kernels for each feature submatrix, and combined them into a single kernel by using either multiple kernel learning algorithms, such as multi kernel SVM (mkSVM) or averaging algorithms, such as mean multi-kernel SVM (mean-mkSVM).
3.5.1. Least-Square Sparse Regression Elastic Net (leastR)
We learn a sparse weight β that, when mapped by Z, best explains Ytrn. This is achieved by solving a l2-norm and l1-norm regularized least-squares problem. That is
| (6) |
The label vector Ytst is predicted based on Ẑtest and is given by Ẑtestβ.
3.5.2. Logistic Sparse Regression Elastic Net (logisticR)
This is similar to leastR classifier, but with the least-squares function replaced by the logistic loss function. That is
| (7) |
The label vector Ytst is given by Ẑtestβ + c.
3.5.3. Support Vector Machine (SVM)
The dual formulation of SVM (Chang and Lin, 2011) is given as
| (8) |
where is a vector of dual variables, C is the regularization parameter, K(Ẑj, Ẑk) is the kernel that indicates the similarity between sample Ẑj ∈ ℝ1×nf and Ẑk ∈ ℝ1×nf in Ẑtrn, and nf is the number of features for each sample. We built linear kernel (Klinear (Ẑj, Ẑk) = 〈Ẑj, Ẑk〉) and Gaussian kernel ( ) using Ẑtrn for the prediction of Ytst.
3.5.4. Multi-Kernel SVM (mkSVM)
Combining multiple kernels (Gönen and Alpaydin, 2011) has been shown to improve classification performance. Thus, instead of using a single kernel, we combined multiple kernels using multi-kernel support vector machine (mkSVM). Specifically, we built multiple kernels (i.e., linear, Gaussian and polynomial kernels with different parameters) for each submatrix in Ẑtrn, and then used multiple kernel learning (MKL) to estimate the kernel combination weights.
The dual formulation of mkSVM (Rakotomamonjy et al., 2008) is given as
| (9) |
where is a vector of dual variables, is the kernel weight matrix, C is the regularization parameter, Q is the total number of kernels, and is the q-th kernel between sample and in . We used three types of kernels: linear kernel Klinear(Ẑj, Ẑk) = 〈Ẑj, Ẑk〉, Gaussian kernel ( , and polynomial kernel (Kpolynomial(Ẑj, Ẑk) = (〈Ẑj, Ẑk〉+1)p). We employed 5 values for s and 3 values for p. Thus, each submatrix in Ẑtrn corresponds to a total of Q = 9 kernels, and for m submatrices, we have a total of 9m kernels. These kernels were combined by using the learned weight matrix η in . The equality constraint in (9), which is similar to l1-norm, causes η to be sparse, and only the most discriminative kernels were selected. After obtaining α and η from the training data, the class label for a test sample Ẑtst was estimated by , where b is the bias term obtained from the support vectors. For more detail on mkSVM, please refer to (Gönen and Alpaydin, 2011).
3.5.5. Mean Multi-Kernel SVM (mean-mkSVM)
Mean-mkSVM is similar to mkSVM, but instead of learning the kernel weights, the kernels are combined by simple averaging and therefore all kernels are combined with equal weighting. Since nonlinear kernel is very sensitive to parameter selection, only the linear kernel is used for mean-mkSVM, similar to (Zhang and Shen, 2012b).
4. Results and Discussions
4.1. Performance Measure
We used accuracy, sensitivity, and specificity to evaluate the performance of the proposed classification framework. In addition, the Receiver Operating Characteristic (ROC) curve was used to summarize the classifier performance over a range of tradeoffs between true positive and false positive error rates (Swets, 1988). The Area Under the ROC Curve (AUC) (Lee, 2000; Duda et al., 2012; Bradley, 1997), used as the fourth measure, is independent to the decision criterion used and is less sensitive to data imbalance. Thus, AUC is the most representative performance measure in this study. All the results reported in this paper are the average of 10 repetitions in 10-fold cross validation.
4.2. Parameter Selection
We evaluated our framework using different classifiers, including leastR, logisticR, linear-kernel SVM (SVMlin), Gaussian-kernel SVM (SVMrbf), mkSVM, and mean-mkSVM. All the hyperparameters (e.g., λ, C, and s) used for the classifiers (and the feature selections) are determined through 5-fold cross validation, using only the training data. Also included are the classification results obtained using low rank label imputation technique (LRMC), as described in our previous work (Thung et al., 2014, 2013). The parameters λm and μ of LRMC are set at 0.1 and 10−5, respectively, based on our previous work (Thung et al., 2014).
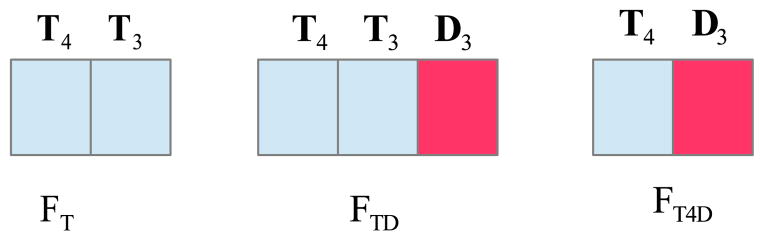
4.3. Feature Combinations
Three feature combinations were tested in this study (see Figure 3), i.e., FT – volumetric features only; FTD – volumetric and all the corresponding dynamic features; FT4D – volumetric features from the fourth (18 month) time point and all the corresponding dynamic features. The number of dynamic features used was determined by the number of time points used in the experimental study. For example, if time point 4 and time point 3 are used, there is only 1 type of dynamic feature, i.e., D3; while if all the time point are used, there are 3 types of dynamic features, i.e., D3, D2 and D1. In the following subsections, we report the results for our framework using different combinations of time points, combinations of features, feature selection methods, and classifiers.
Figure 3.
Three examples of feature combination: FT, FTD, and FT4D, using data from 2 time points, T4 and T3.
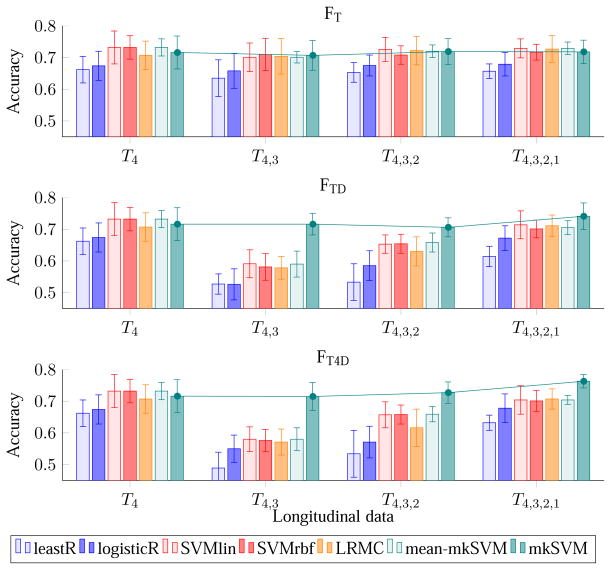
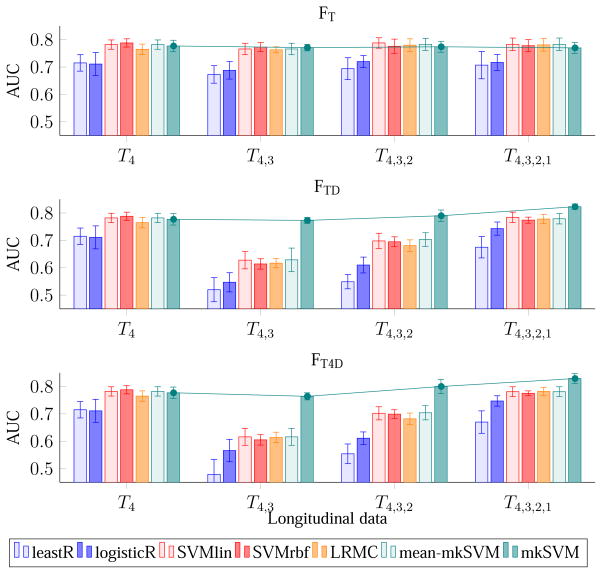
4.4. Evaluation – Effect of Increasing the Number of Time Points
Figures 4 and 5 show the effect of the number of time points on accuracy and AUC using different combinations of features. The first row of both figures indicates that, without dynamic features (i.e., FT), there is no significance difference in performance even using data from more than one time point. In contrary, feature combinations that utilize dynamic features, i.e., FTD and FT4D, perform significantly better. With dynamic features, there is a trend of increasing performance (both in term of accuracy and AUC) when using data from more earlier time points. The plots in Figure 4 and Figure 5 also indicate that the performance of the framework is not always improved when using data from more than one time point. For example, when compared with time point 4 (reference or “latest” time point), the performance of the proposed classifier (i.e., mkSVM) drops slightly when including additional data from time point 3, but increases afterward when using additional data from time points 2 and 1. Similar trend is observed using other classifiers (e.g., leastR, SVMlin, LRMC, mean-mkSVM), but with a much significant drop in performance using the dynamic features from time points 4 and 3. This is potentially due to the relatively smaller time separation between time points 4 and 3 (only 6 months apart). The images are hence relatively similar and do not offer much additional information, and also the dynamic features could be noisy. Nevertheless, unlike other classifiers, the proposed mkSVM, which assigns different weights to the kernels derived from different data, can avoid this issue effectively.
Figure 4.
Average accuracy (over 10 repetitions of 10-fold cross-validation) of pMCI identification using MR data with increasing number of time points. The error bars show the standard deviations. The line plots show the changing trend of the proposed mkSVM method with increasing time points.
Figure 5.
Average AUC of pMCI identification using MR data with increasing number of time points.
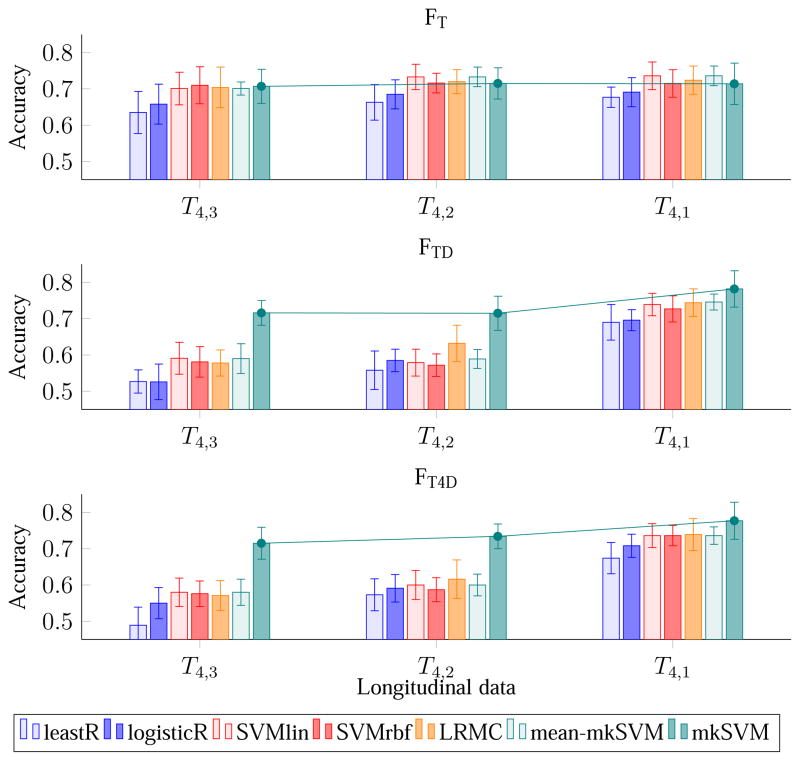
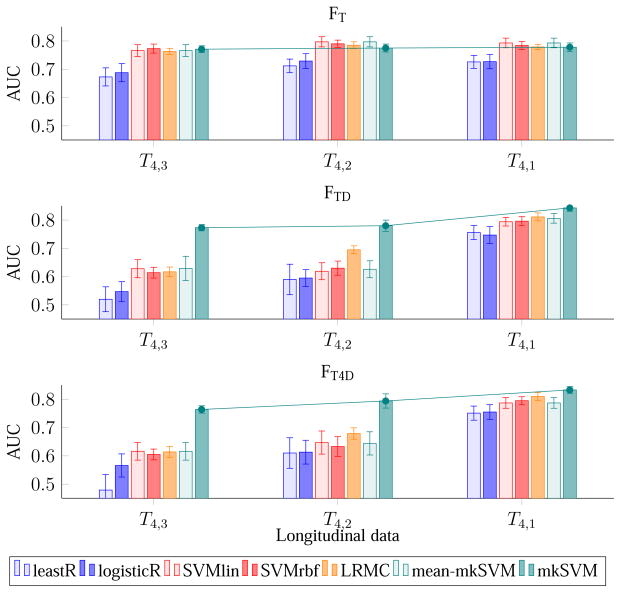
4.5. Evaluation – Effect of Scan Time Interval
We investigate here the effect of scan time interval between two MRI scans on classification accuracy. Figure 6 and Figure 7 show the results of pMCI identification using data from the reference time point and one additional earlier time point. From the figure, it can be seen that when the scanning time interval of the 2 time points increases, so does the classification accuracy and the AUC. This trend is seen for all the three feature combinations and for almost all the classifiers. The reason behind this observation could be that the brain structures of the subjects change more significantly when scan time interval is increased, making the dynamic features more useful. pMCI subjects encounters a greater rate of neurodegeneration than sMCI subjects. The dynamic features capture this difference from the longitudinal data and improve pMCI/sMCI classification accuracy. We also note that the improvement gained by using 2 time points is comparable to that using more time points. This observation indicates that the time interval between scans is a more important factor in pMCI identification than the number of scans.
Figure 6.
Average accuracy of pMCI identification using MR data from two time points of increasing scan time interval.
Figure 7.
Average AUC of pMCI identification using MR data from two time points of increasing scan time interval.
4.6. Evaluation – Effect of Feature Combination
When comparing the performance difference among FT, FTD, and FT4D, we found that FTD, and FT4D, which utilize dynamic features, are significantly better than FT, which uses only MRI ROI-based features. This observation can be seen in Figures 4 to 7. For example, considering all time points, the best AUC values are 0.783, 0.823, and 0.829, for FT, FTD, and FT4D, respectively. If considering only the first and fourth time points, the best AUCs achieved by FT, FTD, and FT4D are 0.793, 0.843, and 0.833, respectively. In other words, using FTD and FT4D gives an increase of accuracy of about 4–5 % over FT, when using time points 1 and 4, achieved by our proposed classifier (mkSVM).
4.7. Evaluation – Effect of Classifier
The performance of the classifiers depends on the feature combination used. For FT, the performances of SVMlin, SVMrbf, LRMC, mean-mkSVM, and mkSVM are comparable, while the performances of leastR and logisticR are relatively inferior. For FTD and FT4D, mkSVM in overall performs better than other classifiers for all combinations of time points. For FTD, the highest AUC value (0.843) is achieved by mkSVM, using data from time points 1 and 4. This is 6.6% higher than its AUC when using only time point 4. Similar conclusions can also be drawn when using FT4D. The complete results in terms of accuracy, sensitivity, specificity and AUC are shown in Tables 2 to 5. In term of sensitivity, mkSVM always performs the best for all these feature combinations.
Table 2.
Classification accuracy. The best results are marked in bold.
| Classifiers | Increasing Time Points | 2 Time Points | 3 Time Points | ||||||
|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||
| 4 | 4,3 | 4,3,2 | 4,3,2,1 | 4,2 | 4,1 | 4,2,1 | 4,3,1 | ||
| FT | leastR | 0.662 | 0.635 | 0.653 | 0.657 | 0.663 | 0.677 | 0.671 | 0.652 |
| logisticR | 0.674 | 0.658 | 0.675 | 0.679 | 0.685 | 0.691 | 0.696 | 0.674 | |
| SVMlin | 0.732 | 0.701 | 0.726 | 0.729 | 0.733 | 0.736 | 0.725 | 0.710 | |
| SVMrbf | 0.732 | 0.710 | 0.708 | 0.717 | 0.716 | 0.715 | 0.708 | 0.705 | |
| LRMC | 0.707 | 0.704 | 0.722 | 0.727 | 0.720 | 0.724 | 0.734 | 0.707 | |
| mean-mkSVM | 0.732 | 0.701 | 0.720 | 0.729 | 0.733 | 0.736 | 0.730 | 0.718 | |
| mkSVM | 0.716 | 0.707 | 0.719 | 0.718 | 0.715 | 0.714 | 0.720 | 0.710 | |
|
| |||||||||
| FTD | leastR | 0.662 | 0.527 | 0.533 | 0.614 | 0.558 | 0.690 | 0.660 | 0.628 |
| logisticR | 0.674 | 0.526 | 0.585 | 0.672 | 0.585 | 0.696 | 0.689 | 0.670 | |
| SVMlin | 0.732 | 0.591 | 0.653 | 0.714 | 0.579 | 0.739 | 0.721 | 0.724 | |
| SVMrbf | 0.732 | 0.581 | 0.654 | 0.701 | 0.572 | 0.727 | 0.721 | 0.700 | |
| LRMC | 0.707 | 0.578 | 0.630 | 0.711 | 0.632 | 0.744 | 0.713 | 0.715 | |
| mean-mkSVM | 0.732 | 0.590 | 0.658 | 0.705 | 0.589 | 0.746 | 0.727 | 0.728 | |
| mkSVM | 0.716 | 0.716 | 0.706 | 0.741 | 0.715 | 0.782 | 0.756 | 0.756 | |
|
| |||||||||
| FT4D | leastR | 0.662 | 0.489 | 0.534 | 0.632 | 0.573 | 0.674 | 0.663 | 0.608 |
| logisticR | 0.674 | 0.550 | 0.571 | 0.678 | 0.591 | 0.708 | 0.695 | 0.671 | |
| SVMlin | 0.732 | 0.580 | 0.657 | 0.704 | 0.600 | 0.736 | 0.720 | 0.722 | |
| SVMrbf | 0.732 | 0.576 | 0.658 | 0.701 | 0.587 | 0.736 | 0.717 | 0.698 | |
| LRMC | 0.707 | 0.571 | 0.616 | 0.707 | 0.616 | 0.739 | 0.721 | 0.716 | |
| mean-mkSVM | 0.732 | 0.580 | 0.659 | 0.704 | 0.600 | 0.736 | 0.729 | 0.726 | |
| mkSVM | 0.716 | 0.715 | 0.727 | 0.763 | 0.734 | 0.777 | 0.749 | 0.756 | |
Table 5.
Classification AUC values.
| Classifiers | Increasing Time Points | 2 Time Points | 3 Time Points | ||||||
|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||
| 4 | 4,3 | 4,3,2 | 4,3,2,1 | 4,2 | 4,1 | 4,2,1 | 4,3,1 | ||
| FT | leastR | 0.715 | 0.673 | 0.694 | 0.707 | 0.712 | 0.726 | 0.721 | 0.707 |
| logisticR | 0.711 | 0.688 | 0.720 | 0.717 | 0.729 | 0.727 | 0.738 | 0.719 | |
| SVMlin | 0.782 | 0.766 | 0.788 | 0.783 | 0.797 | 0.793 | 0.794 | 0.782 | |
| SVMrbf | 0.788 | 0.773 | 0.776 | 0.778 | 0.790 | 0.784 | 0.777 | 0.777 | |
| LRMC | 0.765 | 0.763 | 0.780 | 0.781 | 0.785 | 0.779 | 0.789 | 0.770 | |
| mean-mkSVM | 0.782 | 0.766 | 0.783 | 0.783 | 0.797 | 0.793 | 0.789 | 0.782 | |
| mkSVM | 0.777 | 0.771 | 0.774 | 0.770 | 0.775 | 0.778 | 0.769 | 0.769 | |
|
| |||||||||
| FTD | leastR | 0.715 | 0.520 | 0.549 | 0.675 | 0.590 | 0.756 | 0.717 | 0.688 |
| logisticR | 0.711 | 0.547 | 0.610 | 0.743 | 0.595 | 0.747 | 0.765 | 0.728 | |
| SVMlin | 0.782 | 0.628 | 0.698 | 0.784 | 0.619 | 0.794 | 0.785 | 0.777 | |
| SVMrbf | 0.788 | 0.614 | 0.695 | 0.774 | 0.630 | 0.796 | 0.781 | 0.766 | |
| LRMC | 0.765 | 0.617 | 0.681 | 0.778 | 0.695 | 0.811 | 0.790 | 0.771 | |
| mean-mkSVM | 0.782 | 0.629 | 0.703 | 0.779 | 0.626 | 0.806 | 0.787 | 0.781 | |
| mkSVM | 0.777 | 0.773 | 0.790 | 0.823 | 0.780 | 0.843 | 0.820 | 0.831 | |
|
| |||||||||
| FT4D | leastR | 0.715 | 0.479 | 0.554 | 0.670 | 0.610 | 0.751 | 0.711 | 0.677 |
| logisticR | 0.711 | 0.566 | 0.611 | 0.747 | 0.613 | 0.755 | 0.768 | 0.743 | |
| SVMlin | 0.782 | 0.616 | 0.702 | 0.781 | 0.647 | 0.787 | 0.784 | 0.777 | |
| SVMrbf | 0.788 | 0.605 | 0.699 | 0.775 | 0.633 | 0.795 | 0.783 | 0.764 | |
| LRMC | 0.765 | 0.614 | 0.682 | 0.782 | 0.679 | 0.810 | 0.794 | 0.771 | |
| mean-mkSVM | 0.782 | 0.616 | 0.704 | 0.781 | 0.644 | 0.787 | 0.789 | 0.786 | |
| mkSVM | 0.777 | 0.764 | 0.800 | 0.829 | 0.794 | 0.833 | 0.822 | 0.831 | |
4.8. Evaluation – Effect of Feature Selection Methods
We compared the performance when either Eq.(3) (igLeastR) or Eq.(4) (igLogisticR) is applied independently. Student’s t-test was also applied for feature selection by removing features that are not statistically significantly correlated with the class label (igt-test). We also compared our method with least-squares (glLeastR) and logistic (glLogisticR) group Lasso regressions (Liu et al., 2009). Specifically, regression is performed using the submatrix of complete data extracted from the full feature matrix (Figure 2(a)), and the weight matrix is penalized via l2,1-norm. Weights corresponding to features of the same ROI from different feature submatrices are grouped using the l2-norm and the different groups are associated using the l1-norm. Table 6 shows the average AUC of the proposed mkSVM (over 10 repetitions of 10-fold cross validation) using different feature selection methods and feature combinations (i.e., FT, FTD, and FT4D). The results show that our proposed feature selection method, in most cases, outperforms all other methods in terms of AUC. All feature selection methods, except igt-test, always show better AUC values, when using data FTD and FTD from all time points or from two well-separated time points (e.g., T4,1). The relatively lower performance of group Lasso is probably because 1) group Lasso tends to select ROIs that are discriminant for all time points, which possibly removes discriminant features that only appeared at certain time points, 2) only samples with a complete feature set are used in feature selection. In contrast, the proposed method avoids the weaknesses above by using elastic net regression on each feature submatrix. The superior performance of the proposed method over leastR and logisticR methods also shows the advantage of combining features selected by two elastic net regressions within each feature submatrix while at the same time requiring common feature sets across feature submatrices.
Table 6.
Classification AUC values for the proposed classifier (mkSVM) using different feature selection methods.
| Feature Combination | Feature Selection | Increasing Time Points | 2 Time Points | 3 Time Points | |||||
|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||
| 4 | 4,3 | 4,3,2 | 4,3,2,1 | 4,2 | 4,1 | 4,2,1 | 4,3,1 | ||
| FT | igLeastR | 0.761 | 0.769 | 0.768 | 0.767 | 0.777 | 0.761 | 0.772 | 0.778 |
| igLogisticR | 0.768 | 0.763 | 0.765 | 0.758 | 0.774 | 0.768 | 0.757 | 0.767 | |
| igt-test | 0.757 | 0.748 | 0.742 | 0.738 | 0.746 | 0.743 | 0.732 | 0.740 | |
| glLeastR | 0.761 | 0.750 | 0.757 | 0.750 | 0.746 | 0.751 | 0.753 | 0.762 | |
| glLogisticR | 0.777 | 0.763 | 0.766 | 0.767 | 0.774 | 0.761 | 0.765 | 0.759 | |
| Proposed | 0.777 | 0.771 | 0.774 | 0.770 | 0.775 | 0.778 | 0.769 | 0.769 | |
|
| |||||||||
| FTD | igLeastR | 0.761 | 0.753 | 0.754 | 0.810 | 0.772 | 0.829 | 0.807 | 0.818 |
| igLogisticR | 0.768 | 0.752 | 0.762 | 0.805 | 0.772 | 0.828 | 0.815 | 0.816 | |
| igt-test | 0.757 | 0.711 | 0.724 | 0.739 | 0.705 | 0.752 | 0.727 | 0.758 | |
| glLeastR | 0.761 | 0.675 | 0.691 | 0.790 | 0.716 | 0.810 | 0.794 | 0.800 | |
| glLogisticR | 0.777 | 0.709 | 0.732 | 0.803 | 0.739 | 0.811 | 0.813 | 0.795 | |
| Proposed | 0.777 | 0.773 | 0.790 | 0.823 | 0.780 | 0.843 | 0.820 | 0.831 | |
|
| |||||||||
| FT4D | igLeastR | 0.761 | 0.762 | 0.768 | 0.817 | 0.767 | 0.838 | 0.812 | 0.819 |
| igLogisticR | 0.768 | 0.771 | 0.781 | 0.814 | 0.780 | 0.833 | 0.820 | 0.829 | |
| igt-test | 0.757 | 0.727 | 0.741 | 0.750 | 0.709 | 0.754 | 0.744 | 0.762 | |
| glLeastR | 0.761 | 0.684 | 0.702 | 0.789 | 0.710 | 0.790 | 0.791 | 0.803 | |
| glLogisticR | 0.777 | 0.702 | 0.723 | 0.797 | 0.734 | 0.819 | 0.809 | 0.795 | |
| Proposed | 0.777 | 0.764 | 0.800 | 0.829 | 0.794 | 0.833 | 0.822 | 0.831 | |
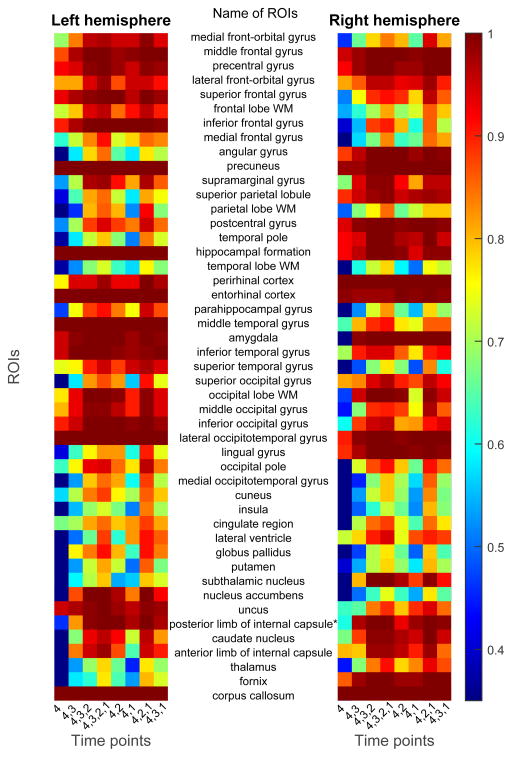
4.9. Frequency Map of Selected Features
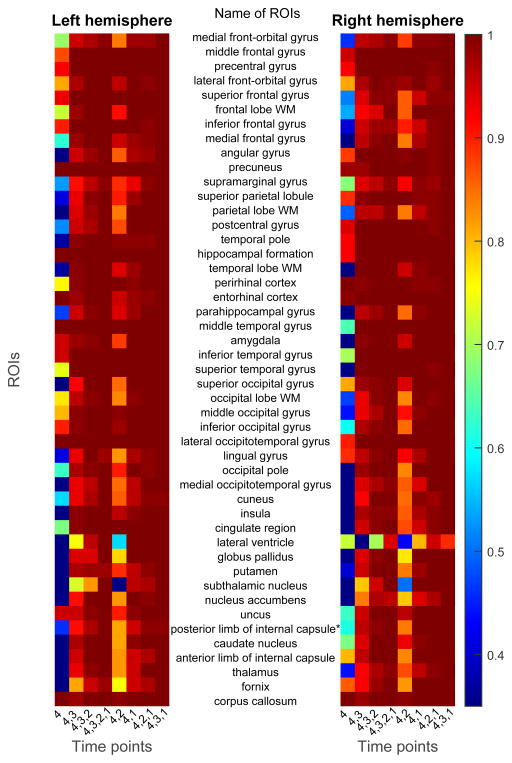
Figures 8 and 9 shows the frequency map of selected features using the proposed feature selection method, for FT and FT4D, respectively. The left and right maps of the figure show the feature selection frequency maps for ROIs from the left hemisphere and right hemisphere of the brain, respectively. Each row of the map denotes feature from one ROI, with its name shown between the two maps. There are 47 rows in each map, corresponding to 46 ROIs for each hemisphere and 1 ROI for the corpus callosum. Each column denotes a combination of time points. Comparing Figures 8 and 9, more ROIs are selected due to the existence of dynamic features. Some frequently selected ROIs include precuneus, hippocampal formation, perrihinal cortex, entorhinal cortex, amygala, middle temporal gyrus, inferior temporal gyrus, and lateral occipitotemporal gyrus. These regions are involved in memory formation, processing and storing (Burgess et al., 2002; Stanislav et al., 2013; Smith and Kosslyn, 2006; Poulin et al., 2011; Ranganath, 2006; Yonelinas et al., 2001). The corpus callosum, which is associated with AD and MCI (Di Paola et al., 2010; Wang et al., 2006), is also frequently selected.
Figure 8.
Frequencies of features selected using the proposed feature selection method and FT data, under different combinations of time points.
Figure 9.
Frequencies of features selected using the proposed feature selection method and FT4D data, under different combinations of time points.
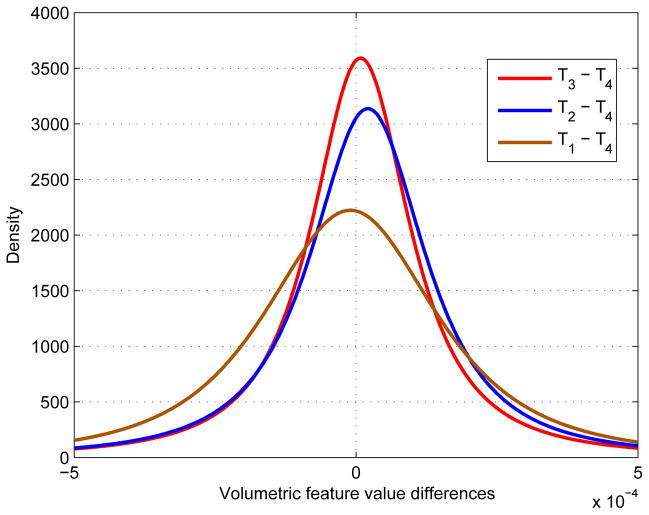
4.10. Probability Density Function of Dynamic Features
We have suggested previously that the improvement of pMCI identification using longitudinal data with longer scan time interval (Figure 6 and Figure 7) is due to the larger volumetric differences and hence more significant dynamic features. To evaluate the validity of this observation, we used 31 most frequently selected ROIs (Figure 9) and plot the distribution of the corresponding volumetric differences (i.e., {Ti – T4}) in Figure 10. The results indicate that the distribution of T1 – T4 is the broadest, followed by T2 – T4 and T3 – T4. This observation is consistent with our assumption that D1, which represents the dynamic features obtained from MRI data with relatively larger scan interval, is able to capture the variability between pMCI and sMCI subjects.
Figure 10.
Probability density function (pdf) of volumetric differences.
5. Conclusion
We have proposed a pMCI/sMCI classification framework that harnesses the additional information given by possibly incomplete longitudinal data. The experimental results demonstrate that classification performance improves when data from multiple time points with sufficient separation in scanning times are used. We also observed that, rather than using only static volumetric features, dynamic features can be used to improve classification performance. Feature selection using combined elastic net regressions has been shown to be more effective than feature selection using these regression techniques independently. The proposed classifier (mkSVM) outperforms other state-of-the-art classifiers when dynamic features are used. The best classification accuracy using two time points was achieved by mkSVM at 78.2%, which is 6.6% more than the accuracy it achieved by using only the reference time point. Similarly, the best AUC using two time points was achieved by mkSVM at 84.3%, which is 6.6% more than the AUC it achieved by using only the reference time point. In the future, we will extend the current framework to work with multiple imaging modalities (e.g., PET and CSF) and multiple clinical scores (e.g., MMSE (Wechsler, 1945) and ADAS (Doraiswamy et al., 1997)) to further improve classification performance.
Table 3.
Classification sensitivity.
| Classifiers | Increasing Time Points | 2 Time Points | 3 Time Points | ||||||
|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||
| 4 | 4,3 | 4,3,2 | 4,3,2,1 | 4,2 | 4,1 | 4,2,1 | 4,3,1 | ||
| FT | leastR | 0.650 | 0.620 | 0.634 | 0.655 | 0.638 | 0.667 | 0.652 | 0.641 |
| logisticR | 0.717 | 0.695 | 0.713 | 0.728 | 0.734 | 0.747 | 0.747 | 0.700 | |
| SVMlin | 0.760 | 0.713 | 0.743 | 0.750 | 0.749 | 0.743 | 0.742 | 0.729 | |
| SVMrbf | 0.765 | 0.734 | 0.738 | 0.749 | 0.732 | 0.722 | 0.729 | 0.738 | |
| LRMC | 0.713 | 0.706 | 0.720 | 0.736 | 0.746 | 0.745 | 0.752 | 0.718 | |
| mean-mkSVM | 0.760 | 0.713 | 0.736 | 0.750 | 0.749 | 0.743 | 0.750 | 0.735 | |
| mkSVM | 0.770 | 0.768 | 0.807 | 0.810 | 0.788 | 0.788 | 0.800 | 0.799 | |
|
| |||||||||
| FTD | leastR | 0.650 | 0.453 | 0.444 | 0.547 | 0.500 | 0.677 | 0.617 | 0.566 |
| logisticR | 0.717 | 0.597 | 0.645 | 0.713 | 0.658 | 0.723 | 0.743 | 0.705 | |
| SVMlin | 0.760 | 0.634 | 0.725 | 0.776 | 0.644 | 0.790 | 0.773 | 0.769 | |
| SVMrbf | 0.765 | 0.652 | 0.756 | 0.774 | 0.671 | 0.777 | 0.777 | 0.746 | |
| LRMC | 0.713 | 0.599 | 0.630 | 0.697 | 0.651 | 0.762 | 0.732 | 0.680 | |
| mean-mkSVM | 0.760 | 0.639 | 0.742 | 0.772 | 0.651 | 0.792 | 0.774 | 0.774 | |
| mkSVM | 0.770 | 0.833 | 0.792 | 0.829 | 0.781 | 0.882 | 0.838 | 0.858 | |
|
| |||||||||
| FT4D | leastR | 0.650 | 0.424 | 0.463 | 0.550 | 0.537 | 0.648 | 0.614 | 0.545 |
| logisticR | 0.717 | 0.608 | 0.610 | 0.713 | 0.663 | 0.760 | 0.752 | 0.688 | |
| SVMlin | 0.760 | 0.637 | 0.740 | 0.762 | 0.670 | 0.782 | 0.767 | 0.769 | |
| SVMrbf | 0.765 | 0.627 | 0.756 | 0.773 | 0.680 | 0.783 | 0.774 | 0.746 | |
| LRMC | 0.713 | 0.590 | 0.609 | 0.692 | 0.632 | 0.758 | 0.742 | 0.690 | |
| mean-mkSVM | 0.760 | 0.637 | 0.745 | 0.762 | 0.670 | 0.782 | 0.770 | 0.772 | |
| mkSVM | 0.770 | 0.819 | 0.801 | 0.848 | 0.793 | 0.875 | 0.822 | 0.869 | |
Table 4.
Classification specificity.
| Classifiers | Increasing Time Points | 2 Time Points | 3 Time Points | ||||||
|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||
| 4 | 4,3 | 4,3,2 | 4,3,2,1 | 4,2 | 4,1 | 4,2,1 | 4,3,1 | ||
| T | leastR | 0.677 | 0.648 | 0.671 | 0.655 | 0.695 | 0.690 | 0.693 | 0.660 |
| logisticR | 0.628 | 0.612 | 0.631 | 0.626 | 0.634 | 0.628 | 0.640 | 0.640 | |
| SVMlin | 0.702 | 0.683 | 0.710 | 0.708 | 0.718 | 0.729 | 0.709 | 0.684 | |
| SVMrbf | 0.694 | 0.678 | 0.679 | 0.683 | 0.702 | 0.707 | 0.689 | 0.663 | |
| LRMC | 0.700 | 0.697 | 0.723 | 0.718 | 0.692 | 0.700 | 0.718 | 0.690 | |
| mean-mkSVM | 0.702 | 0.683 | 0.705 | 0.708 | 0.718 | 0.729 | 0.709 | 0.692 | |
| mkSVM | 0.656 | 0.634 | 0.622 | 0.613 | 0.636 | 0.630 | 0.630 | 0.607 | |
|
| |||||||||
| FTD | leastR | 0.677 | 0.612 | 0.631 | 0.692 | 0.626 | 0.704 | 0.711 | 0.699 |
| logisticR | 0.628 | 0.448 | 0.519 | 0.626 | 0.501 | 0.665 | 0.629 | 0.630 | |
| SVMlin | 0.702 | 0.544 | 0.567 | 0.642 | 0.506 | 0.682 | 0.666 | 0.676 | |
| SVMrbf | 0.694 | 0.504 | 0.535 | 0.618 | 0.462 | 0.671 | 0.662 | 0.651 | |
| LRMC | 0.700 | 0.556 | 0.629 | 0.722 | 0.611 | 0.723 | 0.691 | 0.756 | |
| mean-mkSVM | 0.702 | 0.538 | 0.560 | 0.630 | 0.519 | 0.696 | 0.675 | 0.679 | |
| mkSVM | 0.656 | 0.580 | 0.615 | 0.641 | 0.642 | 0.670 | 0.669 | 0.639 | |
|
| |||||||||
| FT4D | leastR | 0.677 | 0.564 | 0.613 | 0.724 | 0.616 | 0.703 | 0.719 | 0.681 |
| logisticR | 0.628 | 0.486 | 0.525 | 0.637 | 0.513 | 0.648 | 0.634 | 0.652 | |
| SVMlin | 0.702 | 0.518 | 0.561 | 0.637 | 0.518 | 0.686 | 0.669 | 0.671 | |
| SVMrbf | 0.694 | 0.523 | 0.543 | 0.619 | 0.483 | 0.682 | 0.655 | 0.647 | |
| LRMC | 0.700 | 0.553 | 0.621 | 0.719 | 0.598 | 0.717 | 0.696 | 0.746 | |
| mean-mkSVM | 0.702 | 0.518 | 0.560 | 0.637 | 0.518 | 0.686 | 0.684 | 0.676 | |
| mkSVM | 0.656 | 0.595 | 0.644 | 0.668 | 0.671 | 0.667 | 0.673 | 0.626 | |
Acknowledgments
This work was supported in part by NIH grants AG041721, AG042599, EB006733, EB008374, and EB009634.
Data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) National Institutes of Health Grant U01 AG024904. ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering, and through generous contributions from the following: Abbott, AstraZeneca AB, Amorfix, Bayer Schering Pharma AG, Bioclinica Inc., Biogen Idec, Bristol-Myers Squibb, Eisai Global Clinical Development, Elan Corporation, Genentech, GE Healthcare, Innogenetics, IXICO, Janssen Alzheimer Immunotherapy, Johnson and Johnson, Eli Lilly and Co., Medpace, Inc., Merck and Co., Inc., Meso Scale Diagnostic, & LLC, Novartis AG, Pfizer Inc, F. Hoffman-La Roche, Servier, Synarc, Inc., and Takeda Pharmaceuticals, as well as non-profit partners the Alzheimer’s Association and Alzheimer’s Drug Discovery Foundation, with participation from the U.S. Food and Drug Administration. Private sector contributions to ADNI are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Disease Cooperative Study at the University of California, San Diego. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of California, Los Angeles. This research was also supported by NIH grants P30 AG010129, K01 AG030514, and the Dana Foundation.
Footnotes
Contributor Information
Kim-Han Thung, Email: khthung@email.unc.edu.
Dinggang Shen, Email: dgshen@med.unc.edu.
References
- Adeli-Mosabbeb E, Thung KH, An L, Shi F, Shen D. Robust feature-sample linear discriminant analysis for brain disorders diagnosis. Neural Information Processing Systems (NIPS) 2015 [Google Scholar]
- Ashburner J, Friston KJ. Voxel-based morphometrythe methods. Neuroimage. 2000;11:805–821. doi: 10.1006/nimg.2000.0582. [DOI] [PubMed] [Google Scholar]
- Bradley AP. The use of the area under the ROC curve in the evaluation of machine learning algorithms. Pattern recognition. 1997;30:1145–1159. [Google Scholar]
- Burgess N, Maguire EA, O’Keefe J. The human hippocampus and spatial and episodic memory. Neuron. 2002;35:625–641. doi: 10.1016/s0896-6273(02)00830-9. [DOI] [PubMed] [Google Scholar]
- Candès EJ, Recht B. Exact matrix completion via convex optimization. Foundations of Computational Mathematics. 2009;9:717–772. [Google Scholar]
- Chang CC, Lin CJ. LIBSVM: a library for support vector machines. ACM Transactions on Intelligent Systems and Technology (TIST) 2011;2:27. [Google Scholar]
- Davatzikos C, Bhatt P, Shaw LM, Batmanghelich KN, Trojanowski JQ. Prediction of MCI to AD conversion, via MRI, CSF biomarkers, and pattern classification. Neurobiology of aging. 2011;32:2322–e19. doi: 10.1016/j.neurobiolaging.2010.05.023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Paola M, Di Iulio F, Cherubini A, Blundo C, Casini A, Sancesario G, Passafiume D, Caltagirone C, Spalletta G. When, where, and how the corpus callosum changes in MCI and AD- a multimodal MRI study. Neurology. 2010;74:1136–1142. doi: 10.1212/WNL.0b013e3181d7d8cb. [DOI] [PubMed] [Google Scholar]
- Doraiswamy P, Bieber F, Kaiser L, Krishnan K, Reuning-Scherer J, Gulanski B. The Alzheimer’s disease assessment scale patterns and predictors of baseline cognitive performance in multicenter Alzheimer’s disease trials. Neurology. 1997;48:1511–1517. doi: 10.1212/wnl.48.6.1511. [DOI] [PubMed] [Google Scholar]
- Duda RO, Hart PE, Stork DG. Pattern classification. John Wiley & Sons; 2012. [Google Scholar]
- Friedman J, Hastie T, Tibshirani R. A note on the group lasso and a sparse group lasso. 2010 arXiv preprint arXiv:1001.0736. [Google Scholar]
- Gauthier S, Reisberg B, Zaudig M, Petersen RC, Ritchie K, Broich K, Belleville S, Brodaty H, Bennett D, Chertkow H, et al. Mild cognitive impairment. The Lancet. 2006;367:1262–1270. doi: 10.1016/S0140-6736(06)68542-5. [DOI] [PubMed] [Google Scholar]
- Goldberg A, Zhu X, Recht B, Xu J, Nowak R. Transduction with matrix completion: three birds with one stone. Advances in Neural Information Processing Systems. 2010;23:757–765. [Google Scholar]
- Gönen M, Alpaydin E. Multiple kernel learning algorithms. The Journal of Machine Learning Research. 2011;12:2211–2268. [Google Scholar]
- Haacke EM, Brown RW, Thompson MR, Venkatesan R. Magnetic resonance imaging. Wiley-Liss; New York: 1999. [Google Scholar]
- van der Heijden GJ, Donders TAR, Stijnen T, Moons KG. Imputation of missing values is superior to complete case analysis and the missing-indicator method in multivariable diagnostic research: a clinical example. Journal of clinical epidemiology. 2006;59:1102–1109. doi: 10.1016/j.jclinepi.2006.01.015. [DOI] [PubMed] [Google Scholar]
- Hinrichs C, Singh V, Xu G, Johnson S. MKL for robust multimodality AD classification, in: Medical Image Computing and Computer-Assisted Intervention–MICCAI 2009. Springer; 2009. pp. 786–794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hinrichs C, Singh V, Xu G, Johnson SC. Predictive markers for AD in a multi-modality framework: an analysis of MCI progression in the ADNI population. Neuroimage. 2011;55:574–589. doi: 10.1016/j.neuroimage.2010.10.081. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hua X, Leow AD, Parikshak N, Lee S, Chiang MC, Toga AW, Jack CR, Jr, Weiner MW, Thompson PM. Tensor-based morphometry as a neuroimaging biomarker for Alzheimer’s disease: an MRI study of 676 AD, MCI, and normal subjects. Neuroimage. 2008;43:458–469. doi: 10.1016/j.neuroimage.2008.07.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang L, Gao Y, Jin Y, Thung KH, Shen D. Machine Learning in Medical Imaging. Springer; 2015. Soft-split sparse regression based random forest for predicting future clinical scores of Alzheimers disease; pp. 246–254. [Google Scholar]
- Huang S, Li J, Ye J, Wu T, Chen K, Fleisher A, Reiman E. Identifying Alzheimer’s disease-related brain regions from multi-modality neuroimaging data using sparse composite linear discrimination analysis. Advances in Neural Information Processing Systems. 2011:1431–1439. [Google Scholar]
- Jack C, Dickson D, Parisi J, Xu Y, Cha R, Obrien P, Edland S, Smith G, Boeve B, Tangalos E, et al. Antemortem MRI findings correlate with hippocampal neuropathology in typical aging and dementia. Neurology. 2002;58:750–757. doi: 10.1212/wnl.58.5.750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack C, Petersen R, Xu Y, OBrien P, Smith G, Ivnik R, Boeve B, Waring S, Tangalos E, Kokmen E. Prediction of AD with MRI-based hippocampal volume in mild cognitive impairment. Neurology. 1999;52:1397–1397. doi: 10.1212/wnl.52.7.1397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jack CR, Bernstein MA, Fox NC, Thompson P, Alexander G, Harvey D, Borowski B, Britson PJ, Whitwell LJ, Ward C, et al. The Alzheimer’s disease neuroimaging initiative (ADNI): MRI methods. Journal of Magnetic Resonance Imaging. 2008;27:685–691. doi: 10.1002/jmri.21049. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kabani NJ. A 3D atlas of the human brain. Neuroimage. 1998;7:S717. [Google Scholar]
- Kohannim O, Hua X, Hibar DP, Lee S, Chou YY, Toga AW, Jack CR, Weiner MW, Thompson PM. Boosting power for clinical trials using classifiers based on multiple biomarkers. Neurobiology of aging. 2010;31:1429–1442. doi: 10.1016/j.neurobiolaging.2010.04.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lee SS. Noisy replication in skewed binary classification. Computational statistics & data analysis. 2000;34:165–191. [Google Scholar]
- Li F, Tran L, Thung KH, Ji S, Shen D, Li J. A robust deep model for improved classification of AD/MCI patients. Biomedical and Health Informatics. 2015 doi: 10.1109/JBHI.2015.2429556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu F, Wee CY, Chen H, Shen D. Inter-modality relationship constrained multi-modality multi-task feature selection for alzheimer’s disease and mild cognitive impairment identification. Neuro Image. 2014;84:466–475. doi: 10.1016/j.neuroimage.2013.09.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J, Ji S, Ye J. SLEP: Sparse Learning with Efficient Projections. Arizona State University; 2009. [Google Scholar]
- Liu M, Suk HI, Shen D. Multi-task sparse classifier for diagnosis of MCI conversion to AD with longitudinal MR images. In: Wu G, Zhang D, Shen D, Yan P, Suzuki K, Wang F, editors. Machine Learning in Medical Imaging. Springer International Publishing. volume 8184 of Lecture Notes in Computer Science. 2013. pp. 243–250. [Google Scholar]
- Ma S, Goldfarb D, Chen L. Fixed point and Bregman iterative methods for matrix rank minimization. Mathematical Programming. 2011;128:321–353. [Google Scholar]
- MacCallum RC, Browne MW, Sugawara HM. Power analysis and determination of sample size for covariance structure modeling. Psychological methods. 1996;1:130. [Google Scholar]
- Poulin SP, Dautoff R, Morris JC, Barrett LF, Dickerson BC. Amygdala atrophy is prominent in early Alzheimer’s disease and relates to symptom severity. Psychiatry Research: Neuroimaging. 2011;194:7–13. doi: 10.1016/j.pscychresns.2011.06.014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Querbes O, Aubry F, Pariente J, Lotterie JA, Démonet JF, Duret V, Puel M, Berry I, Fort JC, Celsis P, et al. Early diagnosis of Alzheimer’s disease using cortical thickness: impact of cognitive reserve. Brain. 2009;132:2036–2047. doi: 10.1093/brain/awp105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rakotomamonjy A, Bach FR, Canu S, Grandvalet Y. SimpleMKL. Journal of Machine Learning Research. 2008;9 [Google Scholar]
- Ranganath C. Working memory for visual objects: complementary roles of inferior temporal, medial temporal, and prefrontal cortex. Neuroscience. 2006;139:277–289. doi: 10.1016/j.neuroscience.2005.06.092. [DOI] [PubMed] [Google Scholar]
- Sanroma G, Wu G, Thung K, Guo Y, Shen D. Machine Learning in Medical Imaging. Springer; 2014. Novel multi-atlas segmentation by matrix completion; pp. 207–214. [Google Scholar]
- Schneider T. Analysis of incomplete climate data: Estimation of mean values and covariance matrices and imputation of missing values. Journal of Climate. 2001;14:853–871. [Google Scholar]
- Shen D, Davatzikos C. HAMMER: hierarchical attribute matching mechanism for elastic registration. IEEE Transactions on Medical Imaging. 2002;21:1421–1439. doi: 10.1109/TMI.2002.803111. [DOI] [PubMed] [Google Scholar]
- Simon N, Friedman J, Hastie T, Tibshirani R. A sparse-group lasso. Journal of Computational and Graphical Statistics. 2013;22:231–245. [Google Scholar]
- Sled JG, Zijdenbos AP, Evans AC. A nonparametric method for automatic correction of intensity nonuniformity in MRI data. IEEE Transactions on Medical Imaging. 1998;17:87–97. doi: 10.1109/42.668698. [DOI] [PubMed] [Google Scholar]
- Smith EE, Kosslyn SM. Cognitive psychology: Mind and brain. Pearson Prentice Hall; 2006. [Google Scholar]
- Speed T. Statistical analysis of gene expression microarray data. CRC Press; 2003. [Google Scholar]
- Stanislav K, Alexander V, Maria P, Evgenia N, Boris V. Anatomical characteristics of cingulate cortex and neuropsychological memory tests performance. Procedia-Social and Behavioral Sciences. 2013;86:128–133. [Google Scholar]
- Stefan JT, Pruessner JC, Faltraco F, Born C, Rocha-Unold M, Evans A, Möller HJ, Hampel H. Comprehensive dissection of the medial temporal lobe in ad: measurement of hippocampus, amygdala, entorhinal, perirhinal and parahippocampal cortices using MRI. Journal of neurology. 2006;253:794–800. doi: 10.1007/s00415-006-0120-4. [DOI] [PubMed] [Google Scholar]
- Swets JA. Measuring the accuracy of diagnostic systems. Science. 1988;240:1285–1293. doi: 10.1126/science.3287615. [DOI] [PubMed] [Google Scholar]
- Thung KH, Wee CY, Yap PT, Shen D. Machine Learning in Medical Imaging. Springer; 2013. Identification of Alzheimers Disease using incomplete multimodal dataset via matrix shrinkage and completion; pp. 163–170. [Google Scholar]
- Thung KH, Wee CY, Yap PT, Shen D. Neurodegenerative disease diagnosis using incomplete multi-modality data via matrix shrinkage and completion. Neuroimage. 2014;91:386–400. doi: 10.1016/j.neuroimage.2014.01.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thung KH, Yap PT, Adeli-M E, Shen D. Medical Image Computing and Computer-Assisted InterventionMICCAI 2015. Springer; 2015. Joint diagnosis and conversion time prediction of progressive mild cognitive impairment (pmci) using low-rank subspace clustering and matrix completion; pp. 527–534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tibshirani R. Regression shrinkage and selection via the lasso. Journal of the Royal Statistical Society. Series B (Methodological) 1996:267–288. [Google Scholar]
- Troyanskaya O, Cantor M, Sherlock G, Brown P, Hastie T, Tibshirani R, Botstein D, Altman RB. Missing value estimation methods for DNA microarrays. Bioinformatics. 2001;17:520–525. doi: 10.1093/bioinformatics/17.6.520. [DOI] [PubMed] [Google Scholar]
- Wang H, Nie F, Huang H, Risacher SL, Saykin AJ, Shen L, et al. Identifying disease sensitive and quantitative trait-relevant biomarkers from multidimensional heterogeneous imaging genetics data via sparse multimodal multitask learning. Bioinformatics. 2012;28:i127–i136. doi: 10.1093/bioinformatics/bts228. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang PJ, Saykin AJ, Flashman LA, Wishart HA, Rabin LA, Santulli RB, McHugh TL, MacDonald JW, Mamourian AC. Regionally specific atrophy of the corpus callosum in AD, MCI and cognitive complaints. Neurobiology of aging. 2006;27:1613–1617. doi: 10.1016/j.neurobiolaging.2005.09.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Nie J, Yap PT, Li G, Shi F, Geng X, Guo L, Shen D, Initiative ADN, et al. Knowledge-guided robust mri brain extraction for diverse large-scale neuroimaging studies on humans and non-human primates. PloS one. 2014;9:e77810. doi: 10.1371/journal.pone.0077810. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Y, Nie J, Yap PT, Shi F, Guo L, Shen D. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2011. Springer; 2011. Robust deformable-surface-based skull-stripping for large-scale studies; pp. 635–642. [DOI] [PubMed] [Google Scholar]
- Wechsler D. A standardized memory scale for clinical use. The Journal of Psychology. 1945;19:87–95. [Google Scholar]
- Wee CY, Yap PT, Denny K, Browndyke JN, Potter GG, Welsh-Bohmer KA, Wang L, Shen D. Resting-state multi-spectrum functional connectivity networks for identification of mci patients. PLOS ONE. 2012a;7:e37828. doi: 10.1371/journal.pone.0037828. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wee CY, Yap PT, Li W, Denny K, Browndyke JN, Potter GG, Welsh-Bohmer KA, Wang L, Shen D. Enriched white matter connectivity networks for accurate identification of MCI patients. Neuro Image. 2011;54:1812–1822. doi: 10.1016/j.neuroimage.2010.10.026. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wee CY, Yap PT, Shen D. Prediction of alzheimer’s disease and mild cognitive impairment using cortical morphological change patterns. Human Brain Mapping. 2013;34:3411–3425. doi: 10.1002/hbm.22156. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wee CY, Yap PT, Wang L, Shen D. Group-constrained sparse fmri connectivity modeling for mild cognitive impairment identification. Brain Structure and Function. 2014;219:641–656. doi: 10.1007/s00429-013-0524-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wee CY, Yap PT, Zhang D, Denny K, Browndyke JN, Potter GG, Welsh-Bohmer KA, Wang L, Shen D. Identification of MCI individuals using structural and functional connectivity networks. Neuro Image. 2012b;59:2045–2056. doi: 10.1016/j.neuroimage.2011.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weiner MW, Veitch DP, Aisen PS, Beckett LA, Cairns NJ, Green RC, Harvey D, Jack CR, Jagust W, Liu E, et al. The Alzheimer’s disease neuroimaging initiative: A review of papers published since its inception. Alzheimer’s & Dementia. 2013;9:e111–e194. doi: 10.1016/j.jalz.2013.05.1769. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Whitwell JL, Shiung MM, Przybelski S, Weigand SD, Knopman DS, Boeve BF, Petersen RC, Jack CR. MRI patterns of atrophy associated with progression to AD in amnestic mild cognitive impairment. Neurology. 2008;70:512–520. doi: 10.1212/01.wnl.0000280575.77437.a2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yonelinas A, Hopfinger J, Buonocore M, Kroll N, Baynes K. Hippocampal, parahippocampal and occipital-temporal contributions to associative and item recognition memory: an fMRI study. Neuroreport. 2001;12:359–363. doi: 10.1097/00001756-200102120-00035. [DOI] [PubMed] [Google Scholar]
- Zhang D, Liu J, Shen D. Medical Image Computing and Computer-Assisted Intervention–MICCAI 2012. Springer; 2012. Temporally-constrained group sparse learning for longitudinal data analysis; pp. 264–271. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang D, Shen D. Multi-modal multi-task learning for joint prediction of multiple regression and classification variables in Alzheimer’s disease. Neuroimage. 2012a;59:895–907. doi: 10.1016/j.neuroimage.2011.09.069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang D, Shen D. Predicting future clinical changes of MCI patients using longitudinal and multimodal biomarkers. PloS one. 2012b;7:e33182. doi: 10.1371/journal.pone.0033182. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang Y, Brady M, Smith S. Segmentation of brain MR images through a hidden Markov random field model and the expectation-maximization algorithm. IEEE Transactions on Medical Imaging. 2001;20:45–57. doi: 10.1109/42.906424. [DOI] [PubMed] [Google Scholar]
- Zhou J, Liu J, Narayan VA, Ye J. Proceedings of the 18th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM; 2012. Modeling disease progression via fused sparse group lasso; pp. 1095–1103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou L, Wang Y, Li Y, Yap PT, Shen D, et al. Hierarchical anatomical brain networks for MCI prediction: revisiting volumetric measures. PloS one. 2011;6:e21935. doi: 10.1371/journal.pone.0021935. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X, Suk HI, Zhu Y, Thung KH, Wu G, Shen D. Machine Learning in Medical Imaging. Springer; 2015. Multi-view classification for identification of Alzheimers disease; pp. 255–262. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zou H, Hastie T. Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society: Series B (Statistical Methodology) 2005;67:301–320. [Google Scholar]