Abstract
For thermal modeling to play a significant role in treatment planning, monitoring, and control of magnetic resonance-guided focused ultrasound (MRgFUS) thermal therapies, accurate knowledge of ultrasound and thermal properties is essential. This study develops a new analytical solution for the temperature change observed in MRgFUS which can be used with experimental MR temperature data to provide estimates of the ultrasound initial heating rate, Gaussian beam variance, tissue thermal diffusivity, and Pennes perfusion parameter. Simulations demonstrate that this technique provides accurate and robust property estimates that are independent of the beam size, thermal diffusivity, and perfusion levels in the presence of realistic MR noise. The technique is also demonstrated in vivo using MRgFUS heating data in rabbit back muscle. Errors in property estimates are kept less than 5% by applying a third order Taylor series approximation of the perfusion term and ensuring the ratio of the fitting time (the duration of experimental data utilized for optimization) to the perfusion time constant remains less than one.
Keywords: MR thermometry, high-intensity focused ultrasound, SAR, thermal diffusivity, perfusion
1. Introduction
Thermal modeling plays an important role in ongoing efforts to improve magnetic resonance-guided focused ultrasound (MRgFUS) thermal therapies. While current treatment strategies use magnetic resonance temperature imaging (MRTI) during the therapy alone for treatment guidance, effective use of thermal modeling can improve safety and streamline and shorten the overall treatment time, a known treatment limiting factor (Wu et al 2003, Kim et al 2011, 2012). For example, thermal modeling can be used to preemptively adjust treatments to prevent violation of tissue safety constraints and mitigate risks to healthy tissues and critical structures. Thermal modeling can also be used during treatment planning to make therapies more time efficient by tailoring power and duration settings to balance healthy tissue constraints with a desire for fast target treatment without excessive overdosing (Burtnyk et al 2010, Jenne et al 2012, Salgaonkar et al 2014, Schwenke et al 2015). During the treatment, thermal models can provide information to increase the spatial and temporal resolution or volumetric coverage of temperature monitoring (Todd et al 2010, Roujol et al 2012, de Senneville et al 2013, Odéen et al 2015). In addition to improved safety monitoring, these additional data can provide model-predictive controllers with treatment feedback guiding impromptu adjustments for optimized thermal therapies (Salomir et al 2000, Vanne and Hynynen 2003, Arora et al 2006, de Bever et al 2014). In each of these cases, however, the value of thermal models and the treatment predictions they provide depends upon the accuracy of the ultrasound and thermal properties used in those models.
With the development of accurate and robust MRTI capabilities comes the opportunity to develop or improve patient-specific property estimation procedures that are less invasive and less susceptible to positional uncertainties and noise errors than previous methods. In recent years, MRTI has been used in estimation techniques for determining a variety of ultrasound (Salomir et al 2000, Dragonu et al 2009, Dillon et al 2012, 2013, Appanaboyina et al 2013, Alon et al 2013), thermal (Cline et al 1994, Salomir et al 2000, Cheng and Plewes 2002, Huttunen et al 2006, Sumi and Yanagimura 2007, Dragonu et al 2009, Cornelis et al 2011, Zhang et al 2013, Appanaboyina et al 2013, Alon et al 2013, Dillon et al 2013, 2014, Zhang et al 2013, 2015), and perfusion properties (Cheng and Plewes 2002, Huttunen et al 2006, Dragonu et al 2009, Cornelis et al 2011, Appanaboyina et al 2013, Alon et al 2013, Dillon et al 2015).
This paper introduces a new analytical temperature solution that can be used with MRgFUS temperature data to provide estimates of four parameters of interest in patient-specific modeling: the ultrasound initial heating rate (IHR) and Gaussian beam variance (β), the tissue thermal diffusivity (α), and the Pennes perfusion parameter (w). This is the first analytical solution for estimating all of these parameters that incorporates finite duration ultrasound heating and the effects of perfusion. The solution is made possible by replacing the exponential perfusion term in a commonly applied focused ultrasound integral equation with its Taylor series approximation. A parametric simulation study assesses how the order of the Taylor series approximation, optimization fitting parameters, random Gaussian noise, and various ultrasound and thermal properties affect the estimation results. The technique is then demonstrated with in vivo MRTI data from focused ultrasound heating in rabbit back muscle. By applying the extensive dynamic and spatial MRgFUS data to the simultaneous estimation of these important parameters, this technique has unique potential to provide accurate properties for improved thermal modeling of MRgFUS thermal therapies.
2. Theory
2.1. Heating solution
The transverse plane (figure 1) temperature change profile during focused ultrasound heating, Theat (°C), as a function of radial position r (mm) from the beam axis and time t (s) since the onset of heating, assuming a Gaussian power distribution with no axial conduction, uniform thermal properties, and perfusion modeled as a scalar thermal energy sink (Pennes 1948), is expressed by (Cline et al 1994)
Figure 1.
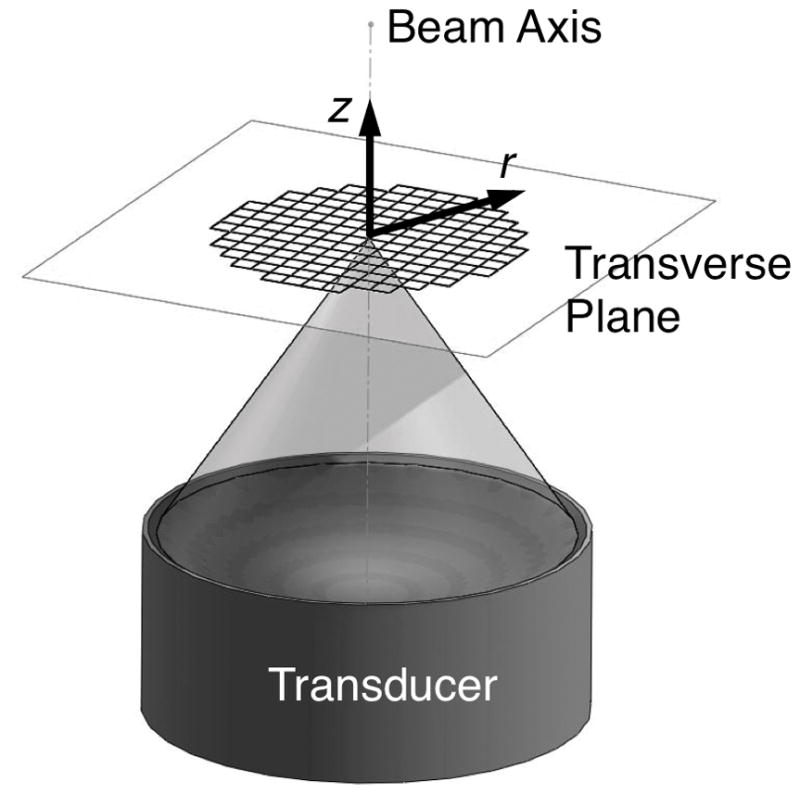
Orientation of coordinate axes for property estimation with respect to the ultrasound transducer.
| (1) |
where IHR is the initial heating rate (°C/s) and β is the Gaussian variance (mm2) of the ultrasound beam. The perfusion time constant τbl (s) is related to the Pennes perfusion parameter w (kg/m3/s), tissue density ρ (kg/m3), and specific heats of tissue cp and blood cbl (J/kg/°C) by the equation τbl=ρcp/(wcbl). The conduction time constant τc (s) depends upon tissue thermal diffusivity α (mm2/s) and β according to τc=β/(4α).
In the past, applying (1) for analytical estimation of ultrasound and thermal properties has required eliminating the time integral through the assumption of instantaneous heating (Parker 1983, Cheng and Plewes 2002, Anand and Kaczkowski 2008, 2009, Dragonu et al 2009, Cornelis et al 2011, Zhang et al 2013, 2015) or simplifying the integrand for evaluation by neglecting perfusion (Cline et al 1994, Dillon et al 2012, 2013, 2014) and/or utilizing only the center-line, on-axis solution (Parker 1985, Kress and Roemer 1987, Cline et al 1994, Dillon et al 2012). To our knowledge, the full analytical solution of (1) cannot be directly evaluated.
2.2. Taylor series expansion of perfusion
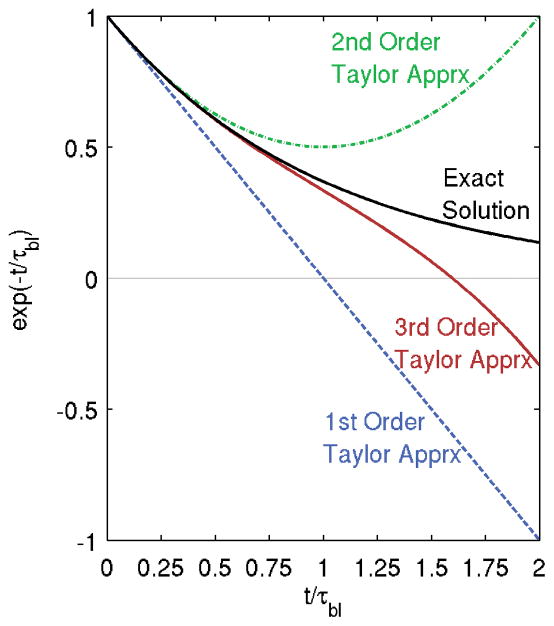
However, by approximating the exponential perfusion term with a low-order Taylor series expansion, obtaining a closed-form analytical solution to (1) is possible. In this study, we evaluate the 1st, 2nd, and 3rd order Taylor series perfusion term approximations (i.e. 3rd order approximation: exp(−t/τbl) ≈ 1 − (t/τbl) + (t/τbl)2/2 − (t/τbl)3/6). Figure 2 shows the exponential perfusion term exp(−t/τbl) and the proposed Taylor series approximations as a function of the exponential argument t/τbl. It is clear that the higher order approximations will remain valid for longer times, with approximation errors greater than 5% occurring at t/τbl> 0.29, 0.58, and 0.88 for the 1st, 2nd, and 3rd order approximations, respectively.
Figure 2.
The exponential perfusion term exp(−t/τbl) and its Taylor series approximations as a function of the argument t/τbl.
2.3. Taylor series-approximated analytical heating solutions
After substituting the appropriate Taylor series approximation into (1), the time integral can be evaluated for a closed-form analytical solution. These solutions are given in table 1, where Ei refers to the exponential integral function (Abramowitz and Stegun 1964). While the higher order approximations should remain valid for longer times, they also increase the complexity of the analytical solution and may increase the computation time required for identifying the parameters of interest.
Table 1.
Closed-form analytical temperature solutions during ultrasound heating.
| Order of Approximation | Temperature solution | ||
|---|---|---|---|
| 1 |
|
||
| 2 |
|
||
| 3 |
|
2.4. Taylor series-approximated analytical cooling solutions
It may be beneficial to include the analytical cooling solution in the estimation process, especially when short ultrasound heating durations, th (s), limit the number of MRTI acquisitions during heating. The desired cooling solutions are obtained by the superposition of heating solutions according to (Cline et al 1994, Dillon et al 2014)
| (5) |
These solutions are presented in table S1 of the supplementary material.
2.5. Estimation of ultrasound, thermal, and blood flow properties
Even though the complexity of the analytical solutions varies for the different order Taylor series approximations, the same parameters are required in each variant. With known times t and th and radial positions r for the MRTI data, the heating [(2), (3), or (4)] and/or cooling [(S1), (S2), or (S3)] solutions can be optimized in a least-squares minimization utilizing four parameters: IHR, β, τc, andτbl. The tissue thermal diffusivity (α) can be calculated from fitting parameters β and τc and the Pennes perfusion parameter (w) from τbl. While many previous methods have employed only single position data or required multi-step estimation procedures, this method can estimate each of these four important parameters using temperature data from multiple locations and times simultaneously.
3. Methods
3.1. Numerical simulations of temperature data
The ultrasound power deposition pattern was simulated as a radial Gaussian in a 2D plane perpendicular to the beam axis at a spatial resolution of 0.1 mm isotropic. As part of the parametric study, the full width at half maximum (FWHM) of the ultrasound varied between 1, 1.5, 3, and 5 mm, with a nominal value of 3 mm. The magnitude of the power deposition was adjusted to yield 10 °C temperature rise during thermal simulations. Temperatures were calculated with a 2D finite-difference time-domain solver at a spatial and temporal resolution of 0.1 mm isotropic and 0.01 s, respectively. The ultrasound heating time th was 24 s (approximately the duration of current clinical sonications) and cooling temperatures were simulated for an additional 24 s. Adiabatic boundary conditions were assumed at the edges of the model and the blood temperature was assumed equal to the uniform, initial tissue temperature. Tissue density was set at 1000 kg/m3 and tissue and blood specific heats were assumed equal at a value of 4000 J/kg/°C. The parameter study adjusted the tissue thermal diffusivity α between values of 0.075, 0.1, 0.125, 0.15, and 0.175 mm2/s (nominal α = 0.125 mm2/s), and the Pennes perfusion parameter w was simulated at 1, 5, 10, 20, 30, 40, and 50 kg/m3/s (nominal w = 5 kg/m3/s). To more realistically represent MRTI data, the temperatures were subsampled to 0.5 mm isotropic spatial resolution and 4 s temporal resolution. In high signal regions, MRI noise distributions can be approximated by a Gaussian function (Anand and Sahambi 2010); therefore, random Gaussian noise was added to the temperatures with a standard deviation (SD) of 0.1, 0.2, 0.5, 1, and 2 °C (nominal noise = 0.2 °C). The study included 250 independent noise trials for each parameterized case. In a few cases, no noise was added to the data to identify errors under ideal conditions.
3.2. Optimization of parameters to estimate properties
The properties of interest were estimated as described in section 2.5 on an Intel Core 2 Duo T6500 Processor (2.10 GHz, 4.00 GB RAM) using MATLAB function fminsearchbnd. This function places constraints on each of the four fitting parameters (IHR: 0–10, β: 0–10, τc:0–25, and τbl:10–∞), but still allows for a range of values larger than would be anticipated clinically. For reference, values of τbl calculated using a tissue property database compiled from many studies are presented in table 2 (Hasgall et al 2015). Fitting parameters for each trial started from a random initial guess. The study assessed the order of the Taylor series approximation in the analytical solutions, and the 3rd order approximation was used in the nominal case. Two parameters related to the selection of data in the optimization process were also considered in the parametric study. First, the fitting time included the first 8, 16, 24, 32, 40, or 48 s of simulated data (nominal fitting time= 48 s). Second, the fitting radius (0, 2, 4, or 6 mm) incorporated all data within that distance of the beam axis (see portrayal in figure 1) in the optimization process (nominal fitting radius= 4 mm). A fitting radius of 0 mm indicates that only the data from the point at the center of the focal zone (r=0) are included, requiring use of the on-axis analytical solution provided by Kress and Roemer (1987) and its corresponding cooling solution evaluated using (5).
Table 2.
Pennes perfusion parameter w and perfusion time constants τbl for various tissues (Hasgall et al 2015).
| Tissue | w (kg/m3/s) | τbl (s) |
|---|---|---|
| Kidney | 63 | 18 |
| Heart Muscle | 17 | 64 |
| Liver | 14 | 74 |
| Brain | 9 | 113 |
| Uterus | 8 | 147 |
| Fat | 0.6 | 1075 |
| Muscle | 0.6 | 1672 |
| Nonperfused tissue | 0 | ∞ |
3.3 Experimental protocol
To demonstrate the technique in vivo, MRgFUS was performed on a female New Zealand white rabbit under IACUC approval. The rabbit was placed supine on the MRgFUS system under general anesthesia, and the back muscle was sonicated with an acoustic power of 8 W for 24 s (see figure 3 for setup). MR temperature images (Siemens 3T Trio, 3D segmented echo planar imaging (EPI), repetition time = 36 ms, echo time = 11 ms, flip angle = 20°, bandwidth = 744 Hz/pixel, EPI factor = 9, spatial resolution = 1×1×3 mm, field of view = 192×114 mm, 8 slices with 25% oversampling, temporal resolution = 4.7 s) were acquired with a single-loop coil positioned under the rabbit and a two-channel surface coil placed on the rabbit’s abdomen. The coil signals were weighted and combined by the inverse covariance matrix (Roemer et al 1990), data were zero-filled interpolated to 0.5 mm isotropic resolution (Todd et al 2011, Dillon et al 2013), and temperatures were calculated with the proton resonance frequency method (De Poorter et al 1995, Ishihara et al 1995) using a 2D referenceless technique with fifth order polynomial (Rieke et al 2004). Tissue properties were estimated with the 3rd order Taylor series approximation using a fitting time of 80 s and fitting radius of 10 mm in the transverse plane where the maximum temperature rise occurred. After the animal was euthanized, invasive thermal diffusivity measurements were made in the back muscle with a commercial thermal property analyzer (KD2 Pro, Decagon Devices, Pullman, WA, USA).
Figure 3.
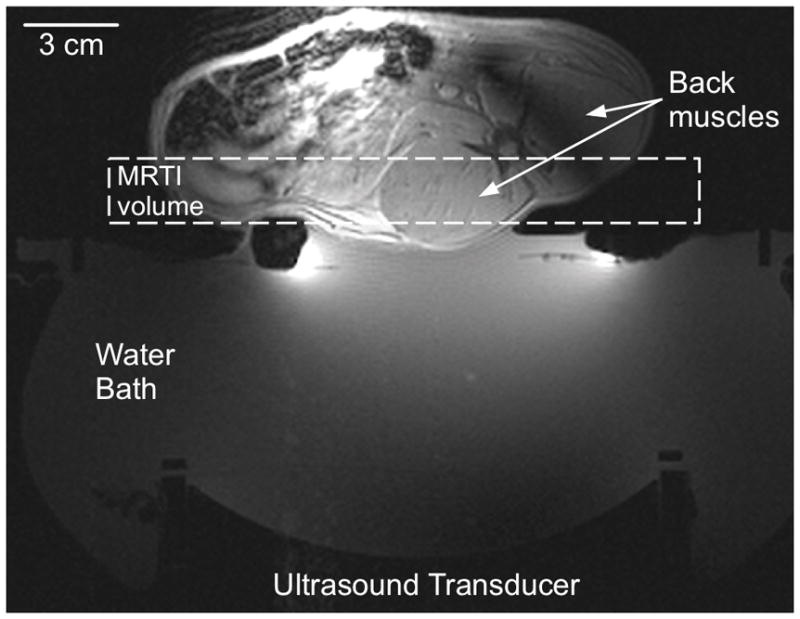
Experimental setup for in vivo estimation of properties in rabbit back muscle. The ultrasound transducer sonicates vertically through a coupling water bath to focus in the center of the back muscle. The MR temperature imaging volume is identified with a dashed box.
4. Results
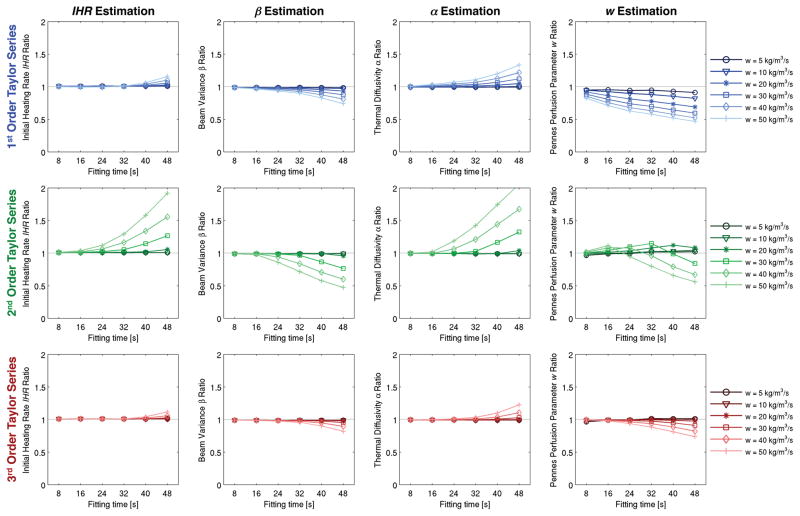
Noise-free simulation results are shown in figure 4, in which the fitting time (x-axis), Taylor series approximation order (rows), and Pennes perfusion parameter w are varied (color gradation). Results are normalized on the y-axis as the ratio of the estimated to true property values. These plots show that, in the absence of noise, results are most accurate for low perfusion levels and short fitting times. In addition, the 3rd order Taylor series approximation is consistently the most accurate. As perfusion and fitting times increase, property estimates using the 2nd order Taylor series approximation degrade significantly.
Figure 4.
Noise-free estimation results with variation of fitting time (x-axis), order of Taylor series approximation (rows), and perfusion levels (color gradations). Property estimates are normalized by their true values.
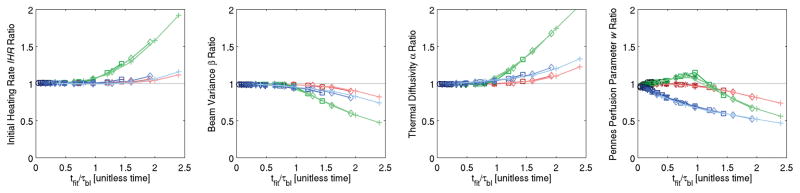
Figure 5 combines all the results of figure 4, and its x-axis (tfit = fitting time) is non-dimensionalized by the perfusion time constant τbl. For each Taylor series approximation order, results for different perfusion levels overlap. Thus, regardless of perfusion level, accurate estimates of IHR, β, and α (< 7% error) can be made using any of the Taylor series approximations with the condition that tfit/τbl < 1. However, accurate estimates of w require a 3rd order Taylor series approximation and that tfit/τbl < 1 for < 5% error or tfit/τbl < 1.5 for < 10% error.
Figure 5.
Combination of all figure 4 results with the x-axis non-dimensionalized by the perfusion time constant τbl. When estimating IHR, β, and α < 7% error is possible using any of the Taylor series approximations if tfit/τbl < 1. When estimating w, a 3rd order Taylor series approximation and tfit/τbl < 1 results in errors <5%. See figure 4 for color legends.
As fitting times increased from 8 to 48 s, average computation times for estimating properties ranged from 42–61 s for the 1st order Taylor series approximation, 42–65 s for the 2nd order approximation, and 52–78 s for the 3rd order approximation.
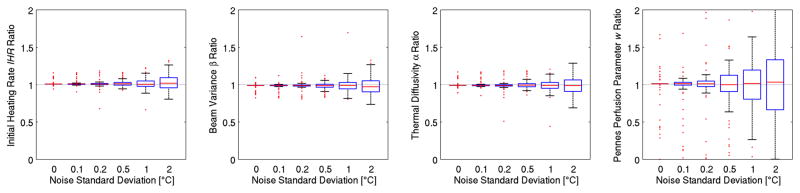
Figure 6 uses box-and-whisker plots of the 250 trials at each noise level to show that increased noise in temperature data leads to more variability in property estimates, as expected. The Pennes perfusion parameter w is the property most sensitive to noise.
Figure 6.
Property estimation as a function of noise in the temperature measurements. The Pennes perfusion parameter w is the property most sensitive to noise.
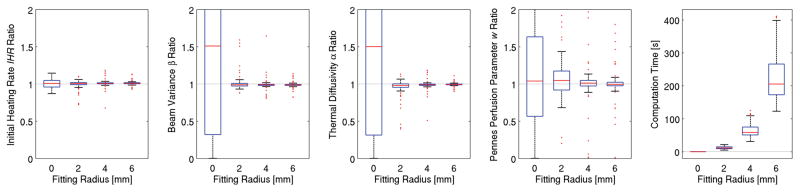
Increasing the fitting radius reduces variability in property estimates as seen in figure 7. The number of voxels included in the optimization process was 1, 45, 193, and 437 for the 0, 2, 4, and 6 mm fitting radius, respectively. The greater computational burden of using more voxels’ data for a larger fitting radius results in longer computation times (rightmost plot of figure 7).
Figure 7.
Property estimation as a function of the fitting radius. As the fitting radius increases, variability in estimates decreases and the computation time increases.
The size of the ultrasound beam has minimal effect upon property estimates, with <5% reduction in the interquartile range (IQR) for all estimates when increasing the beam FWHM from 1 to 5 mm (see supplemental data). In all cases, the median value was within 1% of the true property value.
Variation in the tissue thermal diffusivity α does not produce any observable differences in property estimates (see supplemental data). The entire IQR was contained within ±2%, ±3%, ±3%, and ±6% of the true values for IHR, β, α, and w, respectively.
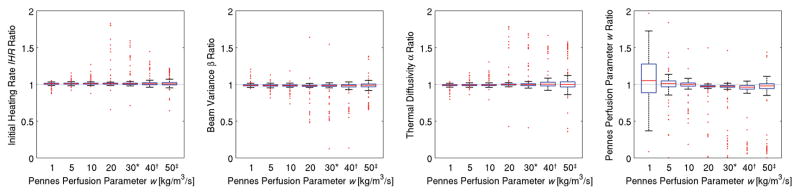
In figure 8, the Pennes perfusion parameter w is varied, and fitting times are adjusted for perfusions greater than 20 kg/m3/s to ensure that tfit/τbl < 1. When estimating IHR, β, and α, changes in perfusion do not result in observable changes in estimation. The variability of w estimates decreases with increasing perfusion values. When fitting times are reduced to ensure tfit/τbl < 1, a slight increase in the variability of results is seen.
Figure 8.
Property estimation as a function of the Pennes perfusion parameter w. By adjusting the fitting time such that tfit/τbl < 1 (*: tfit=32 s, †: tfit=24 s, ‡: tfit=16 s), accurate property estimates are made regardless of perfusion levels. The variability of w estimates first decreases with increasing perfusion but then increases when the fitting times are reduced.
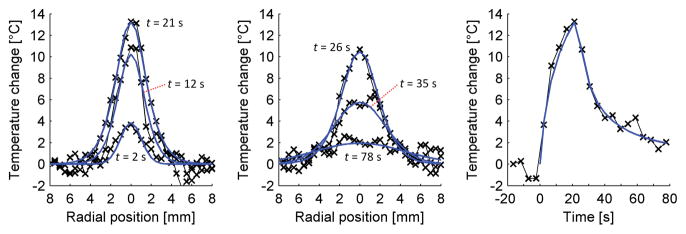
Several locations and times from the least-squares fit (blue line) of (4) to the in vivo MRgFUS data (× markers) are shown in figure 9. The left plot includes data from the heating period at times t = 2, 12, and 21 s. The middle plot shows cooling temperatures at times t = 26, 35, and 78 s. The right plot shows the experimental temperature versus time curve and fit at the location of maximum temperature change (13.9 °C). The properties estimated for these data are IHR = 2.3 °C/s, β= 1.5 mm2, α= 0.146 mm2/s, and w = 1.3 kg/m3/s. Invasive measurements of thermal diffusivity (N=5) have a mean and standard deviation value of 0.155± 0.008 mm2/s.
Figure 9.
Experimental MRgFUS temperature data in rabbit back muscle with optimized least-squares fit. The left plot shows temperatures and fit during heating, while the middle plot includes data during the cooling period. The right plot shows the experimental temperature versus time curve and fit at the location of maximum temperature change.
5. Discussion
The primary finding of this study is that by utilizing a 3rd order Taylor series expansion of the exponential perfusion term, a closed-form analytical temperature solution is attainable that can be used with MRTI data for accurate property estimation independent of beam size, tissue thermal diffusivity and perfusion levels, provided that the data for fitting is selected such that tfit/τbl < 1.
5.1. Effects of solution properties
The 3rd order Taylor series approximation consistently provided the most accurate property estimates and maintained <5% error under the condition tfit/τbl < 1. Somewhat surprisingly, results with the 2nd order Taylor series approximation were generally worse than those of the 1st order approximation. This most likely occurs because the 2nd order expression overpredicts perfusion when the approximation is invalid (see figure 2), thus overemphasizing its contribution in the analytical expression, while the 1st order expression underpredicts perfusion, which reduces the impact of its error in the estimation process.
5.2. Effects of fitting properties
In the noise-free case, better estimates of all properties are obtained when using a short fitting time. With the addition of noise, which is always present in reality, utilizing additional data from more fitting points is desirable. Because the analytical solution becomes invalid for long times, it is recommended that the choice of fitting time be constrained by tfit/τbl < 1. This constraint should only be consequential when high perfusion values are anticipated in the tissue of interest, i.e. in the kidneys (see table 2).
Using a single voxel (fitting radius = 0 mm) eliminates information about the spatial distribution of temperatures and explains why estimates of spatial parameters β and α could not be made for that case (figure 6). While estimates of IHR and w can be made with the center-point solution, increasing the fitting radius led to a dramatic reduction in the variability of results and demonstrates the value of the extensive data available from MRTI. However, there may be diminishing returns with increased fitting radius as temperature changes relative to the noise decrease with increasing distance from the ultrasound beam axis and computation times increase.
5.3. Effects of noise and ultrasound properties
The Pennes perfusion parameter w was found to be the property most sensitive to noise in the temperature data, because it has the smallest effect of all estimated properties upon the temporal and spatial distribution of temperatures. It is noteworthy that in the absence of noise, 9% of the 250 trials failed to converge to within ±5% of the true property values because MATLAB exits the optimization algorithm if the solution has not converged within 800 iterations. This occurs because the search space is shallow, particularly in the perfusion dimension, and errors in one parameter are compensated by offsets in other parameters, slowing convergence to the global minimum, i.e. the true property values. With more advanced optimization algorithms, it is likely that the solution would converge more quickly and these outliers would be eliminated.
Increasing the size of the ultrasound beam led to minor improvements in estimation results. While the effect of IHR was not assessed, a greater IHR will increase the magnitude of temperature changes and should lead to improved estimation results.
5.4. Effects of tissue properties
Accurate property estimates were made for all thermal diffusivity and perfusion values tested. Changes to thermal diffusivity had limited effect upon the variability of property estimates and greater perfusion values led to less variability in property estimates. However, under the constraint tfit/τbl < 1, the shorter fitting times required by high perfusion values led to increased variability in estimates.
5.5. Experimental demonstration of technique
The demonstration of the technique with MRTI data in rabbit back muscle shows that property estimates with in vivo data are possible. The initial slope of the temperature versus time curve and the width of the temperatures over time were well matched by the fitting parameters of IHR and β. The thermal diffusivity estimate was within 6% of the mean measured thermal diffusivity. Differences between the estimated perfusion value (1.3 kg/m3/s) and published values for muscle perfusion (0.6 kg/m3/s) are negligible when considering the minimal impact such low perfusion values have on temperature curves. Ultimately, the ability of the technique to accurately fit the heating and cooling MRTI data both spatially and temporally increases confidence that this technique has potential for property estimation in MRgFUS applications.
5.6. General observations
The accuracy of this property estimation technique depends upon the accuracy of the temperature measurements as well as the appropriateness of the analytical solution’s approximations. Any magnetic field drift, systematic artifacts, or other measurement errors in the temperature data may introduce errors in property estimates. Additionally, assumptions of constant, uniform thermal, acoustic, and perfusion properties will lead to errors if such properties change dynamically or vary spatially. In heterogeneous tissues such as malignant tumors, this technique would likely provide average properties that, while not indicative of true tissue anatomy, would also be useful for thermal modeling and treatment planning purposes. However, in areas of severe property variation, such as in close proximity to large blood vessels, this technique is not likely to converge to meaningful property values. Further studies are needed to more extensively investigate the accuracy and usefulness of property estimates from applying this technique in heterogeneous tissues.
The magnitude of the noise used for much this study (SD = 0.2 °C) may be lower than that encountered clinically, particularly when hardware limitations require the use of the MRI body coil for temperature measurements. However, the effects of greater noise in clinical data upon property estimates would likely be counteracted by the greater temperature rise induced by clinical treatments (20–40 °C instead of 10 °C). Future work will apply retrospective analysis of clinical treatment data to further validate this technique. Also, application-specific coils have the potential to greatly reduce the noise magnitude (Minalga et al 2013) and would make possible pretreatment clinical evaluation of these properties without requiring ablative sonications.
This new approach increases the amount of data utilized for property estimation, both temporally and spatially, when compared with previous analytical solutions. It is the first technique to simultaneously account for and estimate ultrasound properties (IHR and β), tissue thermal diffusivity, and the Pennes perfusion parameter. As such, it has unique potential for improving property estimation for thermal modeling applications in MRgFUS thermal therapies.
6. Conclusion
The new analytical solution has been shown to accurately and robustly estimate ultrasound, thermal, and perfusion properties independent of the ultrasound beam size, thermal diffusivity, and Pennes perfusion parameter. Where possible, longer fitting times and a larger fitting radius should be used to include more MRTI data in the optimization process and mitigate the effects of noise. To obtain estimation results with less than 5% error, it is recommended that the 3rd order Taylor series expansion solution be used with the fitting time constrained such that tfit/τbl < 1.
Supplementary Material
Acknowledgments
The authors gratefully acknowledge support from NIH grants R01 CA172787 and R01 EB013433.
Footnotes
PACS
| 87.50.yt | Therapeutic applications |
| 87.19.Pp | Biothermics and thermal processes in biology |
| 87.80.Lg | Biophysical techniques (magnetic resonance techniques) |
| 87.85.jc | Physical properties of biomaterials |
References
- Abramowitz M, Stegun IA. Handbook of mathematical functions: with formulas, graphs, and mathematical tables. New York, NY: Dover; 1964. [Google Scholar]
- Alon L, Collins C, Carluccio G, Novikov D, Zhu Y, Sodickson D. Tissue thermal property tomography. Proc 21st Ann Mtg ISMRM. 2013:2519. [Google Scholar]
- Anand A, Kaczkowski PJ. Noninvasive determination of in situ heating rate using kHz acoustic emissions and focused ultrasound. Ultrasound Med Biol. 2009;35:1662–71. doi: 10.1016/j.ultrasmedbio.2009.05.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anand A, Kaczkowski PJ. Noninvasive measurement of local thermal diffusivity using backscattered ultrasound and focused ultrasound heating. Ultrasound Med Biol. 2008;34:1449–64. doi: 10.1016/j.ultrasmedbio.2008.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anand CS, Sahambi JS. Wavelet domain non-linear filtering for MRI denoising. Magn Reson Imaging. 2010;28:842–61. doi: 10.1016/j.mri.2010.03.013. [DOI] [PubMed] [Google Scholar]
- Appanaboyina S, Partanen A, Haemmerich D. Non-invasive estimation of thermal tissue properties by high-intensity focused ultrasound. Proc SPIE. 2013:85840W. [Google Scholar]
- Arora D, Minor MA, Skliar M, Roemer RB. Control of thermal therapies with moving power deposition field. Phys Med Biol. 2006;51:1201–19. doi: 10.1088/0031-9155/51/5/011. [DOI] [PubMed] [Google Scholar]
- de Bever J, Todd N, Payne A, Christensen DA, Roemer RB. Adaptive model-predictive controller for magnetic resonance guided focused ultrasound therapy. Int J Hyperthermia. 2014;30:456–70. doi: 10.3109/02656736.2014.968223. [DOI] [PubMed] [Google Scholar]
- Burtnyk M, N’Djin WA, Kobelevskiy I, Bronskill M, Chopra R. 3D conformal MRI-controlled transurethral ultrasound prostate therapy: validation of numerical simulations and demonstration in tissue-mimicking gel phantoms. Phys Med Biol. 2010;55:6817–39. doi: 10.1088/0031-9155/55/22/014. [DOI] [PubMed] [Google Scholar]
- Cheng H-LM, Plewes DB. Tissue thermal conductivity by magnetic resonance thermometry and focused ultrasound heating. J Magn Reson Imaging. 2002;16:598–609. doi: 10.1002/jmri.10199. [DOI] [PubMed] [Google Scholar]
- Cline HE, Hynynen K, Hardy CJ, Watkins RD, Schenck JF, Jolesz FA. MR temperature mapping of focused ultrasound surgery. Magn Reson Med. 1994;31:628–36. doi: 10.1002/mrm.1910310608. [DOI] [PubMed] [Google Scholar]
- Cornelis F, Grenier N, Moonen CT, Quesson B. In vivo characterization of tissue thermal properties of the kidney during local hyperthermia induced by MR-guided high-intensity focused ultrasound. NMR Biomed. 2011;24:799–806. doi: 10.1002/nbm.1624. [DOI] [PubMed] [Google Scholar]
- De Poorter J, De Wagter C, De Deene Y, Thomsen C, Ståhlberg F, Achten E. Noninvasive MRI thermometry with the proton resonance frequency (PRF) method: in vivo results in human muscle. Magn Reson Med. 1995;33:74–81. doi: 10.1002/mrm.1910330111. [DOI] [PubMed] [Google Scholar]
- Dillon C, Roemer R, Payne A. Magnetic resonance temperature imaging-based quantification of blood flow-related energy losses. NMR Biomed. 2015;28:841–51. doi: 10.1002/nbm.3318. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dillon CR, Payne A, Christensen DA, Roemer RB. The accuracy and precision of two non-invasive, magnetic resonance-guided focused ultrasound-based thermal diffusivity estimation methods. Int J Hyperthermia. 2014;30:362–71. doi: 10.3109/02656736.2014.945497. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dillon CR, Todd N, Payne A, Parker DL, Christensen DA, Roemer RB. Effects of MRTI sampling characteristics on estimation of HIFU SAR and tissue thermal diffusivity. Phys Med Biol. 2013;58:7291–307. doi: 10.1088/0031-9155/58/20/7291. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dillon CR, Vyas U, Payne A, Christensen DA, Roemer RB. An analytical solution for improved HIFU SAR estimation. Phys Med Biol. 2012;57:4527–44. doi: 10.1088/0031-9155/57/14/4527. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dragonu I, de Oliveira PL, Laurent C, Mougenot C, Grenier N, Moonen CTW, Quesson B. Non-invasive determination of tissue thermal parameters from high intensity focused ultrasound treatment monitored by volumetric MRI thermometry. NMR Biomed. 2009;22:843–51. doi: 10.1002/nbm.1397. [DOI] [PubMed] [Google Scholar]
- Hasgall PA, Di Gennaro F, Baumgartner C, Neufeld E, Gosselin MC, Payne D, Klingenböck A, Kuster N. IT’IS Database for thermal and electromagnetic parameters of biological tissues. 2015 Online: www.itis.ethz.ch/database.
- Huttunen JMJ, Huttunen T, Malinen M, Kaipio JP. Determination of heterogeneous thermal parameters using ultrasound induced heating and MR thermal mapping. Phys Med Biol. 2006;51:1011–32. doi: 10.1088/0031-9155/51/4/017. [DOI] [PubMed] [Google Scholar]
- Ishihara Y, Calderon A, Watanabe H, Okamoto K, Suzuki Y, Kuroda K, Suzuki Y. A precise and fast temperature mapping using water proton chemical shift. Magn Reson Med. 1995;34:814–23. doi: 10.1002/mrm.1910340606. [DOI] [PubMed] [Google Scholar]
- Jenne JW, Preusser T, Günther M. High-intensity focused ultrasound: principles, therapy guidance, simulations and applications. Z Für Med Phys. 2012;22:311–22. doi: 10.1016/j.zemedi.2012.07.001. [DOI] [PubMed] [Google Scholar]
- Kim Y, Bae D-S, Kim B-G, Lee J-W, Kim T-J. A faster nonsurgical solution very large fibroid tumors yielded to a new ablation strategy. Am J Obstet Gynecol. 2011;205:292, e1–5. doi: 10.1016/j.ajog.2011.07.019. [DOI] [PubMed] [Google Scholar]
- Kim Y, Keserci B, Partanen A, Rhim H, Lim HK, Park MJ, Köhler MO. Volumetric MR-HIFU ablation of uterine fibroids: role of treatment cell size in the improvement of energy efficiency. Eur J Radiol. 2012;81:3652–9. doi: 10.1016/j.ejrad.2011.09.005. [DOI] [PubMed] [Google Scholar]
- Kress R, Roemer R. A comparative analysis of thermal blood perfusion measurement techniques. J Biomech Eng. 1987;109:218–25. doi: 10.1115/1.3138672. [DOI] [PubMed] [Google Scholar]
- Minalga E, Payne A, Merrill R, Todd N, Vijayakumar S, Kholmovski E, Parker DL, Hadley JR. An 11-channel radio frequency phased array coil for magnetic resonance guided high-intensity focused ultrasound of the breast. Magn Reson Med. 2013;69:295–302. doi: 10.1002/mrm.24247. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Odéen H, Todd N, Dillon C, Payne A, Parker DL. Model predictive filtering MR thermometry: Effects of model inaccuracies, k-space reduction factor, and temperature increase rate. Magn Reson Med. 2015 doi: 10.1002/mrm.25622. Online: http://doi.wiley.com/10.1002/mrm.25622. [DOI] [PMC free article] [PubMed]
- Parker KJ. Effects of heat conduction and sample size on ultrasonic absorption measurements. J Acoust Soc Am. 1985;77:719–25. doi: 10.1121/1.392340. [DOI] [PubMed] [Google Scholar]
- Parker KJ. The thermal pulse decay technique for measuring ultrasonic absorption coefficients. J Acoust Soc Am. 1983;74:1356. [Google Scholar]
- Pennes HH. Analysis of tissue and arterial blood temperatures in the resting human forearm. J Appl Physiol. 1948;1:93–122. doi: 10.1152/jappl.1948.1.2.93. [DOI] [PubMed] [Google Scholar]
- Rieke V, Vigen KK, Sommer G, Daniel BL, Pauly JM, Butts K. Referenceless PRF shift thermometry. Magn Reson Med. 2004;51:1223–31. doi: 10.1002/mrm.20090. [DOI] [PubMed] [Google Scholar]
- Roemer PB, Edelstein WA, Hayes CE, Souza SP, Mueller OM. The NMR phased array. Magn Reson Med. 1990;16:192–225. doi: 10.1002/mrm.1910160203. [DOI] [PubMed] [Google Scholar]
- Roujol S, de Senneville BD, Hey S, Moonen C, Ries M. Robust adaptive extended Kalman filtering for real time MR-thermometry guided HIFU interventions. IEEE Trans Med Imaging. 2012;31:533–42. doi: 10.1109/TMI.2011.2171772. [DOI] [PubMed] [Google Scholar]
- Salgaonkar VA, Prakash P, Rieke V, Ozhinsky E, Plata J, Kurhanewicz J, Hsu I-CJ, Diederich CJ. Model-based feasibility assessment and evaluation of prostate hyperthermia with a commercial MR-guided endorectal HIFU ablation array. Med Phys. 2014;41:033301. doi: 10.1118/1.4866226. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Salomir R, Vimeux FC, de Zwart JA, Grenier N, Moonen CTW. Hyperthermia by MR-guided focused ultrasound: Accurate temperature control based on fast MRI and a physical model of local energy deposition and heat conduction. Magn Reson Med. 2000;43:342–7. doi: 10.1002/(sici)1522-2594(200003)43:3<342::aid-mrm4>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- Schwenke M, Strehlow J, Haase S, Jenne J, Tanner C, Langø T, Loeve AJ, Karakitsios I, Xiao X, Levy Y, Sat G, Bezzi M, Braunewell S, Guenther M, Melzer A, Preusser T. An integrated model-based software for FUS in moving abdominal organs. Int J Hyperthermia. 2015;31:240–50. doi: 10.3109/02656736.2014.1002817. [DOI] [PubMed] [Google Scholar]
- de Senneville BD, Roujol S, Hey S, Moonen C, Ries M. Extended Kalman filtering for continuous volumetric MR-temperature imaging. IEEE Trans Med Imaging. 2013;32:711–8. doi: 10.1109/TMI.2012.2234760. [DOI] [PubMed] [Google Scholar]
- Sumi C, Yanagimura H. Reconstruction of thermal property distributions of tissue phantoms from temperature measurements--thermal conductivity, thermal capacity and thermal diffusivity. Phys Med Biol. 2007;52:2845–63. doi: 10.1088/0031-9155/52/10/014. [DOI] [PubMed] [Google Scholar]
- Todd N, Payne A, Parker DL. Model predictive filtering for improved temporal resolution in MRI temperature imaging. Magn Reson Med. 2010;63:1269–79. doi: 10.1002/mrm.22321. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todd N, Vyas U, de Bever J, Payne A, Parker DL. The effects of spatial sampling choices on MR temperature measurements. Magn Reson Med. 2011;65:515–21. doi: 10.1002/mrm.22636. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vanne A, Hynynen K. MRI feedback temperature control for focused ultrasound surgery. Phys Med Biol. 2003;48:31–43. doi: 10.1088/0031-9155/48/1/303. [DOI] [PubMed] [Google Scholar]
- Wu F, Wang Z-B, Chen W-Z, Bai J, Zhu H, Qiao T-Y. Preliminary experience using high intensity focused ultrasound for the treatment of patients with advanced stage renal malignancy. J Urol. 2003;170:2237–40. doi: 10.1097/01.ju.0000097123.34790.70. [DOI] [PubMed] [Google Scholar]
- Zhang J, Fischer J, Warner L, Oto A, Hor P-H, Muthupillai R. Noninvasive, in vivo determination of uterine fibroid thermal conductivity in MRI-guided high intensity focused ultrasound therapy. J Magn Reson Imaging. 2015;41:1654–61. doi: 10.1002/jmri.24724. [DOI] [PubMed] [Google Scholar]
- Zhang J, Mougenot C, Partanen A, Muthupillai R, Hor P-H. Volumetric MRI-guided high-intensity focused ultrasound for noninvasive, in vivo determination of tissue thermal conductivity: initial experience in a pig model. J Magn Reson Imaging. 2013;37:950–7. doi: 10.1002/jmri.23878. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.