Functional Imaging of the Non-Human Primate Placenta With Endogenous BOLD Contrast

Abstract

Purpose

To characterize spatial patterns of $T_2^{\ast }$ in the rhesus macaque placenta, to correlate these patterns with placental perfusion determined using dynamic contrast enhanced (DCE)-MRI, and to evaluate the potential for using the blood oxygen level-dependent (BOLD) effect to quantify placental perfusion without the use of exogenous contrast reagent.

Methods

Magnetic resonance imaging was performed on three pregnant rhesus macaques at gestational day 110. Multi-echo spoiled gradient echo measurements were used to compute maps of $T_2^{\ast }$. Spatial maxima in these maps were compared with foci of early enhancement determined by DCE-MRI.

Results

Local maxima in $T_2^{\ast }$ maps are strongly correlated with spiral arteries identified by DCE-MRI, with mean spatial separations ranging from 2.34 to 6.11 mm in the three animals studied. Spatial patterns of $R_2^{\ast }(=1∕T_2^{\ast })$ within individual placental lobules can be quantitatively analyzed using a simple model to estimate fetal arterial oxyhemoglobin concentration [Hb_o,f] and a parameter v_iPS/Φ, reflecting oxygen transport to the fetus. Estimated mean values of [Hb_o,f] ranged from 4.25 mM to 4.46 mM, while v_iPS/Φ ranged from 2.80×10⁵ cm⁻³ to 1.61×10⁶ cm⁻³.

Conclusions

Maternal spiral arteries show strong spatial correlation with foci of extended $T_2^{\ast }$ observed in the primate placenta. A simple model of oxygen transport accurately describes the spatial dependence of $R_2^{\ast }$ within placental lobules and enables assessment of placental function and oxygenation without requiring administration of an exogenous contrast reagent.

Introduction

There is tremendous clinical need for non-invasive tools for in vivo assessment of maternal blood flow and oxygen delivery within the placenta. Many aspects of placental growth, development, and function are incompletely understood despite the crucial role this organ plays in regulating maternal-fetal exchange of oxygen, nutrients, and waste products. Impairment of placental function is implicated in a range of adverse outcomes (1-4), but our understanding of the specific role of placental pathophysiology is limited by our inability, at present, to characterize maternal placental blood flow in the clinical context. Development of quantitative methods of measuring placental oxygen delivery and transport between the maternal and fetal vasculatures will enable us to better understand the normal function of this organ and to detect abnormal placental function as a critical first step in the formulation and evaluation of potential therapeutic interventions.

The hemochorial structure of the primate placenta, in which maternal blood in the intervillous space bathes villi containing fetal blood vessels, ties placental vascular organization to maternal-fetal oxygen transport. In the following, we will discuss three distinct anatomic structures: first, a placental “lobe”, is a self-contained anatomic structure within which the maternal and fetal blood exchange oxygen, nutrients, and wastes. Second, a “cotyledon”, is an anatomic structure within a lobe that is separated from adjacent cotyledons by a ridge of tissue termed a “septum”. Third, following the nomenclature of Faber and Thornburg (5), a “lobule”, is a functional unit comprised of a maternal spiral artery supplying oxygenated maternal blood to a fetal villous tree. While human placentas are generally comprised of a single disc-shaped lobe, in rhesus macaques (and a number of other primate species), placentas typically have two lobes, each of which is disc-shaped, in which the umbilical cord inserts directly into the primary lobe and the secondary lobe is connected to the umbilical cord via bridging vessels (6). The correspondence between spiral arteries and cotyledons is not consistently one-to-one, with some cotyledons perfused by two or more spiral arteries (7). When a single spiral artery perfuses a cotyledon, the cotyledon and the lobule are essentially identical, while cotyledons having multiple spiral artery sources will contain multiple associated lobules.

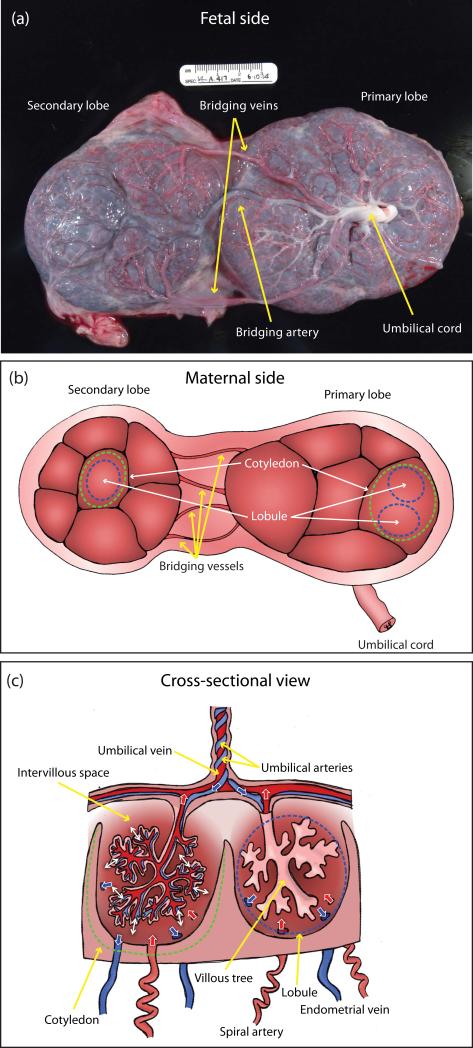
A photograph of the fetal side of a rhesus macaque placenta after Caesarean delivery that shows the primary and secondary placental lobes, the umbilical cord, and the bridging vessels connecting the secondary lobe to the umbilical cord (two bridging veins and one bridging artery in this case) is shown in Figure 1a. A scale bar in centimeters is visible above the specimen. The bridging arteries transport deoxygenated fetal blood from the umbilical arteries to the secondary lobe, while the bridging veins transport oxygenated fetal blood from the secondary lobe to the umbilical vein. Figure 1b presents a schematic illustration of the maternal side of the placenta, clarifying the relationship between the anatomic cotyledons delineated by septa (indicated by the green dashed lines for a single cotyledon in each placental lobe), and the functional lobules, indicated by the blue dashed lines, where individual cotyledons may contain one or more lobules. The bridging vessels directly connect the secondary placental lobe to the umbilical cord, and do not connect with the primary lobe, so the secondary lobe constitutes an independent functional unit. Figure 1c plots a schematic cross section of the placenta identifying major structures including umbilical arteries, umbilical vein, cotyledons, lobules, intervillous space, villous tree, spiral arteries, and endometrial veins. The boundary of the cotyledon is shown by the dashed green line, and the boundary of the lobule by the dashed blue line. Vessels carrying oxygenated blood are indicated in red (corresponding flows indicated by red single-headed arrows) and vessels carrying deoxygenated blood are indicated in blue (corresponding flows indicated by blue single-headed arrows). Oxygenated maternal blood is supplied to the intervillous space of both lobes of the placenta via the spiral arteries, with one spiral artery associated with each lobule, and deoxygenated maternal blood is removed via the endometrial veins located on the periphery of the lobule. Deoxygenated fetal blood flows via the umbilical arteries into the villous trees where oxygen, nutrients, and wastes are exchanged with the maternal blood in the intervillous space indicated in Figure 1c by the doubleheaded white arrows, and oxygenated fetal blood returns to the fetus via the umbilical vein. Readers unfamiliar with the peculiarities of the fetal circulation should note that the umbilical arteries carrying deoxygenated blood to the placenta branch from the fetal iliac arteries, while the umbilical vein, which carries oxygenated blood from the placenta to the fetus, connects to the fetal vena cava. Thus, the conventional association of anatomic arteries with oxygenated blood and veins with deoxygenated blood is reversed in this case.

Figure 1.

An illustration of the anatomy and morphology of the non-human primate placenta showing both the maternal and fetal surfaces along with a cross-sectional view. Major structures including primary and secondary placental lobes, bridging vessels, umbilical arteries, umbilical vein, cotyledons, lobules, villous tree, spiral arteries, and endometrial veins are identified. Panel (a) shows a photograph of the fetal side of a rhesus macaque placenta after Caesarean delivery, with primary placental lobe, secondary placental lobe, umbilical cord, and bridging artery and veins indicated. Panel (b) is a schematic illustration of the maternal side of the placenta, with anatomic cotyledons (green dashed lines) and functional lobules (blue dashed lines) indicated in both primary and secondary lobes. Panel (c) is a schematic cross-section of the placenta, with the cotyledon and the lobule indicated as in panel (b). Vessels carrying oxygenated blood are shown in red (with red arrows indicating flow direction), and vessels carrying deoxygenated blood are shown in blue (with corresponding flow indicated by blue arrows). Oxygen, nutrients, and wastes are exchanged between the maternal blood occupying the intervillous space and the fetal capillaries comprising the villous tree, as indicated by the double-headed white arrows.

In humans, roughly 10-40 cotyledons are distributed within a single placental lobe, with 1-4 lobules per cotyledon, each associated with a single spiral artery supplying maternal blood to the intervillous space (5, 8). Rhesus macaques typically have a comparable number of cotyledons distributed across the primary and secondary placental lobes. Based on our previous DCE-MRI studies, rhesus macaque lobules have volumes on the order of 1-2 cm³. The intervillous space (the placental space accessible to maternal blood) constitutes approximately 40% of the total volume of a cotyledon (9). Recently we have established that dynamic contrast enhanced MRI (DCE-MRI), using bolus injection of a gadolinium-based contrast reagent (CR) into the maternal vasculature, can be used to delineate placental lobules by directly tracking the expanding wavefront of CR (7).

The work presented here is aimed at characterizing the water ¹H transverse relaxation time in the placenta ($T_2^{\ast }$) and correlating those observations with DCE-MRI results. These studies reveal spatially coherent patterns in maps of placental $T_2^{\ast }$ that closely resemble the patterns of early contrast uptake observed in DCE-MRI. Specifically, we find regions of relatively long $T_2^{\ast }$, surrounded by a penumbra of much shorter $T_2^{\ast }$, where the $T_2^{\ast }$ maxima correspond to spatial locations of early arrival of contrast to the placenta. We establish that perfusion domains identified by DCE-MRI closely coincide in location and number with spatial $T_2^{\ast }$ maxima in the primate placenta. This result allows us to infer that the voxels most proximal to spiral artery sources of maternal blood (identified by DCE-MRI) have the lowest deoxyhemoglobin concentration, using the sensitivity of the $T_2^{\ast }$ measurements to blood oxygen level (via the blood oxygen level-dependent, BOLD, effect). Based on this observation, we develop a quantitative geometric model that relates the measured spatial patterns of transverse relaxation rate, $R_2^{\ast }=(1∕T_2^{\ast })$, within individual placental lobules to physiological variables pertinent to fetal and maternal blood oxygenation, and apply this model to our measurements.

Methods

All procedures described in the following were approved by the Institutional Animal Care and Use Committee (IACUC) of the Oregon National Primate Research Center (ONPRC). The ONPRC abides by the Animal Welfare Act and regulations enforced by the U.S. Department of Agriculture, the Public Health Service Policy on Humane Care and Use of Laboratory Animals, in accordance with the U.S. National Institutes of Health Guide for the Care and Use of Laboratory Animals. Magnetic resonance imaging was performed on gestational day 110 (G110) in three pregnant rhesus macaques (Macaca mulatta, typical gestation of 165 days, referred to in this manuscript as animals A, B, and C) who were part of the control group in a study of fetal ethanol exposure. Animals were sedated by intramuscular administration of 10 mg/kg ketamine and intubated. Sedation was maintained by placing animals on a portable anesthesia delivery system providing O₂ with 1.5% isoflurane. Immediately prior to MRI, a catheter was placed in the saphenous vein for the delivery of the gadolinium-based contrast reagent.

MRI studies were performed on a nonhuman primate-dedicated 3T Siemens TIM-Trio scanner (Erlangen, Germany) using a circularly-polarized (CP) transmit, 15-channel receive radiofrequency (RF) “extremity” coil (QED, Cleveland, OH). Following localization of the placenta and acquisition of T₂-weighted half-Fourier acquisition single-shot turbo spin-echo (HASTE) anatomic images in the coronal and axial planes, axial 2D multislice spoiled gradient echo (SPGR) images (TR=418 ms, flip angle=30°, 256×72 matrix, 96 slices, 1.5 mm isotropic spatial resolution), spanning the entire uterus, were acquired at six in-phase echo times (TE=4.92, 9.84, 19.68, 29.52, 36.90, and 44.28 ms) with monopolar readout gradients. Subsequently, 3D SPGR images were acquired in the coronal plane (TR=9.50 ms, TE=2.46 ms, 128×56×44 matrix, 2.5 mm isotropic spatial resolution, flip angles of 3° and 25°), also covering the entire uterus, to allow estimation of T₁ (longitudinal relaxation time) with the variable flip angle (VFA) method (10). Immediately after acquisition of VFA data, 150 volumes of 3D SPGR images were acquired for DCE-MRI (TR=2.00 ms, TE=0.72 ms, flip angle=20°, 6/8 partial Fourier encoding in both phase and slab encode directions, elliptical phase undersampling, parallel imaging with GRAPPA (iPAT factor of 2), acquisition time per frame of 3.64 seconds, total acquisition time of 546 seconds), with field of view and resolution matched to the VFA images. Ten baseline images were acquired prior to intravenous injection of a standard dose of 0.1 mmol/kg of gadoteridol CR (Prohance, Bracco Diagnostics Inc, Princeton, NJ) at a rate of 30 mL/min using a syringe pump (Harvard Apparatus, Holliston, MA). Anatomic and multiecho imaging was performed during expiratory breath-holding, achieved by temporarily suspending ventilation, while DCE-MRI data were acquired during ventilation. Physiological monitoring of pulse rate, arterial blood oxygen saturation, and end-tidal CO₂ partial pressure was performed throughout the imaging study, with no deviations from normal ranges observed in these parameters for any of the three animals studied. Each physiological parameter was recorded at 10 minute intervals, and values reported herein are averages over the final 40 minutes of the MRI exam, which overlapped the time period in which placental multiecho and DCE-MRI data were collected. Immediately following each MRI procedure, fetuses were delivered by Cesarean section, and samples of maternal and fetal blood were collected for determinations of blood hemoglobin concentrations using a Pentra 60 C+ blood analyzer (HORIBA Medical, Irvine, CA).

$T_2^{\ast }$ analysis

Spatial maps of the water ¹H transverse relaxation time ($T_2^{\ast }$) were computed per-voxel from multiecho SPGR measurements using a weighted linear least squares algorithm, implemented in MATLAB (Mathworks, Natick, MA), fitting the signal, S, to the linearized signal equation:

$$\log S\left(TE\right)=\log S\left(0\right)-TE∕T_2^{\ast }.$$ (1)

Mean image noise was estimated from an imaging volume outside the body separately for each echo and incorporated into the model regression, and parameter covariance matrices were computed using standard propagation of uncertainty.

Spatial modeling of $T_2^{\ast }$ distributions

It is well known that arterial and venous blood manifest significantly different transverse relaxation times, with shortening in venous blood due to the paramagnetism of deoxyhemoglobin; this is the basis of the much-studied BOLD effect (11). We hypothesize that a pattern of high-to-low $T_2^{\ast }$ observed with increasing spatial distance from the spiral artery source within individual perfusion domains in the placenta represents a high-to-low gradient in oxygen concentration in maternal blood within the intervillous space. Here, we develop a mathematical model relating the spatial distribution of $R_2^{\ast }(=1∕T_2^{\ast })$ within the perfusion domain representing a single placental lobule to relevant underlying physiological parameters. This model predicts the spatial variation of $R_2^{\ast }$ within individual lobules as a function of distance from the spiral artery supplying oxygenated blood from the mother to the fetus.

Each lobule is approximated as a spherical perfusion domain supplied with oxygenated maternal blood by a spiral artery located at its center. Further, the flow of maternal blood through the intervillous space of the lobule is assumed to be incompressible, with laminar transport from the central source to venous sinks located at the periphery. Mass conservation can then be used to express the radial displacement (ρ) of a parcel of maternal blood as a function of time. Assuming a spiral artery source from which blood is supplied at a rate Φ (ml/min), and a spatially-uniform volume fraction of intervillous space, v_i, the radius at which a Lagrangian element of flowing blood (12) is located increases as

$$\frac{d\rho }{dt}=\frac{\Phi }{4\pi {\rho }^2{v}_i}.$$ (2)

Assuming conventional first order rate kinetics for the transport of oxygen from the intervillous space to the fetal blood (5), the rate of change in oxyhemoglobin ([Hb_o]) in the intervillous space can be expressed as a function of time as

$$\frac{d\left[H{b}_o\right]}{dt}=-PS(\left[H{b}_o\right]-\left[H{b}_{o,f}\right]),$$ (3)

where PS is the permeability-surface area product for oxygen exchange from the intervillous space to the fetal villi, and [Hb_o,f] is the effective (corrected for the increased oxygen affinity of fetal hemoglobin) concentration of oxyhemoglobin in the fetal arterial blood, assumed to be constant within each lobule. Use of the chain rule

$$\frac{d\left[H{b}_o\right]}{d\rho }=\frac{d\left[H{b}_o\right]}{dt}\frac{dt}{d\rho }$$ (4)

yields a first-order differential equation

$$\frac{d\left[H{b}_o\right]}{d\rho }=-PS(\left[H{b}_o\right]-\left[H{b}_{o,f}\right])\frac{4\pi {\rho }^2{v}_i}{\Phi }$$ (5)

that can be solved directly:

$$\left[H{b}_o\right]\left(\rho \right)=\left[H{b}_{o,f}\right]+(\left[H{b}_{o,in}\right]-\left[H{b}_{o,f}\right])e^{-\frac{4\pi PS}{3\Phi }{v}_i{\rho }^3},$$ (6)

where [Hb_o,in] is the maternal oxyhemoglobin concentration at the spiral artery input to the lobule.

In order to express [Hb_o] in terms of $R_2^{\ast }$, we use the observation of Blockley et al. (13) that the $R_2^{\ast }$of blood at a magnetic field strength of 3T depends linearly on deoxyhemoglobin concentration: ([Hb_d]):

$$R_2^{\ast }=R_{20}^{\ast }+r_2^{\ast }\left[H{b}_d\right]=R_{20}^{\ast }+r_2^{\ast }(\left[Hb\right]-\left[H{b}_o\right])$$ (7)

with $R_{20}^{\ast }$ being the intrinsic $R_2^{\ast }$ in the absence of Hb_d and $r_2^{\ast }$ the $R_2^{\ast }$ relaxivity of Hb_d, reported to be 20.2 s⁻¹mM⁻¹ in human blood (13). Combining the two equations above yields an expression for the radial dependence of $R_2^{\ast }$

$$R_2^{\ast }\left(\rho \right)=(R_{20}^{\ast }+r_2^{\ast }(\left[Hb\right]-\left[H{b}_{o,f}\right]))+r_2^{\ast }(\left[H{b}_{o,f}\right]-\left[H{b}_{o,in}\right])e^{-\frac{4\pi PS}{3\Phi }{v}_i{\rho }^3}.$$ (8)

Using [Hb] values obtained from maternal blood draws, [Hb_o,in] from maternal arterial pulse oximetry, and the experimental $r_2^{\ast }$ value for deoxyhemoglobin, this equation can be fit to measured data to estimate $R_{20}^{\ast },\left[H{b}_{o,f}\right]$, and v_iPS/Φ for individual perfusion domains within the placenta. In principle, stereology-based estimates of v_i could also be incorporated to determine the unscaled ratio PS/Φ. However, in this work, the scaled parameter v_iPS/Φ is reported because lobule-specific v_i values were not determined.

A numerical algorithm for spatial modeling of $R_2^{\ast }$ distributions

In order to describe 3D measured data with this model, we have developed and implemented an algorithm in MATLAB (Mathworks, Natick, MA) that reduces our 3D measurements of $R_2^{\ast }$ to a single effective dimension. This algorithm proceeds as follows, where specific MATLAB functions are indicated in italics:

• (1)A separate mask is created to delineate each lobe of the placenta. Regions of interest (ROIs) are initially drawn on axial T2 HASTE images, then resampled and overlaid on $T_2^{\ast }$ maps. Particular care is taken to exclude regions of amniotic fluid and uterine wall from these ROIs.
• (2)The $T_2^{\ast }$ map derived from fitting the multiecho data and the placenta masks from step (1) are linearly interpolated to 0.75 mm isotropic spatial resolution using interpn. This facilitates smoother evolution of the wavefronts computed in step (5).
• (3)Local maxima within the placenta are identified in a smoothed version of the interpolated $T_2^{\ast }$ map (3D gaussian convolution with a 3 voxel kernel width) using the imregionalmax function.
• (4)N_i (i = 1,2) lobules in each lobe are identified with the maxima found in step (3), and the locations of these maxima are chosen as seed points.
• (5)Iteration number maps, corresponding to approximate isosurfaces, are generated from the interpolated $T_2^{\ast }$ map via the multistencil fast marching (MSFM) algorithm (14, 15), as implemented in Mathworks File Exchange submission #24531 by Dirk-Jan Kroon. MSFM is run separately for each lobe, initialized with the N_i seed points from step (4).
• (6)Each lobe is segmented into N_i perfusion domains by running the watershed segmentation algorithm on the iteration number maps computed in step (5).
• (7)Histograms of perfusion domain volume (V), median Euclidean distance from the nearest seed point (ρ_eff), and median $R_2^{\ast }(=1∕T_2^{\ast })$ are computed as functions of iteration number. For each lobule, iteration number is histogrammed into 100 bins (empirically chosen based on observed data) ranging from 0 to the 95^th percentile within that lobule. Uncertainty in $R_2^{\ast }$ is estimated from the interquartile range of $R_2^{\ast }$ values in each histogram bin.
• (8)Median $R_2^{\ast }$ is plotted against ρ_eff out to an empirically chosen cutoff distance of 1.5 cm and Eq. 8 is fit to the resulting curves using weighted nonlinear least squares regression (lsqcurvefit).

DCE-MRI analysis

DCE-MRI data are processed using the methods described previously (7). Briefly, time curves of measured signal intensity are converted to estimates of CR concentration as described in (16). Pre-injection longitudinal relaxation time (T₁₀) is estimated using the variable flip angle (VFA) method with flip angles of 3° and 25° (10), and the full nonlinear relationship between relative signal enhancement (Ξ) and concentration (C) is numerically inverted using measured field-dependent relaxivity values (17) to generate time curves of CR concentration (16). The arterial input function (AIF) is measured in the inferior abdominal aorta, just above the iliac bifurcation. For our data acquisition geometry, this location minimizes potential inflow artifacts and partial-volume effects, and was found to provide consistently reliable measurements. Resulting concentration-time curves for each voxel are fit using weighted nonlinear regression to the Gamma Capillary Transit Time (GCTT) model (16). Maps of the model tissue blood flow parameter, F_T (= C_t(t)/(R(t) * C_b(t))), are resampled and interpolated to match the resolution of the interpolated $T_2^{\ast }$ maps, and local maxima in F_T, corresponding to spiral artery sources, are identified using the same algorithm as described in step (3) above. It is important to note that F_T represents the instantaneous flow in each individual voxel rather than the total spiral artery flow, which is denoted Φ. While it is theoretically possible to derive the latter from the former, there are a number of technical and practical difficulties, and we have not attempted to do so here. Instead, F_T is simply the scale factor between the tissue concentration curve and the impulse response to the input function. There are two principal advantages to using F_T instead of working directly with a purely descriptive quantifier such as early relative enhancement: (1) the modeling procedure automatically compensates for differences in contrast arrival time between lobules, and (2) the model fitting procedure regularizes the time curves, decreasing sensitivity to motion artifacts arising from respiration.

3D point clouds of image maxima determined separately from the interpolated $T_2^{\ast }$ and interpolated F_T maps were co-registered using the iterative closest point (ICP) algorithm (MATLAB File Exchange submission #27804 by Jakob Wilm). The resulting affine transformation was used to estimate both center-of-mass separation (translation) between point clouds and mean between-point separation, compensating for misregistration due to respiratory motion in the DCE-MRI acquisition and allowing us to quantify the spatial concordance between local maxima in transverse relaxation time and in contrast uptake.

Results

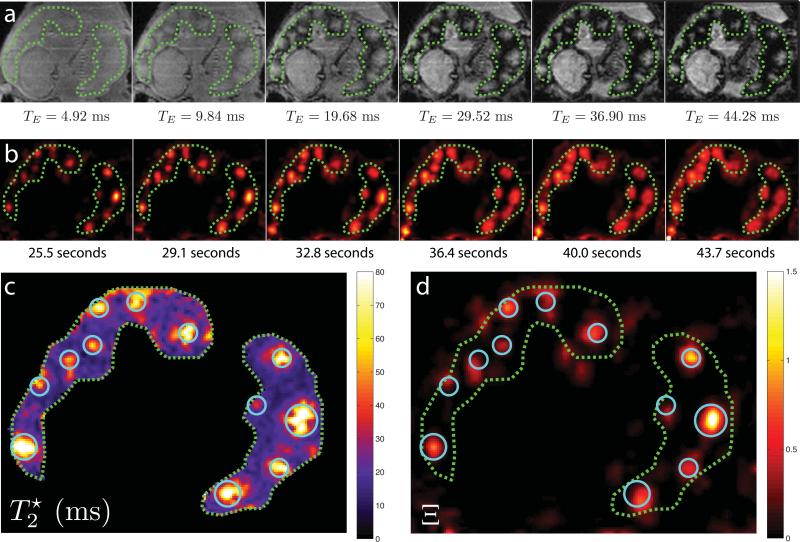
Raw signal measurements for a single axial slice through both placental lobes for each of the six echo times of the multiecho acquisition in animal B are shown in the top panel of Figure 2, with the boundaries of each lobe indicated by the dashed green lines. The fetal brain is visible in the lower left corner of these images. Our acquisition is heavily proton-density weighted for the shortest echo time (4.92 ms), resulting in relatively little contrast between the placenta, fetus, and surrounding tissues, or within the placenta itself. However, inspection of images acquired at progressively longer echo times reveals substantial spatial heterogeneity within the placenta, with focal regions of minimal signal attenuation surrounded by a penumbra of rapidly decreasing signal.

Figure 2.

A comparison of multiecho $T_2^{\ast }$ imaging and DCE-MRI results for a single imaging slice through both placental lobes of Animal B. Panel (a) shows signal magnitude for each of the 6 echo times acquired for $T_2^{\ast }$ measurements, with TE ranging from 4.92 ms for the first image to 44.28 ms for the last image. Panel (b) plots relative enhancement, Ξ(t), from DCE-MRI measurements for six sequential time points ranging from initial contrast arrival at 25.5 seconds to 43.7 seconds after injection of Gd-based contrast reagent. Panel (c) displays the $T_2^{\ast }$ map derived from regression to the data in panel (a), with local maxima in $T_2^{\ast }$ indicated by blue circles. Panel (d) shows a magnified and rescaled view of the relative enhancement data at 25.5 seconds post-injection, with $T_2^{\ast }$ maxima from panel (c) overlaid without image registration. In all images, placental lobes are delineated by green dashed lines, with the primary lobe (defined as the lobe in which the umbilical cord inserts) on the left and the secondary lobe on the right.

Comparison of the spatial location of foci seen in the later echoes of the multiecho data immediately reveals a high degree of spatial correlation with foci of contrast enhancement observed by DCE-MRI. Relative signal enhancement with CR injection is defined as Ξ(t) = (S(t) – S₀)/S₀, where the temporal signal in a voxel is S(t) and the mean baseline signal, averaged over the 10 time points prior to CR injection, is S₀. In panel b of Figure 2, Ξ(t) is shown for six consecutive time points at the same axial position as Figure 2a. In Figure 2b, the Ξ maps have been spatially resampled to match the multiecho measurements, with the two placental lobes indicated by the green dashed curves. The initial arrival of contrast to spiral artery outlets within the placenta is apparent, with localized foci in the first time frame slowly evolving outward as contrast-bearing maternal blood perfuses the intervillous space.

To further emphasize the spatial correlation between multiecho measurements and DCE-MRI measurements, the $T_2^{\ast }$ map resulting from fitting multiecho data is shown in Figure 2c and compared with an expanded map of Ξ at 25.5 seconds post-injection shown in Figure 2d. The local maxima in $T_2^{\ast }$ are indicated with light blue circles and the same locations are shown, without image registration, on the Ξ map. Maxima in DCE-MRI contrast enhancement correlate extremely well with maxima in transverse relaxation time. However, due to the fact that the multiecho images were acquired during breath-holding while the DCE-MRI data were acquired in the presence of motion arising from maternal respiration, a certain degree of misregistration arising from respiratory motion of the diaphragm and abdomen is expected.

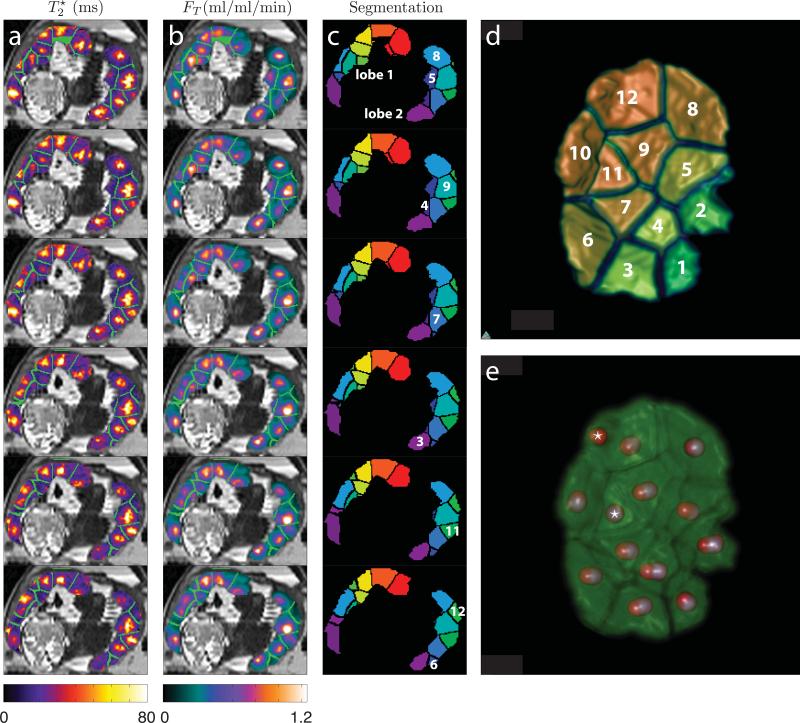
Figure 3a displays $T_2^{\ast }$ maps for six contiguous axial slices through both lobes of the placenta in animal B beginning with the slice shown in Figure 2. Figure 3b shows the corresponding maps of F_T derived from model fitting to the DCE-MRI data. Boundaries between placental lobules, determined by watershed segmentation of the smoothed relaxation time maps, are indicated in bright green. The watershed segmentation domains corresponding to placental lobules are shown in Figure 3c, with several of the lobules in lobe 2 numbered. Colors in Figure 3c represent the (arbitrarily-assigned) lobule numbers that correspond to those shown in the upper right panel (Figure 3d), where a volume rendering of the entirety of lobe 2 viewed from the interior of the uterus is displayed. We chose the secondary lobe for visualization because it was relatively flat, unlike the more highly curved and somewhat involuted primary lobe, making it possible to simultaneously visualize all lobules. Figure 3e is a volume rendering of lobe 2 showing seed points, with spheres of 3 mm radius superimposed on local maxima of the $T_2^{\ast }$ map (gray) and the F_T map (red). Starred maxima indicate the single case where a local maximum in F_T did not closely coincide with a nearby maximum in $T_2^{\ast }$. In this case, F_T and $T_2^{\ast }$ maxima are not centered on the same placental structure, due to misregistration arising from respiratory motion in the DCE-MRI acquisition. Averaged over all 34 lobules identified for animal B, the mean distance between local maxima in the $T_2^{\ast }$ map and the F_T map is 2.34 mm (minimum/maximum of 0.60 mm – 10.5 mm).

Figure 3.

Segmentation of placental $T_2^{\ast }$ measurements. Panel (a) displays $T_2^{\ast }$ for six sequential slices from Animal B, beginning from the top with the slice shown in Figure 2. Boundaries between individual lobules, as determined by the segmentation algorithm described in Methods, are indicated in green. Panel (b) shows the tissue blood flow parameter (F_T), determined from nonlinear regression to DCE-MRI measurements, for the same six slices. Segmentation boundaries are shown in green. Panel (c) plots the lobule segmentation domains (distinct colors correspond to different arbitrarily-assigned lobule numbers), with domains in the secondary lobe that are visible in these slices numerically labeled for comparison with curves in Figure 4. These domains are shown as isosurfaces for the entire secondary lobe in panel (d). Panel (e) shows a volume rendering of the secondary lobe, oriented as in panel (d), with local maxima in $T_2^{\ast }$ indicated by gray spheres and local maxima in F_T indicated by red spheres. In one lobule we observe a discrepancy between the two measurements, indicated by the asterisks, with two maxima in F_T identified within lobule #12 and none identified within lobule #11. The origin of this discrepancy is discussed further in the text.

Model fits to measured placental $R_2^{\ast }$

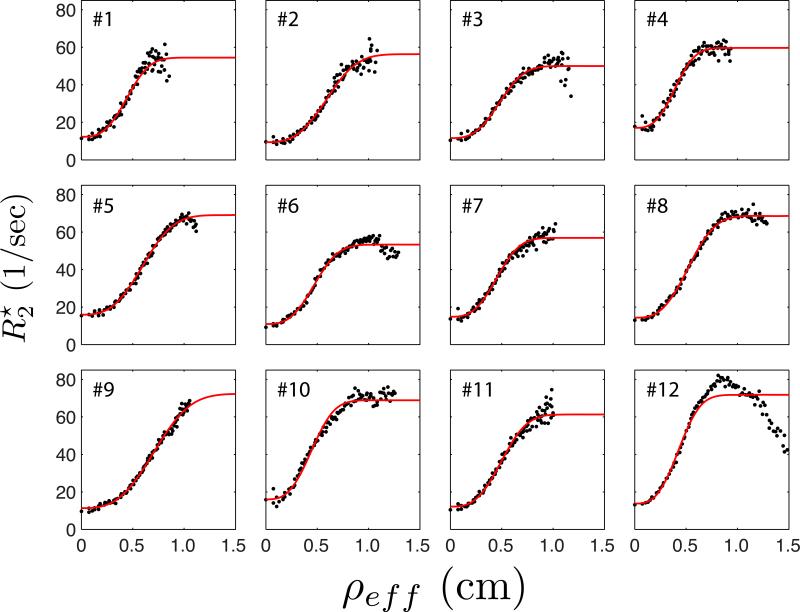
In order to quantitatively characterize the spatial patterns we observe in $R_2^{\ast }$, measured data were fit with Eq. 8. In Figure 4, the dependence of measured $R_2^{\ast }$ for each lobule in lobe 2 of animal B is plotted against effective radius, ρ_eff, computed using the algorithm described above. Each of the twelve curves plotted in Figure 4 correspond to each lobule's numeric label in Figure 3. Model fits (red curves) are shown superimposed on the measured points (black). From the figure, it is clear that Eq. 8 closely approximates the observed changes in $R_2^{\ast }$ as a function of distance from the spiral artery source supplying maternal blood to each lobule.

Figure 4.

Spatial dependence of measured $R_2^{\ast }$ along with model fitting results. Black points show the measured median value of $R_2^{\ast }$ as a function of median distance from the central spiral artery for all 12 lobules in the secondary placental lobe of Animal B, as numbered in panel (d) of Figure 3. Red curves are the results from nonlinear regression to Equation 8. The anomalous drop-off at large effective radius observed in lobule #12 results from inclusion of perfused extra-placental tissue (likely uterine wall) in the region of interest.

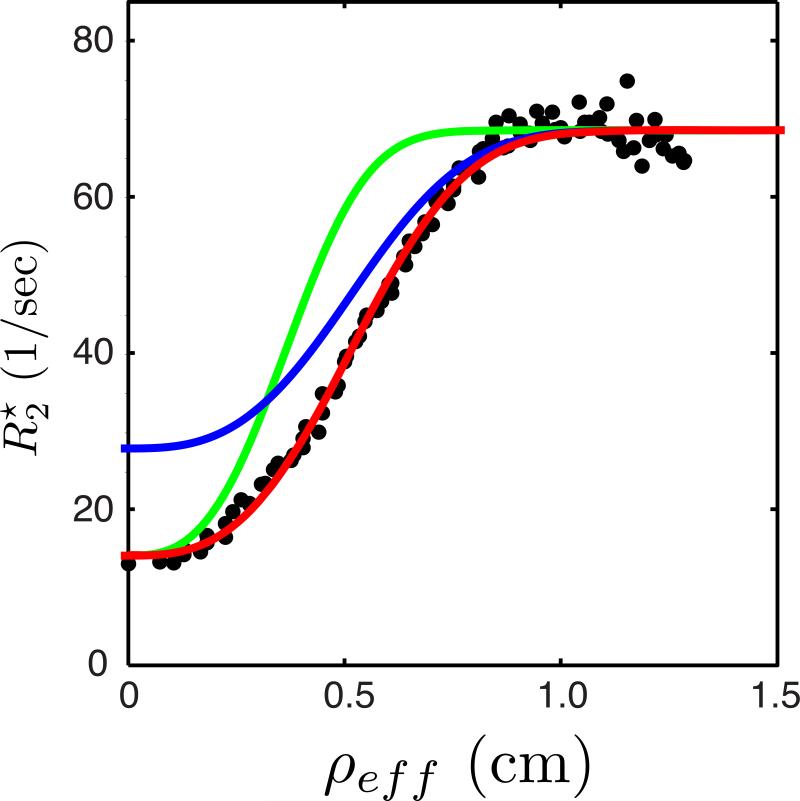
A motivation for our spatial modeling approach is to provide a means of interpreting $R_2^{\ast }$ in terms of physiological parameters relevant to placental function. Figure 5 demonstrates the predicted effects of changes in maternal blood flow and maternal blood oxygen saturation on the spatial distribution of $R_2^{\ast }$. A magnified view of the data from lobule #8 of animal B is shown, with the model regression to the measured data points again indicated by the red curve. The blue curve shows the model prediction for a decrease in maternal S_pO₂ from 100% to 80%, resulting in an increase in maternal arterial blood $R_2^{\ast }$, the y-intercept in Figure 5. Similarly, the green curve simulates the effect of a reduction in the total blood flow, Φ, to this lobule by 40%, resulting in an increase in the steepness of the dependence of $R_2^{\ast }$ on distance from the spiral artery. Conversely, an increase in spiral artery blood flow decreases the steepness of the $R_2^{\ast }$ curve (not shown).

Figure 5.

Model predictions of the sensitivity of the spatial variation in $R_2^{\ast }$ to changes in spiral artery blood flow and maternal oxygen saturation. Black points plot the measured data for lobule #8 from Figure 4, along with the model fit (red). The blue and green curves plot model predictions for changes in the spatial dependence of $R_2^{\ast }$ with a decrease in maternal SpO2 from 100% to 80% (blue) or a decrease of 40% in the spiral artery blood flow (green) to this lobule.

Measurements performed on the two other animals provide further evidence of correspondence between patterns of $T_2^{\ast }$ and F_T contrast in spite of considerable inter-animal variability in the number of lobules identified, as well as in the observed $R_2^{\ast }$ dependencies on ρ_eff, anticipated in the simulations shown in Figure 5. Placentas in animals A and C were found to have 18 and 13 lobules, respectively, substantially fewer than the 34 lobules found in animal B. However, the total placental volumes of 78.8 cm³ and 99.4 cm³ for animals A and C were similar to that of animal B (75.8 cm³, Table 1). As a result, lobules were substantially larger in animals A and C than in animal B. Nevertheless, strong correspondence was observed between $T_2^{\ast }$ and F_T parameter maps, with mean distances between local maxima obtained from the ICP algorithm of 3.17 mm and 6.11 mm for animals studied here, is 3.91 cm³, corresponding to a sphere with 0.98 cm radius.

Table 1.

MRI- and model-derived placental parameters, along with maternal and fetal physiological parameters.

Animal	Placenta volume (cm3)	# of lobules	Median viPS/Φ (×106 cm−3)	Median $R_2^{\ast }$ (s−1)	Median [Hbo,f] (mM)	Arterial O2 saturation (%)	Pulse rate (bpm)	[Hbf] (mM)	[Hbm] (mM)
A	78.8	18	0.88±0.41	15.4±2.6	4.17±0.50	99.5	117	7.82	6.15
B	75.8	34	1.61±0.73	13.1±1.9	4.39±0.43	99.5	105	7.95	6.77
C	99.4	13	0.28±0.41	11.5±1.7	4.52±0.89	100	108	9.44	6.21

[Hb_o,f] is the model estimate of fetal arterial oxyhemoglobin concentration, and [Hb_f] and [Hb_m] are the fetal and maternal total hemoglobin concentrations, measured from blood samples after Caesarean delivery. Arterial oxygen saturation was measured via pulse oximetry.

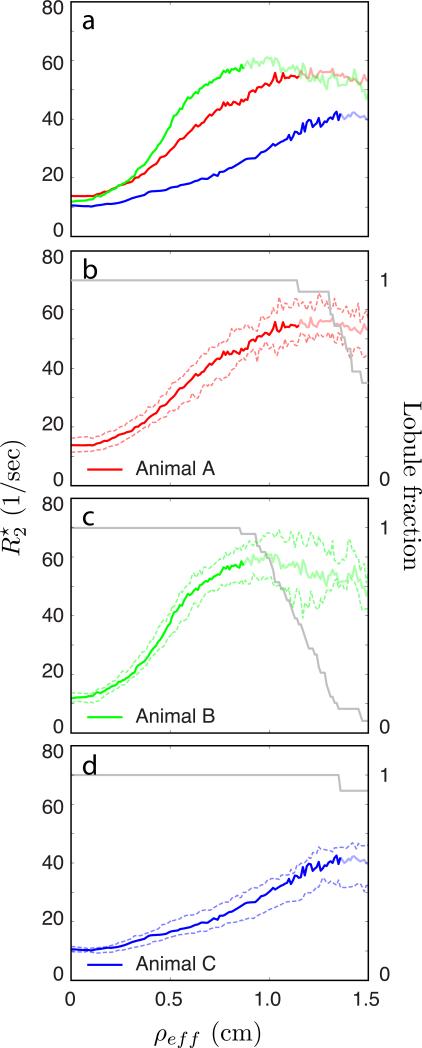
In Figure 6a, the median $R_2^{\ast }$ for voxels in all lobules is plotted versus ρ_eff for all three animals (animal A in red, animal B, displayed in Figures 2-5, in green, and animal C in blue). Figures 6b-d plot $R_2^{\ast }$ versus ρ_eff for each of the three animals separately, animal A in 6b (red), animal B in 6c (green), and animal C in 6d (blue). Solid curves show the median $R_2^{\ast }$ averaged over all lobules, with 25^th and 75^th percentile curves indicated by dashed lines. Because lobules have different sizes, not every lobule extends to the maximum ρ_eff value of 1.5 cm shown in this plot. As a result, the average curves no longer include smaller lobules at larger effective distances, becoming progressively biased by larger lobules. To clarify this, median curves are desaturated for ρ_eff larger than the maximum ρ_eff for the smallest lobule in each animal, so that the fully saturated curves include all lobules out to the maximum effective radius of the smallest lobule. The axes on the right side in Figures 6b-d correspond to the gray curves showing the fraction of lobules in each animal that are at least as large as ρ_eff; curves of $R_2^{\ast }$ are desaturated once this fraction decreases below 1. Most noticeable in comparisons between the three animals are the differences in the spatial gradient of $R_2^{\ast }$ with ρ_eff, with animal B possessing the steepest curve, animal A being intermediate, and animal C exhibiting the least steep increase in $R_2^{\ast }$ with ρ_eff.

Figure 6.

Spatial dependence of measured $R_2^{\ast }$ for all three animals. Panel (a) plots the median dependence of $R_2^{\ast }$ on median distance from the spiral artery, averaged over all lobules in both placental lobes, for Animals A (red), B (green), and C (blue). Panels (b)-(d) show the same median curves along with 25%/75% bounds (dashed lines). Median curves are desaturated for distances beyond the maximum radius of the smallest lobule in each animal. Gray curves in panels (b)-(d), corresponding to the right hand axis, show the fraction of lobules having a minimum radius at least as large as ρ_eff.

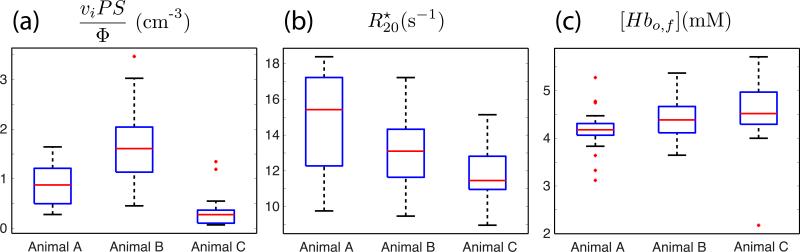
Figure 7 presents box plots for the three different physiological parameters estimated from our model in each of the three animals. Figure 7a shows v_iPS/Φ estimates for all lobules in each of the three animals. T-tests reveal statistically significant differences in the mean v_iPS/Φ between animals A and B (p=0.0002), animals A and C (p=0.002), and animals B and C (p<1e-6). In addition, more subtle differences between animals are observable in the y-intercept of Figure 6a. Model estimates of $R_{20}^{\ast }$ for each animal are shown in Figure 7b. T-tests for differences between animals A and B, A and C, and B and C give p-values of 0.01, 0.001, and 0.03, respectively. Finally, model estimates of [Hb_o,f] are shown in Figure 7c. No statistically significant differences were observed in this parameter between any of the animals. Statistically significant differences were also not observed between the primary and secondary placental lobes for any of the fitted parameters (data not shown). Data obtained for all three animals are summarized in Table 1.

Figure 7.

Box plots of model parameter estimates for all three animals. Parameters for all lobules of both placental lobes are included. Panel (a) shows v_iPS/Φ, panel (b) shows $R_{20}^{\ast }$, and panel (c) shows [Hb_o,f], with Animal A on the left, Animal B in the middle, and Animal C on the right in each panel.

Discussion

This study establishes a direct correspondence between regional patterns of $T_2^{\ast }$ and spiral artery perfusion territories, identified by DCE-MRI, in the primate placenta for the first time. Endogenous, water spin-relaxation-based patterns of MRI contrast similar to the regional pattern of $R_2^{\ast }$ examined here have been seen in previous studies of human subjects performed by other researchers. In the $R_2^{\ast }$-weighted images of Sorensen and colleagues (18) and others (19) (in the former study, the authors referred to the data as “BOLD images”) as well as the R₂-weighted images of Derwig et al. (20, 21), approximately six ~3 cm diameter structures are intersected in axial images of the placenta, and within each structure, a high-signal intensity core is surrounded by a low-intensity rim. In a study of murine placenta (which is morphologically quite unlike primate placenta), Bobek et al. (22) observed that T₂ contrast within the placenta was abolished on elimination of blood flow through terminal anesthesia. Although these results are consistent with our observation of gradients in [Hb_d] that underlie the quantitative framework we have proposed here for interpreting $R_2^{\ast }$ parameter maps, these previous analyses did not attribute the observed spatial patterns to the detailed placental vascular organization. It is the combination of quantitative $R_2^{\ast }$ determinations with DCE-MRI-based delineation of spiral artery locations in nonhuman primate subjects (7) that has enabled us to verify that the lobule structure evident in $R_2^{\ast }$ maps is the same as the structure observed following CR administration into the maternal vasculature. This advance enabled the development of the quantitative framework described here for interpreting $R_2^{\ast }$ measurements in terms of physiological parameters reflecting maternal placental perfusion. We further note that similar structures are visible in T₂-weighted HASTE anatomic imaging in these animals, suggesting that, while non-quantitative, these data, which are commonly used for imaging in pregnancy, may provide a simple means of assessing the functional viability of perfusion domains within the placenta.

A limitation to non-invasive clinical tools used to date for assessing placental function (e.g. Doppler ultrasound) is they are incapable of characterizing perfusion within the intervillous space, the site of oxygen exchange between the maternal and fetal vasculature. Rather, these techniques are directed at the major vessels supporting the placenta. Current MRI indications in human pregnancy generally focus on assessment of fetal developmental abnormalities, with limited applications in characterization of aberrant placental development (23-26). While the DCE-MRI approach we previously applied to nonhuman primate subjects does provide an ability to characterize maternal blood flow in intervillous spaces, to perform such measurements it is necessary to inject a CR into the maternal vasculature. We have recently found that gadolinium chelate (Prohance®) has limited transplacental passage, resulting in minimal fetal tissue exposure and suggesting low risk of adverse fetal effects (27), consistent with observations made by Mühler et al. from high gadolinium chelate exposure measurements made in murine pregnancies (28). Contrast-enhanced imaging has been reported for evaluation of cases of placenta accreta (29). Nevertheless, lingering uncertainties about consequences of fetal CR exposure make it unlikely that gadolinium-based CR will be used routinely for in vivo investigation of placental function in pregnant women. The analysis presented here addresses the above limitations by providing a method for estimating, on an individual lobule basis and using only endogenous MRI contrast, $R_{20}^{\ast }$, v_iPS/Φ, and [Hb_o,f], all of which directly relate to maternal blood flow in the intervillous space and its ability to provide oxygen to the fetal vasculature. It is therefore anticipated that this method can be readily adapted to human subjects, potentially providing a non-invasive means of clinical assessment of placental function in the future.

Among the three animals characterized in this study, notable variability was observed in the number of lobules identified per placenta, the median v_iPS/Φ ratio, and the median $R_{20}^{\ast }$.These animals were clinically-normal rhesus macaques, assessed at the same day of pregnancy (G110 of a 165 day gestation), and thus the variability observed in this study may reflect the distribution of parameters observable in normal rhesus pregnancy at this gestational age. For each of the animals, the number of lobules identified by MRI (18, 34, and 13, respectively for animals A, B, and C, Table 1) was consistently larger than the number of cotyledons identified by observers blinded to the MRI data following Cesarean section delivery (9, 13, and 9, respectively for animals A, B, and C) following previously-described procedures (7). Imperfect correspondence between the pattern of perfusion domains identified by DCE-MRI and the cotyledons observed following delivery was noted in our earlier study in rhesus macaques (7). The results presented here indicate the existence of multiple (as many as 2 to 3) spiral arteries per cotyledon, which is consistent with previous histological examinations of primate placentas.

In addition to variation in the number of lobules, considerable (approximately 5-fold) variation in the median v_iPS/Φ ratios was also observed between animals. At present, it is not possible to attribute this variability to specific factors within the term v_iPS/Φ. For example, differences between lobules could result from variability in the chorion surface area or permeability to oxygen, the volume fraction of the intervillous space, spiral artery blood flow, or a combination of these factors. It is interesting to note that the number of lobules is inversely related to the median v_iPS/Φ ratio for this set of animals. The reason for this association is unknown, and future animal studies will focus on identifying correlations between these parameters. However, if we assume that the dominant source of variation in this parameter is total blood flow (i.e. that intervillous volume and oxygen permeability are fixed), we can compute ∑Φ/v_iPS for the entire placenta to estimate normalized total placental blood flow. This sum is 2.03 × 10⁻⁵ for Animal A, 2.22 × 10⁻⁵ for Animal B, and 4.86 × 10⁻⁵ for Animal C, a considerably tighter range than that observed on the lobule level. This suggests that there may be an adaptive relationship between the number of lobules and per-lobule blood flow that regulates total blood flow available to the fetus.

The significance of observed variability in $R_{20}^{\ast }$ between animals is, at present, unknown. There are numerous factors that could contribute to this term. Some potential candidates are differences in intervillous volume (v_i), maternal and/or fetal hematocrit levels, and magnetic field inhomogeneity. Our sample size was too limited in this study to attempt to correlate these variables, but we intend to investigate these possible factors in future work.

While our model fits the majority of the curves shown in Figure 4 quite well, lobule #12 appears to be an anomaly, with the model fit becoming relatively poor for values of ρ_eff above approximately 0.7 cm accompanied by a pronounced drop-off in $R_2^{\ast }$ at larger distances. This particular lobule also corresponds to the single significant discrepancy between local maxima identified in the $T_2^{\ast }$ maps and local maxima in tissue blood flow identified from DCE-MRI. Further inspection of the raw image data used to specify the placental region of interest (ROI) revealed that the boundary between the placenta and the uterine wall in this particular anatomic location was relatively indistinct, making the ROI difficult to definitively specify. As a result, some non-placental tissue was likely included when the ROI was drawn, exacerbated by the misregistration between DCE-MRI and $T_2^{\ast }$ measurements stemming from the ventilated acquisition (affected by maternal respiratory motion) in the former vs. breath-hold acquisition in the latter. Avid enhancement of the highly vascular uterine wall with contrast administration is consistently observed, so inadvertent inclusion of this tissue can lead to false identification of maxima in the DCE-MRI data. At the same time, uterine wall tissue has a larger $T_2^{\ast }$ value (and, consequently, a lower $R_2^{\ast }$ value) than the peripheral region of the placental lobules, so inclusion of this tissue within the ROI will simultaneously lead to a spurious drop in $R_2^{\ast }$ at larger values of ρ_eff. Although it is possible to eliminate this problem by removing a portion of the secondary lobe ROI containing lobule #12 (data not shown), we chose to present results without further modification because the ROIs were drawn independently of and blinded to the model fit. Doing so prevents the potential for operator bias stemming from fine-tuning of ROIs to optimize quality of model fit.

There are two principal limitations to our $T_2^{\ast }$ data acquisition protocol. First, the presence of pockets of intestinal gas within loops of bowel located in close proximity to the placenta can result in susceptibility-induced artifacts in maps of $T_2^{\ast }$. In the animal studies reported here, gas pockets were sufficiently far from the placenta to have a negligible impact, but this possibility should be considered when performing data analysis as susceptibility artifacts could be misconstrued as regions of placental hypooxygenation. Other than minimizing the presence of intestinal gas via dietary or other interventions, masking of affected regions is the simplest means of mitigation. It is relatively easy to identify gas pockets based on their low signal characteristics, enabling generation of spatially-extended masks by region growing or other similar algorithms. A second limitation is the need to perform multiple breath holds during imaging, resulting in the potential for spatial misregistration between slices if the breath-holds are not completely reproducible. In the primate studies described here this was found to be negligible because respiration was ventilator-controlled under anesthesia, but it has the potential to pose more significant complications for conscious breath-hold imaging in human subjects. While breath-holding might also conceivably affect the maternal and fetal oxyhemoglobin levels no significant changes from baseline saturation were observed during the course of any of the breath-hold measurements.

Conclusion

Our results demonstrate the presence of focally inhomogeneous regions in maps of $T_2^{\ast }$ in non-human primate placenta. Correlation of these regions with the locations of early contrast uptake during injection of gadolinium-based CR further demonstrates that zones of local $T_2^{\ast }$ prolongation are spatially congruent with spiral artery sources supplying maternal blood to placental lobules. In order to quantitatively interpret this spatial pattern in terms of placental physiology, we have proposed a model connecting the observed $T_2^{\ast }$ patterns to the parameters $R_{20}^{\ast }$, v_iPS/Φ, and [Hb_o,f], which relate to intervillous blood flow and oxygen exchange with the fetal vasculature. Our data demonstrate the feasibility of using this novel data acquisition protocol and modeling approach to quantify placental perfusion with endogenous MRI contrast, simplifying its potential application to human pregnancy. The short acquisition time and lack of CR administration alleviate many of the safety concerns of MRI use during pregnancy. Future work will investigate the potential utility of these parameters for noninvasively interrogating placental development and function in human pregnancies.