Diffusion MRI noise mapping using random matrix theory

Abstract

Purpose

To estimate the spatially varying noise map using a redundant magnitude MR series.

Methods

We exploit redundancy in non-Gaussian multi-directional diffusion MRI data by identifying its noise-only principal components, based on the theory of noisy covariance matrices. The bulk of PCA eigenvalues, arising due to noise, is described by the universal Marchenko-Pastur distribution, parameterized by the noise level. This allows us to estimate noise level in a local neighborhood based on the singular value decomposition of a matrix combining neighborhood voxels and diffusion directions.

Results

We present a model-independent local noise mapping method capable of estimating noise level down to about 1% error. In contrast to current state-of-the art techniques, the resultant noise maps do not show artifactual anatomical features that often reflect physiological noise, the presence of sharp edges, or a lack of adequate a priori knowledge of the expected form of MR signal.

Conclusions

Simulations and experiments show that typical diffusion MRI data exhibit sufficient redundancy that enables accurate, precise, and robust estimation of the local noise level by interpreting the PCA eigenspectrum in terms of the Marchenko-Pastur distribution.

INTRODUCTION

The transition from “weighted” MR images to full-scale microstructural modeling is setting a much higher bar on estimating signal parameters in an unbiased way. This is especially relevant for diffusion MRI (dMRI) (1, 2), which holds unrivaled promise for non-invasive quantification of microstructural parameters. Unfortunately, the non-Gaussian nature of noise in magnitude MR data generally biases the diffusion parameters of interest (3). The correction for this noise-induced bias relies on an independent unbiased estimate for the noise map (4).

Accurate, precise, and robust noise estimation has remained a challenging problem. The overarching reason is the non-Gaussian, typically non-central χ (nc-χ) noise statistics, that couples an unknown noise-free signal nonlinearly with the noise in the original complex-valued data from each coil element. This coupling is especially important at low signal-to-noise ratio (SNR), typical of dMRI acquisitions. Further complications arise from low spatial resolution, involuntary motion, and generally spatially varying noise pattern due to the use of parallel imaging (5).

So far, only a few noise estimation methods are able to deal with the spatially varying nature of noise (4, 6–11). The existing techniques depend on (i) the assumption of homogeneous signal intensities in a local neighborhood (10, 11); (ii) diffusion model assumptions (9); (iii) repeated measurements that are often not available (6–8); or (iv) some way of decomposing images into “low frequency” (signal) and “high frequency” (noise), e.g. using wavelets (4, 12, 13), which tends to overestimate the noise level, since sharp edges contribute to the high frequency sub-band. Physiological noise, image misalignment and model inaccuracies, all tend to bias the diffusion model and repetition-based methods (4, 6). The obvious manifestation of this bias is the artifactual anatomical structure visible in the estimated noise maps.

Here we present a model-independent local noise estimation method based on the random matrix theory (RMT) results for noisy covariance matrices. RMT was pioneered by Eugene Wigner and Freeman Dyson in the 1950s-1960s (14, 15) to describe statistics of energy levels in large nuclei and further applied in a wide range of fields. Our method is free of the above limitations and artifacts. Simulations and experiments show it outperforms existing methods in terms of precision and accuracy by an order of magnitude, reducing error in local noise estimation down to about 1% in routine dMRI acquisitions.

Technically, we employ principal component analysis (PCA) coupled with RMT, to exploit the redundancy in multi-directional dMRI data. In the limit of a large covariance matrix size, the noise contribution to the histogram of PCA eigenvalues becomes deterministic, and is given by the universal Marchenko-Pastur (MP) distribution (16) parametrized by the non-Gaussian noise variance σ². This universality allows us to determine the noise level. Hereafter, we will refer to the proposed method as MP-PCA.

Noise level estimation using RMT has previously been explored in the context of finance (17), wireless communication systems (18), cardiac MRI (19), DCE-MRI (20), and fMRI (21). Here we demonstrate for the first time the applicability of this approach in the context of dMRI. In particular, we show with simulations and experiments that typical dMRI data exhibit sufficient redundancy in order to identify the noise bulk from the PCA eigenspectrum using RMT. Next, we make the necessary step from Gaussian to nc-χ distributions in order to resolve noise bias in quantitive MR modalities. For that, we study the manifestation of the nc-χ bias in the PCA eigenspectrum. We demonstrate that by applying the inversion technique (22), the underlying Gaussian noise level σ_c (i.e. the noise standard deviation in the coils) that parameterizes the non-central χ distribution can accurately be determined from σ and the reconstructed signal obtained by nullifying the noise bulk.

THEORY

Noise in magnitude MR data

Phased array coil technology has seen significant developments in the last decades. The introduction of coil systems with a large number of channels, along with new parallel imaging techniques has resulted in significant improvements in scan times or SNR. The resulting magnitude MR data distribution, however, depends on the reconstruction method that is used to combine the complex signals from all independent channels. In general, magnitude MR data is approximately nc-χ distributed with 2L degrees of freedom (23). Here, L corresponds to the effective number of coils and depends on both the hardware and the applied reconstruction technique (24, 25).

The nc-χ distributed magnitude signal m is described by following probability density function:

$$p_L(m\mid \nu ,{\sigma }_c,L)=\frac{m^L}{{\sigma }_c^2}{\nu }^{1-L}\text{exp}\left(-\frac{{\nu }^2+m^2}{2{\sigma }_c^2}\right)I_{L-1}\left(\frac{\nu m}{{\sigma }_c^2}\right),$$ [1]

with ν the noise-free magnitude signal and I_L−1 the (L − 1)^th-order modified Bessel function of the first kind (26). For L = 1, the distribution reduces to the Rice distribution. The expectation value μ of the nc-χ distributed variable m is

$$\mu ={{\beta }_L}_1{F}_1\left(-\frac{1}{2},L,-{\theta }^2\right){\sigma }_c,$$ [2]

with θ = ν/σ_c the SNR, ₁F₁ the confluent hypergeometric function, and

$${\beta }_L=\sqrt{2}\frac{\Gamma (L+\frac{1}{2})}{\Gamma \left(L\right)}=\sqrt{\frac{\pi }{2}}\frac{(2L-1)!!}{2^{L-1}(L-1)!}.$$ [3]

The variance of m equals

$${\sigma }^2=2L{\sigma }_c^2+{\nu }^2-{\mu }^2.$$ [4]

Since the noise bias of the measured signal increases with L, it is beneficial to choose the image reconstruction of the complex coil images that minimizes that parameter. Indeed, reconstructions algorithms such as SENSE, adaptive combine (27) or the recently proposed SENSE1 (28) algorithm always result in L = 1, i.e. a Rician data distribution, even if parallel imaging has been applied, and therefore, they are superior to sum-of-squares reconstructions from a statistical point-of-view.

Principal component analysis (PCA)

Let X be an M × N real-valued measurement matrix, with rows representing M voxels within a sliding window, and columns representing N weighted magnitude MR measurements in each voxel. In what follows, we will take voxels from a square or a cubic patch of a dMRI data set; however, one could also group voxels based on other principles, e.g. within a particular region of interest or tissue type. What will be important is that the matrix X is sufficiently large, i.e. R ≡ min{M, N } ≫ 1.

We expect (as confirmed a posteriori), that the dMRI data is redundant. Namely, due to correlations between many diffusion weighted (DW) signals brought by a generally unknown underlying diffusion process, and/or because the dMRI signal can be efficiently represented by a small number of parameters, X can be approximately viewed as a linear combination of a few, P << R, linearly independent sources, or principal components. In other words, the high-dimensional measurement is effectively reduced to a P-dimensional hyperplane. PCA (29, 30) finds the basis of this hyperplane, the principal components, as eigenvectors of the M × M sample covariance matrix

$$\sum =\frac{1}{N}{\mathit{XX}}^T=\mathit{U}{\Lambda }^2{\mathit{U}}^T.$$ [5]

In Equation [5], U is an orthonormal matrix whose columns are the principal components, and Λ² is an M × M diagonal matrix of eigenvalues λ₁ · · · λ_M. For numerical precision, U and Λ are generally computed via the singular value decomposition of $\mathit{X}=\sqrt{N}\mathit{U}\Lambda {\mathit{V}}^T$.

We will focus on the eigenvalues, which we sort in the descending order, λ₁ ≥ λ₂ ≥ … . In the noise-free population case, corresponding to fixed M and N → ∞, Σ will have exactly P nonzero eigenvalues.

In reality, we are faced with a sample covariance matrix with N ~ M , built from noisy data. Noise propagates through PCA to the eigenvalues and eigenvectors, making all R eigenvalues nonzero, so that rank Σ = R. Remarkably, while noise in each measurement is random, its contribution to the histogram of covariance matrix eigenvalues becomes deterministic in the limit R ≫ P (16).

PCA of a completely random covariance matrix

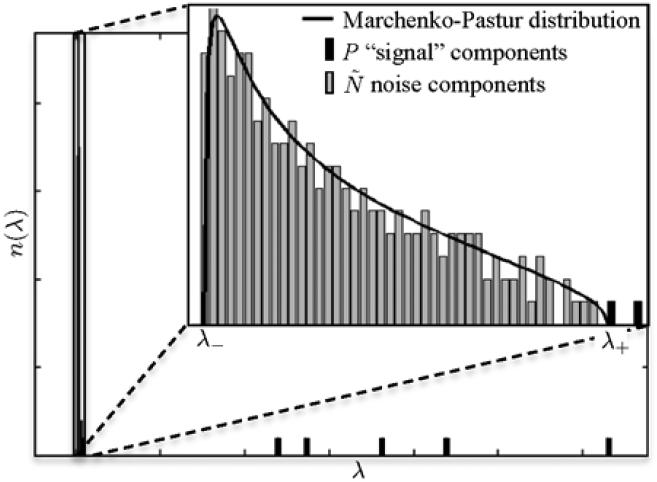
To understand the role played by noise, we first consider the spectrum of Equation [5] when the measurement is pure white noise, P = 0. If X has uncorrelated independent identically distributed (iid) Gaussian entries with variance σ² and zero mean, the nonzero eigenvalues of Σ are distributed according to the following universal “quarter-circle” law (Figure 1):

$$p(\lambda \mid \sigma ,\gamma )=\frac{\sqrt{({\lambda }_{+}-\lambda )(\lambda -{\lambda }_{-})}}{2\pi \gamma \lambda {\sigma }^2},{\lambda }_{-}\le \lambda \le {\lambda }_{+}$$ [6]

and p(λ) ≡ 0 otherwise, where ${\lambda }_{\pm }{\sigma }^2{(1\pm \sqrt{\gamma })}^2$ with γ = M/N the matrix size ratio. Equation [6] has been derived by Vladimir Marchenko and Leonid Pastur in 1967 (16), and is analogous to the celebrated Wigner’s semicircle law for the eigenvalue distribution of random Hamiltonians. For γ < 1, p(λ) is normalized to ${\int }_{{\lambda }_{-}}^{{\lambda }_{+}}pd\lambda =1$, whereas, for γ > 1, p(λ) is normalized to 1/γ, with the (1 − 1/γ)δ(λ) density at zero. The corrections to Equation [6] for finite R decrease fast with R, as ~ 1/R.

Figure 1.

Eigenvalue spectrum of sample covariance matrix of simulated DW data. MP distribution is superimposed. The P significant eigenvalues are separated from the MP “sea”.

We will use the fact that the spectrum resulting from Equation [6] has lower and upper bounds λ_± that depend on the noise level σ and matrix size ratio γ. Physically, the MP distribution arises due to eigenvalue repulsion around the population density δ(λ − σ²) (Equation [6] for γ → 0). The repulsion between levels λ_i,j with the force ~ 1/|λ_i − λ_j | maps finding p(λ) onto an equilibrium profile in an electrostatic problem (15), fixing the bounds λ_± and the spectral shape with square root singularities resulting in Equation [6].

PCA of noisy redundant data

The universality of the MP distribution for the noisy part of PCA still applies if the data X includes P signal sources (significant components), as long as P << R (31). Intuitively, this is guaranteed by the electrostatic analogy (15) — a few charges, representing the significant eigenvalues, cannot noticeably distort the bulk charge density. Figure 1 shows a diffusion tensor based example for P = 7 (1 non-DW signal + 6 DTI elements), N = 256, M = 512, where the shape of the MP “sea” of eigenvalues is very well described by Equation [6].

Depending on the noise level, some of the significant eigenvalues can fall into the MP bulk (31) and become invisible (indistinguishable from noise). Hence, from now on we denote P the number of eigenvalues above the MP edge λ₊. We will develop an iterative noise mapping procedure based on identifying the MP bulk of $\tilde{N}=R-P$ eigenvalues.

METHODS

Noise level estimation

The combination of local PCA with RMT can now be used to estimate the noise level locally. Distribution fitting, that is, minimizing the error between $p(\lambda \mid \sigma ,\tilde{\gamma })$, i.e. the MP distribution of nonzero eigenvalues, and the histogram of the lowest $\tilde{N}$ eigenvalues of Σ by varying the noise level σ and matrix size ratio $\tilde{\gamma }\equiv M∕\tilde{N}$, yields an estimate of the parameters of interest.

An heuristic search algorithm is used to solve this estimation problem. The general idea is to estimate σ and $\tilde{N}$ simultaneously by changing $\tilde{N}$ and estimating the corresponding σ iteratively until $\tilde{N}$ equals the number of eigenvalues ranged by λ₋ and λ₊, which are determined by both $\tilde{N}$ and σ. More specifically, the algorithm is as follows (a schematic overview of the algorithm is shown in Figure 2): (i) At the ith iteration, we have the number ${\tilde{N}}_i=R-P_i$ of MP (noise-only) eigenvalues, i.e. $[{\lambda }_{P_i+1},\cdots ,{\lambda }_R]$. Its initial guess ${\tilde{N}}_1=R-P_1$ is related to the physically expected number P₁ of “observable” model parameters; we take P₁ = 6 for b ≤ 1 ms/μm² DW data and P₁ = 15 for higher b, cf. the number of spherical harmonic coefficients in a 2^nd and 4^th order basis, respectively. Overall, we found the dependency of the algorithm to the initial P₁ to be negligible. (ii) The histogram of the smallest nonzero ${\tilde{N}}_i$ eigenvalues is created by binning $[{\lambda }_{P_i+1},\cdots ,{\lambda }_R]$ into n_b bins with center locations $[{\stackrel{‒}{\lambda }}_1,\cdots ,{\stackrel{‒}{\lambda }}_{n_b}]$ and corresponding bin counts $\rho =[{\rho }_1,\cdots ,{\rho }_{n_b}]$.

Figure 2.

Schematic overview of the MP-PCA algorithm described in section ”Noise level estimation”.

The computation of the number of bins of the histogram, n_b, is data-driven:

$$n_b=\text{arg}\underset{n}{\text{min}}\frac{2\stackrel{‒}{\rho }-\upsilon }{h^2(n,\tilde{N})},$$ [7]

with $h(n,\tilde{N})=|{\lambda }_R-{\lambda }_{P_i+1}|∕n$ being the bin width. Here, $\stackrel{‒}{\rho }=\frac{1}{n}{\sum }_{i=1}^n{\rho }_i\text{and}\upsilon =\frac{1}{n}{\sum }_{i=1}^n{({\rho }_i-\stackrel{‒}{\rho })}^2$ the mean and biased variance of the bin counts, respectively (32).

(iii) A rough estimate of the noise level is computed as ${\tilde{\sigma }}_i=\sqrt{{\lambda }_R}∕|1-\sqrt{{\tilde{\gamma }}_i}|$ with ${\tilde{\gamma }}_i=M∕{\tilde{N}}_i$ and λ_R the lowest nonzero eigenvalue and a proxy for λ₋. Note that we prefer to approximate σ_i by means of an estimate of λ₋ instead of λ₊ as its dependency on $\tilde{N}$ is expected to be weaker. Indeed, conceptually λ_Pi+1 can serve as an estimation for λ₊. However, λ_Pi , λ_Pi+1, and λ_Pi−1 might practically differ by an order of magnitude (the right edge of the MP “sea” fluctuates according to the Tracy-Widom distribution (31)), whereas λ_R is nearly independent of the search variable P_i.

(iv) An extensive grid search, center around ${\tilde{\sigma }}_i$, is done to determine the optimal σ_i. We minimize the weighted squared error between the histogram of ${\tilde{N}}_i$ eigenvalues and the distribution (Equation [6]) with given ${\tilde{\gamma }}_i$:

$${\sigma }_i=\text{arg}\underset{\sigma }{\text{min}}\sum _{n=1}^{n_b}{W}_n({\rho }_n-\varsigma p({\stackrel{‒}{\lambda }}_n\mid \sigma ,{\tilde{\gamma }}_i)),$$ [8]

with $\varsigma =h(n_b,{\tilde{N}}_i){\tilde{N}}_i$ a scaling factor to convert probabilities into counts. The inverse of those predicted counts are chosen as weights, i.e. $W_n={\left(\varsigma p({\stackrel{‒}{\lambda }}_n\mid \sigma ,{\tilde{\gamma }}_i)\right)}^{-1}$, to compensate for the strong non-uniformity of the distribution when $M\approx \tilde{N}$, due to the λ^−1/2 divergency of $p\left(\lambda \right){\mid }_{\tilde{\gamma }-1}$ as λ → 0.

(v) We then compute the right MP edge ${\lambda }_{+,i}={\sigma }_i^2{(1+\sqrt{{\gamma }_i})}^2$ and compute the number P_i+1 of observable parameters, as the number of eigenvalues exceeding λ_+,i.

(vi) We iterate (i) to (v) until P_i+1 = P_i.

The universality of MP law requires both M, the number of voxels, and $\tilde{N}$, the number of noiseonly components, to largely exceed 1. Obviously, $\tilde{N}$ depends on the chosen diffusion protocol and the degree of redundancy (which depends both on M and on the strength of diffusion weighting). The freedom to choose M ≫ 1 enables finding a compromise between spatial resolution and the redundancy. The use of a sliding window (e.g. M = [11 × 11] or M = [5 × 5 × 5]) will yield the 2d or 3d noise map, respectively. We hereby assume the true noise map can be considered to be fairly constant within those local neighborhoods. Because of that assumption, we here opt to analyze the native diffusion-weighted measurement matrix X instead of log(X) to avoid strong signal dependency of the noise level induced by the log transform.

Correction for non-central χ statistics

The standard deviation

$$\sigma =\xi \left(\theta \right)\le 1$$ [9]

of a nc-χ distributed variable with L degrees of freedom is always smaller than the standard deviation σ_c of the Gaussian noise in the individual complex-valued coil images (22). The factor

$$\xi \left(\theta \right)=2L+{\theta }^2-{\beta }_L^2\cdot {{[}_1{F}_1(-1∕2,L,-{\theta }^2∕2)]}^2$$ [10]

is a function of SNR θ. Because the SNR is not known a priori, the correction ξ(θ) needs to be estimated iteratively until convergence, initiated by both the mean, μ(θ), and variance, σ²(θ), of the magnitude signal, cf. Koay’s inversion (22).

We use P significant eigenvalues (i.e. the ones exceeding the right MP edge λ₊) to estimate the signal mean in each voxel and diffusion gradient direction, $\mathit{X}=\sqrt{N}\mathit{U}\Lambda {\mathit{V}}^T$, where $\widehat{\Lambda }$ is obtained from the SVD-derived Λ by nullifying all but the first P eigenvalues. The remaining eigenvalues can further be corrected, cf. (31). We then use Koay’s inversion for each element ${\widehat{X}}_{ij}$ separately.

Overall, we expect the noise map to be slightly underestimated because some of the noise corrupts the P significant eigenvalues and is not accounted in the distribution fitting. We estimate this bias at the level of 1/R.

Aja-Fernández et al. showed that in case of of parallel imaging, the actual magnitude of MR signal may deviate from a pure nc-χ distribution to an unknown degree (23, 25). This happens if the individual coil images are combined using the sum-of-squares while noise correlations exist between the different coil images. Obviously, if an accurate analytical expression for the actual data distribution is lacking, accurate bias correction cannot be performed. However, this potential source of bias roots in noise modeling and the unknown propagation of the coil correlations into the data distribution, and is not inherent to the use of MP-PCA. For more information regarding this related, though independent problem, we refer to (4, 23, 25).

Previous noise mapping approaches

We will compare our method with following state-of-the-art techniques for noise estimation:

Repetitions

In the simplest case, σ is computed as the standard deviation of a set of repeated measurements. If the mean is calculated as well, Koay’s inversion can be applied to correct for nc-χ bias. Physiological noise may interfere with the estimation of the noise level. To overcome that potential source of inaccuracy, one can replace the mean and the standard deviation by their robust counterparts, i.e. median and median absolute deviation (MAD) estimators, respectively (6).

Residuals

Weighted least squares fitting of an adequately chosen signal representation, e.g. DTI, to the data will result in residuals with statistics directly related to the noise variance σ² (33). An estimate of the expectation value of the directional DW signals is found by reconstructing the signal based on the estimated noise parameters, employing Koay’s inversion. Note that this approach is equally accurate as the simultaneous estimation of signal and noise parameters by means of log-likelihood functions (34, 35) if the data is Rician distributed with a minimal SNR of 2 (33, 36).

Wavelets

The wavelet decomposition provides a means to separate low from high frequency information. Assuming the high frequency components contains residual signal that originated in high image gradients in addition to noise, Coupé et al suggested the MAD of the absolute value of the high frequency components as a global estimate of σ (12). Correction for nc-χ statistics is again possible. A local dMRI-specific variant of their approach was presented by Veraart et al (4).

Data

As the overarching issue with noise mapping is our inherent lack of noise-free ground truth, below we employ both the simulated data based on an atlas (37), and a human dMRI measurement with large oversampling for a range of diffusion weightings.

Simulated dMRI data

We simulated whole brain DW data, derived from a hybrid diffusion atlas that was created with 10 healthy subjects (37). The choice for that atlas roots in its high precision and a high order parameterization of the underlying diffusion signal by spherical harmonics, allowing us to employ it as a noise-free “ground truth”. We resampled the b = 1 ms/μm²-shell of the atlas data on 90 isotropically distributed gradient directions (g) to serve as gold standard for the antipodal symmetric signal $S\left(g\right)={\sum }_{l=0,2,4}{\sum }_{m=-l}^l{c}_m^l{Y}_l^m\left(\mathrm{g}\right)$ with $c_m^l$ the real harmonic series coefficients and $Y_l^m$ an orthonormal basis for real functions of the unit sphere with order l and phase factor m (38). After adding complex Gaussian noise with standard deviation σ_c, the magnitude images were computed to generate Rician distributed DW data. In total, 4 noise realizations were made: spatially uniform noise level with average SNR_b=0 = 20 and 40 within a brain mask, and spatially varying noise level with average SNR_b=0 = 20 and 40.

We applied our proposed MP-PCA method and the wavelet-based method to estimate the noise map on each complete simulated data set, i.e. N = 90 gradient directions, as well as on subsets of N = 30 and 60 gradient directions. Subsets were chosen in such a way that each subset was composed out of isotropically distributed directions. For MP-PCA, we additionally varied the sliding window size (M = [n × n × n] with n = {5, 7, 9}). For a quantitative comparison of the different techniques, we use the relative error, i.e. a voxelwise measure that is calculated as the difference between a measurement and the local ground truth value, divided by the ground truth value. The performance of the residual-based method would be misleadingly high due to the lack of physiological noise and motion in the simulation set-up and, as such, not shown here.

Experiment

A 30 year-old healthy volunteer underwent imaging on a Siemens Skyra (3T) MR scanner (Siemens AG, Siemens Medical Solutions, Erlangen, Germany) after obtaining informed consent, using a 20-channel receiver head coil. The body coil was used for transmission. An EPI-DW sequence was used to acquire the dMRI data. Diffusion weighting was applied along 90 isotropically distributed gradient directions with b = 1, 2, and 3 ms/μm². Same gradient direction were applied for each b. Additionally, 4 × 23 additional images were acquired: 23 images without diffusion sensitization and 3 × 23 DW images with diffusion sensitization (b = 1, 2, and 3 ms/μm²) along a single gradient direction. Other imaging parameters were kept constant throughout the data acquisition sequences: TR/TE : 5000/106, ms, matrix: 88 × 88, slice thickness: 2.5 mm, slices: 50, parallel imaging factor: GRAPPA with acceleration factor 2, reconstructed using the adaptive combine algorithm (L = 1), multiband acceleration with factor 2.

Noise maps were estimated from b-value dependent subsets of the measured data, by employing (i) robust noise map estimator using repeated measurements; 23 × {b = 0, 1, 2, 3} ms/μm² (6), (ii) statistics of the residuals after a diffusion tensor imaging (DTI) fit using the weighted linear least squares estimator; subsets were 5 × {b = 0} + 90 × {b = 0, 1, 2, 3} ms/μm² (33, 36), (iii) the local wavelet-based approach; subsets were 90 × {b = 1, 2, 3} ms/μm² (4), and (iv) our proposed MP-PCA with a [7 × 7 × 7] sliding window; 90 × {b = 1, 2, 3} ms/μm². Additionally, we applied our proposed MP-PCA method on subsets of b_i consisting of 30 and 60 isotropically distributed gradient directions, respectively.

RESULTS

nc-χ distributed random matrices

Figure 3 shows the average noise level estimated using MP-PCA from 500 independent realization of a 125 × 90 matrix X of which each entry X_ij is a sample for a nc-χ distribution with ν = SNR and σ_c = 1. The noise level is shown as function of the SNR for L=1, 8, 16, and 32, before ($\widehat{\sigma }$; red) and after (${\widehat{\sigma }}_c$; green) correction for the nc-χ bias, respectively. The standard deviation of the respective nc-χ distributed variables, σ, are shown to demonstrate that in case of nc-χ distributed data, the proposed framework returns an accurate estimate of σ instead of σ_c. As shown in Figure 3, the signal $\widehat{\mu }$ reconstructed from the principal components after nullifying all but the first P eigenvalues matches the expectation value μ instead of the respective noise-free underlying signal ν. In this simulation, P was always determined to be 1 by our algorithm, even in case of SNR=0, which indicates that the nc-χ signal bias leaks out of the noise bulk and contributes to signal component(s). The observation that we can estimate both σ and μ justifies the use of Koay’s inversion technique (22) to compute estimates of the Gaussian noise level σ_c regardless of L. Hence, without loss of generality, we limit rest of the manuscript to L = 1. It can be observed in Figure 3 that for very low SNR, ${\widehat{\sigma }}_c$ is slightly underestimated. However, the underestimation is inherent to the inversion technique, not to the MP-PCA estimation of σ or μ, which is shown to be accurate.

Figure 3.

The bias correction framework relies on the accurate estimation of the expectation value (top row) and standard deviation (bottom row) of the distribution. The theoretical (μ) and the estimated $\left(\widehat{\mu }\right)$ expectation values are shown in the top row in dashed blue and red curves, respectively. The magnitude noise standard deviation $\widehat{\sigma }$ and underlying Gaussian noise level ${\widehat{\sigma }}_c$, estimated from a 125 × 90 matrix X of which each entry X_ij is a sample for a nc-χ distribution with noise free signal ν = SNR and σ_c = 1, are shown as function of the SNR for L=1, 8, 16, and 32, before and after correction for the nc-χ bias, respectively (bottom row). The solid lines (red and green) are the average over 500 independent noise realizations, whereas the shaded colored areas show the confidence interval bounded by the standard deviation.

Simulation data

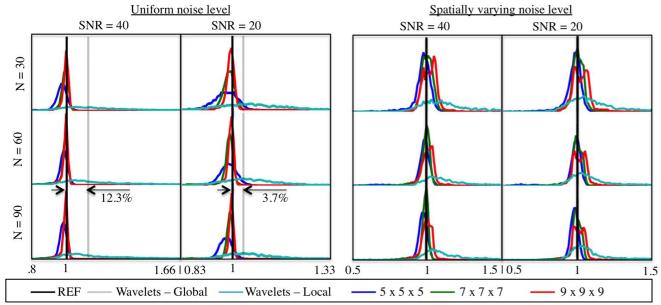
Figure 4 and Figure 5 show the noise maps estimated from Rician distributed simulated data with spatially uniform and spatially varying noise levels, respectively, using (i) our proposed local MP-PCA technique and (ii) the local wavelet-based noise map estimator (4). The spatially varying noise map is shown in Figure 5 (labeled REF) for reference. A visual inspection of the maps shows us that the wavelet approach tends to overestimate the noise, especially near sharp edges in the DW images. As a result, the underlying image is reflected in the estimated noise maps, e.g. CSF. However, this bias depends on the SNR. The lower the SNR, the better the decoupling of noise and high frequency edge information by a wavelet decomposition. Nonetheless, regardless the SNR, our proposed technique, MP-PCA, shows about 99% accuracy and precision in the local estimation of the noise level, even for low N.

Figure 4.

Noise maps estimated from Rician distributed simulated data with spatially uniform noise level. Our proposed method, MP-PCA, was evaluated as function of SNR, number of DW acquisitions N , and 3d sliding window size M. Comparison with a local wavelet-based noise estimator (4) demonstrates the superior performance of MP-PCA, in terms of both accuracy and precision, regardless the underlying signals and noise-uniformity. The advantages of MP-PCA are obvious already by having no artifactual anatomical features, that are present in the wavelet-based method.

Figure 5.

Noise maps estimated from Rician distributed simulated data with spatially varying noise level. Our proposed method, MP-PCA, was evaluated as function of SNR, number of DW acquisitions N , and 3d sliding window size M. Comparison with a local wavelet-based noise estimator (4) demonstrates the superior performance of MP-PCA, in terms of both accuracy and precision, regardless the underlying signals and noise-uniformity. The advantages of MP-PCA are obvious already by having no artifactual anatomical features, that are present in the wavelet-based method.

In Figure 6 we show the histograms of the relative errors in the estimated noise levels within the brain mask. These quantitative comparison includes the results for the global noise estimator based on the wavelet decomposition, proposed by Coupé et al. (12) in case of the spatially uniform noise map. For the global wavelet estimator, a 12.3% overestimation of the noise level is observed for SNR=40, whereas, for SNR=20, the bias reduces to 3.7%.

Figure 6.

Histograms of the relative error of the noise maps estimated from Rician distributed simulated data with spatially uniform (left) and varying noise levels (right). The proposed MP-PCA outperforms local and global wavelet-based noise estimators, both in terms of accuracy and precision. The precision of MP-PCA tend to increase with the size of the sliding window. However, the resolution of the largest window becomes insufficient to capture local variability in noise level in case of spatially varying noise, thereby biasing the results (red curve). This points at the existence of an optimal sliding window size M for a given coil array.

In Table I, we listed the mean relative error (MRE) and the standard deviation of the relative errors (SRE), both calculated within the brain mask. The global wavelet approach resulted in a single noise level for each DW image. The corresponding MRE and SRE were computed from that set of values. The MRE indicates the high accuracy of MP-PCA, regardless of the SNR. In the worst case, we observed a MRE of 2.9%, but in most cases the absolute value of the MRE < 1%. For the local wavelet based approaches, the performance in terms of MRE ranged between 5% and 20%. Similarly, MP-PCA is better in terms of SRE, which probes the precision. In general, SRE decreases with increasing M and N.

Table I.

Quantitative comparison of different noise estimation techniques as function of SNR, N, and, if applicable, sliding window size. MRE = mean relative error; SRE = standard deviation of the relative error. The MRE for MP-PCA is about 1%, an order of magnitude below MRE for wavelet-based methods.

			MP-PCA						WAVELET
			5 × 5 × 5		7 × 7 × 7		9 × 9 × 9		local		global
	SNR	N	MRE	SRE	MRE	SRE	MRE	SRE	MRE	SRE	MRE	SRE
Spatially uniform		30	−0.0209	0.0406	−0.0090	0.0188	−0.0030	0.0117	0.0614	0.1081	0.0376	0.0126
	20	60	−0.0135	0.0308	−0.0084	0.0125	−0.0025	0.0097	0.0537	0.0838	0.0370	0.0134
		90	−0.0179	0.0239	−0.0073	0.0113	−0.0023	0.0083	0.0503	0.0766	0.0366	0.0148
		30	−0.0227	0.0145	−0.0031	0.0088	0.0035	0.0061	0.1601	0.1187	0.1224	0.0153
	40	60	−0.0126	0.0113	−0.0014	0.0071	0.0014	0.0052	0.1450	0.1075	0.1230	0.0154
		90	−0.0135	0.0100	−0.0017	0.0065	−0.0007	0.0055	0.1368	0.1014	0.1247	0.0155
	SNR	N	MRE	SRE	MRE	SRE	MRE	SRE	MRE	SRE
Spatially varying		30	−0.0128	0.0385	0.0075	0.0363	0.0259	0.0569	0.0809	0.1448
	20	60	−0.0075	0.0324	0.0021	0.0330	0.0193	0.0499	0.0852	0.1606
		90	−0.0172	0.0280	−0.0031	0.0301	0.0104	0.0453	0.0754	0.1425
		30	−0.0120	0.0393	0.0101	0.0376	0.0291	0.0487	0.1680	0.2534
	40	60	−0.0102	0.0328	0.0026	0.0255	0.0166	0.0384	0.2029	0.3155
		90	−0.0193	0.0302	−0.0040	0.0220	0.0084	0.0364	0.1965	0.2964

Increasing the window size might lower the performance in case of spatially varying noise. Indeed, the selection of the sliding window size is influenced by two opposing effects. First, the histograms for the spatially uniform noise suggest that increasing the window size increases the precision of the estimator due to increase in the random matrix size. However, for the spatially varying noise case, we observed a slight bias in the local noise estimation due to the reduced resolution of large window sizes. This is visible in both the maps and histograms. We find [7×7×7] the better trade-off in between precision and accuracy in our experiments.

Experiment

Figure 7 shows the noise maps estimated from b-value dependent subsets of the measured data for the different estimators. The following qualitative observations can be made. First, despite the use of robust statistics, noise map estimation based on repeated measurements are prone to artifacts related to physiological noise, CSF pulsation in particular. The use of high b-value largely minimized that effect. Hence, the map estimated from the 23 repetitions with b = 3 ms/μm², i.e. the highest b-value in our study, serves as the most reliable proxy for the ground truth, hereafter termed bronze standard. Second, the noise maps based on residuals after a diffusion model fit are only as accurate as the diffusion model. Unsurprisingly, the accuracy decreases with the increase in b-value, especially noticeable in the major white matter structures. Moreover, although not overly represented in this data set, this technique might suffer from subject motion and physiological noise. Fig. 8 in ref. (4) shows for example how bad it can get in clinical data. Third, wavelet-based approaches suffer from an incomplete separation of noise and signal by a wavelet transformation at high SNR. Therefore, at low b-value, anatomical structure can be observed in the estimated noise maps. Although the effect reduces with b, it does not disappear in our data. Finally, MP-PCA shows a smooth, artifact-free noise map that is more consistent with the bronze standard than other methods for all b-values.

Figure 7.

Experiments show qualitatively and quantitatively (see Table I) that our proposed method (MP-PCA) outperforms the residual and wavelet-based methods if compared to the most reliable proxy for the ground truth. This map was computed from 23 repetitions at the highest b-value to suppress CSF-related physiological noise and is referred to as the bronze standard. In the scatter plots, the best estimated noise maps (gray boxes) of the corresponding row are shown voxel-by-voxel against our bronze standard (gray dots). The black line of unity and the dashed lines (offset of ±10% of window range to unit line) are shown for reference.The highest correspondence is observed for the MP-PCA method. Indeed all MP-PCA maps correlate well with the bronze standard, correlation coefficients are all 0.90, whereas for the residual-based method, the coefficients range between 0.81 and 0.83, and for the wavelet-based technique, they range between 0.41 and 0.88. The images are ranged by [0 50].

Figure 8.

Weak dependence of MP-PCA noise maps on N and sliding window size is shown by evaluation of subets of b = 1 ms/μm²-shell. The images are ranged by [0 20].

Figure 7 shows scatter plots in which the best result of (ii), (iii), and (iv) are shown voxel-by-voxel against our bronze standard (i.e. b = 3 ms/μm²). It can be observed that MP-PCA shows the highest correspondence. Moreover, that technique has the least b-value dependency and, as such, is the most generally applicable one. The high correspondence can also be quantified by the correlation coefficient. All MP-PCA maps correlate well with the bronze standard, correlation coefficients are all 0.90, whereas for the residual-based method, the coefficients range between 1.81 and 0.83, and for the wavelet-based technique, they range between 0.41 and 0.88.

Figure 8 shows the dependence of MP-PCA on the number N of DW images by selecting isotropically distributed subets with N = 30, 60, and 90. Furthermore, the performance of MP-PCA is evaluated as function of the sliding window size. In line with previous experiments, MP-PCA results are very consistent, regardless of N and sliding window size. In general, the precision tends to increase with N and the window size. However, theoretically, the performance is eventually expected to decrease with (a) increasing the window size (potential heteroscedasticity of the underlying noise level) or (b) reducing N (redundancy loss when N approaches P).

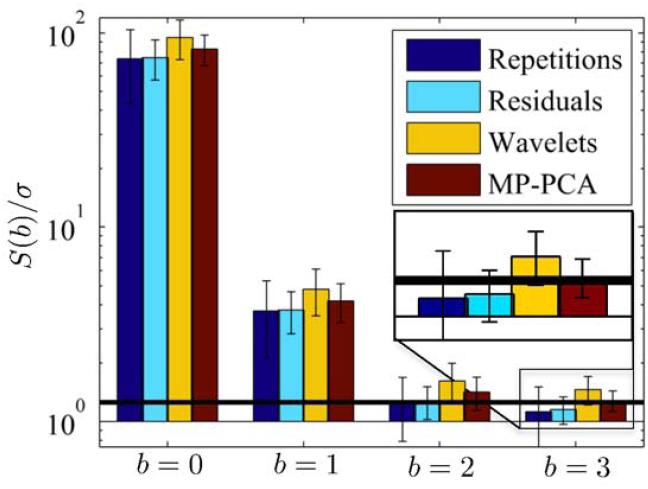
A final demonstration of the high accuracy of MP-PCA in comparison to other approaches is given in Figure 9. The DW signals in the CSF voxels are suppressed down to e^−3×3 ≈ 10⁻⁴ level at b = 3 ms/μm² and, as such, can be assumed to be noise-only. Hence, the average of those signals equals the noise floor, i.e. the minimally measurable signal. Since our data is Rician distributed, the noise floor is given by $\sqrt{\pi ∕2}{\sigma }_c$. After normalization of the DW images with the spatially varying noise maps of σ_c, obtained from the different approaches, we averaged the signals within the CSF. The mean and standard deviation over all the DW images present for each b-value are shown in Figure 9. One can readily observe that the MP-PCA normalized DW signals yield the best correspondence to the normalized noise floor, $\sqrt{\pi ∕2},\text{at}b=3\text{ms}∕\mu {\text{m}}^2$. Normalization of the DW signals was needed to cope with the spatially varying nature of the noise maps.

Figure 9.

Average CSF signal as function of the b-value [ms/μm²]. The DW data was first normalized by the noise maps estimated with the different techniques. The error bars indicate the standard deviation over the different DW images present for each b-value. The black line shows the noise floor, i.e. $\sqrt{\pi ∕2}$ for the normalized data. The CSF signal is suppressed by > 99.99% at b = 3 ms/μm² and can therefore be assumed to be noise-only.

DISCUSSION

We presented an accurate, precise and robust method for the local noise estimation. The method exploits the redundancy in multi-directional diffusion MRI data by identifying the noise-only principal components using the knowledge that the corresponding eigenvalues are described by the universal Marchenko-Pastur distribution, parameterized by the noise level.

Previous noise mapping methods all come with serious limitations. Repeated measurements are often not available due to scan time constraints. Misalignment of data limits the accuracy of all methods other than the wavelet-based approaches. Model inaccuracies due to physiological effects such as CSF pulsation will distort the statistics of the residuals or the accuracy of likelihood functions, and the accuracy of wavelet-based approaches strongly depends on the presence of residual signal in the high frequency sub-band. We demonstrated all those limitations in clinically representative experiments while showing that our MP-PCA technique is much less sensitive to the above complications inherent to a dMRI data set.

Here, we further elaborate on the strengths, limitations, and potential applications of the method.

Redundancy requirement

The Marchenko-Pastur distribution is an asymptotic universal law that holds in the large matrix size limit. In this regard, one must consider the size of the $[M\times \tilde{N}]$ noise-only matrix that we obtain by decomposing the [M × N ] measurement matrix in its principal components. Hence, the noise part $\tilde{N}=N-P$ will only be large if the measurements are highly redundant, P << N. First, small P can be achieved by limiting the diffusion-weighting. Indeed, the complexity of the underlying, generally non-Gaussian diffusion process, and as such P, tends to increase with the bvalue. Second, P increases with the size M of the sliding window due to the potential heterogeneity in noise level within the set of voxels. Simulations showed that the performance of our approach might become lower for large M (see Figure 6). Hence, the beauty of our proposed technique is that it performs best when applied locally. However, one rather chooses M > N to avoid the situation when M becomes the dominating factor in the deviation from the Marchenko-Pastur law, which is of order O(1/ min{M, N }).

Using the above guidelines, we demonstrated high accuracy of the noise estimator even for DW data sets limited to 30 gradient directions. Therefore we showcased the wide applicability of this theoretical framework.

We would like to emphasize that redundancy is not tied to dMRI, the modality of our interest throughout this work. Indeed, the proposed technique can be applied in other modalities including, but not limited to, redundant time series, such as DCE-MRI (20) and fMRI. Neither is application of this technique limited to a single DW shell in q-space.

Ground truth

The main limitation of our study is the lack of ground truth in our experimental part. Due to obvious reasons one cannot measure noise-free signal. Regarding the ground truth for the noise, unfortunately, one cannot measure exactly such a reference map either. On the one hand, the thermal noise level depends on the load of the scanner (39). Hence, an air-only acquisition will not provide the required information. On the other hand, although switching off the excitation pulses might mimic such an acquisition, image reconstructions often require the signal, i.e. autocalibration signal (ACS) lines, for accurate calculation of the coil sensitivity maps that determine the spatially varying nature of the noise map (40).

Given all these limitations, we assessed the accuracy of the proposed technique. First, we tried to create the most reliable proxy (“bronze standard”) for the ground truth by acquiring multiple repetitions of the same DW image. Despite the use of a robust estimator (6), we observed that physiological noise and misalignments between repeated measurements tend to bias the noise estimation. The effect was significantly lower for higher b-values. Second, we used the knowledge that CSF is fully suppressed at b = 3 ms/μm², to evaluate the accuracy of the methods. Indeed, within the CSF the average signal should match the noise floor, which is parameterized by the noise level. As shown in Figure 9, the best correspondence was achieved for MP-PCA.

Applications

Noise bias

To remedy the systematic bias of diffusion parameters that is inherent to the use of least squares estimators in case of nc-χ distributed data, one may prefer using more advanced estimators that explicitly account for the actual MR data distribution (4, 35). Those distributions are parameterized by the noise level. Hence, prior knowledge of that parameter enables an improved precision and accuracy of diffusion model parameter estimators.

Outlier detection

Signal variability in DW images roots in both thermal noise and spatially and temporally varying artifacts such as subject motion and cardiac pulsation. Those spatially and temporally varying artifacts, which are referred to as physiological noise, generally cannot be modeled. Robust parameter estimation techniques such as RESTORE (41, 42) have been introduced to identify the signal outliers and minimize their effect on the the diffusion model parameters. However, the thermal noise level is required in most of the robust estimators in order to identify those outliers with some user-defined probability.

Gibbs ringing

Gibbs ringing has recently been recognized as a confound in diffusion MR analyses (43–45). Moreover, we analytically derived its significant quantitative impact on the diffusion signal and model parameters (45). To remedy the strong bias on diffusion metrics due to the Gibbs ringing artifact, we suggested to extrapolate the k-space beyond the measured part (46) by means of second order total generalized variation minimization (45, 47). These types of regularized optimization problems generally come with a regularization term that controls the data fidelity. Optimal choice of this regularization term is based on the thermal noise level (48).

Denoising

By applying PCA to redundant data and preserving only the significant principal components, the noise can be strongly reduced. Manjon et al. (49) recently proposed image denoising in the context of dMRI by using a sliding window wherein the local PCA transformation matrix was estimated. Denoising is then achieved by canceling all principal components with eigenvalues below some threshold; the key uncertainty in this approach is choosing this threshold. The authors rely on empirically defined thresholds, e.g. 5.29σ² for their particular M and N . Here, we suggest using an objective threshold ${\lambda }_{+}={\sigma }^2{(1+\sqrt{\tilde{\gamma }})}^2$ based on the right edge of the Marchenko-Pastur distribution [6]. Hence we foresee that considering λ₊ as a threshold value will further improve and generalize PCA based denoising methods. However, this is beyond the scope of this work.

Nonetheless, the term denoising must be put in right perspective. Noise is not only represented in a limited number of principal components that can be canceled upon request. Indeed, in practice, all principal components, the eigenvalues and eigenvectors, are corrupted by noise to some degree. Some (or all) significant eigenvalues might be indistinguishable from the noise spectrum in case of low SNR and large γ. Hence, denoising techniques can remove some of the principal components describing the noise-free signal. Next, eigenvalues distinct from the noise bulk are biased by a coherent repulsion of the significant eigenvalues by all the pure noise eigenvalues (31). Additionally, the corruption of the eigenvectors by the noise cannot be undone. These elements explain the negative MREs in Table I and put the term denoising in perspective. Consequently, the standard deviation of the reconstruction of the noise-only signal has systematically lower variance than the estimated noise variance (results not shown). Hence, data variability due to noise is only partially canceled by MP-PCA denoising.

CONCLUSION

We used the universal Marchenko-Pastur distribution to identify the noise-only eigenvalues obtained by a local PCA of nc-χ distributed dMRI data. Typical dMRI data has shown to exhibit sufficient redundancy which allows to distinguish between the noise and signal components in a model-independent way, and without the need to empirically set the PCA threshold value. Our proposed local noise estimator outperforms known spatially varying noise estimation methods in terms of accuracy (~ 99%) and precision, and does not require acquisition of repeated measurements, instead utilizing data redundancy.