A MATHEMATICAL FRAMEWORK FOR EXACT MILESTONING

Abstract

We give a mathematical framework for Exact Milestoning, a recently introduced algorithm for mapping a continuous time stochastic process into a Markov chain or semi-Markov process that can be efficiently simulated and analyzed. We generalize the setting of Exact Milestoning and give explicit error bounds for the error in the Milestoning equation for mean first passage times.

1. Introduction

Molecular Dynamics (MD) simulations, in which classical equations of motion are solved for molecular systems of significant complexity, have proven useful for interpreting and understanding many chemical and biological phenomena (for textbooks see [23, 12, 1]). However, a significant limitation of MD is of time scales. Many molecular processes of interest occur on time scales significantly longer than the temporal scales accessible to straightforward simulations. For example, permeation of molecules through membranes can take hours [6], while MD is usually restricted to the microsecond time scale. One approach to extend simulation times is to use faster hardware [24, 25, 21]. Other approaches focus on developing theories and algorithms for long time phenomena. The emphasis in developing algorithms has been on methodologies for activated processes with a single dominant barrier such as Transition Path Sampling [8, 19]. Approaches for dynamics on rough energy landscapes and for more general and/or diffusive behavior have also been developed [22, 7, 26, 20]. The techniques of Exact Milestoning [3] and Milestoning [10] belong to the latter category.

The acceleration in Milestoning is based on the use of a large number of short trajectories between certain hypersurfaces in phase space that we call milestones, instead of complete trajectories between reactants and products (see Figure 1). The use of short trajectories is trivial to parallelize, making the formulation efficient to use on modern computing resources. Moreover, using short trajectories initiated near bottlenecks of reactions allows for enhanced sampling of improbable but important events. The last enhancement can lead to exponential speed up of the computations. A challenge is how to start the short trajectories and how to analyze the result to obtain the correct long time behavior.

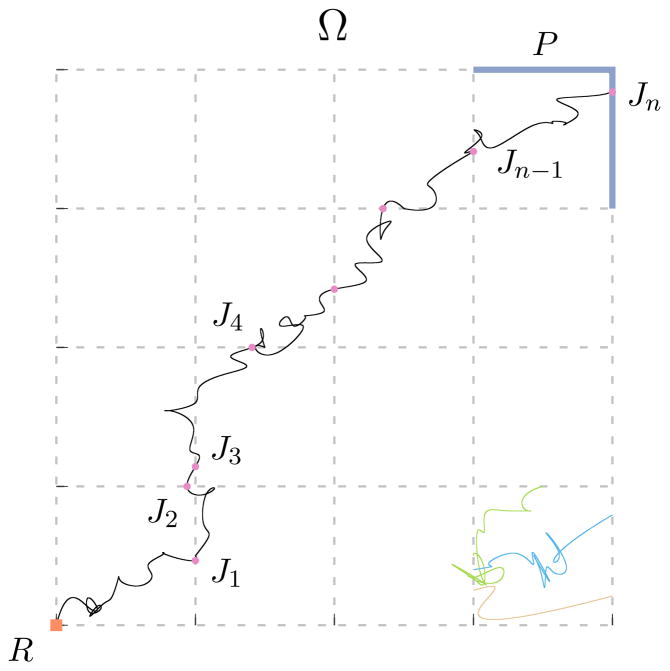
Fig. 1.

Representation of the state space Ω and the milestones. Each milestone is an edge of one of the squares traced by dashed grey lines. The reactant state R is highlighted as a square dot in the left-bottom corner while the product state P is comprised of the two line segments shown in blue at the upper-right corner. A particular realization of a long trajectory appears as a continuous black line and the corresponding values of the process (J_n) are marked with circles. The individual trajectories shown in different colors near the bottom-right corner represent trajectory fragments as used in the Milestoning algorithm.

Milestoning uses an approximate distribution for the initial conditions of the trajectories at the hypersurfaces. The results are then analyzed within the Milestoning theory. This approximation is typically the canonical distribution conditioned to be at the milestones. Exact Milestoning improves over the starting guess of the initial conditions by an iterative process that converges to the correct stationary distribution.

There are related approaches that use short trajectory information to obtain information on long time kinetics such as non-equilibrium umbrella sampling [28] and trajectory tilting [27]. However the overall scope of these methods is more limited than that of Exact Milestoning, which provides a complete statistical mechanical picture of the system.

While Milestoning is an approximate procedure, it shares the same philosophy and core algorithm as the Exact Milestoning approach. In both algorithms the state space Ω is coarse-grained by closed subsets called milestones. The short trajectories are run between nearby milestones and are terminated the first time they reach a milestone different from the one they were initiated on (see Figure 1). The short trajectories in time and space should be contrasted with long continuous trajectories from the reactant R to the products P in straight-forward MD.

In the theoretical analysis of the short trajectories, in Milestoning and Exact Milestoning emphasis is made on the absolute flux. The absolute flux is always positive and is the number of trajectories that pass through a milestone per unit time. While we obtained time-dependent solutions for the kinetics in Milestoning in the past [10], more recently and frequently we use stationary solutions [3, 17]. In stationary systems the flux is time independent and can be used to define a probability measure after a proper normalization. Hence, it is possible to reformulate the algorithms of Milestoning and Exact Milestoning in terms of widely used concepts and tools of probability theory. This formulation and a rigorous mathematical framework are provided in the present manuscript.

This article is organized as follows. In Section 2, we describe the setting for Exact Milestoning and introduce notation used throughout. In Section 3, we show existence of and convergence to a stationary flux under very general conditions. In Section 4 we state precisely the Exact Milestoning algorithm [3]. In Section 5, we establish conditions under which convergence to the stationary flux is consistent in the presence of numerical error (Lemma 5.2 and Theorem 5.3), and we give a natural upper bound for the numerical error arising in Exact Milestoning (Theorem 5.4). Finally, in Section 6 we consider some instructive examples.

2. Setup and notation

2.1. The dynamics and MFPT

In Milestoning we spatially coarse-grain a stochastic dynamics (X_t). The basic idea is to stop and start trajectories on certain interfaces, called milestones, and then reconstruct functions of (X_t) using these short trajectories, which can be efficiently simulated in parallel. We focus here on using Milestoning for the efficient computation of mean first passage times (MFPTs) of (X_t), although similar ideas can be used to compute other non-equilibrium quantities.

To make our arguments we need some assumptions on the process (X_t). We assume (X_t) is a time homogeneous strong Markov process with càdlàg paths taking values in a standard Borel space Ω. These assumptions allow us to stop and restart (X_t) on the milestones without knowing its history. In applications, usually (X_t) is Langevin or overdamped Langevin dynamics, and Ω is a subset of Euclidean space. More generally, (X_t) could be a diffusion and Ω = ℝ^d/ℤ^d could be a torus, or (X_t) could be a continuous time Markov chain on a discrete set Ω = ℕ.

We write ℙ, 𝔼 for all probability measures and expectations. ℙ^ξ and ℙ^x will represent probabilities for a process starting at a distribution ξ or point x, respectively. We write ||·||_TV for total variation norm of signed measures. Our analysis below will mostly take place in an idealized setting where we assume infinite sampling on the milestones. In this setting, distributions are smooth (if state space is continuous) and the total variation norm is the appropriate one. We omit explicit mention of sigma algebras and filtrations, which will always be the natural ones, and we will use the words distribution and probability measure interchangeably.

Recall we are interested in computing the MFPT of (X_t) from a reactant set R to a product set P. Throughout we consider fixed disjoint product and reactant sets P, R ⊂ Ω. When R is not a single point, we will start (X_t) from a fixed probability measure ρ on R. If R is a single point, ρ = δ_R, the delta distribution at R. As discussed above, Milestoning allows for an efficient computation of the MFPT of (X_t) to P, starting at ρ. It is useful to think of P as a sink, and R as a source for (X_t). More precisely, we assume that when (X_t) reaches P, it immediately restarts on R according to ρ. Obviously, this assumption has no effect on the MFPT to P. It will be useful, however, for computational and theoretical considerations.

2.2. The milestones and semi-Markov viewpoint

Milestoning uses a set M ⊂ Ω to spatially parallelize the computation of the MFPT. Each point x ∈ M will belong to a milestone M_x ⊂ M. Thus, M is the union of all the milestones. We assume there are finitely many milestones, each of which is a closed set. Moreover, we assume that (X_t) passes through the intersection of two milestones with probability 0 – thus, (X_t) can only cross one milestone at a time. This can be accomplished for Langevin or overdamped Langevin dynamics by, for example, taking the milestones to be codimension 1 manifolds whose pairwise intersections are codimension 2 or larger. The sets P and R will be two of the milestones. Typically, the milestones are hyperplanes which approximate the level sets of a reaction coordinate, or they are faces of cell boundaries of a Voronoi tesselation obtained by taking points along a high temperature trajectory for (X_t).

Let X₀ ~ ξ, where ξ denotes a generic probability measure on M. We now describe in detail the coarse-graining process. By following the sequence of milestones crossed by (X_t), we obtain a stochastic process defined on M as follows. Let θ₀, θ₁, θ₂, . . . be stopping times for (X_t) defined by

$$\text{if}{X}_{{\theta }_n}=x,\text{then}{\theta }_{n+1}:=inf\{t>{\theta }_n:X_t\in M_y\text{for}\text{some}{M}_y\ne M_x\},{\theta }_0=0.$$

Informally, θ_n corresponds to the time at which (X_t) crosses a milestone for the nth time. It is very important to note that θ_n corresponds to the first time for (X_t) to hit the “next” milestone, that is, a milestone different from the one (X_t) hit at time θ_n−1. Thus, when we refer to milestone crossings, we mean crossings of a milestone different from the last one crossed.

Define also τ₀ = 0 and for n ≥ 1, τ_n = θ_n − θ_n−1. Informally, τ_n is the time between the (n − 1)th and nth milestone crossings. For n ≥ 0, define J_n = X_θnto be the sequence of milestone points visited. That is, J_n is the point on the nth milestone crossed by (X_t). Note that each J_n is an element on some milestone – not the label of a milestone. Thus, (J_n) lives on the possibly uncountable set M.

As discussed above, due to our assumptions on M and (X_t), the law of X_n and τ_n depends only on X_n−1, that is,

$$\mathbb{P}(J_n\in C,{\tau }_n\le t\mid (J_0,{\tau }_0),\dots ,(J_{n-1}=x,{\tau }_{n-1}))=\mathbb{P}(J_n\in C,{\tau }_n\le t\mid J_{n-1}=x).$$ (2.1)

Let (Y_t) be the jump process on M defined by Y_t = J_n if θ_n ≤ t < θ_n+1. Since J_n is the nth milestone point crossed by (X_t), and θ_n is the time at which (X_t) crossed this point, we see that (Y_t) equals (X_t) at each milestone crossing. Thus, (Y_t) can be considered a coarse-grained version of (X_t) which throws away the path of (X_t) between milestones, keeping only the endpoints. When (Y_t) has a probability density, it corresponds to the density p(x, t) from [3] for the last milestone point passed. Due to (2.1), (Y_t) is called semi-Markov. It has transition kernel K(x, dy, dt) given by

$$\mathbb{P}(J_n\in C,{\tau }_n\le t\mid J_{n-1}=x)={\int }_{[0,t]}{\int }_{C}K(x,dy,dt).$$

We adopt the convention that the innermost integral corresponds to the first variable of integration appearing in the integrand. Note that if (Y_t) and (X_t) start at the same distribution ξ on M, then they have the same MFPT to P. Thus, for the purposes of studying the MFPT, it suffices to consider the coarse-grained process (Y_t). Since (X_t) restarts at ρ upon reaching P, so does (Y_t), and so

$$\text{for}\text{all}x\in P,K(x,dy,dt)={\delta }_{t=0}\rho (dy).$$ (2.2)

Following standard terminology in probability theory, we call (J_n) the jump chain of (Y_t). It is a Markov chain with transition kernel

$$K(x,dy):={\int }_{[0,\infty )}K(x,dy,dt).$$

2.3. Stopping times

Note that the sojourn times τ_n between milestones depend on the position of (X_t) on the nth milestone crossed at time t = θ_n−1. The following notation will thus be useful. For x ∈ M, we write

$${\tau }_M^x=inf\{t>0:Y_t\in M_y\text{for}\text{some}{M}_y\ne M_x\}.$$

This is the first time for (Y_t) to hit some milestone other than M_x, starting at x ∈ M. In particular, if X_θn−1 = x was the (n − 1)th crossing point, then ${\theta }_n={\theta }_{n-1}+{\tau }_M^x$ is the next crossing time. As we are concerned with first passage times to P, we will also use the notation

$${\tau }_P=inf\{t>0:Y_t\in P\}.$$

In particular, the MFPT we are interested in is 𝔼^ρ[τ_P]. As discussed above, the MFPT will be estimated via short trajectories between milestones. An important ingredient is the correct starting distribution for these trajectories. Exact Milestoning makes use of a stationary flux of (X_t) on the milestones, which corresponds to the stationary distribution (shown to exist below) of the jump chain (J_n). To study this distribution we need to define also the first hitting time of P for (J_n):

$${\sigma }_P=min\{n\ge 0:J_n\in P\}.$$

Some assumption is required to guarantee the existence of a stationary flux. We adopt the following very general sufficient condition, which we assume holds through the remainder of the paper: 𝔼^ξ[τ_P] and 𝔼^ξ[σ_P] are finite for all probability measures ξ on M. This ensures that (Y_t) reaches P in finite expected time and does not cross infinitely many milestones in finite time. In probabilistic language, the latter condition means that (Y_t) is non-explosive. This sufficient condition can be readily verified in the standard settings for milestoning discussed above. Under only this assumption, we give in Theorem 3.3 an exact milestoning equation for 𝔼^ρ[τ_P]. Moreover we show in Section (4) how the equation leads to an efficient algorithm for computing &Eopf^ρ[τ_P]. The exact equation we give is the same as in [3], except phrased in the semi-Markov framework defined above.

2.4. Dual action of kernels

We use the following notation for the expected value of a bounded function f : M → ℝ with respect to a probability measure ξ on M:

$$\xi f:={\int }_{M}fd\xi .$$

It will be useful to consider K(x, dy) as a stochastic kernel which operates on probability measures from the left and bounded functions on the right. More precisely, by a stochastic kernel we mean an operator P such that

$$\xi P:={\int }_M\xi (dx)P(x,·),Pf:={\int }_{M}P(·,dy)f(y),$$

are maps preserving, respectively, the complete metric space ℘ of probability measures on M with the total variation norm, and the Banach space ℬ of bounded functions on M with the sup norm. Informally, ξK is the distribution of J_n, and ξKf is the expected value of f(J_n), given that J_n−1 was distributed according to ξ. In particular, Kⁿ is a stochastic kernel for each n ≥ 0, with ℙ^ξ(J_n ∈ ·) = ξKⁿ and 𝔼^ξ[f(J_n)] = ξKⁿf, where K⁰ = 1 is the identity operator.

3. Invariant measure and MFPT

3.1. Stationary distribution on the milestones

The formula for the MFPT relies on a stationary distribution, which we denote by μ, for (J_n). Our μ is the same as the appropriately normalized stationary flux q in other Milestoning papers. We use the notation μ instead of q to emphasize that μ is a probability measure on M that may not have a density. We show in Theorem 3.1 below that μ exists. The proof of existence requires only the above assumption of finite MFPTs to P and non-explositivity of (Y_t), along with the special source and sink structure of the dynamics implied by (2.2).

Theorem 3.1

(J_n) has an invariant probability measure μ defined by

$$\mu (·):={\mathbb{E}}^{\rho }\left[\sum _{n=0}^{{\sigma }_P}{𝟙}_{\{J_n\in ·\}}\right]{\mathbb{E}}^{\rho }{[{\sigma }_P+1]}^{-1}.$$

Proof

Define $\nu (·)={\mathbb{E}}^{\rho }[{\sum }_{n=0}^{{\sigma }_P}{𝟙}_{\{J_n\in ·\}}]$ and observe that

$$\nu (·)=\sum _{n=0}^{\infty }\sum _{m=0}^n{\mathbb{P}}^{\rho }(J_m\in ·\mid {\sigma }_P=n){\mathbb{P}}^{\rho }({\sigma }_P=n)=\sum _{n=0}^{\infty }{\mathbb{P}}^{\rho }(J_n\in ·,{\sigma }_P\ge n).$$

If C ∧ R = ∅, by bounded convergence,

$${\int }_M\nu (dx)K(x,C)=\sum _{n=0}^{\infty }{\mathbb{P}}^{\rho }(J_{n+1}\in C,{\sigma }_P\ge n)=\sum _{n=0}^{\infty }{\mathbb{P}}^{\rho }(J_n\in C,{\sigma }_P\ge n)=\nu (C),$$

where the second equality uses ℙ^ρ(J₀ ∈ C) = 0 and J_n+1 ∉ R ⇒ σ_P ≠ n. If C ⊂ R,

$$\begin{array}{l}{\int }_M\nu (dx)K(x,C)=\sum _{n=0}^{\infty }{\mathbb{P}}^{\rho }(J_{n+1}\in C,{\sigma }_P=n)+\sum _{n=0}^{\infty }{\mathbb{P}}^{\rho }(J_{n+1}\in C,{\sigma }_P\ge n+1)\\ =\rho (C)-{\mathbb{P}}^{\rho }(J_0\in C,{\sigma }_P\ge 0)+\sum _{n=0}^{\infty }{\mathbb{P}}^{\rho }(J_n\in C,{\sigma }_P\ge n)=\nu (C).\end{array}$$

We will show below that (J_n) converges to μ under appropriate conditions. In that case μ is unique and we will call μ the stationary measure. We emphasize that the formula on which Exact Milestoning is based – the equation in Theorem 3.3 below – holds true whether or not μ is unique. However, a successful application of the Exact Milestoning algorithm will require some technique for sampling μ. The algorithm we present (Algorithm 1 below) is based on convergence of (J_n) to μ. We consider two types of convergence in Theorem 3.4 and 3.5 below. We also discuss a simple case where (J_n) may not converge following Theorem 3.4 below.

Algorithm 1.

Exact Milestoning algorithm.

Input: Milestones $M={\cup }_{j=1}^m{M}_j$, initial guess ξ, and tolerance ε > 0 for the absolute error in the MFPT.

Output: Estimates for μ, local MFPTs 𝔼μ[τM], and overall MFPT 𝔼ρ[τP].

μ(0) ← ξ

T(0) ← +∞

for all n = 1, 2, . . . do

for i = 1 to m do

Estimate $a_{ij}^{(n)}$ and ${\mathbb{E}}^{{\mu }_i^{(n-1)}}[{\tau }_M]$

${\mathbf{A}}_{ij}^{(n)}\leftarrow a_{ij}^{(n)}(M_j)$

end for

Solve wTA = w T (with $\mathbf{A}=({\mathbf{A}}_{ij}^{(n)})\in {ℝ}_{\ge 0}^{m\times m}$ and $\mathbf{w}=(w_1,\dots ,w_m)\in {ℝ}_{\ge 0}^m$)

for j = 1 to m do

${\mu }_j^{(n)}\leftarrow {\sum }_{i=1}^m{w}_i{a}_{ij}^{(n)}$

end for

Normalize μ(n)

T(n) ← μ(P)−1 𝔼μ(n−1)[τM]

if |T(n) − T(n−1)| < ε then

break

end if

end for

return (μ(n), 𝔼μ(n−1)[τM], T(n))

It is worth noting that the proof of Theorem 3.1 leads to the following representation of μ as a Neumann series. The representation is given in Corollary 3.2 below. In principle, this representation can be used to sample μ even when (J_n) does not converge to μ. The Neumann series is written in terms of the sub-stochastic transient kernel K̄ defined by

$$\overline{K}(x,dy)=\{\begin{array}{ll}K(x,dy),\hfill & x\notin P\hfill \\ 0,\hfill & x\in P\hfill \end{array}.$$ (3.1)

The transient kernel K̄ has the same right action as the stochastic kernel K, but its left action is on the larger Banach space of signed bounded measures with total variation norm. Informally, it corresponds to a version of (J_n) that is “killed” when upon reaching P.

Corollary 3.2

We have

$$\underset{n\to \infty }{lim}{\Vert \nu {(M)}^{-1}\sum _{i=0}^{n-1}\rho {\overline{K}}^i-\mu \Vert }_{TV}=0.$$ (3.2)

Proof

Recall that μ = ν/ν (M) where

$$\nu (·)=\sum _{n=0}^{\infty }{\mathbb{P}}^{\rho }(J_n\in ·,{\sigma }_P\ge n)=\sum _{n=0}^{\infty }\rho {\overline{K}}^n.$$

Moreover,

$$\underset{\mid f\mid \le 1}{sup}\left|\nu {(M)}^{-1}\sum _{i=0}^{n-1}\rho {\overline{K}}^{i}f-\mu f\right|\le \nu {(M)}^{-1}\sum _{i=n}^{\infty }{\mathbb{P}}^{\rho }({\sigma }_P\ge i),$$ (3.3)

and the right hand side of (3.3) is summable since by assumption 𝔼^ρ[σ_P] < ∞.

3.2. Milestoning equation for the MFPT

Equipped with an invariant measure μ, we are now able to state the Milestoning equation (3.4) for the MFPT. In Exact Milestoning, this equation is used to efficiently compute the MFPT. The algorithm is based on two principles: first, many trajectories can be simulated in parallel to estimate ${\tau }_M^x$ for various x; and second, the stationary distribution μ can be efficiently estimated through a technique based on power iteration. (See the right hand side of equation (3.4).) The gain in efficiency comes from the fact that the trajectories used to estimate ${\tau }_M^x$ are much shorter than trajectories from R to P. The second principle above depends somewhat on whether we have a good “initial guess” of μ. When (X_t) is Langevin dynamics, we have found in some cases the canonical Gibbs distribution is a sufficiently good initial guess. See [3] and [4] for details and discussion.

Theorem 3.3

Let μ be defined as above. Then μ(P) > 0 and

$$\mu (P){\mathbb{E}}^{\rho }[{\tau }_P]={\int }_M\mu (dx){\mathbb{E}}^x[{\tau }_M^x]:={\mathbb{E}}^{\mu }[{\tau }_M].$$ (3.4)

Proof

The assumption 𝔼^ρ[σ_P] < ∞ shows that μ(P) > 0. For any x ∈ M,

$$\begin{array}{l}{\mathbb{E}}^x[{\tau }_P]={\int }_M{\mathbb{E}}^x[{\tau }_P\mid Y_{{\tau }_M^x}=y]K(x,dy)\\ ={\int }_M{\mathbb{E}}^x[{\tau }_M^x\mid Y_{{\tau }_M^x}=y]K(x,dy)+{\int }_{M\backslash P}{\mathbb{E}}^x[{\tau }_P-{\tau }_M^x\mid Y_{{\tau }_M^x}=y]K(x,dy)\\ ={\mathbb{E}}^x[{\tau }_M^x]+{\int }_{M\backslash P}{\mathbb{E}}^y[{\tau }_P]K(x,dy).\end{array}$$

Thus,

$$\begin{array}{l}{\mathbb{E}}^{\mu }[{\tau }_P]={\mathbb{E}}^{\mu }[{\tau }_M]+{\int }_{M\backslash P}{\int }_M\mu (dx){\mathbb{E}}^y[{\tau }_P]K(x,dy)\\ ={\mathbb{E}}^{\mu }[{\tau }_M]+{\int }_{M\backslash P}\mu (dy){\mathbb{E}}^y[{\tau }_P],\end{array}$$

and so

$${\mathbb{E}}^{\mu }[{\tau }_M]={\int }_P\mu (dy){\mathbb{E}}^y[{\tau }_P]=\mu (P){\mathbb{E}}^{\rho }[{\tau }_P].$$

In Section 4 below we present the Exact Milestoning algorithm (Algorithm 1) recently used in [3] and [4]. The algorithm uses a technique which combines coarse-graining and power iteration to sample μ. Consistency of power iteration algorithms are justified via Theorem 3.4 below, where we show ξKⁿ → μ as n → ∞. Though we emphasize that there are a range of possibilities for sampling μ (for example, algorithms based on (3.2) or (3.7) below) we note that Algorithm 1 was shown to be efficient for computing the MFPT in the entropic barrier example of [3] and the random energy landscapes example of [4].

3.3. Convergence to stationarity

In this section we justify the consistency of power iteration-based methods for sampling μ by showing that ξKⁿ converges to μ in total variation norm as n → ∞. The theorem requires an extra assumption – aperiodicity of the jump chain (J_n).

Theorem 3.4

Suppose that (J_n) is aperiodic in the following sense:

$$g.c.d.\{n\ge 1:{\mathbb{P}}^{\rho }({\sigma }_P=n-1)>0\}=1.$$ (3.5)

Then for all probability measures ξ on M,

$$\underset{n\to \infty }{lim}{\Vert {\mathbb{P}}^{\xi }(J_n\in ·)-\mu \Vert }_{TV}=0.$$ (3.6)

In particular, μ is unique.

Proof

We use a simple coupling argument. Let (H_n) be an independent copy of (J_n) and let J₀ ~ ξ and H₀ ~ μ. For n ≥ 0, let S_n (resp. T_n) be the times at which (J_n) (resp. (H_n)) hit P for the (n + 1)st time. Then S_n+1 − S_n, n ≥ 0, are iid random variables with finite expected value and nonlattice distribution, and (S_n+1 −S_n)_n≥0 ~ (T_n+1 −T_n)_n≥0. It follows that (S_n −T_n)_n≥0 is a mean zero random walk with nonlattice step distribution. Thus, its first time to hit 0 is finite almost surely. So

$$\zeta :=inf\{n\ge 0:J_n\in P,H_n\in P\}$$

obeys ℙ (ζ ≥ n) → 0 as n → ∞. Note that J_n ~ H_n whenever ζ < n. Thus

$$\mid {\mathbb{P}}^{\xi }(J_n\in C)-{\mathbb{P}}^{\mu }(H_n\in C)\mid \le 2\mathbb{P}(\zeta \ge n).$$

Since μ is stationary for (H_n) we have ℙ^μ(H_n ∈ C) = μ(C). Now

$${\Vert {\mathbb{P}}^{\xi }(J_n\in ·)-\mu \Vert }_{TV}=\underset{C\subset M}{sup}\mid {\mathbb{P}}^{\xi }(J_n\in C)-\mu (C)\mid \le 2\mathbb{P}(\zeta \ge n),$$

which establishes the convergence result. To see uniqueness, suppose ξ is another invariant probability measure for (J_n); then the last display becomes ||ξ − μ||_TV ≤ 2ℙ(ζ ≥ n). Letting n → ∞ shows that ξ ~ μ.

We now consider a class of problems where there is a smooth one-dimensional reaction coordinate ψ : Ω → [0, 1] tracking progress of (X_t) from R to P. In this case ψ|_R ≡ 0, ψ|_P ≡ 1, the milestones M₁, ..., M_m are disjoint level sets of ψ, and R = M₁, P = M_m. The jump chain (J_n) can only hop between neighboring milestones, unless it is at P. That is, if J_n ∈ M_i for i ∉ {1, m}, then J_n+1 ∈ M_i−1 or J_n ∈ M_i+1; if J_n ∈ M₁ then J_n+1 ∈ M₂; and if J_n ∈ M_m, then J_n+1 ∈ M₁. Suppose that if J_n ∈ M_i for i ∉ {1, m}, then J_n+1 ∈ M_i−1 with probability in (0, 1). Such systems satisfy the aperiodicity assumption (3.5) if and only if m is odd. This is due to the fact that, starting at M₁, (J_n) can reach M_m in either m − 1 or m + 1 steps with positive probability, and m and m+2 are coprime when m is odd. On the other hand, if m is even then the conclusion of Theorem 3.4 cannot hold. To see this, let m be even and start (J_n) at an initial distribution supported on an odd-indexed milestone. Then after any even number of steps (J_n) is supported on an odd-indexed milestone, while after any odd number of steps (J_n) is supported on an even-indexed milestone.

Theorem 3.4 estabishes convergence of the time marginals of (J_n), that is, the distributions of J_n at fixed times n. (J_n) also converges in a time-averaged sense, even if (3.5) does not hold. More precisely, we have the following version of the Birkhoff ergodic theorem:

Theorem 3.5

Let J₀ ~ ξ, with ξ a probability measure on M. For bounded f : M → ℝ,

$$\underset{n\to \infty }{lim}\frac{1}{n}\sum _{i=0}^{n-1}f(J_i)\stackrel{a.s.}{=}{\int }_{M}fd\mu \equiv \mu f.$$ (3.7)

Proof

Let S_n be the times at which (J_n) hits P for the (n + 1)st time, and define

$$f_n=\sum _{i=S_n+1}^{S_{n+1}}f(J_i).$$

Note that f_n, n ≥ 0, are iid. Let k(n) = max{k : S_k ≤ n} and write

$$\frac{1}{n}\sum _{i=1}^{n-1}f(J_i)=\frac{1}{n}\sum _{i=0}^{S_0}f(J_i)+\frac{1}{n}\sum _{i=0}^{k(n)-1}{f}_i+\frac{1}{n}\sum _{i=S_{k(n)}+1}^{n}f(J_i)$$

Since (J_n) hits P in finite time a.s., n − S_k(n) and S₀ are finite a.s. Thus,

$$\underset{n\to \infty }{lim}\frac{1}{n}\sum _{i=0}^{n-1}f(J_i)=\underset{n\to \infty }{lim}\frac{k(n)-1}{n}\frac{1}{k(n)-1}\sum _{i=0}^{k(n)-1}{f}_i.$$

Notice R_n := S_n+1 − S_n, n ≥ 0 are iid with finite expectation and

$$\frac{R_0+\dots +R_{k(n)-1}}{k(n)}\le \frac{n-S_0}{k(n)}\le \frac{R_0+\dots +R_{k(n)}}{k(n)}.$$

By the previous two displays and the law of large numbers,

$$\underset{n\to \infty }{lim}\sum _{i=0}^{n-1}f(J_i)=\frac{\mathbb{E}[f_0]}{\mathbb{E}[R_0]}=\frac{1}{\mathbb{E}[{\sigma }_P]}\sum _{i=0}^{{\sigma }_P}{\mathbb{E}}^{\rho }[f(J_i)]=\frac{\nu f}{\nu (M)}=\mu f,$$

with ν defined as in Theorem 3.4.

Theorem 3.5 shows that problems in sampling μ arising from aperiodicity can be managed by averaging over time.

Markov chains for which the conclusion of Theorem 3.4 hold are called Harris ergodic. It is worth noting that Harris ergodicity, together with aperiodicity of the sojourn times, also leads to a limit for the time marginals of of (Y_t). More precisely, suppose (3.5) holds and for each x ∈ M \ P and y ∈ M, ℙ^x(τ₁ ∈ · | J₁ = y) is nonlattice. Then for any C ⊂ M and μ-a.e. x,

$$\underset{t\to \infty }{lim}{\mathbb{P}}^x(Y_t\in C)=\frac{{\int }_C\mu (dy){\mathbb{E}}^y[{\tau }_M^y]}{{\int }_M\mu (dy){\mathbb{E}}^y[{\tau }_M^y]}.$$ (3.8)

See [2] for details and proof. When the right hand side of (3.8) has a density, it is the same as the stationary probability density p(x) in [3] for the last milestone point passed.

4. Exact Milestoning algorithm

We now describe in detail an algorithm for sampling the stationary measure μ and the MFPT 𝔼^ρ[τ_P], used successfully for instance in [3] and [4]. Let ξ be an initial guess for μ. For example, if (X_t) is Brownian or Langevin dynamics, we usually take ξ to the canonical Gibbs distribution. We assume here that the conclusion of Theorem 3.4 holds. We write M_i for the distinct milestones, so that M = ∪_iM_i and M_i, M_j have disjoint interiors when i ≠ j. The algorithm will produce approximations

$$\xi \equiv {\mu }^{(0)},{\mu }^{(1)},{\mu }^{(2)},\dots$$

of μ. Let ${\mu }_i^{(n)}$ be the non-normalized restriction of μ⁽ⁿ⁾ to M_i, and define

$${\mathbb{E}}^{{\mu }_i^{(n)}}[{\tau }_M]:={\mu }^{(n)}{(M_i)}^{-1}{\int }_{M_i}{\mu }_i^{(n)}(dx){\mathbb{E}}^x[{\tau }_M^x],$$

(This is a slight abuse of notation, since ${\mu }_i^{(n)}$ is not a probability distribution: it is not normalized.) For C ⊂ M_j we will also use the notation

$$a_{ij}^{(n)}(C)={\mu }^{(n-1)}{(M_i)}^{-1}{\int }_{M_i}{\mu }_i^{(n-1)}(dx)K(x,C).$$

Below we think of $a_{ij}^{(n)}$ and ${\mu }_i^{(n)}$ as either distributions or densities. The $a_{ij}^{(n)}$ are obtained based on observations of trajectory fragments. We can conceive a simple Monte Carlo scheme for the purpose of approximating these distributions as follows. Let x₁,..., x_L be iid samples from the distribution ${\mu }_i^{(n-1)}/{\mu }^{(n-1)}(M_i)$. From each _i sample point x_ℓ ∈ M_i, we simulate (X_t) until it hits a neighboring milestone, say at the point y_ℓ ∈ M_j. If we idealize by assuming the simulation of (X_t) is done exactly, then by Chebyshev’s inequality,

$$\mathbb{P}\left(\left|a_{ij}^{(n)}(C)-{\int }_C\frac{1}{L}\sum _{\ell =1}^L{\delta }_{y_{\ell }}(dy)\right|>\epsilon \right)\le \frac{a_{ij}^{(n)}(C)-a_{ij}^{(n)}{(C)}^2}{L{\epsilon }^2},$$

where δ_y is the Dirac delta distribution at y. We therefore write, for y ∈ M,

$$a_{ij}^{(n)}(y)\approx \frac{1}{L}\sum _{\ell =1}^L{\stackrel{\sim }{\delta }}_{y_{\ell }}(y),$$ (4.1)

where δ̃_z is either some suitable approximation to the identity at z, or simply a delta function at z. Thus, in Algorithm 1 we think of $a_{ij}^{(n)}$ and ${\mu }_i^{(n-1)}$ as either densities in the former case, or as distributions in the latter. The local mean first passage times, that is, the times between milestone crossings, are approximated by the sample means

$${\mathbb{E}}^{{\mu }_i^{(n-1)}}[{\tau }_M]\approx \frac{1}{L}\sum _{\ell =1}^L{\tau }_M^{x_{\ell }}.$$

It is important to realize that we do not need to store the full coordinates of each y_ℓ in memory. Instead, it suffices to use a data-structure that keeps track of the pairs (y_ℓ, M_j). The actual coordinates of each point can be written to disk and read from it as needed.

The eigenvalue problem in Algorithm 1 involves a stochastic matrix $\mathbf{A}\in {ℝ}_{\ge 0}^{m\times m}$ that is sparse. Indeed, the i-th row corresponds to milestone M_i and may have only as many non-zero entries as the number of neighboring milestones M_j. In practice, to solve the eigenvalue problem we can use efficient and accurate Krylov subspace solvers [15] such as Arnoldi iteration [18] to obtain w without computing all the other eigenvectors.

In Algorithm 1, if ${\mathbf{w}}_i:={\mu }_i^{(n-1)}(M_i)$ is used instead of the solution w to w^TA = w^T, then the algorithm approximates μ by simple power iteration. The reason for defining the weights as the solution to w^TA = w^T is practical: we have found that it gives faster convergence of the iterations, at no apparent cost to accuracy. It can be seen as a version of power iteration that uses coarse-graining. See [3, 4] for applications of the algorithm in Exact Milestoning and [15, 18] for related discussions.

5. Error analysis

5.1. Stationary distribution error

In practice, due to time discretization error, we cannot generate trajectories exactly according to the transition kernel K. Instead, we can generate trajectories according to a numerical approximation K_ε. We investigate here whether such schemes are consistent, that is, whether powers of K_ε of K converge to a distribution μ_ε ≈ μ. We emphasize that, even though we account for time discretization here, we still assume infinite sampling, and thus for a given x ∈ M, K_ε (x, dy) may be a continuous distribution. See Section 5.2 below for related remarks and a discussion of how time discretization errors affect the Exact Milestoning estimate of the MFPT.

The following theorem, restated from [11], establishes consistency of iteration schemes based on Theorem 3.4 when K_ε is sufficiently close to K and (J_n) is geometrically ergodic. After the theorem, in Lemma 5.2 and Theorem 5.3 we give natural conditions for geometric ergodicity of (J_n).

Theorem 5.1

Suppose (J_n) is geometrically ergodic: there exists κ ∈ (0, 1) such that

$$\underset{x\in M}{sup}{\Vert {\delta }_x{K}^n-\mu \Vert }_{TV}=O({\kappa }^n).$$

Let {K_ε} be a family of stochastic kernels with K₀ = K, assumed to act continuously on ℬ, such that

$$\underset{\epsilon \to 0}{lim}\underset{\mid f\mid \le 1}{sup}{\Vert K_{\epsilon }f-Kf\Vert }_{\infty }=0.$$ (5.1)

Then for each κ̂ ∈ (κ, 1), there is δ > 0 such that for each ε ∈ [0, δ), K_ε has a unique invariant probability measure μ_ε, and

$$\begin{array}{l}\underset{\epsilon <\delta }{sup}\underset{x\in M}{sup}{\Vert {\delta }_x{K}_{\epsilon }^n-{\mu }_{\epsilon }\Vert }_{TV}=O({\widehat{\kappa }}^n),\\ \underset{\epsilon \to 0}{lim}{\Vert {\mu }_{\epsilon }-\mu \Vert }_{TV}=0.\end{array}$$

Geometric ergodicity is inconvenient to check directly. We give two sufficient conditions for geometric ergodicity of (J_n). The first condition is a uniform lower bound on the probability to reach P in N steps; see Lemma 5.2. We use this to obtain a strong Feller condition in Theorem 5.3. The latter is a very natural condition and is easy to verify in some cases, for instance when (X_t) is a nondegenerate diffusion and the milestones are sufficiently regular.

Lemma 5.2

Suppose that there exists λ ∈ (0, 1) and N ∈ ℕ such that for all x ∈ M, ℙ^x(J_N−1 ∈ P) ≥ λ > 0. Then (J_n) is geometrically ergodic:

$$\underset{x\in M}{sup}{\Vert {\delta }_x{K}^n-\mu \Vert }_{TV}\le {\lambda }^{-1}{(1-\lambda )}^{\lfloor n/N\rfloor }.$$

Proof

Let ξ₁, ξ₂ ∈ ℘, consider the signed measure ξ = ξ₁ − ξ₂ and compute

$$\begin{array}{l}{\Vert {\xi }_1{K}^N-{\xi }_2{K}^N\Vert }_{TV}=\underset{\mid f\mid \le 1}{sup}\left|{\int }_M{\int }_M\xi (dy)K^N(y,dz)f(z)\right|\\ =\underset{\mid f\mid \le 1}{sup}\left|{\int }_M{\int }_M\xi (dy)(K^N(y,dz)-\lambda \rho (dz))f(z)\right|\\ =\underset{\mid f\mid \le 1}{sup}\left|{\int }_M\xi (dy){\int }_M(K^N(y,dz)-\lambda \rho (dz))f(z)\right|\\ \le (1-\lambda )\underset{\mid f\mid \le 1}{sup}\left|{\int }_M\xi (dy)f(y)\right|=(1-\lambda ){\Vert {\xi }_1-{\xi }_2\Vert }_{TV}.\end{array}$$

The last line uses the fact that K^N(y, dz) − λρ(dz) is a positive measure. This shows that K^N is a contraction mapping on ℘ with contraction constant (1 − λ). Observe also that ||ξ₁K − ξ₂K||_TV ≤ ||ξ₁ − ξ₂||_TV. The result now follows from the contraction mapping theorem. See for instance Theorem 6.40 of [9].

Note that the λ in Lemma (5.2) is a quantity that can be estimated, at least in principle, by running trajectories of (X_t) starting at x which cross N − 1 milestones before reaching P. However, this is likely impractical for the same reason direct estimation of the MFPT is impractical – the trajectories would be too long. One alternative would be to compute the probability $P^i(J_{N-1}^{\mathbf{A}}\in P)$ for the Markov chain ( $J_n^{\mathbf{A}}$) on {1, …, m} with transition matrix A, and use the minimum over i ∈ {1, …, m} as a proxy for λ. Even without a practical way to estimate λ, we believe the characterization of Lemma 5.2 is useful for understanding the convergence rate.

Lemma 5.2 leads to the following condition for geometric ergodicity of (J_n).

Theorem 5.3

Suppose that M is compact and (J_n) is a strong Feller chain which is aperiodic in the sense of (3.5). Then (J_n) is geometrically ergodic.

Proof

Let ε ∈ (0, μ(P)). By Theorem 3.4, for each x ∈ M there is N_x ∈ ℕ such that ℙ^x(J_n ∈ P ) ≥ ε for all n ≥ N_x. Because (J_n) is strong Feller, the map x → ℙ^x(J_n ∈ P) is continuous. By compactness of M, it follows that for any λ ∈ (0, ε) there is N ∈ ℕ such that ℙ^y(J_n ∈ P) ≥ λ for all y ∈ M and n ≥ N − 1. Theorem 5.2 now yields the result.

5.2. MFPT error

As discussed above, Equation 3.4 can be used to estimate the MFPT 𝔼^ρ[τ_P ] by sampling μ and local MFPTs ${\tau }_M^x$. The error in this estimate has two sources. First, in general we only have an approximation μ̃ ≡ μ_ε of μ. The second source of error is in the sampling of ${\tau }_M^x$, due to the fact that we can only simulate a time discrete version (X̃_nδt) of (X_t). In Theorem 5.4 below we give an explicit formula for the numerical error of the MFPT in terms of these two sources. We first need the following notation. Let ${\stackrel{\sim }{\tau }}_M^x$ be the minimum of all n δt > 0 such that the line segment between X̃_nδt and X̃ _(n+1)δt intersects M \ M_x, and define

$${\mathbb{E}}^{\stackrel{\sim }{\mu }}[{\stackrel{\sim }{\tau }}_M]:={\int }_M\stackrel{\sim }{\mu }(dx){\mathbb{E}}^x[{\stackrel{\sim }{\tau }}_M^x].$$

We emphasize that Theorem 5.4 below gives an expression for the error in the original Milestoning as well as in Exact Milestoning.

Theorem 5.4

There exists a nonnegative function ϕ such that

$$\mid {\mathbb{E}}^{\rho }[{\tau }_P]-\stackrel{\sim }{\mu }{(P)}^{-1}{\mathbb{E}}^{\stackrel{\sim }{\mu }}[{\stackrel{\sim }{\tau }}_M]\mid \le c_1\mid \mu {(P)}^{-1}-\stackrel{\sim }{\mu }{(P)}^{-1}\mid +\stackrel{\sim }{\mu }{(P)}^{-1}(c_2{\Vert \mu -\stackrel{\sim }{\mu }\Vert }_{TV}+\varphi (\delta t)),$$ (5.2)

where

$$c_1:={\mathbb{E}}^{\mu }[{\tau }_M],c_2:=\underset{x\in M}{sup}{\mathbb{E}}^x[{\tau }_M^x].$$

Proof

Note that

$$\begin{array}{l}\mid {\mathbb{E}}^{\rho }[{\tau }_P]-\stackrel{\sim }{\mu }{(P)}^{-1}{\mathbb{E}}^{\stackrel{\sim }{\mu }}[{\stackrel{\sim }{\tau }}_M]\mid =\mid \mu {(P)}^{-1}{\mathbb{E}}^{\mu }[{\tau }_M]-\stackrel{\sim }{\mu }{(P)}^{-1}{\mathbb{E}}^{\stackrel{\sim }{\mu }}[{\stackrel{\sim }{\tau }}_M]\mid \\ \le \mid \mu {(P)}^{-1}{\mathbb{E}}^{\mu }[{\tau }_M]-\stackrel{\sim }{\mu }{(P)}^{-1}{\mathbb{E}}^{\mu }[{\tau }_M]\mid +\mid \stackrel{\sim }{\mu }{(P)}^{-1}{\mathbb{E}}^{\mu }[{\tau }_M]-\stackrel{\sim }{\mu }{(P)}^{-1}{\mathbb{E}}^{\stackrel{\sim }{\mu }}[{\tau }_M]\mid +\mid \stackrel{\sim }{\mu }{(P)}^{-1}{\mathbb{E}}^{\stackrel{\sim }{\mu }}[{\tau }_M]-\stackrel{\sim }{\mu }{(P)}^{-1}{\mathbb{E}}^{\stackrel{\sim }{\mu }}[{\stackrel{\sim }{\tau }}_M]\mid \end{array}$$

where we have written ${\mathbb{E}}^{\stackrel{\sim }{\mu }}[{\tau }_M]:={\int }_M\stackrel{\sim }{\mu }(dx){\mathbb{E}}^x[{\tau }_M^x]$. We may write

$$\varphi (\delta t)=\mid {\mathbb{E}}^{\stackrel{\sim }{\mu }}[{\tau }_M]-{\mathbb{E}}^{\stackrel{\sim }{\mu }}[{\stackrel{\sim }{\tau }}_M]\mid$$

for the term depending only on time stepping error. Note that

$$\begin{array}{l}\mid {\mathbb{E}}^{\mu }[{\tau }_M]-{\mathbb{E}}^{\stackrel{\sim }{\mu }}[{\tau }_M]\mid =\left|{\int }_M\mu (dx){\mathbb{E}}^x[{\tau }_M^x]-{\int }_M\stackrel{\sim }{\mu }(dx){\mathbb{E}}^x[{\tau }_M^x]\right|\\ \le \left(\underset{x\in M}{sup}{\mathbb{E}}^x[{\tau }_M^x]\right){\Vert \mu -\stackrel{\sim }{\mu }\Vert }_{TV}.\end{array}$$

Combining the last three expressions yields the result.

Recall that in the above we have ignored errors from finite sampling. We now discuss the implications of those errors. In the original Milestoning, μ̃ is the canonical Gibbs distribution on the milestones. In that setting, we can typically sample independently from μ̃ on the milestones. Thus, the central limit theorem implies that the true error in the Milestoning approximation of 𝔼^ρ [τ_P] is bounded above with high probability by the right hand side of (5.2) plus a constant times $1/\sqrt{N}$, where N is the number of samples. An analogous argument applies to Exact Milestoning if μ̃ is sampled by simple power iteration. For our coarse-grained version of power iteration, however, we obtain samples of μ̃ which are not independent, and thus a more detailed analysis would be required to determine the additional error from finite sampling.

We do not analyze the time discretization error ϕ(δt) and instead refer the reader to [14] and references therein. Here we simply remark that, if (X_t) is a diffusion process, then under certain smoothness assumptions on the drift and diffusion coefficients of (X_t) and on M, we have $\varphi (\delta t)=\theta (\sqrt{\delta t})$ when (X_nδt) is the standard Euler time discretization with time step δt. See [13] for details and proof and see [5, 16] for numerical schemes that mitigate time discretization error in the MFPTs.

6. Illustrative examples

In this section we present two examples of Milestoning on the torus Ω = ℝ²/ℤ². The process (X_t) will be governed by the Brownian dynamics equation,

$$\{\begin{array}{l}d{X}_t=-\nabla U(X_t)dt+\sqrt{2{\beta }^{-1}}d{B}_t,\hfill \\ X_0~\rho \hfill \end{array}$$

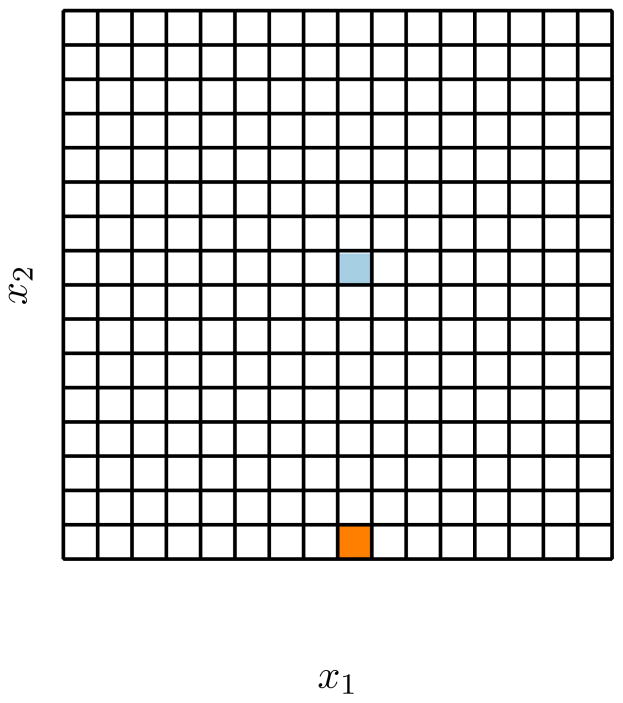
where U : Ω → ℝ is a smooth potential energy function, β > 0 is the inverse temperature, and (B_t) is a standard Brownian motion. For our computations, we consider a uniformly spaced mesh of milestones with fixed product and reactant sets P, R; see Figure 2.

Fig. 2.

Diagram showing the reactant state (orange square) and the product state (blue square) within the set of all milestones for the example in Section 6. Each milestone is an edge of one of the small squares in the diagram. (The total number of milestones has been decreased to enhance visibility.)

6.1. Constant potential energy

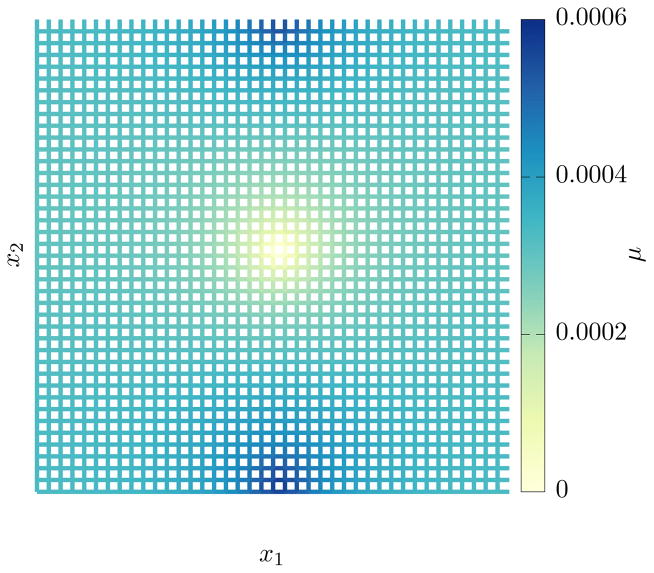
In the case where U is a constant function, the corresponding canonical Gibbs distribution is also constant. However, the stationary distribution μ obtained in Milestoning is not constant. This is because every trajectory reaching the product state P immediately restarts at R according to ρ, as determined by (2.2). The resulting (density of) μ is shown in Figure 3.

Fig. 3.

Stationary distribution μ corresponding to a system with constant potential energy for the example in Section 6. There are 2 × 40 × 40 total milestones.

6.2. Rough energy landscape

In this case, we consider U of the form

$$U(x_1,x_2)=\sum _{k_1=-N}^{N-1}\sum _{k_2=-N}^{N-1}{C}_{k_1,k_2}{f}_{k_1,k_2}(x_1,x_2),$$ (6.1)

where N is a parameter determining the maximum allowed frequency. The constants C_k1,k2 are given by

$$C_{k_1,k_2}=\{\begin{array}{ll}{c}_{k_1,k_2},\hfill & \text{with}\text{probability}\frac{1}{2},\hfill \\ 0,\hfill & \text{with}\text{probability}\frac{1}{2},\hfill \end{array}$$

with c_k1,k2 being uniformly distributed in the interval ( $-\frac{1}{2\pi },\frac{1}{2\pi }$). The random functions f_k1,k2 are defined as

$$f_{k_1,k_2}(x_1,x_2)=\{\begin{array}{ll}cos(2\pi k_1{x}_1)cos(2\pi k_2{x}_2),\hfill & \text{with}\text{probabilit}y1/3,\hfill \\ cos(2\pi k_1{x}_1)sin(2\pi k_2{x}_2),\hfill & \text{with}\text{probability}1/3,\hfill \\ sin(2\pi k_1{x}_1)sin(2\pi k_2{x}_2),\hfill & \text{with}\text{probability}1/3.\hfill \end{array}$$

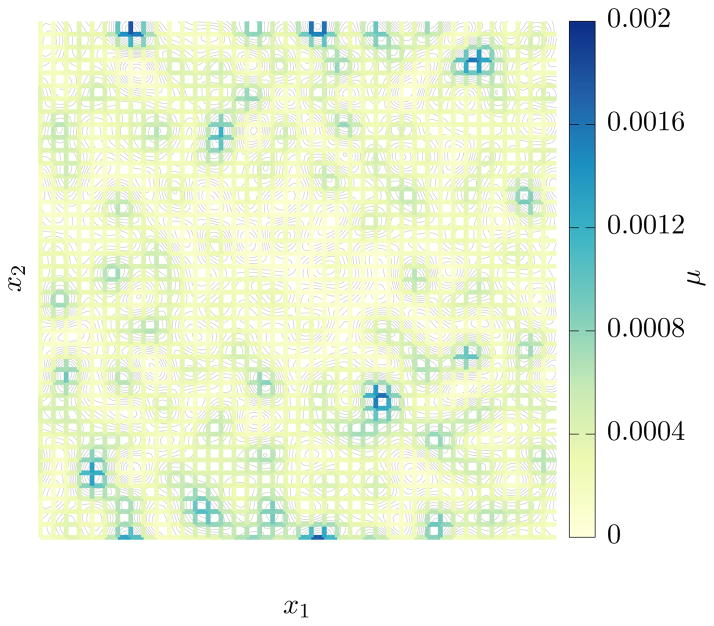
Therefore, the potential energy function U is a sparse, periodic function on the two-dimensional torus. An example of a stationary distribution on a particular realization of the above potential energy functions is displayed in Figure 4, where we see that (the density of) μ is concentrated in a few basins of attraction.

Fig. 4.

Stationary density μ on a rough energy landscape for the example in Section 6. The contour lines are the level sets of U.