Thinner Regions of Intracranial Aneurysm Wall Correlate with Regions of Higher Wall Shear Stress: A 7T MRI Study

Abstract

BACKGROUND AND PURPOSE:

Both hemodynamics and aneurysm wall thickness are important parameters in aneurysm pathophysiology. Our aim was to develop a method for semi-quantitative wall thickness assessment on in vivo 7T MR images of intracranial aneurysms for studying the relation between apparent aneurysm wall thickness and wall shear stress.

MATERIALS AND METHODS:

Wall thickness was analyzed in 11 unruptured aneurysms in 9 patients who underwent 7T MR imaging with a TSE-based vessel wall sequence (0.8-mm isotropic resolution). A custom analysis program determined the in vivo aneurysm wall intensities, which were normalized to the signal of nearby brain tissue and were used as measures of apparent wall thickness. Spatial wall thickness variation was determined as the interquartile range in apparent wall thickness (the middle 50% of the apparent wall thickness range). Wall shear stress was determined by using phase-contrast MR imaging (0.5-mm isotropic resolution). We performed visual and statistical comparisons (Pearson correlation) to study the relation between wall thickness and wall shear stress.

RESULTS:

3D colored apparent wall thickness maps of the aneurysms showed spatial apparent wall thickness variation, which ranged from 0.07 to 0.53, with a mean variation of 0.22 (a variation of 1.0 roughly means a wall thickness variation of 1 voxel [0.8 mm]). In all aneurysms, apparent wall thickness was inversely related to wall shear stress (mean correlation coefficient, −0.35; P < .05).

CONCLUSIONS:

A method was developed to measure the wall thickness semi-quantitatively, by using 7T MR imaging. An inverse correlation between wall shear stress and apparent wall thickness was determined. In future studies, this noninvasive method can be used to assess spatial wall thickness variation in relation to pathophysiologic processes such as aneurysm growth and rupture.

Intracranial aneurysms may rupture; this rupture leads to subarachnoid hemorrhage. The case fatality of aneurysmal SAH has decreased during the past decades but is still around 30%–40%, and almost half of the survivors remain permanently disabled.¹ The prevalence of intracranial aneurysms is approximately 3%.² Several risk and trigger factors for rupture have been identified,^3,4 but these factors explain only a small proportion of the risk of rupture and are insufficient to explain the pathophysiology of rupture.⁵ Thus, we need more risk factors to better predict rupture, and we need to increase knowledge of pathophysiology to better understand rupture.⁶

Hemodynamics play an important role in aneurysm pathophysiology because the endothelial cells are sensitive to mechanical stimuli such as stretch and wall shear stress (WSS, the frictional force on the walls caused by the blood flow).⁷ Time-resolved 3D phase-contrast MR imaging (PCMR) can measure in vivo flow and WSS in aneurysms,⁸ and a recent study showed that the use of 7T MR imaging increases the signal-to-noise ratio and improves flow visualization and quantification.⁹

Aneurysmal wall thickness is another interesting parameter in the pathophysiology of rupture because the wall eventually ruptures. In a previous study, we showed that it is possible to assess the spatial variation in aneurysm wall thickness by using signal intensities of the aneurysm wall on 7T MR imaging.¹⁰ A phantom and histopathologic correlation study validated that there is a linear relation between wall thickness and image intensity.¹⁰ This development has the potential to enable noninvasive assessments of the relation between different pathophysiologic parameters and wall thickness. However, a method to quantitatively assess the wall thickness on in vivo images has not yet been developed. Therefore, we aimed to develop an algorithm to obtain semi-quantitative measurements of the wall thickness to assess the spatial variation of the apparent wall thickness within an aneurysm and to assess the correlation between wall thickness and WSS on 7T images in patients with intracranial aneurysms.

Materials and Methods

Patient Selection

From a series of patients (18, with 20 aneurysms in total) with unruptured intracranial aneurysms from a previous study,¹⁰ we selected the patients who underwent both a magnetization-prepared inversion-recovery turbo spin-echo (MPIR-TSE) scan for vessel wall imaging and a time-resolved PCMR scan for wall shear stress assessment. Patients with artifacts in the PCMR scan due to gradient coil hardware problems were excluded as well as patients with motion artifacts on the MPIR-TSE scan. Patients in whom an insufficient amount of aneurysm wall was free from directly bordering brain tissue (<10%, based on subjective estimation) could not be analyzed and were excluded (in total, 4 aneurysms were excluded for this reason). We performed exclusion blinded to the WSS results.

Imaging Sequences

MR imaging was performed on a 7T MR imaging scanner (Achieva; Philips Healthcare, Best, the Netherlands) with a 32-channel receive head coil and a volume-transmit coil (Nova Medical, Wilmington, Massachusetts).

A previously described¹⁰ T1-weighted 3D MPIR-TSE sequence with whole-brain coverage was used to image the aneurysm wall.¹¹ Briefly, the scan parameters were as follows: acquired resolution, 0.8 × 0.8 × 0.8 mm³; FOV, 250 × 250 × 190 mm³ (feet to head × anterior to posterior × right to left); scan duration, approximately 11 minutes.

A time-resolved 3D PCMR sequence was used to determine wall shear stress. Briefly, we used the following scan parameters⁹: acquired resolution, 0.5 × 0.5 × 0.5 mm³; FOV, 190 × 190 × 20 mm³ (anterior to posterior × right to left x feet to head); velocity-encoding limit, 150 cm/s for each velocity-encoding direction. Five (n = 1) or 6 (n = 10) cardiac phases were obtained, retrospectively gated, by using a peripheral pulse unit. Acquired temporal resolution ranged between 209 and 286 ms, depending on the heart rate. The scan duration was approximately 13 minutes.

Image Processing

Wall Thickness from Intensity: Theory.

For walls thinner than the voxel size, the intensity on the MPIR-TSE images is proportional to the vessel wall thickness.¹⁰ Under idealized circumstances, the observed intensity in MPIR-TSE images could be used to compute the absolute wall thickness, w, by using a simple linear relationship:

where S_w is the signal for a voxel with isotropic voxel size d, containing the vessel wall with surrounding blood and CSF. S₀ is the signal of a voxel completely filled with vessel wall.

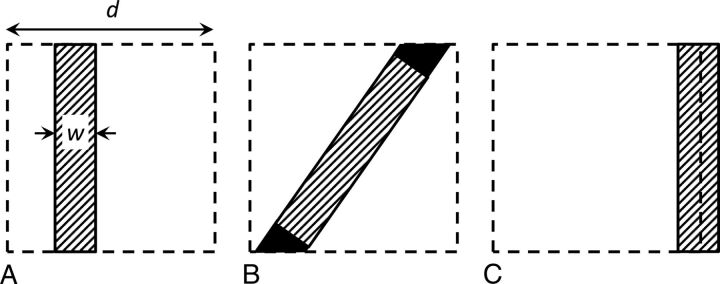
To render signal intensity a true reflection of the wall thickness (relative to the voxel size), one should have the following (long) list of requirements for a voxel with a piece of vessel wall inside: First, the partial volume effect should occur only among the vessel wall, blood, and CSF, and the signal from blood and CSF should be perfectly suppressed (Fig 1A). Second, the signal intensity of a voxel that is fully filled with vessel wall (S₀) should be known. Third, there should be no variation of vessel wall signal across the wall due to, for example, heterogeneous tissue composition in combination with the contrast-weighting of the MPIR-TSE sequence. Fourth, the vessel wall should be parallel with one of the sides of the voxel because oblique walls will lead to a higher filling factor than just the proportion of the wall thickness to the voxel size (Fig 1B). Fifth, the partial volume effect of the thin vessel wall should not be divided over 2 voxels; thus, there may be no boundary of 2 voxels within the vessel wall, parallel to the vessel wall (Fig 1C). Last, the nominal acquired resolution of the MPIR-TSE images (0.8 mm) should be equal to the true physical resolution, without blurring due to motion or an imperfect point spread function.

Fig 1.

A, Illustration of a voxel (dashed square, size d) partly filled with aneurysm wall (filled rectangle) with thickness w. In case of perfect suppression of the surrounding CSF and blood, the signal from the voxel is directly proportional to the wall thickness w, as given by the equation. B, If the vessel wall is oblique, the filling factor is higher, leading to a different proportionality constant between the wall thickness and the signal obtained from the voxel (extra signal is indicated by black areas). C, If the voxel boundary falls within the vessel wall, the partial volume effect is spread over 2 voxels, leading to apparently thinner walls (less signal compared with A).

Apparent Wall Thickness Estimation Algorithm

Because the above-mentioned requirements will not be met, in practice, an algorithm was developed to obtain an estimation of the ratio S_w/S₀ from the signal intensities in the vessel wall (MPIR-TSE) images, and this ratio was termed “apparent wall thickness” (AWT). With the limitations of the requirements in mind, one might think of the AWT as a fractional thickness of the vessel wall relative to the voxel size. As a surrogate for the unknown intensity of a voxel completely filled with vessel wall, S₀, the intensity of the adjacent brain tissue, was used. Brain tissue was chosen because the vessel wall has T1 similar to that of brain tissue at 7T¹² and because the MPIR-TSE yields only limited T1-weighted contrast (almost no contrast between gray and white matter, Fig 2). A schematic overview of the analysis method, including the correlation with WSS measurements, is shown in Fig 2.

Fig 2.

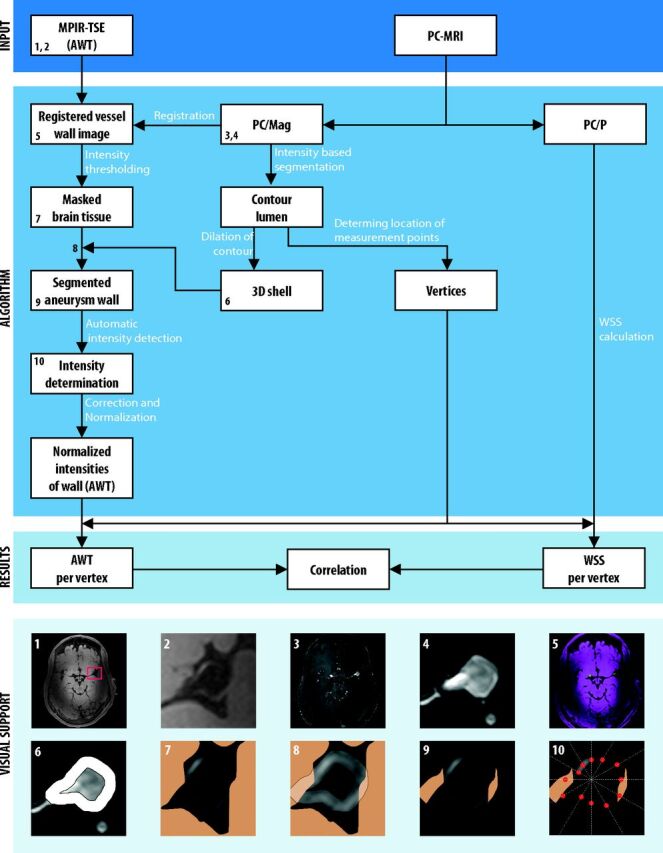
Schematic overview of the algorithm to determine the apparent wall thickness and its correlation to wall shear stress in intracranial aneurysms on 7T MR imaging. Blocks represent in- and outputs, and arrows represent procedures within the algorithm. The numbers in the boxes refer to the visualizations of several steps at the bottom of the image: 1) MPIR-TSE image (transverse orientation); the red box indicates the area of brain tissue that is used for the correction (by fitting a second-order polynomial function to the brain tissue intensities) and normalization of the vessel wall intensities; 2) cropped MPIR-TSE image clearly showing the aneurysm wall and its varying intensity; 3) the PC/mag image used for segmentation of the aneurysm lumen; 4) cropped PC/mag image; 5) registered images: pink is MPIR-TSE; green, PC/mag; 6) 3D shell encompassing the aneurysm wall; 7) brain tissue mask; 8) overlay of the 3D shell on the MPIR-TSE image with tissue mask; 9) segmented aneurysm wall; and 10) radial intensity profiles to sample vessel wall intensities (ie, signal maxima within the 3D shell, indicated by red dots). The profiles were rotated by stepping with 1°; here only a few profiles are shown. The images are taken from aneurysm 1 (Table). PC/P indicates phase-contrast MRI phase images.

First, to be able to relate measurements and segmentations of either images, the MPIR-TSE images were registered to the PCMR magnitude (PC/Mag) images by using a standard rigid body registration in MeVisLab (MeVis Medical Solutions, Bremen, Germany). The registration was performed on the entire image, which leads, in a minority of cases, to slightly suboptimal registration at the location of the aneurysm. Therefore, when automatic registration was not optimal, small manual adjustments were made. After registration, no deviations between the lumen derived from the PC/mag and the lumen of the MPIR-TSE images were observed.

Second, the aneurysm lumen/wall boundary was obtained by segmentation of the PC/Mag by using a level set evolution algorithm.¹³ To obtain the segmentation of the aneurysm wall on MPIR-TSE images, we dilated the contour of the segmented lumen to generate a 3D shell (ROI) that encompassed the aneurysm wall (Fig 2, image panel 6). This step and the remaining postprocessing steps of the analysis method were performed in a custom built Matlab program (MathWorks, Natick, Massachusetts).

Next, the intensities of the wall within the 3D shell were automatically sampled by using radial-intensity profiles crossing the aneurysm wall in the MPIR-TSE images. Maximum intensities along the profiles within the 3D shell (ie, where the profile crossed the aneurysm wall) were saved. The profiles were rotated with a step of 1° through all 2D sections containing the aneurysm, in transversal, sagittal, and coronal planes. Because the aneurysm wall has nearly the same intensity as brain tissue, the wall was indistinguishable from the brain tissue in areas where the aneurysm bordered the brain tissue. Therefore, a brain tissue mask based on an intensity threshold and connected components was used to avoid intensity measurements in the bordering brain tissue. Intensities of parent vessels were manually deleted, as well as intensities that were evidently located outside the wall (errors).

Finally, the AWT was computed by normalizing to the local brain tissue intensity. Care was taken to use only local brain tissue to also correct for intensity inhomogeneity, which is typically present on the 7T images (Fig 2, image panel 1). The inhomogeneity in local brain tissue intensity was corrected for by fitting the intensities to a second-order polynomial function, by using brain signal from a manually drawn box around the aneurysm. The brain signal was selected by removing CSF and blood signal (based on their low intensities) and the aneurysmal wall (based on the segmented 3D shell described above). The resulting fitted brain tissue intensity field was used to normalize the aneurysm wall intensities. The normalized aneurysm wall intensities were used as AWT.

Wall Shear Stress Calculation

Wall shear stress was determined as previously described.¹⁴ After smoothing of the lumen/wall boundary segmentation mentioned above, a spline was fitted through the velocity values derived from PCMR phase images perpendicular to the wall. A blood viscosity of 4.0¹⁰⁻³ Pa × s, which is commonly used in similar algorithms,^15–17 was used in this algorithm and the wall shear stress during peak systole was used for correlation with the AWT measurements. Peak systole was defined as the cardiac timeframe with the highest average velocity in the aneurysm segmentation.

Comparison of Apparent Wall Thickness and Wall Shear Stress

To obtain common measurement locations for both the AWT and WSS, we divided the aneurysm lumen contour into different faces (individual surfaces) and vertices (corners of faces) by using the isosurface function in Matlab. The amount of vertices was determined by the algorithm used in the isosurface function of Matlab and depended on the size of the aneurysm. At each vertex point, the WSS was computed from the 3D velocity data, and the corresponding AWT was obtained by averaging the AWT samples that were closest to the vertex. Because the amount of vertices was much higher (approximately 10 times) than the amount of voxels on the aneurysm lumen contour, the AWT and WSS values at each vertex cannot be regarded as independent or unique measurements. Accordingly, the resolution of the AWT map (or WSS map) is determined by the resolution of the underlying MPIR-TSE images (or PCMR images), and not by the density of the vertices. Visual comparisons were made for all aneurysms, to illustrate the results of the statistical analysis. The 3D lumen contours of each aneurysm were presented, colored by an interpolated color map representing the WSS and AWT.

Statistical Analyses

Spatial variation in AWT was defined as the interquartile range of the AWT within an aneurysm (ie, the number specifies the range that contains the middle 50% of the AWT). A higher range reflects more variation in wall thickness across the aneurysm. The interquartile range was chosen to avoid the effect of outliers on the AWT variation assessment. A visual estimation of the coverage and the amount of data points were reported to give an impression of the area of the aneurysm wall that was covered by the analysis.

Because the potential relation between WSS and AWT is not necessarily linear, Spearman correlation coefficients were computed to compare AWT and WSS in the aneurysms. The correlation coefficients between AWT and WSS were calculated for each individual aneurysm, after which a 1-sample t test was used to test whether the mean correlation coefficient was significantly different from zero, with significance set at P < .05. The correlation coefficients were weighted by the amount of measured points, to decrease the influence of aneurysms with fewer data points. We decided to not pool all the data to calculate the overall correlation coefficient because the amount of points were different per aneurysm. If the data were pooled, the observed correlation between WSS and AWT could be dominated by the data of the largest aneurysm. The significance of each individual correlation coefficient was not determined because the artificially high number of data points (from the high number of vertices on the lumen contour) would yield unrealistically low P values.

The correlation between AWT and WSS was further visualized with histograms for each aneurysm. To reduce the amount of data in these histograms, the WSS was divided into quartiles, with an equal amount of data points per quartile.

Results

Population

Eighteen patients (with 20 aneurysms in total) underwent both MPIR-TSE scans and PCMR. Four patients were excluded on the basis of PCMR artifacts due to a gradient hardware problem; 1 patient, due to motion artifacts on MPIR-TSE; and 4, due to an insufficient proportion of visible wall. Thus, 9 patients with, in total, 11 aneurysms were available for analysis. Their mean age was 59 years, and 44% were women. Baseline characteristics are shown in the Table.

Baseline characteristics and AWT results of 11 unruptured intracranial aneurysms

Aneurysm	Age (yr), Sex	Aneurysm (mm), Largest Diameter (Height × Width in mm)	Location of Aneurysm	Analyzed Points	Coverageb	AWT Heterogeneityc	Correlation (ρ)
1	50, Ma	9.1 (5.9 × 6.3)	MCA	864	50%–75%	0.17	−0.4
2	55, M	9.6 (6.1 × 9.6)	MCA	769	50%–75%	0.53	−0.6
3	70, M	9.5 (7.8 × 7.8)	AcomA	714	25%–50%	0.22	−0.1
4	64, M	10.1 (8.8 × 7.7)	MCA	466	25%–50%	0.15	−0.3
5	60, Fa	6.8 (6 × 4.7)	MCA	428	50%–75%	0.21	−0.5
6	55, F	7.4 (6.0 × 5.8)	MCA	406	50%–75%	0.11	−0.2
7	56, M	12.6 (10.1 × 9.4)	AcomA	298	<25%	0.31	−0.5
8	50, Ma	6.4 (4.8 × 3.9)	ICA	166	25%–50%	0.21	−0.5
9	74, F	6.1 (6.1 × 5.7)	AcomA	163	25%–50%	0.13	−0.1
10	50, F	12.9 (12.9 × 6.3)	MCA	130	<25%	0.31	−0.3
11	60, Fa	5.6 (4.5 × 3.9)	Pericallosal artery	33	<25%	0.07	−0.4

Note:—AcomA indicates anterior communicating artery.

^aTwo aneurysms in 1 patient.

^bCoverage indicates the visual estimated percentage of the area of the wall that could be analyzed.

^cHeterogeneity is defined as the interquartile range in AWT, and reflects the spatial wall thickness variation.

Apparent Wall Thickness and Wall Shear Stress

Color maps of the AWT showed spatial variation in almost all aneurysms (Fig 3), which ranged from 0.07 to 0.53, with a mean variation of 0.22 (Table). A variation of 1.0 roughly means a thickness variation of 1 voxel.

Fig 3.

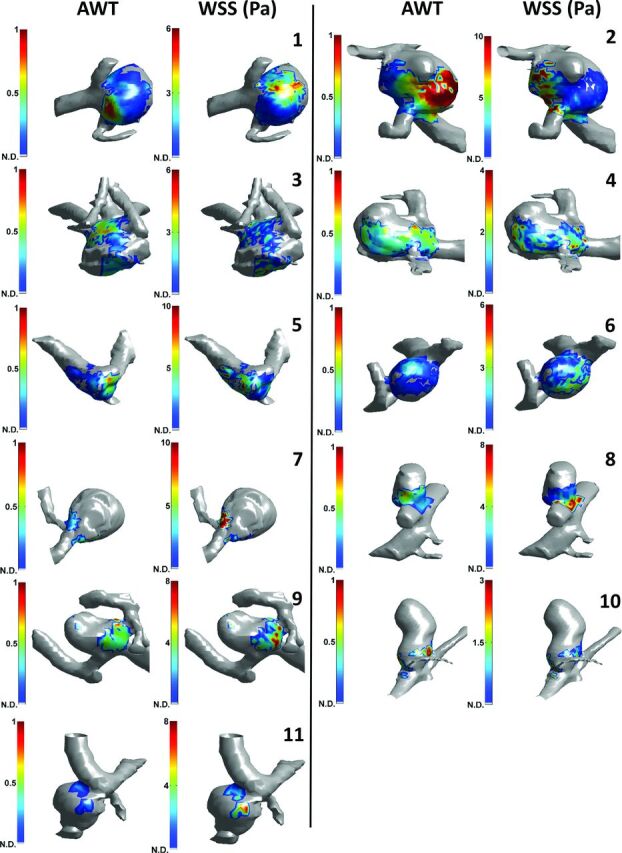
Visual comparison between apparent wall thickness and wall shear stress in intracranial aneurysms on 7T MR imaging. 3D color map with AWT (left images) and 3D color map with WSS (right images) are shown. The color scaling for all AWT images is equal, while the WSS images were individually scaled as indicated by the color scale bars. Parent vessels and wall areas where no AWT data (N.D.) were available are displayed in gray. Numbers correspond to the numbering of the aneurysms in the Table. The other side of the aneurysms is shown in the On-line Figure.

A correlation between AWT and WSS was visible in most aneurysms (Fig 3), particularly where the coverage and the spatial variation was high (Table).

In all aneurysms, AWT and WSS were inversely correlated (though sometimes close to zero, Table). The mean correlation coefficient was −0.35, which was significantly different from zero (P < .05).

The inverse relation between AWT and WSS is also visible in the individual and pooled plots, as shown in Fig 4. In the lowest WSS quartile, there was more variety in AWT between different aneurysms than in the highest WSS quartile. In other words, low WSS at thinner walls was present, but high WSS at thicker walls was rarely observed (Fig 4B).

Fig 4.

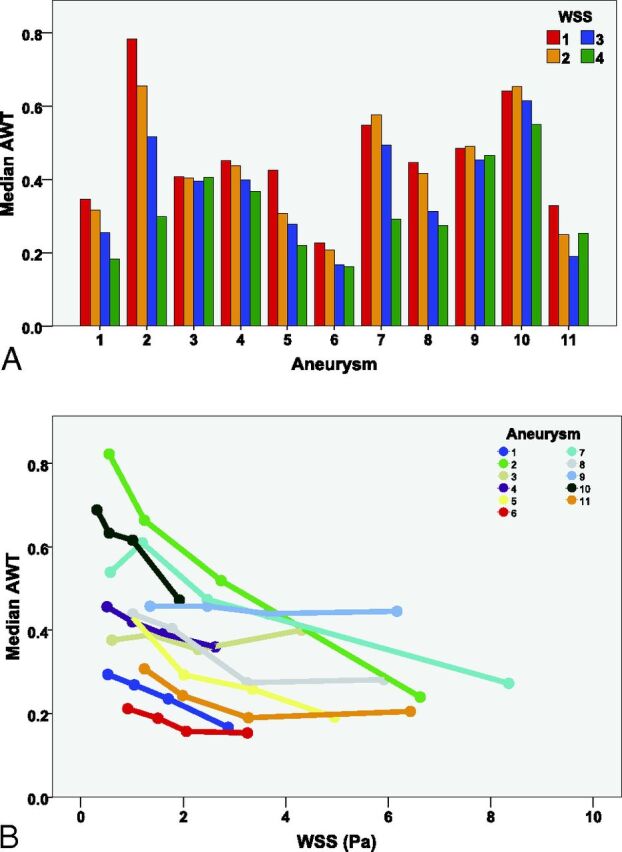
Comparison of apparent wall thickness and wall shear stress in intracranial aneurysms on 7T MR imaging. A, Histogram for each aneurysm is sorted from the aneurysm with the highest amount of measurements points (n = 864) to the aneurysm with the least measurement points (n = 33). The 4 colors represent the WSS, divided into 4 quartiles per aneurysm with increasing WSS (1 = lowest WSS quartile, 4 = highest WSS quartile). B, AWT is plotted against WSS in all aneurysms (different colors). The dots represent the 4 WSS quartiles.

Discussion

On the basis of previous work, a semi-automatic algorithm was developed to measure apparent aneurysm wall thickness from the signal intensity of the wall on 7T MR vessel wall images of patients with unruptured intracranial aneurysms. Semi-quantitative measurements of the wall thickness were obtained, which showed wall thickness variation in all analyzed aneurysms. Furthermore, by calculating WSS from PCMR data, we found an inverse relation between apparent wall thickness and wall shear stress.

Our results are in contrast with the results of a previous study, which found a positive correlation between wall thickness and wall shear stress.¹⁸ The relation between WSS and wall thickness is probably complex and may differ between large, thick-walled aneurysms and small, thin-walled ones.⁶ Kadasi et al¹⁸ studied predominantly smaller aneurysms because 12 of 54 aneurysms (22%) were >7 mm, and we studied relatively large aneurysms (7 of 11 (63%) were >7 mm), which might partly explain the different observations. However, the different observations can also be related to methodologic differences. Kadasi et al used intraoperative images for a dichotomous visual scoring of wall thickness, while we semi-quantitatively assessed wall thickness on noninvasive MR images. Furthermore, although they did not validate thickness measurements with ex vivo histopathologic assessment, they visually assessed actual wall appearance. On the other hand, while we did validate our thickness assessments with an ex vivo study on 2 samples with heterogeneous composition,¹⁰ we did so in the absence of flowing blood or fluid. Wall shear stress was, in our study, measured by 3D PCMR, while the previous study used computational fluid dynamics simulations, which depend on certain assumptions and boundary conditions such as rigid vessel walls and inflow velocity at the entrance of the simulated vessel segment. However, general WSS patterns should be similar for either method (computational fluid dynamics or PCMR).¹⁴ A clear advantage of our method is the avoidance of invasive methods (such as aneurysm surgery) to obtain information on wall thickness. An elaborate study by using both approaches on small and large aneurysms with ex vivo (postsurgery) validation is warranted to determine the impact of the differences in methodology.

The observed inverse correlation in the present study is consistent with the hypothesis that high WSS is associated with the process of intracranial aneurysm wall remodelling that might cause wall thinning, such as activation of proteases by mural cells, matrix degradation, and apoptosis.⁶ Furthermore, low WSS is associated with increased inflammatory cell infiltration and smooth muscle cell proliferation,^6,7 which may lead to wall thickening.

The WSS computations require sufficiently high velocity-to-noise ratios. We used a higher velocity-encoding (150 cm/s) than the velocity-encoding of 100 cm/s that was used by van Ooij et al,¹⁴ who showed good qualitative agreement between WSS measured with PCMR and computational fluid dynamics simulations. However, the study of van Ooij et al was performed at 3T, whereas we performed PCMR at 7T, which yields a higher SNR and, therefore, improved accuracy of the velocity vector direction and magnitude.⁹ Thus, we are confident that the low WSS values are of at least comparable reliability with those presented before.¹⁴ The lumen segmentations were performed on the PC/mag images, in which the SNR depends on the blood velocity (inflow effect). The segmentations appear to be robust because no mismatches were observed with the lumens obtained from the MPIR-TSE images. Besides, comparisons of velocity direction and magnitude obtained from PCMR at 3T and the segmentation algorithm showed good agreement with computational fluid dynamics in regions of both high and low SNR and velocity-to-noise ratio in intracranial aneurysms.¹⁹

This study has several strengths. First, it uses a noninvasive method to quantify wall thickness, which provides a unique means for in vivo quantification of wall thickness variation in unruptured aneurysms. Second, the method is based on the relation between aneurysm wall thickness and image intensity, which has been validated by a phantom and histopathologic correlation study.¹⁰ Finally, the analyzed methods for WSS and wall thickness have been shown useful in aneurysms of various sizes, providing that an appropriate signal-to-noise ratio of the MR images is obtained and that the walls are surrounded by CSF.

Some limitations should be mentioned. First, the relation between the aneurysm wall parts bordering brain tissue and WSS could not be analyzed because measurement of thickness in these parts is not possible. Therefore, the association between thickness of wall bordering the parenchyma and WSS remains unknown. Unfortunately, this association frequently concerned the apex of the aneurysm, which is especially of interest because it is known to be the predominant site of rupture. Second, the observed correlation coefficients were relatively weak, which may partly be due to noise. The influence of noise is suggested by the fact that aneurysms with larger variation in wall thickness, and thus a larger dynamic range in the AWT parameter, tended to show a stronger correlation than aneurysms with a more narrow range in AWT. Last, despite the AWT, in theory, being directly related to the absolute vessel wall thickness, it depends on too many requirements that are not met in practice to claim that we have found a tool to measure absolute wall thickness. The most important requirement is the nulling of CSF and blood. The found inverse correlation may be partly caused by imperfect nulling of blood with very low flow velocities. The MPIR-TSE is used to obtain black blood, which is based on the high flow sensitivity of the long turbo spin-echo train with low refocusing angles. However, very slow blood flow may still yield some signal. If that is the case, the wall seems thicker at locations with low velocities and thus low WSS. This feature leads to overestimation of the negative correlation.

We previously validated the correlation between signal intensity and wall thickness with an ex vivo imaging experiment on an aneurysm wall of heterogeneous composition and histopathologic validation, and with a tapering phantom study, in which flow could not affect the wall thickness.¹⁰ However, although these validation experiments show that thickness variation can explain the observed signal variation, they cannot exclude a potential additional confounding role of slow-flowing blood in the in vivo situation. The long turbo spin-echo trains with low reduced refocusing angles are very sensitive to motion, up to diffusion-related motion.²⁰ The refocusing angles of the MPIR-TSE sequence used in this work were very low, with a range of 12°–40°. Although we think the low refocusing angles will protect against the effect of low-flow velocities, this should be confirmed in future studies by using a dedicated phantom setup with flow or by performing additional validation studies on postoperative material from patients who have been scanned with the MPIR-TSE sequence before an operation.

Future Directions

The conflicting results of our study and a previous study on the relation between aneurysm wall thickness and WSS¹⁸ call for further studies in which both approaches are applied and compared in the same patients. The presented method for in vivo wall thickness determination, in combination with the aneurysm-specific WSS, might provide a valuable means to noninvasively study how wall thickness and hemodynamic parameters are related to aneurysm growth and rupture. This study may yield new insights in the pathophysiology of intracranial aneurysms. Therefore, studies to correlate rupture of aneurysms with WSS and wall thickness may help in the search for new rupture predictors. In particular, the spatial variation in AWT might be an interesting parameter for those future studies. Whether thickness variation indicates higher rupture risks is currently unknown. Nevertheless, it seems plausible that much variation in thickness calls for a pathologic wall, prone to rupture.

Conclusions

A method was developed to measure the wall thickness semi-quantitatively, using 7T MR imaging. An inverse correlation between wall shear stress and AWT was determined. In future studies, this noninvasive method can be used to assess spatial wall thickness variation in relation to pathophysiologic processes such as aneurysm growth and rupture.

ABBREVIATIONS:

AWT

apparent wall thickness

MPIR-TSE

magnetization-prepared inversion-recovery turbo spin-echo

PC/mag

phase-contrast MR magnitude images

PCMR

phase-contrast MR imaging

WSS

wall shear stress