Skip to main content
PMC home page
Scientific Reports logoLink to Scientific Reports
. 2016 May 26;6:26680. doi: 10.1038/srep26680

Experimental Demonstration of a Hybrid-Quantum-Emitter Producing Individual Entangled Photon Pairs in the Telecom Band

Geng Chen 1,2, Yang Zou 1,2, Wen-Hao Zhang 1,2, Zi-Huai Zhang 1,2, Zong-Quan Zhou 1,2, De-Yong He 1,2, Jian-Shun Tang 1,2, Bi-Heng Liu 1,2, Ying Yu 2,3, Guo-Wei Zha 2,3, Hai-Qiao Ni 2,3, Zhi-Chuan Niu 2,3,a, Yong-Jian Han 1,2,b, Chuan-Feng Li 1,2,c, Guang-Can Guo 1,2
PMCID: PMC4881037  PMID: 27225881

Abstract

Quantum emitters generating individual entangled photon pairs (IEPP) have significant fundamental advantages over schemes that suffer from multiple photon emission, or schemes that require post-selection techniques or the use of photon-number discriminating detectors. Quantum dots embedded within nanowires (QD-NWs) represent one of the most promising candidate for quantum emitters that provide a high collection efficiency of photons. However, a quantum emitter that generates IEPP in the telecom band is still an issue demanding a prompt solution. Here, we demonstrate in principle that IEPPs in the telecom band can be created by combining a single QD-NW and a nonlinear crystal waveguide. The QD-NW system serves as the single photon source, and the emitted visible single photons are split into IEPPs at approximately 1.55 μm through the process of spontaneous parametric down conversion (SPDC) in a periodically poled lithium niobate (PPLN) waveguide. The compatibility of the QD-PPLN interface is the determinant factor in constructing this novel hybrid-quantum-emitter (HQE). Benefiting from the desirable optical properties of QD-NWs and the extremely high nonlinear conversion efficiency of PPLN waveguides, we successfully generate IEPPs in the telecom band with the polarization degree of freedom. The entanglement of the generated photon pairs is confirmed by the entanglement witness. Our experiment paves the way to producing HQEs inheriting the advantages of multiple systems.

As reliable quantum emitters, single semiconductor QDs have been shown to be excellent building blocks in the fields of quantum computation1, quantum cryptography2 and quantum optics3. Single QDs’ desirable optical properties substantially meet the requirements of a single-photon emitter, including high-fidelity anti-bunching, narrow emission lines and high brightness. Moreover, they can potentially be integrated into monolithic structures, such as optical microcavities4,5 and electrical charge-tuning devices6. A popular realization involves Stranski-Krastanow InGaAs QDs embedded in a three-dimensional matrix7. However, extracting photons from a bulk semiconductor is highly inefficient because of the large mismatch in the refractive indices of GaAs and vacuum. To address this issue, an attractive approach is to embed the quantum dots in a nanowire8,9,10, which serves as a photonic waveguide. High coupling of the quantum emitter into the fundamental waveguide mode compared with higher order modes (β-factor ~1), thereby enabling near-unity light-extraction efficiency11. The only limitation preventing this QD-NW structure from use in practical quantum communication is its emission in the red, which is not suitable for long-distance transmission in an optical fiber.

Compared to single photons, IEPPs are considered more advanced tools for use in quantum information. IEPPs can function as single photons in all of the above-mentioned fields, but they are irreplaceable in long-distance quantum key distribution12, quantum teleportation13 and distributed quantum computation14. However, developing a quantum emitter that generates IEPPs remains a technological challenge. Recently, both polarization15 and time-bin entangled photon pairs16 were realized in a quantum dot system through a cascade radiation process. IEPPs in the telecom O band (1260–1360 nm) were also demonstrated utilizing an additional InGaAs strain relaxation layer to increase the emission wavelength of the quantum dot17. However, increasing the wavelength also increases the fine structure splitting, which allows only classical correlations to be observed. Moreover, similar to the single photon emitters based on a single QD, the wavelength tunability of the emission is extremely limited. To the best of our knowledge, generating IEPPs in the most commonly used ~1550 nm telecom band has not previously been demonstrated.

In contrast to a single QD, the wavelength of the photon pairs from the SPDC process can be directly tuned by changing the temperature or cut angle of the nonlinear crystal18. The SPDC process was used to generate entangled photon pairs in the telecom band19. However, the occurrence of the SPDC process is random; furthermore, it always has a finite probability of generating some multiple entangled pairs. Such multiple pairs induce errors and have a large negative impact on the rate of successful generating of long-distance entangled pairs. Even a small probability of generating multiple pairs will significantly reduce the efficiency when single photon detectors are employed20.

The zero multiple photon probability of single QD and the wavelength tunability of SPDC are prerequisites for producing an ideal IEPP emitter. Currently, as far as we know, there is no system that unifies these two properties. Principally, a hybrid system, i.e., the nonlinear crystal pumped by deterministic single photons, can evolve into a IEPP emitter. In previous systems, the nonlinear crystals always had to be pumped by a high-power laser due to the low conversion efficiency of the SPDC process. In nonlinear optical materials, such as β-barium borate (BBO) crystal, the efficiency is approximately 10−11 per pump photon21. However, technical progress has shown that it is possible to pump the nonlinear crystals by using a single-photon-level beam22,23,24. Major advances in nonlinear optics, such as the quasi-phase-matching of optical materials, have recently enabled access to higher inherent nonlinearities, such as that of the PPLN crystal. The downconversion efficiencies demonstrated in these materials can reach 10−9 in bulk18. The introduction of optical waveguides etched in a PPLN crystal has further increased the conversion efficiencies to 10−6 25, thus enabling single-photon-level SPDC. In principle, the conversion efficiency can be further improved by increasing the length of the waveguide of PPLN. There is no physical limit to prevent the conversion efficiency from approaching the value of 1.

The existing techniques are adequate to fabricate an efficient single QD-NW and PPLN waveguide; however, the compatibility of a single QD-QW and PPLN is the main obstacle to producing this novel HQE. Generally, these limitations include matched emission wavelength, high-fidelity anti-bunching, narrow emission lines and high brightness. One can directly design a PPLN waveguide for a stable CW laser; however, for a single QD-NW it is quite another matter due to the uncertainty of both the emission wavelength and the optical quality. In our scheme, to generate non-degenerate IEEPs in the telecom band, the QD-NW emission should be as close to 775 nm as possible, resulting in the grestest wavelength tunability.

Using the current growth technique, it is not easy to control the QD emission to a certain wavelength with an accuracy of several nanometers. One feasible approach is to restrain the emission within a range of tens of nanometers covering the required wavelength. Based on the study of massive QD-NWs, several candidate QD-NWs can be selected at approximately 775 nm. Fine matching of the QD-NW and the PPLN waveguide can be realized through either tuning of the QD-NW (e.g., lateral strain or vertical electric field)26,27,28,29, or the temperature of the PPLN waveguide. Considering it is difficult to tuning the QD-NW while maintaining high single photon collection efficiency, temperature tuning of PPLN waveguide is more adoptable for this scheme. By assigning the emission wavelength of the QD-NW, one can design the PPLN waveguide that is most compatible with it; the details of this process are discussed below. Furthermore, a tradeoff exists between the brightness and linewidth for quantum emitters, i.e., a narrow linewidth corresponds to a long lifetime, which yields low photon counting rate. Due to the high β-factor, the reported QD-NW can realize >1 MHz count rate using a standard detector11,30. Another expected effect of QD-NW is luminescence linewidth broadening due to surface states31. To achieve efficient SPDC process, the linewidth of the pumping photons should be narrower than the PPLN waveguide conversion bandwidth.

In this work, we experimentally demonstrate a HQE generating IEPPs in the telecom band with the polarization degree of freedom. We fundamentally achieve the compatibility of the QD-PPLN interface, and the quantum witness result indicates the entanglement characteristic of the generated photon pairs. Our results are the first step toward distributing entanglement over a long distance32,33,34,35.

Results

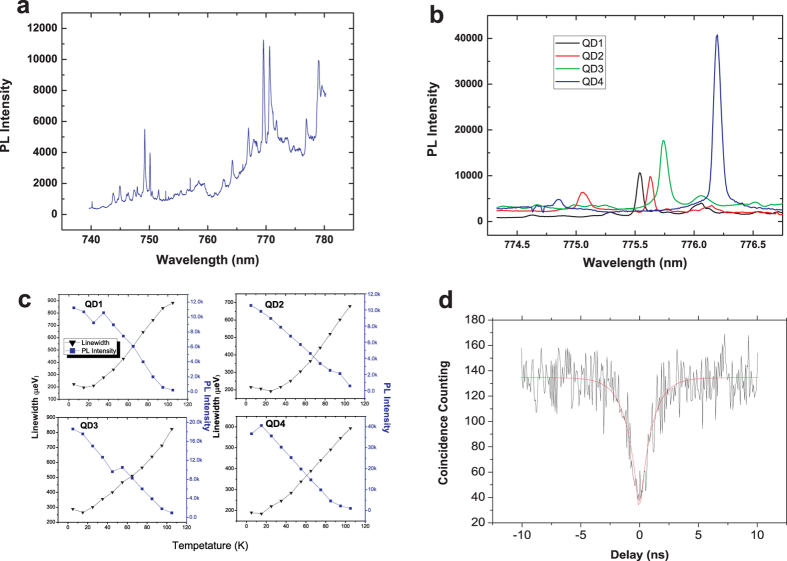
In this work, a newly designed QD-NW is used as the single photon emitter. The details of the growth methods and the micro-spectrum techniques are provided in the Methods section. The Photoluminescence (PL) study results show that the emission range of this QD-NW assemble is from 740 to 780 nm, which covers the target wavelength of 775 nm for our scheme, as shown in Fig. 1(a). To identify the most suitable QD-NW to achieve the highest compatibility of the PPLN waveguide, we narrow the search range within 10 nm around 775 nm. The PL of approximately one hundred possible candidate QD-NWs are investigated; four of them are shown in Fig. 1(b). For each of these four QDs, the temperature dependency of both emission intensity and linewidth are studied; the results are shown in Fig. 1(c). Tuning the cryostat temperature can achieve the largest β-factor, thus yielding a maximum counting of photons. The maximum counting points for these four QDs are 35 K, 95 K, 55 K and 15 K. The linewidth also substantially depend on the temperature and undergoes a narrowing trend, as previously reported36. It can be concluded that the narrowest points (15 K, 25 K, 15 K and 15 K) are generally not consistant with the maximum counting points. As a result, we have to determine the best balance temperature point that accounts for both the counting rate and the linewidth, instead of performing one-sided optimization. Comprehensively considering all of the desirable optical properties, QD4 emitting at 776.2 nm was selected as the single photon emitter to construct the HQE. The linewidth of this QD-NW is 185 μeV at 15 K, which is significantly narrower than the conversion bandwidth of the PPLN waveguide (approximately 320 μeV) applied in this experiment. The corresponding count rate is 3.3 MHz and the Hanbury Brown and Twiss (HBT) measurement shows a pronounced anti-bunching characteristic, with a multi-photon probability of g2(0) = 0.187 (Fig. 1d), which confirms that it is indeed a high purity single-photon source.

Figure 1. The optical characteristics of the QD-NW sample.

Figure 1

Open in a new tab

(a) The PL spectrum of a QD assemble on one certain NW. (b) The PL spectrum of four candidate QD-NWs, the measuring temperature is 15 K. (c) The temperature dependence of the PL intensity and linewidth of four candidate QD-NWs. (d) HBT measurement result of QD4 emission using continuous wave above-band gap excitation. The error bars are smaller than the dimension of the markers and are not shown.

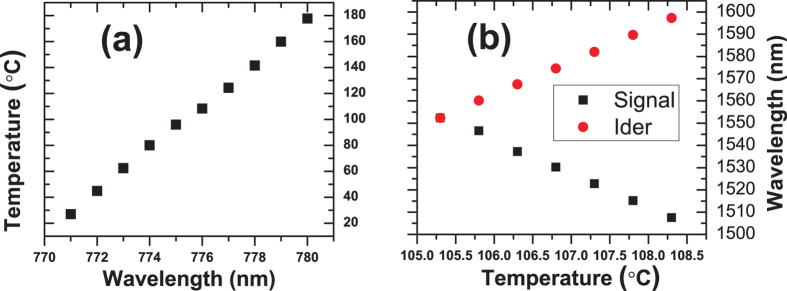
Using this QD-NW sample, the down-conversion characteristics of the PPLN waveguide are studied using theoretical calculation of two scenarios. First, the pump beam wavelength is changed and we calculate the temperature points to achieve degenerate down-conversion. Theoretical results show that, corresponding to 1 nm increasing on pumping beam, the temperature must be raised by 18.2 °C. The temperature controller can be tuned from room temperature to 200 °C, which restricts the feasible range to approximately 10 nanometers. In this scheme the PPLN feasible range should be from 770 to 780 nm, i.e., the occurrence of 775 nm down-conversion should be better at the centering of the tunable temperature range. Second, the pumping beam wavelength is fixed at 775 nm and we calculate the spectrum distribution of the IEPP. It can be concluded that the spectral separation increases with the temperature; the rate is measured as ~30 nm/°C. With these calculation results and considering that long crystals yielding more photon pairs and narrower bandwidths, we customized a 50-mm long flux-grown PPLN crystal with etched waveguides from HC Photonics with a grating period of 18.50 μm for type-0 phase matching. The PPLN crystal is tested in the above two scenarios with a tunable cw laser resonant with the QD-NWs’ emission. As shown in Fig. 2, the measured results fundamentally fit with the theoretical calculations and the degenerate down-conversion point for 776.2 nm is 106.4 °C.

Figure 2. Experimental test results of the PPLN waveguide.

Figure 2

Open in a new tab

(a) The degenerate down-conversion temperature points for varying pumping wavelength. (b) The wavelength-temperature dependence relationship of the telecom band photon pairs with 776.2 nm CW laser pumping. The error bars are smaller than the dimension of the markers and are not shown.

As shown in Fig. 3, the experimental setup consists of two parts. The top-right portion is the single photon emitter, which uses a single QD-NW. The bottom-left portion is the entanglement generator based on the PPLN waveguide. After being filtered by the grating, the single photons are collected into a single mode fiber. The emitted single photons from the fiber are collimated by an achromatic lens. The polarization state is controlled by a combination of a polarizer and HWP. To generate the maximally entangled state, the photons’ polarization is set to the 45 degree diagonal state, written as 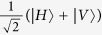Inline graphic.

Figure 3. Experimental setup for the generation of IEPP of telecom band.

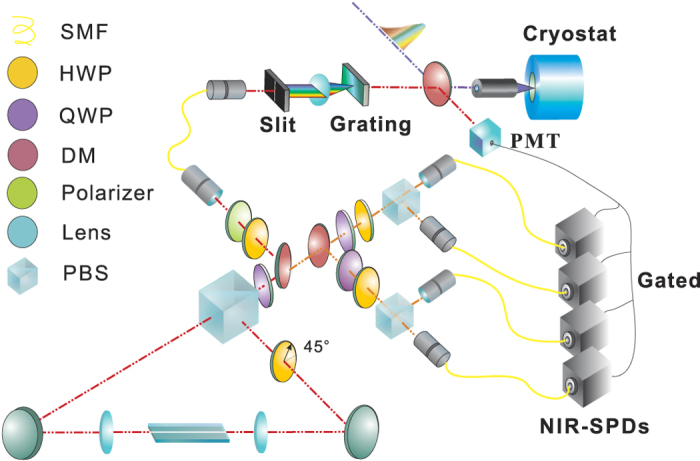
Figure 3

Open in a new tab

The single QD-NW in the cryostat is excited by the pulsed ultraviolet (UV) beam and generates visible single photons with wavelengths of approximately 775 nm. The polarization Sagnac interferometer (PSI) apparatus with a PPLN waveguide at the center is used to generate polarization entanglement. The single photons coupled into the PPLN waveguide have a probability of splitting into IEPP, which are detected by near-infrared single-photon detectors (NIR-SPDs). The four NIR-SPDs are gated by the electrical pulses from the photo-multiple tube (PMT). SMF - single mode fiber, HWP - half wave plate, QWP - quarter wave plate, DM - dichroic mirror, PBS - polarized beam splitter.

To separate the visible pump and telecom down-conversion photons, a dichroic mirror is applied to guide the visible pump photons into the entangled photon source setup, which is mainly a PSI. The bidirectional pumping of the crystal in counter-propagating directions creates a coherent superposition of the counter-propagating down-conversion outputs at the PBS, whose output photons are in polarization entangled state written as |HsHl〉 + eiϕ|VsVl〉. The interferometric combination of two outputs is typically sensitive to pathlength perturbations, however, the PSI configuration eliminates the need for path-length stabilization through its common path arrangement37,38. Moreover, the phase ϕ of the output state can be chosen by simply adjusting the relative phase between the horizontally and vertically polarized components of the pump. Details of the PSI and the entanglement generation process are provided in the Method section. The PPLN crystal was temperature stabilized at a phase-matching temperature of 107.3 °C above the degenerate point for 776.2 nm down-conversion, using a thermoelectric heater with a temperature stability better than 0.1 °C. The wavelengths of the signal and idler photons are centered at 1522.4 and 1583.7 nm, respectively. These telecom photons are split by a dichroic mirror. The two photons are measured by two standard polarization analyzers, either of which consists of a quarter wave plate (QWP), a half wave plate (HWP), a polarized beam splitter (PBS) and two near infrared single photon detectors (NIR-SPDs). The time stamps of all events were recorded when two photons were detected within 3 ns of each other by using a time-tagger with a resolution of 100 ps.

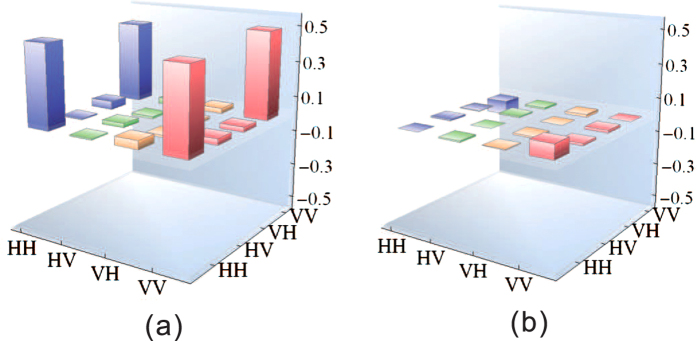
To verify that this setup is reliable for generating entanglement, first, a 776.2 nm continuous laser is adopted instead of the single photons to pump the PPLN waveguide. With a pumping power of 10 nW, we detect 3,000 pairs of telecom photons per second. The combined coupling and detection efficiency for the 1522.4 nm and 1583.7 nm photons is η1 = η2 = 0.08, as measured from the ratio of photon detections to coincident photon detections. The density matrix of the output state can be reconstructed by quantum state tomography. The coincidence counts recorded in 16 projective measurements can be used to obtain individual density matrix elements by using a maximum likelihood algorithm. The real and imaginary parts of the density matrix are plotted in Fig. 4. This density matrix estimation yields a level of fidelity of 0.936 ± 0.013 for the matching to a maximally entangled Bell state. The concurrence is measured to be 0.918 ± 0.011, which confirms that the PSI can generate high-quality entanglement.

Figure 4.

Figure 4

Open in a new tab

(a) Real and (b) Imaginary parts of the reconstructed density matrix of the PSI outcome state when the PPLN waveguide is pumped with a 776.2 nm continuous laser.

For the single photon case with the QD-NW excited by the pulsed UV beam, approximately 0.6 M/s single photons are coupled into the PPLN waveguide for the SPDC process. The combined coupling and detection efficiency of the 1522.4 nm and 1583.7 nm photons is η1 = η2 = 0.036. The reduced efficiency likely results from the relatively long lifetime of the QD-NW (which is measured as 1.02 ns after fitting the HBT results), which leads to an exponential decay wave-package that cannot be completely covered by the 1-ns gate of the NIR-SPDs.

In contrast to quantum state tomography, the measurement of witness operators does not provide a complete reconstruction of the original quantum state, however, it does allow us to check the entanglement character of a quantum state by using a minimal number of local measurements for an39,40,41. The witness operator can be measured locally by select correlated measurement in the three complementary bases, which are linear(H/V), diagonal(D/J), and circular(R/L), with |L〉=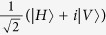Inline graphic and |R〉=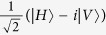Inline graphic. To verify that the two photons are actually in an entangled state, the expectation value of the corresponding witness operator is expected to take a negative value. The entanglement witness is given by

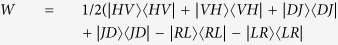graphic file with name srep26680-m4.jpg

There are four possible settings for each complementary base. A certain expectation value E[ij] (i, j = H, V, D, J, R, L) of a correlation function is obtained by making a von Neumann measurement along a specific basis and computing the probability over all the possible events. For example, for a HV correlation Tr(ρHV), we perform measurements along the H/V basis. Next, its value E[HV] is given by the number of coincidence counts of HV over the sum of all coincidence counts of HH, HV, VH, and VV. Benefiting from the application of four NIR-SPDs, for each basis, the data for four settings can be recorded simultaneously. The experimental integration time for each basis is 35 h, and we record approximately 450 events of desired two-qubit coincidences for non-vanishing item, including the coincidence from the NIR-SPDs’ dark counts. To calculate W, six correlation functions are measured; their expectation values are shown in Fig. 5. The witness can then be directly evaluated as Tr(ρW) = −0.11 ± 0.021. When the coincidence from the NIR-SPDs’ dark count is eliminated, the result is Tr(ρW) = −0.28 ± 0.037. The error is obtained from Monte Carlo estimation. The negativity of the measured witness implies clearly that the telecom photon pairs are entangled. The imperfection of our data is due to the relatively low extinction ratio of the dual-wavelength devices and the PSI phase fluctuation during the long data recording time.

Figure 5. Experimental expectation values for every correlation function of the entanglement witness for the generated state.

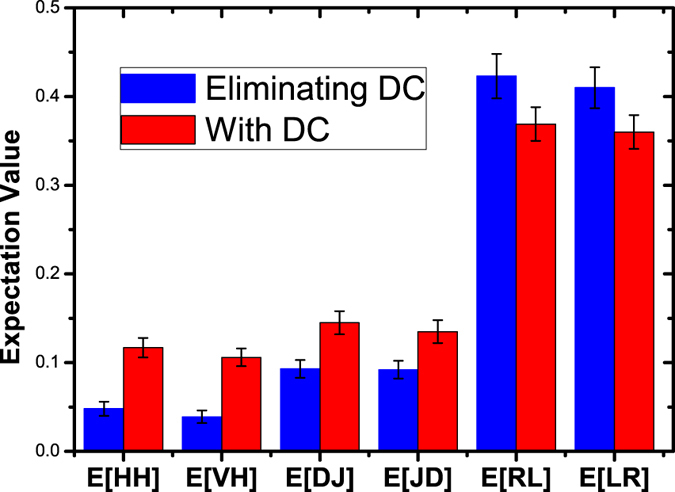
Figure 5

Open in a new tab

The results are derived by twofold coincidence measurements along three complementary common bases: linear(H/V), diagonal(+/−), and circular(R/L), conditioned by the pulsed signals from PMT. The blue bars are results after eliminating coincidence from the NIR-SPDs’ dark count, whereas the red bars include this noise.

Our scheme provides a sub-Poissionian distribution of the IEPP in the telecom band that is inherited from the QD-NW emission. To further verify this result, the probability of multiple-photon-pairs is estimated by the autocorrelation g2(0) of either down-converted photon. The autocorrelation can be measured by analyzing the histogram of coincidence counts of the two NIR-SPDs in either polarization analyzer, and the generation of multiple-photon-pairs gives rise to photon coincidences at zero delay. The results for long and short wavelength photons are 0.176 and 0.182 respectively, when the coincidence from the NIR-SPDs dark count is eliminated. The fairly low values of g2(0) indicate sub-Poissonian distribution of the IEPP.

Discussion

The main issues preventing our scheme from being applied in quantum communication are the dephasing of QD-NW and the low counting rate. On the one hand, the dephasing from QD can be dramatically suppressed by near-resonant excitation and coupling to a microcavity. Combining these two techniques single photons can be deterministically generated with extremely high single-photon purity and indistinguishability42. However, due to the difficulty in fabrication, the lack of microcavity is one main obstacle preventing QD-NW from high quality single photon emitter. Recently, ref. 11 integrated a gold mirror at the nanowire base to reflect downward-emitted photons and it is possible to form a microcavity with high-reflection coating fiber placed at the top the QD-NW43. On the other hand, there are several existing techniques to increase the IEPP count rate and each of the sections in our scheme can likely be improved. First, the coupling efficiency of the QD-NW emission can still be significantly increased by configuring the emission direction. Chu et al. designed an optical antenna to convert the dipolar radiation of an arbitrarily oriented quantum emitter to a directional beam with an efficiency more than 99%44. Second, in a periodically poled waveguide with high-reflectivity dielectric mirrors deposited on the waveguide end faces, the SPDC can be significantly enhanced at the resonances of the cavity45. Third, with the modern superconducting NIR-SPDs, the detection efficiency can be close to unity46. For any of these improvements, the IEPP count rate can be raised by at least one order of magnitude. Furthermore, the wavelength tunability of our scheme makes it more flexible for multi-user quantum communications. A programmable temperature controller for the PPLN waveguide can enable the compatibility with quantum wavelength-division multiplexing (WDM)47.

In summary, to the best of our knowledge, for the first time a HQE was experimentally demonstrated to generate IEPPs in the telecom band. The QD-NW employed in this experiment is a uniquely designed single-photon source and has a extremely high luminescence efficiency. The 50-mm-long PPLN waveguide used here possesses the highest conversion efficiency in SPDC process. A QD-NW meeting all of the desirable conditions for the QD-PPLN interface is found to construct this HQE. The quantum witness results show that the generated photon pairs are strongly entangled. Our scheme is the first step toward the fabrication of a practical IEPP source in the telecom band.

Methods

Single photon emitter

The formation of the QD-NW utilizes epitaxial growth, that is, “bottom-up” approaches, including the vapor-liquid-solid (VLS)48 and selective area epitaxy methods. This type of QD-NW system has also been proven to be a better gain medium than the homogeneous systems49,50. The QD-NW structure consists of a GaAs core, and a single separated GaAs QD can be achieved by using single Al0.58Ga0.42As quantum ring (QR) on the facet of a NW as the bottom surrounding barrier and an Al0.7Ga0.3As shell as the top barrier, which serves as single-photon emission source. This QD-NW sample is placed in a cryostat and cooled down with liquid Helium. In the PL study, the pump beam uses the 632.8 nm line of a cw He-Ne laser, which is focused on the sample through a confocal microscopy system. With one piece of a 1,200 groove/mm grating, followed by a lens and slit. Single emission lines from QD-NWs can be isolated to implement the HBT measurement.

For the generation of IEPPs in the telecom band, the QD-NW is excited with a pulsed uv pump centered at 388.1 nm. This UV beam was generated through the secondary harmonic generation (SHG) process in a BBO crystal pumped by femtosecond 776.2 nm pulsed laser, at a repetition rate of 76 MHz. After the SHG process, the light passes through a DM, that is highly transmissive at 776.2 nm and highly reflective at 388.1 nm, and the residual 776.2 nm light is transmitted to a photo-multiple tube (PMT). The generated electronic pulses from the PMT are used to trigger the four NIR-SPDs. The reflected UV pulses excite the QD-NW to generate single photons.

PSI and entanglement generation

The PSI is composed of two silver mirrors and a PBS that serves as the input and output optical element. A PPLN waveguide for generating entangled photons by SPDC is located within the interferometer. The Sagnac configuration calls for an input-output PBS that operates at both the pump and down-conversion wavelengths. Instead, we used a commercially available broad band PBS cube. The PBS provides acceptable extinction ratio of (150:1) and (35:1) for the visible pump and telecom photon pair, respectively. The PBS serves to produce counter-propagating pumps for the bidirectional pumping of the down-conversion crystal. The 50-mm PPLN crystal is mounted in a crystal oven at the center of the PSI. For dual-wavelength capability, the PPLN crystal is uncovered without any tail optical fiber. The pumping single photons are coupled to the waveguide directly using a pair of aspheric lenses. These f = 11.17 mm coupling aspheric lens are customized with a dual-color AR coating. A dual-wavelength half-wave plate (DW-HWP) designed for both 776.2 nm and the telecom band rotates the V-polarized pump to the H polarization that is required (along the crystal’s y axis) for type-0 phase matching. 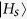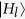It creates non-degenerate photon pairs with identical polarizations Inline graphic↻ and Inline graphic↻, that propagate in clockwise direction. The subscripts s and l denote the short and long wavelengths centered at 1522.4 and 1583.7 nm, respectively. 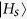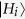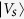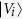The horizontal component of the beam is transmitted through the PBS and creates pairs Inline graphic↺ and Inline graphic↺, propagating in the counterclockwise direction; these pairs are flipped to Inline graphic↺ and Inline graphic↺, respectively, by the DW-HWP. 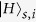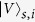A small amount of both the Inline graphic and Inline graphic components leak from the idle exit port of the low extinction ratio PBS; however, the balance between these two components can be maintained by adjusting the pump polarization slightly. 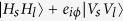The counterpropagating pairs in the ↻ and ↺ modes are then combined at the PBS, where again the horizontal photons are transmitted and the vertical photons are reflected such that the outcome state is Inline graphic.

Additional Information

How to cite this article: Chen, G. et al. Experimental Demonstration of a Hybrid-Quantum-Emitter Producing Individual Entangled Photon Pairs in the Telecom Band. Sci. Rep. 6, 26680; doi: 10.1038/srep26680 (2016).

Acknowledgments

We thank for the invaluable discuss with HC Photonics for the fabrication of the PPLN waveguide. This work was supported by the National Basic Research Program of China (Grants No. 2011CB921200, 2013CB933304), the Strategic Priority Research Program (B) of the Chinese Academy of Sciences (Grant No. XDB01030300), National Natural Science Foundation of China (Grant Nos 11274297, 11105135, 11474267, 11004185, 60921091, 11274289, 10874170, 61322506, 11325419, 61327901, 90921015, 61308010), the Fundamental Research Funds for the Central Universities (Grant No. WK2030020019, WK2470000011).

Footnotes

Author Contributions C.-F.L. and G.C. plan and design the experiment. G.C. out the quantum-dot part of the experiment assisted by W.-H.Z. and Z.-H.Z., Y.Z. and J.-S.T. designs the computer programs. D.-Y.H. assists on operating the NIR-SPDs. Y.Y., G.-W.Z., H.-Q.N. and Z.-C.N. grow the quantum dot sample. G.C. analyzes the experimental results and writes the manuscript with the help of C.-F.L., B.-H.L. and Z.-Q.Z. and Y.-J.H., G.-C.G. and C.-F.L. supervise the project. All authors discuss the experimental procedures and results.

References

  1. Knill E., Laflamme R. & Milburn G. J. A scheme for efficient quantum computation with linear optics. Nature 409, 46–52 (2001). [DOI] [PubMed] [Google Scholar]
  2. Gisin N., Ribordy G., Tittel W. & Zbinden H. Quantum cryptography. Rev. Mod. Phys. 74, 145–195 (2002). [Google Scholar]
  3. Strauf S. Quantum optics: towards efficient quantum sources. Nature Photon. 4, 132–134 (2010). [Google Scholar]
  4. Englund D. et al. Controlling the spontaneous emission rate of single quantum dots in a two-dimensional photonic crystal. Phys. Rev. Lett. 95, 013904 (2005). [DOI] [PubMed] [Google Scholar]
  5. Reitzenstein S. Semiconductor quantum dot¨Cmicrocavities for quantum optics in solid state. IEEE J. Sel. Top. Quantum Electron. 18, 1733 (2012). [Google Scholar]
  6. Yuan Z. et al. Electrically driven single-photon source. Science 295, 102 (2002). [DOI] [PubMed] [Google Scholar]
  7. Santori C., Fattal D., Vuckovicacute J., Solomon G. S. & Yamamoto Y. Indistinguishable photons from a single-photon device. Nature 419, 594–597 (2002). [DOI] [PubMed] [Google Scholar]
  8. Borgström M. T., Zwiller V., Muller E. & Imamoglu A. Optically bright quantum dots in single nanowires. Nano Lett. 5, 1439–1443 (2005). [DOI] [PubMed] [Google Scholar]
  9. Minot E. D. et al. Single Quantum Dot Nanowire LEDs. Nano Lett. 7, 367–371 (2007). [DOI] [PubMed] [Google Scholar]
  10. Heiss M. et al. Self-assembled quantum dots in a nanowire system for quantum photonics. Nature Mat. 12, 439 (2013). [DOI] [PubMed] [Google Scholar]
  11. Reimer M. E. et al. Bright single-photon sources in bottom-up tailored nanowires. Nat. Comms. 3, 737 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Ekert A. Quantum cryptography based on Bell’s theorem. Phys. Rev. Lett. 67, 661–663 (1991). [DOI] [PubMed] [Google Scholar]
  13. Bennett C. H. et al. Teleproting an unkonwn quantum state via dual classical and Einstein-Podolsky-Rosen Channels. Phys. Rev. Lett. 70, 1895–1899 (1993). [DOI] [PubMed] [Google Scholar]
  14. Serafini A., Mancini S. & Bose S. Distributed Quantum Computation via Optical Fibers. Phys. Rev. Lett. 96, 010503 (2006). [DOI] [PubMed] [Google Scholar]
  15. Jayakumar H. et al. Time-bin entangled photons from a quantum dot. Nat. Comms. 5, 4251 (2014). [DOI] [PMC free article] [PubMed] [Google Scholar]
  16. Stevenson R. M. et al. A semiconductor source of triggered entangled photon pairs. Nature 439, 179–182 (2006). [DOI] [PubMed] [Google Scholar]
  17. Ward M. B. et al. Coherent dynamics of a telecom-wavelength entangled photon source. Nat. Comms. 10, 4316 (2014). [DOI] [PubMed] [Google Scholar]
  18. Fedrizzi A., Herbst T., Poppe A., Jennewein T. & Zeilinger A. A wavelength-tunable fiber-coupled source of narrowband entangled photons. Opt. Exp. 15, 15377–15386 (2007). [DOI] [PubMed] [Google Scholar]
  19. Takesue H., Inoue K., Tadanaga O., Nishida Y. & Asobe M. I. Generation of pulsed polarization-entangled photon pairs in a 1.55-mu m band with a periodically poled lithium niobate waveguide and an orthog onal polarization delay circuit. Opt. Lett. 30, 293–295 (2005). [DOI] [PubMed] [Google Scholar]
  20. Guha S. et al. Rate-loss analysis of an efficient quantum repeater architecture. arXiv 1404.7183 (2014).
  21. Kurtsiefer C., Oberparleiter M. & Weinfurter H. Generation of correlated photon pairs in type-II parametric down conversion-revisited. J. Mod. Opt. 48, 1997–2007 (2001). [Google Scholar]
  22. Hübel H. et al. Direct generation of photon triplets using cascaded photon-pair sources. Nature 466, 601–603 (2010). [DOI] [PubMed] [Google Scholar]
  23. Shalm L. K. et al. Three-photon energy-time entanglement. Nature Phys. 9, 19–22 (2012). [Google Scholar]
  24. Hamel D. R. et al. Direct generation of three-photon polarization entanglement. Nature Photon. 8, 801–807 (2014). [Google Scholar]
  25. Tanzilli S. et al. Highly efficient photon-pair source using periodically poled lithium niobate waveguide. Electron. Lett. 37, 26–28 (2001). [Google Scholar]
  26. Seidl S. et al. Effect of uniaxial stress on excitons in a self-assembled quantum dot Appl. Phys. Lett. 88, 203113 (2006). [Google Scholar]
  27. Ding F. et al. Tuning the Exciton Binding Energies in Single Self-Assembled InGaAs/GaAs Quantum Dots by Piezoelectric-Induced Biaxial Stress. Phys. Rev. Lett. 104, 067405 (2010). [DOI] [PubMed] [Google Scholar]
  28. Bennett A. J. M. et al. Electric-field-induced coherent coupling of the exciton states in a single quantum dot. Nat. Phys. 6, 947 (2010). [Google Scholar]
  29. Ghali1 M., Ohtani K., Ohno Y. & Ohno H. Generation and control of polarization-entangled photons from GaAs island quantum dots by an electric field. Nat. Comms. 3, 661 (2012). [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Yu Y. et al. Self-Assembled Quantum Dot Structures in a Hexagonal Nanowire for Quantum Photonics. Adv. Mat. 26, 2710–2717 (2014). [DOI] [PubMed] [Google Scholar]
  31. Uccelli E., Arbiol J., Morante J. R. & Morral A. F. i. InAs Quantum Dot Arrays Decoratingthe Facets of GaAs Nanowires. ACS Nano. 4, 5895–5993 (2010). [DOI] [PubMed] [Google Scholar]
  32. Duan L. M., Lukin M. D., Cirac J. I. & Zoller P. Long-distance quantum communication with atomic ensembles and linear optics. Nature 414, 413–418 (2001). [DOI] [PubMed] [Google Scholar]
  33. Sangouard N., Simon C., de Riedmatten H. & Gisin N. Quantum repeaters based on atomic ensembles and linear optics. Rev. Mod. Phys. 83, 33–80 (2011). [Google Scholar]
  34. Jiang L. et al. Quantum repeater with encoding. Phys. rev. A 79, 032325 (2009). [Google Scholar]
  35. Muralidharan S., Kim J., Lutkenhaus N., Lukin M. D. & Jiang L. Ultrafast and Fault-Tolerant Quantum Communication across Long Distances. Phys. Rev. Lett. 112, 250501 (2014). [DOI] [PubMed] [Google Scholar]
  36. Peng Y., Niu Y., Cui N. & Gong S. Cavity linewidth narrowing by voltage-controlled induced transparency in asymmetry quantum dot molecules Opt. Commun. 284, 824–827 (2011). [Google Scholar]
  37. Shi B. S. & Tomita A. Generation of a pulsed polarization entangled photon pair using a Sagnac interferometer. Phys. Rev. A. 69, 013803 (2004). [Google Scholar]
  38. Kim T., Fiorentino M. & Wong F. N. C. Phase-stable source of polarization-entangled photons using a polarization Sagnac interferometer. Phys. Rev. A 73, 012316 (2006). [Google Scholar]
  39. Gühne O. et al. Detection of entanglement with few local measurements. Phys. Rev. A 66, 062305 (2002). [Google Scholar]
  40. Barbieri M. et al. Detection of entanglement with polarized photons: Experimental realization of an entanglement witness. Phys. Rev. Lett. 91, 227901 (2003). [DOI] [PubMed] [Google Scholar]
  41. Goebel A. M. et al. Multistage entanglement swapping. Phys. Rev. Lett. 101, 080403 (2008). [DOI] [PubMed] [Google Scholar]
  42. He Y. M. et al. On-demand semiconductor single-photon source with near-unity indistinguishability. Nat. Nanotechnol. 8, 213 (2013). [DOI] [PubMed] [Google Scholar]
  43. Albrecht R., Bommer A., Deutsch C., Reichel J. & Becher C. Coupling of a Single Nitrogen-Vacancy Center in Diamond to a Fiber-Based Microcavity. Phys. Rev. Lett. 110, 243602 (2013). [DOI] [PubMed] [Google Scholar]
  44. Chu X. L. et al. Experimental realization of an optical antenna designed for collecting 99% of photons from a quantum emitter. Optica 1, 203–208 (2014). [Google Scholar]
  45. Luo K. H. Two-color narrowband photon pair source with high brightness based on clustering in a monolithic waveguide resonator. et al. arXiv. 1306.1756 (2013).
  46. Marsili F. et al. Detecting single infrared photons with 93% system efficiency. Nature Photon. 7, 210–214 (2013). [Google Scholar]
  47. Chen W. et al. Field Experiment on a Star Type Metropolitan Quantum Key Distribution Network. IEEE Photon. Tech. L. 21, 575–577 (2009). [Google Scholar]
  48. Dick K. A. et al. The morphology of axial and branched nanowire heterostructures. Nano Lett. 7, 1817–1822 (2007). [DOI] [PubMed] [Google Scholar]
  49. Qian F. et al. Multi-quantum-well nanowire heterostructures for wavelength-controlled lasers. Nat. Mater. 7, 701–706 (2008). [DOI] [PubMed] [Google Scholar]
  50. Yan X. et al. Formation Mechanism and Optical Properties of InAs Quantum Dots on the Surface of GaAs Nanowires. Nano Lett. 12, 1851–1856 (2012). [DOI] [PubMed] [Google Scholar]

Articles from Scientific Reports are provided here courtesy of Nature Publishing Group

RESOURCES