Forgotten topological index of chemical structure in drugs

Abstract

A massive of early drug tests implies that there exist strong inner relationships between the bio-medical and pharmacology characteristics of drugs and their molecular structures. The forgotten topological index was defined to be used in the analysis of drug molecular structures, which is quite helpful for pharmaceutical and medical scientists to grasp the biological and chemical characteristics of new drugs. Such tricks are popularly employed in developing countries where enough money is lacked to afford the relevant chemical reagents and equipment. In our article, by means of drug molecular structure analysis and edge dividing technology, we present the forgotten topological index of several widely used chemical structures which often appear in drug molecular graphs.

1. Introduction

With rapid development of medicine manufacture, a large number of new drugs have been developed each year. Hence, it demands a tremendous amount of work to determine the pharmacological, chemical and biological characteristics of these new drugs, and such workloads become more and more fussy and clustered. It requires enough reagents equipment and assistants to test the performances and the side effects of existing new drugs. Nevertheless, in lower income countries and areas (such as certain cities and countries in South America, Africa and Southeast Asia), there is no sufficient money to defray reagents and equipment which can be employed to measure the biochemical properties. Fortunately, many previous studies have pointed that chemical and pharmacodynamics characteristics of drugs and their molecular structures are closely linked. If we calculate indicators of these drug molecular structures in view of defining the topological indices, the medical and pharmaceutical scholars could find it useful to well know their medicinal properties, which can make up the defects of medicine and chemical experiments. From this standpoint, the methods on topological index computation are very suitable and serviceable for developing countries in which they can yield the available biological and medical information of new drugs without chemical experiment hardware.

In medicine mathematical model, the structure of drug is represented as an undirected graph, where each vertex indicates an atom and each edge represents a chemical bond between these atoms. Let G be a simple graph corresponding to a drug structure with atom (vertex) set $V(G)$ and chemical bond (edge) set $E(G)$. A topological index defined on molecule structure G can be considered as a real-valued function f: G → ${\mathbb{R}}^{+}$ which maps each drug molecular structure to certain real numbers. In the past 40 years, scientists have introduced several important indices, such as Wiener index, PI index, Zagreb index and eccentric index, to measure the characters of drug molecules. There were several reports contributing to determine these topological indices of special molecular graph in chemical, nanomaterials and pharmaceutical engineering (Yan et al., 2015, Gao et al., 2016a, Gao et al., 2016b, Gao and Farahani, 2016a, Gao and Farahani, 2016b, Gao and Shi, 2015, Gao and Wang, in press-a, Gao and Wang, in press-b, Gao and Wang, 2014, Gao and Wang, 2015). The notations and terminologies used but not clearly stated in our article can be referred in Bondy and Mutry (2008).

Followed by the first and second Zagreb indices, Furtula and Gutman (2015) introduced forgotten topological index (also called F-index) which was defined as

$$F(G)={\displaystyle \sum _{v\in V(G)}}d{(v)}^3={\displaystyle \sum _{\mathit{uv}\in E(G)}}(d{(u)}^2+d{(v)}^2)\text{,}$$

where $d(v)$ is denoted as the degree of vertex v (the number of vertex adjacent to vertex v). Furtula and Gutman (2015) raised that the predictive ability of forgotten topological index is almost similar to that of first Zagreb index and for the acentric factor and entropy, and both of them obtain correlation coefficients larger than 0.95. This fact implies the reason why forgotten topological index is useful for testing the chemical and pharmacological properties of drug molecular structures. Sun et al. (2014) deduced some basic nature of forgotten topological index and reported that this index can reinforce the physico-chemical flexibility of Zagreb indices. Very recently, Gao et al. (2016a) manifested the forgotten topological index of some significant drug molecular structures.

Although there have been several contributions on distance-based indices and degree-based molecular structures, the researches of forgotten topological index for certain special drug structures are still largely limited. Because of these, tremendous academic and industrial interest has been attracted to research the forgotten topological index of drug molecular structure from a mathematical point of view.

Let $\delta (G)$ and $\mathrm{\Delta }(G)$ be the minimum and maximum degree of G, respectively. The edge set E(G) can be divided into several partitions: for any i and j, $\delta (G)⩽$ i,j $⩽\mathrm{\Delta }(G)$, let $E_{\mathit{ij}}$ = {e = uv $\in$ E(G)| $d(v)$ = i, $d(u)$ = j} and $n_{\mathit{ij}}=|E_{\mathit{ij}}|$.

With continued work on Gao et al. (2016a), we get the forgotten topological index of several important chemical structures which have high frequency in drug structures.

2. Forgotten topological index of graphene $G(m\text{,}n)$

As a kind of two-dimensional material, graphene is a planar sheet of carbon atoms that is densely packed in a honeycomb crystal lattice, and it is the main element of certain carbon allotropes including charcoal, fullerenes and graphite, see Fig. 1.

Theorem 1

Let $G(m\text{,}n)$ be a graphene sheet with n rows and m columns. We obtain

$$F(G(m\text{,}n))=\left\{\begin{array}{cc}18\left(\lceil \frac{n}{2}\rceil (5m+1)+\lfloor \frac{n}{2}\rfloor (m+3)\right)-20m-20n-20\text{,}\hfill & n\equiv 1(\text{mod}2)\hfill \\ 18\left(\lceil \frac{n}{2}\rceil (5m+1)+\lfloor \frac{n}{2}\rfloor (m+3)\right)+16m-20n-38\text{,}\hfill & n\equiv 0(\text{mod}2)\hfill \end{array}.\right)$$

Proof

In terms of structure analysis, we get

$$|E(G(m\text{,}n))|=\left\{\begin{array}{cc}\lceil \frac{n}{2}\rceil (5m+1)+\lfloor \frac{n}{2}\rfloor (m+3)\text{,}\hfill & n\equiv 1(\text{mod}2)\hfill \\ \lceil \frac{n}{2}\rceil (5m+1)+\lfloor \frac{n}{2}\rfloor (m+3)+2m-1\text{,}\hfill & n\equiv 0(\text{mod}2)\hfill \end{array}.\right)$$

In view of further calculating, we have $n_{22}=n+4$, $n_{23}=4m+2n-4$, and $n_{33}=|E(G(m\text{,}n))|-4m-3n$. Therefore, using the definition of forgotten topological index, we obtain

$$\begin{array}{c}F(G(m\text{,}n))={\displaystyle \sum _{\mathit{uv}\in E(G(m\text{,}n))}}(d{(u)}^2+d{(v)}^2)\hfill \\ ={\displaystyle \sum _{\mathit{uv}\in E_{22}}}(2^2+2^2)+{\displaystyle \sum _{\mathit{uv}\in E_{23}}}(2^2+3^2)+{\displaystyle \sum _{\mathit{uv}\in E_{33}}}(3^2+3^2)\hfill \\ =8(n+4)+13(4m+2n-4)+18(|E(G(m\text{,}n))|-4m-3n)\hfill \\ =\left\{\begin{array}{cc}18\left(\lceil \frac{n}{2}\rceil (5m+1)+\lfloor \frac{n}{2}\rfloor (m+3)\right)-20m-20n-20\text{,}\hfill & n\equiv 1(\text{mod}2)\hfill \\ 18\left(\lceil \frac{n}{2}\rceil (5m+1)+\lfloor \frac{n}{2}\rfloor (m+3)\right)+16m-20n-38\text{,}\hfill & n\equiv 0(\text{mod}2)\hfill \end{array}\right)\hfill \end{array}$$

Hence, we obtain the expected result. □

Figure 1.

2-Dimensional graph of graphene sheet.

3. Forgotten topological index of three family of dendrimer stars

In this section, we determine three famous infinite classes ${\mathit{NS}}_1[n]$, ${\mathit{NS}}_3[n]$ and of dendrimer stars which widely appear in the drug structures.

Theorem 2

Let n be the number of steps of growth in this type of dendrimer stars. We infer

$$\begin{array}{cc}\hfill & F({\mathit{NS}}_1[n])=306·2^n-47\text{,}\hfill \\ \hfill & F({\mathit{NS}}_2[n])=408·2^n-70\text{,}\hfill \\ \hfill & F({\mathit{NS}}_3[n])=668·2^n-134\text{.}\hfill \end{array}$$

Proof

By observing the structures of these three dendrimer stars, we deduce its edge dividing as follows:

$$\begin{array}{cc}\hfill & •\text{for}{\mathit{NS}}_1[n]:n_{23}=18·2^n-12\text{,}{n}_{22}=9·2^n+3\text{,}{n}_{13}=1\text{and}{n}_{34}=3\text{;}\hfill \\ \hfill & •\text{for}{\mathit{NS}}_2[n]:n_{23}=24·2^n-8\text{,}{n}_{22}=12·2^n+2\text{and}{n}_{33}=1\text{;}\hfill \\ \hfill & •\text{for}{\mathit{NS}}_3[n]:n_{23}=28·2^n-6\text{,}{n}_{22}=22·2^n-7\text{,}{n}_{33}=6·2^n\text{and}{n}_{13}=2^{n+1}\text{.}\hfill \end{array}$$

Therefore, according to the definition of forgotten topological index, we check

$$\begin{array}{c}F({\mathit{NS}}_1[n])={\displaystyle \sum _{\mathit{uv}\in E({\mathit{NS}}_1[n])}}(d{(u)}^2+d{(v)}^2)\hfill \\ ={\displaystyle \sum _{\mathit{uv}\in E_{22}}}(2^2+2^2)+{\displaystyle \sum _{\mathit{uv}\in E_{23}}}(2^2+3^2)+{\displaystyle \sum _{\mathit{uv}\in E_{13}}}(1^2+3^2)+{\displaystyle \sum _{\mathit{uv}\in E_{34}}}(4^2+3^2)\hfill \\ =8(9·2^n+3)+13(18·2^n-12)+10+25·3\hfill \\ =306·2^n-47\text{.}\hfill \end{array}$$

$$\begin{array}{c}F({\mathit{NS}}_2[n])={\displaystyle \sum _{\mathit{uv}\in E({\mathit{NS}}_2[n])}}(d{(u)}^2+d{(v)}^2)\hfill \\ ={\displaystyle \sum _{\mathit{uv}\in E_{22}}}(2^2+2^2)+{\displaystyle \sum _{\mathit{uv}\in E_{23}}}(2^2+3^2)+{\displaystyle \sum _{\mathit{uv}\in E_{33}}}(3^2+3^2)\hfill \\ =8(12·2^n+2)+13(24·2^n-8)+18\hfill \\ =408·2^n-70\text{.}\hfill \end{array}$$

$$\begin{array}{c}F({\mathit{NS}}_3[n])={\displaystyle \sum _{\mathit{uv}\in E({\mathit{NS}}_3[n])}}(d{(u)}^2+d{(v)}^2)\hfill \\ ={\displaystyle \sum _{\mathit{uv}\in E_{22}}}(2^2+2^2)+{\displaystyle \sum _{\mathit{uv}\in E_{23}}}(2^2+3^2)+{\displaystyle \sum _{\mathit{uv}\in E_{13}}}(1^2+3^2)+{\displaystyle \sum _{\mathit{uv}\in E_{33}}}(3^2+3^2)\hfill \\ =8(22·2^n-7)+13(28·2^n-6)+20·2^n+108·2^n\hfill \\ =668·2^n-134\text{.}\hfill \end{array}$$

Thus, the expected result is obtained. □

4. Forgotten topological index of polyomino chains of n-cycles and triangular benzenoid

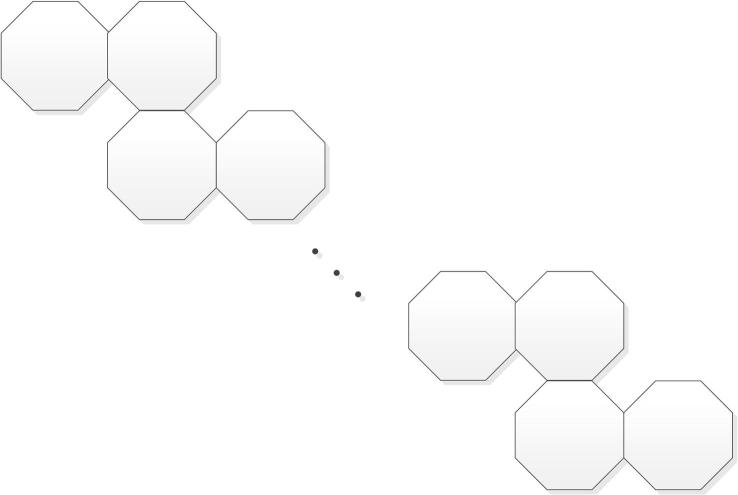
From a mathematical point of view, polyomino system is a finite 2-connected plane graph in which each interior face (i.e. cell) is surrounded by a $C_4$. It is an edge-connected union of cells, and more details can be found in Klarner and Polyominoes (1997) and Ghorbani and Ghazi (2010). As an example, the polyomino chains of 8-cycles can be shown in Fig. 2.

Theorem 3

Let $G$ be a molecular graph described above. We have

$$F(G)=344n-22\text{.}$$

Proof

By means of structure analysis, we infer $n_{22}=12n+4\text{,}{n}_{23}=8n$, and $n_{33}=8n-3$. Therefore, using the definition of forgotten topological index, we obtain

$$\begin{array}{c}F(G)={\displaystyle \sum _{\mathit{uv}\in E(G)}}(d{(u)}^2+d{(v)}^2)\hfill \\ ={\displaystyle \sum _{\mathit{uv}\in E_{22}}}(2^2+2^2)+{\displaystyle \sum _{\mathit{uv}\in E_{23}}}(2^2+3^2)+{\displaystyle \sum _{\mathit{uv}\in E_{33}}}(3^2+3^2)\hfill \\ =8(12n+4)+13·8n+18(8n-3)\hfill \\ =344n-22\text{.}\hfill \end{array}$$

Hence, we obtain the expected result. □

Figure 2.

The zig-zag chain of 8-cycles.

Next, we compute forgotten topological index of triangular benzenoid molecular graph $T(n)$. Its structure can be referred to Fig. 3.

Theorem 4

Let $T(n)$ be a triangular benzenoid. We deduce

$$F(T(n))=\frac{39}{2}{n}^2+\frac{177}{2}n-60\text{.}$$

Proof

Using the edge dividing technology, we derive $n_{22}=6\text{,}{n}_{23}=\frac{3n(n-1)}{2}$, and $n_{33}=6(n-1)$. Hence, by means of the definition of forgotten topological index, we get

$$\begin{array}{c}F(T(n))={\displaystyle \sum _{\mathit{uv}\in E(T(n))}}(d{(u)}^2+d{(v)}^2)\hfill \\ ={\displaystyle \sum _{\mathit{uv}\in E_{22}}}(2^2+2^2)+{\displaystyle \sum _{\mathit{uv}\in E_{23}}}(2^2+3^2)+{\displaystyle \sum _{\mathit{uv}\in E_{33}}}(3^2+3^2)\hfill \\ =48+13·\frac{3n(n-1)}{2}+18(6n-6)\hfill \\ =\frac{39}{2}{n}^2+\frac{177}{2}n-60.\square \hfill \end{array}$$

Figure 3.

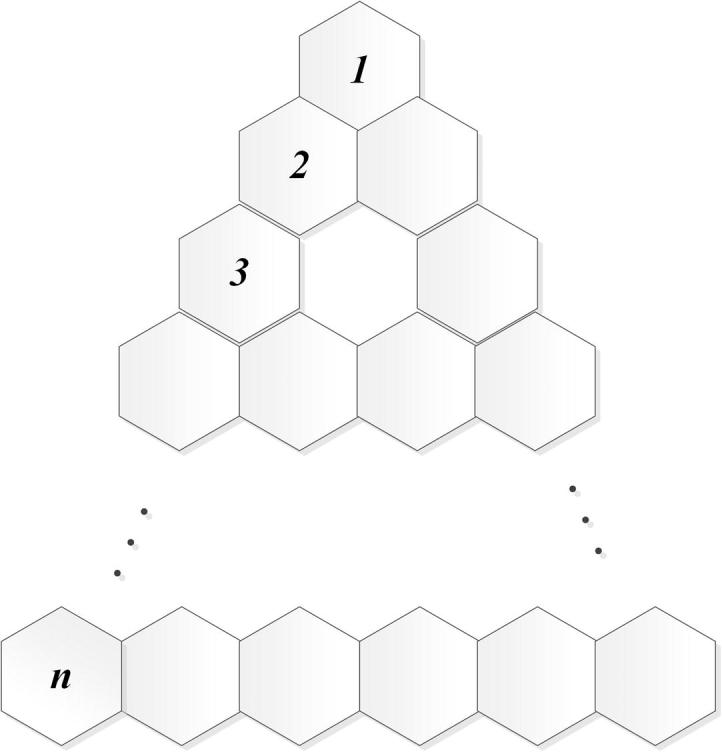
Molecular graph of triangular benzenoid.

5. Forgotten topological index of bridge molecular structures

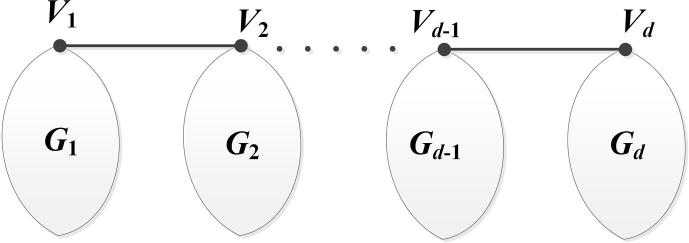
Let ${\{G_i\}}_{i=1}^d$ be a set of finite pairwise disjoint molecular graphs with $v_i\in V(G_i)$. The bridge molecular graph $B(G_1\text{,}\dots \text{,}{G}_d)=B(G_1\text{,}\dots \text{,}{G}_d\text{;}{v}_1\text{,}\dots \text{,}{v}_d)$ of ${\{G_i\}}_{i=1}^d$ with respect to the vertices ${\{v_i\}}_{i=1}^d$ is yielded from the molecular graphs $G_1\text{,}\dots \text{,}{G}_d$ in which the vertices $v_i$ and $v_{i+1}$ are connected by an edge for $i=1\text{,}2\text{,}\dots \text{,}d-1$. The main result of this section is determining the formulas of some degree based indices for the infinite family of drug structures of bridge molecular graph with $G_1\text{,}\dots \text{,}{G}_d$ (see Fig. 4). We set $G_d(H\text{,}v)=B(H\text{,}\dots \text{,}H\text{,}v\text{,}\dots \text{,}v)$ for special situations of bridge molecular graphs.

Figure 4.

The bridge molecular graph.

In the following context of this section, we discuss the bridge graphs in which the main parts of graphs are path, cycle and complete molecular graph, respectively.

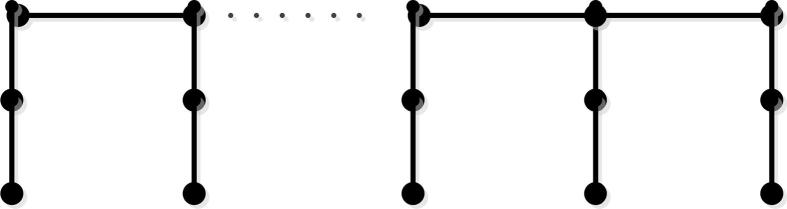
• •Let $P_n$ be the path with n vertices. We have $\mathit{dn}$ vertices and $\mathit{dn}-1$ edges for bridge molecular graph $G_d(P_n\text{,}v)$ (see Fig. 5 for more details). Additionally, the edge set of bridge graph $G_d(P_n\text{,}v)$ can be divided into four partitions: $n_{22}=d(n-3)+2\text{,}{n}_{23}=n_{12}=d$, and $n_{33}=d-3$.
• •Let $C_n$ be the cycle with n vertices. We have $\mathit{dn}$ vertices and $\mathit{dn}+d-1$ edges for bridge molecular graph $G_d(C_n\text{,}v)$ (see Fig. 6 for more details). Additionally, the edge set of bridge molecular graph $G_d(C_n\text{,}v)$ can be divided into five partitions: $n_{22}=d(n-2)\text{,}{n}_{23}=4\text{,}{n}_{24}=2d-4\text{,}{n}_{34}=2$ and $n_{44}=d-3$.
• •Let $K_n$ be compete molecular graph with n vertices. We have $\mathit{dn}$ vertices and $\frac{\mathit{dn}(n-1)}{2}+d-1$ edges for bridge molecular graph $G_d(K_n\text{,}v)$ (see Fig. 7, $G_d(K_3\text{,}v)$ as an example). Additionally, the edge set of bridge molecular graph $G_d(K_n\text{,}v)$ can be divided into five partitions: $n_{55}=n_{5(n-1)}=d-2\text{,}{n}_{45}=n_{4(n-1)}=2$ and $n_{(n-1)(n-1)}=\frac{d(n-1)(n-2)}{3}$.

Figure 5.

The bridge molecular graph $G_d(P_n\text{,}v)$.

Figure 6.

The bridge molecular graph $G_d(C_n\text{,}v)$.

Figure 7.

The bridge molecular graph $G_d(K_3\text{,}v)$.

Using the definition of forgotten topological index, we get the main result in this section which is stated as follows. We skip the detail proof here.

Theorem 5

$$F(G_d(P_n\text{,}v))=8\mathit{dn}+12d-38\text{,}$$

$$F(G_d(C_n\text{,}v))=8\mathit{dn}+56d-74\text{,}$$

$$F(G_d(K_n\text{,}v))=(6n^2-12n+312)+d(n^2-2n+76)+\frac{2d{(n-1)}^3(n-2)}{3}\text{.}$$

6. Forgotten topological index of carbon tube networks

In this section, we focus on the $m\times n$ quadrilateral section $P_m^n$ with $m⩾2$ hexagons on the top and bottom sides and $n⩾2$ hexagons on the lateral sides cut from the regular hexagonal lattice L, see Fig. 8 for its detailed chemical structure.

Figure 8.

Quadrilateral section $P_m^n$ cuts from the regular hexagonal lattice.

The tube ${\mathit{NA}}_m^n$ with $2m(n+1)$ vertices and $(3n+2)m$ edges is obtained by identifying two lateral sides of $P_m^n$ via identifying the vertices $u_0^j$ and $u_m^j$ $(j=0\text{,}1\text{,}\dots \text{,}n$).

Let $n\in \mathbb{N}$ be even so that $n\text{,}m⩾2$. The tube ${\mathit{NC}}_m^n$ of order $n(2m+1)$ with size $n(3m+\frac{1}{2})$ can be yielded by identifying the top and bottom sides of the quadrilateral section $P_m^n$ in a similar way in which the vertices $u_i^0$ and $u_i^n$ for $i=0\text{,}1\text{,}\dots \text{,}m$ and vertices $v_i^0$ and $v_i^n$ for $i=0\text{,}1\text{,}\dots \text{,}m$ are identified. See Baca et al. (2015) for more details.

Theorem 6

$$F\left({\mathit{NA}}_m^n\right)=54\mathit{mn}-16m\text{,}$$

$$F\left({\mathit{NC}}_m^n\right)=54\mathit{mn}-11n\text{.}$$

Proof

For tube ${\mathit{NA}}_m^n$, we derive $n_{23}=4m$, and $n_{33}=m(3n-2)$. Hence, by means of the definition of forgotten topological index, we get

$$\begin{array}{c}F({\mathit{NA}}_m^n)={\displaystyle \sum _{\mathit{uv}\in E({\mathit{NA}}_m^n)}}(d{(u)}^2+d{(v)}^2)\hfill \\ ={\displaystyle \sum _{\mathit{uv}\in E_{23}}}(2^2+3^2)+{\displaystyle \sum _{\mathit{uv}\in E_{33}}}(3^2+3^2)\hfill \\ =13·4m+18m(3n-2)=54\mathit{mn}-16m\text{.}\hfill \end{array}$$

For tube ${\mathit{NC}}_m^n$, we derive $n_{22}=n\text{,}{n}_{23}=2n$, and $n_{33}=n(3m-\frac{5}{2})$. Hence, by means of the definition of forgotten topological index, we get

$$\begin{array}{c}F({\mathit{NC}}_m^n)={\displaystyle \sum _{\mathit{uv}\in E({\mathit{NC}}_m^n)}}(d{(u)}^2+d{(v)}^2)\hfill \\ ={\displaystyle \sum _{\mathit{uv}\in E_{22}}}(2^2+2^2)+{\displaystyle \sum _{\mathit{uv}\in E_{23}}}(2^2+3^2)+{\displaystyle \sum _{\mathit{uv}\in E_{33}}}(3^2+3^2)\hfill \\ =8n+26n+18n\left(3m-\frac{5}{2}\right)\hfill \\ =54\mathit{mn}-11n.\square \hfill \end{array}$$

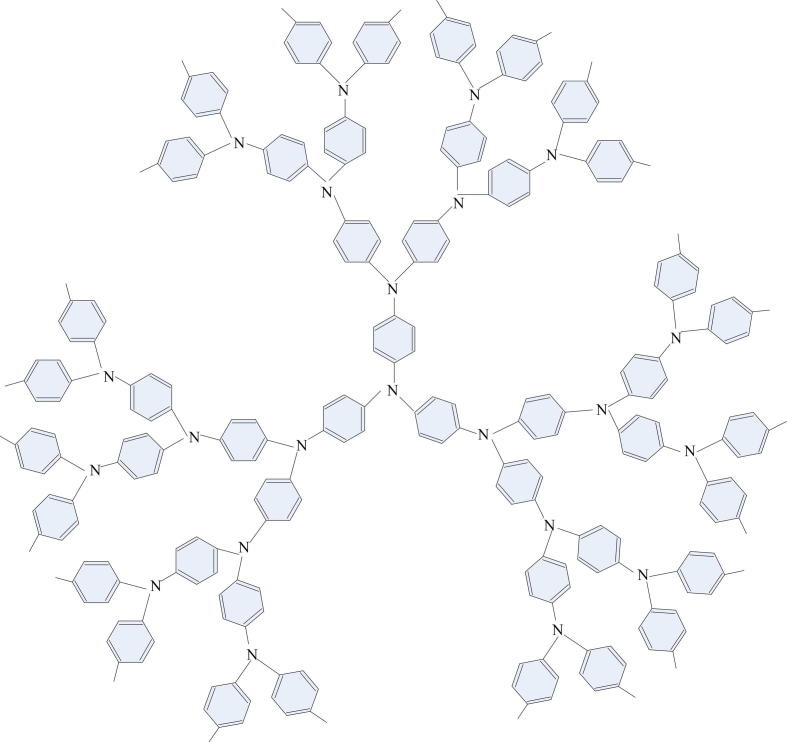
7. Forgotten topological index of dendrimer stars $D_3[n]$

In this section, we discuss an important chemical structure $D_3[n]$ which denotes the n-th growth of star dendrimer for $\forall n\in \mathbb{N}\cup \{\mathbb{0}\}$. See Fig. 9 for more details on the structure of this chemical molecular graph which widely appear in drug structures.

Figure 9.

The 2-Dimensional of the n-th growth of star dendrimer $D_3[n]$.

According to the analysis in Farahani (2013), we know that $E(D_3[n])$ can be divided into four parts: $n_{13}=3·2^n\text{,}=6(2^{n+1}-1)\text{,}{n}_{23}=12(2^{n+1}-1)$, and $n_{33}=9·2^n-6$. Hence, we directly get the following conclusion for these molecular structures.

Theorem 7

$$F(D_3[n])=600·2^n-312\text{.}$$

8. Forgotten topological index of two classes of benzenoid series

Finally, we aim to determine the forgotten topological index of two classes of benzenoid series.

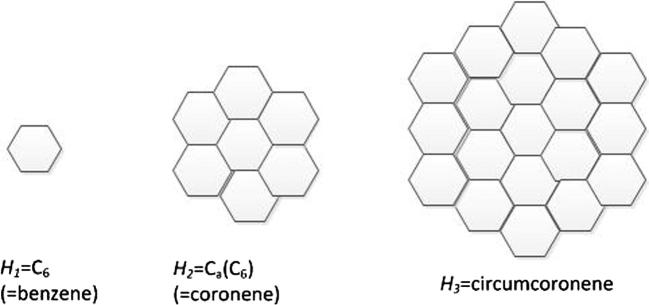
First, we consider circumcoronene series of benzenoid $H_k$. When k = 1, 2, 3, the structures are presented in Fig. 10.

Figure 10.

The first, second and third molecular graphs $H_1$, $H_2$ and $H_3$ from the circumcoronene series of benzenoid.

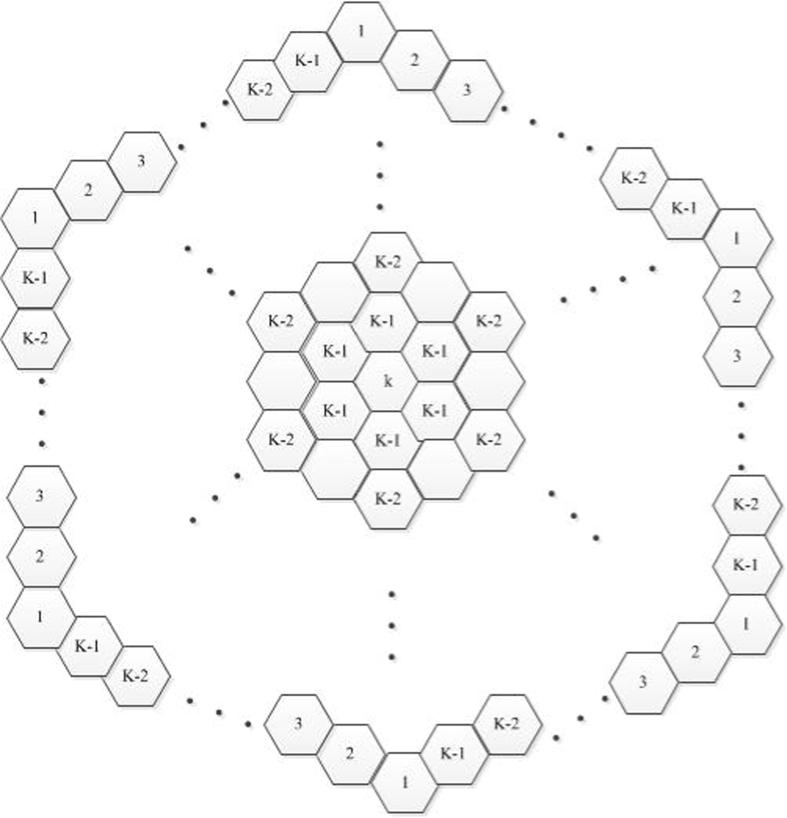
Thus, this family of circumcoronene homologous series of benzenoid is consisted of several copies of benzene $C_6$ on circumference, and the more details for this structure can be referred to Fig. 11.

Theorem 8

$$F(H_k)=162k^2-114k\text{.}$$

Proof

Consider circumcoronene series of benzenoid $H_k$ for $k⩾1$. It is not hard to check $\mathit{that}|V(H_k)|=6k^2$ and $|E(H_k)|=9k^2-3k$. Moreover, we deduce $n_{33}=9k^2-15k+6$, $n_{23}=12(k-1)$, and $n_{22}=6$. Thus, using the definition of forgotten topological index, we infer

$$\begin{array}{c}F(H_k)={\displaystyle \sum _{\mathit{uv}\in E(H_k)}}(d{(u)}^2+d{(v)}^2)\hfill \\ ={\displaystyle \sum _{\mathit{uv}\in E_{22}}}(2^2+2^2)+{\displaystyle \sum _{\mathit{uv}\in E_{23}}}(2^2+3^2)+{\displaystyle \sum _{\mathit{uv}\in E_{33}}}(3^2+3^2)\hfill \\ =48+156(k-1)+18(9k^2-15k+6)\hfill \\ =162k^2-114k.\square \hfill \end{array}$$

Figure 11.

The circumcoronene series of benzenoid $H_k$ for $k⩾1$.

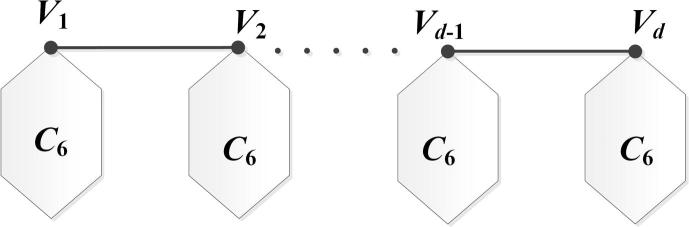
Next, we consider capra-designed planar benzenoid series (the structure can be referred to Farahani and Vlad (2013) for more details). By means of intermediate results presented in Farahani and Vlad (2013), we present the forgotten topological index of ${\mathit{Ca}}_k(C_6)$ which is stated as follows:

Theorem 9

$$F({\mathit{Ca}}_k(C_6))=54·7^k+24·3^k-30\text{.}$$

Proof

By analyzing the molecular structure of ${\mathit{Ca}}_k(C_6)$, we check that the edge set of ${\mathit{Ca}}_k(C_6)$ can be divided into three partitions: $n_{22}=3^k+3\text{,}{n}_{23}=4·3^k$, and $n_{33}=3·7^k-2·3^k-3$. Thus, using the definition of forgotten topological index, we infer

$$\begin{array}{c}F({\mathit{Ca}}_k(C_6))={\displaystyle \sum _{\mathit{uv}\in E({\mathit{Ca}}_k(C_6))}}(d{(u)}^2+d{(v)}^2)\hfill \\ ={\displaystyle \sum _{\mathit{uv}\in E_{22}}}(2^2+2^2)+{\displaystyle \sum _{\mathit{uv}\in E_{23}}}(2^2+3^2)+{\displaystyle \sum _{\mathit{uv}\in E_{33}}}(3^2+3^2)\hfill \\ =8(3^k+3)+52·3^k+18(3·7^k-2·3^k-3)\hfill \\ =54·7^k+24·3^k-30.\square \hfill \end{array}$$

9. Conclusion

Due to the contentiously evolving viruses, a great deal of new diseases can be discovered each year. This requires us to develop more new drugs to treat new diseases. Forgotten topological index was introduced to measure the medicinal properties of new drugs which is largely popular in developing areas. In our article, in terms of drug structure analysis and edge dividing trick, we determine the forgotten topological index of certain molecular graphs which widely appear in drug structures. The conclusions achieved in our paper illustrate the promising prospects of the application for pharmacy engineering.