Extruding Loops to Make Loopy Globules?

Main Text

Each human cell contains over two meters worth of DNA, and this DNA is not only packed in the nucleus, but also organized in three dimensions (3D) as an addressable memory. Furthermore, it is becoming clear that 3D organization is actively used in biological world to realize and control a variety of functions and feedback loops. The advent of chromosome conformation capture, 3C, and subsequent family of 4C, 5C, and Hi-C methods, mostly due to Dekker and coworkers (1, 2), revolutionized the field. While modern superresolution microscopy is also very informative (see a recent neat example in Kirmes et al. (3)), the C-methods provide information not only about spatial contacts between pairs of genetic loci, but also simultaneously their genetic coordinates along the chromatin fiber—the type of information a polymer physicist could only dream of. With such data in hand, it is not surprising, then, that the genome literature became suddenly littered with the language of polymer physics: folding, contact maps, equilibrium and nonequilibrium globules, scaling exponents, etc. Initially, there was an obvious excitement about the fact that Hi-C contact maps pretty convincingly ruled out the equilibrium globule structure and instead pointed to the viability of the crumpled globule model (which on this occasion was renamed “fractal”). But several questions and controversies sprang up very soon thereafter. The article by Goloborodko and colleagues (4), in this issue of the Biophysical Journal, along with closely related studies (5, 6, 7) promise to shed a new light on this closely knit coil of controversies. In the simplest form (see cartoon in Fig. 1), the model postulates the existence of a certain active free-energy-consuming protein system that can simultaneously capture two neighboring sites on the same chromatin fiber, and then walk in two opposite directions along the fiber, thus extruding a loop of gradually increasing size. By construction, this loop is not concatenated with other loops, but the loops can be nested, larger loops tend to be replaced by smaller ones, and rich dynamics arises with the possibility of a nontrivial steady state. Why is this so exciting?

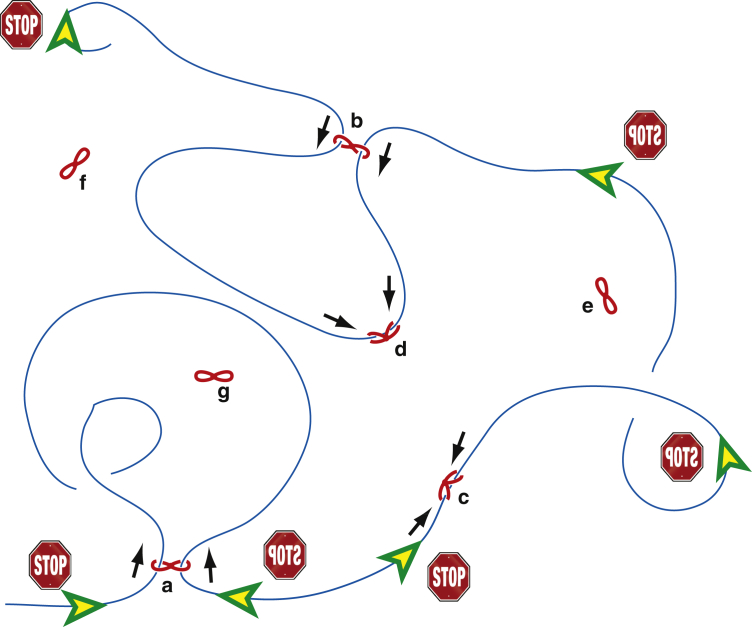
Figure 1.

Cartoon representation of the loop extrusion model. Extruders (a) and (b) have already produced large loops; (c) and (d) are only starting. Extruders (e–g) are presently disconnected from the fiber; they diffuse around, and will initiate new loops once they absorb somewhere on the fiber. Extruder (a) is already approaching the (mirror symmetric) stop signs, while (b) and (d) have a long way to go. (Black arrows) Directions in which fiber is pushed by every extruder. Two large loops are shown to collide in three dimensions. To see this figure in color, go online.

First, equilibrium and crumpled/fractal globules are all models of a homopolymer, while most of the observed contact maps have a distinct checkerboard appearance, suggesting some sort of microsegregation elements, called topologically associated domains (where the word “topology” is abused, apparently without any relation to the branch of mathematics). This domain structure hints on the connections with heteropolymer (same as copolymer) globules, inviting us to view genome folding as a close relative of protein folding, on a gigantic scale. While protein folding is controlled by a set of simple molecular interactions (hydrophobic, electrostatic, etc.), in the case of a genome, the volume interactions between various pieces of chromatin fiber are mediated by a variety of chromatin-related proteins some of which may bind more or less specifically to certain sequence motifs. An important hint in this direction came from a high resolution Hi-C study (8), where ∼10⁴ pair contacts were identified as loop anchors, and their sequence motifs were found to be antiparallel, oriented along the genome such as to face one another. Now, in hindsight, these motifs are beautifully interpreted as natural stop signs for the loop extruding proteins (5, 6).

Second, it turned out that the very concept of crumpled/fractal globule is more intricate than was realized before. While polymer systems with simple topology (where the word “topology” is used in explicit reference to the proper branch of mathematics), such as a concentrated solution of long unconcatenated loops, do exhibit peculiar fractal and physical properties, their details are sensitive to the specific features of the polymers in question (9, 10). Furthermore, these systems tend to exhibit a very wide crossover, so that their asymptotic scaling may not be sufficient to understand real experiments. For instance, contact probability P(s) as a function of genomic distance s, with its scaling exponent γ (defined such that P(s) ∼ s^−γ), exhibits γ slightly larger than 1 at s ≳1000 kbp, which is indicative of a crumpled/fractal globule; but at smaller s (say 50 kbp ≲ 500 kbp), the local slope of double logarithmic plot P(s) is significantly more shallow, γ ≈ 0.75. The fact that γ depends on scale tells us, of course, that the system is not a mathematical fractal, boringly similar to itself on all scales; as with every interesting fractal in the real world, it is self-similar over a limited range of scales. Furthermore, γ < 1 cannot be a property of any true fractal embedded in real 3D space (because ${\int }_1^{\infty }P\left(s\right)ds$ is the total number of contacts for one locus, which must be finite). Therefore, the observation of γ ≈ 0.75 hints at some peculiar cross-over behavior over the range of length scales s. What could it be? A simple mean field argument relates γ to a more common index ν, which describes the root-mean-squared gyration radius of a subchain of length s, 〈r²(s)〉 ∼s^2ν, namely, γ = 3ν (because the second end of an s-long loop is roughly uniformly distributed in a sphere of radius r(s) around first end). This argument then implies ν ≈ 0.25—which is very suggestive: 1/4 is the size exponent of a randomly branched polymer without excluded volume. For any real system, the ν = 1/4 scaling can exist only over a limited range of s, and this is indeed observed in a variety of models with unconcatenated loops. It is thus not surprising—again, in hindsight—that the loop extrusion model does exhibit the right γ ≈ 0.75 over a limited range of s. This also raises an intriguing parallel with the physics of RNA, where secondary structures force molecules to behave like a branched polymer, which exhibits territories and contact statistics reminiscent of chromatin (11).

Third, an equilibrium globule is in equilibrium, while a crumpled/fractal globule is either a long-lived pseudo-equilibrium object, or may be made into a state of equilibrium by replacing slow relaxation with (artificial, but permanent) topological constraints of closed loops. These states correspond to a minimum—global or local—of a free energy (or another appropriate thermodynamic potential). This is in an obvious contradiction to the fact that chromatin dynamics is definitely an actively driven process (12) that violates the fluctuation-dissipation theorem, with all the familiar far-reaching consequences. Active processes in the nucleus are hypothesized to be behind the microphase segregation between eu- and hetero-chromatin (13). Thus, it is only fitting that loop extrusion is an active, free-energy-consuming process. Because loop extruders not only engage chromatin fiber, but can also fall off (with an appropriate rate), some steady state arises (4)—which is time-independent (on average), but not equilibrium; that means it does not correspond to any minimum of any thermodynamic potential. In this sense, it is surprisingly similar to, for instance, self-organized phase segregation of such active systems as suspensions of bacterial swimmers (14). One can hardly overemphasize the difference of this view from the idea of static chromatin loops stabilized by a passive protein cross linker. Nicely, different theoretical regimes (“sparse” and “dense” in the language of Goloborodko et al. (4)) seem to be appropriate for interphase and metaphase.

Fourth, it was always puzzling how chromosome territories can be reconciled with the fact that each chromosome interacts with 10 or more others. The natural assumption is that boundaries between territories are very wiggly, with a high fractal dimension d (which corresponds to significant protrusions from other chromosomes into the body of any given one). While the direct test of this hypothesis will have to wait for superresolution microscopy (3), we can at least start to make the assumption quantitative. To this end, there is a relation between scaling exponents γ and β = d/3, namely, β + γ = 2 (see Halverson et al. (9) for derivation and explanation and Sanborn et al. (6) for a more formal treatment): the range of scales with γ < 1 leads therefore to β > 1, which means that the “surfaces” between domains may possess a fractal dimension >3!

Thus, one loop extrusion model untangles several puzzles in one stroke. Of course, it leaves some open questions. First, and foremost, when loops get extruded, they generate together an osmotic pressure that counteracts further extrusion. This may slow down the extrusion and make the process more intricate. This effect is probably present in the advanced simulations (see, e.g., Sanborn et al. (6) and Goloborodko et al. (7)). In some way, this suggests that the resulting structure may be not too dissimilar from the recently proposed “loopy globule” (10).

It looks like many strings of this exciting problem are starting to come together.

Editor: Michele Vendruscolo.