Knowledge-Based Methods To Train and Optimize Virtual Screening Ensembles

Abstract

Ensemble docking can be a successful virtual screening technique that addresses the innate conformational heterogeneity of macromolecular drug targets. Yet, lacking a method to identify a subset of conformational states that effectively segregates active and inactive small molecules, ensemble docking may result in the recommendation of a large number of false positives. Here, three knowledge-based methods that construct structural ensembles for virtual screening are presented. Each method selects ensembles by optimizing an objective function calculated using the receiver operating characteristic (ROC) curve: either the area under the ROC curve (AUC) or a ROC enrichment factor (EF). As the number of receptor conformations, N, becomes large, the methods differ in their asymptotic scaling. Given a set of small molecules with known activities and a collection of target conformations, the most resource intense method is guaranteed to find the optimal ensemble but scales as O(2^N). A recursive approximation to the optimal solution scales as O(N²), and a more severe approximation leads to a faster method that scales linearly, O(N). The techniques are generally applicable to any system, and we demonstrate their effectiveness on the androgen nuclear hormone receptor (AR), cyclin-dependent kinase 2 (CDK2), and the peroxisome proliferator-activated receptor δ (PPAR-δ) drug targets. Conformations that consisted of a crystal structure and molecular dynamics simulation cluster centroids were used to form AR and CDK2 ensembles. Multiple available crystal structures were used to form PPAR-δ ensembles. For each target, we show that the three methods perform similarly to one another on both the training and test sets.

Introduction

Virtual screening (VS) is a valuable hit discovery tool with tremendous potential to improve the efficiency and reduce the costs of modern high throughput screens (HTS). Despite the increasing trend toward miniaturization and greater well plate density, reagents and other consumables drive up HTS costs, particularly when large corporate or commercial databases are screened.¹ Rationally prioritizing compounds for experimental testing can reduce costs. For example, during a virtual high throughput screen, a computational model is developed and applied to rank compounds for testing.^2,3 When paired with high quality compound libraries, carefully constructed computational models can generate hit rates many fold above random.^4,5 This can result in novel, structurally diverse actives from which several lead series can be selected. Structural diversity ultimately helps circumvent ADME-Tox and patent liabilities that can increase lead optimization costs.^6,7

Computational virtual screening models primarily fall into two classes, ligand-based⁸ and structure based, or docking methods.⁹ Ligand-based methods predict the activity of novel compounds by assessing their similarity to known actives. Docking methods, on the other hand, use predicted interactions between a small molecule and a target receptor to predict activity. Numerous benchmarking studies have reported that ligand-based methods yield greater hit rates than structure-based methods.^5,10,11 However, a reliance on chemical similarity may limit their ability to identify novel chemical matter. In contrast, the diversity of actives determined using docking methods is only constrained by the shape of the receptor-binding pocket. In principal, docking can enable the discovery of actives more novel and diverse than ligand-based methods. Consistently, numerous successful examples of docking in early stage discovery can be found in the literature.¹²⁻¹⁴

Despite these successes, docking has traditionally been to a single static representation of the target. This static view is far from reality. In solution, a drug target is highly dynamic, and two notable models have been advanced that suggest a tight coupling between protein motion and small molecule binding. In 1958, Koshland proposed the induced fit model, which suggests that ligand binding induces a conformational change of the protein that enhances its affinity for the ligand.¹⁵ Conformational selection is a more recent explanation of small molecule binding that incorporates energy landscape theory.¹⁶ It proposes that binding stabilizes one of many preexisting conformers of the unbound target.^17,18 Both models imply that the collection of low-energy receptor conformers defining the bound state depend upon ligand identity; by extension, successful docking requires the receptor to be in, or at least near, the appropriate ligand-dependent bound state. Ensemble docking, in which each ligand is docked to a set of receptor conformers, was introduced in an effort to address this requirement.¹⁹

There are a variety of means to generate structures for ensemble docking, including crystallography²⁰ and NMR²¹ techniques. However, while experimental methods have shown promise, the materials, time, and expertise required to determine multiple, high quality structures is a significant bottleneck. In contrast, molecular dynamics (MD) simulations offer a relatively inexpensive alternative to generate diverse, realistic conformational states. This is largely the result of the recent implementation of MD codes on commodity graphical processor units (GPUs)^22,23 and the dramatic speedup of simulation benchmarks.

Regardless of whether structures are generated by experiment or simulation, for ensemble docking to be successful, a subset of conformations likely to offer the best VS performance must be identified. Though several studies have provided hints,²⁴⁻²⁶ others have been unable to determine a meaningful relationship between observable receptor characteristics and virtual screening performance.^27,28 Even with insights from a growing body of careful studies, it remains difficult or impossible to know a priori which receptor conformations will result in an ensemble with virtual screening utility.

The difficulties of selecting effective virtual screening conformations are compounded by the combinatorial nature of the ensemble selection process. When the number of receptor conformations is large, the problem results in a significant number of possibilities, and it can be difficult or impossible to know which of these ensembles will produce the best virtual screening performance.

Though systematic training and data-fusion methods exist that address similar issues in ligand-based VS, there is a relative paucity of knowledge-based structural selection methods. Despite this, other knowledge-based ensemble selection methods have been described in the literature. For example, Yoon and Welsh²⁹ proposed an ensemble docking method in which ensemble members are selected to maximize the correlation between the experimental and predicted binding affinities. The combinatorial problem was addressed by assigning each compound an ensemble score that consisted of a linear combination of score weights to each receptor conformation using a Monte Carlo scheme. Using estrogen receptor α, they demonstrated that the approach leads to more accurate classification than docking to the crystal structure alone.

While Yoon’s and Welsh’s method can produce stronger correlation with experimental binding affinities and result in enhanced VS performance, experimental binding measurements are required. This precludes the use of single-point HTS data and limits the method to compounds whose binding affinities have been measured or to those with dose–response curves, from which binding affinities may be inferred.

Rather than optimizing the correlation with experimental binding affinities, selecting ensembles to maximize the value of a binary classification metric offers greater flexibility. Since binary classification is categorical, once an appropriate activity threshold has been determined, any assay that delivers an activity measurement can be used. This opens the door to the use of single-point data, which is less expensive to determine and typically can be found in greater abundance than careful binding affinity measurements.

For example, following a slightly different approach, Xu and Lill developed a knowledge-based ensemble selection technique that can be used with any type of affinity measurement.³⁰ In it, receptor conformers are first ranked by their ability to separate the average docking scores of active and inactive compounds. Then, by assuming that effective ensembles must be constructed from effective conformations, ensembles of successively larger size are formed by aggregating conformers from highest to lowest rank. While the assumption avoids the combinatorial problem, its severity went unexamined. For example, does the procedure ignore ensembles with significantly greater classification power? While the underlying assumption went unexamined, the approach appeared promising. When classification ability was examined as a function of ensemble size, the performances of the trained ensembles were comparable or better than the those of ensembles selected by aggregating structurally diverse receptor conforms.

A final approach, developed and widely applied by the Cavasotto and Abagyan groups, utilizes virtual screening performance on a small training set to select the most promising structure from an ensemble generated using either Monte Carlo side-chain sampling or normal-mode analysis.³¹ By including a ligand with the desired properties, for example, a high affinity binder or a receptor agonist/antagonist, the search may be biased toward structures that enrich ligands with similar properties. During model generation, the VS ability of each target conformer is evaluated, and conformational sampling continues until VS performance converges. Following convergence, a single best performing structure can be derived and used for cross docking, selectivity studies, or VS. Alternatively, multiple conformers may be extracted and combined into useful ensembles, and the methods we introduce here may prove useful in such an approach.

In this work, we present three new training methods that select structure-based ensembles for VS use. All three methods construct ensembles by optimizing one of two binary classification metrics, which makes them flexible and enables their use with single-point data, competition assay data (e.g., IC₅₀ values), or other binding data. To address the combinatorial problem, the population of ensembles is generated by complete enumeration, and two different heuristics are designed to generate population samples biased to exclude low performing ensembles. These approaches lead to different asymptotic scaling as the number of receptor conformations becomes large, and they allow us to examine the severity of the approximations underlying each heuristic relative to the enumerative solution.

Each method is evaluated on three different target proteins with active and decoy molecules taken from the DUD-E:³² the androgen nuclear hormone receptor (AR), the cyclin-dependent kinase 2 (CDK2), and the peroxisome proliferator-activated receptor δ (PPAR-δ). Target conformations were selected from a range of sources, including RMSD and volumetric clustering of conventional MD simulations, as well as multiple crystal structures.

Methods

Data Sets and Target Proteins

The knowledge-based training methods were tested on three protein targets: the androgen receptor, the cyclin-dependent kinase 2 (CDK2), and the peroxisome proliferator-activated receptor δ (PPAR-δ). Conformations generated by volumetric clustering of conventional MD trajectories along with the crystal structure PDBID 2AM9 were used to train androgen receptor ensembles. Similarly, conformations generated by RMSD clustering of MD trajectories, along with the crystal structure PDBID 4GCJ, were used to train ensembles of CDK2. Clustering and simulation details are provided in subsequent sections. For PPAR-δ, ensemble training was performed using 12 crystal structure conformations with the following PDBIDs (Uniprot Q03181): 2AWH, 2B50, 2J14, 2Q5G, 2XYJ, 2ZNP, 3DY6, 3ET2, 3GZ9, 3PEQ, 3SP9, and 3TKM. Structures were selected to ensure a resolution of 3.0 Å or lower and to ensure that each ligand was unique. Additionally, all of the structures are antagonist bound, which is consistent with the antagonists that make up the actives of the training and test sets, as described below.

Active and decoy ligand sets from the Directory of Useful Decoys-Ehanced (DUD-E)³² were used to perform virtual screening for each target. While a complete description of ligand set curation can be found in the original reference, we briefly describe the process here. Compounds in ChEMBL whose affinities (IC₅₀, EC₅₀, K_i, K_d) were less than or equal to 1 μM were clustered by their Bemis Murcko (BM) frameworks.³³ Compounds with the highest affinity from each cluster were pooled and resulted in sets of actives with unique BM frameworks. For each active, 50 decoys were selected from the Zinc database by matching the molecular weight, logP, number of rotatable bonds, hydrogen bond donor and acceptor counts, and net formal charge (determined in a pH range from 6 to 8) of the active. To reduce the number of false negatives, only the 25% most dissimilar decoys, as judged by Tanimoto scores using ECF4P fingerprints, were retained.

Evaluating the classification performance of a knowledge-based model on the training set will generally provide an overly optimistic estimate of the model’s ability to correctly distinguish active and inactive molecules.³⁴ To provide a more realistic estimate of the trained model’s classification ability, DUD-E compounds were randomly split in half, while maintaining the decoy-to-active ratio, forming training and test sets. The androgen receptor training and test sets were composed of 7150 compounds, 133 of which were active compounds. The CDK2 training and test sets were composed of 14,162 compounds, 237 of which were active compounds. The PPAR-δ training and test sets were composed of 6245 compounds, 120 of which were active.

Molecular Dynamics

Except as noted, CDK2 and androgen simulations were performed identically. Simulations were initiated from a crystal structure of either the androgen receptor (PDBID 2AM9) or CDK2 (PDBID 4GCJ). The sulfate ion, glycerol, and the dithiotheritol molecule were deleted from 2AM9, while four molecules of ethanediol were deleted from 4GCJ. In 2AM9, K836, K846, N848, and E893 are far from the receptor-binding pocket and have unresolved side-chain atoms. Schrödinger’s Prime^35,36 was used to add them. In 4CGJ, atoms from the following residues had multiple occupancy values: D38, S46, D127, K129, R169, L212, M233, K237, K250, S264, and H268. In each case, the position with the larger value was retained. Protonation states for both 2AM9 and 4GCJ were predicted at pH 7.0 using the program PROPKA3,³⁷⁻³⁹ and hydrogen atom positions were assigned and optimized using Schrödinger’s Protein Preparation Wizard. Following protonation, water molecules with fewer than three hydrogen bonds to nonwater molecules were removed. The protonated crystal structures were built for MD simulation using the xLEaP program that accompanies AMBER14.⁴⁰ The cholesterol and RC-3-89 ligand parameters were generated using the Antechamber program in AMBER14. Ligand atomic partial charges were determined from the crystallographic conformations using the AM1-BCC method,⁴¹ and all other force field terms were assigned according to the generalized Amber force field (GAFF).⁴² Each system was immersed in a box of pre-equilibrated TIP4PEW water⁴³ that provided a minimum 10 Å water pad between the protein and the boundary of the periodic box in the x-, y-, and z-directions. Each system was brought to electric neutrality by the addition of an appropriate number of chloride or sodium ions, modeled using the parameters developed by Joung and Cheatham.⁴⁴ The androgen receptor system was comprised of 54,014 atoms, and the CDK2 system was composed of 50,644 atoms. The potential energy was described by the AMBER14 force field with the Stony Brook correction.⁴⁵ A 20,000-step minimization was performed with 2 kcal mol^–1 Å^–2 heavy atom backbone restraint in two stages. During the first step, a 19,500-steepest descent minimization was conducted. The second step entailed a 500-step conjugate gradient minimization. Following minimization, a 200 ps NPT simulation was carried out at 300 K and 1 atm. Pressure was maintained with a Monte Carlo barostat with 100 steps between volume changes and a pressure relaxation time of 2 ps^–1. Following the NPT simulation, a 5 ns NVT simulation was conducted, and restart files were written every 1 ns. These restart files were used to initiate five 20 ns NVT simulations, and frames were written every 2000 fs. All 50,000 frames were concatenated yielding a 100 ns trajectory. During NPT and all NVT simulations, hydrogen heavy atom bonds were constrained using the SHAKE algorithm,⁴⁶ and a 2 fs time step was used. Temperature was maintained in all simulations using a Langevin thermostat with a collision frequency of 2 ps^–1. The Particle Mesh Ewald method was used to treat long-range electrostatics,²³ and simulations were performed using pmemd.cuda on a GeForce GTX TITAN card from NVIDIA. During NVT production runs, the simulation setup resulted in an average timing of 30.29 ns/day on the androgen receptor system and 31 ns/day on the CDK2 system.

Binding Site Clustering

The 100 ns trajectories were each subsampled at an interval of 40 ps, or every 20th frame, resulting in a total of 2500 frames, which were then clustered. Prior to clustering, external translation and rotation were removed from each trajectory by minimizing the RMSD distance of the Cα backbone atoms to the equivalent atoms of the first sampled frame of the trajectory.

For the androgen receptor trajectory, the binding site shape of each sampled structure was determined using POVME 2.0.⁴⁷ Inclusion regions were autodetected using the testosterone ligand as input. Following binding site characterization, the Tanimoto volume overlap between all pairs of structures was calculated, from which a normalized volume overlap matrix was generated. Finally, hierarchical clustering was applied to the overlap matrix, 10 clusters were generated, and the structures corresponding to each of the cluster centroids were retained for docking. Ligand-based autodetection of inclusion regions and hierarchical clustering are features that will be released in the forthcoming version of POVME.

For the CDK2 trajectory, RMSD clustering was performed using the algorithm described in Daura et al.⁴⁸ as implemented in version 5.0.3 of the GROMACS g_cluster program. Clustering was performed on the heavy atoms of all residues within 10 Å of the bound inhibitor RC-3-89 in the crystal structure PDBID 4GCJ. A cutoff of 1.6 Å resulted in five clusters, and cluster centroids were retained for docking.

Docking

The Glide SP algorithm, from Schrödinger, was used to perform docking to all target conformations.⁴⁹ The algorithm generates a series of ligand poses. Relative to the protein receptor, each pose has a unique position and orientation. Each pose is also distinguished by a unique conformation. Following generation, all poses are independently subjected to a set of hierarchical filters that utilize precomputed grids to estimate ligand–receptor interaction energies. In the initial filter, the steric complementarities of ligand poses with the receptor are computed using a grid-based version of ChemScore. Poses that pass the initial filter are minimized in a grid-based approximation of the OPLS pose–receptor interaction energy. Following minimization, Emodel, an empirical scoring function optimized to compare pose energetics, is used to identify the best pose for each ligand. Finally, a “docking score” is reported for each ligand. The docking score is an empirical ligand binding affinity estimate, which incorporates Epik state penalties that are based on the predicted populations of alternative ligand protonation and tautomerization states.⁵⁰

Prior to docking, two-dimensional representations of active and decoy molecules were downloaded from the DUD-E in SDF format. Schrödinger’s LigPrep program⁵¹ was used to add hydrogen atoms and generate three-dimensional ligand structures. Alternative protonation and tautomer states were determined at pH 7 using the Epik program, with default settings. Alternative ring conformations were not generated since these are produced by Glide during docking. Input chiralities were retained, and all other options were set to their default values.

Receptor conformations were prepared for docking as follows. TIP4PEW water and chloride ions were removed from the MD trajectory. The resulting trajectory, which consisted of either the androgen receptor and the testosterone ligand or CDK2 and the inhibitor RC-3-89 were clustered as described above, resulting in 10 and 6 cluster centroids, respectively. Schrödinger’s Protein Preparation Wizard was used to generate correct atom types for Glide grid generation. Atom coordinates were not altered in the process. Protonation states from the MD simulation were retained, and neither hydrogen bond network optimization nor structural minimizations were conducted. For each cluster centroid, the grid center was positioned on the center of geometry of the ligand; all other options were set to their default values.

Docking was performed using Glide with the SP scoring function. All other options were set to their default values. Docking was conducted locally on a Dell Precision T7500n workstation with a dual six-core Intel X5680 processor, and each compound required roughly 15 s to dock.

Performance Analysis

Receiver operating characteristic, or ROC, curves were used to evaluate the performance of each ensemble. ROC curves provide two useful measures of binary classification performance: the area under the curve (AUC) and the ROC enrichment factor (EF).

A ROC curve is determined by successively moving a threshold through compounds ranked by their docking scores. By assuming all compounds with scores better than the threshold are active, a true positive fraction (TPF) and false positive fraction (FPF) can be calculated at each threshold. For example, the TPF is the fraction of active compounds whose docking scores are equal to or better than the threshold, ΔG_T. TPF can be calculated as an average over an indicator function, γ, as described by eq 1.

1

In eq 1, N_A is the total number of active compounds. For a given active, the indicator function γ takes a value of 1 if the value of the docking score, ΔG_i, is better than or identical to the threshold and a value of 0 otherwise. Similarly, the FPF is the fraction of inactive compounds whose docking scores are equal to or better than the threshold. It is also determined as an average of γ, but over the inactive compounds.

2

In eq 2, N_I is the total number of inactive compounds, and all other terms are defined identically to eq 1. Once the TPF and FPF values have been calculated at each threshold, they are plotted along the y-axis and x-axis, respectively, resulting in a ROC curve.

The area under the ROC curve (AUC) is equivalent to the probability that a virtual screening protocol will rank a randomly selected active compound ahead of a randomly selected inactive compound.⁵² An AUC value of 0.5 corresponds to random selection, or a method with no classification power, while a value of 1 indicates perfect separation of active and inactive compounds. Additionally, the value of the AUC is independent of the fraction of actives in the database, it has no free parameters, and an analytic estimate of its standard error is known.⁵² The AUC value can be estimated using a left-handed Riemann sum, which is equivalent to averaging the TPF values at each inactive compound of the ranked list.

3

While the AUC is a useful measure of global classification performance, the early enrichment, or the preferential ranking of active compounds early in the ranked list, is often used to judge the quality of a virtual screen. Enrichment factors are frequently calculated as the ratio of the fraction of actives found in a given percent of the ranked database to the fraction of actives in the total database. Unfortunately, the maximum value of this popular metric depends on the ratio of inactive to active compounds in the screened database.⁵² This makes retrospective method comparison difficult. To circumvent this complicating factor, we use the so-called “ROC enrichment”, whose maximum value is independent of the ratio of decoy to active compounds. The ROC enrichment factor (EF) is the ratio of the TPF, determined at some FPF of interest, to the FPF of interest.⁵²

4

Random classification is indicated by an EF value of 1, and perfect separation of actives and decoys is given by a maximum value of FPF^–1. Like the AUC, the standard error of the ROC enrichment factor may be calculated analytically, which facilitates statistical analysis.⁵²

Statistical Analysis

For any VS protocol, classification performance will vary as a result of having different compounds in the screened database. Confidence intervals capture the magnitude of this variability. For example, assuming repeated screens are performed identically on different databases, the true mean should be found within identically constructed 95% confidence intervals (CI₉₅) in 95% of the measurements. CI₉₅ values were constructed according eq 5.⁵³

5

The standard error, SE, of the calculated classification metric (AUC or EF) is given and is calculated differently for AUC and ROC-EF values. The exact form that each takes is provided in the Supporting Information. The value of l is selected such that ± l bounds 95% of Student’s t-distribution, where the number of degrees of freedom was determined by subtracting one from the sum of the number of active and inactive compounds.

Ensemble Scoring

Several different methods for combining multiple docking scores into a single docking score have been suggested. Reported protocols include creating composite grids of all ensemble members,^19,54 treating conformations as an independent variables during docking,^55,56 and using different weighted averages, which include arithmetic¹⁷ and Boltzmann weighted averages,⁵⁷ as well as averages using weights determined by knowledge-based methods.²⁹ One simple approach, and the one used in this work, takes the best scoring function value across all ensemble members. For example, a compound docked to an ensemble composed of N protein conformations will have N docking scores, {ΔG₁, ΔG₂, ..., ΔG_N}, and the ensemble score of the compound is defined as the smallest score of the set, i.e., min{ΔG₁, ΔG₂, ..., ΔG_N}. If a compound has more than one protonation or tautomer state, the state with the lowest docking score is retained.

Results

Given an arbitrary collection of target conformations, it is difficult to know which set will result in the best VS performance. Here, we provide three knowledge-based methods designed to systematize the selection process: the exhaustive method, the slow heuristic method, and the fast heuristic method, which are each introduced below.

Knowledge-Based Ensemble Selection

In the “exhaustive” method, at each ensemble size, all combinatorial possibilities are enumerated, and the complete ensemble population is constructed. As shown in the Supporting Information, if N is the total number of target conformations considered, the enumerative approach generates 2^N – 1 ensembles. Using big O notation, this is expressed as O(2^N). For example, given three conformations, labeled A, B, and C, seven ensembles can be constructed: three of size one (A, B, C), three of size two (AB, AC, BC), and one of size three (ABC). Both AUC and EF values are used to rank the performance of each, and the best performing ensemble is retained. Thus, the exhaustive method generates the entire population of ensembles, performs a census, and only retains the individual member with the desired performance characteristics.

In the “slow heuristic” method, ensembles are assembled recursively. In the first step, the performance of each receptor conformation is considered individually, and the best performer becomes the first ensemble member. Next, the remaining receptor conformations are added in turn, forming a series of two-membered ensembles, and the best ensemble is retained. The process is repeated until all receptor conformations have been added to the ensemble, and the top performer of any size is identified. In the Supporting Information, we show that the slow heuristic method generates N(N + 1)/2 ensembles. Using big O notation, this is expressed as O(N²). For example, given three conformations A, B, and C, three one-membered ensembles (A, B, C) will be considered, and the best performer will be retained. If B is the top performing one-member ensemble, then two two-membered ensembles (BA and BC) will be constructed, and one three-membered ensemble (ABC) will be constructed. Thus, the slow heuristic method is designed to construct a biased sample of the ensemble population that excludes individuals that do not contain the best performing ensembles of smaller sizes.

Like the slow heuristic method, the “fast heuristic” method also assembles ensembles recursively. First, the classification performance of each individual conformation is ranked by either AUC or EF. Ensembles of increasing size are then constructed by merging conformers of successively decreasing performance. The performance of each conformation is considered only once. To identify the ensemble that performs best, each of the resulting ensembles must also be evaluated once. Thus, for N conformers, 2N – 1 performance evaluations are required, and the scaling is linear. Using big O notation, this is expressed as O(N). For example, if the performance of three conformations is given as A > B > C, then one one-membered ensemble (A), one two-membered ensemble (AB), and one three-membered ensemble (ABC) are formed. The fast heuristic results in a small biased sample that neglects the worst performing conformers at each ensemble size.

Each method was implemented in a program called “Ensemble Builder,” which was written in the Python language⁵⁸⁻⁶⁰ and was used to produce the results reported here. An alpha-version of the Ensemble Builder software is freely available for download through PyPi.

The performance of the three methods was evaluated on the androgen receptor, CDK2, and PPAR-δ. Conformations for these targets were selected from a variety of sources, as summarized in Table 1. Androgen receptor and CDK2 structures were selected from pools of five 20 ns MD simulations using two different clustering methods. Volumetric clustering was performed on the binding pocket of the androgen receptor to select 10 conformations, and RMSD clustering was performed on the active site of CDK2, which lead to the selection of five conformations. The crystal structures used to initiate the simulations were also included and resulted in heterogeneous collections of simulation and experimentally determined conformations of sizes 11 and 6 for the androgen receptor and CDK2, respectively. Twelve human PPAR-δ crystal structures were selected from the protein data bank.⁶¹ Sets of active and decoy compounds for each target were taken from the DUD-E.

Table 1. Summary of Structures Used To Construct Ensembles.

target	structural source	number of structures
androgen receptor	volumetric clustering of five 20 ns MD simulations; one crystal structure	11
CDK2	RMSD clustering of five 20 ns MD simulations; one crystal structure	6
PPAR-δ	wwPDB; Uniprot Q03181	12

The remainder of the Results section is organized as follows. First, the relationship between the ensemble selection algorithms, the anticipated results, and the actual results are examined in the Population and Heuristic Samples section. The dependence of the classification ability on ensemble size is then assessed in the Performance vs Size section, and the results conclude with a comparison of each method on training and test sets in the section entitled Comparing Ensemble Performance on Training and Sets.

Population and Heuristic Samples

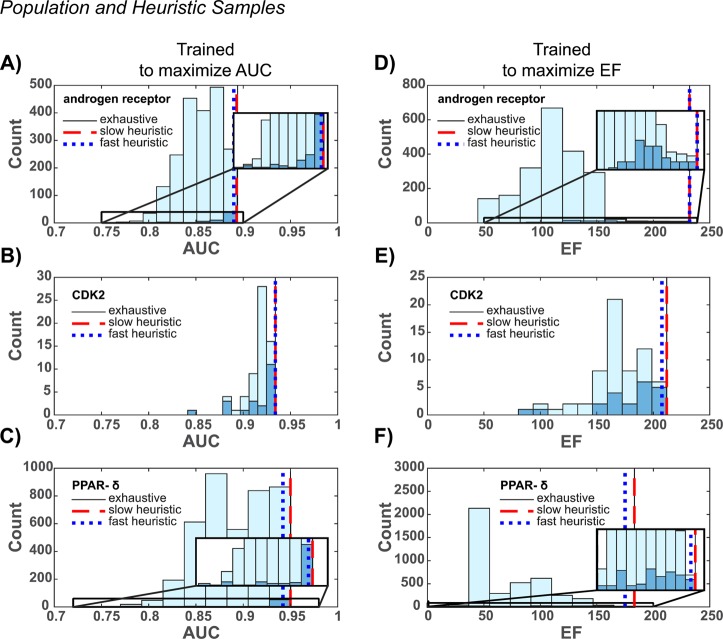
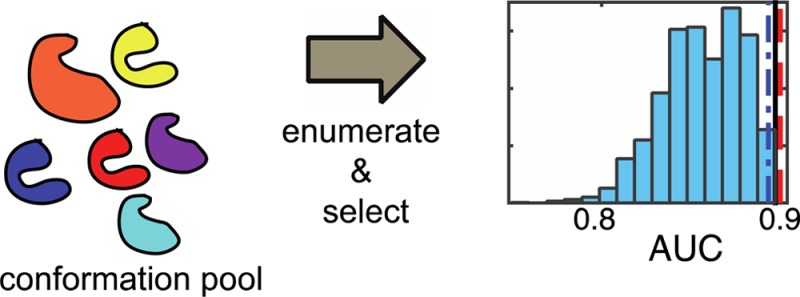
Given docking results for an arbitrary collection of target conformers, the exhaustive method enumerates the population of all possible ensembles and identifies the ensemble with the largest objective function value (AUC or EF at a false positive fraction of 0.001). Since the exhaustive method performs a census on the ensemble population and records the performance of each individual, it is guaranteed to identify the best performing ensemble. It follows that if the performance values of the population are represented as a distribution, the value of the best ensemble should reside on the edge of the distribution.

To verify that the best ensemble is found on the edge of the population distribution, ensembles were enumerated, and the corresponding training set performance values (AUC or EF) were sorted into 10 histogram bins. The resulting distributions are shown in light blue in Figure 1.

Figure 1.

AUC and EF histograms. The exhaustive method was used to enumerate all possible ensembles, and the AUC and EF values of the corresponding population were sorted into 10 bins and plotted in light blue. The slow heuristic method was used to sample a subset of the ensemble population, and the AUC and EF values were sorted into 10 bins and plotted in dark blue. Insets provide expanded views for the androgen receptor and PPAR-δ. AUC values for ensembles trained to maximize the AUC are reported as vertical lines in (A)–(C), and EF values for ensembles trained to maximize the EF are reported as vertical lines in (D)–(F).

Consistent with expectations, the values of the ensembles identified by the exhaustive method appear at the edges of the distributions. This is true across all the targets considered, independent of whether target conformations came from simulation or experiment (Table 1) and provides some confidence in the generality of the approach.

Because the exhaustive method can be computationally expensive, we have developed a more efficient approach, called the “slow heuristic method,” which may have greater utility. To reduce expense, the slow heuristic assumes that the next largest ensemble must contain the current ensemble. Following this assumption, target conformers not yet ensemble members are each grouped with the current best performing ensemble, and the resulting collections are ranked by the values of their objective functions. Hence, the heuristic should result in a population sample biased to favor higher performing ensembles.

To confirm the slow heuristic results in a biased sample that favors higher performance, it was used to construct ensembles, and the corresponding training set AUC and EF values were sorted into 10 bins. The resulting distributions are shown in dark blue in Figure 1.

For each target and both objective functions, the majority of the slow heuristic sample distributions reside on the right side of the corresponding population distributions, which correspond to higher performance values. This is consistent with expectations and indicates that recursively generating ensembles from high performing target conformations results in a sample biased to favor performance. The consistency of this result across targets and both AUC and EF values suggests that the approach is generally applicable for a variety targets and ROC-based objective functions.

To further confirm that the slow heuristic produces biased samples, we plotted the performance values of the best ensembles identified by the method as dashed red vertical lines in Figure 1. In five of the six cases considered, the slow heuristic and exhaustive methods result in ensembles that perform identically. In the last case (Figure 1A), the difference was small: an AUC of 0.893 for the slow heuristic compared to a value of 0.894 for the exhaustive method. Since identical results imply that the edges of the samples and populations overlap, these results provide additional evidence that the slow heuristic is able to sample ensembles biased to perform well.

Compared to the population generated by the exhaustive method, the dark blue slow heuristic sample is smaller. The discrepancy between sample and population size becomes larger when a greater number of target conformations is considered. For example, of the three targets, the greatest number of conformations (12) was considered for PPAR-δ, and the difference between the sample and population sizes is largest. This observation is consistent with the scaling of each method: given N conformations, the exhaustive method enumerates a population of size 2^N – 1, and the slow heuristic method considers samples of size N(N + 1)/2.

By assuming that ensembles can be constructed by successively merging target conformations of decreasing performance, the number of ensembles considered is reduced further still, and an approach we call the fast heuristic method is the result. The fast heuristic only considers the performance of each target conformation once. While this results in the greatest computational efficiency, the method considers the smallest number of ensembles, and the likelihood of failing to sample the best performing ensemble of the population is largest.

Our results indicate that considering a drastically smaller sample of ensembles with the fast heuristic approach does not significantly alter the performance of the best determined ensemble (Figure 1). In four out of six cases, the fast heuristic fails to sample the highest performing ensemble. However, in all cases, the differences in performance are relatively small, and the fast heuristic performance values reside near the edges of the distributions. This indicates that the fast heuristic is able to sample ensembles that perform similarly to the best performing ensemble of the population.

Performance vs Size

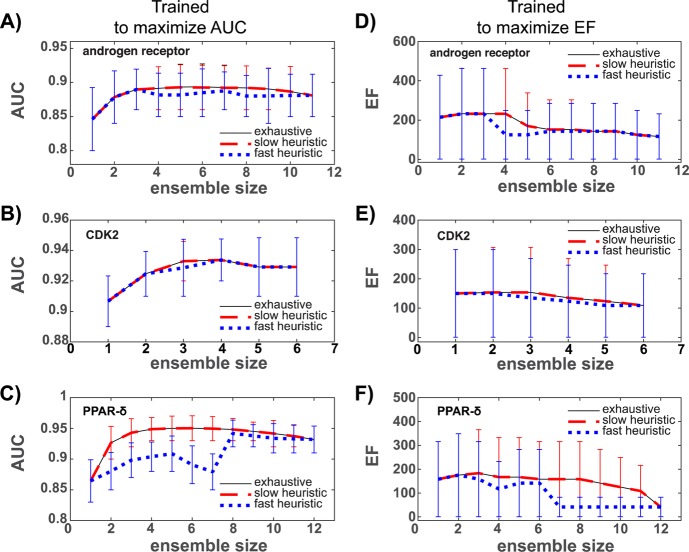
When performance is measured as a function of ensemble size (Figure 2), it is notable that for each target the exhaustive method provides an upper bound: this is expected since the exhaustive method identifies ensembles by selecting the top performer from the entire population of a given size.

Figure 2.

Training set performance as a function of ensemble size for three proteins using DUD-E. AUC is the area under the ROC curve. EF is the ROC enrichment factor at a false positive fraction of 0.001. AUC values for ensembles trained to maximize the AUC are shown in (A)–(C), and EF values for ensembles trained to maximize the EF are reported in (D)–(F). Shown are 95% confidence intervals.

The slow heuristic and exhaustive methods perform identically, or nearly identically, across the range of ensemble sizes and targets considered. These results are consistent with the distributions shown in Figure 1. However, the trends in Figure 2 go further to imply that the slow heuristic is able to sample the best performing ensemble of the population at each size or an ensemble that performs nearly identically.

While the fast heuristic realizes linear scaling by drastically reducing the number of ensembles considered during training, it is the poorest performing method, particularly for PPAR-δ where the deviations are largest. However, across all targets and for the majority of the sizes considered, the performance values of the fast heuristic fall within the confidence intervals of the exhaustive and slow heuristic methods. Since this implies performance differences may be attributed to training set variability, the fast heuristic performs reasonably well in comparison to the other two methods.

For a given target and objective function, the smallest and largest ensembles identified by each method perform identically, as the identical bounds of the plots shown in Figure 2 indicate. This behavior is anticipated. Each method forms one-membered ensembles from the single best performing target conformer, and the largest ensembles are formed by merging all target conformations.

Finally, the EF confidence intervals reported in (D)–(F) are larger than those reported for the AUC values in (A)–(C). Because enrichment factors quantify classification performance on a smaller subset of the total data, the larger variability is expected: smaller sample sizes lead to greater standard errors and, by extension, larger confidence intervals.

Comparing Ensemble Performance on Training and Test Sets

When developing knowledge-based classification methods, evaluating the performance of the trained model on an independent test set is a prerequisite to performing a prospective screen. Doing so ensures that the model can correctly classify compounds distinct from the training compounds.³⁴ To further validate the classification ability of the highest performing ensembles identified by each method, the ensembles were used to screen an independent test set, and the test and training set performances were compared.

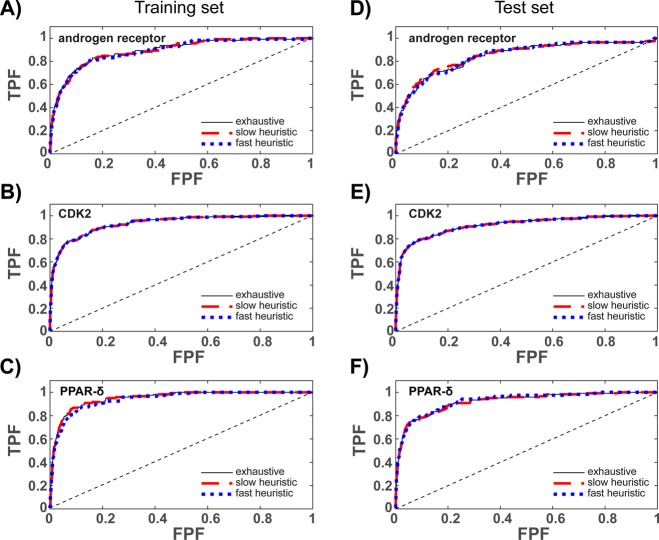
As can be seen by examining the androgen receptor entry in Table 2, despite variations in ensemble size and training set performance, the test set results are identical for each method when ensembles are trained using the AUC as an objective function. The variations in ensemble size imply that the samples generated by the slow and fast heuristic do not contain the best performing ensemble of the population. However, the training set performances, which are within confidence intervals of each other, imply that the best performing members of the samples have classification abilities that are similar to the best performing population member. This is consistent with the ROC curves illustrated in Figure 3A and D, which illustrate that the three methods result in ensembles with nearly identical global classification abilities.

Table 2. AUC Values Determined on Training and Test Sets of Best Performing Ensembles Selected To Maximize AUC^a.

	androgen receptor			CDK2			PPAR-δ
method	size	training	test	size	training	test	size	training	test
exhaustive	6	0.894 ± 0.05	0.850 ± 0.04	4	0.934 ± 0.014	0.919 ± 0.019	6	0.950 ± 0.020	0.923 ± 0.023
slow heuristic	5	0.893 ± 0.04	0.850 ± 0.04	4	0.934 ± 0.014	0.919 ± 0.019	6	0.950 ± 0.020	0.923 ± 0.02
fast heuristic	3	0.890 ± 0.03	0.850 ± 0.04	4	0.934 ± 0.014	0.919 ± 0.019	8	0.942 ± 0.022	0.928 ± 0.03

^aThe column labeled “size” gives the number of target conformations in the optimally performing ensemble identified by each method; 95% confidence intervals are given. Androgen receptor ensembles were constructed from 10 MD conformations identified using pocket volume clustering and a crystal structure. CDK2 ensembles were constructed from five MD conformations identified using RMSD-based pocket clustering and a crystal structure. PPAR-δ ensembles were constructed from 12 crystal structures.

Figure 3.

Receiver operating characteristic (ROC) curves for ensembles trained to maximize the AUC of the ROC curve. Dashed black lines illustrate random classification. Training set values are shown in (A)–(C). Test set values are shown in (D)–(F).

Similar results are realized for CDK2, where the three training methods result in identically sized ensembles with identical performance values on both training and test sets; consistently, the ROC curves in Figure 3B and E overlap. Collectively, these results imply that the slow and fast heuristic methods were able to sample the best performing ensemble of the population.

Consistent with the androgen receptor and CDK2 results, the three methods perform nearly identically on PPAR-δ. By comparing training and test set entries in Table 3, along with Figure 3C and F, it is apparent that the slow heuristic method was able to sample the best performing ensemble from the population, but the fast heuristic method was not. Compared to the best ensemble of the population, the best ensemble sampled by the fast heuristic is slightly larger and performs slightly worse on the training set but slightly better on the test set. However, for both training and test sets, the differences in performance are small, and the AUC values of each method are within confidence intervals of one another. In other words, the best performing ensemble in the fast heuristic sample has similar classification ability as the best performing member of the ensemble population.

Table 3. EF at FPF of 0.001 Determined on Training and Test Sets of Best Performing Ensembles Selected To Maximize EF at FPF of 0.001^a.

	androgen receptor			CDK2			PPAR-δ
method	size	training	test	size	training	test	size	training	test
exhaustive	4	232.1 ± 87.2	151.8 ± 73.9	2	211.9 ± 57.9	148.3 ± 50.3	3	183.3 ± 83.0	116.7 ± 64.04
slow heuristic	4	232.1 ± 87.2	151.8 ± 73.9	2	211.9 ± 57.9	148.3 ± 50.3	3	183.3 ± 83.0	116.7 ± 64.04
fast heuristic	3	232.1 ± 87.2	133.9 ± 70.1	1	207.63 ± 57.5	152.5 ± 50.9	2	175.0 ± 76.6	125.0 ± 62.2

^aThe column labeled “size” gives the number of target conformations in the optimally performing ensemble identified by each method; 95% confidence intervals are given. Androgen receptor ensembles were constructed from 10 MD conformations identified using pocket volume clustering and a crystal structure. CDK2 ensembles were constructed from five MD conformations identified using RMSD-based pocket clustering and a crystal structure. PPAR δ ensembles were constructed from 12 crystal structures.

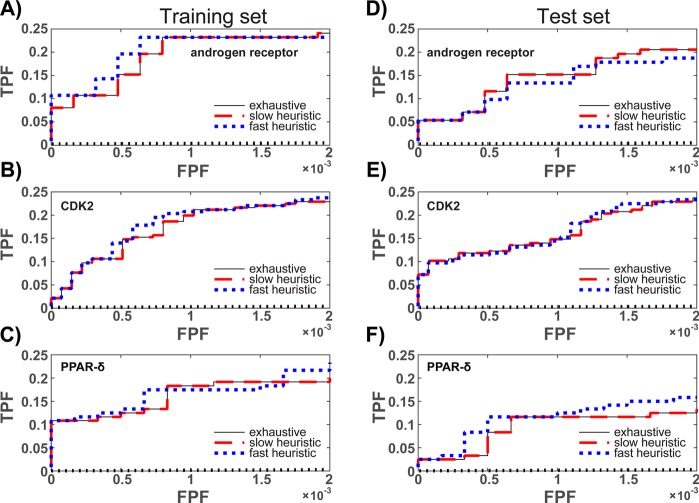
Similar to the results produced when using an AUC objective function, each method produces androgen receptor ensembles that perform identically, or nearly so, when ensembles are selected by maximizing the EF. For example, Table 3 shows that the ensembles identified by the exhaustive and slow heuristic methods have identical sizes and performance values. Consistently, Figure 4A and D, which show the early portion of the ROC curves determined on the training and test sets, respectively, are identical for the exhaustive and slow heuristic methods. While the fast heuristic sample did not contain the optimal population member, the method sampled an ensemble that performed comparably: the performance was identical on the training set and within confidence intervals on the test set.

Figure 4.

Receiver operating characteristic (ROC) curves for ensembles trained to maximize the EF at a FPF of 0.001. Dotted black lines illustrate random classification. Training set values are shown in (A)–(C). Test set values are shown in (D)–(F). To be consistent with the training condition, the early portion of the ROC curve, with FPF values between 0 and 0.002, is shown.

The pattern is similar when the EF is maximized to identify CDK2 and PPAR-δ ensembles: the slow heuristic samples the best performing member of the population, and the fast heuristic samples an ensemble that performs comparably. In all cases, the performance differences are small, and the averages are within confidence intervals of one another. Collectively, these results provide further evidence that the fast and slow heuristic methods effectively sample ensembles biased to favor high performing members of the population.

Across all the targets considered, the training and test set performances are similar for each method, and similar classification accuracy implies an underlying similarity in the structure of the compounds that make up each set. That is, if training and test set compounds are chemically similar, then they should be classified similarly. To analyze the extent of training and test set overlap, we utilize a popular invariant scaffold representation: graph frameworks.³³ A graph framework can be generated from any molecule by converting all atoms to Sp3 hybridized carbon atoms and removing acyclic substructures that do not connect ring systems.

Training and test set similarity was estimated by determining the percentage of molecules whose graph frameworks were unique to each set and the percentage that was shared by each set (Figure 5). Across the three targets, between 65% and 76% of molecules can be represented by frameworks that are found in both the training and test sets, and between 12% and 18% of molecules are represented by graph frameworks found only in the training or test sets. Hence, the underlying chemical similarities shared by the training and test sets help explain the similar classification performance observed for these sets. However, the existence of molecules whose graph frameworks are unique suggests that the trained ensembles are able to correctly classify molecules structurally distinct from those used during training.

Figure 5.

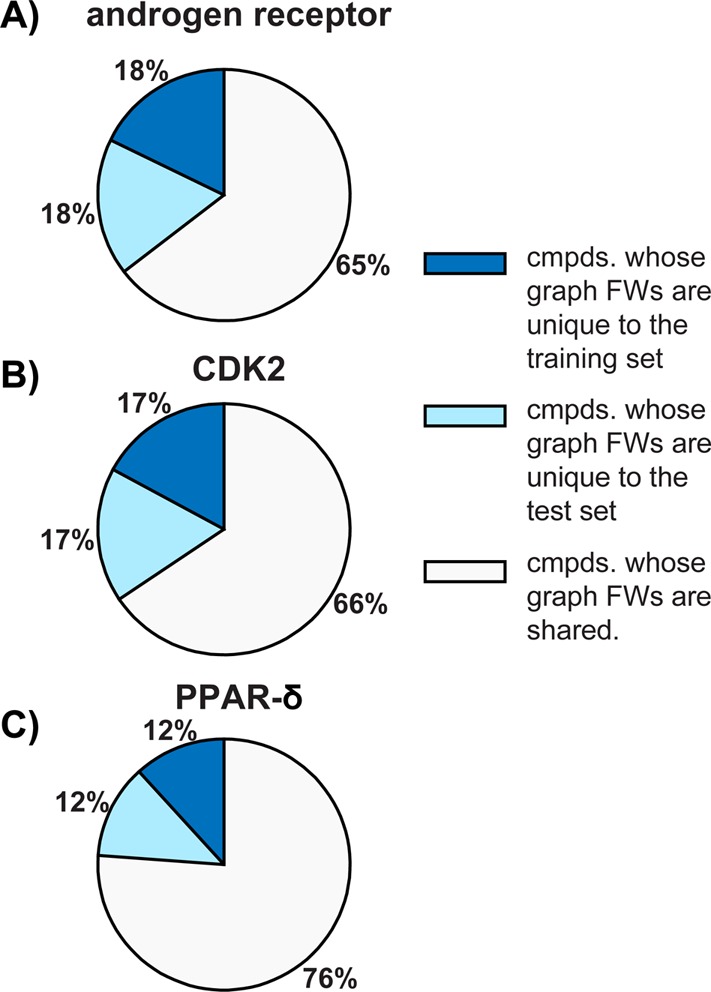
Percentages of compounds whose graph frameworks (FWs) are unique to, and shared between, training and test sets. Percentages are given for (A) androgen receptor, (B) CDK2, and (C) PPAR-δ.

Discussion

Given a collection of target conformations generated either by experiment or by simulation, it is difficult or impossible to know a priori which subset will result in the best VS performance. The problem becomes increasingly challenging as the number of target conformations grows, and this is the result of the combinatorial nature of the problem. To address this problem, we presented three knowledge-based ensemble selection methods: the exhaustive method, the slow heuristic method, and the fast heuristic method. For each method, the discussion includes schematic illustrations that describe the underlying selection algorithm and an examination of performance, scaling, and limitations; results from the androgen receptor, CDK2, and PPAR-δ provide context.

Exhaustive Method

By enumeration of all possible combinations of conformers, the exhaustive method generates the complete ensemble population and only retains the highest performing individual; that is, the exhaustive method is guaranteed to identify the best performing member of the population. This is illustrated schematically in the “Exhaustive” column of Figure 6. Three receptor conformers, colored red, green, and blue are shown, and the ensembles that can be constructed at each size are also shown. The population constitutes all of the ensembles at each size, and in the simple schematic, contains seven members. By performing a census of the population, the best performing ensemble is readily identified. This was realized for each target considered here.

Figure 6.

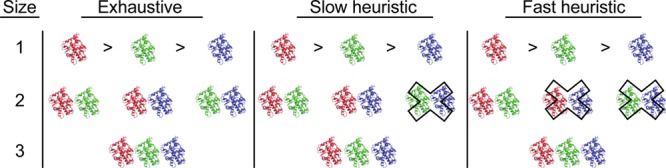
Training method schematic: selecting the best performing ensemble from three target conformers. As indicated by the greater than symbols, the VS performance, measured by either the AUC or EF, is greatest for the red conformer, followed by the green conformer, and the blue conformer is the poorest performer. Each method is found in a column, and all combinatorial possibilities are shown. The VS performance of enumerations marked with an “X” are not explicitly evaluated. Hence, the exhaustive method evaluates all combinatorial possibilities. The slow heuristic assumes the next largest optimal ensemble is formed only from a combination of the current ensemble and one of the remaining conformers. The fast heuristic method ranks the VS performance of each target conformer and assembles ensembles by successively including conformers of decreasing performance.

Applying conformation enumeration to generate ensembles is not new, and the idea has appeared in the literature. For example, to retrospectively compare the VS performance of ensemble and single crystal structure VS protocols, Korb et al.⁶² used a similar enumerative approach. However, in their work, enumeration was not tied to ensemble training, and we later proposed that enumeration could be used to identify ensembles with the greatest VS utility.⁶³ It is that concept that we demonstrated here.

Slow Heuristic

Performing a population census, as the exhaustive method does, guarantees that the best performing ensemble will be identified, but the process is computationally expensive. To reduce expense, we introduced the slow heuristic, which builds ensembles recursively. Beginning with the best performing target conformer, each conformation not yet assigned to an ensemble is grouped with the best performing ensemble of the current size. This produces a sample of ensembles, each with one additional conformation and a characteristic VS performance, from which the best ensemble is selected. The process continues until all conformers have been included in an ensemble, and the ensemble that performs best overall is retained. Following this heuristic produces a biased sample that neglects population members that do not contain the best performing ensembles of smaller sizes.

To clarify how the slow heuristic results in biased samples, we have illustrated the process schematically in the “Slow heuristic” column in Figure 6. Of the three conformations, the red one performs best, the green next best, and the blue conformation performs worst. The one-membered ensemble is made up of the single best performing target conformer, or the red conformer, in this case. After identifying the one-membered ensemble, two two-membered ensembles are then generated. Each contains the best one-membered ensemble: red-blue and red-green. Since the blue-green ensemble does not contain the best performing one-membered ensemble, it is neglected.

While it is not a given that the slow heuristic will result in samples biased to favor high performing ensembles, that did prove to be the case in the three targets considered in this work. This was illustrated in part by the overlap of the population and slow heuristic sample distributions in Figure 1 and in part by the ability of the method to identify the best performing ensemble from the population. For example, in Figure 1, the slow heuristic sample favored ensembles that produced larger values of both classification metrics considered, and this was true across all three targets. Additionally, the slow heuristic identified the best performing ensemble from the population in five out of the six cases considered (Tables 2 and 3). These observations provide further support for the claim that the method produces biased samples favoring high performing ensembles, and they suggest that the method may be generally applicable across different target classes and ROC-based objective functions.

Nevertheless, because the slow heuristic samples the population, it may miss ensembles in which synergism between poor performing conformations can lead to a higher performing ensemble. To help clarify this, consider the blue and green conformations in Figure 6. Despite their poorer individual performances, if they pair to form a high performing two-membered ensemble, it will not be sampled by the slow heuristic. However, while missing potential synergism is possible, when the sample is biased toward high performing ensembles, the best performing sample member may perform comparably to the highest performing population member. This proved true in this study. For example, when the slow heuristic was used to train androgen receptor ensembles to maximize the AUC, the sample did not contain the optimal ensemble from the population; however, the performances of the best ensemble from the sample and the best ensemble from the population were within confidence intervals of one another (Table 2).

The slow heuristic appears to offer a reasonable compromise between computational efficiency and performance. To illustrate the computationally efficiency, in the Supporting Information, we show that the exhaustive method scales as O(2^N), given N target conformations, while the slow heuristic scales as O(N²). For example, if 23 receptor conformations are considered, the exhaustive method considers roughly 8.3 million ensembles, while the slow heuristic method only evaluates 264 ensembles. However, since each of the enumerated ensembles can be evaluated on a single processor, it is noteworthy to point out that the exhaustive method is embarrassingly parallel.

Fast Heuristic

By constructing ensembles of increasing size by successively merging conformations of decreasing performance, the fast heuristic ignores the pools of ensembles generated at each size by the slow heuristic and further reduces computational expense. Thus, the fast heuristic produces a small, biased sample that neglects the poorest performing conformations at each ensemble size.

To clarify how the fast heuristic produces biased samples, we have illustrated the process schematically in the “Fast heuristic” column in Figure 6. Since the red conformation performs best, it is selected as the one-membered ensemble, and the poorer performing conformations are neglected. By merging the one-membered ensemble with the next best performing conformation, the two-membered red-green ensemble is produced. The green-blue ensemble is ignored, just as it is by the slow heuristic, but the red-blue ensemble is also ignored, which results in a smaller sample.

Relative to the exhaustive solution, which generates the entire ensemble population, the fast heuristic sample is significantly smaller. In general, given N target conformations, the ensemble population has a size 2^N – 1, and the fast heuristic only considers 2N – 1 of these. In practice, this can quickly amount to thousands of possibilities. For example, with 11 androgen receptor conformations, the fast heuristic method ignores 2026 of the 2047 possible ensembles.

The fast heuristic is nearly identical to the method of Xu and Lill,³⁰ which was described in the Introduction. However, rather than using the value of a ROC classification metric, they ranked target conformations by the differences in average docking scores of decoy and active molecules to each conformer. While Xu’s and Lill’s results were promising, the effect of ignoring a significant fraction of the ensemble population was not assessed.

To provide insight into the severity of the heuristic relative to the enumerative solution, we compare the exhaustive and fast heuristic results. Consistent with the small sample size, the fast heuristic was only able to identify the best performing population member in one of the six cases considered (Tables 2 and 3). Despite this, the ensembles identified performed similarly to the best performing ensemble of the population: fast heuristic performance values were within confidence intervals of the best performing members of the population for all three targets and both objective functions. Despite the much smaller sample size, the fast heuristic may be a generally applicable approach that offers linear scaling without a dramatic sacrifice in classification ability.

Conclusions

Docking to structural ensembles is a promising means of identifying novel, structurally diverse active compounds. Despite the potential of ensemble docking, it is difficult to know which structures will synergize and perform well during a virtual screen. This problem emerges from the combinatorial nature of ensemble selection. To address the selection problem, we presented three promising knowledge-based methods. Each method scales differently in the limit of a large number of receptor conformations but can perform similarly, which was demonstrated by constructing ensembles of the androgen receptors, CDK2, and PPAR-δ and with either X-ray crystallographic structures or snapshots from all-atom molecular dynamics trajectories. As with all other knowledge-based methods, those presented here are fundamentally limited by the availability of high quality ligand sets. Nevertheless, virtual screens are often carried out on targets for which active and inactive molecules are known. In these cases, the ensemble selection methods presented have broad applicability.

Glossary

Abbreviations

ROC

receiver operating characteristic

TPF

true positive fraction

FPF

false positive fraction

AUC

area under the curve

EF

ROC enrichment factor

VS

virtual screening

CDK2

cyclin-dependent kinase 2

PPAR-δ

peroxisome proliferator-activated receptor delta

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jcim.5b00684.

• Expressions used to determine the standard error of the reported AUC and EF values. Derivations of the big O scaling reported for the exhaustive and slow heuristic methods. (PDF)

Author Contributions

S. A. Jusoh and T. L. Offutt contributed equally to the production of this work.

This work was supported by an NIH Director’s New Innovator Award (DP2-OD007237) and an NSF XSEDE Supercomputer resource grant (RAC CHE060073N) to R.E.A. Support from the National Biomedical Computation Resource (NBCR, P41 GM103426) is also gratefully acknowledged. S.A.J. gratefully acknowledges financial support from the Ministry of Education Malaysia and Universiti Teknologi MARA Malaysia.

The authors declare no competing financial interest.