Abstract
AC electrokinetics is a collection of processes for manipulating bulk fluid mass and embedded objects with AC electric fields. The ability of AC electrokinetics to implement the major microfluidic operations, such as pumping, mixing, concentration and separation, makes it possible to develop integrated systems for clinical diagnostics in non-traditional healthcare settings. The high conductivity of physiological fluids presents new challenges and opportunities for AC electrokinetics based diagnostic systems. In this review, AC electrokinetic phenomena in conductive physiological fluids are described followed by a review of the basic microfluidic operations and the recent biomedical applications of AC electrokinetics. The future prospects of AC electrokinetics for clinical diagnostics are presented.
Keywords: electrokinetics, microfluidics, electrothermal flow, physiological fluid, point-of-care diagnostics
Introduction
In the past decades, micro total analysis systems (μ-TAS) have been widely studied for various biological and medical applications.1, 2 A prominent advantage of μ-TAS is the ability to integrate multiple components, such as liquid handling, cell and molecule manipulation, and detection into an automated, sample-in-answer-out system. Despite intensive efforts, most developed microfluidic systems have limited applications as automated biomedical analysis tools. Developing μ-TAS for laboratory automation is often constrained by complex sample preparation procedures and the inability to resolve full system integration.3, 4 Numerous microfluidic approaches, such as paper-based microfluidics, lab-on-a-CD, electrowetting-on-dielectric and multiphase flow4, 5, are therefore being developed to address these challenges.
Among various microfluidic techniques alternating current (AC) electrokinetics represents a promising approach towards the development of a fully integrated μ-TAS. The advantages of AC electrokinetics include rigorous micro and nano manipulation methods, low power consumption, cost-effectiveness, simplicity in microelectrode fabrication, and advancement in portable electronics.6, 7 AC electrokinetic phenomena include dielectrophoresis (DEP), AC electroosmosis (ACEO), and AC electrothermal flow (ACEF). These techniques are capable of performing most fundamental microfluidic operations, such as sample pumping, mixing, concentration, and separation, to develop automated biomedical analysis systems.
Biomedical applications often require manipulation of physiological samples and biological buffers with high conductivity. Table 1 summarizes the conductivities of typical physiological fluids and media. Nevertheless, most conventional electrokinetic studies were performed in low conductivity buffers to avoid unwanted side effects, such as electrolysis and heating. To design electrokinetics based μ-TAS for laboratory automation applications, proper electrokinetic phenomena for manipulating conductive fluids should be considered. For example, ACEO is most effective in low conductivity solution (< 0.1 S/m) and has limited applicability in conductive biological buffers and physiological fluids. In contrast, ACEF is effective in a wide range of conductivities, and it is commonly used at frequencies greater than 100 kHz.8, 9 Understanding the dominant electrokinetic phenomena and their limitations throughout a wide range of conductivities is essential in the design of electrokinetics based μ-TAS.
Table 1.
| Physiological fluid | Cell culture medium and buffer solution | ||
|---|---|---|---|
| Urine | 1.1 to 2.5 | Lysogeny broth (LB) | 1.0 to 1.2 |
| Cerebrospinal fluid (CSF) | 1.4 to 1.8 | Mueller Hinton Broth | 1.0 to 1.2 |
| Bile | 1.1 to 1.4 | Phosphate buffered saline (PBS 1X) |
1.3 to 1.6 |
| Blood | 0.4 to 0.8 | Dulbecco's Modified Eagle Medium (DMEM) |
1.4 to 1.5 |
| Saliva | 0.4 to 0.6 | Sodium phosphate buffer (1M) |
5.0 to 6.0 |
In this review, electrokinetic techniques for manipulating conductive physiological fluids are discussed. In particular, ACEF and DEP are focused on due to their effectiveness in manipulating fluids with a wide conductivity range. After a summary of the theory and characteristics of DEP and ACEF, recent device designs and applications using these electrokinetic techniques for pumping, mixing, and bio-particle manipulation are presented. Finally, the potential areas in need of development and application of AC electrokinetics are discussed.
AC Electrothermal Flow
ACEF arises from temperature gradients developed within a fluid when an external electric field is applied. The local temperature gradients create conductivity, permittivity, viscosity, and density gradients in the solution. These gradients and their interactions with the electric field, in turn, create bulk fluid forces and fluid motion (Figure 1A). For instance, the interaction between the conductive gradient and the non-uniform electric field induces the Coulomb force. The vertical density gradient generates the buoyancy force. A theoretical model has been developed for estimating the electrothermal force.6, 10, 11 In this model, the charge density and the electric field are described by Gauss’s law (1) and the charge conservation equation (2):
| (1) |
| (2) |
where ε, ρq, σ and u are the electrical permittivity, the charge density, the solution conductivity and the fluid velocity. E is the electric field. By using perturbation analysis, the electrical potential ϕ in the medium can be estimated by:
| (3) |
Joule heating is induced by the electrical field according to the Ohm’s Law and the temperature field can be determined by considering the energy equation:
| (4) |
where k, ρm, and c are the thermal conductivity, density, and specific heat of the fluid, respectively. In a typical microfluidic device, the Péclet number is small (Pe = ρmCpuL/k ≪ 1, where Cp is the heat capacity and L the characteristic length). The thermal convection can be neglected, and the energy equation is simplified to:
| (5) |
The temperature field can then be determined to estimate the time averaged electrothermal force:
| (6) |
where for water, and f is the applied frequency. The first term of equation (6) is the Coulomb force due to the conductivity gradient and the second term is the dielectric forces due to the permittivity gradient. From equation (6), the electrothermal force depends on the applied frequency. In particular, the Coulomb force will dominate at low frequencies while the dielectric force will dominate at high frequencies with a crossover frequency (fc) depending on the charge relaxation time ((τc)). The crossover frequency fc is given by:
| (7) |
The charge relaxation time of the liquid is given by τc ≈ τ = ε/σ.
Figure 1.
(A) Schematic of AC electrothermal flow. Arrows induced the direction of the bulk fluid force and fluid circulation. (B) The frequency dependence of the electrothermal force, M(ω,T), at different fluid conductivities.
For a parallel electrode with a small gap, the gradient of temperature can be estimated by:
| (8) |
The time-averaged force with an applied alternating potential is:
| (9) |
where θ is the angular coordinate and
| (10) |
is a dimensionless factor describing the frequency dependence.
ACEF creates fluid motion in samples with a wide range of conductivity.8 Figure 1B shows the frequency dependence of the electrothermal force in different conductivities. For physiological conductivities (~1 S/m), the ACEF velocities is constant and effective at high frequency range (~1MHz),10, 11 which can minimize electrolysis of the fluid. This presents a great advantage of ACEF flow. From equation (9), the ACEF is proportional to V4. For a sample with a higher conductivity, only a low voltage is required for biomedical applications. By properly designing the electrode and microchannel structures, ACEF can be applied to perform necessary microfluidic operations.
Dielectrophoresis
DEP arises from the interaction between a non-uniform electric field and the induced dipole of a polarizable object (Figure 2A). The dielectrophoretic force can move the object toward the high electric field region or low electric field region depending on the effective polarization between the object and the medium. If the object has a higher polarizability, the force will push the object toward the high electric field strength region (positive DEP); otherwise, the force will point toward the low electric field strength region (negative DEP). DEP has been demonstrated to effectively manipulate various types of molecules, particles and cells.7, 12
Figure 2.
(A) Principle of dielectrophoresis. B) Modeling of dielectric responses of red blood cells (RBC) and E. coli in media of different conductivities.
The time-averaged dielectrophoretic force on a spherical object is given by:13
| (11) |
where R is the particle radius, Erms is the root mean square electric field, ω is the angular frequency, and K(ω) is the Clausius-Mossotti factor, which describes the frequency variation of the effective polarizability of the particle in the medium. The Clausius-Mossotti factor is defined by:
| (12) |
where and are the complex permittivities of the particle and medium, respectively.
For a homogenous material, the complex permittivity is given by:
| (13) |
where ε is the permittivity and σ is the conductivity of the particle and medium.
Several major characteristics of DEP should be noticed. First, DEP is most effective near the edge of the electrode, where the gradient of the electric field is strongest (F ~ ∇|Erms|2). The force rapidly decays with distance away from the electrode. Second, DEP depends on the applied frequency (F ~ K(ω)). For biological cells, the effective polarization of the cells (i.e., the frequency dependence) is determined by the cellular structures and their electrical properties. Distinct DEP spectra are observed for different cell types. Figure 2B shows the dielectric responses of mammalian cells and bacteria in different conductive conditions.14 Furthermore, DEP force is sensitive to the particle dimension (F ~ R3).
Microfluidic operations
Using AC electrokinetics, multiple microfluidic operations, such as pumping, mixing, and particle manipulation, can potentially be implemented within a single system with the proper microelectrode design and electronic interface.8, 15 This renders AC electrokinetics a promising strategy for microfluidic system integration. Recent advancements in microfluidic operations utilizing AC electrokinetics for physiological fluids are summarized in this section.
Pumping
Existing microfluidic systems often require external driving mechanisms (e.g., pumps or pressure sources) to accomplish transportation of reagents or samples within the devices. Incorporation of such mechanisms, however, greatly reduces the portability of the device for point-of-care applications.16, 17 This represents a fundamental hurdle for implementing μ-TAS in point-of-care diagnostic applications. Electrokinetic pumps, which do not involve any mechanical moving parts, can be fabricated easily and resolve the need of external driving mechanisms necessary for microfluidic system integration.18 Various electrokinetic pump designs have been proposed.19, 20 The electrolysis pump, for instance, can be applied to generate fluid motion in a microchannel.16 ACEF flow represents another promising method for fluid pumping in microchannels.21, 22 Recently, various ACEF pumps have been designed.
With a proper electrode design, an imbalance of the temperature and electric fields is created to break the symmetric competitive vortices and create a net fluid flow (Figure 3A). ACEF pump with an array of asymmetric microelectrode pairs has been demonstrated.23, 24 The study reported an asymmetric electrode design with low voltages (<15 Vrms) for driving fluids with conductivities between 0.02 and 1 S/m. Fluid velocities of 100 - 1,000 μm/s were reported. Furthermore, an asymmetric electrode array with biased AC signals has been reported (Figure 3B).25 Compared to pure AC signals, the DC bias increased the local ionic strength near the electrodes leading to a substantial conductivity gradient. This gradient could in turn induce a stronger ACEF. The design reached a linear velocity of 2.5 mm/s with 4.42 Vrms AC signal and 1.0 V DC bias. The volumetric flow rate or pumping pressure, however, was not specified in these studies.
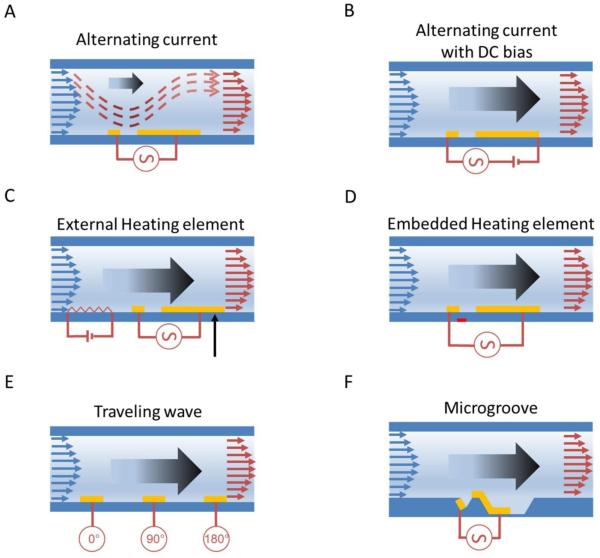
Figure 3.
Schematic illustration of six AC electrothermal pump designs. (A) Asymmetric electrodes design, (B) DC-biased AC electrothermal pump, (C) AC electrothermal pump with an external heating element, (D) enhanced AC electrothermal pumping with thin film resistive heaters embedded, (E) traveling-wave AC electrothermal pump, and (F) AC electrothermal fluidic pumping in micro-grooved channels
An important consideration for ACEF pumps is the creation of the temperature gradient by Joule heating, which depends on the sample conductivity. For a relatively low conductive medium (< 0.1 S/m), a high voltage is required to generate a large temperature gradient. This can be resolved via two approaches: 1) external heat source or 2) ACEF pump with voltage phase change. Inclusion of an external heat source can create a longitudinal temperature gradient and allows independent control of the temperature gradient and the electric field. For instance, Gimsa et al incorporated a separate heating electrode, in addition to the asymmetric electrode, in the microchannel (Figure 3C).26 The pump velocity was measured at conductivities varying from 0.1 S/m to 1.3 S/m and reached 20 μm/s with a voltage of 30 V peak-to-peak (Vpp). The velocities were shown to be relatively independent of the medium conductivity. Another approach of ACEF pump with external heating was also proposed.27 For this design, the heating element was embedded in the glass substrate (Figure 3D). Numerical simulation showed that the design provided over two times higher volumetric flow than Joule heating alone for the same input power.
The second type of ACEF pump designed involves a phase change of the electrical signal. A two-phase AC voltage was applied to the asymmetric electrode array in a high conductivity solution (0.224 S/m).28 The major advantage of the two-phase ACEF pump, as compared to the single phase pump, is enhanced electric field magnitude due to superposition of the electric fields produced by the different-phased electrodes. Numerically, the two-phase ACEF pump achieved at least 25% faster fluid flow rates than the single phase ACEF pump. Recently, a multi-phase ACEF pump with improved performance shown by theoretical and numerical simulation is also studied (Figure 3E).29 These results suggest design information necessary to build micro-pump systems for lab-on-chip applications. However, these concepts have not been verified experimentally.
Theoretically, a net pumping action can be generated as long as the design breaks the symmetric competitive vortices over the electrodes. In the asymmetric electrode design, the large effective vortices provide the major force pumping the fluid forward. However, the existence of small reversal vortices can greatly reduce the overall pumping capacity.30 Channel geometry modification has proven effective in addressing this issue. This concept was first demonstrated by Du et al via incorporation of microgrooved channels in the asymmetric electrode array design (Figure 3F).30 The microgrooves on the channel floor significantly reduced the effects of the reversal flows, which enhanced the overall pumping efficiency. In the study, the fluid conductivity was 0.1 S/m. The microgrooved structure increased the pumping capacity by five to six-fold as compared to a simple asymmetric electrode arrangement with the same effective dimensions.30, 31
Mixing
Mixing is essential in most biochemical assays. It is especially important for μ-TAS due to the laminar nature of microfluidic flows. The small characteristic length of a microchannel typically leads to a low Reynolds number (Re < 1), indicative of laminar flow. Without turbulent mixing, molecular advection in the microscale only relies on diffusion. The diffusion time scale can be estimated by T=L2/D, where L is the diffusion length and D is the mass diffusion coefficient. In a biochemical assay, e.g. protein or nucleic acid detection, the reaction time can be greatly limited by the low mass diffusion coefficient of the macromolecules. Therefore, effective mixing in microfluidic devices represents a key component towards the development of μ-TAS.5
Several methods have been developed for microfluidic mixing and can be categorized to two types: passive or active mixers. For passive mixers an external actuation mechanism other than fluid pumping is not required. Mixing can be enhanced by split-and-recombine, multi-laminating, Dean vortex, or 3D channel geometry dependent on the Reynolds number regime. For active mixers, external driving forces, such as pressure, ultrasound, magnetism, and electrohydrodynamics, are required.32 However, advantages of active mixers include shorter mixing time and simpler microchannel design. Numerous electrokinetic micromixers have been designed due to the effectiveness of electrokinetic mixing and the simplicity of the microelectrode fabrication compared to other active mixing approaches.33, 34 ACEF mixing, in particular, has received extensive attention for biomedical applications. Various ACEF mixers have been studied extensively using numerical approaches, and effective mixing can be accomplished in a shorter period of time compared to diffusion. Two ACEF mixer designs for reagent mixing are shown in Figure 4A and B. The mixer in Figure 4A consists of a pair of coplanar electrodes under two fluid streams. By applying a DC-biased AC voltage, an electrokinetic flow is induced with a flow profile perpendicular to that of incoming laminar streams of liquids to be mixed.35 An improved design has also been reported recently (Figure 4B).36 In this design, a pair of coplanar electrodes with a sinusoidal interelectrode gap was used to enhance the mixing in a microchannel.
Figure 4.
Schematic illustrations of electrode configurations for fluid mixing by AC electrothermal effect with (A) symmetric electrodes with AC voltage and DC bias, and (B) asymmetric meandering electrodes with AC voltage. Schematic illustrations of (C) AC electrothermal enhancement of heterogeneous assays, and (D) AC electrothermal enhancement of an electrochemical pathogen sensor.
In addition to reagent mixing, ACEF can be incorporated for assay enhancement. There are several advantages of ACEF for enhancement of biochemical assays, particularly for electrochemical assays. First, ACEF can be generated by the application of an AC potential to sensing electrodes, which can be easily integrated into the sensing platform.37, 38 Second, ACEF can apply on-chip stirring and heating, both of which enhance the sensor signal. Lastly, the ACEF can also reduce the background noise and enhance the specificity of the assay.
The biomedical applications for ACEF assay enhancement have been demonstrated.37, 39-42 Electrothermal assay enhancement was first demonstrated with biotin-streptavidin binding by optical detection (Figure 4C).39 More recently, an ACEF enhanced electrochemical biosensor was confirmed for pathogen identification and antimicrobial susceptibility testing.37, 43 In this design, ACEF enhancement was directly performed on a self-assembled-monolayer-based electrochemical sensor. The same set of electrodes was used for both electrochemical signal enhancement and electrochemical sensing leading to enhanced results. In particular, the sensitivity of the bacterial 16S rRNA hybridization assay was improved at least one order of magnitude and the incubation time was reduced 6-fold. The ACEF enhanced biosensor can be implemented within an enclosed microfluidic system leading to automated molecular diagnostics at the point of care (Figure 4D).16, 38
Another challenge of clinical diagnostics is the matrix effects of the physiological fluids, which can affect the assay performance.44 ACEF was shown to mitigate the matrix effect in an electrochemical biosensor.43, 45 ACEF enhancement was able to not only increase the specific bonding efficiency, but also reduce the background noise due to the matrix effect in clinical urine and blood samples. The study also showed multiplex detection of three uropathogenic clinical isolates with similar 16S rRNA sequences, illustrating the enhanced specificity of the assay. These results demonstrated that ACEF can significantly improve the signal-to-noise ratio of the biosensor for multiplex urinary tract infection diagnosis.
Bio-particles manipulation
The ability to selectively manipulate bio-particles, such as cells, DNA, and proteins, is important for various biological applications. Physical positioning of bio particles through techniques, such as trapping, focusing and isolation, is required to perform the biomedical analysis. Various manipulation techniques, such as optical tweezers,46 acoustic forces,47 and surface modification,48 have been reported. For clinical diagnostics at the point of care, the advantages of electrokinetics include simple system requirements, label-free manipulation and cost effectiveness. Particle manipulation can be applied to a wide spectrum of biomedical applications such as: rapid bacteria separation for antimicrobial susceptibility testing49, DNA extraction for pathogen identification50, and proteins concentration for biomarker discovery51 to name a few.
Dielectrophoresis (DEP) is one effective strategy for manipulation of bio-particles, such as mammalian cells, bacteria, yeast, DNA, and proteins. DEP-based cell manipulation has been demonstrated for different applications.49, 52-54 Figure 5A shows a schematic of using positive DEP to concentrate bacteria.55, 56 Positive DEP is typically performed in media with low conductivity in order to assure that the cells are more polarizable than the media. In contrast, negative DEP is more commonly observed in media with high conductivity. For instance, negative DEP force has been shown for cell manipulation, such as separation,14, 57, 58 concentration,14, 59 and patterning.60, 61 One of the designs of negative DEP patterning was proposed by Mittal et al (Figure 5B).60 The device was demonstrated to effectively position HeLa cells and 3T3 fibroblasts in conductive media by using negative DEP. The biocompatibility of their method was demonstrated by showing the patterned cells could proliferate and express a normal morphology. Cell separation can also be achieved by negative DEP.14, 57 One example is using DEP continuously to separate and to concentrate bacteria in physiological samples (Figure 5C,D).14 The device separates bacteria from diluted blood and cerebrospinal fluid. The separation efficiency of the device reached 90% at 30 μL/h. The bacteria were further captured and concentrated into a collection chamber using positive DEP. The bacteria capture efficiency was around 95% at 800 μL/h.
Figure 5.
Bioparticle manipulation: Schematic illustrations of (A) nanoscale bioparticle trapping, (B) DEP-based single-cell patterning for patterning, proliferating, and/or migrating cells, continuous cell (C) separation and (D) concentration, hybrid electrokinetic device for manipulating (E) bacteria and (F) cancer cells (focusing and separation).
During DEP manipulation, electrokinetics induced fluid motion should be considered as it can change the efficiency of DEP. The fluid motion introduces hydrodynamic drag force that washes away the DEP trapped particles or on the other hand, the fluid motion could enhance the performance of the DEP manipulation by introducing long range fluid motion. A hybrid electrokinetic manipulation system was proposed by Sin et al.34 In this hybrid electrokinetic device, the combination of DEP and ACEF allows separation, mixing, and concentration of colloidal particles ranging from nanometers to micrometers. Furthermore, Gao et al. demonstrated a 3-parallel-electrode configuration for continuous isolation of various bacteria and mammalian cells (figure 5E,F).62, 63 By properly designing the channel and operating condition, they demonstrated ACEF constrains target cells (E. coli) far away from the bulk solution toward the electrode surface, where DEP is most effective. Target cells can further trapped on the edges of the central electrode by DEP and EP (Figure 5E).62 Using a similar electrode design, the combination of DEP and ACEF resulted in different equilibrium positions of cancer cells and white blood cells in the flow channel, effectively separating the cells (Figure 5F).
Future Direction
AC electrokinetics has been demonstrated as a promising technique for fluid and particle manipulation, including pumping, mixing, concentration, and separation, in microfluidic systems. Although the potential of AC electrokinetics is established in numerous biomedical applications, little work has been done to integrate multiple electrokinetic sample preparation and sensing modules for laboratory automation. Since only microelectrodes and electronic interfaces are required, systems integration with AC electrokinetics can potentially cost-effective. The development of fully integrated electrokinetic systems is an important step to realize the potential of electrokinetics based μ-TAS for infectious disease diagnostics, early stage cancer detection, cell biology and other applications.
ACEF often occurs in electrokinetic manipulation of high conductivity media. By properly applying knowledge of the phenomenon, ACEF could be an effective AC electrokinetic technique for system integration leading towards point-of-care diagnostics because of its effectiveness at physiological conductivity.17 The technique is further applicable to various types of samples and applications. Since molecular advection and molecular binding efficiency are the fundamental barriers that are commonly observed in various biomedical assays, ACEF enhancement has a great potential to benefit other sensing platforms found in clinical and biochemical applications.
Another challenge for current electrokinetics-based μTAS is the volume mismatch between the microfluidic system and the physiological sample. For infectious disease diagnostics, samples from microliter to tens of milliliters are collected from patients. However present microfluidic system can typically handle on the order of ten to one hundred microliter solution. It is a fundamental obstacle that is necessary to surpass in order to move the technology toward clinical applications. In future research, it is important to develop a better strategy to handle a large volume of physiological sample within a short period of time.
Efforts should also be devoted to the fundamental understanding of electrokinetics. Most of the classical theories of electrokinetics are derived based on simplified assumptions, such as small temperature elevation and constant electrical properties of the fluids and the bio-particles. As the techniques and applications are expanding, these classical assumptions may not be valid and should be reconsidered. For instance, as the length scale of the system increases, natural convection, such as buoyancy, should be considered in ACEF design. Furthermore, heat convection has to be considered in systems handling a large volume. The effects of DC bias and hybrid electrokinetics should also be studied systematically.
Conclusions
The characteristics of two AC electrokinetic phenomena, DEP and ACEF, for manipulation of conductive physiological fluids have been discussed. These phenomena are particularly important in clinical diagnostics, as they relate to conductive samples. AC electrokinetics based operation, such as pumping, mixing and bio-particle manipulation, in microfluidics are reviewed. Future studies will lead to a fully integrated platform, which can quickly handle a large volume of physiological samples. It is important that a fully integrated ACEF model be created as it is lacking currently. Further understanding of the ACEF model would be useful to predict the electrohydrodynamic phenomenon in novel electrokinetic devices. Additionally, new ACEF techniques hold promise as a better tool for developing new biotechnology applications.
ACKNOWLEDGEMENTS
The authors thank Jose Miguel Valdez for his helpful suggestions and technical support. This work was supported by NIH Health Director's New Innovator Award (DP2OD007161) and NIAID (U01AI082457 and R44AI088756).
Nomenclature
- c
specific heat of the fluid
- Cp
heat capacity
- E
magnitude of the electric field
- Erms
root mean square electric field
- f
frequency of the AC voltage
- fc
crossover frequency
- 〈FE〉
time-averaged electrothermal force
- FDEP
dielectrophoretic force
- k
thermal conductivity
- K(ω)
Clausius-Mossotti factor
- L
characteristic length
- M(ω,T)
dimensionless factor of electrothermal force
unit vector in tangential direction
- Pe
Péclet number
- r
radial direction in cylindrical coordinate system
- R
particle radius
- T
temperature
- u
fluid velocity
- Vrms
root mean square voltage
Greek symbols
- α
parameter defined as α = (∂ε/∂T)/ε
- β
parameter defined as β = (∂σ/∂T)/σ
- ε
electrical permittivity
complex permittivity of the medium
complex permittivity of the particle
- θ
tangential direction in cylindrical coordinate system
- ρm
medium density
- ρq
charge density
- σ
the solution conductivity
- τ
charge relaxation time, τ = ε/σ
- ϕ
electrical potential
- ω
angular frequency of the AC voltage, ω = 2πf
Reference
- 1.Wang TH, Wong PK. Transforming Microfluidics into Laboratory Automation. Journal of Association for Laboratory Automation. 2010;15:A15–A16. [Google Scholar]
- 2.Whitesides G. Solving problems. Lab on a chip. 2010;10:2317–2318. doi: 10.1039/c0lc90036b. [DOI] [PubMed] [Google Scholar]
- 3.Culbertson CT, Mickleburgh TG, Stewart-James SA, Sellens KA, Pressnall M. Micro Total Analysis Systems: Fundamental Advances and Biological Applications. Anal Chem. 2014;86:95–118. doi: 10.1021/ac403688g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Sin ML, Gao J, Liao JC, Wong PK. System Integration - A Major Step toward Lab on a Chip. J Biol Eng. 2011;5:6. doi: 10.1186/1754-1611-5-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Sin ML, Mach KE, Wong PK, Liao JC. Advances and challenges in biosensor-based diagnosis of infectious diseases. Expert Rev Mol Diagn. 2014;14:225–244. doi: 10.1586/14737159.2014.888313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Ramos A, Morgan H, Green NG, Castellanos A. Ac electrokinetics: a review of forces in microelectrode structures. Journal of Physics D-Applied Physics. 1998;31:2338–2353. [Google Scholar]
- 7.Wong PK, Wang TH, Deval JH, Ho CM. Electrokinetics in micro devices for biotechnology applications. IEEE-ASME Transactions on Mechatronics. 2004;9:366–376. [Google Scholar]
- 8.Sin MLY, Gau V, Liao JC, Wong PK. Electrothermal Fluid Manipulation of High-Conductivity Samples for Laboratory Automation Applications. Jala-J Lab Autom. 2010;15:426–432. doi: 10.1016/j.jala.2010.05.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Castellanos A, Ramos A, Gonzalez A, Green NG, Morgan H. Electrohydrodynamics and dielectrophoresis in microsystems: scaling laws. Journal of Physics D-Applied Physics. 2003;36:2584–2597. [Google Scholar]
- 10.Green NG, Ramos A, Gonzalez A, Castellanos A, Morgan H. Electrothermally induced fluid flow on microelectrodes. Journal of Electrostatics. 2001;53:71–87. [Google Scholar]
- 11.Gonzalez A, Ramos A, Morgan H, Green NG, Castellanos A. Electrothermal flows generated by alternating and rotating electric fields in microsystems. Journal of Fluid Mechanics. 2006;564:415–433. [Google Scholar]
- 12.Wong PK, Chen CY, Wang TH, Ho CM. Electrokinetic bioprocessor for concentrating cells and molecules. Analytical chemistry. 2004;76:6908–6914. doi: 10.1021/ac049479u. [DOI] [PubMed] [Google Scholar]
- 13.Pohl HA. The Motion and Precipitation of Suspensoids in Divergent Electric Fields. J Appl Phys. 1951;22:869–871. [Google Scholar]
- 14.Park S, Zhang Y, Wang TH, Yang S. Continuous dielectrophoretic bacterial separation and concentration from physiological media of high conductivity. Lab on a chip. 2011;11:2893–2900. doi: 10.1039/c1lc20307j. [DOI] [PubMed] [Google Scholar]
- 15.Honegger T, Peyrade D. Comprehensive analysis of alternating current electrokinetics induced motion of colloidal particles in a three-dimensional microfluidic chip. J Appl Phys. 2013;113 [Google Scholar]
- 16.Sin MLY, Gau V, Liao JC, Wong PK. A Universal Electrode Approach for Automated Electrochemical Molecular Analyses. J Microelectromech S. 2013;22:1126–1132. doi: 10.1109/JMEMS.2013.2253545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Sin MLY, Gau V, Liao JC, Wong PK. Integrated microfluidic systems for molecular diagnostics: A universal electrode platform for rapid diagnosis of urinary tract infections. Nanotechnology Magazine, IEEE. 2013;7:31–37. [Google Scholar]
- 18.Laser DJ, Santiago JG. A review of micropumps. J Micromech Microeng. 2004;14:R35–R64. [Google Scholar]
- 19.Studer V, Pepin A, Chen Y, Ajdari A. An integrated AC electrokinetic pump in a microfluidic loop for fast and tunable flow control. Analyst. 2004;129:944–949. doi: 10.1039/b408382m. [DOI] [PubMed] [Google Scholar]
- 20.Shin W, Shin SJ, Lee JM, Nagarale RK, Heller A. A miniature, single use, skin-adhered, low-voltage, electroosmotic pumping-based subcutaneous infusion system. Drug Delivery and Translational Research. 2011;1:342–347. doi: 10.1007/s13346-011-0021-7. [DOI] [PubMed] [Google Scholar]
- 21.Fuhr G, Schnelle T, Wagner B. Traveling Wave-Driven Microfabricated Electrohydrodynamic Pumps for Liquids. J Micromech Microeng. 1994;4:217–226. [Google Scholar]
- 22.Muller T, et al. Trapping of micrometre and sub-micrometre particles by high-frequency electric fields and hydrodynamic forces. J Phys D Appl Phys. 1996;29:340–349. [Google Scholar]
- 23.Jie W, Lian M, Yang K. Micropumping of biofluids by alternating current electrothermal effects. Applied Physics Letters. 2007;90 234103-234103-234103. [Google Scholar]
- 24.Hong FJ, Cao J, Cheng P. A parametric study of AC electrothermal flow in microchannels with asymmetrical interdigitated electrodes. Int Commun Heat Mass. 2011;38:275–279. [Google Scholar]
- 25.Lian M, Wu J. Ultrafast micropumping by biased alternating current electrokinetics. Appl Phys Lett. 2009;94 [Google Scholar]
- 26.Stubbe M, Holtappels M, Gimsa J. A new working principle for ac electro-hydrodynamic on-chip micro-pumps. J Phys D Appl Phys. 2007;40:6850–6856. [Google Scholar]
- 27.Williams SJ. Enhanced electrothermal pumping with thin film resistive heaters. Electrophoresis. 2013;34:1400–1406. doi: 10.1002/elps.201200377. [DOI] [PubMed] [Google Scholar]
- 28.Zhang RM, Dalton C, Jullien GA. Two-phase AC electrothermal fluidic pumping in a coplanar asymmetric electrode array. Microfluid Nanofluid. 2011;10:521–529. [Google Scholar]
- 29.Liu WY, Ren YK, Shao JY, Jiang HY, Ding YC. A theoretical and numerical investigation of travelling wave induction microfluidic pumping in a temperature gradient. J Phys D Appl Phys. 2014;47 [Google Scholar]
- 30.Du E, Manoochehri S. Enhanced ac electrothermal fluidic pumping in microgrooved channels. J Appl Phys. 2008;104 [Google Scholar]
- 31.Du E, Manoochehri S. Microfluidic pumping optimization in microgrooved channels with ac electrothermal actuations. Applied Physics Letters. 2010;96 [Google Scholar]
- 32.Di Carlo D. Inertial microfluidics. Lab Chip. 2009;9:3038–3046. doi: 10.1039/b912547g. [DOI] [PubMed] [Google Scholar]
- 33.Sasaki N. Recent Applications of AC Electrokinetics in Biomolecular Analysis on Microfluidic Devices. Anal Sci. 2012;28:3–8. doi: 10.2116/analsci.28.3. [DOI] [PubMed] [Google Scholar]
- 34.Sin MLY, Shimabukuro Y, Wong PK. Hybrid electrokinetics for separation, mixing, and concentration of colloidal particles. Nanotechnology. 2009;20 doi: 10.1088/0957-4484/20/16/165701. [DOI] [PubMed] [Google Scholar]
- 35.Ng WY, Goh S, Lam YC, Yang C, Rodriguez I. DC-biased AC-electroosmotic and AC-electrothermal flow mixing in microchannels. Lab on a chip. 2009;9:802–809. doi: 10.1039/b813639d. [DOI] [PubMed] [Google Scholar]
- 36.Sasaki N, Kitamori T, Kim HB. Fluid mixing using AC electrothermal flow on meandering electrodes in a microchannel. Electrophoresis. 2012;33:2668–2673. doi: 10.1002/elps.201200099. [DOI] [PubMed] [Google Scholar]
- 37.Sin MLY, et al. In Situ Electrokinetic Enhancement for Self-Assembled-Monolayer-Based Electrochemical Biosensing. Analytical chemistry. 2012;84:2702–2707. doi: 10.1021/ac203245j. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Ouyang MX, et al. An AC electrokinetics facilitated biosensor cassette for rapid pathogen identification. Analyst. 2013;138:3660–3666. doi: 10.1039/c3an00259d. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Sigurdson M, Wang DZ, Meinhart CD. Electrothermal stirring for heterogeneous immunoassays. Lab on a chip. 2005;5:1366–1373. doi: 10.1039/b508224b. [DOI] [PubMed] [Google Scholar]
- 40.Feldman HC, Sigurdson M, Meinhart CD. AC electrothermal enhancement of heterogeneous assays in microfluidics. Lab on a chip. 2007;7:1553–1559. doi: 10.1039/b706745c. [DOI] [PubMed] [Google Scholar]
- 41.Huang KR, et al. Simulation on binding efficiency of immunoassay for a biosensor with applying electrothermal effect. J Appl Phys. 2008;104 [Google Scholar]
- 42.Li SS, Ren YK, Jiang HY. Convection and mass transfer enhanced rapid capacitive serum immunoassay. Rsc Adv. 2014;4:9064–9071. [Google Scholar]
- 43.Liu T, Lu Y, Gau V, Liao JC, Wong PK. Rapid Antimicrobial Susceptibility Testing with Electrokinetics Enhanced Biosensors for Diagnosis of Acute Bacterial Infections. Annals of biomedical engineering. 2014 doi: 10.1007/s10439-014-1040-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Chiu ML, et al. Matrix Effects-A Challenge Toward Automation of Molecular Analysis. Jala-J Lab Autom. 2010;15:233–242. [Google Scholar]
- 45.Liu TT, et al. Electrokinetic stringency control in self-assembled monolayer-based biosensors for multiplex urinary tract infection diagnosis. Nanomed-Nanotechnol. 2014;10:159–166. doi: 10.1016/j.nano.2013.07.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Wang XL, et al. Enhanced cell sorting and manipulation with combined optical tweezer and microfluidic chip technologies. Lab Chip. 2011;11:3656–3662. doi: 10.1039/c1lc20653b. [DOI] [PubMed] [Google Scholar]
- 47.Ding XY, et al. On-chip manipulation of single microparticles, cells, and organisms using surface acoustic waves. P Natl Acad Sci USA. 2012;109:11105–11109. doi: 10.1073/pnas.1209288109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Riahi R, et al. A microfluidic model for organ-specific extravasation of circulating tumor cells. Biomicrofluidics. 2014;8 doi: 10.1063/1.4868301. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Lu Y, et al. Single Cell Antimicrobial Susceptibility Testing by Confined Microchannels and Electrokinetic Loading. Anal Chem. 2013;85:3971–3976. doi: 10.1021/ac4004248. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Kalyanasundaram D, et al. Rapid extraction and preservation of genomic DNA from human samples. Anal Bioanal Chem. 2013;405:1977–1983. doi: 10.1007/s00216-012-6637-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Liao KT, Tsegaye M, Chaurey V, Chou CF, Swami NS. Nano-constriction device for rapid protein preconcentration in physiological media through a balance of electrokinetic forces. Electrophoresis. 2012;33:1958–1966. doi: 10.1002/elps.201100707. [DOI] [PubMed] [Google Scholar]
- 52.Albrecht DR, Underhill GH, Wassermann TB, Sah RL, Bhatia SN. Probing the role of multicellular organization in three-dimensional microenvironments. Nat Methods. 2006;3:369–375. doi: 10.1038/nmeth873. [DOI] [PubMed] [Google Scholar]
- 53.Taff BM, Voldman J. A scalable addressable positive-dielectrophoretic cell-sorting array. Anal Chem. 2005;77:7976–7983. doi: 10.1021/ac0513616. [DOI] [PubMed] [Google Scholar]
- 54.Chiou PY, Ohta AT, Wu MC. Massively parallel manipulation of single cells and microparticles using optical images. Nature. 2005;436:370–372. doi: 10.1038/nature03831. [DOI] [PubMed] [Google Scholar]
- 55.Chaurey V, et al. Scaling down constriction-based (electrodeless) dielectrophoresis devices for trapping nanoscale bioparticles in physiological media of high-conductivity. Electrophoresis. 2013;34:1097–1104. doi: 10.1002/elps.201200456. [DOI] [PubMed] [Google Scholar]
- 56.Chaurey V, Polanco C, Chou CF, Swami NS. Floating-electrode enhanced constriction dielectrophoresis for biomolecular trapping in physiological media of high conductivity. Biomicrofluidics. 2012;6 doi: 10.1063/1.3676069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Cheng IF, Froude VE, Zhu YX, Chang HC, Chang HC. A continuous high-throughput bioparticle sorter based on 3D traveling-wave dielectrophoresis. Lab Chip. 2009;9:3193–3201. doi: 10.1039/b910587e. [DOI] [PubMed] [Google Scholar]
- 58.Sabuncu AC, Beskok A. A separability parameter for dielectrophoretic cell separation. Electrophoresis. 2013;34:1051–1058. doi: 10.1002/elps.201200411. [DOI] [PubMed] [Google Scholar]
- 59.Park S, Koklu M, Beskok A. Particle Trapping in High-Conductivity Media with Electrothermally Enhanced Negative Dielectrophoresis. Analytical chemistry. 2009;81:2303–2310. doi: 10.1021/ac802471g. [DOI] [PubMed] [Google Scholar]
- 60.Mittal N, Rosenthal A, Voldman J. NDEP microwells for single-cell patterning in physiological media. Lab Chip. 2007;7:1146–1153. doi: 10.1039/b706342c. [DOI] [PubMed] [Google Scholar]
- 61.Voldman J. Electrical forces for microscale cell manipulation. Annu Rev Biomed Eng. 2006;8:425–454. doi: 10.1146/annurev.bioeng.8.061505.095739. [DOI] [PubMed] [Google Scholar]
- 62.Gao J, et al. Hybrid electrokinetic manipulation in high-conductivity media. Lab Chip. 2011;11:1770–1775. doi: 10.1039/c1lc20054b. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Gao J, Riahi R, Sin MLY, Zhang SF, Wong PK. Electrokinetic focusing and separation of mammalian cells in conductive biological fluids. Analyst. 2012;137:5215–5221. doi: 10.1039/c2an35707k. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Gabriel C, Gabriel S, Corthout E. The dielectric properties of biological tissues .1. Literature survey. Phys Med Biol. 1996;41:2231–2249. doi: 10.1088/0031-9155/41/11/001. [DOI] [PubMed] [Google Scholar]
- 65.Gabriel C, Peyman A, Grant EH. Electrical conductivity of tissue at frequencies below 1 MHz. Phys Med Biol. 2009;54:4863–4878. doi: 10.1088/0031-9155/54/16/002. [DOI] [PubMed] [Google Scholar]