Comment on “Cortical folding scales universally with surface area and thickness, not number of neurons”

Abstract

Mota and Herculano-Houzel (Reports, 3 July 2015, p.74) assign power functions to neuroanatomical data and present a model to account for evolutionary patterns of cortical folding in the mammalian brain. We detail how the model assumptions are in conflict with experimental and observational work and show that the model itself does not accurately fit the data.

How brains evolve to store more information has always been of interest to neurobiologists. There is clear evidence that changes in neuron production during development affect cortical morphology in adulthood (e.g., primary microcephaly), and that both neuron production and cortical morphology vary considerably across mammalian species. However, there remains considerable controversy over what developmental mechanisms and evolutionary selective pressures drive the cortex to fold as it does. Mota and Herculano-Houzel (1) recently presented a model which aims to explain both the developmental and evolutionary drivers of cortical folding through a single, universal power law. They arrive at their model using regression analyses on interspecific data and mathematical evaluations of the fractal folding patterns of paper. We think, however, that the authors have overlooked some key findings that may call into question some of their analytical assumptions, and that giving a second thought to some of the decisions the authors made in their analyses can only help to strengthen what we know about development and evolution of the mammalian brain.

The authors conclude that the cortical folding index regresses against brain mass with a “fairly low r²”. There are several issues here. Firstly, it is never explained how surface area and cortical thickness are calculated across all species and studies. No single method is indicated or explicated. Considering data were collected from studies that used different source material (histological slides, MRIs), different preservation techniques (formalin immersion, paraformaldehyde fixation), different methods (stereology, pachymetry), and that span 40 years of data collection, we think some deliberation on the effect of measurement variability on the authors’ results is warranted. Secondly, an r² = 0.75 (P < 0.0001) is considerably robust, and should really only be considered “fairly low” if compared to other models, which the authors do not do. Thirdly, Fig. 1E shows that “the folding index does not vary as a significant power function of cortical thickness across gyrencephalic species”, something that was previously shown (2), but the authors fail to cite. Fourthly, the regression analysis is conducted on only a selection of species (i.e., those below a certain folding index). As folding index is a continuous trait, the authors need to present some statistical justification for removing those data from their analysis. Previous work has found that the relationship between folding index and brain mass (and cortical neuron number) is best fit by two linear functions, leading to two mammalian groups (3), a result that is further supported by clustering analyses and phylogenetic modeling on gyrencephaly and life-history traits. Therefore, we think the authors’ claim that there are not “two clusters of gyrencephaly” is not justified. Rather, as in all scientific disputes, if they are confident that their model fits the data better than previous models, then it is incumbent on them to demonstrate it.

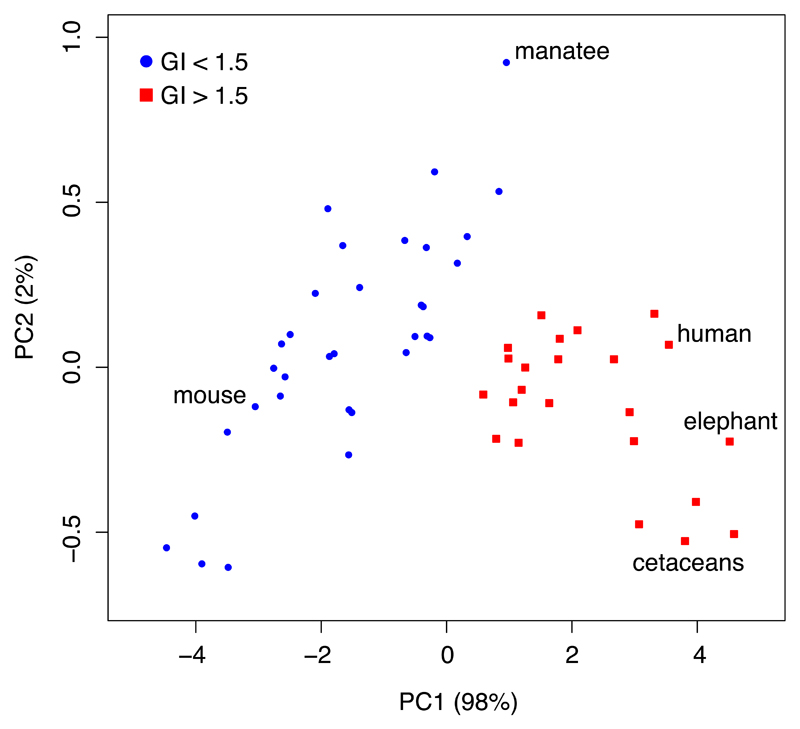
Fig. 1.

Two clusters of mammalian species with GI values either below (blue circle) or above (red square) 1.5. Total cortical surface area (A_G) and cortical thickness (T) data (Table S1 in 1) were log-transformed and a mixed clustering algorithm that utilises factorial analysis and a combination of hierarchical (Ward’s method) and K-means clustering was used to sort the species into distinct groups (implemented in the R package ‘FactoClass’ (9)). The clusters are shown using the two principal components of the data. Relevant species, or groups of species, are highlighted. The cat (Felis catus) is not shown (see 3).

Further to this point, we re-analysed the Mota and Herculano-Houzel data in Table S1, which contains cortical surface area (A_G) and thickness (T) estimates for 57 species. We show that A_G and T predict two clusters of species, one with a gyrencephaly index (GI) below 1.5 and one with a GI above 1.5 (Fig. 1). This recovers the original result reported in (3), in which high- and low-GI groups were identified with a boundary GI value of 1.5. Fig. 1 helps to clarify that species transitioning from the low- to the high-GI group must do so by increasing their cortical surface area with relatively little change in their cortical thickness.

The authors make several more statistical assertions without proper justification. If, as the authors assert, “the degree of gyrification is much larger in artiodactyls than in primates”, “a better fit is found for total surface area” as a function of folding index, and “the precise relationship between T and A_G across gyrencephalic species differs across orders”, then some statistical support needs to be implemented. This last statement, in particular, requires further analysis, as previous work has shown that the relationship between T and A_G disappears when phylogenetic relatedness, a hallmark of species comparisons (4), is taken into account (2). The authors cite (2,3) as corroborating evidence that “gyrification actually scales differently across mammalian orders”, even though the cited work shows quite the opposite. If statistical rigor is not implemented, then the authors’ assertions appear, to the reader, to be subjective interpretations of the data. Likewise the (mis)representation of previous work.

The most recent common mammalian ancestor was gyrencephalic (3,5). There have been many transitions in mammalian evolution from gyrencephaly to lissencephaly (3,6). Experimental work in the marmoset has shown that, despite being a lissencephalic species, it retains the neurogenic program of a gyrencephalic species (6). Together, these studies strongly suggest that species may evolve a lissencephalic phenotype from a gyrencephalic one, exemplifying secondary lissencephaly. The authors do not address this evidence in their claim that “there is no such thing as “secondary lissencephaly” ”, nor in their interjection that “Remarkably, there is no a priori reason for lissencephaly”. They furthermore suggest that the earliest mammalian brain was “smooth”, not only omitting contradictory evidence (3,5), but citing as evidence work that makes no claim whatsoever to the smoothness of the earliest mammalian brain (ref. 31 in their paper).

Finally, there is formidable corroboration for a positive role of the developmental neurogenic program in determining the folding pattern of the adult cortex. Experimental work in mammals has demonstrated a predictive relationship between the distribution of neuron progenitors along the ventricle during development and the programmed pattern of gyri and sulci in the adult (7). These patterns are preceded by distinct gene expression profiles particular to prospective gyri and sulci in the developing neocortex (8). This explains, in part, why we see conserved patterns of cortical folding across closely related species, even when those species have considerably different folding indices (see 2). The authors’ “crumpled paper” model, which claims that gyrencephaly is not achieved “through the generation of larger numbers of neurons”, but is instead the mechanistic byproduct of surface area expanding faster than cortical thickness over evolutionary time, does not account for these phenomena observed across species at the morphological, cellular, and genomic level.

The analytical and conceptual approach that Mota and Herculano-Houzel bring to the study of cortical development is crucially important and presents great potential in moving the field forward. However, in light of the statistical errors and failures to address work that challenges their conclusions, we think the claims they make are not sufficiently supported and therefore should not yet be taken as rote formulae for explaining mammalian brain evolution.