Confounding, effect modification and the odds ratio: Common misinterpretations

Introduction

When investigators report the results of observational studies or randomized controlled trials (RCTs), they often adjust for covariates using multivariable regression models, or stratify analyses. The intervention effect estimate is often expressed as an adjusted odds ratio (OR_adj). In an RCT where confounding bias is absent, many investigators would interpret differences in stratum-specific ORs to mean that the actual causal effect of the intervention is dependent on the presence or absence of the covariate (causal effect modification). However, even in the absence of both bias and causal effect modification, it is a mathematical certainty that the OR in each stratum of a variable will differ if the stratifying variable increases the risk of the outcome independent of intervention!

How significant is this problem? Analyses stratified by sex are often recommended by authors [1] and granting agencies (http://grants.nih.gov/grants/guide/pa-files/PA-13-018.html). In a recent review examining subgroup analyses in RCTs with dichotomous outcomes, 52% (120/229) conducted subgroup analyses[2]. Of these, 86/120 (72%) studies reported subgroup analyses using the OR or hazard ratio. If logistic or Cox regression is the analysis conducted, and the outcome is common (e.g. some cardiovascular diseases), this under-recognized fact may lead investigators and clinicians to inappropriate conclusions such as suggesting treatment effectiveness is different in diabetics vs. non-diabetics, male vs. female, etc. The same issues also affect conclusions about confounding when the crude (unadjusted) OR is different from the multiple logistic regression OR_adj. The purpose of this article is to explain why this occurs through simple extensions of commonly known principles.

Background

Although more precise statistical language is sometimes used, for simplicity, in this paper 1) “adjustment” refers to including a variable in a regression analysis unless otherwise specified, and 2) causal effect modification means that the biological effect of the intervention is either stronger or weaker in the presence of the covariate (causal effect modifier) [3, 4]. We will use a restricted definition of causal effect modification, where it only exists if the effects across strata are different on both the additive and multiplicative scales. For example, we consider that there is no causal effect modification if a variable’s mechanism of action is such that mortality increases by an absolute 10% regardless of baseline risk (i.e. from 10% to 20%, 30% to 40%, 40% to 50%; RD is constant across strata) even though the RR across strata are different. Similarly, there is no causal effect modification if the variable’s mechanism of action is such that mortality increases 1.5-fold regardless of baseline risk (i.e. from 10% to 15%, 20% to 30%, 30% to 45%; RR constant across strata) even though the RD across strata are different.

Several authors have previously illustrated that the crude estimate of the OR from logistic regression (and hazard ratio from Cox regression), is not equal to the adjusted estimate even in the absence of confounding [5–7], but they have always used examples where the risk ratios in each stratum were also different. However, the problem of misinterpretation of effect modification using OR has not been widely under concern. In this report, we focus on causal effect modification and illustrate an example in the absence of both bias and differences in stratum-specific risk ratios. We further explain that one way to view the results of others [5–7] is simply as a more complex example of our illustration. Finally, we provide three examples from the literature (1 RCT and 2 observational studies) where the authors interpreted the interaction term from an odds ratio derived by logistic regression as causal effect modification, without providing the information necessary to determine if the observed differences were truly due to causal effect modification, or simply an example where the stratum-specific OR are different for mathematical reasons alone (i.e. no causal effect modification), or a combination of the two.

Example

To illustrate the effect, let us consider a serious illness where the 1-year untreated mortality in the population is 52%. Let us consider a randomized controlled trial (RCT) of 1,000 patients comparing Drug A vs. placebo (Table 1). The proportion of diabetic patients (and severity of diabetes) in each group is identical at 30% so there is no confounding by diabetes, or baseline differences between intervention groups. We will use a multiplicative causal mechanism and say that Drug A reduces mortality by 50% regardless of baseline risk, with the specific example showing a mortality reduction from 52% to 26%. Further, the 50% reduction is true for both non-diabetics and diabetics.

Table 1.

Simulated data for a randomized study of 1,000 participants where 30% of participants are diabetics. Diabetes increases the risk of death, but the treatment reduces mortality by 50% (on a multiplicative scale) in both diabetics and non-diabetics. The relative risk is collapsible. The crude odds ratio is a population weighted average of the odds ratio in the two strata (population standardized odds ratio).

	Dead	Alive	Total	Risk	Relative Risk (95%CI)	Odds Ratio (95%CI)
All Patients
Treated	130	370	500	26%	0.50 (0.42 to 0.59)	0.32 (0.25 to 0.43)
Control	260	240	500	52%
Total	390	610	1000
Non-Diabetic Patients
Treated	70	280	350	20%	0.50 (0.39 to 0.64)	0.38 (0.26 to 0.53)
Control	140	210	350	40%
Total	210	490	700
Diabetic Patients
Treated	60	90	150	40%	0.50 (0.40 to 0.62)	0.17 (0.10 to 0.29)
Control	120	30	150	80%
Total	180	120	300

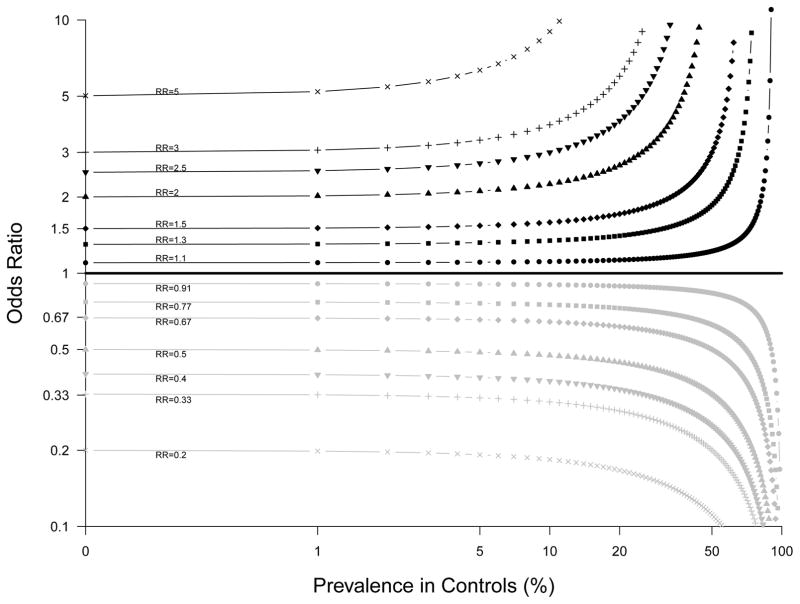
At the top of Table 1, we see the RR for the overall group is indeed 0.5, and the OR is 0.32. The difference between the RR and OR is simply illustrating the well-known fact that the OR represents an overestimation of the risk as expressed by the RR when the disease is common [8–11], which is the context of the current example (untreated mortality equals 52%). This overestimation is illustrated in Figure 1.

Figure 1.

The relationship between odds ratio (OR) and relative risk (RR) using log scales (adapted from [8, 9, 11]). The relationship is curvilinear for each RR, with the slope increasing as the prevalence in controls increases, and as RR increases.

In the bottom of Table 1, the results are presented for diabetics and non-diabetics separately. Once again, the RR is 0.5 for each group as previously stated – there is no confounding or causal effect modification. However, when we examine the results for OR, we see that the OR for diabetics is 0.17 (95%CI: 0.10 to 0.29), and the OR for non-diabetics is 0.38 (95%CI: 0.26 to 0.53). Finally, when intervention, diabetes and the interaction term intervention*diabetes are all entered into a logistic regression model with death as the outcome, the interaction term in the example has a p-value of 0.01. A naïve interpretation of the OR estimates in Table 1 (without knowing the RR because it is not usually reported in logistic regression analyses) is that there is strong evidence for a biological interaction between Drug A and diabetes (or that diabetes is a marker for another causal effect modifier). However, there is neither confounding nor causal effect modification in our hypothetical data, and the RR results across the strata in Table 1 are consistent with absence of causal effect modification, in that the decreased risk with treatment on the multiplicative scale is independent of the baseline risk.

Explanation of the Stratum Specific OR Effect

Although other authors have provided more elaborate explanations and examples of similar effects [5, 6, 12–14], one perspective is simply to view our example as an extension of the fact that the OR and RR are two different effect measures, and the OR is known to overestimate the RR when the disease is common. In Figure 1, the slope of the relationship between OR and RR increases as the prevalence of the outcome in controls increases. Therefore, when the RR is constant across different strata of a covariate (as in our simulated data), the OR will overestimate the RR by different magnitude if the prevalence of the control risk within each of the stratum is different. In other words, the stratum-specific OR must be different even though there is no confounding or causal effect modification. Although the magnitude of the differences between conditional and marginal OR has recently been characterized across a wide range of conditions [15], the magnitude of the differences in stratum-specific OR is revealed in Figure 1. These differences will increase as the proportion of controls with the outcome increases, and as the RR increases. Further, increasing the causal effect of the stratifying variable on the outcome would also lead to an increased difference between stratum-specific results. These relationships are illustrated in Figure 2. Practically speaking, if the rare disease assumption holds within each stratum (e.g. <10% of participants have the outcome), the effect would be minimal except at very high RR. Therefore, if the OR is used as the effect measure, as is common with logistic regression, these assumptions need to be verified for appropriate interpretation. Of note, the effect we report only occurs with regression-adjusted OR and stratum-specific OR, but does not occur if one uses population-standardized OR (or population standardized RR/RD) [5].

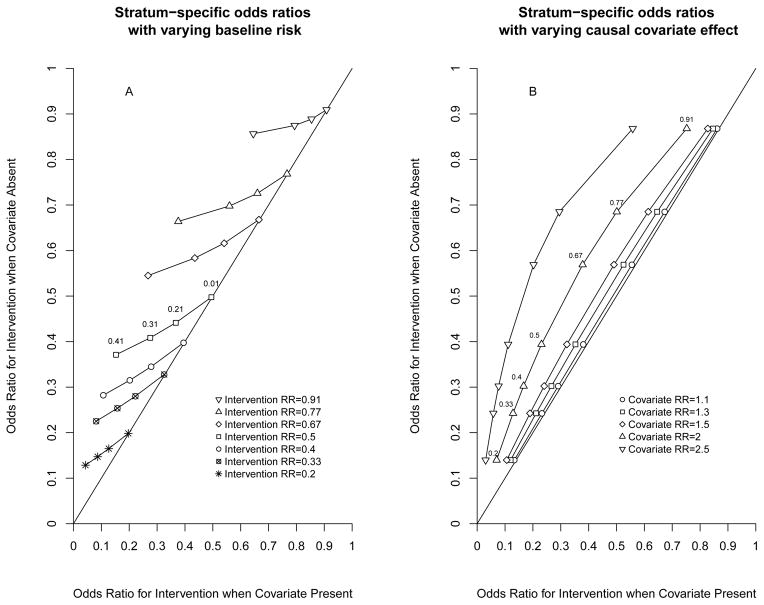
Figure 2.

Graphs illustrating how stratum specific odds ratios (OR) will differ even when there is no bias or causal effect modification. In both panels, the OR for the intervention when the covariate is absent (y-axis) is plotted against the OR for the intervention when the covariate is present (x-axis). Any deviation from the line of identity on the graph means that the OR in the two different strata are different. In A, the effect of the covariate is held constant and doubles the risk of the outcome. Each set of symbols represent a particular relative risk (RR) for the intervention, but at increasing baseline risks from 0.01 (rightmost point) to 0.41 (leftmost point). The difference between the stratum-specific OR increases as the baseline risk increases, and as the RR increases, but is negligible at very low baseline risks. In B, the baseline risk under control conditions in the absence of the covariate is held constant at 35%. Each set of symbols represents a particular strength for the covariate effect (e.g. upright triangles Covariate RR=2 mean the covariate doubles the risk of the outcome), with each symbol representing the OR at intervention RR ranging from 0.2 (lowest point) to 0.91 (highest point). The difference between stratum-specific OR increases as the strength of the covariate increases (from left to right). Because the baseline probability is held constant at 35%, the maximum covariate RR shown is 2.5 (e.g. covariate RR=3 would give an impossible probability of 1.05).

Although the current example described results from an RCT and explored causal effect modification, the same principle holds true for confounding within observational studies, or for analyses examining chance baseline imbalances of prognostic factors in RCTs. In the example in Table 1, by definition, the strength of the potential confounder (diabetes)-treatment assignment is nil. Had we changed the strength of this association to any non-zero value, diabetes would have been considered a confounder. However, there would still have been differences in the prevalence of the outcome across the different strata. In this context, differences between the crude OR and the stratum-specific OR are more complex because they depend on the balance between changing prevalence, bias, and causal effect modification. For example, others have illustrated that the effect can appear in the reverse: in the presence of causal effect modification without bias, the stratum-specific OR may appear the same as each other, but different from the crude OR (which might be misinterpreted as bias rather than causal effect modification because the stratum-specific OR are the same) [13, 15]. Finally, the same principle applies to rate ratios and hazard ratios [5, 16]. Intuitively, this must be true because the OR estimated using an incidence-density sampling approach approximates the rate ratio.

Specific Examples from the Literature

In a RCT investigating the effect of lottery-based incentives on warfarin adherence [17], the proportion of participants who ended up with the primary or secondary outcome was approximately 20–40% depending on the subgroup and analysis. In the subgroup with INR below target range (under anticoagulated), the probability of non-adherence was approximately 0.26 in the lottery group and 0.4 in the control group, and the OR for non-adherence using lottery-based incentives is 0.53. In the subgroup where INR was within the target range, the probability of non-adherence was approximately 0.18 in the lottery group and 0.19 in the control groups, and the OR for non-adherence using lottery-based incentives was 0.94. Nevertheless, if we calculate the RR using these probabilities, the RR would be 0.26/0.4=0.65 in the subgroup with INR below target range, whereas the RR would be 0.18/0.19=0.95 in the subgroup with INR within the target range. Therefore, effect modification suggested by the differences in the subgroup OR (0.53 and 0.94) is greater than the effect modification suggested by the differences in the subgroup RR (0.65 and 0.95), even though both use a multiplicative scale. As the prevalence of the outcome is different across strata, the divergence between the two reported ORs must be different than the difference between the two unreported stratum-specific risk ratios, and the p-value for interaction on the OR scale does not represent the p-value for interaction on the RR scale.

In an observational study on activity (independent variable) and obesity (outcome), Steeves et al [18] categorized subjects in the NHANES data as having high or low occupational activity (equivalent to diabetes in our example). Each subject was also categorized as having non-occupational activity equal to none, insufficient and sufficient (equivalent to treatment in our example). Using logistic regression and odds ratios, they report an interaction between occupational and non-occupational activity on the outcome obesity. However, the authors adjusted for some variables in the logistic regression results but did not present the prevalence adjusted for the same set of variables (required to calculate the effect we describe). Therefore, we cannot determine the magnitude of the effect, and their results should not be interpreted as evidence for causal effect modification.

Finally, Dye et al [19], examined the NHANES data to see if there was an interaction between race and smoking on the outcome of perceived need for filling or replacing teeth (one outcome among many). In this study, the prevalence of the outcome varied by smoking and by race. The odds ratio results from a logistic regression were reported as “smoking status did produce a significant interaction with race/ethnicity…”. Without an analysis of the prevalence of the outcome within the levels of the intervention (i.e. smoking status) for the levels of the control group (e.g. reference category for ethnicity), such an interpretation is inappropriate.

In conclusion, logistic regression is an important tool and reporting adjusted OR (or Cox regression and rate ratios) is appropriate in many contexts. However, investigators and readers should be wary of claims of effect modification or biological interaction when the covariate is known to be an independent cause of the outcome, and the disease is common.

Appendix

Let us consider a hypothetical study with binary outcome Y, treatment A, a binary covariate X. Denote the prevalence of outcome in control within the stratum X=1 as: P₀₁ = P(Y = 1|A = 0, L = 1), and the prevalence of outcome in control within the stratum X=0 as : P₀₀ = P(Y = 1|A = 0, L = 0). Let us assume that there is not effect modification in multiplicative scale. Therefore, the risks of outcome in treatment groups are increased or decreased by the common RR for both strata. It follows that:

$$\begin{array}{l}{P}_{11}=P(Y=1\mid A=1,L=1)=RR\times P_{01}\\ P_{10}=P(Y=1\mid A=1,L=0)=RR\times P_{00}\end{array}$$

We can then calculate the stratum-specific OR. For X=1:

$$O{R}_1=\frac{P_{11}/(1-P_{11})}{P_{01}/(1-P_{01})}=\frac{RR\times P_{01}/(1-RR\times P_{01})}{P_{01}/(1-P_{01})}=\frac{RR(1-P_{01})}{1-RR\times P_{01}}$$

where RR × P₀₁ ≠ 1, Similarly, for X=0:

$$O{R}_0=\frac{RR(1-P_{00})}{1-RR\times P_{00}}$$

where RR × P₀₀ ≠ 1. The stratum-specific OR can be then expressed as a function of the common RR and the prevalence in controls (denoted by P):

$$OR=\frac{RR(1-P)}{1-RR\times P}.$$

If we consider the common RR fixed, the first derivative of the function is given by:

$$\frac{RR(RR-1)}{{(1-RR\times P)}^2}.$$

When the fixed common RR>1, the first derivative is always positive, therefore the function is monotonically increasing. We have OR₁ > OR₀ if P₀₁ > P₀₀. When the fixed common RR<1, the first derivative is always negative, therefore the function is monotonically decreasing. We have OR₁ < OR₀ if P₀₁ > P₀₀. When the fixed common RR=1, we have OR₁ = OR₀ and there is no effect modification by either RR or OR.