Skip to main content
PMC home page
ACS Central Science logoLink to ACS Central Science
. 2016 May 5;2(5):316–324. doi: 10.1021/acscentsci.6b00063

A Direct Mechanism of Ultrafast Intramolecular Singlet Fission in Pentacene Dimers

Eric G Fuemmeler †, Samuel N Sanders §, Andrew B Pun §, Elango Kumarasamy §, Tao Zeng †, Kiyoshi Miyata §, Michael L Steigerwald §, X-Y Zhu §, Matthew Y Sfeir ∥,*, Luis M Campos §,*, Nandini Ananth †,*
PMCID: PMC4882733  PMID: 27280166

Abstract

graphic file with name oc-2016-00063r_0003.jpg

Interest in materials that undergo singlet fission (SF) has been catalyzed by the potential to exceed the Shockley–Queisser limit of solar power conversion efficiency. In conventional materials, the mechanism of SF is an intermolecular process (xSF), which is mediated by charge transfer (CT) states and depends sensitively on crystal packing or molecular collisions. In contrast, recently reported covalently coupled pentacenes yield ∼2 triplets per photon absorbed in individual molecules: the hallmark of intramolecular singlet fission (iSF). However, the mechanism of iSF is unclear. Here, using multireference electronic structure calculations and transient absorption spectroscopy, we establish that iSF can occur via a direct coupling mechanism that is independent of CT states. We show that a near-degeneracy in electronic state energies induced by vibronic coupling to intramolecular modes of the covalent dimer allows for strong mixing between the correlated triplet pair state and the local excitonic state, despite weak direct coupling.

Short abstract

We identify a specific, high-frequency, intramolecular vibrational mode that assists direct population transfer from the LE state to the ME state through an avoided crossing.

Singlet fission, the process by which one singlet exciton splits into two triplet excitons, is proving an important property for materials used in third-generation solar cells and photodetectors, among other optoelectronic devices.1−3 Unfortunately, technological applications are limited by the small number of organic chromophores that undergo efficient singlet fission,4,5 and are largely restricted to molecular crystals of oligoacenes and related materials that exhibit intermolecular singlet fission (xSF).6−10 Insights into the mechanism of xSF have been obtained by tuning spatial interchromophore interactions;6,11−14 however, the sensitivity of the mechanism to crystal packing orientations poses a significant challenge. As such, devices based on xSF are limited by the lack of high throughput processing strategies to create highly ordered molecular structures. In contrast, recently reported efficient intramolecular singlet fission (iSF) materials15−22 offer significant advantages in terms of their tunable molecular and electronic structure, solution processability, and the ability to form tailored interfaces.23−27 However, a limited understanding of the fundamental process of triplet pair (2×T1) formation hinders the design of versatile iSF materials. It is therefore imperative to uncover the detailed mechanism of iSF and to establish its relationship to chemical structure. Current literature on the mechanism of xSF is in general agreement that charge-transfer (CT) states play a significant role in mediating the coupling between local excitonic (LE) singlet states formed upon photon absorption and the correlated triplet pair1(TT) or multiexcitonic (ME) state.28−34 In addition, the CT-mediated mechanism has been implicated in iSF polymers, using strong-donor/strong-acceptor interactions along the conjugated backbone and leading to high yields of triplet pairs upon photoexcitation in dilute solution.16,35 However, iSF materials that operate by this mechanism can suffer from relatively short triplet lifetimes and parasitic loss pathways involving charge-separated and dark singlet states,16 decreasing the net yield of triplet pairs.

Recently, covalently coupled pentacene dimers were synthesized and demonstrated to yield triplet pairs nearly quantitatively (∼200% triplet yield) by ultrafast, sub-picosecond iSF.15,18,22 From a practical standpoint, bipentacenes are the first family of iSF chromophores with excited state dynamics on time scales comparable to xSF in crystals. Although it is known that pentacenes meet the energetic criteria for singlet fission, where the energy of the singlet state is at least twice the energy of the triplet state, E[S1] ≥ 2E[T1], the mechanism of iSF in pentacene dimers is unclear. In particular, the role of CT states in mediating iSF is called into question: low-lying CT states are not expected based on the molecular structure, and experimental measurements of iSF rates show relative insensitivity to changes in solvent properties. This raises the possibility of an alternate direct coupling mechanism, where the correlated triplet state is directly populated from the singlet manifold, a pathway previously ruled out in the case of xSF materials (Figure 1A).30,31,34,36,37 Since the rates of iSF and triplet–triplet recombination vary dramatically as a function of the coupling interactions in the bipentacene, it is clear that structure–property relationships can be exploited to control excited state dynamics and to test different mechanisms for the SF process.38

Figure 1.

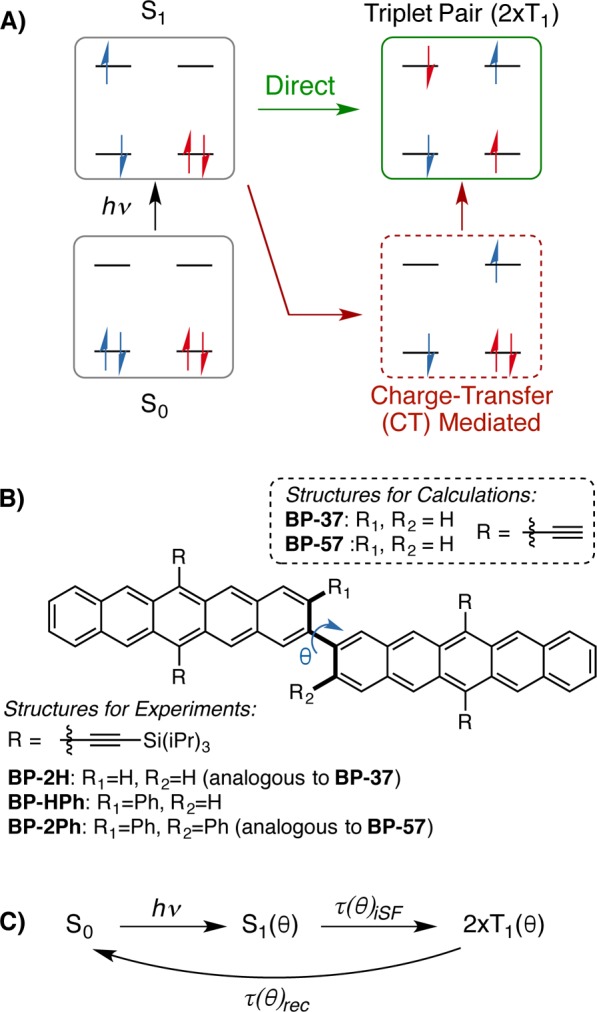
Figure 1

Open in a new tab

(A) Direct (in green) and charge transfer mediated (in red) mechanisms of singlet fission. (B) Molecules studied in this manuscript, where the abbreviations represent bipentacene and its dihedral angle θ (BP-θ) where θ = 37°, 42°, and 57° for the various twist angles. (C) Schematic excited state rates that depend on dihedral angle, θ, after excitation (hν) to the singlet state (S1): rate of intramolecular singlet fission (τiSF) and the rate of triplet pair (2×T1) recombination (τrec).

Here, we start by investigating the direct coupling mechanism, where a vibronically induced degeneracy between the local excitonic (LE) and multiexcitonic (ME) states leads to ultrafast iSF despite a small coupling matrix element between the LE and ME states. We identify a specific, high-frequency, intramolecular vibrational mode that assists direct population transfer from the LE state to the ME state through an avoided crossing (see Supporting Information movie). This demonstrates that ultrafast iSF can occur via the direct coupling mechanism in covalently linked pentacene dimers and does not require CT mediation. We note that an avoided crossing previously identified along an intermonomer mode in cofacial pentacene dimers was shown to be an artifact of the calculation method,32,36 and although intramonomer ring-breathing modes have been identified as important in xSF,39,40 their role has not been clearly established. We also investigate the possibility of a CT-mediated superexchange mechanism for iSF in bipentacenes. We show that although iSF rates sensitively depend on the dihedral angle, CT state energies are largely independent of this factor. Experimental measurements establish the independence of iSF rates on solvent properties, specifically orientational polarizability. Furthermore, using both theory and experiment, we quantify the role of structural factors (Figure 1B) by studying the change in rates of iSF with the dihedral angle, θ, between monomers (Figure 1C). While the direct coupling mechanism correctly predicts the observed change in iSF rate with dihedral angle, the indirect couplings that drive CT-mediated singlet fission do not show concomitant change. Taken together, these insights into the mechanism of iSF from experiment and theory suggest a new class of materials where the direct coupling mechanism is important.

The Excited Adiabatic and Diabatic States of BP-37

We begin our theoretical investigation with the parent bipentacene, BP-37, where the notation indicates the calculated dihedral angle of the minimum energy structure, θ = 37°. This compound is a simplified version of the experimentally measured BP-2H, which undergoes iSF with a 0.76 ps time constant in ∼200% triplet yield, followed by triplet pair recombination with a time constant of 450 ps.15 In the truncated version, the solubilizing tri-isopropylsilyl groups are replaced with hydrogens. We establish that the solubilizing groups present in the experimental study do not affect the electronic structure of the monomer significantly (Supporting Information), in agreement with previous work.41 We optimize the geometry of the substituted pentacene monomer and establish that its geometry changes little upon dimerization. This allows us to define the dimer reference geometry as two substituted pentacene monomers linked through a covalent bond of length 1.48 Å at the 2- and 2′-positions (Figure 1B). The excited state energies of BP-37 are obtained from complete active space self-consistent field theory (CASSCF) calculations with extended multiconfiguration quasi-degenerate perturbation theory (XMCQDPT).32,42 The adiabatic eigenstates obtained from these calculations are labeled Si, where i = 0 indicates the ground state and higher values of i represent the excited states. Throughout this manuscript, we also employ quasi-diabatic states constructed by rotating the adiabatic states into a local state basis. The reference diabatic states are labeled following standard notation where the first index of the label refers to monomer A and the second index refers to monomer B in the dimer. The low-lying diabatic states are shown in Figure 2 and correspond to the ground state gg, the ME state, tt, the two singlet LE states, eg and ge, the two CT states, ac and ca, and the doubly excited states, dg and gd. We will use these adiabatic and diabatic states to aid in the analysis of both the direct coupling and CT-mediated superexchange pathways for iSF in bipentacenes.

Figure 2.

Figure 2

Open in a new tab

Eight lowest diabatic configurations (excited states in gray boxes) represented using the highest occupied molecular orbital (HOMO) and lowest unoccupied molecular orbital (LUMO) on each monomer (A and B), highlighting the various states: charge transfer (CT), multiexcitonic (ME), doubly excited (DE), and local excitonic (LE).

The Direct Coupling Mechanism

We find that an eight-orbital/eight-electron (8o8e) active space is necessary to yield accurate excited adiabatic state energies for the dimer,17,43,44 and our results are shown in Table 1. In order to quantify the direct coupling mechanism we perform a rotation of the adiabatic states into a localized, diabatic state basis.29,30,45−47 Unfortunately, using the 4-fold diabatization scheme48,49 (Supporting Information) in the 8o8e active space yields inaccurate quasi-diabatic state configurations that account for <85% of the higher lying adiabatic states. Therefore, we construct an accurate diabatic state representation of the Hamiltonian at the 8o8e level of theory by including only the three lowest lying adiabatic excited states shown in Table 2. We analyze the contribution to the excited adiabatic states from individual state configurations and find no significant CT character in states within 1 eV of the first excited state. The adiabatic state with primarily ME character (S1) is slightly higher in energy than the adiabatic states that have primarily LE character (S2 and S3). We find that there is weak direct coupling between the LE and ME states,

graphic file with name oc-2016-00063r_m001.jpg

at the reference dimer geometry and that the energy difference between the LE and ME states (∼50 meV) is small, as compared to previously reported values for other acenes.12,30−32 The near coincidence of energies of the LE and ME states and the large energy gap between these states and the states with significant CT character suggests a difference in the mechanism of iSF in the present molecules from an earlier study of xSF in a staggered cofacial pentacene dimer.32

Table 1. Lowest Vertical Excitation Energies of the Covalent Dimer at the Reference Geometry.

state 8o8e vertical energy (eV)
S1 1.96a
S2 1.96
S3 2.01
Open in a new tab
a

Experimental bright state at 1.88 eV.

Table 2. Diabatic 4-State Hamiltonian Matrix Calculated Using an 8o8e Active Space (in meV) at the Reference Geometry of BP-37.

  gg ge eg tt
gg 0.0 –18.7 –18.7 –27.0
ge –18.7 1961.2 0.8 –2.2
eg –18.7 0.8 1961.2 –2.2
tt –27.0 –2.2 –2.2 2009.7
Open in a new tab

The small energy separation suggests that vibrational relaxation might induce a change in the character of the lowest singlet state, necessary for efficient iSF. The next step is to identify key vibrational modes that couple strongly to the electronic states and to evaluate their role in promoting mixing of the LE and ME states. Since BP-37 is a weakly coupled dimer, we focus on the normal modes of the substituted pentacene monomer. We project the geometric distortion accompanying relaxation, from the ground state structure (vertical excitation) to the optimized S1 and T1 monomer structures, onto the corresponding set of normal modes. We find a dominant monomer ring-breathing mode at 1435 cm–1 based on the magnitude of energy changes along the relaxation pathway and a significant Huang–Rhys factor (Supporting Information). Not surprisingly, this mode is consistent with the vibronic progression spectrum of an unsubstituted pentacene monomer50,51 and in agreement with previous work that suggests the importance of a ring-breathing mode,39,40 although an avoided crossing has not been identified.

We use this ring-breathing mode to generate a two-dimensional potential energy surface (PES) for the excited states along the dimensionless coordinate, Q, corresponding to the two monomer normal modes at 1435 cm–1. We use an inexpensive and efficient occupation restricted multiple active space spin flip (ORMAS-SF) approach to rapidly scan the PES and identify geometries of interest.52,53 A limited number of XMCQDPT calculations are then performed with an 8o8e active space at these geometries to obtain accurate excited state energies. Performing a diabatization as described earlier, we obtain three excited diabatic state potential energy surfaces along the diagonal of vector Q, where Q = (0,0) corresponds to the vertical excitation geometry. Figure 3A shows that as we move along the diagonal, the initially higher lying ME state rapidly becomes degenerate with the LE states, and then significantly lower in energy. At the point of degeneracy (an avoided crossing) there is mixing between the ME and LE diabatic states that leads to a change in character of the lowest adiabatic excited state (S1): Figure 3B shows the composition of the three lowest excited adiabatic states as a function of the normal mode coordinates demonstrating the change in character of the lowest adiabatic state as a function of Q.

Figure 3.

Figure 3

Open in a new tab

(A) A slice of the potential energy surface along the diagonal of the normal mode coordinate, Q, as each substituted pentacene monomer in the dimer relaxes along the 1435 cm–1 mode. The values at each point are calculated at the 8o8e level of theory (see the Supporting Information for details). The ME state is higher than the LE states at Q = (0,0), and the avoided crossing is Q = (0.33,0.33). (B) Percent diabatic state composition of the three lowest excited adiabatic states of BP-37 as a function of Q demonstrating strong mixing at Q = (0.33,0.33) and the change in character of adiabatic states S1 and S3 as we move from Q = (0,0) to Q = (1.3,1.3). (C) Representation of the 1435 cm–1 mode in pentacene and the postulated structure of T1 in a pentacene monomer, achieved through the avoided crossing.

It is clear that despite the overall weak direct-coupling strength, strong mixing occurs as the adiabatic states become sufficiently close in energy. We note that the involvement of a high-frequency mode is in keeping with the observed ultrafast time scale for iSF. In Figure 3C, we provide physical insight into the direct coupling mechanism for iSF, mediated by a vibrational mode. Starting from a vertical excitation at Q = (0,0), where the bond character shown is deduced from the reported X-ray structure15 (Supporting Information), the vibrational mode of a substituted pentacene monomer points to a structure where the vectors guide the shortening of the carbon–carbon bonds highlighted in red (double-bond character in Figure 3C), concomitant with the elongation of the other bonds. The bond-stretching and contraction suggests stabilization of a biradical structure with triplet character localized in the central pentacene ring (animation of Q available as Supporting Information). This biradical character results in rapid lowering of the ME state energy, resulting in the near-degeneracy (avoided crossing) necessary for strong direct mixing of the LE and ME states.54−58 It must be noted that the structure on the right is not a minimum energy structure, but one that represents the bond character along the important mode in iSF. It is clear from the analysis above that the rate of iSF will be intimately tied to the direct coupling matrix elements. This coupling can be tuned by the extent of orbital overlap, in particularly via geometric changes. For instance, as the monomers rotate around the central bond and approach orthogonality, we expect coupling to reach a minimum. We consider a rotation of the dihedral angle from 37° to 57° and find a 2-fold decrease in the direct coupling matrix element at the avoided crossing region (∼3 meV vs ∼1.5 meV). Assuming a golden-rule like expression for the rate of singlet fission where the rate is proportional to the square of the direct coupling strength,4 we predict a decrease in the iSF rate by a factor of 4; a key result that will be compared to the predicted CT-mediated value in the next section, and confirmed by experimental results below.

Quantifying the Role of Charge Transfer States

While the identification of an avoided crossing is essential to make the direct coupling mechanism viable, this does not in any way rule out a contribution from the CT-mediated superexchange mechanism. In this section, we investigate the role of CT states and we quantify the change in iSF rate associated with the CT-mediated mechanism as the dihedral angle is varied.

As previously mentioned, we find that accurate quasi-diabatic CT states cannot be obtained at the 8o8e level of theory. In order to quantify the extent of CT involvement we move to a reduced, four-orbital/four-electron (4o4e) active space that includes only the HOMO and LUMO on each pentacene for BP-37. Table 3 lists the adiabatic state energies and the corresponding diabatic state contributions from 4o4e calculations and illustrates the minimal mixing observed between different “types” of diabatic states.

Table 3. Energies (in eV) and Diabatic Contributions (in %) of the Eight Lowest Adiabatic Singlet Statesa Calculated at the 4o4e Level of Theory.

(adiabatic state) and energy gg tt ge eg gd dg ac ca
(S0) 0.00 88.2 0.0 0.0 0.0 5.6 5.6 0.3 0.3
(S1) 1.53 0.2 98.2 0.0 0.0 0.1 0.1 0.8 0.8
(S2) 1.67 0.0 0.0 48.5 48.5 0.3 0.3 1.2 1.2
(S3) 1.69 0.1 0.0 48.9 48.9 1.0 1.0 0.0 0.0
(S4) 1.86 10.6 0.2 1.1 1.1 43.1 43.2 0.4 0.4
(S5) 2.01 0.0 0.0 0.3 0.3 49.7 49.7 0.0 0.0
(S6) 2.81 0.9 1.6 0.0 0.0 0.2 0.2 48.7 48.4
(S7) 2.81 0.0 0.0 1.2 1.2 0.0 0.0 48.7 48.9
Open in a new tab
a

See Figure 2 for representation of the diabats.

The adiabatic states largely correspond to a single type of diabatic state, with the exception of S0 and S4, where the inherent biradical character of BP-37 results in low energy doubly excited states, dg and gd, mixing with the gg diabat. In the less accurate 4o4e level of theory, S1 is largely composed of tt character, while the other states exhibit linear combinations of similar types of diabats (eg + ge, dg + gd, or ac + ca). This is in agreement with the 8o8e calculations where we see no CT character in states within ∼1 eV of the low-lying singlet excited states. We also find that calculations at the 4o4e level underestimate energies, particularly the ME state, but are able to reproduce the qualitative picture of high-lying CT states and very little diabatic mixing.

Previous work investigating the mechanism of xSF unfavorably compared the direct coupling mechanism against superexchange mediated by high-lying CT states.28−33,59 Here, the experimentally observed 0.76 ps iSF time constant in BP-37,15 the large energy separation (∼1 eV) of the CT states, and the relatively small energy separation between the ME and LE states suggest a mechanism that may be independent of CT mediation. Although the magnitude of the coupling between the ME/LE states and the CT states in BP-37 is comparable to values reported for pentacene and tetracene dimers that undergo xSF,30,32,33,39,43,60,61 the energetic separation of the CT states for iSF in BP-37 is significantly larger.12,31,32,34 This difference is expected since the dimer lacks the HOMO/LUMO energy bands found in crystalline pentacene, in addition to the longer intermonomer distance (monomer center-of-mass separated by 13.6 Å in BP-37 vs 5 Å in crystalline pentacene) that leads to a reduction in stabilizing Coulomb binding energy.

graphic file with name oc-2016-00063r_m002.jpg 1

Unlike the direct coupling mechanism, the CT-mediated mechanism is second-order in nature, and depends on two factors: the coupling matrix elements and energy differences between states. The effective indirect coupling is defined by eq 1 and likewise for the ge diabat.

Because CT mediation is an inherently nonlocal phenomenon, it is expected that CT energies and the indirect coupling may depend strongly on the intermonomer geometry of the covalently linked pentacene units. We examine two degrees of freedom that affect the interactions between the pentacene chromophores: the length of the covalent bond between the two monomers and the dihedral angle θ. We find that CT state energies are at a minimum near the reference C–C bond length of 1.48 Å, and increase only slightly in energy as the σ bond length decreases (Figure 4A). Similarly, Figure 4B shows that the energies of the CT states remain high in energy and fairly constant relative to the lower lying excited states as a function of dihedral angle.

Figure 4.

Figure 4

Open in a new tab

Energies of the 4o4e diabatic states as a function of (A) intermonomer C–C bond length in BP-37 and (B) the dihedral angle shown in Figure 1B. (C) CT-mediated superexchange Veff as defined in the text as a function of the bipentacene dihedral angle.

Although CT states are substantially higher in energy, this does not necessarily preclude an efficient CT-mediated mechanism.30 A better method to establish the role of CT state mediation is to examine the effective coupling as a function of chemical structure, and compare the predictions of this mechanism to the experimentally observed iSF rates. Drawing parallels to our analysis of the direct mechanism, we show the indirect coupling as a function of dihedral angle in Figure 4C. Further, the indirect coupling decreases by a factor of ∼6 as the dihedral angle changes from 37° to 57°, while the CT state energies remain roughly constant relative to the ME and LE sates. Assuming, again, a golden-rule rate expression, this would predict slower iSF by a factor of ∼36 in contrast to the factor of 4 predicted by the direct coupling pathway. We note that, despite the high-level multireference methods used here, we cannot directly compare the magnitude of coupling for the direct and CT-mediated mechanisms, rather we rely on trends in coupling to predict changes in iSF rates. We now turn to experimental evidence to distinguish between these two different scaling relationships and to identify the dominant mechanism.

Experimental Results

In order to experimentally investigate how the excited state dynamics are affected by modifying interplanar angle between the two substituted pentacene monomers, we synthesize compounds BP-HPh (θ = 42°) and BP-2Ph (where θ is analogous to BP-57), where the dihedral angle twist is imposed by steric hindrance from the R groups shown in Figure 1B. Since the phenyl groups are twisted orthogonal to the pentacene core, they do not have significant contributions to the electronic structure, as evidenced in the UV–vis spectrum where their addition does not shift the onset of absorption (i.e., the phenyl groups do not participate in delocalization with pentacene). The transient absorption (TA) spectra (Figure 5) of BP-HPh and BP-2Ph show qualitatively similar features to the parent BP-2H (which is analogous to BP-37), and the iSF rates and yields can be similarly obtained.15 The spectrally deconvoluted singlet and triplet transient features are evaluated using global analysis methods,62 and all three exhibit a broad singlet excited state transition that spectrally overlaps with a narrower triplet absorption feature at ∼520 nm. A triplet absorption feature on the red side of the ground state bleach is prominent in BP-2H but decreases in intensity as the molecule becomes more twisted. We have seen a similar effect in bipentacene molecules with conjugated spacers and believe that this trend can be attributed to coupling of the T1 → Tn triplet transition dipole moments, oriented along the long axis of the molecule when the pentacenes are both aligned (planar) and in close proximity.63

Figure 5.

Figure 5

Open in a new tab

(A–C) Raw transient absorption (ΔA) data for dilute solutions of BP-2H, BP-HPh, and BP-2Ph in chloroform plotted as a function of wavelength and time. Regions of large pump scatter at ∼600 nm have been removed for clarity. (D–F) Corresponding singlet and triplet spectral deconvolution for BP-2H, BP-HPh, and BP-2Ph, respectively, solved by singular value decomposition and global analysis.

As in BP-2H, we quantify the iSF yield from the ground state bleach signal in the deconvoluted spectral transients for the singlet and triplet.15,18,64 This method is valid since the entirety of the molecule is bleached when populated by one singlet or two triplets.15,18 We establish that increased twisting of the molecule does not violate this condition by measuring each sample under the identical excitation conditions and verifying that the quantity ΔA/(ε(1 – T)) is conserved for the ground state bleach, where ε is the extinction coefficient at the absorption maximum and T is the transmission at the pump wavelength. In other words, the singlet is fully delocalized on the whole molecule.

We observe that the area of the ground state bleach, when corrected for overlap with induced absorption signals, is unchanged after singlet fission. Thus, all initially populated states are converted to triplet pairs and a quantitative iSF yield of ∼200% is observed. This high yield is consistent with a simple rate analysis, since singlet fission is orders of magnitude faster than competing deactivation processes such as the ∼12.3 ns fluorescence decay in TIPS-pentacene monomer.64 While qualitatively similar dynamics are observed in all three compounds, quantitative differences in the rates of singlet fission and triplet recombination are observed. In Figure 6, we show the TAS kinetics associated with the peak of the triplet absorption in chloroform at 517, 516 and 528 nm for BP-2H, BP-HPh and BP-2PH, respectively. It should be noted that there is some overlap with induced absorption from the singlet state, which gives an instantaneous rise at time zero. Global fitting of the full data set is used to achieve high accuracy of the extracted time constants.

Figure 6.

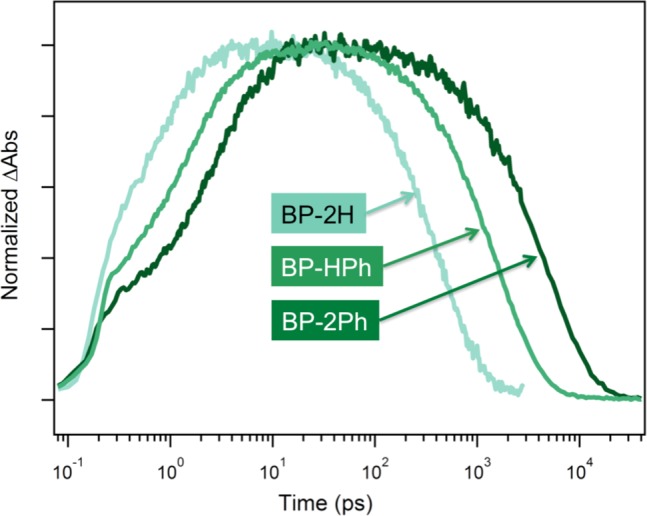
Figure 6

Open in a new tab

Single wavelength transient absorption kinetics monitoring the peak in the triplet excited state absorption spectrum in chloroform, between 0.1 and 0.2 mW and less than 100 μM for all samples. While both iSF and the corresponding triplet decay rates slow with increased interplanar angle, there is a larger change in the rate of triplet decay.

The ultrafast time constant for iSF monotonically increases as the dihedral angle increases, from 0.76 ps to 1.69 ps to 3.38 ps. The iSF rate constant changes from BP-2H (least twisted) to BP-2Ph (most twisted) by a factor of ∼4.5, very close to the factor of 4 predicted by the direct coupling mechanism comparing BP-37 to BP-57, and an order of magnitude different from the slow-down in rate predicted by the CT-mediated superexchange mechanism. We note that the rate of triplet recombination is similarly affected, with the time constant monotonically increasing from 450 ps to 1600 ps to 5200 ps, as the dimer becomes more twisted. We find that the change in electronic coupling strength for the recombination of two triplets appears to be more dramatic than for iSF, with recombination rates scaling even more strongly than iSF rates with the twist-induced reduction in coupling. Since fast iSF but slow triplet recombination are desired, this observation suggests a viable way to optimize the overall excited state lifetime, an important result for technological applications.

Effect of Solvent Properties on iSF Rates

Finally, using both theory and experiments, we establish that solvent properties do not significantly and systematically change the rate of iSF, suggesting that iSF proceeds primarily through a direct coupling mechanism in the bipentacenes studied here. We calculate diabatic excited state energies in solution by employing the polarizable continuum model (PCM) to simulate solvent effects.48,65 Even for solvents as polar as water, we observe only a minimal 50 meV shift in CT state energies relative to all other states (further details provided in the Supporting Information). Experimental studies reveal a weak and complex dependence of the electronic energy levels on the properties (in particular orientation polarizability) of the solvent, consistent with the idea that direct coupling mediates iSF and CT states are not necessarily involved. While small changes in the energy of the S0 → S1, S1 → SN, and T1 → T3 transitions are observed, there is a nonmonotonic dependence on the solvent dielectric constant, index of refraction, or orientation polarizability (Supporting Information). The singlet fission rate constants change by less than a factor of 2 over the entire range of solvents used (including hexane, xylenes, chloroform, THF, acetone), which is consistent with a dominant mechanism that does not involve CT states to mediate iSF. We note that other pentacene dimers with a markedly different connectivity were recently shown to exhibit weakly solvent-dependent iSF dynamics.17,18 That result suggests that molecules with varying degrees of conjugation and through-space interactions may adopt intramolecular conformations capable of accessing lower lying CT states.

In summary, we find a novel mechanism for ultrafast iSF in pentacene dimers: direct coupling of the singlet to multiexciton state facilitated by vibronic coupling induced degeneracy. Furthermore, we rule out dominant contributions of a CT-mediated mechanism, unlike in the case of xSF. Experimental characterization of iSF rates of molecules with different dihedral angles confirms that the direct coupling mechanism accurately reproduces measured trends and further raises the interesting point that slowing the rate of iSF in highly twisted dimers is accompanied by dramatically slower rates of triplet pair recombination. Establishing the mechanism for iSF in these materials is the first step toward designing new materials with optimized excited state properties for high efficiency organic solar cells.

Experimental Section

Calculations

All geometry optimizations described in the manuscript are performed using DFT-B3LYP with a 6-31G* basis set. Following earlier work on xSF in pentacene,32 excited state energies for the dimer are obtained from multiconfiguration quasi-degenerate perturbation theory (XMCQDPT) calculations42 with a 0.02 au intruder state avoidance shift49 using the SBKJC pseudopotential with its corresponding double-ζ basis set66plus a d-polarization function taken from the standard 6-31G* basis set for carbon.67 We find that an 8o8e active space is necessary to yield accurate excited state energies for the dimer, a conclusion similarly reached for related acene dimers.17,43,44 Diabatization of the eight (four) lowest lying states is performed at the 4o4e (8o8e) level employing the 4-fold approach of Nakamura and Truhlar to obtain our diabatic states.68,69 Reference orbitals are generated from a Hartree–Fock calculation at large intermonomer distances which allows for each orbital to be unambiguously associated with only one monomer. To investigate the effects of solvent polarity, diabatization calculations utilizing the polarizable continuum model (PCM) are performed at the CASSCF level using a minimal active space so as to explicitly construct charge transfer diabats.48,65 A state specific shift, defined as E(XMCQDPT) – E(CASSCF) in vacuo, is applied to the resulting energies to account for the absent dynamical correlation. All calculations are performed using the electronic structure package GAMESS-US.70,71

Transient Absorption Spectroscopy

Transient absorption spectroscopy was performed using a commercial Ti:sapphire laser system (SpectraPhysics) operating at a repetition rate of 1 kHz. A commercial optical parametric amplifier (LightConversion) was used to generate resonant pump pulses with ∼100 fs time duration. Supercontinuum probe light was generated by focusing a small portion of the 800 nm fundamental into a sapphire disk. The probe light was split into signal and reference beams, which were detected on a shot-by-shot basis by a fiber-coupled silicon (visible) or InGaAs (infrared) diode array. The pump–probe delay was controlled by a mechanical delay stage. Excitation fluence in each measurement was approximately 50 μJ/cm2. Method details and results for additional ultrafast experiments, including triplet photosensitization and photoluminescence upconversion measurements, can be found in the Supporting Information.

Acknowledgments

L.M.C. acknowledges support from the Office of Naval Research Young Investigator Program (Award N00014-15-1-2532), ACS Petroleum Research Fund, 3M Non-Tenured Faculty Award, Arthur C. Cope Scholar Award, and Cottrell Scholar Award. N.A. acknowledges support from a Sloan Foundation Research Fellowship and a Cornell Startup Grant. S.N.S. and A.B.P. thank the NSF for GRFP (DGE 11-44155). X.-Y.Z. acknowledges support from the DOE, Grant DE-SC0014563. This research used resources of the Center for Functional Nanomaterials, which is a U.S. DOE Office of Science Facility, at Brookhaven National Laboratory under Contract No. DE-SC0012704. We are grateful to the Nuckolls lab for use of their UV–vis spectrophotometer.

Glossary

Abbreviations

SF

singlet fission

xSF

intermolecular singlet fission

CT

charge transfer

iSF

intramolecular singlet fission

LE

local excitonic

ME

multiexcitonic

CASSCF

complete active space self-consistent field theory

XMCQDPT

extended multiconfiguration quasi-degenerate perturbation theory

PES

potential energy surface

ORMAS-SF

occupation restricted multiple active space spin flip

8o8e

eight orbitals/8 electrons

4o4e

four orbitals/four electrons

PCM

polarizable continuum model

THF

tetrahydrofuran

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acscentsci.6b00063.

  • Synthetic procedures, steady state absorption spectra, solvent studies, photoluminescence upconversion spectroscopy and photosensitization experiment details and results, and details of calculations (PDF)

  • Animation of the pentacene dimer vibrational modes (MOV)

Author Present Address

(T.Z.) Department of Chemistry, Carleton University, Ottawa, Canada.

Author Contributions

‡ E.G.F., S.N.S., and A.B.P. contributed equally

The authors declare no competing financial interest.

Supplementary Material

oc6b00063_si_001.pdf (2.1MB, pdf)
oc6b00063_si_002.mov (8.9MB, mov)

References

  1. Hanna M. C.; Nozik A. J. Solar conversion efficiency of photovoltaic and photoelectrolysis cells with carrier multiplication absorbers. J. Appl. Phys. 2006, 100, 074510. 10.1063/1.2356795. [DOI] [Google Scholar]
  2. Green M. A. Third generation photovoltaics: Ultra-high conversion efficiency at low cost. Prog. Photovoltaics 2001, 9, 123–135. 10.1002/pip.360. [DOI] [Google Scholar]
  3. Lee J.; Jadhav P.; Baldo M. A. High efficiency organic multilayer photodetectors based on singlet exciton fission. Appl. Phys. Lett. 2009, 95, 033301. 10.1063/1.3182787. [DOI] [Google Scholar]
  4. Smith M. B.; Michl J. Recent Advances in Singlet Fission. Annu. Rev. Phys. Chem. 2013, 64, 361–386. 10.1146/annurev-physchem-040412-110130. [DOI] [PubMed] [Google Scholar]
  5. Congreve D. N.; Lee J.; Thompson N. J.; Hontz E.; Yost S. R.; Reusswig P. D.; Bahlke M. E.; Reineke S.; Van Voorhis T.; Baldo M. A. External Quantum Efficiency Above 100% in a Singlet-Exciton-Fission–Based Organic Photovoltaic Cell. Science 2013, 340, 334–337. 10.1126/science.1232994. [DOI] [PubMed] [Google Scholar]
  6. Eaton S. W.; Miller S. A.; Margulies E. A.; Shoer L. E.; Schaller R. D.; Wasielewski M. R. Singlet Exciton Fission in Thin Films of tert-Butyl-Substituted Terrylenes. J. Phys. Chem. A 2015, 119, 4151–4161. 10.1021/acs.jpca.5b02719. [DOI] [PubMed] [Google Scholar]
  7. Smith M. B.; Michl J. Singlet Fission. Chem. Rev. 2010, 110, 6891–6936. 10.1021/cr1002613. [DOI] [PubMed] [Google Scholar]
  8. Eaton S. W.; Shoer L. E.; Karlen S. D.; Dyar S. M.; Margulies E. A.; Veldkamp B. S.; Ramanan C.; Hartzler D. A.; Savikhin S.; Marks T. J.; Wasielewski M. R. Singlet Exciton Fission in Polycrystalline Thin Films of a Slip-Stacked Perylenediimide. J. Am. Chem. Soc. 2013, 135, 14701–14712. 10.1021/ja4053174. [DOI] [PubMed] [Google Scholar]
  9. Minami T.; Ito S.; Nakano M. Theoretical Study of Singlet Fission in Oligorylenes. J. Phys. Chem. Lett. 2012, 3, 2719–2723. 10.1021/jz3011749. [DOI] [PubMed] [Google Scholar]
  10. Zeng T.; Ananth N.; Hoffmann R. Seeking Small Molecules for Singlet Fission: A Heteroatom Substitution Strategy. J. Am. Chem. Soc. 2014, 136, 12638–12647. 10.1021/ja505275m. [DOI] [PubMed] [Google Scholar]
  11. Lee J.; Jadhav P.; Reusswig P. D.; Yost S. R.; Thompson N. J.; Congreve D. N.; Hontz E.; Van Voorhis T.; Baldo M. A. Singlet Exciton Fission Photovoltaics. Acc. Chem. Res. 2013, 46, 1300–1311. 10.1021/ar300288e. [DOI] [PubMed] [Google Scholar]
  12. Yost S. R.; Lee J.; Wilson M. W. B.; Wu T.; McMahon D. P.; Parkhurst R. R.; Thompson N. J.; Congreve D. N.; Rao A.; Johnson K.; Sfeir M. Y.; Bawendi M. G.; Swager T. M.; Friend R. H.; Baldo M. A.; Van Voorhis T. A transferable model for singlet-fission kinetics. Nat. Chem. 2014, 6, 492–497. 10.1038/nchem.1945. [DOI] [PubMed] [Google Scholar]
  13. Piland G. B.; Bardeen C. J. How Morphology Affects Singlet Fission in Crystalline Tetracene. J. Phys. Chem. Lett. 2015, 6, 1841–1846. 10.1021/acs.jpclett.5b00569. [DOI] [PubMed] [Google Scholar]
  14. Dillon R. J.; Piland G. B.; Bardeen C. J. Different Rates of Singlet Fission in Monoclinic versus Orthorhombic Crystal Forms of Diphenylhexatriene. J. Am. Chem. Soc. 2013, 135, 17278–17281. 10.1021/ja409266s. [DOI] [PubMed] [Google Scholar]
  15. Sanders S. N.; Kumarasamy E.; Pun A. B.; Trinh M. T.; Choi B.; Xia J.; Taffet E. J.; Low J. Z.; Miller J. R.; Roy X.; Zhu X. Y.; Steigerwald M. L.; Sfeir M. Y.; Campos L. M. Quantitative Intramolecular Singlet Fission in Bipentacenes. J. Am. Chem. Soc. 2015, 137, 8965–8972. 10.1021/jacs.5b04986. [DOI] [PubMed] [Google Scholar]
  16. Busby E.; Xia J.; Low J. Z.; Wu Q.; Hoy J.; Campos L. M.; Sfeir M. Y. Fast Singlet Exciton Decay in Push–Pull Molecules Containing Oxidized Thiophenes. J. Phys. Chem. B 2015, 119, 7644–7650. 10.1021/jp511704r. [DOI] [PubMed] [Google Scholar]
  17. Zirzlmeier J.; Lehnherr D.; Coto P. B.; Chernick E. T.; Casillas R.; Basel B. S.; Thoss M.; Tykwinski R. R.; Guldi D. M. Singlet fission in pentacene dimers. Proc. Natl. Acad. Sci. U. S. A. 2015, 112, 5325–5330. 10.1073/pnas.1422436112. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Lukman S.; Musser A. J.; Chen K.; Athanasopoulos S.; Yong C. K.; Zeng Z.; Ye Q.; Chi C.; Hodgkiss J. M.; Wu J.; Friend R. H.; Greenham N. C. Tuneable Singlet Exciton Fission and Triplet–Triplet Annihilation in an Orthogonal Pentacene Dimer. Adv. Funct. Mater. 2015, 25, 5452–5461. 10.1002/adfm.201501537. [DOI] [Google Scholar]
  19. Varnavski O.; Abeyasinghe N.; Aragó J.; Serrano-Perez J. J.; Ortí E.; López Navarrete J. T.; Takimiya K.; Casanova D.; Casado J.; Goodson T. III High Yield Ultrafast Intramolecular Singlet Exciton Fission in a Quinoidal Bithiophene. J. Phys. Chem. Lett. 2015, 6, 1375–1384. 10.1021/acs.jpclett.5b00198. [DOI] [PubMed] [Google Scholar]
  20. Busby E.; Xia J.; Wu Q.; Low J. Z.; Song R.; Miller J. R.; Zhu X.-Y.; Campos L. M.; Sfeir M. Y. A Design Strategy for Intramolecular Singlet Fission Mediated by Charge-Transfer States in Donor-Acceptor Organic Materials. Nat. Mater. 2014, 14, 426–433. 10.1038/nmat4175. [DOI] [PubMed] [Google Scholar]
  21. Sanders S. N.; Kumarasamy E.; Pun A. B.; Steigerwald M. L.; Sfeir M. Y.; Campos L. M. Intramolecular Singlet Fission in Oligoacene Heterodimers. Angew. Chem., Int. Ed. 2016, 55, 3373–3377. 10.1002/anie.201510632. [DOI] [PubMed] [Google Scholar]
  22. Sakuma T.; Sakai H.; Araki Y.; Mori T.; Wada T.; Tkachenko N. V.; Hasobe T. Long-Lived Triplet Excited States of Bent-Shaped Pentacene Dimers by Intramolecular Singlet Fission. J. Phys. Chem. A 2016, 120, 1867–1875. 10.1021/acs.jpca.6b00988. [DOI] [PubMed] [Google Scholar]
  23. Low J. Z.; Sanders S. N.; Campos L. M. Correlating Structure and Function in Organic Electronics: From Single Molecule Transport to Singlet Fission. Chem. Mater. 2015, 27, 5453–5463. 10.1021/cm502366x. [DOI] [Google Scholar]
  24. Burdett J. J.; Bardeen C. J. The Dynamics of Singlet Fission in Crystalline Tetracene and Covalent Analogs. Acc. Chem. Res. 2013, 46, 1312–1320. 10.1021/ar300191w. [DOI] [PubMed] [Google Scholar]
  25. Müller A. M.; Avlasevich Y. S.; Schoeller W. W.; Müllen K.; Bardeen C. J. Exciton Fission and Fusion in Bis(tetracene) Molecules with Different Covalent Linker Structures. J. Am. Chem. Soc. 2007, 129, 14240–14250. 10.1021/ja073173y. [DOI] [PubMed] [Google Scholar]
  26. Müller A. M.; Avlasevich Y. S.; Müllen K.; Bardeen C. J. Evidence for exciton fission and fusion in a covalently linked tetracene dimer. Chem. Phys. Lett. 2006, 421, 518–522. 10.1016/j.cplett.2006.01.117. [DOI] [Google Scholar]
  27. Kumarasamy E.; Sanders S. N.; Pun A. B.; Vaselabadi S. A.; Low J. Z.; Sfeir M. Y.; Steigerwald M. L.; Stein G. E.; Campos L. M. Properties of Poly- and Oligopentacenes Synthesized from Modular Building Blocks. Macromolecules 2016, 49, 1279–1285. 10.1021/acs.macromol.5b02711. [DOI] [Google Scholar]
  28. Tao G. Electronically Nonadiabatic Dynamics in Singlet Fission: A Quasi-Classical Trajectory Simulation. J. Phys. Chem. C 2014, 118, 17299–17305. 10.1021/jp5038602. [DOI] [Google Scholar]
  29. Berkelbach T. C.; Hybertsen M. S.; Reichman D. R. Microscopic theory of singlet exciton fission. I. General formulation. J. Chem. Phys. 2013, 138, 114102. 10.1063/1.4794425. [DOI] [PubMed] [Google Scholar]
  30. Berkelbach T. C.; Hybertsen M. S.; Reichman D. R. Microscopic theory of singlet exciton fission. II. Application to pentacene dimers and the role of superexchange. J. Chem. Phys. 2013, 138, 114103. 10.1063/1.4794427. [DOI] [PubMed] [Google Scholar]
  31. Berkelbach T. C.; Hybertsen M. S.; Reichman D. R. Microscopic theory of singlet exciton fission. III. Crystalline pentacene. J. Chem. Phys. 2014, 141, 074705. 10.1063/1.4892793. [DOI] [PubMed] [Google Scholar]
  32. Zeng T.; Hoffmann R.; Ananth N. The Low-Lying Electronic States of Pentacene and Their Roles in Singlet Fission. J. Am. Chem. Soc. 2014, 136, 5755–5764. 10.1021/ja500887a. [DOI] [PubMed] [Google Scholar]
  33. Chan W.-L.; Berkelbach T. C.; Provorse M. R.; Monahan N. R.; Tritsch J. R.; Hybertsen M. S.; Reichman D. R.; Gao J.; Zhu X. Y. The Quantum Coherent Mechanism for Singlet Fission: Experiment and Theory. Acc. Chem. Res. 2013, 46, 1321–1329. 10.1021/ar300286s. [DOI] [PubMed] [Google Scholar]
  34. Beljonne D.; Yamagata H.; Bredas J. L.; Spano F. C.; Olivier Y. Charge-Transfer Excitations Steer the Davydov Splitting and Mediate Singlet Exciton Fission in Pentacene. Phys. Rev. Lett. 2013, 110, 226402. 10.1103/PhysRevLett.110.226402. [DOI] [PubMed] [Google Scholar]
  35. Aryanpour K.; Dutta T.; Huynh U. N. V.; Vardeny Z. V.; Mazumdar S. Theory of Primary Photoexcitations in Donor-Acceptor Copolymers. Phys. Rev. Lett. 2015, 115, 267401. 10.1103/PhysRevLett.115.267401. [DOI] [PubMed] [Google Scholar]
  36. Zimmerman P. M.; Musgrave C. B.; Head-Gordon M. A Correlated Electron View of Singlet Fission. Acc. Chem. Res. 2013, 46, 1339–1347. 10.1021/ar3001734. [DOI] [PubMed] [Google Scholar]
  37. Monahan N.; Zhu X.-Y. Charge Transfer–Mediated Singlet Fission. Annu. Rev. Phys. Chem. 2015, 66, 601–618. 10.1146/annurev-physchem-040214-121235. [DOI] [PubMed] [Google Scholar]
  38. Meylemans H. A.; Hewitt J. T.; Abdelhaq M.; Vallett P. J.; Damrauer N. H. Exploiting Conformational Dynamics To Facilitate Formation and Trapping of Electron-Transfer Photoproducts in Metal Complexes. J. Am. Chem. Soc. 2010, 132, 11464–11466. 10.1021/ja1055559. [DOI] [PubMed] [Google Scholar]
  39. Casanova D. Electronic Structure Study of Singlet Fission in Tetracene Derivatives. J. Chem. Theory Comput. 2014, 10, 324–334. 10.1021/ct4007635. [DOI] [PubMed] [Google Scholar]
  40. Yamagata H.; Norton J.; Hontz E.; Olivier Y.; Beljonne D.; Brédas J. L.; Silbey R. J.; Spano F. C. The nature of singlet excitons in oligoacene molecular crystals. J. Chem. Phys. 2011, 134, 204703. 10.1063/1.3590871. [DOI] [PubMed] [Google Scholar]
  41. Kaur I.; Jia W.; Kopreski R. P.; Selvarasah S.; Dokmeci M. R.; Pramanik C.; McGruer N. E.; Miller G. P. Substituent Effects in Pentacenes: Gaining Control over HOMO–LUMO Gaps and Photooxidative Resistances. J. Am. Chem. Soc. 2008, 130, 16274–16286. 10.1021/ja804515y. [DOI] [PubMed] [Google Scholar]
  42. Granovsky A. A. Extended multi-configuration quasi-degenerate perturbation theory: The new approach to multi-state multi-reference perturbation theory. J. Chem. Phys. 2011, 134, 214113. 10.1063/1.3596699. [DOI] [PubMed] [Google Scholar]
  43. Parker S. M.; Seideman T.; Ratner M. A.; Shiozaki T. Model Hamiltonian Analysis of Singlet Fission from First Principles. J. Phys. Chem. C 2014, 118, 12700–12705. 10.1021/jp505082a. [DOI] [Google Scholar]
  44. Coto P. B.; Sharifzadeh S.; Neaton J. B.; Thoss M. Low-Lying Electronic Excited States of Pentacene Oligomers: A Comparative Electronic Structure Study in the Context of Singlet Fission. J. Chem. Theory Comput. 2015, 11, 147–156. 10.1021/ct500510k. [DOI] [PubMed] [Google Scholar]
  45. Greyson E. C.; Vura-Weis J.; Michl J.; Ratner M. A. Maximizing Singlet Fission in Organic Dimers: Theoretical Investigation of Triplet Yield in the Regime of Localized Excitation and Fast Coherent Electron Transfer. J. Phys. Chem. B 2010, 114, 14168–14177. 10.1021/jp907392q. [DOI] [PubMed] [Google Scholar]
  46. Teichen P. E.; Eaves J. D. A Microscopic Model of Singlet Fission. J. Phys. Chem. B 2012, 116, 11473–11481. 10.1021/jp208905k. [DOI] [PubMed] [Google Scholar]
  47. Difley S.; Voorhis T. V. Exciton/Charge-Transfer Electronic Couplings in Organic Semiconductors. J. Chem. Theory Comput. 2011, 7, 594–601. 10.1021/ct100508y. [DOI] [PubMed] [Google Scholar]
  48. Cossi M.; Rega N.; Scalmani G.; Barone V. Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J. Comput. Chem. 2003, 24, 669–681. 10.1002/jcc.10189. [DOI] [PubMed] [Google Scholar]
  49. Witek H. A.; Choe Y.-K.; Finley J. P.; Hirao K. Intruder state avoidance multireference Møller--Plesset perturbation theory. J. Comput. Chem. 2002, 23, 957–965. 10.1002/jcc.10098. [DOI] [PubMed] [Google Scholar]
  50. Halasinski T. M.; Hudgins D. M.; Salama F.; Allamandola L. J.; Bally T. Electronic Absorption Spectra of Neutral Pentacene (C22H14) and Its Positive and Negative Ions in Ne, Ar, and Kr Matrices. J. Phys. Chem. A 2000, 104, 7484–7491. 10.1021/jp0011544. [DOI] [Google Scholar]
  51. Haas S.; Matsui H.; Hasegawa T. Field-modulation spectroscopy of pentacene thin films using field-effect devices: Reconsideration of the excitonic structure. Phys. Rev. B: Condens. Matter Mater. Phys. 2010, 82, 161301. 10.1103/PhysRevB.82.161301. [DOI] [Google Scholar]
  52. Krylov A. I. Spin-Flip Equation-of-Motion Coupled-Cluster Electronic Structure Method for a Description of Excited States, Bond Breaking, Diradicals, and Triradicals. Acc. Chem. Res. 2006, 39, 83–91. 10.1021/ar0402006. [DOI] [PubMed] [Google Scholar]
  53. Ivanic J. Direct configuration interaction and multiconfigurational self-consistent-field method for multiple active spaces with variable occupations. I. Method. J. Chem. Phys. 2003, 119, 9364–9376. 10.1063/1.1615954. [DOI] [Google Scholar]
  54. Akdag A.; Havlas Z.; Michl J. Search for a Small Chromophore with Efficient Singlet Fission: Biradicaloid Heterocycles. J. Am. Chem. Soc. 2012, 134, 14624–14631. 10.1021/ja3063327. [DOI] [PubMed] [Google Scholar]
  55. Wen J.; Havlas Z.; Michl J. Captodatively Stabilized Biradicaloids as Chromophores for Singlet Fission. J. Am. Chem. Soc. 2015, 137, 165–172. 10.1021/ja5070476. [DOI] [PubMed] [Google Scholar]
  56. Ito S.; Minami T.; Nakano M. Diradical Character Based Design for Singlet Fission of Condensed-Ring Systems with 4nπ Electrons. J. Phys. Chem. C 2012, 116, 19729–19736. 10.1021/jp3072684. [DOI] [Google Scholar]
  57. Minami T.; Ito S.; Nakano M. Fundamental of Diradical-Character-Based Molecular Design for Singlet Fission. J. Phys. Chem. Lett. 2013, 4, 2133–2137. 10.1021/jz400931b. [DOI] [Google Scholar]
  58. Minami T.; Nakano M. Diradical Character View of Singlet Fission. J. Phys. Chem. Lett. 2012, 3, 145–150. 10.1021/jz2015346. [DOI] [PubMed] [Google Scholar]
  59. Aryanpour K.; Shukla A.; Mazumdar S. Theory of Singlet Fission in Polyenes, Acene Crystals, and Covalently Linked Acene Dimers. J. Phys. Chem. C 2015, 119, 6966–6979. 10.1021/jp5124019. [DOI] [Google Scholar]
  60. Alguire E. C.; Subotnik J. E.; Damrauer N. H. Exploring Non-Condon Effects in a Covalent Tetracene Dimer: How Important Are Vibrations in Determining the Electronic Coupling for Singlet Fission?. J. Phys. Chem. A 2015, 119, 299–311. 10.1021/jp510777c. [DOI] [PubMed] [Google Scholar]
  61. Havenith R. W. A.; de Gier H. D.; Broer R. Explorative computational study of the singlet fission process. Mol. Phys. 2012, 110, 2445–2454. 10.1080/00268976.2012.695810. [DOI] [Google Scholar]
  62. Snellenburg J. J.; Laptenok S. P.; Seger R.; Mullen K. M.; van Stokum I. H. M. Glotaran: A Java-Based Graphical User Interface for the R Package TIMP. J. Stat. Soft. 2012, 49, 1–22. 10.18637/jss.v049.i03. [DOI] [Google Scholar]
  63. Marciniak H.; Pugliesi I.; Nickel B.; Lochbrunner S. Ultrafast singlet and triplet dynamics in microcrystalline pentacene films. Phys. Rev. B: Condens. Matter Mater. Phys. 2009, 79, 235318. 10.1103/PhysRevB.79.235318. [DOI] [Google Scholar]
  64. Walker B. J.; Musser A. J.; Beljonne D.; Friend R. H. Singlet exciton fission in solution. Nat. Chem. 2013, 5, 1019–1024. 10.1038/nchem.1801. [DOI] [PubMed] [Google Scholar]
  65. Barone V.; Cossi M. Quantum Calculation of Molecular Energies and Energy Gradients in Solution by a Conductor Solvent Model. J. Phys. Chem. A 1998, 102, 1995–2001. 10.1021/jp9716997. [DOI] [Google Scholar]
  66. Stevens W. J.; Basch H.; Krauss M. Compact effective potentials and efficient shared-exponent basis sets for the first- and second-row atoms. J. Chem. Phys. 1984, 81, 6026–6033. 10.1063/1.447604. [DOI] [Google Scholar]
  67. Hehre W. J.; Ditchfield R.; Pople J. A. Self-Consistent Molecular Orbital Methods. XII. Further Extensions of Gaussian-Type Basis Sets for Use in Molecular Orbital Studies of Organic Molecules. J. Chem. Phys. 1972, 56, 2257–2261. 10.1063/1.1677527. [DOI] [Google Scholar]
  68. Nakamura H.; Truhlar D. G. The direct calculation of diabatic states based on configurational uniformity. J. Chem. Phys. 2001, 115, 10353–10372. 10.1063/1.1412879. [DOI] [Google Scholar]
  69. Nakamura H.; Truhlar D. G. Direct diabatization of electronic states by the fourfold way. II. Dynamical correlation and rearrangement processes. J. Chem. Phys. 2002, 117, 5576–5593. 10.1063/1.1500734. [DOI] [Google Scholar]
  70. Schmidt M. W.; Baldridge K. K.; Boatz J. A.; Elbert S. T.; Gordon M. S.; Jensen J. H.; Koseki S.; Matsunaga N.; Nguyen K. A.; Su S.; Windus T. L.; Dupuis M.; Montgomery J. A. General atomic and molecular electronic structure system. J. Comput. Chem. 1993, 14, 1347–1363. 10.1002/jcc.540141112. [DOI] [Google Scholar]
  71. Gordon M. S.; Schmidt M. W.. Advances in electronic structure theory: GAMESS a decade later. In Theory and Applications of Computational Chemistry: the first forty years; Dykstra C. E., Frenking G., Kim K. S., Scuseria G. E., Eds.; Elsevier: Amsterdam, 2005; pp 1167–1189. [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

oc6b00063_si_001.pdf (2.1MB, pdf)
oc6b00063_si_002.mov (8.9MB, mov)

Articles from ACS Central Science are provided here courtesy of American Chemical Society

RESOURCES