The Optical Signature of Charges in Conjugated Polymers

Abstract

Electrical charge flowing through organic semiconductors drives many of today’s mobile phone displays and television screens, suggesting an internally consistent model of charge-carrier properties in these materials to have manifested. In conjugated polymers, charges give rise to additional absorption of light at wavelengths longer than those absorbed by the electrically neutral species. These characteristic absorption bands are universally being related to the emergence of localized energy levels shifted into the forbidden gap of organic semiconductors due to local relaxation of the molecular geometry. However, the traditional view on these energy levels and their occupation is incompatible with expected changes in electron removal and addition energies upon charging molecules. Here, I demonstrate that local Coulomb repulsion, as captured by nonempirically optimized electronic-structure calculations, restores compatibility and suggests a different origin of the charge-induced optical transitions. These results challenge a widely accepted and long-established picture, but an improved understanding of charge carriers in molecular materials promises a more targeted development of organic and hybrid organic/inorganic (opto-)electronic devices.

Short abstract

The historical view of charge-induced intragap states in conjugated polymers and the optical transitions between them is challenged. An alternative picture is developed, highlighting local Coulomb interaction as the key ingredient.

Introduction

The transport of charge carriers through light-emitting organic semiconductors is one of the fundamental processes enabling the current evolution of display technology. Since the discovery of metallic conduction in doped polyacetylene,¹ the presence of charges in π-conjugated and aromatic polymers has been inferred from the emergence of distinct features in their near-infrared/visible absorption spectrum.^2,3 These features have historically been assigned to one-electron transitions involving single-particle energy levels situated within the band gap of the electrically neutral polymer.^4,5 In the more common case of nondegenerate ground-state systems, these intragap states are thought to arise from local, adiabatic lattice relaxation around excess charges, and the envisioned self-localized electrons or holes are habitually referred to as polarons.³⁻⁵ The picture illustrating the charge-induced energy levels, and the associated optical transitions, has pervaded pertinent scientific literature over the past three decades,³⁻⁸ it is featured in topical textbooks,^9,10 and it is invoked to interpret spectroscopic data to the present day.^7,8 Here, I argue that the occupation of the charge-induced intragap states in this picture entails implausible consequences for electron removal and addition energies. On the basis of state-of-the-art first-principles calculations, I then demonstrate that local Coulomb repulsion dictates a different occupation scheme. With only a minor increase in complexity, this revised picture lifts undesirable inconsistencies and suggests a different origin for the ubiquitously observed optical signature of charges in conjugated polymers. I expect the present work to lead to new insights into the nature and transport of charge carriers in organic semiconductors—central to understanding and improving organic as well as hybrid organic/inorganic (opto-)electronic devices—both through the critical re-examination of past results and through the informed design of new experiments.

Results and Discussion

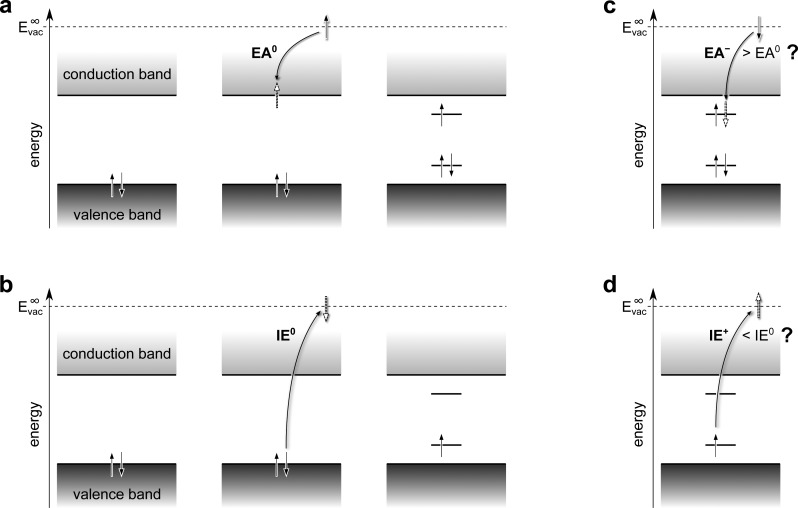
The process by which polarons are widely perceived to form in conjugated polymers with nondegenerate ground states is schematically depicted in Figure 1. By adding an electron to the bottom of the conduction band, an energy corresponding to the vertical electron affinity of the neutral system, EA⁰, is gained (Figure 1a). Subsequently, the nuclei around the added electron are envisioned to adiabatically rearrange so as to stabilize the excess charge—now spatially confined to a polymer segment of finite length—in energy. The resulting, singly occupied energy level below the conduction-band edge is accompanied by a comparably localized, but doubly occupied, energy level that relaxes upward in energy from the valence-band edge owing to the local lattice distortion. This local distortion, together with the charge that both causes it and is trapped by it, is then termed a negative polaron. In full analogy, a positive polaron is understood to form by investing the vertical ionization energy of the neutral polymer, IE⁰, to remove an electron from the top of the valence band (Figure 1b). Again, the nuclei around the excess charge—now a hole—are then thought to adiabatically rearrange so as to localize it and to stabilize it in energy, which is represented by a singly occupied energy level above the valence-band edge, accompanied by a comparably localized but empty energy level, which relaxes downward from the conduction-band edge of the neutral polymer into its fundamental gap.

Figure 1.

Traditional view on the charge-induced energy levels in nondegenerate conjugated polymers. (a) In the charge-neutral ground state of the polymer, its valence band (VB) is completely filled with spin-paired electrons, as indicated by the two antiparallel arrows at the upper VB edge (left). On addition of an electron from the vacuum level, E_vac^∞ (that is, the energy of an electron at rest in a vacuum infinitely far away from the system of interest), to the bottom of the conduction band (CB), the vertical electron affinity, EA⁰, of the neutral polymer is gained (center). Adiabatic relaxation of the local geometry around the excess electron leads to a localized, singly occupied energy level below the CB edge and a doubly occupied, comparably localized level above the VB edge (right). (b) Investing the vertical ionization energy, IE⁰, of the neutral polymer promotes an electron from the VB edge to E_vac and creates two localized energy levels within its fundamental gap, the lower of which is singly occupied and the upper empty. (c) The picture in (a) implies that EA^–, the energy gained when adding a second electron into the upper, singly occupied intragap state, is always larger than EA⁰. (d) The picture in (b) implies that IE⁺, the energy required to remove the remaining electron from the lower, singly occupied intragap state is always smaller than IE⁰.

The picture just described obviously portrays a static, zero-Kelvin situation, and it could be criticized for treating the nuclear degrees of freedom as a classical deformation potential^4,5 rather than as quantized vibrations at finite temperature.^11,12 That it (spuriously) implies the breaking of translational symmetry in idealized one-dimensionally periodic systems^13,14 might be acceptable because some degree of disorder is inherent to realistic polymers and, with it, the possibility for localized electronic states.^15,16 Less accepted,¹⁷ however, are the implications of the established polaron picture for the electron addition and removal energies of singly charged polymer chains.

The fact that, in the anion case, the horizontal line representing the upper, singly occupied intragap state is drawn as long as that representing the lower, doubly occupied state implies that also the former can accept a second electron (Figure 1c). This, however, entails that the vertical electron affinity of the anion, EA^–, that is, the second electron affinity of the neutral polymer, is always larger than EA⁰, its first electron affinity. Likewise, in the cation case, the arrow on the horizontal line representing the lower, singly occupied intragap state suggests that the vertical ionization energy of the cation, IE⁺, that is, the second ionization energy of the neutral polymer, is always smaller than IE⁰, its first ionization energy (Figure 1d).

It is the central tenet of the present work that neither of these notions, EA^– > EA⁰ and IE⁺ < IE⁰, is borne out in reality and that, in fact, the opposite is the case. If, indeed, a negative charge should be (self-)confined to a finite spatial region, then a second negative charge added to the same region in space will experience Coulomb repulsion, thereby lowering EA^–. Likewise, removing a second electron from an already positively charged spatial region will cost additional energy to overcome Coulomb attraction, thereby increasing IE⁺. In spite of the fact, however, that the neglect of Coulomb interaction has been explicitly acknowledged early on,^2,4,5 and despite its foreseen impact on the optical signature of charges in conducting polymers,^18,19 the qualitative features of the underlying energy-level diagrams in Figure 1 have long stood unchallenged. Notwithstanding ongoing progress in calculating the spectral function, that is, the equivalent to the density of states (DOS) in many-electron systems that are correlated through Coulomb and electron-phonon interactions,²⁰ a much simpler, still adiabatic, picture has recently been proposed for the molecular semiconductor C₆₀ (ref (21)). It suggests that local Coulomb interaction, already when treated at the mean-field level of theory, dramatically alters the energies and occupations of the charge-induced intragap states, observed there by (inverse) photoelectron spectroscopy. No attempt, however, has been made to assess the compatibility of this picture with the optical signature of charges in the system, and the impact of intermolecular hybridization has been disregarded entirely. While this might be permissible for C₆₀, where the widths of conduction and valence bands are small compared to local Coulomb repulsion,²¹⁻²³ the chemical repeat units in polymers are linked by covalent bonds and band widths can, therefore, be substantial.²⁴

Electronic Structure

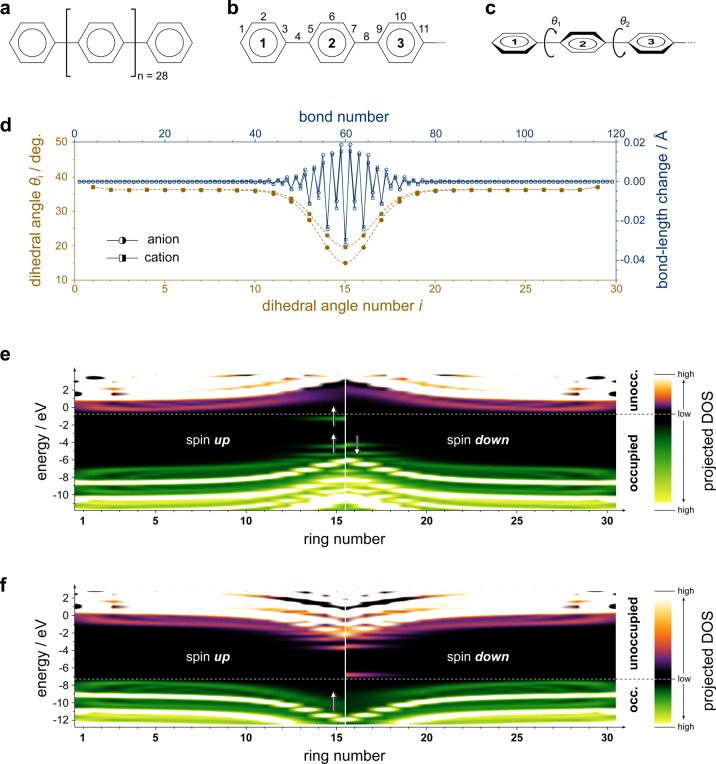
To illustrate the consequences of the competition between (mean-field) Coulomb interaction, adiabatic lattice relaxation, and the delocalization of excess charges on the energy levels of conducting-polymer ions, I performed density functional theory (DFT) calculations on the archetypical example of poly(para-phenylene) or, rather, a 30 repeat-unit oligomer thereof (Figure 2a). Adiabatic relaxation after adding or removing an electron leads to local changes in its geometry (Figure 2b–d), which reflect the more quinoidal nature of the ionic species.^25,26 The DOS around the localized charges might at first appear reminiscent of that in Figure 1, but recent advances in DFT (see Methods) allow highlighting critical differences.

Figure 2.

Charge-induced structural relaxation and electronic density of states in a prototypical polymer. (a) Chemical structure of the investigated compound. (b) Schematic illustrating the numbering of bonds. (c) Schematic illustrating the numbering and sign of the interring dihedral angles; bold numbers refer to the numbering of rings. (d) Dihedral angles θ_i (in degrees) in the anion (brown, filled circles) and in the cation (brown, filled squares); connecting lines are spline interpolations to guide the eye. Also shown are the changes in bond lengths upon adding (blue, open circles) and removing (blue, open squares) an electron from the neutral oligomer. (e) Calculated density of states (DOS) for the radical anion, projected onto individual rings. The spin-up channel is shown for rings 1 through 15 and the spin-down channel for rings 16 through 30. The respective other half of the oligomer is symmetry equivalent. The color scheme indicates the magnitude of the projected DOS from low (black) to high (white) as well as its occupation (green and violet tones for occupied and unoccupied, respectively). The horizontal, white, dashed line marks the boundary between the occupied and the unoccupied states. The white arrows indicate electrons with according spin to facilitate juxtaposition to Figure 1. (f) Same as (e) for the radical cation.

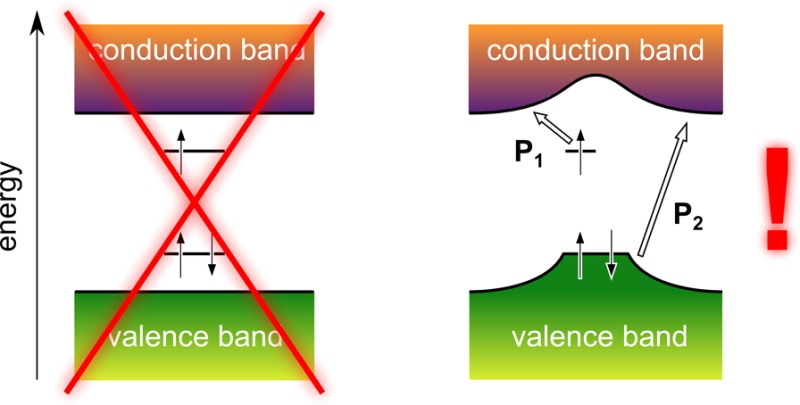
In the anion case (Figure 2e), a singly occupied, localized intragap state just below the conduction-band edge indeed emerges in the spin-up manifold. Its counterpart in the spin-down manifold, however, is notably absent. Consequently, no second electron can be added at this energy (cf. Figure 1c), and the unlikely notion of EA^– > EA⁰ is refuted. Rather, all unoccupied levels “bulge upward” around the localized negative charge, visualizing that a second electron brought into its vicinity would be repelled and that, therefore, EA^– < EA⁰ locally.

Results for the cation case (Figure 2f) are even more striking in that the energy level locally relaxing upward from the valence-band edge is, in fact, completely empty. It is a hole state and no electron can, therefore, be removed from it (cf. Figure 1d). Its occupied counterpart in the spin-up manifold merges into the locally downward-bulging valence band, which affirms that removing a second electron from an already positively charged spatial region costs more energy than removing it from a neutral polymer segment—not less—and that, therefore, IE⁺ > IE⁰ locally.

Qualitatively, the results in Figure 2 thus corroborate the validity of the view proposed in ref (21) also for polymers and its signature is actually visible in previous computational studies.^27,28 Discrepancies to the established polaron picture, however, have not been commented there and neither have their far-reaching implications for the expected optical transitions.

Optical Absorption

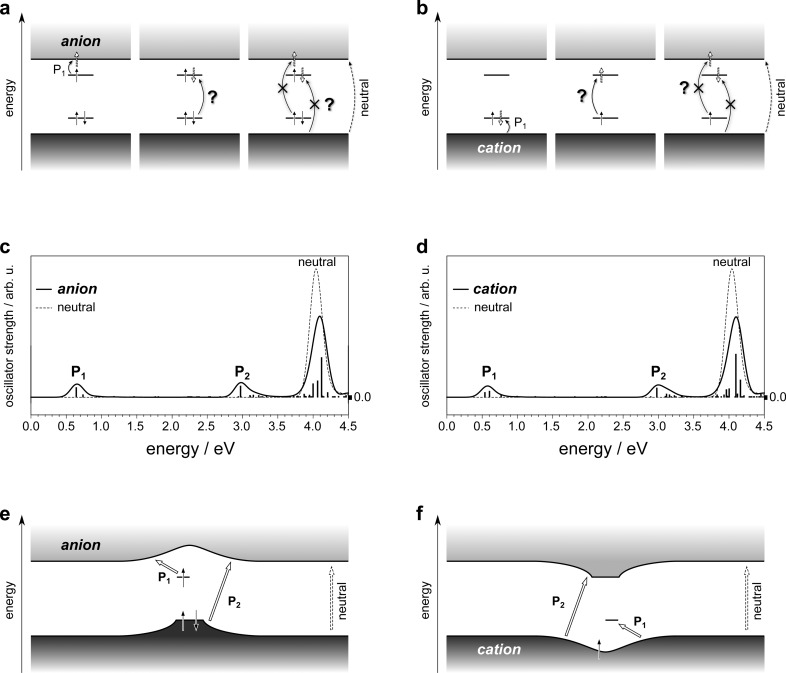
The historical energy-level diagram (Figure 1) suggests three optical transitions to be, in principle, observable in polymer ions of either sign, all at lower energies than the onset of absorption in the neutral system.³⁻⁵ According to this view, the lowest-energy transition in the anion, labeled “P1” in Figure 3a (left), corresponds to promoting the single electron from the upper intragap level into the conduction band. Such a transition still seems plausible in the revised DOS (Figure 2e). Next in energy, the traditional picture suggest a transition promoting an electron from the lower, doubly occupied intragap level into the upper, single occupied state (Figure 3a, center). Previously argued to have appreciable oscillator strength,^26,29−31Figure 2e shows that, on the contrary, it does not even exist owing to the absence of the upper, accepting intragap state. The third, highest-energy subgap absorption is predicted to comprise two transitions in the historical picture. The first, from the lower, doubly occupied intragap state into the conduction band (Figure 3a, right) has been attributed vanishing oscillator strength,^26,29−31 but it is still plausible in the revised DOS (Figure 2e). The last transition, however, from the valence band into the upper, singly occupied intragap state is no longer possible in the picture emerging from the present study, again owing to the manifest absence of the upper, accepting level (Figure 2e). For the cation case (Figure 3b) similar revisions are necessary. While, again, P1 is certainly plausible and so is a transition from the valence band into the upper, unoccupied intragap state, no electron can be promoted from the lower intragap state to anywhere because this state is empty (Figure 2f).

Figure 3.

Historical and revised assignment of charge-induced optical transitions in conjugated polymers. (a) Dark- and light-gray shaded boxes indicate the valence and conduction bands, respectively. Straight, solid, and vertical arrows signify electrons with according spin. Straight, dashed, and empty arrows highlight where electrons are promoted to following the optical excitations indicated by curved arrows. The lowest-energy absorption is labeled P1, question marks near optical transitions underline that they are no longer possible in the revised picture based on Figure 2, and they are crossed out if their observability has been questioned in the literature.^26,29−31 The fundamental absorption of the neutral polymer is indicated on the far right. (b) Same as (a) for the cation. (c) TDDFT-calculated absorption spectra of the negatively charged (solid line) and the neutral oligomer (dashed line). The individual transitions contributing to the anion spectrum are indicated by vertical bars at the respective transition energies with their height reflecting the respective oscillator strength in arbitrary units (arb. u.). (d) Same as (c) for the cation. (e) Schematic of the charged-induced energy levels and resulting optical transitions in polymer anions according to the revised picture proposed in the present work. (f) Same as (e) for cations.

Going beyond the single-particle picture just discussed, which suggests at most two out of three optical transitions to survive the revision of the underlying DOS, I performed time-dependent DFT (TDDFT) calculations on the neutral and ionic oligomers to capture the intrinsically excitonic nature of excited states in such systems. Figure 3c,d clearly shows that, indeed, two broad, subgap absorption features (P1 and, at higher energies, “P2”), are to be expected. Both are composed of a multitude of individual transitions, each of which is by itself a linear combination of many single-electron excitations from an occupied into an unoccupied energy level. Analysis of the expansion coefficients leads to the cartoons in Figure 3e,f, which I suggest should replace the historical picture of charge-induced energy levels and optical transitions in conjugated polymers: In the anion case, feature P1 is composed of transitions that all start from the upper, single occupied intragap level and that end first at the conduction-band edge and then in successively higher-lying unoccupied states. In the cation, the corresponding transitions all end in the lower, unoccupied intragap level and they start first from the valence-band edge and then from successively lower-lying occupied states. The transitions contributing to feature P2 in the anion case start in the lower, doubly occupied intragap state (and lower-lying occupied levels) and end at the conduction-band edge (and higher-lying unoccupied levels). In the cation, they start from the valence-band edge (and lower-lying occupied levels) and end in the upper, empty intragap state (and higher-lying unoccupied levels).

Conclusions

It is possible that even this revised picture, which is still adiabatic, still breaks translational symmetry, and treats Coulomb interaction only at the mean-field level, will eventually be further refined in the future. The minimum physics required for doing so, however, would seem to be captured only by a fully quantized, two-band Holstein-Peierls-Hubbard model, possibly extended to finite temperature,^11,12 disorder,^15,16 and intersite Coulomb interaction.^18,19 My hope is that the present study might stimulate the theoretical community to meet the challenge of finding the spectral function and the optical conductivity of such a model for realistic parameters and band fillings. These efforts could further support the critical re-examination of past experimental data, where the observation of only two (rather than three) subgap absorption features is often attributed to the formation of bipolarons,^3,4,7,8 which I do not, however, discuss here because they are not stable in the present system (see Methods).^17,25 Conversely, if more than two subgap absorption features are observed,^7,32 these can no longer all be attributed to polarons and different explanations are called for. I envision the insights emerging from such a re-examination to enable further progress in the understanding and design of organic (opto-)electronic devices and to cross-fertilize research also on other potentially polaronic materials, such as the recently popularized lead-halide methylammonium perovskites used in photovoltaic applications.³³

Methods

All calculations were performed with the Gaussian 09 quantum chemistry suite (Revision C.01)³⁴ on isolated oligomers in a vacuum employing the 6-31+G** contracted-Gaussian basis set.³⁵⁻³⁷ The molecular symmetry was restrained to point group D₂, which implies alternating interring dihedral angles (rather than a helical molecular conformation). Calculations on the neutral oligomer were performed in a closed-shell, spin-restricted manner and calculations on its radical ions within an open-shell, spin-unrestricted scheme.

The most important aspect of the present DFT calculations, however, is the choice of the exchange-correlation functional: To discuss shifts in the energies of (generalized) Kohn–Sham eigenstates upon changing their occupation, care has to be taken that—if such shifts should indeed occur—they do so for physical reasons and not due to inherent shortcomings of the underlying theory. This can be accomplished by using optimally tuned, long-range corrected hybrid functionals,³⁸ of which the Perdew–Burke–Ernzerhof (PBE) variety was chosen for the present study.³⁹ This functional employs pure Hartree–Fock exchange in the long-range and pure PBE exchange in the short-range, with a smooth (error-function) transition between the two regimes.³⁸ This transition is governed by a (system-dependent) range-separation parameter ω, which is chosen such that the energy of the highest occupied molecular orbital (HOMO) of the neutral system equals the total-energy difference to the radical cation,⁴⁰ and that the HOMO of the radical anion corresponds to the total-energy difference to the neutral system.⁴¹ The optimal value of ω = 0.1882 bohr^–1 was determined by repeatedly cycling through geometry optimization of the neutral oligomer and single-point calculations on the radical ions in that geometry. With this value for ω, both the HOMO of the neutral system and that of the radical anion changed by less than 14 meV upon reducing their respective occupation by one electron. The functional obtained through this nonempirical tuning procedure was then employed to optimize the geometries also of the radical ions. Both the interring dihedral angles⁴² and, with ω close to the “ideal” value of 0.188 bohr^–1 for correctly capturing the bond-length alternation in trans-polyenes,⁴³ the charge-induced changes in bond lengths can be expected to be reasonably well described, as can the relaxation energies of 0.23 eV for the anion and 0.17 eV for the cation.

The total DOS obtained with this functional for the relaxed radical ions was then projected (in a Mulliken sense) onto the individual phenyl(ene) rings of the oligomer and broadened with a Gaussian peak-shape function (full width at half-maximum 0.4 eV) for better visualization.⁴⁴ Linear-response TDDFT calculations were also performed with the same functional, which should be well suited to capture the intramolecular charge-transfer nature of the subgap optical transitions in the ionic species.⁴¹ To make these calculations computationally feasible, the range of occupied and unoccupied orbitals, from/to which single-electron excitations are considered, was restricted to 6 per phenyl(ene) unit, i.e., one per carbon p_z-orbital, on either side of the gap. The discrete absorption spectra so obtained (that is, lists of transition energies and corresponding oscillator strengths) were broadened by a Gaussian peak-shape function with a full width at half-maximum of 0.2 eV.

To assess the possibility of bipolaron formation, which—in the historical picture—corresponds to the coalescence of two spin-antiparallel excess charges of the same sign onto the same (locally geometry-relaxed) polymer segment, also calculations on diions were attempted. Adhering to the bipolaron picture of spin-less charge carriers, these calculations were restricted to a singlet and, therefore, conducted in a closed-shell manner. Relaxing the atomic positions (with those of the radical ions as starting guesses) led to an additional stabilization of 0.20 and 0.16 eV for the dianion and dication, respectively, but the centrally localized geometry distortion—clearly visible in Figure 2d—disappeared. More importantly, the total energy of two isolated, noninteracting radical anions was still lower by 1.20 eV than the total energy of one neutral and one dianionic oligomer, and the total energy of two radical cations was lower by 1.14 eV than that of one neutral and one dicationic oligomer, suggesting Coulomb repulsion between two like charges on the same chain to significantly outweigh the energy gained through additional lattice relaxation. This is also manifest in the fact that the spin-restricted, closed-shell wave functions of the diions exhibit external instabilities toward spin-unrestricted solutions. Indeed, reoptimization as triplets lowers the energies of the dianion and the dication by 0.67 and 0.66 eV, respectively. In the absence of charge-stabilizing counterions,²⁵ the formation of bipolarons in the traditional sense is, therefore, unlikely on isolated strands of poly(para-phenylene) in a vacuum.

The author declares no competing financial interest.