Abstract
The classical maximum entropy clustering (MEC) algorithm usually cannot achieve satisfactory results in the situations where the data is insufficient, incomplete, or distorted. To address this problem, inspired by transfer learning, the specific cluster prototypes and fuzzy memberships jointly leveraged (CPM-JL) framework for cross-domain MEC (CDMEC) is firstly devised in this paper, and then the corresponding algorithm referred to as CPM-JL-CDMEC and the dedicated validity index named fuzzy memberships-based cross-domain difference measurement (FM-CDDM) are concurrently proposed. In general, the contributions of this paper are fourfold: 1) benefiting from the delicate CPM-JL framework, CPM-JL-CDMEC features high-clustering effectiveness and robustness even in some complex data situations; 2) the reliability of FM-CDDM has been demonstrated to be close to well-established external criteria, e.g., normalized mutual information and rand index, and it does not require additional label information. Hence, using FM-CDDM as a dedicated validity index significantly enhances the applicability of CPM-JL-CDMEC under realistic scenarios; 3) the performance of CPM-JL-CDMEC is generally better than, at least equal to, that of MEC because CPM-JL-CDMEC can degenerate into the standard MEC algorithm after adopting the proper parameters, and which avoids the issue of negative transfer; and 4) in order to maximize privacy protection, CPM-JL-CDMEC employs the known cluster prototypes and their associated fuzzy memberships rather than the raw data in the source domain as prior knowledge. The experimental studies thoroughly evaluated and demonstrated these advantages on both synthetic and real-life transfer datasets.
Index Terms: Cross-domain clustering, maximum entropy clustering (MEC), privacy protection, transfer learning, validity index
I. Introduction
Clustering analysis is one of the primary branches in pattern recognition. The conventional clustering approaches can be divided into the following major categories: the partition-based [1]–[12], the hierarchy-based [13], [14], the density-based [15]–[18], the grid-based [19]–[21], and the graph-based [22]–[25], etc. Among them, the partition-based approach, such as the well-known K-means [1] and fuzzy C-means (FCM) [2]–[5], is the most popular approach because of its general applicability to real-life problems. Recently, there is a growing interest in another partition-based method, i.e., maximum entropy clustering (MEC) [6], [7], [26], [27], which integrates two theories of probability-based soft partition and information entropy. Karayiannis [6] proposed MEC based on this understanding that the information entropy (such as Shannon’s entropy [28], Renyi’s entropy [28], and Havrda–Charvat’s entropy [28]) is an essential measure of uncertainty or disorder of a system. Consequently, he devised the objective function by combining two items, i.e., one measures the distortion between the samples and the cluster prototypes, and the other is the Shannon’s entropy in terms of fuzzy memberships.
MEC aims to search for the optimal partitions via simultaneously minimizing the distortion and maximizing the entropy. Because of the simplicity of its essence as well as the meaningful physical connotation, the research with respect to MEC has triggered extensive interests. We briefly summarized the representatives as follows. Two convergence analyses regarding MEC were studied in [26] and [27]. Quite a few of model improvements related to MEC have also been presented to date. For example, Li and Mukaidono [29] designed a complete Gaussian membership function for MEC; Ghorbani [30] devised a L1-norm-based MEC objective expression with better robustness; Lao et al. [31] manipulated the conventional MEC framework into a weighted modality; Yu [32] presented a general fuzzy clustering theory via summarizing several soft-partition clustering prototypes, e.g., MEC and FCM; Yu and Yang [33] further proposed the optimality test and the complexity analysis methods, based on [32], for guaranteeing desirable clustering performance; Wang et al. [34] incorporated the concepts of Vapnik’s ε-insensitive loss function as well as weight factor into the MEC framework to improve the identification of outliers; and Zhi et al. [35] presented a meaningful joint framework by combing fuzzy linear discriminant analysis and the original MEC objective function. In addition, some application studies with respect to MEC were also developed, such as image compression [36], image segmentation [37], and real-time target tracking [38].
Traditional clustering approaches, such as MEC, K-means, and FCM, usually work well in the ideal condition where the data is sufficient and pure. However, in reality, the noise and interference information is omnipresent in real life. In addition, there are more challenges regarding the data completeness, in light of the fast developments as well as the rapid requirement changes in modern information systems. In particular, in the early course of a new system, it is extremely difficult to collect sufficient reliable data. Such data shortage severely restricts the practicability of clustering algorithm to a large extent.
Several advanced clustering models have been developed to overcome the challenges of data incompleteness and impureness, such as semi-supervised clustering [39]–[42], co-clustering [43]–[45], multitask learning [46]–[48], and transfer learning [49]–[53]. In our view, transfer learning is the most promising one because of its specific mechanism. Transfer learning works in at least two connected data domains, i.e., one source domain and one target domain, and it allows more than one source domain as needed. It first identifies helpful information from the source domain, in the form of either data or knowledge, and then it migrates this information into the target domain to guide the learning procedure. This auxiliary guidance usually enhances the learning performance in the target domain. In the case where current data is insufficient or impure but there is plenty of useful information coming from related fields or previous studies, transfer learning is an appropriate approach that can significantly improves the clustering performance. Up to now, many methodologies regarding transfer learning have also been reported. For instance, Pan and Yang [49] offered us an outstanding survey on transfer learning. References [50]–[54] investigated the transfer learning-based classification methods. The classification problem could be the most extensive research field on transfer learning by now. References [55]–[58] proposed several transfer regression models. Wang et al. [59] and Pan et al. [60] presented two dimensionality reduction approaches via transfer learning. In addition, References [45], [61]–[63] connected transfer learning with clustering problems and presented several transfer clustering models.
Based on transfer learning, we comprehensively study the cluster prototypes and fuzzy memberships jointly leveraged (CPM-JL) framework for the cross-domain MEC (CDMEC) issue in this paper. The corresponding algorithm is referred to as CPM-JL-CDMEC. Furthermore, we devise the dedicated validity index, i.e., fuzzy membership-based cross-domain difference measurement (FM-CDDM), in order to aid self-adaptive parameter setting in CPM-JL-CDMEC. Owing to this delicate jointly leveraged transfer mechanism as well as the dedicated FM-CDDM validity index, the effectiveness and practicability of CPM-JL-CDMEC are distinctly improved.
The rest of this paper is organized as follows. In Section II, the classical MEC algorithm and transfer learning are reviewed in brief. In Section III, the CPM-JL framework, the CPM-JL-CDMEC algorithm, the convergence analyses, the parameter setting, and the FM-CDDM index are introduced step-by-step. In Section IV, the experimental validations of the correlated algorithms are presented and discussed. The conclusion is summarized in Section V.
II. Related Work
A. MEC
In a broad sense, MEC implies a series of clustering methods whose objective function is composed of one modality of maximizing entropy. The detailed clustering framework may vary to a certain extent in different algorithms [5], [28]–[34], and herein, we review [5], which is a good representative for this category of approach.
Let X = {xi|xi ∈ Rd, i = 1, 2, …, N} denote a given data set, where d is the data dimensionality and N is the data size. Suppose it can be separated into C(2 ≤ C < N) clusters according to a similarity measure. The objective function of the classical MEC algorithm can be rewritten as
| (1) |
where, ||xj − vi||2 denotes the distance between the pattern xj and the cluster prototype vi; U ∈ RC×N is the membership matrix consisting of μij(i = 1, …, C; j = 1, …, N), and μij denotes the membership of the pattern xj to the cluster prototype vi; V ∈ Rd×C is the cluster prototype matrix composed of all cluster prototypes vi(i = 1, …, C); and γ > 0 is the regularization parameter of the Shannon’s entropy.
Using the Lagrange optimization, the update equations of the cluster prototype vi and the membership μij in (1) can be derived as
| (2) |
| (3) |
B. Transfer Learning
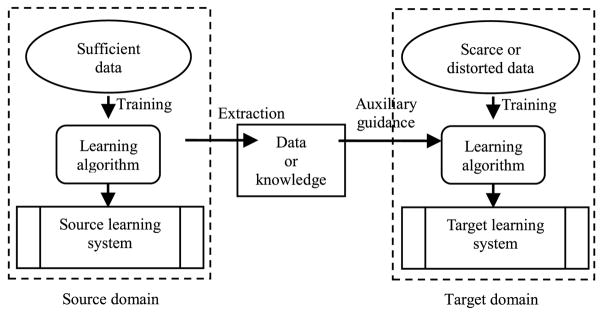
Transfer learning aims to improve the learning performance in the target domain by using the reference information from the source domain [49]. The overall framework of transfer learning is illustrated in Fig. 1. In general, there are two kinds of information that the target domain can obtain from the source domain: raw data or knowledge. Raw data in the source domain is the least sophisticated type of prior information. It may be the most common form to sample the source domain dataset and acquire some representatives and their labels. Knowledge in the source domain is another type of advanced information. Because the original data is not always accessible in the source domain, we may need to conclude knowledge from it sometimes. For example, for the purpose of privacy protection, some raw data maybe cannot be opened and other reasons also could cause the raw data cannot be directly employed even they can be opened. For instance, if there are some underlying drifts between two domains and an unexpected negative influence may occur in the target domain if some improper data are adopted from the source domain. This is the so-called phenomenon of negative transfer. To avoid this potential risk, it is a good choice to draw useful knowledge from the source domain instead of the raw data, e.g., the cluster prototypes in the source domain can be regarded as the good references for the target domain.
Fig. 1.
Overall framework of transfer learning.
So far, transfer learning has been successfully applied in various real-world modeling and learning tasks, such as classification, clustering, and regression [50]–[63].
III. CDMEC Based on Transfer Learning
A. Meaningful Transfer Optimization Formulations for CDMEC
As the two most important elements affecting the clustering performance, cluster prototypes and fuzzy memberships are generally rich in information for reference. Therefore, they are reliable knowledge that can be extracted from the source domain for transfer learning. Based on this idea, for the CDMEC issue, we first devise several transfer optimization formulations from the simple to the complex, and then, we eventually present the complete optimization framework.
1) Cluster Prototypes Leveraged Transfer Optimization Formulation
Definition 1
Let V = [v1, …, vC] ∈ Rd×C denote the cluster prototype matrix in the target domain, where vi(i = 1, …, C) is the estimated cluster prototype, and d and C are the data dimensionality and the cluster number, respectively. Meanwhile, let Ṽ = [ṽ1, …, ṽC] ∈ Rd×C denote the cluster prototype matrix consisting of each known cluster prototype ṽi(i = 1, …, C) in the source domain. Furthermore, make λ be a regularization parameter. Then, the cluster prototype leveraged transfer optimization formulation for CDMEC is defined as
| (4) |
Equation (4) represents the total gap between the estimated cluster prototypes in the target domain and the known ones in the source domain. The regularization coefficient λ controls the reference values of the cluster prototypes in the source domain to those in the target domain. Usually, the larger the coefficient λ, the greater the reference values are.
2) CPM-JL Transfer Optimization Formulation
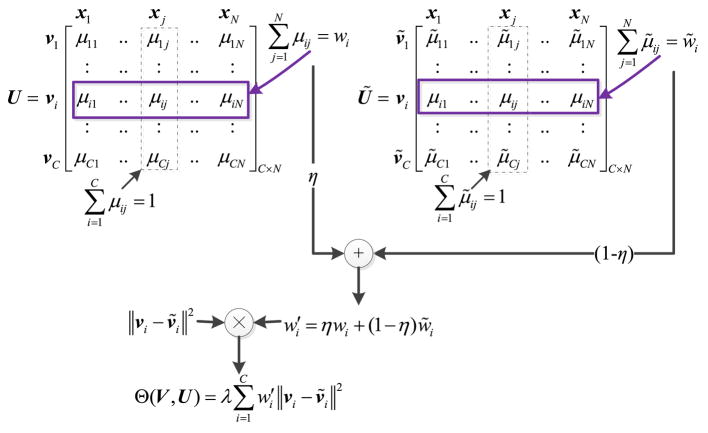
Definition 2
Let Ũ ∈ RC×N denote the membership matrix composed of μ̃ij(i = 1, …, C; j = 1, …, N), where μ̃ij denotes the membership of the pattern xj in the target domain to the known cluster prototype ṽi(i = 1, …, C) in the source domain and it can be derived from (3). By introducing a trade-off factor η ∈ [0, 1] and with the other denotations being the same as those in (4), then CPM-JL transfer optimization formulation can be defined as
| (5a) |
where
| (5b) |
For easily interpreting the meaning of Definition 2, we specifically illustrate its overall composition in Fig. 2. As explained in Definition 1, can be used to measure the approximation degree between the estimated cluster prototypes in the target domain and the given cluster prototypes in the source domain. However, from the perspective of weighted sum, we need to further differentiate the importance of each ||vi − ṽi||2, i.e., the individual weight w′i. In our view, it is reasonable that major clusters, i.e., the clusters composed of many individuals, play primary influence to the total measurement. Therefore, the issue is now converted to find the major clusters in the target domain dataset. As we are aware, each column [μ1j, …, μij, …, μCj]T in the membership matrix U ∈ RC×N in the target domain indicates the potential affiliation of each individual xj in the target dataset, and the greater the value of μij, the more strongly xj belongs to the estimated cluster i in the target domain. Let us analyse the problem in the other point of view, i.e., each row [μi1, …, μij, …, μiN] in U. It is definite that cluster i necessarily contains plenty of samples if many entries of [μi1, …, μij, …, μiN ] take larger values, and which also equals that takes great values. Therefore, as indicated in Fig. 2, can be intuitively used to measure the probability of cluster i that whether it belongs to the major clusters, i.e., whether it consists of many individuals. Moreover, in light of the similarity between the source domain and the target domain in transfer learning, the membership μ̃ij of xj in the target domain to the known cluster prototype ṽi in the source domain can be employed as a reference for μij, and recursively, can be adopted as a reference for . Consequently, as shown in Fig. 2, the combination of wi and w̃i with a trade-off factor η ∈ [0, 1] is devised in (5). Here, the value of η controls the reference degree with respect to μ̃ij, i.e., η → 1 implies that the contribution of μij dominates the optimization formulation Θ(V, U), whereas η → 0 indicates the membership μ̃ij is significantly emphasized. By the way, in light of , and , thus the sum of all the weights in Θ(V, U), i.e., , equals N rather than 1 in our case.
Fig. 2.
Illustration of Definition 2.
Both the known cluster prototypes and their associated fuzzy memberships in the source domain are simultaneously utilized in (5), therefore the designed formulation is named as CPM-JL transfer optimization.
B. Novel CDMEC Framework and Matching Algorithm
In the classical MEC algorithm [see (1)], the term is utilized to evaluate the total deviation of all patterns to all cluster prototypes. Obviously, it is also in the form of weighted sum and the membership μij is employed as the weight factor. Inspired by (5), we introduce the transfer trick into this term, and it can be represented as
| (6) |
where parameter η and membership μ̃ij are the same as those in (5).
1) Specific CPM-JL Framework for CDMEC
Based on (5) and (6), we herein present a novel, integrated framework for solving the general CDMEC problem.
Definition 3
Let XT = xi|xi ∈ Rd, i = 1, 2, …, N} denote the target domain where d is the data dimensionality and N is the data size. Assume there are C clusters in both the source domain and the target domain. The notations of vi, ṽi,μij,μ̃ij, η, and λ are the same as those in (5) or (6). Make γ > 0 be the regularization parameter of the Shannon’s entropy. In addition, have η ∈ [0, 1] and λ ≥ 0, λ ≠ = 1, then the CPM-JL framework for CDMEC can be defined as
| (7) |
There are four items in (7). Both the first and the second terms are inherited from the classical MEC algorithm with only introducing the transfer trade-off coefficient η into the first one. The last two terms, as presented in (5) or (6), are introduced to incorporate additional knowledge from transfer learning.
Theorem 1
The necessary conditions for minimizing the objective function JCPM−JL−CDMEC in (7) yields the following cluster prototype and membership update equations:
| (8) |
| (9) |
Proof
Using the Lagrange optimization, the minimization of JCPM−JL−CDMEC can be transformed into the following unconstrained minimization problem:
| (10) |
where αj(j = 1, …, C) are the Lagrange multipliers.
By separately setting the derivatives to zero with respect to μij and vi, we arrive at
| (11) |
As , based on (11), we get exp ((αj − γ )/γ)
| (12) |
and then by substituting (12) into (11), we can attain (9).
Algorithm 1.
CPM-JL-CDMEC
| Inputs: | The target domain dataset XT, the cluster number C, the maximum iteration number maxiter, the iteration termination threshold ε, the known cluster prototypes Ṽ or the source domain dataset XS, the parameter values in Eq. (7), such as η, λ, and γ. |
| Outputs: | The memberships U, the cluster prototypes V. |
| Extracting knowledge in the source domain: | |
| Setp1: | Obtain the cluster prototypes in Ṽ XS by the classical MEC algorithm; (Skip this step if the cluster prototypes Ṽ in XS are known beforehand) |
| Step2: | Calculate the reference memberships Ũ of all patterns in XT to the cluster prototypes Ṽ in XS via Eq. (3); |
| Cross-domain MEC in the target domain: | |
| Step 1: | Set the iteration counter t = 1 and initialize the memberships U(t); |
| Step 2: | Calculate the cluster prototypes V(t) via Eq. (8), U(t), Ũ, and Ṽ; |
| Step 3: | Calculate the memberships U(t+1) via Eq. (9), V(t) and Ṽ |
| Step 4: | If ||U(t + 1) − U(t)|| < ε or t = maxiter go to Step 5, otherwise, t = t + 1 and go to Step 2; |
| Step 5: | Output the final cluster prototypes V and memberships U in the target domain. |
| (13) |
2) CPM-JL-CDMEC Algorithm
Based on (7)–(9), we now present the core algorithm for CDMEC problems, i.e., CPM-JL-CDMEC, as specifically described in Algorithm 1.
CPM-JL-CDMEC relies essentially on the knowledge coming from the source domain, therefore, the overall workflow of CPM-JL-CDMEC can be divided into two phases: extracting knowledge from the source domain and CDMEC in the target domain.
C. Convergence of CPM-JL-CDMEC
It is well known that the Zangwill’s convergence theorem [9], [64], [65] can be adopted for the convergence proof for almost all iterative optimization algorithms. We aim to prove the convergence of CPM-JL-CDMEC by demonstrating it is a special case of Zangwill’s theorem that can be summarized as follows.
Lemma 1 (Zangwill’s Convergence Theorem)
Let V be a domain of a certain continuous function g, and S ⊂ V be the solution set of g. Define A : V → P(V) is a point to set mapping, which creates an iterative sequence {z(t) = A(t)(z(0))}, where z(0)∈V. If the following conditions hold:
{z(t)} ⊂ Γ ⊆ V, Γ is a compact set;
-
the function g : V → R, satisfying:
if z ∉ S, then for any y ∈ A(z), g(y) < g(z);
if z ∈ S, then either the algorithm terminates or for any y ∈ A(z), g(y) = g(z).
The map A is closed at z if z ∉ S.
Then, either the algorithm stops at a solution or the limit of any converged subsequence is a solution.
Now, we need to prove that our CPM-JL-CDMEC satisfies the three conditions in Lemma 1. Using the similar strategy proposed in [65], we can prove the corresponding Theorems 2a–2c with the auxiliary Definitions 4–7. In light of limited space, we omit the proof details of Theorems 2a–2c, please refer to [65] for detailed derivations.
Definition 4
Let X = {x1, … , xN} be a finite dataset in the Euclidean space Rd, then the set of all fuzzy C-partition of X is defined as .
Definition 5
Define G1 : MC → Rd×C to be a function: G1(U) = V = (v1, … , vC), where vi = (vi1, … , vid)T ∈ Rd, 1 ≤ i ≤ C, are calculated according to (8) and U ∈ Mc.
Definition 6
Define G2 : Rd×C → P(MC) to be a point-to-set map: G2(V) = {U|U ∈ Mc and it is computed by (9)}.
Definition 7
Define a point-to-set map TCPM–JL–CDMEC : Rd×C × MC → P(Rd×C × MC) for the iteration in CPM-JL-CDMEC: TCPM–JL–CDMEC(V,U) = {( V̑, Ȗ)|V̑ = G1(U), Ȗ∈ G2(V̑)}. Specifically, such map can be rewritten as the following composition TCPM–JL–CDMEC = A2 ∘ A1, where A1(V,U) = (G1(U),U) and A2(V, U) = {(V, U)|U ∈ G2(V)}. Thus, (V̑, Ȗ) ∈ TCPM–JL–CDMEC(V, U) = A2 ∘ A1(V, U) = A2(G1(U),U) = A2(V̑, U) = {( V̑, Ȗ)|Ȗ∈ G2(V̑)}.
Theorem 2a
Let η ∈ [0, 1], λ ≥ 0 and λ ≠ 1, and γ > 0 take the specific values as well as Ũ and Ṽ be fixed, suppose X = {x1, … , xN} contains at least C (C < N) distinct points, and make the solution set S of the optimization problem be defined as
| (14) |
Then, it holds that JCPM–JL–CDMEC(V̑, Ȗ) ≤ JCPM–JL–CDMEC(V̄,Ū) for each (V̑, Ȗ) ∈ TCPM–JL–CDMEC(V̄,Ū), and the inequality is strict if (V̄,Ū) ∉ S.
Theorem 2b
Suppose X = {x1, … , xN} contains at least C(C < N) distinct points and (V(0),U(0)) is the starting point of iteration of TCPM–JL–CDMEC with U(0) ∈ MC and V(0) = G1 (U(0)), then the iteration sequence {V(t), (U(t))}, t = 1, 2, … , is contained in a compact subset of Rd×C ×MC.
Theorem 2c
Let η ∈ [0, 1], λ ≥ 0 and λ ≠ 1, and γ > 0 take the specific values as well as Ũ and Ṽ be fixed, suppose X = {x1, … , xN} contains at least C(C < N) distinct points, then the point-to-set map TCPM–JL–CDMEC : Rd×C × MC → P(Rd×C × MC) is closed at each point in Rd×C × MC.
As the objective function JCPM–JL–CDMEC defined in (7) is continuous, the convergence of the CPM-JL-CDMEC algorithm, as summarized in following Theorem 3, is immediately guaranteed from Theorems 2a–2c and Lemma 1.
Theorem 3
(Convergence of CPM-JL-CDMEC). Let η ∈ [0, 1], λ ≥ 0 and λ ≠ 1, and γ > 0 take the specific values as well as Ũ and Ṽ be fixed, have X = {x1, … , xN} contain at least C(C < N) distinct points and JCPM–JL–CDMEC(V, U) be defined in (7), make (V(0), U(0)) be the starting point of the iterations via TCPM–JL–CDMEC with U(0) ∈ MC and V(0) = G1(U(0)), then the iteration sequence {V(t), (U(t))}, t = 1, 2, … , either terminates at a point (V*, U*) in the solution set S or there is a subsequence converging to a point in S.
D. Parameter Setting
There are three important parameters in CPM-JL-CDMEC, i.e., the Shannon’s entropy parameter γ, the transfer regularization coefficient λ, and the trade-off factor η. As usual, the well-known grid search strategy is used for parameter setting in this paper. As we are aware, the grid search strategy depends on some validity indices and current validity indices can be divided roughly into two categories: external criteria (label-based) and internal criteria (label-free) [66]. Those existing external indices, such as normalized mutual information (NMI) [23], [42], [67] and rand index (RI) [67], or internal ones, e.g., Davies–Bouldin index (DBI) [68] and Dunn index [68], can be certainly deployed for the grid search process in this paper. However, for our specific CPM-JL-CDMEC algorithm, especially when it runs on real-life datasets, it is necessary that a dedicated validity index is developed for further enhancing its practicability. For this purpose, we establish the following new validity index.
Definition 8
Let Q̃ = {x̃l}(l = 1, … , m) denote the subset constructed by extracting the pi(i = 1, … , C) nearest samples to each cluster prototype ṽi(i = 1, … , C) in the source domain, where denotes the total data size in Q̃. Let Q = {xj}(j = 1, … , m) signify the subset constructed by extracting one of the nearest neighbors in the target domain to each sample in Q̃. Furthermore, have denote the membership matrix where , l = 1, … , m, represents the fuzzy membership vector of each sample x̃l in Q̃ to the known cluster prototypes Ṽ in the source domain; denote the membership matrix where , j = 1, … , m, represents the fuzzy membership vector of each sample xj in Q to the known cluster prototypes Ṽ in the source domain; and denote the membership matrix where , j = 1, … , m, signifies the fuzzy membership vector of each sample xj in Q to the estimated cluster prototypes V in the target domain, respectively. Thus, the new validity index, named FM-CDDM, for our proposed CPM-JL-CDMEC can be defined as
| (15) |
FM-CDDM, in the form of (15), is designed according to this idea: to measure the differences between the source domain and the target domain, the average distances of each pair of membership vectors in “ ” and “ ” are separately employed and calculated. Actually, the individuals in subset Q̃ are the representatives of each cluster in the source domain, and those in subset Q in the target domain can be regarded as the most similar variations of the corresponding samples in Q̃. Hence, we aim to utilize these two subsets to estimate the differences between the source domain and the target domain from two perspectives. One is that, we fix the cluster prototypes and vary the data samples, i.e., we first separately compute the fuzzy memberships and of Q̃ and Q to the same known cluster prototypes Ṽ in the source domain, and then figure out the average distance via the first term in (15) as one estimated difference. The other is converse, i.e., we adopt the same data samples but different cluster prototypes. Specifically, we firstly compute the fuzzy memberships and of Q to the known cluster prototypes Ṽ in the source domain and the estimated cluster prototypes V in the target domain, respectively, and then calculate the average distance via the second term in (15) as the other estimated difference.
As a result, the best settings of all the parameters η, λ, and γ involved in (15), in principle, can be simultaneously determined via the grid search strategy when FM-CDDM achieves the smallest value. It should be pointed out that, however, the sample size m of Q̃ and Q influences the effectiveness of FM-CDDM to a certain extent. According to our extensive empirical studies, it is an acceptable setting with and , where C is the cluster number and | | denotes the data capacity of the ith cluster in the target domain.
IV. Experimental Results
A. Setup
In this section, we focus on evaluating the performance of the developed CPM-JL-CDMEC algorithm and the FM-CDDM index. Besides CPM-JL-CDMEC and MEC, we employ four other algorithms for comparison, i.e., learning shared subspace for multitask clustering (LSSMTC) [48], combining K-means (CombKM) [48], self-taught clustering (STC) [61], and transfer spectral clustering (TSC) [45]. These algorithms are good representatives of the state-of-the-art algorithms related to our studies. MEC and CPM-JL-CDMEC belong to soft partition clustering; CombKM and LSSMTC belong to hard partition clustering; LSSMTC, TSC, and CombKM belong to multitask clustering; STC, TSC, and CPM-JL-CDMEC belong to transfer clustering. In addition, STC and TSC also belong essentially to co-clustering.
Our experiments were implemented on both synthetic and real-life datasets. To verify the clustering performance of these involved algorithms, three popular validity indices were adopted in this paper, i.e., NMI, RI, and DBI. Among them, NMI and RI belong to external criteria, whereas DBI is an internal criterion. In addition, for CPM-JL-CDMEC, the dedicated FM-CDDM index, proposed by ourselves in (15), was also calculated. Next, we briefly review the particular definitions of NMI, RI, and DBI as follows.
1) NMI
| (16) |
where Ni,j denotes the number of agreements between cluster i and class j, Ni is the number of data points in cluster i, Nj is the number of data points in class j, and N is the size of the whole dataset.
2) RI
| (17) |
where f00 denotes the number of any two sample points belonging to two different clusters, f11 denotes the number of any two sample points belonging to the same cluster, and N is the total number of sample points.
3) DBI
| (18a) |
where
| (18b) |
and C denotes the cluster number in the dataset, denotes the data point belonging to cluster Ck, nk, and vk denote the data size and the centroid of cluster Ck separately.
Both NMI and RI take values within the interval from 0 to 1. Larger values of NMI and RI indicate better clustering performance. In contrast, smaller values of DBI are preferred, and which mean that the levels of both intercluster separation and intracluster compactness are concurrently high. Nevertheless, similar to other internal criteria, DBI has the potential drawback that good values do not necessarily imply better information retrievals. As for FM-CDDM, as previously analysed, smaller values of FM-CDDM are also preferred.
The grid search strategy was adopted in our experiments for parameter optimization. The values or the trial intervals of the primary parameters in each algorithm are listed in Table I.
TABLE I.
Values or Intervals of Primary Parameters in Six Algorithms
| Algorithm | Parameter setting |
|---|---|
| ComKM | K equals to the number of cluster |
| LSSMTC | Task number T = 2 Regularization parameter l ∈ {2,22,23,24}∪{100:100:1000} Regularization parameter λ ∈ {0.25, 0.5, 0.75} |
| STC | Trade-off parameter λ = 1 |
| TSC | K=27, λ = 3, and step = 1 |
| MEC | Entropy regularization parameter γ∈{0.01:0.01:0.09}∪{0.1:0.1:l}∪{2:l:10}∪{20:10:100} |
| CPM-JL-CDMEC | Entropy regularization parameter γ∈{0.01:0.01:0.09}∪{0.1:0.1:l}∪{2:l:10}∪{20:10:100} Transfer regularization parameter γ∈{0:0.01:0.09}∪{0.1:0.1:0.9}∪{2:l:10}∪{20:10:100} Transfer trade-off factor η∈ {0:0.05:1} |
The experimental results are reported in terms of the means and the standard deviations of the employed validity indices, and which were calculated after 20 repeated runs of each algorithm on each dataset. All experiments were carried out on a personal computer with Intel Core i3-3240 3.4 GHz CPU and 4 GB RAM, Microsoft Windows 7, and MATLAB 2010a.
B. On Synthetic Datasets
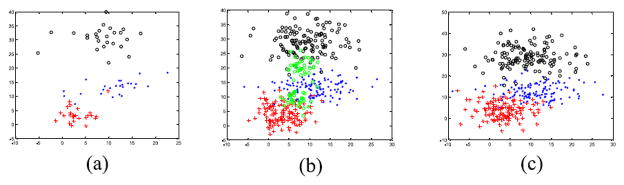
In order to simulate the data scenes for transfer clustering, we generated four synthetic datasets: X̃, X1, X2, and X3. These datasets all contain three base clusters but pose different data distributions, and they were all generated by using the MATLAB built-in function: mvnrnd(). As illustrated in Fig. 3, X̃ simulates the source domain dataset and each cluster consists of 250 samples, so its total capacity is 750.
Fig. 3.
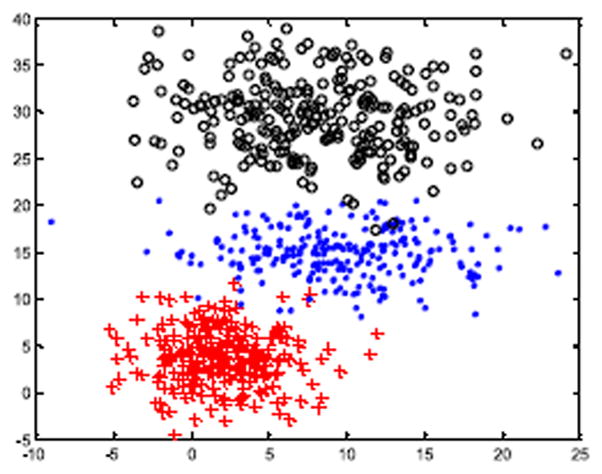
Source domain X̃.
Let ECi and ΣCi denote the mean vector and the covariance matrix of the ith cluster in one dataset, respectively. Thus, X̃ was created with EC1 = [2 4], EC1 = [10 0;0 10], EC2 = [9 15], EC2 = [25 0;0 7], and EC3 = [8 30], EC3 = [30 0;0 20]. X1, X2, and X3 are three cases of target domain, as shown in Fig. 4. X1 simulates the condition where the data in the target domain is insufficient, and which was constructed with EC1 = [3 4], EC1 = [10 0;0 11], EC2 = [10.5 12.5], EC2 = [25 0;0 7], EC3 = [9 29], EC3 = [30 0;0 19.5], and each cluster only consisting of 25 data samples. X2 and X3 were generated using the same data distribution as X1 but each cluster containing 125 samples. Further, two additional clusters were incorporated into X2 as the interference data with EA1 = [7 10], EA1 = [4 0;0 4], EA2 = [8 20], EA2 = [4 0;0 4], and each interference cluster consisting of 35 individuals; and X3 was added the Gaussian noise with the mean and the deviation being 0 and 2, respectively. In general, the eventual data capacities of X̃, X1, X2, and X3 are separately 750, 75, 445, and 375.
Fig. 4.
Target domains. (a) X1. (b) X2. (c) X3.
LSSMTC, CombKM, STC, MEC, and CPM-JL-CDMEC were separately carried out on X1, X2, and X3. Among them, except for MEC, the others need to use the source domain X̃ in different manners. Specifically, CPM-JL-CDMEC utilizes the advanced knowledge concluded from X̃, i.e., the known cluster prototypes and the memberships of those patterns in the target domain to these known cluster prototypes in X̃, whereas the others thoroughly use the raw data in X̃. The clustering effectiveness of each algorithm is listed in Table II in terms of the means and the standard deviations of NMI, RI, and DBI, respectively. In addition, in order to validate the reliability of our devised FM-CDDM index, its value was also calculated in CPM-JL-CDMEC with in (15). Due to the limited space of this paper, we only report the correspondences between FM-CDDM and NMI and RI on X2 and X3 in Tables III and IV, respectively.
TABLE II.
Clustering Performance (NMI, RI, and DBI) of Related Algorithms on Synthetic Datasets
| Dataset | Metrics | Algorithm | ||||
|---|---|---|---|---|---|---|
| LSSMTC | CombKM | MEC | STC | CPM-JL-CDMEC | ||
| X1 | NMI-mean | 0.7626 | 0.7859 | 0.7730 | 0.8552 | 0.9144 |
| NMI-std | 1.17E-16 | 9.79E-17 | 1.17E-16 | 0 | 0 | |
| RI-mean | 0.9023 | 0.9168 | 0.9089 | 0.9443 | 0.9654 | |
| RI-std | 1.17E-16 | 2.34E-16 | 1.17E-16 | 0 | 1.17E-16 | |
| DBI-mean | 0.6153 | 0.6676 | 0.6229 | 0.5928 | 0.5929 | |
| DBI-std | 0 | 1.17E-16 | 1.17E-16 | 0 | 0 | |
| X2 | NMI-mean | 0.6443 | 0.6960 | 0.6498 | 0.7335 | 0.7138 |
| NMI-std | 1.17E-16 | 0.0036 | 1.17E-16 | 0 | 1.17E-16 | |
| RI-mean | 0.8382 | 0.8738 | 0.8405 | 0.8822 | 0.8891 | |
| RI-std | 1.17E-16 | 0.0014 | 1.17E-16 | 0 | 1.17E-16 | |
| DBI-mean | 0.8835 | 0.7931 | 0.8418 | 0.8897 | 0.6503 | |
| DBI-std | 9.72E-5 | 0 | 0.0151 | 0 | 0 | |
| X3 | NMI-mean | 0.7263 | 0.7163 | 0.7523 | 0.7782 | 0.7954 |
| NMI-std | 1.17E-16 | 1.17E-16 | 0 | 0 | 0 | |
| RI-mean | 0.8984 | 0.8917 | 0.9111 | 0.9168 | 0.9296 | |
| RI-std | 0 | 2.34E-16 | 1.17E-16 | 0 | 0 | |
| DBI-mean | 0.8820 | 1.0552 | 0.8802 | 0.8806 | 0.6605 | |
| DBI-std | 0 | 0.0119 | 1.17E-16 | 0 | 0 | |
TABLE III.
Correspondences Between FM-CDDM and NMI and RI on X2 (in the Ascending Order of the Means of FM-CDDM)
| FM-CDDM-mean | 0.03969 | 0.03985 | 0.04019 | 0.04039 | 0.04046 | 0.04049 |
| FM-CDDM-std | 1.627E-17 | 1.552E-17 | 1.151E-17 | 1.552E-17 | 9.180E-18 | 1.097E-17 |
| NMI-mean | 0.66410 | 0.66332 | 0.66410 | 0.66846 | 0.66154 | 0.66154 |
| NMI-std | 0 | 0 | 0 | 0 | 0 | 0 |
| RI-mean | 0.85444 | 0.85200 | 0.85444 | 0.85942 | 0.85461 | 0.85461 |
| RI-std | 1.241E-16 | 0 | 1.241E-16 | 1.241E-16 | 1.241E-16 | 1.241E-16 |
TABLE IV.
Correspondences Between FM-CDDM and NMI and RI on X3 (in the Ascending Order of the Means of FM-CDDM)
| FM-CDDM-mean | 0.04216 | 0.04220 | 0.04223 | 0.04225 | 0.04226 | 0.04227 |
| FM-CDDM-std | 0 | 1.963E-17 | 1.836E-17 | 6.939E-18 | 1.552E-17 | 4.001E-17 |
| NMI-mean | 0.77214 | 0.77214 | 0.77214 | 0.77820 | 0.77214 | 0.77820 |
| NMI-std | 0 | 0 | 0 | 0 | 0 | 0 |
| RI-mean | 0.91997 | 0.91997 | 0.91997 | 0.92298 | 0.91997 | 0.92298 |
| RI-std | 1.241E-16 | 1.241E-16 | 1.241E-16 | 0 | 1.241E-16 | 0 |
The TSC algorithm did not run on these synthetic datasets, because it requires that the data dimensionality must be greater than the number of clusters, and which is not met in these synthetic datasets.
Based on the results presented in Tables II–IV, we make some analyses as follows.
The data in the target domain X1 is relatively scarce and clusters 1 and 2 even overlap a bit. In this situation, the clustering outcomes of those approaches working only based on the data itself in the target domain, such as MEC, are prone to inefficient. Furthermore, the data distribution in X1 is different clearly from that of X̃, so that the clustering performances of LSSMTC, CombKM, and STC are worse than that of CPM-JL-CDMEC. This is because that, even though these competitive clustering algorithms could extract some supporting information from the source domain, the reference value of this information was unreliable in this case. Conversely, CPM-JL-CDMEC utilized the advanced knowledge coming from the source domain as the guidance and such advanced knowledge was more robust than those raw data in this case, therefore it outperformed the others.
Although the data capacities in X2 and X3 are comparatively sufficient, these two cases were polluted by either the interference data or the noise. In general, one of the merits of transfer learning-based methods is the comparatively high anti-noise capability. Consequently, as we see, CPM-JL-CDMEC and STC performed better than the others on X2 and X3.
The pursuits of multitask clustering and transfer clustering are different, and which results in the different performance. Multitask clustering focuses on finishing multiple tasks at the same time, and there exist certainly interactivities between these tasks. By comparison, transfer clustering emphasizes the useful information from the source domain which can enhance the learning performance in the target domain. In summary, because of the guidance of transfer information, the performance of transfer clustering approaches, such as CPM-JL-CDMEC and STC, is distinctly better than the others, if we just focus on the clustering results on the target domain datasets.
Benefitting from the delicate CPM-JL framework, the clustering effectiveness of CPM-JL-CDMEC is always better than that of MEC. This implies the impact of negative transfer was eliminated in these synthetic scenarios.
CPM-JL-CDMEC overcomes the others from the perspective of privacy protection, because CPM-JL-CDMEC merely employs the advanced knowledge (i.e., the known cluster prototypes and their associated fuzzy memberships) in the source domain which cannot be inversely mapped into the original data. Oppositely, the others thoroughly use the raw data in the source domain if they need.
In addition, Tables III and IV indicate that the values of NMI and RI of CPM-JL-CDMEC tend to stay within better ranges when FM-CDDM takes the smallest six values on X2 and X3. For example, on X3, as shown in Table II, the best means of NMI and RI of CPM-JL-CDMEC are 0.7954 and 0.9296, respectively, and in Table IV, the means of NMI and RI are separately around 0.77 and 0.92 when CPM-JL-CDMEC is at the top six. Actually, the correlation between FM-CDDM and NMI/RI exists on all testing datasets, and which indicates that the reliability of FM-CDDM is close to NMI and RI with the distinctive merit that it does not need the sample labels and thus it exhibits stronger practicability.
C. On Real-Life Datasets
In this section, we evaluated the performance of all six algorithms in four real-life transfer scenes, i.e., texture image segmentation, text database, human face recognition, and recognition of real-time human motions (RTHMs). We first introduce the details of these involved real-life datasets, and then present the clustering results of all six algorithms on these datasets.
1) Constructions of Real Transfer Scenes
Texture image segmentation [datasets: texture data 1 (TD1) and texture data 2 (TD2)]: For the scenes of texture image segmentation, we chose seven different textures from the Brodatz texture database,1 and based on them, we firstly constructed two original texture images with the same resolution being 100 × 100 = 10 000 pixels, as shown in Fig. 5(a) and (b). To simulate the transfer scenes, we subsequently generated one derivative of each original image by adding noise as shown in Fig. 5(c) and (d) originating separately from Fig. 5(a) and (b). Based on these four texture images, we generated two datasets for transfer clustering: TD1 and TD2. The specific compositions of these two datasets are listed in Table V. Each dataset was obtained by using the Gabor filter method [69] to extract texture features from the corresponding texture images.
Text data clustering [dataset: rec versus talk]: The New20 text database2 was used in this paper to construct the transfer scenes for text data clustering. Two categories of text data, i.e., rec and talk, and a few of their sub-categories were employed to deploy the source domain and the target domain. We generated the dataset for our experiment: rec versus talk. The categories and their sub-categories involved in rec versus talk are listed in Table VI. Furthermore, the Bow toolkit [70] was also adopted to reduce the data dimensionality which was originally up to 43 586. The final data used for clustering contains 350 effective features.
Human face recognition [dataset: ORL]: The widely-used human face repository, i.e., the ORL database of face,3 was employed for our experiment. We generated the dataset also named ORL in this paper by the following steps. We selected 8 × 10 = 80 facial images from the original ORL database, i.e., eight persons and ten images per person. One facial image of each person is illustrated in Fig. 6. We arbitrarily put eight images per person in the source domain, and the leftover in the target domain. For the purpose of further widening the deviation between the source domain and the target domain as well as enlarging the data capacity in each domain, we also rotated each image anticlockwise with 10° and 20°, respectively. Thus, the eventual image numbers in the source domain and the target domain were separately 192 and 48. In light of the resolution of each image being 92 × 112 = 10304 pixels, we cannot directly use the pixel-gray values of each image as the data features. So we performed the principal component analysis processing on the original gray features, and got the final ORL dataset with data dimensionality being 239.
Recognition of RTHMs [dataset: RTHM]: The dataset for activities of daily living (ADL) recognition with wrist-worn accelerometer data set in the UCI machine learning repository4 was adopted in this paper. It was originally composed of numerous three-variate time series which recorded three signal values of the sensors worn on 16 volunteers’ wrists when they conducted 14 categories of ADL. To simulate the transfer scenario, we first divided the volunteers into two groups according their genders and selected ten categories of activities from the original dataset whose series number are greater than 15, i.e., climb_stairs, comb_hair, descend_stairs, drink_glass, getup_bed, liedown_bed, pour_water, sitdown_chair, standup_chair, and walk. In light of the fact that the female’s total records are distinctly more than the male’s, we used all the female’s time series as the source domain and the male’s as the target domain. Because the time series dimensions (also, series lengths) of different categories of activities are inconsistent and they vary from hundreds to thousands, the multiscale discrete Haar wavelet decomposition [71] strategy was adopted in this paper for dimensionality reduction. After three to six levels of Haar discrete wavelet transform [71] performed on these raw time series, we truncated the intermediates with the same length being 17 and reshaped them into the forms of vectors, thus, we attained the eventual dataset denoted as RTHM in our experiment with the final data dimension being 17 × 3 = 51.
Fig. 5.
Texture images adopted in our experiment. (a) Original texture image 1. (b) Original texture image 2. (c) Derivative image from original image 1. (d) Derivative image from original image 2.
TABLE V.
Compositions of Texture Datasets Involved in Our Experiment
TABLE VI.
Categories and Sub-Categories of New20 Adopted in Our Experiment
| Dataset | Source domain | Target domain |
|---|---|---|
| rec VS talk | rcc.autos | rec.sport.baseball |
| talk.politics.guns | talk.politics.mideast |
Fig. 6.
Human facial dataset: ORL.
The details of all of the real-life datasets involved in our experiments are shown in Table VII. All these datasets had been normalized before they were adopted in our experiments.
TABLE VII.
Details of Real-Life Datasets Involved in This Paper
| Dataset | Transfer domain | Data size | Dimension | Cluster number |
|---|---|---|---|---|
| TD1 | Source domain | 10,000 | 49 | 7 |
| Target domain | 10,000 | 49 | ||
| TD2 | Source domain | 10,000 | 49 | 7 |
| Target domain | 10,000 | 49 | ||
| rec VS talk | Source domain | 1,500 | 350 | 2 |
| Target domain | 500 | 350 | ||
| ORL | Source domain | 192 | 239 | 8 |
| Target domain | 48 | 239 | ||
| RTHM | Source domain | 494 | 51 | 10 |
| Target domain | 312 | 51 |
2) Results of the Experiments
Table VIII reports the means and the standard deviations of NMI, RI, and DBI obtained by the six algorithms on all the real-life datasets. These results clearly prove that CPM-JL-CDMEC is generally of the best performance among all of the candidates. It should be mentioned that these real-life datasets are good representatives aside from their different application backgrounds. In details, rec versus talk and ORL both assume high-dimensionality; TD1 and TD2 are of medium-large scales; and RTHM originating from real-time time series belongs to one of hot topics with respect to the applications of intelligent techniques. This implies that, generally speaking, our CPM-JL-CDMEC algorithm can cope effectively with all of these data situations. Moreover, compared with MEC, the average performance improvement of CPM-JL-CDMEC is more than 50% in terms of the NMI index, which further indicates that the CPM-JL framework is an effective way for the CDMEC problem, even if in some complex data scenarios.
TABLE VIII.
Clustering Performance (NMI, RI, and DBI) of Different Clustering Algorithms on Real Datasets
| Dataset | Metrics | Algorithm | |||||
|---|---|---|---|---|---|---|---|
| LSSMTC | CombKM | MEC | STC | TSC | CPM-JL-CDMEC | ||
| TD1 | NMI-m | 0.5347 | 0.5153 | 0.6087 | 0.4333 | 0.6198 | 0.6489 |
| NMI-s | 0.0600 | 0.0828 | 0.0309 | 0 | 0 | 1.17E-16 | |
| RI-m | 0.8010 | 0.7744 | 0.8838 | 0.8304 | 0.8982 | 0.9077 | |
| RI-s | 0.0653 | 0.1054 | 0.0147 | 0 | 0 | 2.34E-16 | |
| DBI-m | 2.4851 | 3.0258 | 2.3648 | 4.5092 | 2.8825 | 2.3205 | |
| DBI-s | 0.0911 | 0.0574 | 0.1139 | 0 | 0 | 0 | |
| TD2 | NMI-m | 0.6004 | 0.5434 | 0.5930 | 0.3421 | 0.6661 | 0.6817 |
| NMI-s | 0.0838 | 0.1031 | 0.0032 | 0 | 0 | 0.0025 | |
| RI-m | 0.8375 | 0.7923 | 0.8913 | 0.8042 | 0.9148 | 0.9150 | |
| RI-s | 0.0698 | 0.0706 | 0.0031 | 0 | 0 | 0.0015 | |
| DBI-m | 2.6604 | 2.4835 | 2.7696 | 4.9633 | 2.3927 | 2.3369 | |
| DBI-s | 0.0859 | 0.0544 | 0.1510 | 0 | 0 | 0 | |
| rec VS talk | NMI-m | 0.0818 | 0.0572 | 0.2691 | 0.1865 | 0.4224 | 0.6470 |
| NMI-s | 1.46E-17 | 0.0201 | 0 | 0.0055 | 0 | 1.17E-16 | |
| RI-m | 0.5021 | 0.5002 | 0.5960 | 0.5747 | 0.7359 | 0.8593 | |
| RI-s | 0 | 0.0004 | 0 | 0.0078 | 0 | 1.17E-16 | |
| DBI-m | 2.2505 | 2.5320 | 2.4388 | 3.9824 | 1. 7190 | 1.4448 | |
| DBI-s | 0 | 4.68E-16 | 4.68E-16 | 0 | 0 | 0 | |
| ORL | NMI-m | 0.3582 | 0.2124 | 0.2909 | 0.3310 | 0.2950 | 0.5218 |
| NMI-s | 0 | 0.0954 | 0 | 0.0183 | 0.0054 | 0 | |
| RI-m | 0.7748 | 0.5870 | 0.7996 | 0.8116 | 0.8124 | 0.8667 | |
| RI-s | 0 | 0.1806 | 0 | 0.0034 | 0.0004 | 2.34E-16 | |
| DBI-m | 5.7024 | 6.1604 | 3.2747 | 1.5186 | 3.2241 | 3.1124 | |
| DBI-s | 0 | 9.36E-16 | 0.0934 | 0.0361 | 0 | 0 | |
| RTHM | NMI-m | 0.4491 | 0.5120 | 0.5655 | 0.5914 | 0.5986 | 0.6737 |
| NMI-s | 0 | 0 | 0.0154 | 0.0101 | 0.0040 | 1.36E-16 | |
| RI-m | 0.7515 | 0.7745 | 0.7929 | 0.8686 | 0.8862 | 0.8985 | |
| RI-s | 0 | 1.17E-16 | 0.0065 | 0.0003 | 0.0002 | 0 | |
| DBI-m | 1.0867 | 1.0951 | 1.4513 | 1.4873 | 0.74337 | 1.2232 | |
| DBI-s | 2.34E-16 | 2.34E-16 | 0.1386 | 0 | 0.0046 | 0.0003 | |
Note: *-m and *-s denote the values of the mean and the standard deviation, respectively.
Table VIII also reveals two other facts.
The LSSMTC and ComKM approaches good at multitask processing are inefficient in high-dimensional data scenarios.
The DBI metric, which is calculated based on the internal criterion, cannot always catch the inherent information in the data even if it reaches a good value, such as the value of DBI of STC on ORL. In this regard, our proposed FM-CDDM index demonstrates better versatility as well as practicability. The values of FM-CDDM in CPM-JL-CDMEC on all the real-life datasets were computed during our experiments. Similar to that on the synthetic datasets, the values of NMI and RI in CPM-JL-CDMEC correlate well with FM-CDDM because they really rank near the top when FM-CDDM takes the top six values in all these real-life transfer scenarios. For saving paper length, we only present the cases on three datasets: TD2, ORL, and RTHM, as shown in Tables IX–XI.
TABLE IX.
Correspondences Between FM-CDDM, NMI, and RI on Dataset TD2 (in the Ascending Order of the Means of FM-CDDM)
| FM-CDDM-mean | 0.00271 | 0.00348 | 0.00426 | 0.00503 | 0.00581 | 0.00777 |
| FM-CDDM-std | 5.753E-12 | 3.283E-12 | 6.455E-12 | 9.554E-13 | 2.418E-12 | 7.090E-13 |
| NMI-mean | 0.64061 | 0.63896 | 0.63837 | 0.63816 | 0.63927 | 0.63860 |
| NMI-std | 0 | 0 | 0 | 0 | 0 | 0 |
| RI-mean | 0.90631 | 0.90601 | 0.90589 | 0.90583 | 0.90603 | 0.90411 |
| RI-std | 0 | 0 | 0 | 0 | 1.124E-16 | 0 |
TABLE XI.
Correspondences Between FM-CDDM, NMI, and RI on Dataset RTHM (in the Ascending Order of the Means of FM-CDDM)
| FM-CDDM-mean | 1.031E-2 | 1.144E-2 | 1.215E-2 | 1.344E-2 | 1.393E-2 | 1.399E-2 |
| FM-CDDM-std | 5.759E-12 | 4.534E-12 | 6.040E-12 | 1.483E-11 | 5.373E-09 | 2.462E-08 |
| NMI-mean | 0.59089 | 0.57838 | 0.65040 | 0.62803 | 0.64682 | 0.63962 |
| NMI-std | 0 | 0 | 0.00126 | 0.01648 | 0.00182 | 0.00157 |
| RI-mean | 0.85854 | 0.85442 | 0.89190 | 0.87966 | 0.88904 | 0.88724 |
| RI-std | 0 | 0 | 0.00613 | 0.01111 | 0.00251 | 0.01293 |
The segmentation results of six algorithms on Fig. 5(d) are illustrated in Fig. 7. The pixels with the same labels are displayed in the same colors in each sub-graph corresponding to each algorithm. Intuitively, CPM-JL-CDMEC and TSC achieved the better segmentations.
Fig. 7.
Segmentation results of six algorithms on Fig. 5(d). Results of (a) LSSMTC, (b) CombKM, (c) MEC, (d) STC, (e) TSC, and (f) CPM-JL-CDMEC.
D. Robustness Analyses
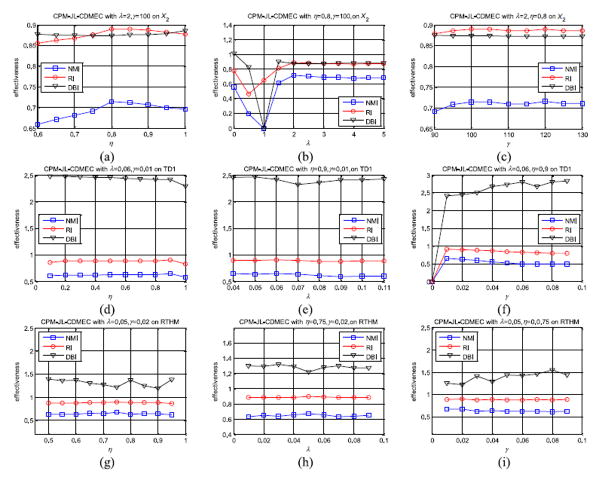
Last but not least, we have evaluated the robustness of our CPM-JL-CDMEC algorithm with respect to its three core parameters, i.e., the transfer trade-off factors η, the transfer regularization parameter λ, and the entropy regularization parameter γ, on both the synthetic and the real-life datasets. On each dataset, we took turns fixing two of the three parameters and gradually changed the third one until CPM-JL-CDMEC achieved the optima by grid search. We calculated the values of the three metrics: NMI, RI, and DBI. Due to the limit of paper length, here, we only report the experimental results on the synthetic dataset X2, the texture image dataset TD1, and the human motion recognition dataset RTHM.
On X2, CPM-JL-CDMEC roughly reached the optima with λ = 2, γ = 100, and η = 0.8; on TD1, with λ = 0.06, γ = 0.01, and η = 0.9; and on RTHM, with λ = 0.05, γ = 0.02, and η = 0.75. The performance curves of CPM-JL-CDMEC on these three datasets are illustrated in Fig. 8, where Fig. 8(a)–(c) shows the cases on X2, Fig. 8(d)–(f) are on TD1, and Fig. 8(g)–(i) are on RTHM.
Fig. 8.
Performance curves of CPM-JL-CDMEC with respect to parameters η, λ, and γ on X2, TD1, and RTHM. (a) On X2, λ and γ are fixed and η varies. (b) On X2, η and γ are fixed and λ varies. (c) On X2, λ and η are fixed and γ varies. (d) On TD1, λ and γ are fixed and η varies. (e) On TD1, η and γ are fixed and λ varies. (f) On TD1, λ and η are fixed and γ varies. (g) On RTHM, λ and γ are fixed and η varies. (h) On RTHM, η and γ are fixed and λ varies. (i) On RTHM, λ and η are fixed and γ varies.
As revealed in Fig. 8, the clustering effectiveness of CPM-JL-CDMEC is relatively stable when the three major parameters are within proper ranges, which demonstrates that CPM-JL-CDMEC features a good robustness against parameter setting.
V. Conclusion
Inspired by transfer learning, we propose the CPM-JL-CDMEC algorithm as well as the dedicated FM-CDDM index in this paper to deal with cross-domain partition-based clustering issues, especially in the situations where the data could be insufficient or polluted by unknown noise or outliers.
In summary, owing to the delicate, CPM-JL framework and the reliable strategy for avoiding negative transfer issues, CPM-JL-CDMEC proves satisfactory clustering effectiveness and robustness in both the artificial and the real-life transfer scenarios. Besides these, by means of the dedicated FM-CDDM index, another contribution of this paper, the combination of “CPM-JL-CDMEC + FM-CDDM” can cope with most of cross-domain data cases. In addition, the intrinsic mechanism of privacy protection in CPM-JL-CDMEC further strengthens the practicability of our research in this paper.
TABLE X.
Correspondences Between FM-CDDM, NMI, and RI on Dataset ORL (in the Ascending Order of the Means of FM-CDDM)
| FM-CDDM-mean | 1.761E-05 | 2.888E-04 | 3.936E-04 | 3.916E-04 | 4.780E-04 | 5.474E-04 |
| FM-CDDM-std | 3.861E-13 | 1.182E-11 | 1.501E-11 | 1.538E-11 | 8.326E-12 | 4.929E-12 |
| NMI-mean | 0.50611 | 0.50611 | 0.50611 | 0.50611 | 0.52054 | 0.52054 |
| NMI-std | 0 | 0 | 0 | 0 | 0 | 0 |
| RI-mean | 0.76596 | 0.76596 | 0.76596 | 0.76596 | 0.77748 | 0.77748 |
| RI-std | 0 | 0 | 0 | 0 | 0 | 0 |
Acknowledgments
This work was supported in part by the National Natural Science Foundation of China under Grant 61202311 and Grant 61272210, in part by the Natural Science Foundation of Jiangsu Province under Grant BK201221834, in part by the Research and Development Frontier Grant of Jiangsu Province under Grant BY2013015-02, in part by the Ministry of Education Program for New Century Excellent Talents under Grant NECT-120882, in part by the Fundamental Research Funds for the Central Universities under Grant JUSRP51321B, and in part by the Jiangsu Province Outstanding Youth Fund under Grant BK20140001. This paper was recommended by Associate Editor A. F. Skarmeta Gomez.
Biographies

Pengjiang Qian (M’12) received the Ph.D. degree from Jiangnan University, Wuxi, China, in 2011.
He is an Associate Professor with the School of Digital Media, Jiangnan University, and Case Western Reserve University, Cleveland, OH, USA, as a Research Scholar in medical image processing. His current research interests include data mining, pattern recognition, bioinformatics and their applications, such as analysis and processing for medical imaging, intelligent traffic dispatching, and advanced business intelligence in logistics. He has authored/co-authored over 30 papers in international/national journals and conferences.

Yizhang Jiang (M’12) is currently pursuing the Ph.D. degree from the School of Digital Media, Jiangnan University, Wuxi, China.
He is currently a Research Assistant with the Department of Computing, Hong Kong Polytechnic University, Hong Kong. His current research interests include pattern recognition, intelligent computation, and their applications. He has published several papers in international journals including the IEEE Transactions on Fuzzy Systems and the IEEE Transactions on Neural Networks and Learning Systems.

Zhaohong Deng (SM’13) received the Ph.D. degree from Jiangnan University, Wuxi, China, in 2008.
He is currently an Associate Professor with the School of Digital Media, Jiangnan University. He visited the University of California, Davis, Davis, CA, USA, and the Hong Kong Polytechnic University, Hong Kong, for over two years. His current research interests include neuro-fuzzy systems, pattern recognition, and their applications. He has authored/co-authored over 40 research papers in international/national journals.

Lingzhi Hu received the Ph.D. degree in medical imaging from Washington University, St. Louis, St. Louis, MO, USA, in 2012.
He is currently a Research Scientist with Philips Electronics North America, Cleveland, OH, USA. His current research interests include system design, image reconstruction, and processing for radiological imaging device. He has authored and co-authored over 30 papers on internationally recognized journals and conferences. He has been invited to review for top journals and conferences in medical imaging for over 20 times.

Shouwei Sun is currently pursuing the M.S. degree from the School of Digital Media, Jiangnan University, Wuxi, China.
His current research interests include pattern recognition, bioinformatics, and their applications. He has authored or co-authored several papers in international/national journals and conferences.

Shitong Wang received the M.S. degree in computer science from the Nanjing University of Aeronautics and Astronautics, Nanjing, China, in 1987.
He visited London University, London, U.K., and Bristol University, Bristol, U.K., the Hiroshima International University, Hiroshima, Japan, Osaka Prefecture University, Osaka, Japan, Hong Kong University of Science and Technology, Hong Kong, and the Hong Kong Polytechnic University, Hong Kong, as a Research Scientist, for over six years. He is currently a Full Professor with the School of Digital Media, Jiangnan University, Wuxi, China. His current research interests include artificial intelligence, neuro-fuzzy systems, pattern recognition, and image processing. He has published over 100 papers in international/national journals and has authored seven books.

Raymond F. Muzic, Jr. (SM’00) received the Ph.D. degree from Case Western Reserve University, Cleveland, OH, USA, in 1991.
He is currently an Associate Professor of Radiology, Biomedical Engineering, and General Medical Sciences—Oncology, Case Western Reserve University. His current research interests include development and application of quantitative methods for medical imaging. He has authored/co-authored approximately 50 peer-reviewed articles. He has led or been a team member on numerous funded research projects. He has also had the pleasure to serve as an advisor for doctoral students.
Footnotes
Contributor Information
Pengjiang Qian, Email: qpengjiang@gmail.com, School of Digital Media, Jiangnan University, Wuxi 214122, China.
Yizhang Jiang, School of Digital Media, Jiangnan University, Wuxi 214122, China.
Zhaohong Deng, School of Digital Media, Jiangnan University, Wuxi 214122, China.
Lingzhi Hu, Philips Electronics North America, Cleveland, OH 44143 USA.
Shouwei Sun, School of Digital Media, Jiangnan University, Wuxi 214122, China.
Shitong Wang, School of Digital Media, Jiangnan University, Wuxi 214122, China.
Raymond F. Muzic, Jr., Department of Radiology and Case Center for Imaging Research, University Hospitals, Case Western Reserve University, Cleveland, OH 44106 USA.
References
- 1.MacQueen JB. Some methods for classification and analysis of multivariate observations. Proc. 5th Berkeley Symp. Math. Stat. Probab; Berkeley, CA, USA. 1967. pp. 281–297. [Google Scholar]
- 2.Dunn J. A fuzzy relative of the ISODATA process and its use in detecting compact well separated clusters. J Cybern. 1974;3(3):32–57. [Google Scholar]
- 3.Höppner F, Klawonn F, Kruse R. Fuzzy Cluster Analysis: Methods for Classification, Data Analysis, and Image Recognition. New York, NY, USA: Wiley; 1999. [Google Scholar]
- 4.Bezdek J, Hathaway R. Numerical convergence and interpretation of the fuzzy c-shells clustering algorithms. IEEE Trans Neural Netw. 1992 Sep;3(5):787–793. doi: 10.1109/72.159067. [DOI] [PubMed] [Google Scholar]
- 5.Liu Z, Xu S, Zhang Y, Chen CLP. A multiple-feature and multiple-kernel scene segmentation algorithm for humanoid robot. IEEE Trans Cybern. 2014 Nov;44(11):2232–2240. doi: 10.1109/TSMC.2013.2297398. [DOI] [PubMed] [Google Scholar]
- 6.Karayiannis NB. MECA: Maximum entropy clustering algorithm. Proc. IEEE Int. Conf. Fuzzy Syst; Orlando, FL, USA. 1994. pp. 630–635. [Google Scholar]
- 7.Li RP, Mukaidono MA. A maximum entropy approach to fuzzy clustering. Proc. IEEE Int. Conf. Fuzzy Syst; Yokohama, Japan. 1995. pp. 2227–2232. [Google Scholar]
- 8.Bradley PS, Mangasarian QL. K-plane clustering. J Glob Optim. 2000;16(1):23–32. [Google Scholar]
- 9.Wu KL, Yu J, Yang MS. A novel fuzzy clustering algorithm based on a fuzzy scatter matrix with optimality tests. Pattern Recognit Lett. 2005;26(5):639–652. [Google Scholar]
- 10.Bezdek JC. A convergence theorem for the fuzzy ISODATA clustering algorithm. IEEE Trans Pattern Anal Mach Intell. 1980 Jan;PAMI-2(1):1–8. doi: 10.1109/tpami.1980.4766964. [DOI] [PubMed] [Google Scholar]
- 11.de Luis Balaguer MA, Williams CM. Hierarchical modularization of biochemical pathways using fuzzy-c means clustering. IEEE Trans Cybern. 2013 Aug;44(8):1473–1484. doi: 10.1109/TCYB.2013.2286679. [DOI] [PubMed] [Google Scholar]
- 12.Jiang Y, et al. Collaborative fuzzy clustering from multiple weighted views. IEEE Trans Cybern. doi: 10.1109/TCYB.2014.2334595. to be published. [DOI] [PubMed] [Google Scholar]
- 13.Heller KA, Ghahramani Z. Bayesian hierarchical clustering. Proc. 22th Int. Conf. Mach. Learn; Bonn, Germany. 2005. pp. 297–304. [Google Scholar]
- 14.Guha S, Rastogi R, Shim K. CURE: An efficient clustering algorithm for large database. Proc. ACM SIGMOD Int. Conf. Manage. Data; Seattle, WA, USA. 1998. pp. 73–84. [Google Scholar]
- 15.Zhuang X, Huang Y, Palaniappan K, Zhao Y. Gaussian mixture density modeling, decomposition, and applications. IEEE Trans Image Process. 1996 Sep;5(9):1293–1302. doi: 10.1109/83.535841. [DOI] [PubMed] [Google Scholar]
- 16.Figueiredo M, Jain A. Unsupervised learning of finite mixture models. IEEE Trans Pattern Anal Mach Intell. 2002 Mar;24(3):381–396. [Google Scholar]
- 17.McLachlan GJ, Peel D. Finite Mixture Models. New York, NY, USA: Wiley; 2000. [Google Scholar]
- 18.McLachlan GJ, Krishnan T. The EM Algorithm and Extensions. New York, NY, USA: Wiley; 1997. [Google Scholar]
- 19.Wang W, Yang J, Muntz R. STING: A statistical information grid approach to spatial data mining. Proc. 23rd Int. Conf. Very Large Data Bases (VLDB); San Francisco, CA, USA. 1997. pp. 186–195. [Google Scholar]
- 20.Sheikholeslami G, Chatterjee S, Zhang A. WaveCluster: A multi-resolution clustering approach for very large spatial databases. Proc. 24th Int. Conf. Very Large Data Bases (VLDB); New York, NY, USA. 1998. pp. 428–439. [Google Scholar]
- 21.Agrawal R, Gehrke J, Gunopolos D. Automatic subspace clustering of high dimensional data for data mining applications. Proc. ACM SIGMOD Int. Conf. Manage. Data; Seattle, WA, USA. 1998. pp. 94–105. [Google Scholar]
- 22.Shi J, Malik J. Normalized cuts and image segmentation. IEEE Trans Pattern Anal Mach Intell. 2000 Aug;22(8):888–905. [Google Scholar]
- 23.Sarkar S, Soundararajan P. Supervised learning of large perceptual organization: Graph spectral partitioning and learning automata. IEEE Trans Pattern Anal Mach Intell. 2000 May;22(5):504–525. [Google Scholar]
- 24.Qian P, Chung FL, Wang S, Deng Z. Fast graph-based relaxed clustering for large data sets using minimal enclosing ball. IEEE Trans Syst, Man, Cybern B, Cybern. 2012 Jun;42(3):672–687. doi: 10.1109/TSMCB.2011.2172604. [DOI] [PubMed] [Google Scholar]
- 25.Xu X, Huang Z, Graves D, Pedrycz W. A clustering-based graph Laplacian framework for value function approximation in reinforcement learning. IEEE Trans Cybern. 2014 Dec;44(12):2613–2625. doi: 10.1109/TCYB.2014.2311578. [DOI] [PubMed] [Google Scholar]
- 26.Zhang Z, Zheng N, Shi G. Maximum-entropy clustering algorithm and its global convergence analysis. Sci China E, Technol Sci. 2001;44(1):89–101. [Google Scholar]
- 27.Ren S, Wang Y. A proof of the convergence theorem of maximum-entropy clustering algorithm. Sci China F, Inf Sci. 2010;53(6):1151–1158. [Google Scholar]
- 28.Xu D. PhD dissertation. Dept. Electr. and Comput. Eng., Univ. Florida; Gainesville, FL, USA: 1999. Energy, entropy and information potential for neural computation. [Google Scholar]
- 29.Li RP, Mukaidono M. Gaussian clustering method based on maximum-fuzzy-entropy interpretation. Fuzzy Sets Syst. 1999;102(2):253–258. [Google Scholar]
- 30.Ghorbani M. Maximum entropy-based fuzzy clustering by using L1-norm space. Turk J Math. 2005;29(1):431–438. [Google Scholar]
- 31.Lao L, Wu X, Cheng L, Zhu X. Maximum weighted entropy clustering algorithm. Proc. IEEE Int. Conf. Netw. Sens. Control; Fort Lauderdale, FL, USA. 2006. pp. 1022–1025. [Google Scholar]
- 32.Yu J. General C-means clustering model. IEEE Trans Pattern Anal Mach Intell. 2005 Aug;27(8):1197–1211. doi: 10.1109/TPAMI.2005.160. [DOI] [PubMed] [Google Scholar]
- 33.Yu J, Yang MS. A generalized fuzzy clustering regularization model with optimality tests and model complexity analysis. IEEE Trans Fuzzy Syst. 2007 Oct;15(5):904–915. [Google Scholar]
- 34.Wang S, Chung KL, Deng Z, Hu D, Wu H. Robust maximum entropy clustering with its labeling for outliers. Soft Comput. 2006;10(7):555–563. [Google Scholar]
- 35.Zhi X, Fan J, Zhao F. Fuzzy linear discriminant analysis-guided maximum entropy fuzzy clustering algorithm. Pattern Recognit. 2013;46(6):1604–1615. [Google Scholar]
- 36.Karayiannis NB, Zervos N. Entropy-constrained learning vector quantization algorithms and their application in image compression. J Electron Imag. 2000 Oct;9(4):495–508. [Google Scholar]
- 37.Li K, Guo Z. Image segmentation with fuzzy clustering based on generalized entropy. J Comput. 2014;9(7):1678–1683. [Google Scholar]
- 38.Li L, Ji H, Gao X. Maximum entropy fuzzy clustering with application to real-time target tracking. Signal Process. 2006;86(11):3432–3447. [Google Scholar]
- 39.Zhu X, Ghahramani Z, Lafferty JD. Semi-supervised learning using Gaussian fields and harmonic functions. Proc. 20th Int. Conf. Mach. Learn. (ICML); Washington, DC, USA. 2003. pp. 912–919. [Google Scholar]
- 40.Zhou D, Bousquet O, Lal TN, Weston J, Schölkopf B. Learning with local and global consistency. Proc. Neural Inf. Process. Syst. (NIPS); Vancouver, BC, Canada. 2004. pp. 321–328. [Google Scholar]
- 41.Breitenbach M, Grudic GZ. Clustering through ranking on manifolds. Proc. 22nd Int. Conf. Mach. Learn. (ICML); Bonn, Germany. 2005. pp. 73–80. [Google Scholar]
- 42.Nie F, Xu D, Li X. Initialization independent clustering with actively self-training method. IEEE Trans Syst, Man, Cybern B, Cybern. 2012 Feb;42(1):17–27. doi: 10.1109/TSMCB.2011.2161607. [DOI] [PubMed] [Google Scholar]
- 43.Dhillon IS, Mallela S, Modha DS. Information-theoretic co-clustering. Proc. 9th ACM SIGKDD Int. Conf. Knowl. Disc. Data Min. (KDD); Washington, DC, USA. 2003. pp. 89–98. [Google Scholar]
- 44.Dhillon IS. Co-clustering documents and words using bipartite spectral graph partitioning. Proc.7th ACM SIGKDD Int. Conf. Knowl. Disc. Data Min. (KDD); San Fransisco, CA, USA. 2001. pp. 269–274. [Google Scholar]
- 45.Jiang WH, Chung FL. Machine Learning and Knowledge Discovery in Databases. Berlin, Germany: Springer; 2012. Transfer spectral clustering; pp. 789–803. (LNCS 7524) [Google Scholar]
- 46.Caruana R. Multitask learning. Mach Learn. 1997;28(1):41–75. [Google Scholar]
- 47.Ando RK, Zhang T. A framework for learning predictive structures from multiple tasks and unlabeled data. J Mach Learn Res. 2005 Dec;6:1817–1853. [Google Scholar]
- 48.Gu Q, Zhou J. Learning the shared subspace for multi-task clustering and transductive transfer classification. Proc. 9th Int. Conf. Data Min. (ICDM); Miami, FL, USA. 2009. pp. 159–168. [Google Scholar]
- 49.Pan J, Yang Q. A survey on transfer learning. IEEE Trans Knowl Data Eng. 2010 Oct;22(10):1345–1359. [Google Scholar]
- 50.Tao J, Chung FL, Wang S. On minimum distribution discrepancy support vector machine for domain adaptation. Pattern Recognit. 2012;45(11):3962–3984. [Google Scholar]
- 51.Gao J, Fan W, Jiang J, Han J. Knowledge transfer via multiple model local structure mapping. Proc. 14th ACM SIGKDD Int. Conf. Knowl. Disc. Data Min. (KDD); Las Vegas, NV, USA. 2008. pp. 283–291. [Google Scholar]
- 52.Mihalkova L, Huynh T, Mooney RJ. Mapping and revising Markov logic networks for transfer learning. Proc. Conf. Artif. Intell. (AAAI); Vancouver, BC, Canada. 2007. pp. 608–614. [Google Scholar]
- 53.Mihalkova L, Mooney RJ. Transfer learning by mapping with minimal target data. Proc. Conf. Artif. Intell. (AAAI); Chicago, IL, USA. 2008. [Google Scholar]
- 54.Duan L, Tsang IW, Xu D. Domain transfer multiple kernel learning. IEEE Trans Pattern Anal Mach Intell. 2012 Mar;34(3):465–479. doi: 10.1109/TPAMI.2011.114. [DOI] [PubMed] [Google Scholar]
- 55.Yang P, Tan Q, Ding Y. Bayesian task-level transfer learning for non-linear regression. Proc. Int. Conf. Comput. Sci. Softw. Eng; Hubei, China. 2008. pp. 62–65. [Google Scholar]
- 56.Borzemski L, Starczewski G. Application of transfer regression to TCP throughput prediction. Proc. 1st Asian Conf. Intell. Inf. Database Syst; Dong Hoi, Vietnam. 2009. pp. 28–33. [Google Scholar]
- 57.Mao W, Yan G, Bai J, Li H. Advances in Neural Networks. Berlin, Germany: Springer; 2010. Regression transfer learning based on principal curve; pp. 365–372. (LNCS 6063) [Google Scholar]
- 58.Deng Z, Jiang Y, Choi KS, Chung FL, Wang S. Knowledge-leverage-based TSK fuzzy system modeling. IEEE Trans Neural Netw Learn Syst. 2013 Aug;24(8):1200–1212. doi: 10.1109/TNNLS.2013.2253617. [DOI] [PubMed] [Google Scholar]
- 59.Wang Z, Song YQ, Zhang CS. Machine Learning and Knowledge Discovery in Databases. Berlin, Germany: Springer; 2008. Transferred dimensionality reduction; pp. 550–565. (LNCS 5212) [Google Scholar]
- 60.Pan SJ, Kwok JT, Yang Q. Transfer learning via dimensionality reduction. Proc. Conf. Artif. Intell. (AAAI); Chicago, IL, USA. 2008. pp. 677–682. [Google Scholar]
- 61.Dai W, Yang Q, Xue G, Yu Y. Self-taught clustering. Proc. 25th Int. Conf. Mach. Learn. (ICML); Helsinki, Finland. 2008. pp. 200–207. [Google Scholar]
- 62.Gu Q, Zhou J. Transfer heterogeneous unlabeled data for unsupervised clustering. Proc. 21st Int. Conf. Pattern Recognit; Tsukuba, Japan. 2012. pp. 1193–1196. [Google Scholar]
- 63.Sun S, Jiang Y, Qian P. Transfer learning based maximum entropy clustering. Proc. 4th IEEE Int. Conf. Inf. Sci. Technol; Shenzhen, China. 2014. pp. 829–832. [Google Scholar]
- 64.Zangwill W. Nonlinear Programming: A Unified Approach. Englewood Cliffs, NJ, USA: Prentice-Hall; 1969. [Google Scholar]
- 65.Gan G, Wu J. A convergence theorem for the fuzzy subspace clustering (FSC) algorithm. Pattern Recognit. 2008;41(6):1939–1947. [Google Scholar]
- 66.Liu Y, et al. Understanding and enhancement of internal clustering validation measures. IEEE Trans Cybern. 2013 Jun;43(3):982–993. doi: 10.1109/TSMCB.2012.2220543. [DOI] [PubMed] [Google Scholar]
- 67.Liu J, et al. Distance-based clustering of CGH data. Bioinformatics. 2006;22(16):1971–1978. doi: 10.1093/bioinformatics/btl185. [DOI] [PubMed] [Google Scholar]
- 68.Desgraupes B. Clustering Indices. Univ. Paris Ouest, Lab Modal’X; Nanterre, France: 2013. [Google Scholar]
- 69.Kyrki V, Kamarainen JK, Kalviainen H. Simple Gabor feature space for invariant object recognition. Pattern Recognit Lett. 2004;25(3):311–318. [Google Scholar]
- 70.McCallum AK. Bow: A Toolkit for Statistical Language Modeling, Text Retrieval, Classification and Clustering [EB/OL] 1996 [Online]. Available: http://www.cs.cmu.edu/mccallum/bow.
- 71.He X, Shao C, Xiong Y. A new similarity measure based on shape information for invariant with multiple distortions. Neurocomputing. 2014 Apr;129:556–569. [Google Scholar]