Importance of Diffuse Metal Ion Binding to RNA

Abstract

RNAs are highly charged polyanionic molecules. RNA structure and function are strongly correlated with the ionic condition of the solution. The primary focus of this article is on the role of diffusive ions in RNA folding. Due to the long-range nature of electrostatic interactions, the diffuse ions can contribute significantly to RNA structural stability and folding kinetics. We present an overview of the experimental findings as well as the theoretical developments on the diffuse ion effects in RNA folding. This review places heavy emphasis on the effect of magnesium ions. Magnesium ions play a highly efficient role in stabilizing RNA tertiary structures and promoting tertiary structural folding. The highly efficient role goes beyond the mean-field effect such as the ionic strength. In addition to the effects of specific ion binding and ion dehydration, ion-ion correlation for the diffuse ions can contribute to the efficient role of the multivalent ions such as the magnesium ions in RNA folding.

1. INTRODUCTION

RNA structure and stability are intrinsic to RNA function and RNA-based therapeutic strategies. Recent breathtaking new discoveries on the functions of non-coding RNAs have opened a new door for many potential therapeutic applications of RNAs. This further presses the demand for quantitative understanding and prediction of RNA structure and stability. RNA structural formation is driven by the intramolecular forces, such as base pairing/stacking, ion-mediated electrostatic interactions and the effects of conformational entropies [1,2]. The primary concern of this chapter is on the role of ion-mediated electrostatic interactions in RNAs.

Metal ions, especially Mg²⁺, play a critical role in RNA folding. Because each RNA nucleotide carries a unit negative charge on the phosphate, RNA folding causes massive build-up of negative charges. There are two electrostatic effects involved in RNA folding. First, the charge build-up would lead to a strong intrachain Coulombic repulsion to oppose RNA folding. For example, folding of a 400-nt RNA could cause an increase in the electrostatic energy of about 1000 kcal/mol [3]. Second, the charge build-up would attract the counterions in the solution and induce significant ion binding to RNA. Specifically, metal ions in the solution can cluster around the polyanionic RNA to effectively reduce the electrostatic energy and to promote folding and stabilize a folded RNA structure. Therefore, RNA structure and stability are strongly coupled to ion electrostatic interactions [1–8].

The main focus of this chapter is on the effect of diffuse (bound) ions in RNA folding. What is a diffuse (bound) ion? To answer this question, we need first to clarify the use of the phrases “bound ions” and “diffuse ions”. Firstly, ion-RNA interaction is predominantly determined by ions in the close vicinity of the RNA surface. The phrase “bound ions” has been used in widely different senses in the literature. Because electrostatic interactions are long-range, all counter ions are “bound” with all nucleic acids in a solution. Therefore, the bound ions for an RNA have been defined as the surrounding ions in excess of the bulk ion concentration. In other literature, bound ions are reserved for interactions that involve specific ion-RNA interactions. In this chapter, we use “bound ion” in the former sense to refer to the diffuse ions accumulated around RNA in excess of the bulk ion concentration away from the RNA.

Secondly, a bound ion can remain hydrated and interact non-specifically with the RNA. These ions are often called “diffuse ions”. Other ions can coordinate to specific groups of the RNA. Due to the close interaction with specific RNA groups, a specifically bound ion could be energetically important (in addition to its catalytic role). However, due to the long-range nature of the Coulomb interaction, the (large number of) diffuse ions can result in a significant electrostatic force on the charged (phosphate) groups of RNA and have a critical impact on the structural formation of RNA [4–8].

2. DIFFUSE IONS PROVIDE A SIGNIFICANT STABILIZING FORCE FOR RNA STRUCTURE

Quantitative study of the effects of diffuse ions is difficult due to several reasons: (a) the long-range nature of the electrostatic interaction, (b) the intriguing interplay between ion-ion and ion-RNA interactions, (c) the dependence on the concentration, charge and size of the ions, and (d) the effect of the complex three-dimensional shape of the RNA. These factors directly impact the answers to several key questions about the important roles of the (diffuse) ions. Where do bound ions distribute on the RNA surface? How many ions are bound to the RNA? How large is the ion-dependent stabilizing free energy? How does the free energy vary for different RNA structures? How is the ion electrostatic free energy compared to the other stabilizing and destabilizing free energies in RNA folding? Why do some ions show “unusually” high efficiency in stabilizing RNA structure than other ions? These questions have provided a strong motivation for the measurements of ion distribution and ion electrostatic folding free energies for the different RNA structures.

2.1. Distribution of the Bound Ions

The first key issue in the ion electrostatics is how diffuse ions are distributed around the RNA molecule [9–19]. There have been several useful experimental methods developed for the quantification of the ion atmosphere around nucleic acids. The methods include small angle X-ray scattering (SAXS) [9–12], the ion-counting method [13], and the thermodynamic method [14–19]. These methods have been successfully used to quantify the ion distribution, the competition between the different species of the ions, and the folding thermodynamics [16,17]; see Table 1.

Table 1.

Experimental measurements for RNA (and DNA) ion atmosphere.

RNAs (or DNAs)	Refs.	Ionic conditions	Thermodynamic quantities
25-bp DNA duplex	[9]	divalent ions	SAXS profiles
	[11]	mixed Rb+/Sr2+	SAXS profiles
	[11]	mixed Rb+/(Co(NH3)6)3+	SAXS profiles number of bound ions
25-bp RNA duplex	[12]	Rb+, Mg2+	SAXS profiles
25-bp DNA duplex	[12]	Rb+, Mg2+	SAXS profiles
24-bp DNA duplex	[13]	mixed Na+/Mg2+	number of bound ions
	[13]	mixed monovalent ions	number of bound ions
	[13]	mixed divalent ions	number of bound ions
24-bp DNA triplex	[13]	mixed Na+/Mg2+	number of bound ions
poly(A · U)	[14]	mixed Na+/Mg2+	number of bound Mg2+
calf thymus DNA	[15]	mixed Na+/Mg2+	number of bound Mg2+
BWYV pseudoknot	[16]	Na+, mixed Na+/Mg2+	number of bound Mg2+
58-nt rRNA fragment	[17]	mixed K+/Mg2+	number of bound Mg2+
yeast tRNA	[18]	mixed Na+/Mg2+	number of bound Mg2+
	[19]	mixed Na+/Mg2+	number of bound Mg2+

BWYV: beet western yellow virus.

The experimental measurements have led to several important findings. For example, for oligomeric DNA and RNA duplexes in a mixed monovalent/divalent ion solution, SAXS profiles showed that in the titration of the ions, although the number of the bound ions for each species varies due to the competition of the different ions, the shape of the ion distribution (for each species) is invariant [10]. In addition, smaller ionic size causes a stronger ion-RNA interaction and thus, the ion size needs to be explicitly taken into account in the theoretical analysis [10,12,13]. Moreover, experimental data on ion binding for RNA and DNA duplexes showed that metal ions can give more efficient charge neutralization for RNA than for DNA, and the difference likely comes from the higher backbone phosphate charge density for an A-form helix than for a B-form helix [12].

A more direct quantification of bound ions comes from the ion-counting method and thermodynamic method, which have been applied to RNAs and DNAs, including yeast tRNA [18,19], poly(A · U) [14], polymeric calf thymus DNA [15], 58-nt ribosomal RNA fragment [17], BWYV (beet western yellow virus) pseudoknot fragment [16], oligomeric DNA and RNA duplexes [13], and DNA triplex [13]. The experimental data from these experiments have revealed several important features of ion binding.

1. The detailed distribution of the bound ions is highly sensitive to the atomic structure of the RNA [12].

2. Ion-binding of the different (monovalent and divalent) ions shows anti-cooperativity [13].

3. Multivalent ions (e.g., Mg²⁺) are much more efficient in charge neutralization than monovalent ions. The unusually high efficiency of the multivalent ions over the monovalent ions is beyond the mean-field effect such as the ionic strength. For example, millimolar Mg²⁺ can achieve the similar ion neutralization as molar Na⁺.

4. The efficiency of multivalent ions (e.g., Mg²⁺) in neutralization is more pronounced for more highly charged nucleic acids, i.e., larger molecules with more compact structures. For example, For a 24-bp DNA duplex and the yeast tRNA^Phe, 0.4mM Mg²⁺ can approximately achieve the same ion neutralization as 20 mM and 32 mM Na⁺, respectively [13,19].

2.2. Stabilization of Helices and Hairpins

Helix and loop are the fundamental segments of RNA secondary structure. A hairpin is the simplest secondary structural motif and plays a variety of structural and functional roles in RNA. The findings about the ion effects in hairpin stability mainly come from the thermodynamic experiments on RNA hairpin folding. Most of the experiments were performed in a Na⁺ solution or a mixed Na⁺/Mg²⁺ solution; see Table 2 for a brief summary [16,20–32]. These thermodynamic measurements revealed several significant features for ion binding and ion-mediated folding stability for helices and hairpins:

Table 2.

Thermodynamic measurements for the ion dependence of RNA and DNA secondary structural stability.

RNAs and DNAs	Refs.	Ionic conditions	Thermodynamic quantities
6-bp DNA duplex	[20]	mixed Na+/Mg2+	Tm, ΔG
9-bp DNA duplex	[21]	Na+, Mg2+	Tm, ΔG
12-bp DNA duplex	[22]	Mg2+	Tm
25-bp DNA duplex	[23]	Mg2+	Tm
RNA duplexes (6–14 bp)	[24]	mixed Na+/Mg2+	ΔG, Tm
DNA duplexes (10–30 bp)	[25]	Na+	Tm
RNA and DNA hairpins (4–34 nt loop)	[26]	Na+, Mg2+	Tm
RNA hairpins (49–124 nt)	[27]	K+, Na+	ΔG
DNA duplexes	[28]	Na+, Mg2+	ΔG, Tm
RNA duplexes	[29]	Na+, Mg2+	ΔG, Tm
DNA and RNA hairpins	[3]	Na+, Mg2+	ΔG, Tm
BWYV pseudoknot hairpin	[16]	Na+, Mg2+	ΔH, ÄS
T4 gene pseudoknot hairpin	[31]	mixed K+/Mg2+	Tm
T2 gene pseudoknot hairpin	[32]	mixed K+/Mg2+	ΔG

T_m: melting temperature; ΔG = ΔH – TΔS: folding stability.

1. Metal ions can stabilize DNA and RNA helices/hairpins in a similar way, with the linear dependence of the folding stability on the logarithm of monovalent salt concentration at low salt (e.g., <0.3M Na⁺), and a saturation tendency at a high monovalent concentration (e.g., >0.3M Na⁺).

2. Compared with the monovalent ions, divalent ions (e.g., Mg²⁺) are more efficient in stabilizing helices/hairpins. The stability in a multivalent ion solution cannot be explained by the mean-field description such as ionic strength. For example, the stabilities for short DNA and RNA oligomers and hairpins in a 10mM Mg²⁺ solution is approximately equivalent to the stabilities in a 1 M Na⁺ solution [20,28–30].

3. Because the binding of Na⁺ competes against the (more efficient) binding of the Mg²⁺ ions a mixed Na⁺/Mg²⁺ solution could lead to less stability than a pure Mg²⁺ solution [29].

The thermodynamic parameters have been measured quite extensively at the standard ion condition (1 M Na⁺). These parameters form the basis for the predictions of RNA (DNA) secondary structure and folding stabilities [33–37]. For monovalent ion condition other than 1 M NaCl, RNA thermodynamic data for various ionic conditions yields a set of fitted formulas for the enthalpy/entropy parameters for RNA and DNA helices as functions of the different (monovalent) ion concentrations [25,28,29,33]. These empirical extensions have been shown to give good estimates for the thermodynamic stabilities for RNA and DNAs in different Na⁺ conditions [25,28,29,38,39].

In contrast to the thermodynamic studies in Na⁺ solutions, experimental data on Mg-mediated helix/hairpin stability has been quite limited [20–24]. The experiments for the Mg²⁺ effects have motivated the attempt to derive the [Mg²⁺]-dependent thermodynamic parameters [28,29]. Though these empirical formulas lack extensive experimental validations due to the limited experimental data, the theory-experiment agreements for the tests against the available experimental data suggest that the derived formulas may be reliable.

Recently, based on statistical mechanical modeling [29], Tan and Chen [30] derived the hairpin loop stability as functions of [Na⁺] and [Mg²⁺]. The results suggest an interplay between the loop entropy and the ion-induced stabilization of the loop. The formation of a loop causes charge build-up of the nucleotide backbone and a stronger ion-RNA interaction. A higher ion concentration would cause a stronger reduction in the electrostatic intrachain repulsion upon loop formation. Therefore, ions help stabilizing the loop. Such ion-induced stability competes against the loss in the conformational entropy upon the loop formation [30].

2.3. Stabilization of Nucleic acid Helix Assembly

Helix-helix packing is fundamental to tertiary structural folding. Osmotic pressure measurements have led to quantitative characterization for the ion-mediated helix-helix assembly [40,41]. These measurements provided several novel insights for the assembly of long (DNA) helices: (a) multivalent ions, such as Co³⁺, can induce attraction between the helices, (b) monovalent ions (e.g., Na⁺) can only modulate the strength of helix-helix repulsion [40], (c) certain types of divalent ions (e.g., Mn²⁺) can induce a helix-helix attractive force that results in DNA condensation [42], while other divalent ions (e.g., Ca²⁺) cannot, and (d)Mg²⁺ ions in the presence of methanol could induce a helix-helix attraction [41]. The different roles of divalent ions might be attributed to different ion-binding affinities to the various groups [1].

Helices in natural RNA structures are usually in the range of several to ten base pairs. In contrast to long helices, short helices have great rotational degrees of freedom and strong end effects. As a result, short helices can have different ion effects than long helices. Aiming to uncover the mechanism for ion-induced helix packing in RNA folding, several experiments have focused on the ion-mediated interactions between short helices [3,43–45]. In addition, SAXS experiments for a system of dispersed short DNA helices suggested that Mg²⁺ ions can significantly reduce the Coulomb repulsion between the helices and induce helix-helix attraction (through end-end base stacking) [11,44,45]. SAXS experiments for a system of loop-tethered short helices revealed a possible weak side-side attraction for helices in a Mg²⁺ solution of concentrations up to 0.6 M [3]. Furthermore, the experiments [3] showed that high-concentration ions (including 1+, 2+ and 3+ ions) can induce a random relaxed state [3] and Mg²⁺ is much more efficient than Na⁺ in causing such a state. A mean-field Poisson-Boltzmann (PB) calculation showed that the PB theory underestimates the efficient role of Mg²⁺ by over 10 times [43]. However, despite the extensive experimental studies, several key issues remain: (a) Is the electrostatic relaxation state a random disordered state or a collapsed compact state? (b) How do the different ions cause the different helix-helix packing states? (c) How does a junction/loop assist ion-induced helix packing?

2.4. Stabilization of Tertiary Structures

Because RNA tertiary structural folding involves massive charge build-up, ion-RNA interaction is significant for tertiary structural folding. In the past decades, extensive experiments have been performed to investigate how metal ions promote RNA tertiary structural folding and stabilize tertiary structures; see Table 3 [16,19,32,46–60]. These experiments have revealed several important roles of metal ions, especially Mg²⁺, in tertiary structural folding as shown below:

Table 3.

Thermodynamic measurements for the ion dependence of RNA and DNA tertiary structural stability.

RNAs or complexes	Refs.	Ionic conditions	Thermodynamic quantities
BWYV pseudoknot	[16]	Na+, mixed Na+/Mg2+	ΔH, ΔS
58-nt rRNA fragment	[46]	mixed NH+/Mg2+	ΔG
yeast tRNA	[19]	mixed Na+/Mg2+	ΔG
HIV-1 kiss complex 1	[59]	Na+, mixed Na+/Mg2+	Tm
HIV-1 kiss complex 2	[60]	Na+, mixed Na+/Mg2+	Tm
T2 pseudoknot	[32]	K+, mixed K+/Mg2+	ΔG
MMTV pseudoknot	[47]	Na+, mixed K+/Mg2+	Tm
T4-35 pseudoknot	[48]	mixed Na+/Mg2+	ΔG, Tm
T4-32 pseudoknot	[48]	mixed Na+/Mg2+	ΔG, Tm
T4-28 pseudoknot	[48]	mixed Na+/Mg2+	ΔG, Tm
Tetrahymena ribozyme	[55]	K+, Na+, Mg2+, spermidine	fraction folded
	[50]	Na+, Mg2+	Rg
	[51]	Na+, Mg2+	Rg
	[54]	Mg2+	Rg
	[49]	Mg2+, Ca2+, Sr2+, Ba2+	fraction folded
	[52]	Mg2+, Ca2+, Sr2+, Ba2+	Rg
	[53]	Na+, Mg2+	lP
hairpin ribozyme	[57]	Na+, Mg2+	fraction folded
	[58]	Na+, Mg2+	fraction folded
A-riboswitch	[56]	Li+, Na+, K+, Rb+, Cs+	Kobs
Azoarzus ribozyme	[52]	K+, Na+, Mg2+, Ca2+, Co3+, spermidine3+	Rg, lP

R_g: radius of gyration; K_obs: equilibrium constant; l_P: persistence length; MMTV: mouse mammary tumor virus.

1. The high efficiency of the Mg²⁺ ions (compared to the Na⁺ ions) is significantly more pronounced for tertiary structures than for secondary structures. This is due to the much higher backbone charge density and the much stronger electrostatic effect in tertiary structural folding. For example, 10 mM Mg²⁺ and 1MNa⁺ can achieve a similar stability for short DNA and RNA duplexes [20,28,29], while for the tertiary structural folding of Tetrahymena ribozyme, the transition mid-points are at 0.5 mM and 0.5 M for Mg²⁺ and Na⁺ solutions, respectively [55].

2. Even with high monovalent ion concentration, Mg²⁺ can make a significant contribution to RNA tertiary structural stability. For example, for a 58-nt ribosomal RNA fragment in the background of 1.6 M monovalent ions, Mg²⁺ ions at 0.1 M can contribute about −6 kcal/mol to the tertiary structural folding stability [46].

3. Mg²⁺ can induce much more compact tertiary structures than Na⁺. For Tetrahymena ribozyme, the folded structure in Mg²⁺ solution is about 7 Å more compact than the one in Na⁺ solutions [50].

4. Metal ions with higher charge and smaller size are more efficient than those with lower charge and bulkier size. Ions of higher charge density (charge/volume) would have stronger ability to stabilize RNA tertiary folds [49,55].

Furthermore, Brownian dynamics simulations for a model RNA tertiary structural folding system provided more detailed insights into the role of metal ions in RNA tertiary structural folding [49]: (a) The condensed ions near the RNA surface show a liquid-like correlated distribution; (b) for the RNA molecule (Tetrahymena ribozyme) studied, non-specific electrostatic interaction alone can account for the collapsed state and the dependence on the ion charge density [6,49]. However, other experiments suggested that, depending on the sequence, specific interactions (binding) of ions with the RNA could contribute significant stability for RNA tertiary structure [7,16,17]. Such distinctive findings on the roles of specific binding ions suggest the necessity for the further more careful and more extensive studies, especially theoretical studies, on the role of the diffuse ions.

Kissing loop complex is a typical tertiary structural motif formed by base pairing between two hairpin loops. Several experiments have pointed to the critical role of diffuse ions in stabilizing the different structures of kissing loop complexes. For HIV-1 DIS-type kissing loop-loop complexes, the melting temperature for the kissing complex shows much more sensitive ion-dependence than for the corresponding duplex of the same sequence at the kissing interface [59,60]. Moreover, the high efficiency of Mg²⁺ over Na⁺ is much more pronounced for the kissing loop complex than for the duplex [59]. The underlining physics for the above findings may stem from the significantly high charge density of RNA backbone at the kissing interface. For the kissing complex, depending on the RNA sequence, Mg²⁺ may also bind to specific locations at the kissing interface. The specific binding of the ions could further contribute to the highly sensitive [Mg²⁺]-dependence of the kissing thermodynamics [60]. For the Tar-tar RNA complex, a bulkier ion would weaken the folding stability, in accordance with the observations that bulkier ions have lower efficiency in stabilizing RNA tertiary folds [56]

3. DIFFUSE ION IS CRITICAL TO RNA FOLDING KINETICS

The Coulombic interaction between RNA backbone charges causes a tremendous kinetic barrier for RNA folding. By lowering the electrostatic barrier for the kinetics, ions can promote the kinetic process of RNA folding and control the folding rate and pathways. There have been tremendous experimental efforts on the role of metal ions in RNA (and DNA) folding kinetics (see Table 4) at both secondary and tertiary structural levels [20,61–68].

Table 4.

Measurements of the ion-dependent folding kinetics of RNAs and DNAs.

RNAs or DNAs	Refs.	Ionic conditions	Folding or unfolding rates
6-bp DNA duplex	[20]	Na+, Mg2+	folding rates
8-bp DNA duplex	[61]	Na+	folding and unfolding rates
DNA duplex	[62]	Na+	folding and unfold rates
DNA hairpins	[63]	Na+	folding and unfolding rates
hairpin ribozyme	[64]	Na+, Mg2+	folding and unfolding rates
RNA three-way junction	[65]	Na+, Mg2+	folding and unfolding rates
Tetrahymena ribozyme	[66]	Mg2+	Rg versus time
	[67]	Na+, Mg2+, Ba2+	folding rate
	[67]	spermidine, (Co(NH3)6)3+	folding rate
	[68]	Na+, Mg2+	folding rates to I and to N

I: the partially unfolded intermediate state; N: the native state.

3.1. Secondary Structural Folding Kinetics

Experiments on the kinetics of helix formation showed that addition of Na⁺ ions would accelerate the folding process [20,61,62] and cause nearly no change to the unfolding rate [20,62]. The findings may be interpreted by a model for the kinetic barrier: The ion causes a decrease in the folding entropy loss and thus an increase in the folding rate (if the kinetic barrier for folding is caused by the entropic loss). In contrast, the loop enthalpy would not change with the ion and thus, the unfolding rate is unchanged (if the kinetic barrier for unfolding is caused by the enthalpic increase) [33,39]. In addition, the folding kinetic data suggests an approximate equivalence between 1M Na⁺ and 10mM Mg²⁺ [20] in promoting folding helix formation.

A hairpin is the simplest secondary structure consisting of a helix and a loop, thus, its folding kinetics is associated with the kinetics of the helix as well as the loop formation [29–30,33]. If the hairpin formation is rate-limited by the slow formation of a base stack in the helix, the dependence of folding and unfolding rates would be similar to the one for helices as described above. If the hairpin folding is rate-limited by the loop formation, addition of metal ions would lead to the acceleration of the loop formation due to the enhanced loop stability and the chain flexibility and thus, a lower kinetic barrier. The unfolding rate decreases with the addition of metal ions probably due to the lowered enthalpy in the folded hairpin state [63].

Recently, a laser temperature-jump spectroscopy experiment showed that for higher ion concentration (e.g., >100mM Na⁺), the loop closure time is not sensitive to the salt concentration. For a low salt solution (e.g., <50mM Na⁺), however, a notable increase in loop closure time has been predicted theoretically [26]. The above ion dependence may arise from the saturation of ion binding at high ion concentrations.

3.2. Tertiary Structural Folding Kinetics

Experimental studies on RNA tertiary structural folding kinetics have provided novel insights into the role of metal ions in folding kinetics. Though these studies focused on different RNA molecules, such as hairpin ribozyme, specific three-way junctions and Tetrahymena ribozyme, many of the conclusions drawn from the studies are general.

3.2.1. Hairpin Ribozyme

The folding and unfolding rate constants of a minimal hairpin ribozyme have been measured using the fluorescence resonance energy transfer (FRET) method. The rate constants were measured with a broad range of ionic conditions, including Na⁺, Mg²⁺, and mixedNa⁺/Mg²⁺ solutions [57,64]. When [Mg²⁺] increases from 1mM to 500mM, the folding rate increases by more than 40-fold, while the unfolding rate remains invariant with [Mg²⁺] in the range [2mM,500mM] and decreases with [Mg²⁺] between 1mM and 2mM [64]. In contrast, adding Na⁺ ions to a pure Na⁺ solution or adding Mg²⁺ to a mixed Na⁺/Mg²⁺ solution causes an increase in the folding rate and a decrease in the unfolding rate [64]. The distinctive ion dependence can be explained by the more significant ion binding and more compact RNA transition state in a Mg²⁺ solution than in a Na⁺ solution. The transition state in a Mg²⁺ solution is highly compact and the folding from the transition state involves a small change in the compactness and no further uptake of ions. In contrast, the transition state in a Na⁺ solution is less compact and the transition from the transition state to the folded state involves further uptake of ions.

3.2.2. A Three-Way Junction

For an RNA three-way junction in 16S rRNA, Mg²⁺ and protein binding are found to induce similar conformational switches from an extended Y-shaped (unfolded) state to a folded y-shaped state [65]. Therefore, understanding the role of Mg²⁺ may provide useful insights into the different forces that lead to a conformational switch. With the addition of Na⁺, the folding rate increases and the unfolding rate decreases, thus, adding Na⁺ favors the formation of the tertiary structure. Adding Mg²⁺ to a Na⁺ solution causes similar qualitative changes in the rate constants as above for a Na⁺ solution. The experiment shows that Mg²⁺ is highly efficient compared to Na⁺, indicating the efficient role of Mg²⁺ in driving the formation of the folded (y-)state. When Mg²⁺ exceeds 100mM, the folding/unfolding rates become saturated in the presence of 50mM Na⁺ [65].

3.2.3. Tetrahymena Ribozyme

Tetrahymena ribozyme has a large, complex native structure with multiple helices, cross-linked loops, and tertiary contacts (such as the tetraloop-receptor interaction). Extensive experimental findings suggest that the structural formation of the Tetrahymena ribozyme involves multi-state kinetics governed by a highly rugged energy landscape [54]. The folding rates and pathways are sensitive to the ionic condition of the solution [6]. For example, SAXS experiments with millisecond resolution indicate that Mg²⁺ ions induce a rapid collapse in 10 ms with the global compactness decreasing from 75 Å to 55 Å. With the formation of the tertiary contacts, further compaction to 45 Å is achieved at ~100 ms [66].

The ion-induced collapsed intermediate state is critical for the folding speed and kinetic partitioning of the folding pathways [4]. Native gel electrophoresis experiments [67] showed that higher [Mg²⁺] and metal ions of higher charge density (charge/volume) would significantly stabilize the non-specific collapsed intermediates. The stabilization of the non-specific collapsed state slows down the (productive) folding to the final native state which requires the formation and stabilization of specific native contacts [49,67]. In addition, a recent experiment showed that, depending on the ionic condition of the solution, the kinetic partitioning of the folding flux can be dependent on the initial conformational ensemble [68].

4. THEORETICAL PREDICTIONS FOR THE DIFFUSE ION BINDING TO RNAs

Several theoretical methods have been used to predict the ion distribution and ion-RNA interaction:

1. Counterion condensation theory [69,70]. The model successfully predicts the logarithmic dependence of the melting temperature for the DNA helix on the ion concentration [33,69]. However its prediction on the ion-mediated helix-helix attraction [71] is not consistent with the experimental results [40,44] and computer simulations [72,73].

2. Poisson-Boltzmann (mean-field) theory [74–79]. The theory gives an accurate prediction for ion binding to RNA in aqueous/monovalent ion solutions [80]. However, the model, which ignores ion size and electrostatic correlation, cannot predict the multivalent ion-mediated attraction between helices [40–41,44] and underestimates the Mg²⁺-mediated folding stability.

3. Models beyond mean-field approximation

   • Tightly bound ion model [81]. The model accounts for ion correlation, finite size, and ion fluctuation effects. Extensive tests against experiments show that the model is highly promising for treating the effects of multivalent (such as Mg²⁺) diffuse ions in RNA folding; see below for more details.

   • Size-modified Poisson-Boltzmann model [82]. By considering the ion size effect, the model with the APBS PB solver [78] gives reliable predictions on monovalent ion binding and the ionic saturation effect at high ion concentration caused by the finite size of the ions. For multivalent ion solutions, such as of Mg²⁺, further improvement of the model is required to account for the long-range inter-ion correlation.

   • Modified Poisson-Boltzmann model based on the Kirkwood/Bogoliubov-Born-Green-Yvon hierarchy [74,83,84]. The model considers the mean effect of ion fluctuation and size exclusion. Tests with the Monte Carlo simulations for simple macroion systems indicate that the model gives improved predictions for multivalent ion distributions than the conventional PB theory. However, the application of the model to treat realistic RNA structures remains computationally challenging [83].

   • Correlation-corrected Poisson-Boltzmann model [85]. With an ad hoc correlation-corrected inter-ion potential, the model successfully predicts an attractive force between the two planes [85]. Comparisons with computer simulations suggest that the model is able to generate improved predictions on multivalent ion distributions compared to the conventional PB theory. For realistic RNA structures, the model is computationally demanding.

   • Other models beyond the mean-field approximation [86–88]. Other theories, such as the density function theory [87], integration theory [86], and local molecular field theory [88], can account for the inter-ion correlation effects. However, the application of these methods to treat realistic three-dimensional RNA structures remains a challenge.

5. CORRELATED DISTRIBUTION OF MULTIVALENT DIFFUSE IONS: THEORY VERSUS EXPERIMENT

Multivalent diffuse bound ions may show a correlated distribution. Consider counterions clustering around a (negatively charged) RNA. Thermal agitation tends to cause disordered distributions of the counterions. However, the Coulombic force between charges tends to bring the ions into an ordered low-energy state. In such a low-energy state, an ion is “networked” (“correlated” or “coupled”) with many other ions. For multivalent counterions such as Mg²⁺, the large ionic charge may cause the Coulombic energy U_Coulomb for an ion-pair to out-compete the thermal agitation energy (k_BT=1.99 cal/mol; k is the Boltzmann constant and T is the temperature). As a result, ions can be in an ordered strongly correlated state. For a realistic RNA, such correlation could easily happen. For instance, [Mg²⁺] near the yeast tRNA^Phe surface can be higher than 8 M [80], causing U_Coulomb >10 k_BT and hence a strong correlation between the ions. Because of the correlation between the ions, the likelihood of finding an ion at a location is sensitive to the discrete locations of other ions. Therefore, the ion correlation effect is intrinsically tied to the ensemble of discrete ion distributions, i.e., “ion fluctuations” (see Figure 1). To replace the discrete (correlated) ion configurations by an average fluid-like continuous distribution is not appropriate.

Figure 1.

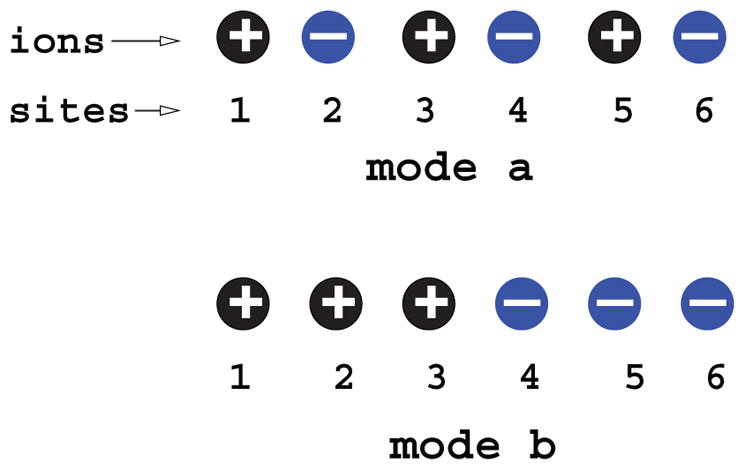
(i) Modes a and b have an identical net average charge (= 0, i.e., neutral), but mode a has a much lower energy than mode b, causing the system to have higher tendency to stay in mode a. It is important to distinguish the different discrete ion distributions and the use of net average “charge neutralization” may not be appropriate. (ii) The likelihood of finding a positive or negative charge at a site (such as site 2) depends on the discrete distribution (locations) of all the other ions instead of the ensemble average distribution of the ions. (iii) A strongly correlated state (such as mode a) can reach much lower energy than a “mean” state. So correlation lowers the energy. Such a correlation-induced low energy effect is more pronounced for a folded RNA structure due to its higher RNA backbone charge density, leading to correlation-enhanced stabilization of the folded structure. Therefore, the unusual efficiency of Mg²⁺ ions, which can be strongly correlated, in RNA stabilization may be attributed to the enhanced stabilization effect due to correlation.

Several experimental and theoretical studies have pointed to the potential importance of correlation/fluctuation effects for diffuse ions. For example, SAXS experiments for the ion-induced structural relaxation of DNA duplexes [43] showed that the Poisson-Boltzmann equation, which ignores the correlation effect, overestimates the [Mg²⁺] midpoint for the transition (structural relaxation) by more than 10 times. Correlation is most likely the reason to cause the discrepancy between PB and the experiment. In addition, computer simulations for metal ions surrounding a model three-dimensional RNA structure showed a liquid-like correlated distribution for the Mg²⁺ ions [49].

Inspired by the potential importance of correlation and fluctuation effects for multivalent counterions such as Mg²⁺ ions, Tan and Chen developed the “Tightly Bound Ion” (TBI) model [81]. Through a classification of the diffuse ions according to the correlation strength, the model considers the different modes for the strongly correlated bound ions while treating the weakly correlated ions using the Poisson-Boltzmann theory. Applications of the TBI model to a broad range of nucleic acid systems such as RNA/DNA helices, RNA/DNA hairpins, DNA helix assembly, DNA bending, RNA three-way junction, and HIV-1 DIS kissing loop complexes [28–30,89–92] provide reliable theoretical predictions for the effect of diffuse ions, especially Mg²⁺ ions, in RNA folding.

Furthermore, TBI theory-experiment agreements for a wide variety of systems led to a set of highly useful formulas for the ion-dependent thermodynamic parameters such as the enthalpy ΔH, entropy ΔS, free energy ΔG, and the melting temperature of RNA. The following set of formulas give the ion-dependent stability (at 37 °C) for an RNA helix in a mixed Na⁺/Mg²⁺ solution [29].

$$\mathrm{\Delta }{G}_{37}^0[{\text{Na}}^{+}/{\text{Mg}}^{2+}]=\mathrm{\Delta }{G}_{37}^0(1\mathrm{M})+(\mathrm{N}-1)(x_1\mathrm{\Delta }{g}_1+x_2\mathrm{\Delta }{g}_2)+\mathrm{\Delta }{g}_{12}$$

where x₁ and x₂ denote the fractional contributions of Na⁺ andMg²⁺ to the whole stability, respectively:

$$x_1=[{\text{Na}}^{+}]/([{\text{Na}}^{+}]+(8.1-32.4/N)(5.2-ln[{\text{Na}}^{+}])[{\text{Mg}}^{2+}]);x_2=1-x_1.$$

Here Δg₁, Δg₂, and Δg₁₂ are given by

$$\begin{array}{ll}\hfill \mathrm{\Delta }{g}_1& =a_1+b_1/N\hfill \\ \hfill a_1& =-0.075ln[{\text{Na}}^{+}]+0.012{ln}^2[{\text{Na}}^{+}]\hfill \\ \hfill b_1& =0.018{ln}^2[{\text{Na}}^{+}]\hfill \\ \hfill \mathrm{\Delta }{g}_2& =a_2+b_2/N^2\hfill \\ \hfill a_2& =-0.6/N+0.025ln[{\text{Mg}}^{2+}]+0.0068{ln}^2[{\text{Mg}}^{2+}]\hfill \\ \hfill b_2& =ln[{\text{Mg}}^{2+}]+0.38{ln}^2[{\text{Mg}}^{2+}]\hfill \\ \hfill \mathrm{\Delta }{g}_{12}& =-0.6x_1{x}_{2}ln[{\text{Na}}^{+}]ln((1/x_1-1)[{\text{Na}}^{+}])/N.\hfill \end{array}$$

Through theory-experiment comparison, the TBI theory also gave a similar set of formulas for the ion-dependent hairpin stability [30].

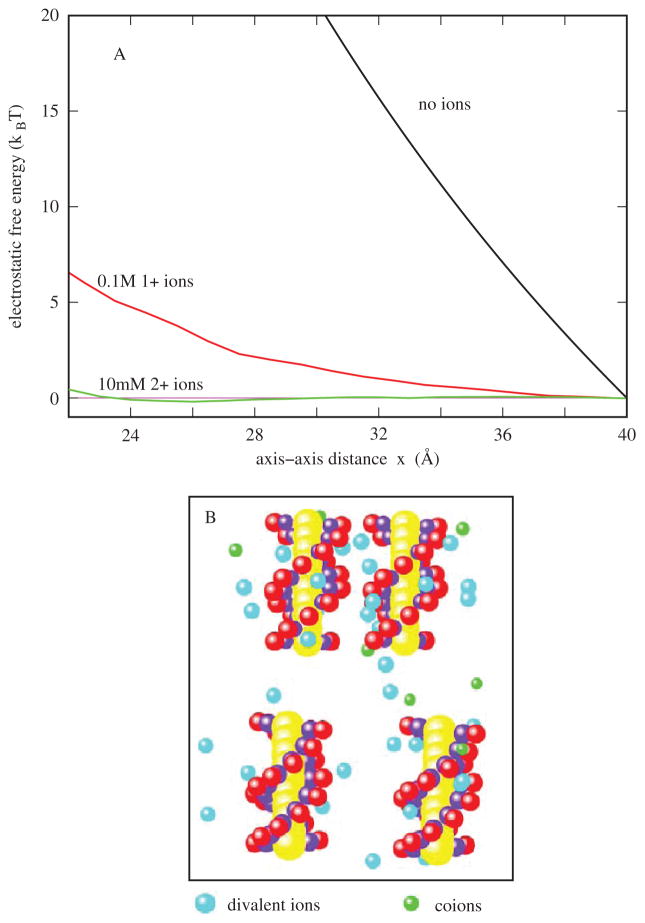
More recently, a Monte Carlo simulation gives the results for the electrostatic free energy landscape for a system of the two nucleic acid helices [93] (see Figure 2A). In the absence of ions, the electrostatic free energy profile shows a large repulsion between the helices. For example, to push the 10-bp two helices from 40Å to 22 Å (axis-axis distance) requires a work of 48 k_BT. With the addition of ions, such repulsion would be greatly reduced (see Figure 2A). In 0.1M Na⁺ solutions, the work is reduced to about 6.5 k_BT. In divalent ion solution, the ion effect becomes more pronounced. 10mM of divalent ions can cause the work to be reduced to 0.5 k_BT. Moreover, the simulation shows a slight attractive force between the helices in a divalent ion solution. At 26 Å, 10mM divalent ions can cause a stabilizing electrostatic free energy of −0.3 k_BT.

Figure 2.

Illustration of the importance of diffuse ion binding in a two-helix system. A. The calculated electrostatic free energy ΔG(x)=G(x) – G(40 Å) as a function of the axis-axis distance x. B. The snapshots for the ion distributions around the helices at x=26 Å (top panel) and x=38 Å (bottom panel), respectively.

How can the ions reduce the folding electrostatic repulsion so dramatically? For the helices immersed in ion solutions shown in the bottom panel of Figure 2B, metal ions are diffusively bound around the helices to lower the intramolecular electrostatic energy. When two helices approach each other, such ion binding becomes more pronounced due to the increased charge density for RNA backbone. The ion binding in the region between the two helices causes a significant reduction in the electrostatic repulsion. For multivalent ions, the high affinity of ion binding in the region between two helices causes a high concentration of the ion cloud and, hence, strong correlation between the ions. The correlation between the bound ions tends to bring the system to ordered low-energy states. For multivalent ions, the correlation effect out-competes the Coulomb repulsion. Such a correlation effect is stronger for a closer approach between the helices, resulting in an attractive force between the helices.

6. GENERAL CONCLUSIONS

Extensive theoretical and experimental investigations show that Mg²⁺ plays a role distinctive from that of Na⁺, as described below:

1. Mg²⁺ is much more efficient than Na⁺ in stabilizing RNA folded structures, including helix, hairpin, helix assembly, and tertiary folds. For the stabilization of secondary structural segments (helices, loops), 10mM Mg²⁺ is approximately equivalent to 1M Na⁺. Such an efficient role of Mg²⁺ becomes more pronounced for more compact and larger molecules.

2. Mg²⁺ ions are essential for RNA to fold into the native tertiary structure. Insufficient Mg²⁺ would lead to partially folded intermediates or a near-native-like structure. In addition, the high efficiency of Mg²⁺ over Na⁺ is much more pronounced for tertiary structural folding than for secondary structural folding. For the folding of the Tetrahymena ribozyme, 0.3mM Mg²⁺ and 0.5M Na⁺ show similar efficiency in stabilizing the tertiary fold [55].

3. For a given RNA, Mg²⁺ ions induce a much more compact (tertiary) structure than Na⁺ ions [50].

4. For ion-mediated nucleic acid helices, Na⁺ can only modulate the repulsive interaction, while Mg²⁺ could induce a (weak) attractive force.

5. Due to the Mg²⁺-induced stabilization of misfolded states and the non-specific collapsed state, the most efficient folding occurs likely in the mixture of monovalent Na⁺ and Mg²⁺ instead of a pure highly concentrated Mg²⁺ solution [67].

The potential correlation between the bound ions may contribute to the distinctively high efficiency of multivalent ions such as Mg²⁺. For multivalent ions, the correlation could be strong. The strong ion correlation drives the ions to self-organize (cooperatively) for reaching low-energy states. Such a correlation-induced bias toward the low-energy states enhances the stability of the (bound) ion clouds, which leads to a high affinity for ion binding and a high stability of the RNA structure.

Metal ions can bind to specific groups in RNA either directly or through water as a ligand. Such specific ion binding has been observed in many know structures. For example, the crystal structure of the P4–P6 domain of the group I intron contains 27 specifically bound Mg²⁺ ions [94]. These specifically bound ions can play essential roles in RNA-related catalysis. However, it is not clear how important these specifically bound ions are for RNA stability and folding kinetics. Nevertheless, based on extensive experiments, the following conclusions about specific binding of metal ions such as Mg²⁺ can be drawn: First, because specific binding of Mg²⁺ has not been observed for many simple RNA systems that show the high efficiency of Mg²⁺, the distinctively more efficient role of Mg²⁺ compared to Na⁺ is unlikely to stem from specific binding, though specifically bound Mg²⁺ ions can enhance the efficient role of Mg²⁺. Second, the formation of specific ion binding often involves a high energy barrier arising from ion dehydration. In contrast, the diffuse ions are much more highly populated. Therefore, for most RNAs, the ion stabilizing force may be dominated by the diffuse ions.

In the past two decades, experimental and theoretical studies have provided quantitative insights into the ion (especially the Mg²⁺ ion) effects in RNA folding. However, due to the complexity of the RNA/water/ion system, many questions about the ion effects in RNA folding remain unanswered: Is the efficient role of Mg²⁺ from ion-ion correlation? Can Mg²⁺ induce RNA helix-helix attraction? Can such an attraction cause a compact collapsed state? Do the specifically bound Mg²⁺ ions make important contributions to the folding stability? The answers to these questions will likely come from further synergistic efforts of theory and experiment.

ABBREVIATIONS

APBS

adaptive Poisson-Boltzmann solver

bp

base pair

BWYV

beet western yellow virus

DIS

dimerization initiation signal

FRET

fluorescence resonance energy transfer

HIV

human immunodeficiency virus

MMTV

mouse mammary tumor virus

nt

nucleotide

PB

Poisson-Boltzmann

Rg

radius of gyration

rRNA

ribosomal ribonucleic acid

SAXS

small angle X-ray scattering

Tar

transactivation response

TBI

tightly bound ion

T_m

melting temperature