Complex, non-monotonic dose-response curves with multiple maxima: Do we (ever) sample densely enough?

Abstract

We usually expect the dose-response curves of biological responses to quantifiable stimuli to be simple, either monotonic or exhibiting a single maximum or minimum. Deviations are often viewed as experimental noise. However, detailed measurements in plant primary tissue cultures (stem pith explants of kale and tobacco) exposed to varying doses of sucrose, cytokinins (BA or kinetin) or auxins (IAA or NAA) revealed that growth and several biochemical parameters exhibit multiple reproducible, statistically significant maxima over a wide range of exogenous substance concentrations. This results in complex, non-monotonic dose-response curves, reminiscent of previous reports of analogous observations in both metazoan and plant systems responding to diverse pharmacological treatments. These findings suggest the existence of a hitherto neglected class of biological phenomena resulting in dose-response curves exhibiting periodic patterns of maxima and minima, whose causes remain so far uncharacterized, partly due to insufficient sampling frequency used in many studies.

Abbreviations

AGPase

ADP-glucose pyrophosphorylase

BA

benzyladenine

IAA

indole-3-acetic acid

NAA

naphthaleneacetic acid.

Measurement of biological responses toward quantitatively scaled stimuli can produce a variety of dose-response curve shapes (Fig. 1). While linear response toward external physical or chemical stimuli has been documented for some biological phenomena in both animals and plants,^1,2 dose-response curves are often non-linear, although usually monotonic (i.e. either rising or falling over the whole range examined), and simple (i.e., exhibiting not more than one inflection point). The notorious Michaelis-Menten enzyme kinetics provides a good example of a simple, monotonic dose-response curve. In some cases simple non-monotonic dose-response curves exhibiting a single maximum or minimum have been reported. Examples of either variety of simple dose responses on cell, tissue and organ levels can be found both in the plant literature^3-5 and in physiological studies dealing with other organisms including mammals.⁶

Figure 1.

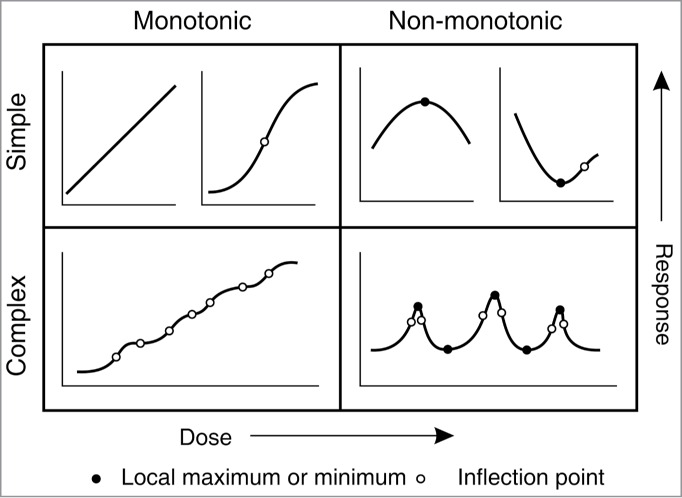
Examples of possible shapes of dose response curves. While monotonic curves are either increasing or decreasing over the whole range of doses examined, non-monotonic ones change direction and thus exhibit at least one (local) maximum or minimum inside the studied interval. We define simple curves as those with at most one inflection point (i.e., change from convex to concave shape or vice versa) within the interval studied.

However, those working in fields involving digital data processing are familiar with the Nyquist sampling theorem, stating that periodic patterns can be accurately detected only if the sampling interval does not exceed half of the period of the pattern studied.⁷ Analogously, non-periodic changes in slope or direction of dose-response curves cannot be reliably detected if occurring on a scale not considerably larger than the sampling interval. Unfortunately, in most biological studies the stimulus doses used (such as, e.g., exogenous signaling molecule concentrations) are rather widely spaced. Changes in response corresponding to dose differences comparable to, or even shorter than, the interval between subsequent sampling points are thus bound to be missed, or dismissed as experimental noise (Fig. 2).

Figure 2.

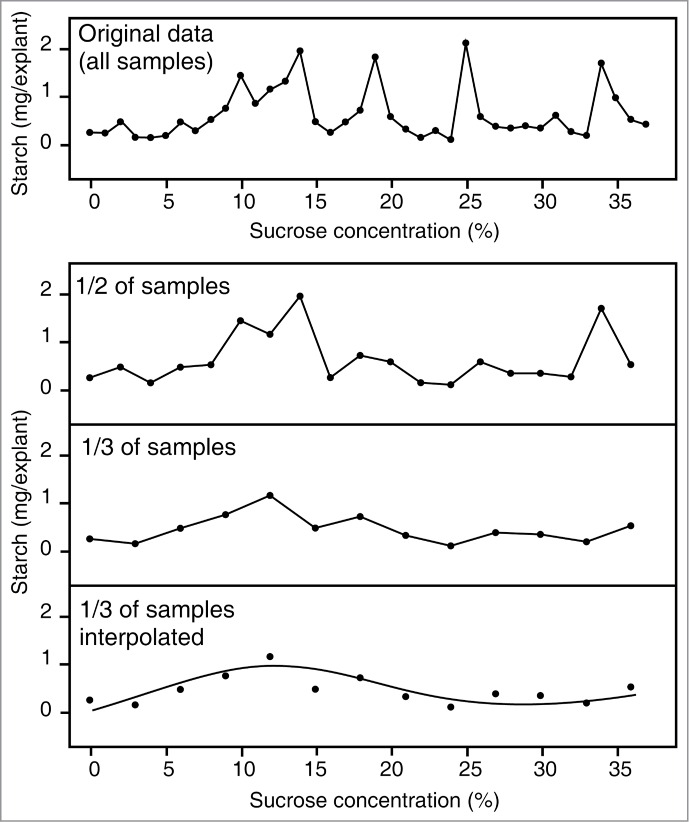
Top: a complex, non-monotonic dose response curve showing the dependence of starch content in kale stem pith explants on sucrose concentration in culture media (from ref. 8). Bottom: reduced sampling frequency substantially alters the apparent dose-response curve. A simple curve with a single maximum and single inflection point can be interpolated between sparsely sampled data points. Note that similar effects of varying sampling frequency would occur also for a complex monotonic dose-response curve, which may appear simple if sampled sparsely.

Indeed, with sufficiently dense sampling, Nissen et al. in the 1970ies to 1980ies detected complex monotonic dose-response curves (“multiphasic curves” with multiple inflection points) for both inorganic and organic solute uptake by various plant tissues and organs,^9,10 attributed nowadays most probably to differential gene expression of low- vs. high-affinity transport systems. They also obtained complex non-monotonic dose-response curves (i.e. curves exhibiting multiple maxima and minima) when following the extent of chlorophyll retention in senescing barley leaves as a function of exogenous cytokinin concentration,¹¹ but this line of research has never been followed up. Similar complex non-monotonic curves have been, however, recorded in pharmacological studies on diverse metazoan systems, especially for responses to low doses of endocrine disruptors, antidepressants and other possible environmental pollutants.^12-15

In a recently published study,⁸ Luštinec et al., building on over 4 decades of previous research,^16-18 used stem pith explants from either tobacco (Nicotiana tabacum) or kale (Brassica oleracea) to examine the effects of varying sucrose, auxin and cytokinin doses on the uptake and accumulation of these biologically active compounds, as well as on tissue growth and selected metabolic parameters. In nearly all cases complex, non-monotonic dose-response curves with several reproducible, statistically significant maxima have been obtained (Table 1, see top panel of Figure 2 for an example). Remarkably, when multiple parameters (such as contents of several metabolites or uptake of multiple compounds) were measured simultaneously, the maxima usually coincided at or around the same concentration of the biologically active compound studied. Given the diversity of conditions and biological parameters producing complex non-monotonic dose-response curves, these results point toward the existence of some underlying general phenomenon whose mechanism, however, remains obscure.

Table 1.

Conditions and parameters found to produce complex non-monotonic dose-response curves toward varying concentrations of biologically active solutes in kale and tobacco explant cultures (data from ref.⁸). Maxima marked by the same letter symbols have been detected at the same solute concentrations within the same experiment(s). * – see Figure 2, top panel for an example; ** – depending on presence of other plant growth regulators.

Explant source	Solute	Concentration range	Dependent variable	Number of maxima
kale	sucrose	0 – 20 %	tissue dry or fresh mass	4 – 5
kale	sucrose	0 – 35 %	starch content	7a*
tobacco	sucrose	0 – 26 %	starch content	6
kale	sucrose	0 – 35 %	AGPase activity	7a
kale	sucrose	0 – 35 %	soluble saccharide content	7a
kale	sucrose	0 – 16 %	sucrose uptake	5b
kale	sucrose	0 – 16 %	NAA uptake	5b
tobacco	NAA	10−14 – 10−4 M	starch content	12–13
kale	IAA	10−6 – 10−4 M	tissue dry mass	7
kale	IAA	10−8 – 10−5 M	IAA uptake	8c
kale	IAA	10−8 – 10−5 M	sucrose uptake	8c
kale	IAA	10−8 – 10−5 M	soluble protein content	8c
tobacco	kinetin	10−10 – 10−4 M	starch content	4–7**
kale	BA	10−8 – 10−4 M	sucrose uptake	5d
kale	BA	10−8 – 10−4 M	soluble protein content	5d

One possibility is that diverse cellular populations, inevitably present in the stem explants (which are heterogeneous e.g., with respect to cell ploidy and possibly contain cells with diverse epigenetic modifications), react differently to the varying culture conditions.⁸ The complex, non-monotonic dose-response curves might, however, also reflect endogenous properties of metabolic processes (understood in a broader sense as including also gene expression and regulatory interactions) in the tissues studied. A massive body of work documents the inherently oscillatory nature of metabolic processes, resulting sometimes in macroscopically manifest periodic behavior of biological systems in both time (e.g. circadian clocks, cell cycle oscillators) and space (e.g., periodic waves of Dictyostelium cells aggregation, embryonic patterning).^19-22 However, theoretical models – for example those of eukaryotic cell cycle regulation²³ or of effects of glucose concentration on glucose-regulated miRNA levels in tumor cells²⁴ – show that some parameters of a system of metabolic reactions mutually linked by regulatory feedback relationships may also exhibit complex, non-monotonic responses as a function of parameters other than time or space, such as e.g. cell size or concentration of one of the system´s components. Moreover, such behavior can be robust over a wide range of model parameters. It is thus conceivable that sensitivity or responsivity of a biological system toward an external stimulus may show an analogous complex, non-monotonic response to the stimulus dose, resulting from the collective behavior of the participating mutually interlinked metabolic processes. Theoretical understanding of such systems, sometimes referred to as “bistable” or “multistable,” is so far limited to relatively simple examples.²⁵

In any case, evidence for existence of complex, non-montonic dose-responses in a well-characterized, experimentally accessible and relatively simple plant system provides a hopeful first step toward elucidating the mechanisms responsible for this enigmatic and so far overlooked phenomenon.

Disclosure of Potential Conflicts of Interest

No potential conflicts of interest were disclosed.

Funding

We thank the Ministry of Education, Youth and Sports of the Czech Republic for financial support by means of the NPUI LO1417 project.