Skip to main content
PMC home page
Social Cognitive and Affective Neuroscience logoLink to Social Cognitive and Affective Neuroscience
. 2016 Feb 12;11(6):973–980. doi: 10.1093/scan/nsw017

Beta- and gamma-band activity reflect predictive coding in the processing of causal events

Stan van Pelt 1,✉, Lieke Heil 1, Johan Kwisthout 1, Sasha Ondobaka 1,2, Iris van Rooij 1, Harold Bekkering 1
PMCID: PMC4884316  PMID: 26873806

Abstract

In daily life, complex events are perceived in a causal manner, suggesting that the brain relies on predictive processes to model them. Within predictive coding theory, oscillatory beta-band activity has been linked to top-down predictive signals and gamma-band activity to bottom-up prediction errors. However, neurocognitive evidence for predictive coding outside lower-level sensory areas is scarce. We used magnetoencephalography to investigate neural activity during probability-dependent action perception in three areas pivotal for causal inference, superior temporal sulcus, temporoparietal junction and medial prefrontal cortex, using bowling action animations. Within this network, Granger-causal connectivity in the beta-band was found to be strongest for backward top-down connections and gamma for feed-forward bottom-up connections. Moreover, beta-band power in TPJ increased parametrically with the predictability of the action kinematics-outcome sequences. Conversely, gamma-band power in TPJ and MPFC increased with prediction error. These findings suggest that the brain utilizes predictive-coding-like computations for higher-order cognition such as perception of causal events.

Keywords: causal inference, action perception, predictive coding, magnetoencephalography, connectivity

Introduction

The view that predictions and prediction errors provide fundamental principles for making sense of perception and cognition is gaining increased interest from the neuroscience community. Predictive coding suggests that perception is a result of a probabilistic inference, in which prior expectations are combined with incoming sensory inputs to infer causes of sensory inputs (Friston, 2010; Bastos et al., 2012). Crucially, a predictive model requires that prediction errors are generated at each level of neuronal processing, so also beyond low-level, sensory brain areas (Clark, 2013; Hohwy, 2013). However, while there is much experimental support for predictive coding activity in low-level perception (Colby et al., 1996; Wolpert et al., 2003; Wacongne et al., 2012; Summerfield and de Lange, 2014; Bastos et al., 2015b), experimental evidence supporting the notion that it generalizes to abstract, higher-order cognitive domains is scarce (Clark, 2013). The current study concentrates on predictive processes in causal inference, a higher-order domain that is central to human cognition (Tenenbaum et al., 2011).

Causal inference is a necessary corollary of modeling our world. Technically, this inference is known as model inversion, in which we invert the mapping from cause to effect to infer the cause given observed effects or consequences. Predicting cause and effect not only allows us to understand physical systems but also other people’s consequential actions. These models build on the world knowledge reflected by the (Bayesian) statistics of causal events that we experience throughout life (Friston, 2010). These models allow us to predict for example the Michotte-like ‘launching effects’ of colliding objects (Michotte, 1950; Kerzel et al., 2000) and the trajectories and impact of a ball thrown by a human agent. Such predictions require an integration of kinematic, (somato)sensory and agent information with different temporal relations. A cortical network encompassing the superior temporal sulcus (STS), temporoparietal junction (TPJ) and medial prefrontal cortex (MPFC) has been associated with inference of potential higher-level (mental) causes of external events (Castelli et al., 2000; Blakemore et al., 2001, 2007; Den Ouden et al., 2005; Fugelsang et al., 2005; Decety and Lamm, 2007; Wheatley et al., 2007; Tavares et al., 2008; Koster-Hale and Saxe, 2013; Murdaugh et al., 2014).

In this study, we use real-world simulated bowling stimuli to unravel if perceptual models for causal inference in the STS-TPJ-MPFC network are governed by predictive coding mechanisms. We recorded brain activity of participants using magnetoencephalography (MEG), while they viewed an agent on a bowling lane throwing balls that knocked over a variable number of pins (see Supplementary Method and Figure S1). Our hypothesis is that for optimal causal inference, the brain will construct a generative model which integrates top-down predictions based on previous bowling events with bottom-up sensory information about the combination of sequential aspects of the current bowling action to predict the complete action. This requires more complex modeling than for Michotte-like collisions, since the agent-related goal directness of the actions needs to be taken into account, i.e. the (score) intentions that are attributed to the agent, independent of the physical (visual) configuration of that score. To this end, top-down predictive signals (Figure 1A, in red) are sent from the higher abstract knowledge areas (MPFC) to motion perception areas (STS) via intermediate integration areas (TPJ), while bottom-up prediction error signals (Figure 1A, blue) flow in the opposite direction (Figure 1A), following the principles of predictive coding. At each level, the predictions are contrasted against the bottom-up evidence that is ascending from lower regions, resulting in sparse, prediction error activity that is in turn sent upstream. Critical to causal inference, the model is assumed to integrate action outcome information (the score—i.e. the effect) with the preceding action kinematics information (throwing direction—i.e. the cause). We will refer to the throwing of the ball and its direction as the “kinematics”, and to the hitting and falling of the pins as the “outcome”. The “full action” will be reserved for the entire sequence of movement and outcome stimuli.

Fig. 1.

Fig. 1.

Open in a new tab

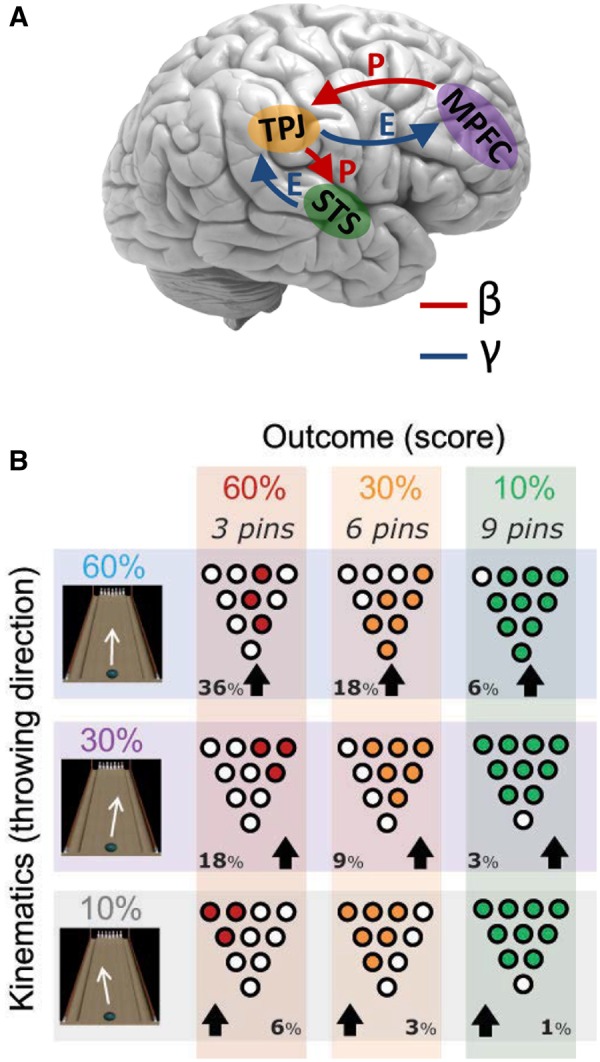
Hypothesized direction of brain activity and experimental design. (A) Schematic of proposed flow of oscillatory activity in a hierarchically organized causal inference network. Predictive, beta-band signals (P, red arrows) run in the top down-direction, from the MPFC, via the intermediate TPJ, to the STS. Prediction error signals (E, blue arrows) are conveyed by the gamma-band and flow in the opposite direction, from STS, via TPJ to MPFC. (B) Experimental design. Subjects viewed animations of a bowler throwing a ball that subsequently knocks over a number of pins. Both the kinematic aspect (throwing direction) and outcome aspect (# of pins hit, i.e. score) were manipulated independently from each other, at three probability levels: 10, 30 and 60%. In conjunction, this made up a total of nine possible complete actions, each with a probability that was the product of the separate probabilities of the action’s kinematic and outcome aspects. Thus, these full actions could be presented at frequencies that ranged from 1% (10 × 10%) to a maximum of 36% (60 × 60%). See Supplementary Movies S1–S9 for the video animations and Supplementary Figure S1 for the trial timelines.

To test the predictive integrative model, we parametrically manipulated the probabilities of both the outcome aspect (score) and kinematic aspect (throwing direction) of the action separately (Figure 1B), each at three levels (10, 30 and 60). The combination of outcome and kinematics, which is hypothesized to be modeled by the proposed integration model, yields nine unique complete actions with probabilities between 1 and 36%. In other words, the combination of kinematics and outcomes had varying degrees of probability or predictability, in which an outcome could not be uniquely associated with any observed kinematics. Prior to the MEG session, subjects underwent a training sessions in which they learned the action probabilities to ensure that these are incorporated in their top-down predictions from the start of the experiment.

We analyzed the model by exploiting the functional segregation between beta- and gamma-band oscillatory activity in terms of predictive coding. This spectral dissociation assumes that gamma-band activity reflects (feed-forward) prediction errors and that beta-band activity reflects the precision of feedback predictive signals (Bastos et al., 2012, 2015a; Bressler and Richter, 2015; Friston et al., 2015). Recent findings in human and non-human primate studies are congruent with these notions (Arnal et al., 2011; Bosman et al., 2012; Bauer et al., 2014; Brodski et al., 2015; Bastos et al., 2015b). We hypothesize that higher-order cognition such as causal inference is based on predictive-coding-like computations in the brain. Consequently, gamma-band activity should decrease parametrically with the probability of the complete action (consistent with reflecting prediction error), whereas beta-band activity should increase with this probability (consistent with reflecting the precision of the prediction). Our results suggest a dissociation in the directionality of beta and gamma connectivities within the causal inference network and show that beta and gamma power modulations are consistent with a predictive coding-based modeling of causal aspects of actions.

Method

See Supplementary Material.

Results

Twenty-three human participants viewed a sequence of 400 animated videos of causal events situated on a bowling lane, while their brain activity was recorded using MEG (see Supplementary Method). The videos consisted of an agent throwing a ball that subsequently knocked over a number of pins. The stimuli could differ in action kinematics (ball throwing direction toward left, center or right), and action outcome (score of 3, 6 or 9 pins hit), together constituting a total of nine unique video’s (Figure 1B). The probabilities at which these video’s could occur were 10, 30 and 60%, for both kinematics and outcome separately, and 1, 3, 3, 6, 6, 9, 18, 18 and 36% for the full action (specific outcome, in combination with specific preceding kinematics). Before going into the MEG, subjects performed a training session with the same stimuli (200 trials), to allow for internalization of the probabilities of the different actions. We subsequently analyzed beta- and gamma-band connectivities in the STS-TPJ-MPFC network as well as spectral power modulations by condition probabilities.

Directionality of beta and gamma connectivity between STS, TPJ and MPFC

We first assessed to what extent the beta-gamma dissociation as observed in lower perceptual areas was also present in the causal inference network. According to the cortical processing hierarchy, top-down predictions flow from MPFC to TPJ, and from there to STS (Figure 1A). Bottom-up prediction error signals are propagated upwards, from STS to TPJ, and from TPJ to MPFC. Because of the lack of direct connections between STS and MPFC (Öngür and Price, 2000; Ethofer et al., 2011), we did not consider this connection in our analyses. The effective STS-TPJ-MPFC network hierarchy should be reflected in a dissociation in the directionality of beta- and gamma-band connectivity between the nodes in this network.

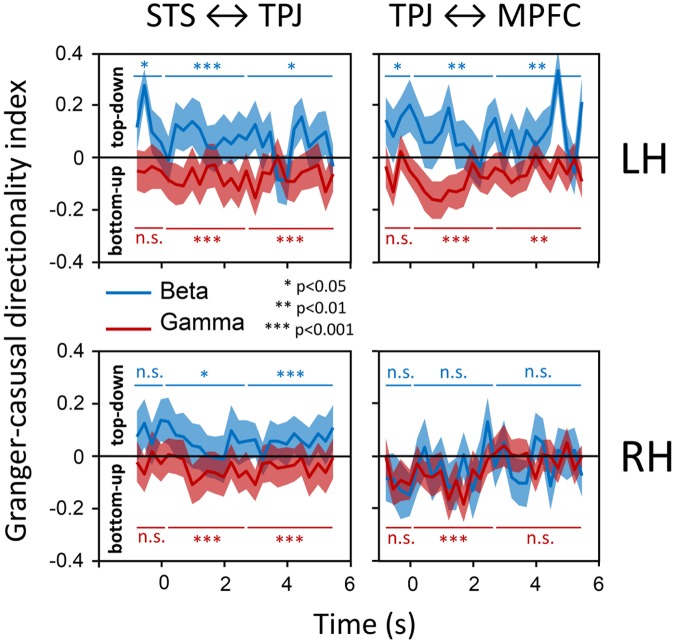
To test this, we reconstructed virtual time courses (bilaterally) in the STS, TPJ and MPFC (see Supplementary Method, and Coricelli and Nagel (2009) for Montreal Neurological Insititute coordinates), separately for beta and gamma-band activity (15–31 Hz and 32–90 Hz, respectively). We subsequently determined the directionality of the beta- and gamma-band connections between STS and TPJ, and between TPJ and MPFC, during the epochs that subjects viewed the bowling videos, independently of the probability of combinations. We computed the Granger-causal connectivity (GC) of their data time courses. For a given set of two time series A and B, GC quantifies the variance in series B that can be predicted on basis of data from series A from an earlier point in time (Geweke, 1982; Kamiński et al., 2001; Dhamala et al., 2008; Schippers et al., 2010). If the past of series A can significantly predict an additional amount of series B than the history of series B alone, series A is said to Granger-cause series B. From this GC data, we constructed an index of the net GC directionality (Schippers et al., 2010; Seth et al., 2015). Figure 2 shows this GC directionality index in the left hemisphere between STS and TPJ (left panels), and TPJ and MPFC (right-hand panels), over the time course of the trial, as averaged over all participants and conditions (t = 0 s denotes movie onset). GC influences in the beta-band are shown in blue, and those in the gamma-band in red. The net directionality of the beta-band connectivity in the left hemisphere (upper panels) is toward the top-down direction (TPJ toward STS and MPFC toward TPJ; indicated by positive values), both for the STS to TPJ and the TPJ to MPFC connections. These effects are significant for the baseline epoch (−1.0 to 0.0 s), the kinematics epoch (0.5–3.0 s) and the outcome epoch (3.0–5.5 s) of the trial (P < 0.05 for all six epochs, signed Mann–Whitney U-test; epochs indicated with blue horizontal lines). In contrast, for the gamma-band, both STS to TPJ and TPJ to MPFC connectivities are stronger in the bottom-up than in the top-down directions (so, TPJ toward MPFC and STS toward TPJ; indicated by negative values). Again, these signals were significantly different from zero in the kinematics epoch (P < 0.001, both connections) as well as in the outcome epoch (P < 0.01). During the baseline however, gamma-band directionality was not different from zero (P > 0.05), in contrast to the beta-band.

Fig. 2.

Fig. 2.

Open in a new tab

GC influences of gamma and beta-band connectivity. The index of the net GC directionality (GC-index) is shown as a function of time (t = 0 s denotes trial onset) for connections between STS and TPJ (left panels), and for the connections between TPJ and MPFC (right-hand panels), for the left (upper panels) and right (lower panels) hemisphere separately. Blue lines depict group-level averaged beta-band directionalities (±s.d.), red lines the directionality in the gamma-band. The individual-subject GC-index is defined as (GC top-down − GC bottom-up)/(GC top-down + GC bottom-up). Horizontal blue and red lines above and below the data traces indicate the baseline, kinematics and outcome epochs within the trial, over which the statistics are computed. Per subject, data are averaged over all trials. LH, left hemisphere; RH, right hemisphere; n.s., not significant.

Similar patterns in the directionality in the connectivity between the same regions are observed in the right hemisphere (Figure 2, lower panels). The gamma-band connectivity between STS and TPJ was stronger in the bottom-up direction during both epochs (P < 0.001), and between TPJ and MPFC during the kinematics epoch (P < 0.001). GC influences in the beta-band were stronger top-down than bottom-up for the connection between STS and TPJ (P < 0.05 and P < 0.001, for kinematics and outcome, respectively). There was no significant directionality (P > 0.05; indicated with not significant) for the other connections and epochs in the right hemisphere (i.e. beta TPJ-MPFC kinematics and outcome epochs; gamma TPJ-MPFC outcome epoch; all baseline epochs). In conjunction, these connectivity findings are congruent with the notion that, also in the causal inference network, beta and gamma-band activity are functionally dissociated, respectively, reflecting top-down and bottom-up signals during the different stages of observation of causal actions.

Modulation of beta and gamma power by action probabilities

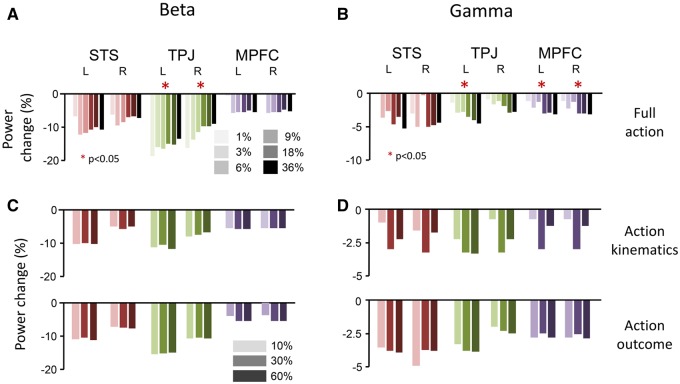
Having established that beta-band activity is indeed related to top-down activity and gamma-band activity to bottom-up signaling in the causal inference network, just as in visual processing areas, we hypothesized that beta and gamma-band activity within these regions should be modulated by the probabilities of the different bowling actions. Beta-band activity should increase when the probability of a condition is higher (higher precision), while gamma-band activity should go down with decreasing prediction error. The predictive causal inference model suggest the oscillatory activity to be modulated by the combination of the probabilities of the action kinematics and the action outcome, rather than by the probabilities of both aspects alone (Figure 1B, see Introduction). Figure 3A shows how beta-band activity during the action outcome stage in STS, TPJ and MPFC is modulated by the probability of the full action (so, a specific action outcome, in combination with specific action kinematics). Averaged over subjects, beta-band power increases parametrically with probability of the full action. This effect is significant in both left and right TPJ (P < 0.05, two-sided t-test, fdr-corrected) but not in STS and MPFC (P > 0.1). So, the larger the probability of the full action, the higher the beta-band activity. In contrast, this positive correlation was not present when we repeated the same regression analysis for the probabilities of the action kinematics and outcome separately (Figure 3C), neither for action kinematics (upper panel) nor for action outcome (lower panel; P > 0.05 in all cases).

Fig. 3.

Fig. 3.

Open in a new tab

Modulation of beta and gamma power by action probabilities. (A) Modulation of the beta-band power change (relative to a common pre-stimulus baseline) as function of probability of the full action, i.e. an outcome in combination with specific preceding kinematics, for the three bilateral regions-of-interests. (B) Results of the same analysis but now for gamma-band power change. (C,D) Modulation of beta-band (C) and gamma-band (D) power change by only the kinematic aspect (upper panel) or the outcome aspect (lower panel) of the bowling action probability. Both oscillatory activity bands show a significant a modulation by action probability but only when the full action is considered (A,B; indicated by asterisks). Note that the relative values between the conditions are crucial here, since baseline was always common.

This result suggests that within the analyzed regions, predictions are not made for the kinematic and outcome components of the action separately but for their combination, i.e. on basis of the probabilities of the full action. In other words, the entire causal event—reflected in the joint probability of kinematics and outcome—is modeled.

Figure 3B and 3D show the same analyses as in Figure 3A and 3C but now for the gamma-band activity. As was the case for beta-band power, there is a modulation by probability of the full action, when kinematics and outcome are combined (Figure 3B). Crucially, the direction of this effect is in opposite direction as for the beta-band, with significant decreases with probability for left TPJ, and left and right MPFC (P < 0.05 in each case). So, the higher the probability of the full action is—and thus the lower the prediction error—the lower the gamma-band response. In contrast, the probabilities of either action kinematics or action outcome in isolation did not significantly modulate power changes in the gamma-band (Figure 3D).

In conjunction with the directionality findings, the power modulation data are supportive of a causal inference model that integrates top-down predictions based on previous events with bottom-up sensory information about the action perceived.

Discussion

The present results deliver a significant insight into the computational properties underlying higher-order cognition. The findings show that our brains make predictive models of causal events, integrating top-down predictions based on previous events with bottom-up sensory information about the action currently being perceived. The results provide novel empirical evidence for predictive coding in higher-order cognitive functioning including its neurophysiological implementation. Our GC analyses of the directionality of spectral connectivity within the causal inference network revealed that the directionality of the gamma-band connectivity is biased toward the bottom-up direction, both for the STS to TPJ and the TPJ to MPFC connections (Figure 2)—but only in the presence of the stimulus. In contrast, for the beta-band, both STS to TPJ and TPJ to MPFC connectivities are stronger in the top-down than in the bottom-up directions, both during and (in the left hemisphere) before stimulus presentation. In conjunction, these connectivity findings are congruent with the notion that beta and gamma-band activity are functionally dissociated. Here, beta-band activity reflects top-down predictive signals, which start being conveyed already before an expected action. Gamma-band activity relays prediction error signals in the bottom-up direction but only when the actual action is presented. Furthermore, we show that beta and gamma signals in these regions are directly modulated by action probabilities. Gamma-band power shows an increase with increasing sensory prediction errors in TPJ and MPFC, whereas beta-band power is positively correlated to the precision of the predicted causal event derived from the generative model.

Oscillatory connectivity and probability modulation

The net direction of the GC connectivity that we observed between the cortical regions within the causal inference network follows the cortical processing hierarchy: the beta-band connectivity is strongest in the feedback (top-down) direction, from MPFC to TPJ to STS, whereas gamma-band connectivity is strongest in the reverse, feed-forward bottom-up direction. This directionality is in line with neurophysiology. Anatomical tracer studies have revealed that feed-forward connections mainly originate from pyramidal cells in the superficial layers and target the granular layer of the (hierarchically) next area, whereas anatomical feedback connections originate from the infragranular layers of the next area and project onto the supragranular and infragranular layers of the previous area (Felleman and Van Essen, 1991; Markov et al., 2013). Computational simulations at the micro and macro network level have indicated that there is an asymmetry in the spectral characteristics of these feed-forward and feedback connections (Bastos et al., 2012; Lee et al., 2013). Indeed, in in vivo experiments, beta-band synchronization is strongest in pyramidal neurons in the infragranular layers, whereas gamma-band activity is mainly observed in pyramidal cells in the supragranular layers (Buffalo et al., 2011; Xing et al., 2012; Roberts et al., 2013; Bastos et al., 2015a). In conjunction with predictive coding theory, this suggests that beta-band activity conveys predictive signals, while gamma-band activity reflects prediction errors (Bastos et al., 2012). This idea is experimentally supported by recent results from both human and non-human primate work (Arnal et al., 2011; Bosman et al., 2012; Bauer et al., 2014; Bressler and Richter, 2015; Brodski et al., 2015; Bastos et al., 2015b; see Friston et al., 2015, for a review). For example, Bressler and Richter (2015) show that the size of visually evoked potentials in V1 are predicted by beta-band activity originating in higher visual areas. The current findings confirm this notion and extend it to higher-level cognition involved in causal inference beyond (extra-striate) visual areas.

The modulation of beta- and gamma-band activity by the probabilities of the observed causal events further support that causal inference follows a predictive coding mechanism that is neurophysiologically implemented by complementary roles of these oscillations. In the predictive coding view of propagation of sensory information, gamma-band activity reflects the unexplained part of the sensory input that is propagated to the next brain area (Friston, 2010; Bastos et al., 2012). Thus, the lower the probability of a stimulus, the larger the prediction error is, and thus, the larger the gamma-band activity.

The parametric increase of beta power with probability that we report suggest that lower frequencies including beta, encode the precision of top-down predictions. The higher the precision of the event predicted by the generative model, the stronger the beta-band activity. This is consistent with message passing in predictive coding and is in line with recent work reporting an increase of attentional alpha-modulation with target predictability (Bauer et al., 2014). It also fits comfortably with active inference and predictive coding in action per se (Friston et al., 2011). For example, there is profound beta suppression during sustained movements (see e.g. Pfurtscheller and Lopes da Silva, 1999) that may be the correlate of sensory attenuation; in other words, the attenuation of sensory precision during movement. Indeed, one might speculate that pathological beta activity in Parkinson’s disease may reflect a loss of precision control, necessary for action selection and subsequent execution.

The modulation of beta- and gamma-band activity (Figure 3) was less pronounced in the STS, which may indicate that the implementation of the full action model mainly takes place at the higher conceptual levels in the network (Ondobaka et al., 2015). This is in agreement with the notion that such a model needs to take internal motivational aspects of the agent into account—namely the desired score—that go beyond the pure visual (kinematic) aspects of the action that are proposed to be encoded by STS. Thus, the predictions of the upcoming full action are made by the TPJ (implemented in the beta-band), on basis of information from STS and MPFC, as suggested by the connectivity results (Figure 2). The absence of oscillatory modulation in STS does not imply that there are no predictions or prediction errors present in STS, only that these do not reflect the full action model with respect to its incorporation of agent-related information encoded in the TPJ and MPFC.

Causal inference in goal-directed action

We only observed a modulation of beta and gamma-band power within the causal inference network when considering the joint probability of the full action, causally integrating kinematics and outcome. When the probabilities of kinematics and outcome aspects of the action were assessed separately, modulatory effects were absent. This suggests that the generative models for the inference of intentional actions incorporate the causal relations between events, in line with previous work on causal inference (Den Ouden et al., 2005; Fugelsang et al., 2005), and mental state attribution in causal inference (Castelli et al., 2000; Blakemore et al., 2001; Wheatley et al., 2007). These inferential processes as investigated in this study are conceptually strongly interrelated to action observation (Hari et al., 1998), theory-of-mind (ToM) and social cognition in general. Many studies in these areas of research observe activity in the same regions that we have currently investigated (Frith and Frith, 2000; Tavares et al., 2008; Coricelli and Nagel et al., 2009) and have also taken a Bayesian perspective for conceptualizing unifying theories (Kilner et al., 2007; Pellicano and Burr, 2012; Baker and Tenenbaum, 2014). For ToM, for example, Koster-Hale and Saxe (2013) proposed a hierarchical model of predictive coding in STS, TPJ and MPFC, that predicts a flow and modulation of bottom-up and top-down activity in this network that is similar to what we found in this study.

A major challenge for future studies will be to assess model updating principles more closely. How do prediction errors enable the updating of the generative model to entail better prediction of future events on the basis of beta and gamma-band activity? It remains an open question how bottom-up and top-down signals interact at a neurophysiological level to modulate gamma-oscillations that are proposed to reflect perceptual surprise at each level of the cortical hierarchy. The nature of this cross-frequency interaction remains to be established and may be implemented by phase–power, power–power or phase–frequency coupling (Jensen and Colgin, 2007). This would be best investigated in a learning paradigm, in which the experimental manipulation systematically targets model updating. On a behavioral level, the relation between score predictions and the errors in the preceding trial(s) could then also be quantified (Wolpert et al., 2003).

The current results stress the importance of higher-level predictions: in this case the outcome of actions. As has been suggested before, our brains predict consequences of actions rather than an agent’s kinematics per se (Majdandžić et al., 2007; Grafton, 2009). Nevertheless, processing of kinematics and outcomes do go hand in hand since neural activation reflects context-dependent action probabilities. Furthermore, the question remains open how and to which extent the framework can be generalized. Do we make context-dependent probabilities for social aspects like observing an in or out-group agent? In any case, the current results suggest it is interesting to follow this path to create a more computationally directed social neuroscience.

Conclusion

This study provides the first direct experimental evidence that higher-order cognitive processes such as causal inference are based on predictive coding-like computations in the brain.

Supplementary Material

Supplementary Data
supp_11_6_973__index.html (854B, html)

Acknowledgements

The authors thank Dr Jan-Mathijs Schoffelen for data analysis advice, Dr Karl Friston for valuable comments on an earlier version of the article and Erik van den Berge for generating the bowling animations. They also thank James Trujillo for critically assessing the manuscript in terms of style.

Funding

S.P., L.H., J.K., I.R. and H.B. were supported by a TOP grant from the Netherlands Organization for Scientific Research (NWO) (407-11-040) to H.B. and I.R. S.O. is funded by a NWO Rubicon Fellowship (446-14-002).

Supplementary data

Supplementary data are available at SCAN online.

Conflict of interest. None declared.

References

  1. Arnal L.H., Wyart V., Giraud A.-L. (2011). Transitions in neural oscillations reflect prediction errors generated in audiovisual speech. Nature Neuroscience, 14, 797–801. [DOI] [PubMed] [Google Scholar]
  2. Baker C.L., Tenenbaum J.B. (2014). Modeling human plan recognition using Bayesian theory of mind. In: Sukthankar G., Goldman R.P., Geib C., Pynadath D., Bui H., editors. Plan, Activity and Intent Recognition: Theory and Practice. Morgan Kaufmann, 177–203. [Google Scholar]
  3. Bastos A.M., Litvak V., Moran R., Bosman C.A., Fries P., Friston K.J. (2015a). A DCM study of spectral asymmetries in feedforward and feedback connections between visual areas V1 and V4 in the monkey. NeuroImage, 108, 460–75. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Bastos A.M., Usrey W.M., Adams R.A., Mangun G.R., Fries P., Friston K.J. (2012). Canonical microcircuits for predictive coding. Neuron, 76, 695–711. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Bastos A.M., Vezoli J., Bosman C.A., Schoffelen J.-M., Oostenveld R., Dowdall J.R., et al. (2015b). Visual areas exert feedforward and feedback influences through distinct frequency channels. Neuron, 85, 390–401. [DOI] [PubMed] [Google Scholar]
  6. Bauer M., Stenner M.-P., Friston K.J., Dolan R.J. (2014). Attentional modulation of alpha/beta and gamma oscillations reflect functionally distinct processes. Journal of Neuroscience, 34, 16117–25. [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Blakemore S.J., den Ouden H., Choudhury S., Frith C. (2007). Adolescent development of the neural circuitry for thinking about intentions. Social Cognitive and Affective Neuroscience, 2, 130–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Blakemore S.J., Fonlupt P., Pachot-Clouard M., Darmon C., Boyer P., Meltzoff A.N., et al. (2001). How the brain perceives causality: an event-related fMRI study. Neuroreport, 12, 3741–6. [DOI] [PubMed] [Google Scholar]
  9. Bosman C.A., Schoffelen J.-M., Brunet N., Oostenveld R., Bastos A.M., Womelsdorf T., et al. (2012). Attentional stimulus selection through selective synchronization between monkey visual areas. Neuron, 75, 875–88. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Bressler S.L., Richter C.G. (2015). Interareal oscillatory synchronization in top-down neocortical processing. Current Opinion in Neurobiology, 31, 62–6. [DOI] [PubMed] [Google Scholar]
  11. Brodski A., Paasch G.-F., Helbling S., Wibral M. (2015). The faces of predictive coding. Journal of Neuroscience, 35, 8997–9006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  12. Buffalo E.A., Fries P., Landman R., Buschman T.J., Desimone R. (2011). Laminar differences in gamma and alpha coherence in the ventral stream. Proceedings of the National Academy of Sciences, 108, 11262–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Castelli F., Happé F., Frith U., Frith C. (2000). Movement and mind: a functional imaging study of perception and interpretation of complex intentional movement patterns. NeuroImage, 12, 314–25. [DOI] [PubMed] [Google Scholar]
  14. Clark A. (2013). Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behavioral and Brain Science, 36, 181–204. [DOI] [PubMed] [Google Scholar]
  15. Colby C.L., Duhamel J.R., Goldberg M.E. (1996). Visual, presaccadic, and cognitive activation of single neurons in monkey lateral intraparietal area. Journal of Neurophysiology, 76, 2841–52. [DOI] [PubMed] [Google Scholar]
  16. Coricelli G., Nagel R. (2009). Neural correlates of depth of strategic reasoning in medial prefrontal cortex. Proceedings of the National Academy of Sciences of the United States of America, 106, 9163–8. [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Decety J., Lamm C. (2007). The role of the right temporoparietal junction in social interaction: how low-level computational processes contribute to meta-cognition. Neuroscientist, 13, 580–93. [DOI] [PubMed] [Google Scholar]
  18. Den Ouden H.E., Frith U., Frith C., Blakemore S.J. (2005). Thinking about intentions. Neuroimage, 28, 787–96. [DOI] [PubMed] [Google Scholar]
  19. Dhamala M., Rangarajan G., Ding M. (2008). Estimating granger causality from Fourier and wavelet transforms of time series data. Physical Review Letters, 100, 018701. [DOI] [PubMed] [Google Scholar]
  20. Ethofer T., Gschwind M., Vuilleumier P. (2011). Processing social aspects of human gaze: a combined fMRI-DTI study. NeuroImage, 55, 411–9. [DOI] [PubMed] [Google Scholar]
  21. Felleman D.J., Van Essen D.C. (1991). Distributed hierarchical processing in the primate cerebral cortex. Cerebral Cortex, 1, 1–47. [DOI] [PubMed] [Google Scholar]
  22. Friston K.J. (2010). The free-energy principle: a unified brain theory? Nature Reviews Neuroscience, 11, 127–38. [DOI] [PubMed] [Google Scholar]
  23. Friston K.J., Bastos A.M., Pinotsis D., Litvak V. (2015). LFP and oscillations—what do they tell us? Current Opinion in Neurobiology, 31, 1–6. [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Friston K.J., Mattout J., Kilner J. (2011). Action understanding and active inference. Biological Cybernetics, 104, 137–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Frith C.D., Frith U. (2000). The physiological basis of theory of mind. In: Baron-Cohen S., Tager-Flusberg H., Cohen D., editors. Understanding Other Minds: Perspective From Developmental Social Neuroscience New York: Oxford University Press, 335–56. [Google Scholar]
  26. Fugelsang J.A., Roser M.E., Corballis P.M., Gazzaniga M.S., Dunbar K.N. (2005). Brain mechanisms underlying perceptual causality. Brain Research. Cognitive Brain Research, 24, 41–7. [DOI] [PubMed] [Google Scholar]
  27. Geweke J. (1982). Measures of conditional linear dependence and feedback between time series. Journal of the American Statistical Association, 77, 304–13. [Google Scholar]
  28. Grafton S. (2009). Embodied cognition and the simulation of action to understand others. Annals of the New York Academy of Sciences, 1156, 97–117. [DOI] [PubMed] [Google Scholar]
  29. Hari R., Forss N., Avikainen S., Kirveskari E., Salenius S., Rizzolatti G. (1998). Activation of human primary motor cortex during action observation: a neuromagnetic study. Proceedings of the National Academy of Sciences of the United States of America, 95, 15061–5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Hohwy J. (2013). The Predictive Mind. New York: Oxford University Press, ix + 282. [Google Scholar]
  31. Jensen O., Colgin L.L. (2007). Cross-frequency coupling between neuronal oscillations. Trends in Cognitive Sciences, 11, 267–9. [DOI] [PubMed] [Google Scholar]
  32. Kamiński M., Ding M., Truccolo W.A., Bressler S.L. (2001). Evaluating causal relations in neural systems: granger causality, directed transfer function and statistical assessment of significance. Biological Cybernetics, 85, 145–57. [DOI] [PubMed] [Google Scholar]
  33. Kerzel D., Bekkering H., Wohlschläger A., Prinz W. (2000). Launching the effect: representations of causal movements are influenced by what they lead to. Quarterly Journal of Experimental Psychology. A, 53, 1163–85. [DOI] [PubMed] [Google Scholar]
  34. Kilner J.M., Friston K.J., Frith C.D. (2007). The mirror-neuron system: a Bayesian perspective. NeuroReport, 18, 619–23. [DOI] [PubMed] [Google Scholar]
  35. Koster-Hale J., Saxe R. (2013). Theory of mind: a neural prediction problem. Neuron, 79, 836–48. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Lee J., Whittington M., Kopell N. (2013). Top-down beta rhythms support selective attention via interlaminar interaction: a model. PLoS Computational Biology, 9, e1003164. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Majdandžić J., Grol M.J., van Schie H.T., Verhagen L., Toni I., Bekkering H. (2007). The role of immediate and final goals in action planning: an fMRI study. Neuroimage, 37, 589–98. [DOI] [PubMed] [Google Scholar]
  38. Markov N.T., Vezoli J., Chameau P., Falchier A., Quilodran R., Huissoud C., et al. (2013). The anatomy of hierarchy: feedforward and feedback pathways in macaque visual cortex. Journal of Comparative Neurology, 522, 225–59. [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Michotte A. (1950). The emotions regarded as functional connections. In: Reymert M.L., editor. Feelings and Emotions: the Mouseheart Symposium. New York: McGraw Hill, 128–44. [Google Scholar]
  40. Murdaugh D.L., Nadendla K.D., Kana R.K. (2014). Differential role of temporoparietal junction and medial prefrontal cortex in causal inference in autism: an independent component analysis. Neuroscience Letters, 568, 50–5. [DOI] [PubMed] [Google Scholar]
  41. Ondobaka S., Kilner J., Friston K. (2015). The role of interoceptive inference in theory of mind. Brain and Cognition. doi: 10.1016/j.bandc.2015.08.002. [Google Scholar]
  42. Öngür D., Price J.L. (2000). The organization of networks within the orbital and medial prefrontal cortex of rats, monkeys and humans. Cerebral Cortex, 10, 206–19. [DOI] [PubMed] [Google Scholar]
  43. Pellicano E., Burr D. (2012). When the world becomes ‘too real’: a Bayesian explanation of autistic perception. Trends in Cognitive Sciences, 16, 504–10. [DOI] [PubMed] [Google Scholar]
  44. Pfurtscheller G., Lopes da Silva F.H. (1999). Event-related EEG/MEG synchronization and desynchronization: basic principles. Clinical Neurophysiology, 110, 1842–57. [DOI] [PubMed] [Google Scholar]
  45. Roberts M.J., Lowet E., Brunet N.M., TerWal M., Tiesinga P., Fries P., et al. (2013). Robust gamma coherence between macaque V1 and V2 by dynamic frequency-matching. Neuron, 78, 523–36. [DOI] [PubMed] [Google Scholar]
  46. Schippers M.B., Roebroeck A., Renken R., Nanetti L., Keysers C. (2010). Mapping the information flow from one brain to another during gestural communication. Proceedings of the National Academy of Sciences of the United States of America, 107, 9388–93. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Seth A.K., Barrett A.B., Barnett L. (2015). Granger causality analysis in neuroscience and neuroimaging. Journal of Neuroscience, 35, 3293–7. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Summerfield C., de Lange F.P. (2014). Expectation in perceptual decision making: neural and computational mechanisms. Nature Reviews Neuroscience, 15, 745–56. [DOI] [PubMed] [Google Scholar]
  49. Tavares P., Lawrence A.D., Barnard P.J. (2008). Paying attention to social meaning: an FMRI study. Cerebral Cortex, 18, 1876–85. [DOI] [PubMed] [Google Scholar]
  50. Tenenbaum J.B., Kemp. C., Griffiths T.L., Goodman N.D. (2011). How to grow a mind: statistics, structure, and abstraction. Science, 331, 1279–85. [DOI] [PubMed] [Google Scholar]
  51. Wacongne C., Labyt E., Van Wassenhove V., Bekinschtein T., Naccache L., Dehaene S. (2011). Evidence for a hierarchy of predictions and prediction errors in human cortex. Proceedings of the National Academy of Sciences, 108(51), 20754–9. [DOI] [PMC free article] [PubMed] [Google Scholar]
  52. Wacongne C., Changeux J.P., Dehaene S. (2012). A neuronal model of predictive coding accounting for the mismatch negativity. Journal of Neuroscience, 32, 3665–78. [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Wheatley T., Milleville S.C., Martin A. (2007). Understanding animate agents: distinct roles for the social network and mirror system. Psychological Science, 18, 469–74. [DOI] [PubMed] [Google Scholar]
  54. Wolpert D.M., Doya K., Kawato M. (2003). A unifying computational framework for motor control and social interaction. Philosophical transactions of the Royal Society of London. Series B, 358, 593–602. [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Xing D., Shen Y., Burns S., Yeh C.-I., Shapley R., Li W. (2012). Stochastic generation of gamma-band activity in primary visual cortex of awake and anesthetized monkeys. Journal of Neuroscience, 32, 13873–80a. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Data
supp_11_6_973__index.html (854B, html)
supp_nsw017_suppl_data.zip (3.4MB, zip)

Articles from Social Cognitive and Affective Neuroscience are provided here courtesy of Oxford University Press

RESOURCES