Mechanistic Modeling of the Effects of Acidosis on Thrombin Generation

Supplemental Digital Content is available in the text.

Published ahead of print April 2, 2015

Abstract

BACKGROUND:

Acidosis, a frequent complication of trauma and complex surgery, results from tissue hypoperfusion and IV resuscitation with acidic fluids. While acidosis is known to inhibit the function of distinct enzymatic reactions, its cumulative effect on the blood coagulation system is not fully understood. Here, we use computational modeling to test the hypothesis that acidosis delays and reduces the amount of thrombin generation in human blood plasma. Moreover, we investigate the sensitivity of different thrombin generation parameters to acidosis, both at the individual and population level.

METHODS:

We used a kinetic model to simulate and analyze the generation of thrombin and thrombin–antithrombin complexes (TAT), which were the end points of this study. Large groups of temporal thrombin and TAT trajectories were simulated and used to calculate quantitative parameters, such as clotting time (CT), thrombin peak time, maximum slope of the thrombin curve, thrombin peak height, area under the thrombin trajectory (AUC), and prothrombin time. The resulting samples of parameter values at different pH levels were compared to assess the acidosis-induced effects. To investigate intersubject variability, we parameterized the computational model using the data on clotting factor composition for 472 subjects from the Leiden Thrombophilia Study. To compare acidosis-induced relative parameter changes in individual (“virtual”) subjects, we estimated the probabilities of relative change patterns by counting the pattern occurrences in our virtual subjects. Distribution overlaps for thrombin generation parameters at distinct pH levels were quantified using the Bhattacharyya coefficient.

RESULTS:

Acidosis in the range of pH 6.9 to 7.3 progressively increased CT, thrombin peak time, AUC, and prothrombin time, while decreasing maximum slope of the thrombin curve and thrombin peak height (P < 10^–5). Acidosis delayed the onset and decreased the amount of TAT generation (P < 10^–5). As a measure of intrasubject variability, maximum slope of the thrombin curve and CT displayed the largest and second-largest acidosis-induced relative changes, and AUC displayed the smallest relative changes among all thrombin generation parameters in our virtual subject group (1-sided 95% lower confidence limit on the fraction of subjects displaying the patterns, 0.99). As a measure of intersubject variability, the overlaps between the maximum slope of the thrombin curve distributions at acidotic pH levels with the maximum slope of the thrombin curve distribution at physiological pH level systematically exceeded analogous distribution overlaps for CT, thrombin peak time, and prothrombin time.

CONCLUSIONS:

Acidosis affected all quantitative parameters of thrombin and TAT generation. While maximum slope of the thrombin curve showed the highest sensitivity to acidosis at the individual-subject level, it may be outperformed by CT, thrombin peak time, and prothrombin time as an indicator of acidosis at the subject-group level.

Acidosis (arterial pH ≤ 7.35) is a major contributor to trauma-associated coagulopathy.^1–3 Acidosis arises when trauma is accompanied by severe hemorrhage and shock, and the resulting hypoperfusion leads to the accumulation of lactic acid.^3,4 Moreover, the infusion of resuscitation fluids, such as normal saline, can exacerbate acidosis.² Similar factors can trigger acidosis in patients undergoing complex surgery.⁵

The molecular mechanisms by which acidosis affects thrombin formation and activity have not been definitively elucidated. Blood coagulation is a complex phenomenon comprising cell-dependent thrombin generation, fibrin formation, and fibrinolysis. While each of these stages could potentially be impaired by acidosis, its effects on the biochemistry of thrombin generation are of particular interest because of the central role of thrombin in thrombus formation.^6,7 Several studies using different experimental methodologies showed that thrombus formation is considerably impaired in acidosis,^8,9 and this effect can even exceed that observed from hypothermia.¹⁰ However, other reports suggest that acidosis without hypothermia has a very limited impact on blood coagulation.^11,12 Direct experimental evidence demonstrates that key coagulation enzymes are inhibited by decreasing pH,¹³ but the effects of acidosis on thrombin generation kinetics in human blood plasma have not been investigated. Furthermore, it is not known how intersubject variability would influence acidosis-induced effects.

Computational modeling can be used to integrate the available knowledge of individual biochemical reactions and make predictions about their cumulative effect on thrombin generation kinetics.^6,14 Such approaches have been applied to analyze how thrombin generation is influenced by dilution^15,16 and hypothermia,¹⁷ as well as by the action of therapeutic agents, such as recombinant factor VIIa^15,18 and prothrombin complex concentrates.¹⁵ These results were obtained by applying, and extending the capabilities of, the Hockin-Mann kinetic model^19,20 of thrombin generation. This model is a simplified representation of thrombin generation biochemistry in human plasma in vitro and can serve as a framework for simulating complex combinations of factors affecting blood clotting.^6,14,18

In this study, we extend the Hockin-Mann model to represent the effects of acidic pH on thrombin generation. We hypothesize that acidosis has the ability to affect the kinetics of free thrombin and thrombin-antithrombin complex (TAT) by both delaying their accumulation and reducing their maximum levels. Moreover, we hypothesize that these effects will be consistent throughout a large population of subjects. Finally, we compare the sensitivity to acidosis for different quantitative parameters of thrombin generation both at the single-subject level and at the subject-group level.

METHODS

Study Group

This work is a computational modeling study; no actual blood samples were drawn or analyzed. This study was conducted in compliance with the document defining our organization’s (BHSAI) Standard Operating Procedure for acquisition, warehousing, and sharing human data, which has been approved by the U.S. Army. Because this study only used previously obtained data, it was exempt from IRB review based on these procedures. Our computational analyses were performed for a virtual subject defined based on average values of coagulation protein concentrations in human plasma.^18,20 Moreover, we analyzed virtual subjects defined using the clotting factor composition data for 472 individual subjects in the Leiden Thrombophilia Study (LETS)²¹ control group, as described below.

Model Parameters, Inputs, Outputs, and the Basic Simulation Protocol

The Hockin-Mann model of thrombin generation is a system of 34 ordinary differential equations reflecting the mass action kinetics of essential biochemical reactions in the thrombin generation network (i.e., in the system of biochemical reactions responsible for thrombin generation).^19,20 Each equation represents one of the coagulation proteins or their complexes. The model’s parameters are the initial concentrations of the coagulation proteins and 44 kinetic constants that determine the rates of the constituent biochemical reactions (the reactions are listed in Table S1 in the Supplemental Digital Content, http://links.lww.com/AA/B118). The default initial concentrations are equal to the corresponding average values in human plasma, and the default values of the kinetic constants correspond to physiological pH level (i.e., pH 7.4). The main input of the model is the initial concentration of tissue factor, which is a biological trigger of thrombus formation. The model’s outputs are temporal curves, called “kinetic trajectories,” that reflect the time dependence of the concentrations of the coagulation proteins. The 2 main outputs considered in this work correspond to the concentration of thrombin (primary end point) and TAT complex (secondary end point).

To run the model and generate output trajectories for the chosen parameter values, we used a software function that computes the trajectories spanning a preselected time interval (in our case, 0–80 minutes). The model trajectories were subjected to further numerical analyses and/or plotted against time. All computations were performed in the software suite MATLAB R2012a (MathWorks, Natick, MA). Additional details pertaining to the computational procedures are provided in the Supplemental Digital Content (http://links.lww.com/AA/B118).

To model thrombin and TAT generation in the individual LETS subjects, we followed our previously described approach^15–17 and substituted the default values of the initial coagulation protein concentrations in the model with the corresponding values determined experimentally for each of the 472 individual subjects in the LETS control subject group. The resulting 472 variants of the Hockin-Mann model can be regarded, and are henceforth referred to, as virtual LETS subjects. After this adjustment to the initial concentrations, we generated and processed output trajectories as described above.

Modeling the pH Dependence of Thrombin and TAT Generation

To represent the pH dependence of thrombin and TAT generation, the basic simulation protocol (suitable only for pH 7.4) had to be modified. Because it is known that the rates of individual enzymatic reactions depend on pH,^22–24 we represented the pH-dependent modulation of the thrombin/TAT generation kinetics by adjusting the catalytic rates of the enzymatic reactions in the Hockin-Mann model. Specifically, we used the expression k(pH) = f(pH)*k(7.4), where k(pH) is the catalytic rate constant of an enzymatic reaction at a given pH level, k(7.4) is the rate constant’s value for physiological pH = 7.4, and f(pH) is a pH-dependent quantity that we refer to as “pH factor.” We considered the following acidotic pH levels: 6.9, 7.0, 7.1, 7.2, and 7.3.

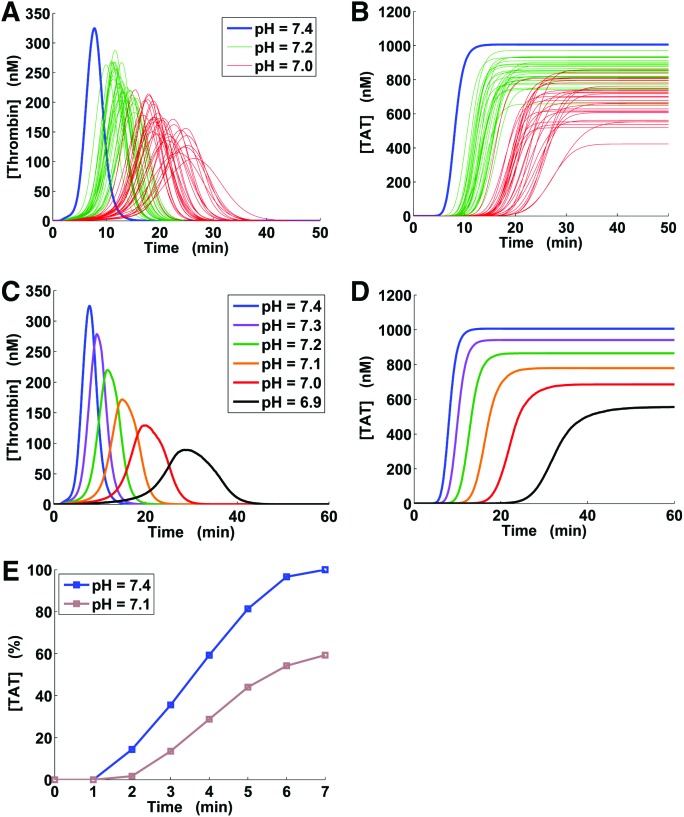
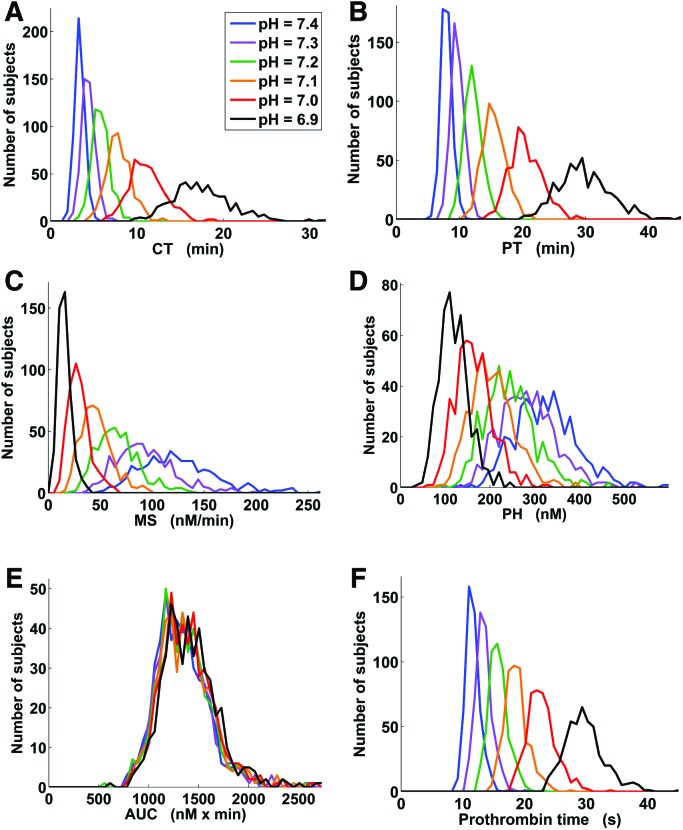
We developed and compared 2 strategies, designated “full” and “reduced,” for the pH-dependence simulations; these strategies were analogous to our recently developed approach to model the effects of hypothermia on thrombin generation.¹⁷ The full strategy involved pH factor random sampling from a pH-dependent interval (shown in Fig. 1), which accounted for the uncertainty in the pH factor values. For a given acidotic pH value, this strategy produced a large number (by default, 5000) of random pH factor sets, each of which was used to adjust the kinetic constants in the model. After the adjustments, the model was run according to the basic simulation protocol (see previous subsection) to produce a group of 5000 distinct trajectories for thrombin and TAT generation. These distinct trajectories were subjected to further analyses, such as quantitative parameter calculation, or plotted against time (Figs. 2–4). For trajectory comparisons and plotting, the default 80-minute time interval was divided into 800 evenly spaced points, and the value of each trajectory at each time point was recorded. Thus, for each time point, we obtained a sample of 5000 trajectory values, which were used for statistical analyses. For example, for each sample at each time point, we calculated the median (Fig. 2, C and D) and quartiles (Fig. 3) and plotted them against time. Moreover, the samples for each model output (i.e., thrombin or TAT), each acidotic pH level, and each time point were tested for normality using the Jarque-Bera test.²⁵

Figure 1.

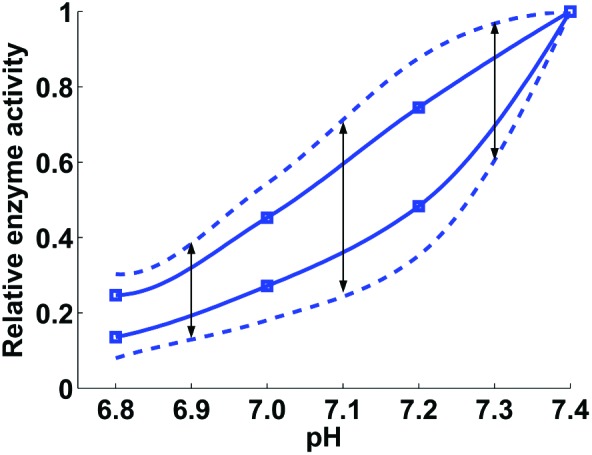
Relative enzyme activity as a function of pH. For every considered acidotic pH level, the pH factor values (which express enzymatic activity relative to that at pH 7.4) were sampled uniformly from the interval delimited by the dashed lines at that pH level. For the pH levels of 6.9, 7.1, and 7.3, such intervals are indicated by black arrows. The dashed lines were obtained by increasing (by 100%) the distance between the solid lines, which approximate the experimental data (extracted from Figs. 2 and 3 in Meng et al.¹³) shown with square markers. The markers on the upper and lower solid lines correspond to the enzymatic activity of the extrinsic tenase and prothrombinase coagulation factor complexes, respectively. The solid lines were fitted to the experimental data using the MATLAB function PCHIP. See Supplemental Digital Content for further details.

Figure 2.

Thrombin generation versus time under physiological and acidotic conditions. TAT = thrombin-antithrombin complex. Subplots A and B: each subplot shows 30 green and 30 red kinetic trajectories, with each trajectory corresponding to a randomly generated set of pH factors; the blue lines correspond to trajectories at the physiological pH level. Subplots C and D represent kinetic trajectories at the physiological pH level (blue) and median trajectories corresponding to the 5000-trajectory groups computed for acidotic pH levels (other colors) as described in Methods (via the full pH-dependence simulation strategy). E, Normalized thrombin-antithrombin complex (TAT) data on induced acidosis for an in vivo porcine model; the data values are designated with square markers and were extracted from Figure 5 in Martini et al.⁹

Figure 4.

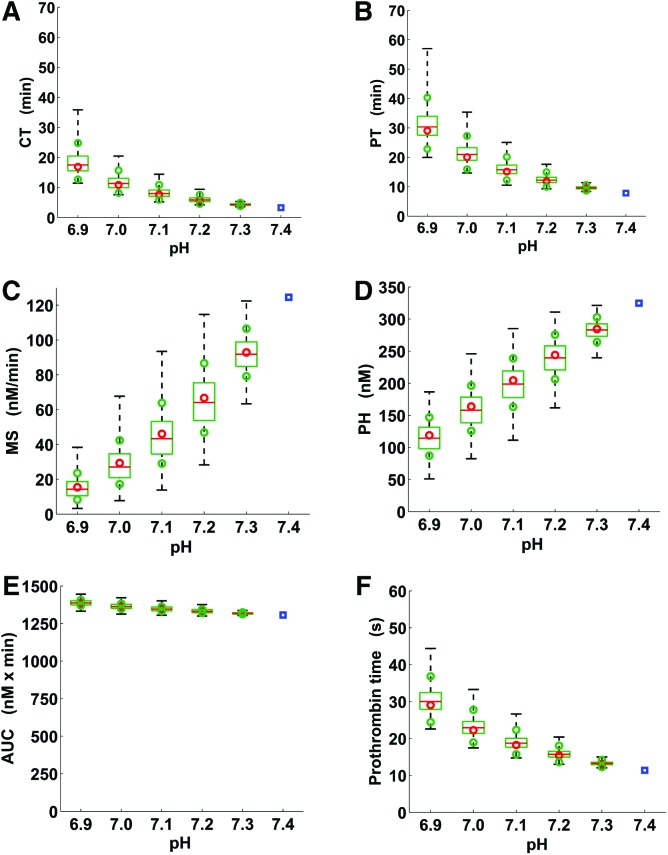
Box and whisker plot of the quantitative parameters of thrombin generation trajectories under physiological and acidotic pH conditions. A, Clotting time; B, Thrombin peak time; C, Maximum slope of the thrombin trajectory; D, Thrombin peak height; E, Area under the thrombin trajectory (or “curve”); F, Prothrombin time. The blue squares correspond to single values for physiological pH, whereas the box plots show thrombin generation parameter distributions corresponding to the groups of 5000 thrombin trajectories generated via the full pH-dependence simulation strategy. Dashed whiskers, green boxes, and red lines show the ranges, interquartile ranges, and medians of the parameter distributions, respectively. The red circles correspond to the estimates of the median values calculated using our reduced pH-dependence simulation strategy (see Methods). The green circles were calculated similarly to the red circles as an estimate of the interquartile ranges shown as green boxes. Acidosis-induced median fold changes in the area under the thrombin trajectory with respect to its physiological value were smaller than corresponding median fold changes for every other thrombin generation parameter (P = 0 to machine precision, Wilcoxon rank sum test; comparisons for each acidotic pH level performed independently.) For each (acidotic) thrombin trajectory and each thrombin generation parameter, fold_change = AV/NV if AV > NV and fold_change = NV/AV otherwise, where AV and NV are the (acidotic) value of the parameter for that thrombin trajectory and the parameter’s physiological value, respectively.

Figure 3.

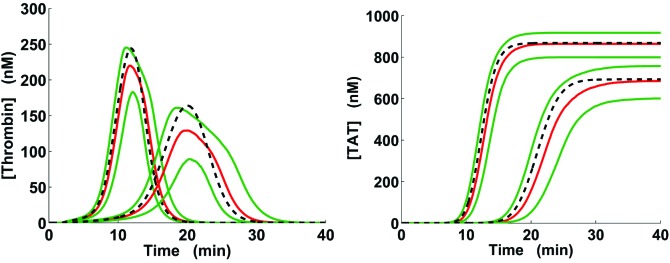
Thrombin generation ranges for acidotic pH levels. Solid green and red lines correspond to the interquartile range and median, respectively, calculated for the groups of 5000 kinetic trajectories generated via the full pH-dependence simulation strategy as described in Methods (the medians, also shown in Fig. 2, C and D, are shown here for comparison purposes). The dashed lines correspond to the acidotic-pH kinetic trajectories calculated using our reduced pH-dependence simulation strategy. For each subplot, the left and right groups of trajectories correspond to pH 7.2 and 7.0, respectively.

Because the full pH-dependence simulation strategy is computationally intensive, a simpler simulation algorithm might be preferable for the LETS subject group analysis. The reduced strategy that we developed did not rely on pH factor randomization, but provided a method for direct estimation of the median and quartiles for the quantities of interest (Figs. 3 and 4). This was achieved by adjusting all the catalytic rate constants in the Hockin-Mann model using 1 appropriately selected pH factor set (see Supplemental Digital Content, http://links.lww.com/AA/B118), which was followed by running the model with these new kinetic constants according to the basic simulation protocol. Thus, in the case of the default initial concentrations, we used both the full and the reduced strategies, whereas in our virtual LETS subject analysis (Figs. 5 and 6), we only used the reduced strategy.

Figure 5.

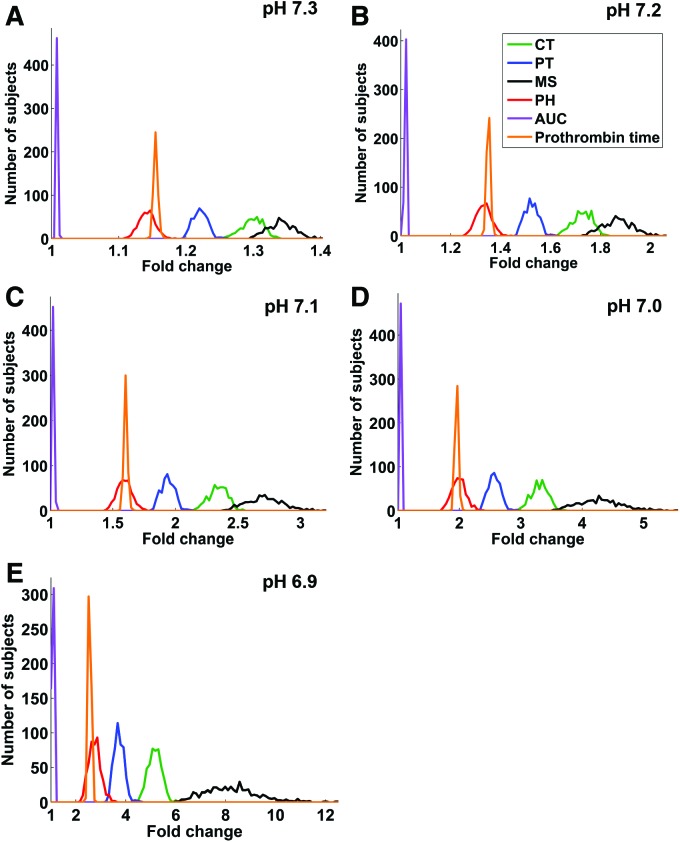
Fold change distributions in the virtual Leiden Thrombophilia Study (LETS) subject group for the 5 thrombin generation parameters and prothrombin time. For each virtual LETS subject, each parameter, and each acidotic pH level, fold_change = AV/NV if AV > NV and fold_change = NV/AV otherwise, where AV and NV are the acidotic and physiological values of the parameter in that subject, respectively. The plots show distribution histograms generated using the MATLAB function HIST with 100 bins splitting up the interval between 1 and the maximum parameter fold change value for a given pH level. CT = clotting time; PT = thrombin peak time; MS = maximum slope of the thrombin trajectory; PH = thrombin peak height; AUC = area under the thrombin trajectory (or “curve”).

Figure 6.

Thrombin generation parameter distributions (including prothrombin time) in the virtual Leiden Thrombophilia Study (LETS) subject group for different pH levels. The plots show distribution histograms generated using the MATLAB function HIST with 50 bins splitting up the interval between 0 and the maximum value for a given thrombin generation parameter. CT = clotting time; PT = thrombin peak time; MS = maximum slope of the thrombin trajectory; PH = thrombin peak height; AUC = area under the thrombin trajectory (or “curve”).

Quantitative Parameter Analysis for Kinetic Trajectories

For the simulated thrombin trajectories, we calculated quantitative parameters of thrombin generation^16,18: clotting time (CT) (i.e., time to 10 nM thrombin), thrombin peak time, maximum slope of the thrombin trajectory (also known as the maximum rate of thrombin generation), thrombin peak height, and the area under the thrombin trajectory (AUC). We also analyzed prothrombin time, which was computed as CT for an initial tissue factor concentration of 17 nM¹⁷ (its default concentration in the model was 5 pM, a standard value for in vitro thrombin generation assays). Likewise, for the simulated TAT trajectories, we calculated the following quantitative parameters: onset time (i.e., time to 10 nM TAT), activation time (i.e., time to 50% of the TAT final level), maximum slope of the TAT trajectory, and TAT final level (i.e., the TAT level at 80 minutes).

For each acidotic pH level, application of the full pH-dependence simulation strategy resulted in the generation of 5000 values for each quantitative parameter (i.e., 1 parameter value for each kinetic trajectory). The samples were tested for normality using the Jarque-Bera test. To compare these parameter samples with the physiological values of the corresponding parameters, we used the Wilcoxon rank sum test.²⁶ In our virtual LETS subject analysis (performed using the reduced pH-dependence simulation strategy), for each considered pH level and each quantitative parameter, we generated a sample of 472 values (i.e., 1 value per 1 virtual subject). Such samples were also tested for normality using the Jarque-Bera test. To test for statistically significant differences between such parameter samples for physiological and acidotic pH levels, we used the Wilcoxon signed rank test.²⁶ The differences between the samples were illustrated by calculating their medians and interquartile ranges. The P values resulting from the Wilcoxon tests were Bonferroni-corrected to account for multiple comparisons. The denominator for the Bonferroni correction was equal to 5, which reflects comparisons between a sample for the physiological pH level and the corresponding samples for each of the considered five acidotic pH levels.

Intrasubject Parameter Change Analysis for the LETS Subject Group

The magnitude of pH-induced change in different thrombin generation parameters for the same subject was assessed via intrasubject fold change comparisons. For each virtual LETS subject, each parameter, and each acidotic pH level, fold_change = AV/NV if AV > NV and fold_change = NV/AV otherwise, where AV and NV are the acidotic and physiological values of the parameter, respectively. We then followed our previous work^15,16 and estimated the probability of fold change patterns by calculating the fraction of virtual subjects for which the pattern of interest was detected. For example, we considered the pattern FC(AUC) < FC(X), where FC(AUC) is the fold change in the AUC and FC(X) is the fold change in any other thrombin generation parameter in the same virtual subject at the same pH level. The SE of a probability estimate q was computed as 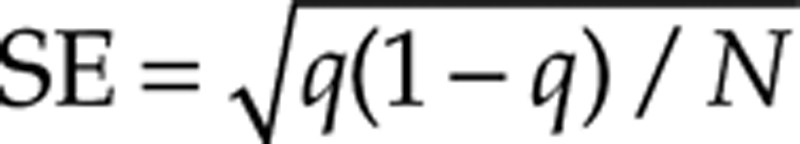, where N = 472 is the LETS subject group size.²⁶ We also report a 95% confidence interval (95% CI) for q; its upper boundary point is 1.00, and its lower boundary point was calculated as the exact (Clopper-Pearson) 1-sided 95% lower confidence limit.²⁷

Intersubject Variability Analysis for the LETS Subject Group

We analyzed the intersubject variation of the parameter fold changes and parameter values by visualizing the fold-change and parameter histograms (Figs. 5 and 6) and calculating the interquartile ranges for the parameter distributions (Tables 1 and 2). The overlap between 2 distributions (or histograms) of a thrombin generation parameter (with the 2 distributions corresponding to 2 distinct pH levels) was quantified via the Bhattacharyya coefficient ρ (Table 3) defined as follows.²⁸ Let x and y be histograms with m bins each, and let x_i and y_i be the numbers of observations from x and y, respectively, falling into the ith bin. (In our analysis, the number of observations in the ith bin is the number of virtual LETS subjects whose thrombin generation parameter values fall within that bin.) The Bhattacharyya coefficient was defined by the expression

Table 1.

Thrombin Generation Parameters in the Virtual Leiden Thrombophilia Study (LETS) Subject Group Under pH Variation

Table 2.

Thrombin–Antithrombin Complex (TAT) Generation Parameters in the Virtual Leiden Thrombophilia Study (LETS) Subject Group Under pH Variation

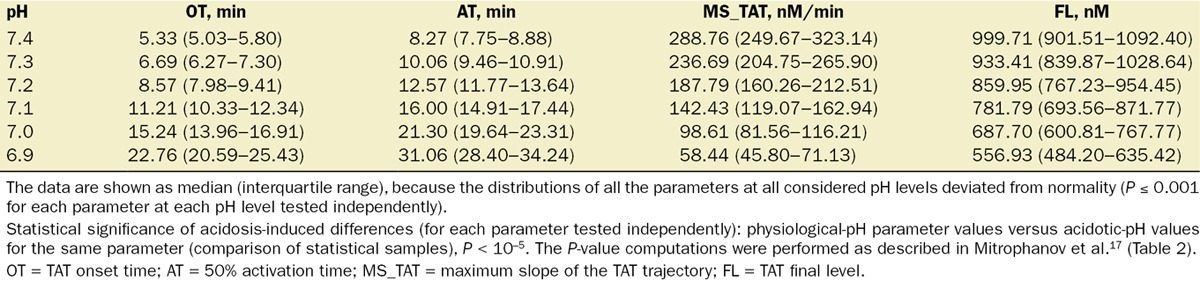
Table 3.

Bhattacharyya Coefficients for the Thrombin Generation Parameters in the Virtual Leiden Thrombophilia Study (LETS) Subject Group

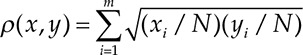where N = 472. It follows that 0 ≤ ρ(x,y)≤1; ρ(x,y) = 0 when x and y do not overlap (i.e., when none of the bins contain observations from both x and y), and ρ(x,y) = 1 when x and y coincide (i.e., when x_i = y_i, i = 1,...,m).

RESULTS

pH Dependence of Thrombin Generation

Examples of distinct thrombin and TAT kinetic trajectories generated using the full pH-dependence simulation strategy are shown in Figure 2, A and B, respectively. In each 5000-trajectory group (1 group corresponded to 1 acidotic pH level), all thrombin trajectories possessed a characteristic one-peaked shape, and all TAT trajectories were monotonically increasing. Trajectories from the groups corresponding to different pH levels often overlapped (Fig. 2, A and B), which reflects the variations in the randomly sampled pH factors. Yet, for each distinct thrombin trajectory and each acidotic pH level, the values of CT, peak time, and prothrombin time were larger, and the values of maximum slope and peak height were smaller, than the corresponding values at pH 7.4. The AUC (i.e., the area under the curve) for acidotic pH levels was larger than that for pH 7.4 in 99.54% of the trajectories. Likewise, for each distinct TAT trajectory and each acidotic pH level, the values of onset time and activation time were larger, and the values of maximum slope were smaller, than the corresponding values at pH 7.4. The TAT final level for acidotic pH levels was smaller than that for pH 7.4 in 99.49% of the trajectories.

To elucidate major trends in the 5000-trajectory groups at each acidotic pH level, we analyzed the corresponding median trajectories. Median trajectories were used because the distributions of thrombin and TAT concentrations in each 5000-trajectory group deviated from normality (P ≤ 0.001, thrombin and TAT samples at each time point and each acidotic pH level tested independently). Acidosis progressively delayed the time of onset and reduced the amount of thrombin and TAT generation, as reflected by median trajectories (Fig. 2, C and D). These model predictions were consistent with experimental results for a porcine model of acidosis (Fig. 2E).⁹

The interquartile distances for the simulated groups of distinct trajectories could be considerable (up to 89.00% of the maximum median value for thrombin generation and up to 64.22% of the maximum median value for TAT generation; see examples in Fig. 3). One reason for this could be imprecise estimation of the median and quartile trajectories owing to insufficient sample size. To test this possibility, we repeated the computations with trajectory group size increased to 10,000 (trajectories generated using our full strategy for pH-dependence simulation, as described in Methods). The resulting median and quartile trajectories practically coincided with the corresponding trajectories for the 5000-trajectory groups (results not shown). This finding suggests that the interquartile value spread may primarily reflect the uncertainty in the pH factor values, which is captured in the full pH-dependence simulation strategy. Yet, the domain shapes defined by the interquartile distances were consistent with the trends shown by the median trajectories (Fig. 2, C and D, and Fig. 3).

To test our reduced pH-dependence simulation strategy, we used it to approximate the median trajectories generated via the full simulation strategy. Yet, the temporal trajectories generated via the reduced strategy (see examples shown for pH 7.2 and 7.0, dashed black lines in Fig. 3) could noticeably deviate from the 5000-trajectory group medians (red lines in Fig. 3) for both thrombin and TAT, especially at pH 6.9 and 7.0 (comparison of statistical samples using Wilcoxon’s rank sum test, P < 10^–5 for certain time points and acidotic pH levels). This result indicates that the use of the full pH-dependence simulation strategy is preferable for accurate estimation of the thrombin and TAT time courses at acidotic pH levels.

Quantitative Parameters of Thrombin Generation

The groups of quantitative parameter values for thrombin and TAT corresponding to each group of 5000 trajectories (generated via the full pH-dependence simulation strategy) were characterized using medians and interquartile ranges because all corresponding distributions deviated from normality (P ≤ 0.001 for each parameter at each pH level tested independently). Acidosis caused a progressive increase in median CT, thrombin peak time, the AUC, and prothrombin time, while the medians for both maximum slope of the thrombin trajectory and thrombin peak height progressively decreased (statistical sample comparisons for each parameter tested independently: physiological-pH parameter values versus acidotic values for the same parameter, P = 0 to machine precision) (Fig. 4). Interestingly, the median value of the AUC at pH 6.9 was only 1.06-fold (95% CI, 1.061–1.062, calculated using the large sample CI approximation for the median²⁹) larger than its value at physiological pH, which is a small change compared with other parameters.

The interquartile ranges for CT, thrombin peak time, the AUC, and prothrombin time were comparatively small in relation to the median values, particularly for higher pH levels (Fig. 4). This suggests that the full simulation strategy can produce informative estimates of the quantitative thrombin generation parameters. Interestingly, the parameter values calculated using the reduced pH-dependence simulation strategy nearly coincided with the corresponding parameter values calculated as sample medians for the 5000-trajectory groups from the full pH-dependence simulation strategy (Fig. 4). Moreover, the parameter distributions’ 1st and 3rd quartiles could also be approximated using the reduced simulation strategy. These approximations were particularly accurate for pH 7.2 and 7.3 (Fig. 4).

For TAT, acidosis progressively increased median onset time and activation time, and progressively decreased the median maximum slope of the TAT trajectory and TAT final level (statistical sample comparisons for each parameter tested independently: physiological-pH parameter values versus acidotic values for the same parameter, P = 0 to machine precision). Accuracy of approximation of the median and quartile parameter values using our reduced pH-dependence simulation strategy was similar to the case of thrombin trajectories (Fig. 4). Taken together, these results suggest that the application of our reduced simulation strategy can be particularly effective in the analysis of individual quantitative trajectory parameters (Fig. 4), rather than whole trajectories (Fig. 3).

pH Effects in the Group of Virtual LETS Subjects

Because our virtual LETS subject analysis focused only on quantitative parameters (rather than the whole trajectories) of thrombin generation, we performed the simulations using only the reduced pH-dependence simulation strategy. Indeed, its use was justified by the sufficiently high accuracy of this approximation detected in the case of average initial concentrations of coagulation proteins (Fig. 4). While the calculated thrombin and TAT generation parameter values in the LETS group displayed substantial intersubject variability (Tables 1 and 2), the general patterns characterizing the effects of acidosis were robust and consistent with our results for the case of average initial concentrations of coagulation proteins. Indeed, for every virtual subject, CT, thrombin peak time, the AUC, and prothrombin time monotonically increased with acidosis, whereas maximum slope of the thrombin trajectory and thrombin peak height monotonically decreased. Likewise, for TAT trajectories, onset time and activation time increased, while maximum slope and final level decreased.

For every acidotic pH level, the pattern FC(MS) > FC(CT) > FC(X) occurred in every virtual subject. Therefore, estimated probability of the pattern’s occurrence in the same subject was equal to 1.00 (SE, 0.00; 95% CI, 0.99–1.00). [Here, FC(·) denotes fold change in a thrombin generation parameter, and MS, CT, and X designate maximum slope of the thrombin trajectory, clotting time, and any other thrombin generation parameter, respectively.] This result suggests that maximum slope and CT can be regarded as the 2 most sensitive thrombin generation parameters in each virtual LETS subject. The least sensitive parameter was the AUC because the pattern FC(AUC) < FC(X) (with X being any other thrombin generation parameter) occurred in every virtual subject and, therefore, its estimated probability was equal to 1.00 (SE, 0.00; 95% CI, 0.99–1.00). Interestingly, while these results reflect the intrasubject variability, our conclusions regarding the most- and the least-sensitive parameters can also be reached by visually comparing the fold change distributions reflecting the intersubject variability in the virtual subject group (Fig. 5).

These findings imply that maximum slope of the thrombin trajectory could potentially be used to discriminate between physiological and acidotic thrombin generation—a question related to the problem of coagulopathy diagnostics. Specifically, would it be possible to tell whether a thrombin trajectory was generated under physiological (pH 7.4) or acidotic pH (for example, pH 7.0) conditions just by looking at its maximum slope value? To investigate this possibility in the context of intersubject variability in the LETS group, we estimated the overlaps between the parameter distributions for different pH values (Fig. 6) using the Bhattacharyya coefficients (Table 3). Surprisingly, maximum slope was inferior to other parameters in its discriminative capacity. Indeed, the maximum slope distributions for pH 7.4 and pH 7.0 overlapped (Fig. 6C, Table 3), thereby thwarting the possibility to tell whether a given maximum slope value has arisen under a physiological (pH 7.4) or acidotic (pH 7.0) condition. By contrast, the pH 7.4 and pH 7.0 distributions for CT (Fig. 6A), thrombin peak time (Fig. 6B), and prothrombin time (Fig. 6F) were fully separated (Table 3), even though thrombin peak time and prothrombin time displayed only moderate fold change magnitudes (Fig. 5). In fact, the overlaps between the maximum slope distributions at acidotic pH levels with the maximum slope distribution at physiological pH level exceeded the corresponding distribution overlaps for CT, thrombin peak time, and prothrombin time for all acidotic pH levels except 6.9 (Table 3). This effect could be understood by noticing the large spread of the fold change distribution for maximum slope (Fig. 5), which suggests that its high sensitivity to intersubject variability causes its distributions for different pH levels to overlap (Fig. 6C). This sensitivity to intersubject variability thus prevents maximum slope from being an informative indicator of acidosis in a subject population, despite its high sensitivity to acidosis in individual subjects.

DISCUSSION

It is generally known that enzymatic activity is influenced by the pH of the biochemical milieu.^22–24 Therefore, it can be expected that the phases of the complex enzymatic aspects of the blood coagulation process would be significantly affected by acidosis. Our computational modeling methodology allowed us to link the pH dependence of individual reactions in the thrombin generation network with the final end points of the study. We used the LETS data in the definition of the initial concentrations for the model and incorporated the pH dependence by adjusting the values of the model’s kinetic constants. We analyzed the model’s ability to qualitatively predict the effects of acidosis. Our results support our hypothesis that acidosis may progressively delay, and reduce the levels of, thrombin generation. Moreover, we found this combined effect to be pronounced, despite considerable intersubject variability in the LETS subject group.

The assessment of thrombin generation can be divided into 2 categories: assessment of thrombus formation (CT, thrombin peak time, and maximum slope of the thrombin trajectory) and the assessment of the quantity of thrombin generated (thrombin peak height and the AUC).¹⁸ Likewise, the TAT trajectory parameters that we used in this study are an indicator of the latency of thrombus formation as measured by onset time, activation time, and maximum slope, whereas TAT final level represents a measurement of the quantity of thrombus. Our results indicate that acidosis strongly influenced all of the above parameters except the AUC. In our analysis, acidosis acted by delaying thrombin generation, as evidenced by an increase in CT, thrombin peak time, the prothrombin time, TAT onset time, and TAT activation time, and by reducing the maximum thrombin level, as evidenced by a decrease in thrombin peak height and TAT final level. The relative insensitivity of the area under the curve to acidosis may be explained by noticing that lower rates of thrombin accumulation and the resulting lower levels of active thrombin lead to a decreased rate of thrombin inhibition by antithrombin. This, in turn, may result in a relatively wider thrombin trajectory, thereby compensating for the acidosis-induced reduction in the thrombin peak height.

Trauma-associated coagulopathy can have several causes, including plasma dilution and hypothermia. Our results suggest that the effect of acidosis on thrombin generation is similar to that expected from hemodilution.¹⁶ There is, however, a considerable difference. The maximum slope of the thrombin curve is the most sensitive parameter for both acidosis and hemodilution, and CT is the second most sensitive parameter for acidosis. In contrast, thrombin peak height is the second most sensitive parameter for hemodilution.¹⁶ Hypothermia is expected to considerably delay thrombin generation and increase the area under the thrombin trajectory, and to leave thrombin peak height and TAT final level practically unchanged.¹⁷ Thus, each of these 3 coagulopathy-inducing factors (i.e., hemodilution, hypothermia, and acidosis) is characterized by unique “signature” effects on thrombin generation. It can be anticipated that a combination of hypothermia and acidosis, similarly to a combination of hypothermia and dilution,¹⁷ would both strongly delay the onset and decrease the levels of thrombin generation.^1,3

Our results are consistent with those reported by Martini et al.,⁹ who showed that acidosis induced in an in vivo porcine model (by infusion of hydrochloric acid in lactated Ringer’s solution) delays the onset and decreases the levels of TAT generation. Further, Darlington et al.,^30,31 using a porcine model of acidosis, found that CT and prothrombin time (which, like TAT onset time, reflect the time of onset of thrombin generation) significantly increased when acidosis was induced by hydrochloric acid infusion.^30,31 In contrast, when acidosis was induced by hemorrhage/hypoventilation, it resulted in a thrombin peak height decrease, with no significant effect on the prothrombin time and CT measured via the Calibrated Automated Thrombogram (Thrombinoscope BV, Maastricht, The Netherlands).^30,31 These discrepancies between experimental results using different strategies to induce acidosis and different types of measurement assays suggest that these (and perhaps other) factors influence the observed effects of acidosis on the onset (and perhaps other aspects) of thrombus formation. This conclusion is supported by evidence obtained from human blood in vitro.¹⁰ Indeed, it was shown that acidosis induces delays in prothrombin time and the onset of thrombus formation determined using thromboelastography.¹⁰ Yet, other studies reported a lack of significant acidosis-induced changes in clotting initiation time measured by viscoelastic assays in whole human blood.^8,12 Paradoxically, Bladbjerg and Jespersen³² reported accelerated clotting initiation upon pH reduction from 7.4 to 7.0. These disparities highlight the limits of our current knowledge about acidosis and illustrate the necessity of further experimental work.

Thrombin generation assays have been proposed as an alternative to traditional laboratory tests, such as prothrombin time and partial thromboplastin time, for accurate assessment of the functional status of the blood coagulation system and diagnosis of its abnormalities.^33,34 While their utility in the specific settings of trauma and complex surgery require further studies, in this study we investigated the concept of using numerical parameters of thrombin generation to distinguish between healthy and diseased states. It is conceivable that a high sensitivity of a thrombin generation parameter based on intrasubject comparisons (i.e., its larger acidosis-induced fold change in comparison with that of the other parameters in the same subject) may lead to better diagnostic dicrimination between healthy and diseased states, because decreasing the pH would lead to large, easily detectable shifts in the parameter distribution. However, our results demonstrate that the most sensitive parameter to lowered pH, that is, the maximum slope of the thrombin curve, is also highly sensitive to intersubject variability in clotting factor composition, which leads to increased overlaps between maximum slope distributions corresponding to different pH levels. Thus, our results suggest that the best discriminating parameters for determining the impact of lowered pH on thrombin kinetics should demonstrate both a sufficiently high intrasubject sensitivity to acidosis and only moderate intersubject variability. This general principle can be applied to other coagulation measurement techniques suggested for coagulopathy diagnostics, such as thromboelastography.^35,36

There are several limitations to this study. Because our investigation strategy builds on the computational model of thrombin generation (i.e., the Hockin-Mann model),^6,19,20 our approach has the conceptual limitations of the original model. First, it primarily reflects biochemical reactions in synthetic plasma; therefore, it does not represent platelet activation kinetics and only partially represents the hemostatic proteome of human blood. Second, the model reflects a static assay that cannot be used to investigate the effects of blood flow or spatial heterogeneity on blood coagulation. Third, this is a thrombin generation model that does not account for other processes that contribute to thrombus formation, such as fibrin generation, fibrin polymerization, and fibrinolysis. Yet, the Hockin-Mann model, which reflects a frequently used in vitro setup and has been extensively validated, has demonstrated its ability to yield valuable mechanistic insights and informative predictions regarding thrombin generation kinetics.^6,18,20,37 Finally, our modeling strategy does not reproduce subtle but important phenomena associated with acidosis, such as the possible differences between specific acidosis-inducing agents and insufficiency of physiological pH restoration to fully reverse the negative impact of acidosis on blood clotting.^30,38 These questions call for separate, focused investigations and motivate the development of computational models of blood coagulation processes beyond thrombin generation.

Computational kinetic modeling has recently been described as a “thinking tool” in blood coagulation research.³⁹ The value of this tool lies in its capacity to establish a connection between our mechanistic understanding of thrombus formation and relevant end points that may reflect pathological conditions. Here, we applied this tool to obtain insights into the effects of acidosis on thrombin generation kinetics in a large group of (virtual) subjects. Our study revealed well-defined patterns that can be tested experimentally. Such experiments will facilitate evaluation of the existing understanding of acidosis and its impact on blood coagulation. The resulting knowledge will contribute to future efforts aimed at therapeutic reversal of the consequences of traumatic coagulopathy.

ACKNOWLEDGMENTS

The authors are grateful to the Editor and 2 anonymous reviewers whose comments have helped to improve the paper, and to Dr. Franklin Dexter for his comments and suggestions regarding the statistical methods used in this work.

DISCLOSURES

Name: Alexander Y. Mitrophanov, PhD.

Contribution: This author designed and conducted the study, analyzed the data, and prepared the manuscript.

Attestation: Alexander Y. Mitrophanov approved the final manuscript, attests to the integrity of the original data and the analysis reported in this manuscript, and is the archival author.

Name: Frits R. Rosendaal, MD, PhD.

Contribution: This author contributed to data collection and analysis.

Attestation: Frits R. Rosendaal approved the final manuscript.

Name: Jaques Reifman, PhD.

Contribution: This author designed the study, analyzed the data, and edited the manuscript.

Attestation: Jaques Reifman approved the final manuscript, and attests to the integrity of the original data and the analysis reported in this manuscript.

This manuscript was handled by: Charles W. Hogue, Jr., MD.

Supplementary Material

ane-121-278-s001.pdf ^{(183.2KB, pdf)}