The Neural Representation of Unexpected Uncertainty During Value-Based Decision Making

Summary

Uncertainty is an inherent property of the environment and a central feature of models of decision-making and learning. Theoretical propositions suggest that one form, unexpected uncertainty, may be used to rapidly adapt to changes in the environment, while being influenced by two other forms: risk and estimation uncertainty. While previous studies have reported neural representations of estimation uncertainty and risk, relatively little is known about unexpected uncertainty. Here, participants performed a decision-making task while undergoing functional magnetic resonance imaging (fMRI), which, in combination with a Bayesian model-based analysis, enabled each form of uncertainty to be separately measured. We found representations of unexpected uncertainty in multiple cortical areas, as well as the noradrenergic brainstem nucleus locus coeruleus. Other unique cortical regions were found to encode risk, estimation uncertainty and learning rate. Collectively, these findings support theoretical models in which several formally separable uncertainty computations determine the speed of learning.

Introduction

Both in our physical and social environment, we regularly encounter situations in which performance depends on maintaining accurate internal representations of the statistics of an unstable external environment. This is a complex task because samples from such an environment may vary in their relevance for predicting future outcomes. For example, if the statistics underlying the environment have changed, then recently acquired samples are more representative of the new environment, and should be weighted accordingly. It has been emphasized (Behrens et al., 2007; Yu and Dayan, 2005) that uncertainty may be used to the advantage of learners, allowing them to optimally weigh new data against old when updating their beliefs. One approach, which could be regarded as a form of novelty detection, suggests that learners quantify at each time point the likelihood that the environment has just changed based on the current sample (Nassar et al., 2010; Payzan-LeNestour and Bossaerts, 2011; Yu and Dayan, 2005). This quantity, termed unexpected uncertainty, can be used to flexibly modulate the weight given to new data as evidence for a change in the underlying structure of the environment varies. The computation of unexpected uncertainty is non-trivial, because improbable data samples may be attributed to a change in the statistics underlying the environment, or alternatively to the known unreliability of predictive relationships, dubbed expected uncertainty (Yu and Dayan, 2005). Importantly, the definition of unexpected uncertainty does not imply that the agent is unaware that his environment is subject to change. Instead, a data sample with high unexpected uncertainty indicates that it is surprising given the cue-outcome association acquired through sampling, even when expected uncertainty, or the known, learned unreliability of this association, is accounted for.

One form of expected uncertainty is risk, or the inherent stochasticity of the environment that remains even when the contingencies are fully known. For example, when sampling in an environment in which a reward is delivered on 50% of occasions versus one in which reward is delivered 95% of the time, risk is higher for the former. The perceptions of risk and unexpected uncertainty are antagonistic (Yu and Dayan, 2005) in the sense that when risk is high, as in the former case, changes in the environment are hard to detect and hence, unexpected uncertainty is low, whereas when risk remains low, as in the latter example, changes in the environment lead to strong increases in unexpected uncertainty.

Unexpected uncertainty is also influenced by estimation uncertainty or the imprecision of the learner's current beliefs about the environment (Chumbley et al., 2012; Frank et al., 2009; Payzan-LeNestour and Bossaerts, 2011; Prévost et al., 2011; Yoshida and Ishii, 2006), which is also referred to as second-order uncertainty (Bach et al., 2011). If beliefs are acquired through learning as opposed to instruction, this quantity decreases with sampling. When estimation uncertainty is high, improbable samples may be partially attributed to the agent's inaccurate beliefs about the structure of the environment, rather than to a change in that structure itself.

Recent behavioural work suggests that subjects' choices may indeed reflect a learning scheme that makes use of unexpected uncertainty (Nassar et al., 2010; Payzan-LeNestour and Bossaerts, 2011). In addition, recent studies tracking pupil size dynamics (Nassar et al., 2012; Preuschoff et al., 2011) demonstrated a correlation of unexpected uncertainty with phasic changes in pupil diameter. Although it has been noted (Yu, 2012) that the action of the cholinergic system also influences pupil size, this modulatory effect was attributed (Nassar et al., 2012) to the activity of the locus coeruleus (LC), a nucleus in dorsorostral pons whose neurons represent the sole source of noradrenaline to the cerebral cortices, cerebellum and hippocampus (Aston-Jones and Cohen, 2005; Moore and Bloom, 1979). Transient shifts in the activity of LC during contingency changes in a target reversal task with non-human primates (Aston-Jones et al., 1997) have also been noted; specifically a transition from the phasic mode, characterized by both relatively low baseline firing rate and high phasic responsiveness to task-relevant stimuli, to the tonic mode, characterized by both relatively high baseline firing rate and diminished phasic responsiveness to task-relevant stimuli. Finally, pharmacological activation of the noradrenergic system in rats has been found to speed behavioral adaptation to change in environmental contingencies (Devauges and Sara, 1990) while noradrenergic, and not cholinergic, deafferentation of rat medial frontal cortex has been found to impair it (McGaughy et al., 2008). These finding are consistent with the theoretical claim that signaling of unexpected uncertainty is mediated by the action of the noradrenergic modulatory system (Yu and Dayan, 2005).

Despite this accumulating behavioral and psychophysical evidence for unexpected uncertainty, to our knowledge, no study to date has directly investigated the neural substrates of unexpected uncertainty in human subjects. To that end, we present results from a study in which participants underwent functional magnetic resonance imaging (fMRI) while they played a six-armed restless bandit decision task, in which the payoff probabilities of the bandit arms changed without notice, and hence, unexpected uncertainty fluctuated constantly. To properly distinguish between changes in unexpected uncertainty and changes in the probability of a jump, or volatility (Behrens et al., 2007; Bland and Schaefer, 2012), we kept the latter constant. We applied a model-based Bayesian learning algorithm (Payzan-LeNestour and Bossaerts, 2011) to track subjects' estimates of the outcome probabilities on each arm. This algorithm provides a principled way to measure unexpected uncertainty, as well as estimation uncertainty and risk, while prescribing how they should influence the rate of learning. Given the complex interrelations between the different components of uncertainty, we included each of the uncertainty signals in our fMRI analysis to minimize potential confounds. We also controlled for changes in the learning rate, because its strong dependence on unexpected uncertainty would otherwise mean that neural activity superficially correlating with unexpected uncertainty could merely reflect generic changes in the learning rate.

We hypothesized that we would observe separately identifiable neural effects of unexpected uncertainty, estimation uncertainty and risk. We predicted that unexpected uncertainty would be encoded at the time of outcome along with the learning rate, as these signals are needed for the purpose of updating values to guide choice on the subsequent trial (Figure 1c). In particular, we aimed to test for activity pertaining to unexpected uncertainty within the noradrenergic brainstem nucleus locus coeruleus. Several studies from the neuroeconomics literature have reported neural correlates of risk during choice in insular cortex/IFG (d' Acremont et al., 2009; Huettel et al., 2005a; Preuschoff et al., 2008), but also anterior cingulate (Christopoulos et al., 2009), striatum (Hsu et al., 2005) and intraparietal sulcus (Huettel et al., 2005a). Moreover, other studies have reported activation correlating with the degree of ambiguity present in a decision-gamble (Hsu et al., 2005) or the degree of estimation uncertainty in a learning task (Bach et al., 2011; Behrens et al., 2007; Chumbley et al., 2012; Prévost et al., 2011). However, such studies have typically used discrete variations in risk and estimation uncertainty, or have limited their attention to specific brain regions, while the present task design permits full parametric variation of these signals in a naturalistic learning environment.

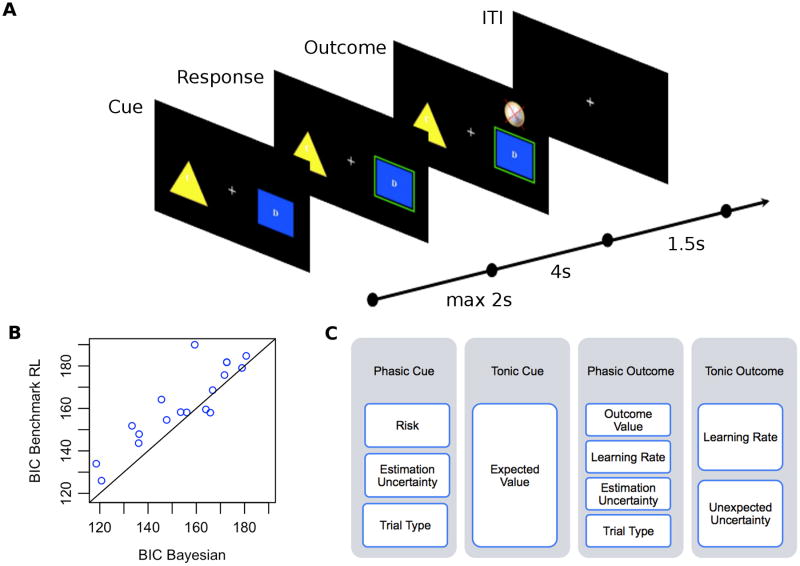
Figure 1.

(a) Illustration of task. On free choice trials participants chose one of two cue stimuli within 2s of cue onset. The chosen cue probabilistically delivered an outcome of +€1, -€1 or no change after a 4s delay. Each trial was followed by a variable length ITI. Forced choice trials were also included, on which only a single cue was available for play. (b) Bayesian Information Criterion (BIC) values of the benchmark RL model relative to the Bayesian model. Each point represents a single participant, with a point above the line indicating greater evidence for the Bayesian model. (c) Schematic of GLM used in analysis of BOLD data; columns denote onset regressors, white boxes denote parameteric modulators.

We were also interested in the role played by the limited set of cortical regions that have been shown to project directly to locus coeruleus in rats and nonhuman primates; those areas being anterior cingulate cortex, dorsomedial and dorsolateral prefrontal cortex and orbitofrontal cortex (Arnsten and Goldman-Rakic, 1984; Aston-Jones et al., 2002; Jodo et al., 1998). It has been suggested (Aston-Jones and Cohen, 2005) that descending projections from these prefrontal regions mediate the influence of important task-related information on the activity of locus coeruleus. We hypothesized that estimation uncertainty, which interacts with unexpected uncertainty to drive learning, might also be encoded in these prefrontal areas, giving it the potential to influence the computations there. Alternatively, unexpected uncertainty signals may be computed in these prefrontal regions and subsequently relayed to locus coeruleus. Given the broad distribution of our regions of interest, a whole brain imaging approach was used to test for regions yielding correlations with our uncertainty signals.

Results

Behavioral

Consistent with prior findings (Payzan-LeNestour and Bossaerts, 2011), the Bayesian learning model fit choices better than the benchmark reinforcement learning model for the majority (89%) of participants (Figure 1b). A one-tailed paired t-test on the differences of the goodness-of-fits (BIC) found the fit of the Bayesian model to be significantly better (p=0.0012; N=18). As a consistency check, we fitted the parameters across subjects by minimizing the negative log-likelihoods of the choice data pooled over all the participants. The results obtained were consistent with those reported here.

Neuroimaging

We did not observe a significant BOLD response at our significance threshold of p_FWE < 0.05 to two of our regressors of interest, namely estimation uncertainty at phasic outcome and learning rate at tonic outcome (see Table S1 in supplemental materials for coordinates of all significant activations).

Unexpected uncertainty at outcome

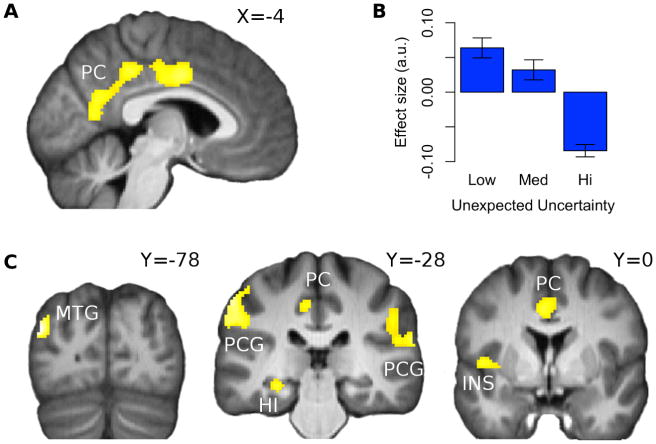
Tonic activity at outcome correlated significantly (p_FWE < 0.05) and negatively with unexpected uncertainty in posterior cingulate cortex, bilateral post-central gyrus, left middle temporal gyrus (MTG), left hippocampus (Hi), and left posterior insula (Ins). See Figure 2. In separate analyses we included unexpected uncertainty as a modulator of (i) phasic activity at outcome presentation and (ii) the 1.5 second period while the outcome was onscreen. The BOLD responses we found overlapped with those illustrated in Figure 2, but were weaker and less extensive (See Figure S3 in the supplemental materials).

Figure 2.

(a, c) SPM showing negative effects of unexpected uncertainty at time of outcome at left middle temporal gyrus [MTG; peak at x,y,z = -44,-78,26], bilateral postcentral gyrus [PCG; peaks at x,y,z = -58,-28,46; x,y,z = 54,-24,20], left hippocampus [Hi; peak at x,y,z = -28,-36,-10], posterior cingulate [PCG; peak at x,y,z = -8,-34,44], and left posterior insula [Ins; peak at x,y,z = -42,-6,2]; p_FWE < 0.05 after extent thresholding. (b) Bar plot shows average effect of low, medium and high unexpected uncertainty at left middle temporal gyrus. To generate this, trials were sorted according to their unexpected uncertainty value into one of three equal-sized bins, which were then fitted to the BOLD signal. Error bars indicate SEM.

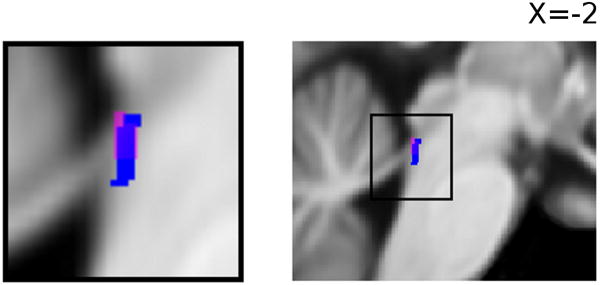
In order to test for the effect of unexpected uncertainty at locus coeruleus, we employed a preprocessing and analysis procedure optimized for this location (see Methods). We applied a small volume correction to the results of this analysis using an anatomical mask of human locus coeruleus in MNI space, generated by (Keren et al., 2009) from high resolution T1-weighted MR imaging of the brainstem. This mask served the dual purpose of correcting the activations for multiple comparisons and delineating the locus coeruleus - a nucleus that is difficult to discriminate on standard T1-weighted images. Following correction, we observed a significant (p_FWE < 0.05, SVC) negative response in left locus coeruleus (LC) to unexpected uncertainty. See Figure 3. The activity in this cluster does not extend significantly into surrounding pontine structures, and the peak of this cluster before masking matches that of the masked cluster at a strict (p_UNC < 0.0002) uncorrected threshold. (See Figure S2 in the supplemental materials for axial slices illustrating activation in pons).

Figure 3.

SPM showing negative effect of unexpected uncertainty (magenta) at locus coeruleus [LC; peak at x,y,z, = -2,-37,-17; p_UNC < 0.001], and anatomical ROI (blue) of human locus coeruleus taken from Keren et al. (2009).

Estimation uncertainty at cue

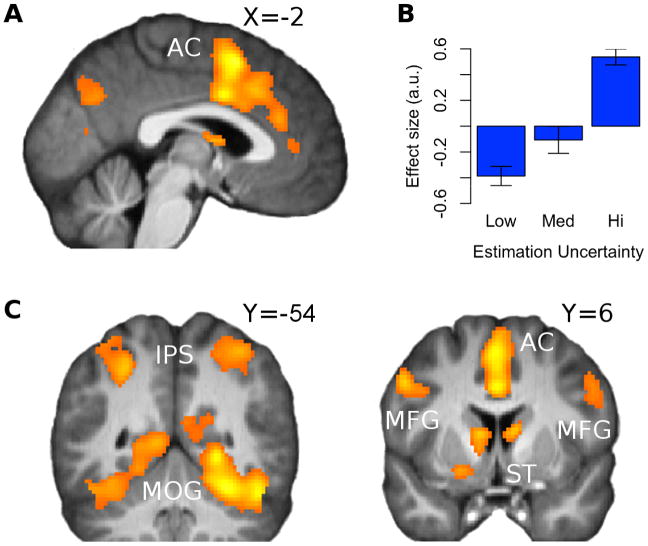
Phasic activation correlated significantly and positively (p_FWE< 0.05) with estimation uncertainty of the chosen option in intraparietal sulcus (IPS), bilateral middle occipital gyrus (MOG) with activation extending bilaterally into parahippocampal gyrus, striatum (St), bilateral middle frontal gyrus (MFG) and anterior cingulate (AC). With the exception of a cluster at right MFG [x,y,z=30,-4,64], activation increased linearly in estimation uncertainty at all regions. See Figure 4.

Figure 4.

(a, c) SPM showing effects of estimation uncertainty at time of cue at intraparietal sulcus [IPS; peak at x,y,z = -42,-40,52], bilateral middle occipital gyrus [MOG; peak at x,y,z = 38,-88,6], striatum [St; peak at x,y,z = 8,-2,12], bilateral middle frontal gyrus [MFG; peaks at x,y,z = -34,58,10; x,y,z=-52,10,38; x,y,z = 48,36,24; x,y,z = 30,-4,64], anterior cingulate [AC; peak at x,y,z = 0,10,54] and inferior frontal gyrus [x,y,z = 48,18,-4]; p_FWE < 0.05 after extent thresholding. Activation increased linearly in estimation uncertainty at all regions, with the exception of a cluster at right MFG [x,y,z = 30,-4,64]. (b) Bar plot shows the average effect of low, medium and high estimation uncertainty at anterior cingulate. To generate these plots, trials were sorted according to their estimation uncertainty value into one of three equal-sized bins, which were then fitted to the BOLD signal. Error bars indicate SEM.

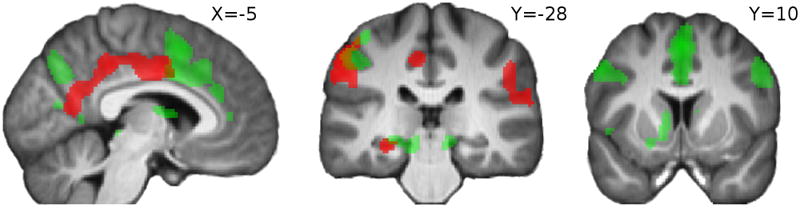
Areas correlating with unexpected and estimation uncertainty are also shown overlayed on the same figure in Figure 5 in order to illustrate more clearly the differential neural patterns associated with each.

Figure 5.

SPMs showing effects of esimation uncertainty at time of cue (green) and negative effect of unexpected uncertainty at outcome (red); p_FWE < 0.05.

Risk at cue

Phasic activation correlated significantly and positively (p_FWE < 0.05) with the risk of the chosen option at cue presentation in right inferior frontal gyrus (IFG) and bilateral lingual gyrus (LG). These activations were found to increase linearly in risk. See Figure 6. A subsequent analysis did not find a modulation by risk of activity in the period between cue and outcome presentation.

Figure 6.

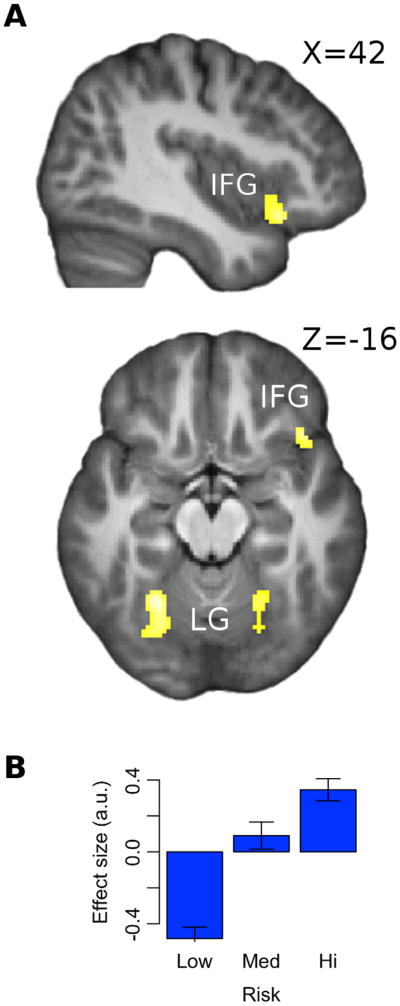
(a) SPM showing effects of risk at time of cue at right inferior frontal gyrus [IFG; peak at x,y,z = 56,16,-6] and bilateral lingual gyrus [LG; peaks at x,y,z = 18,-52,-2; x,y,z = -26,-56,-16]; shown at p_FWE < 0.05 after extent thresholding. (b) Bar plot shows the average effect of low, medium and high risk at inferior frontal gyrus. To generate this, trials were sorted according to their risk value into one of three equal-sized bins, which were then fitted to the BOLD signal. Error bars indicate SEM.

Learning rate at outcome

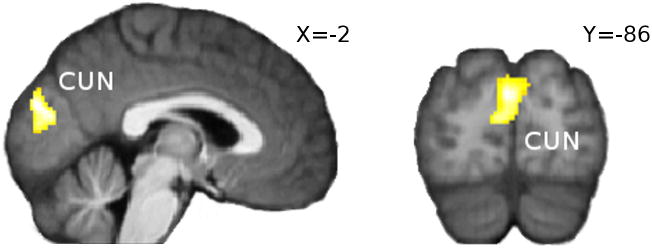
The learning rate at outcome correlated significantly (p_FWE < 0.05) with phasic BOLD activity in cuneus. See Figure 7. We also tested whether subjects' BOLD activity in this cluster was a better predictor of learning than the model-derived Bayesian learning rate, by extracting an averaged and normalized BOLD time course from the cuneal cluster and substituting it for the Bayesian learning rate in our model. The goodness of fit (log-likelihood) of this modified model was poorer than that of our original Bayesian learning model. This remained the case when the BOLD time course was high-pass filtered before inclusion in the learning model and when free parameters were included to scale and offset the BOLD time course.

Figure 7.

Effect of learning rate at time of outcome at cuneus [CUN; peak at x,y,z = -2,-86,22]; p_FWE < 0.05 after extent thresholding.

Expected value at cue

In order to confirm that our model was also capturing neural correlates of expected value as shown in many previous studies (FitzGerald et al., 2009; Hampton et al., 2006; Plassmann et al., 2007) we tested for areas correlating with the expected value of the chosen option at cue presentation. Although we did not find significant effects at our whole brain threshold, for this analysis we could motivate a focused region of interest analysis because such signals are consistently reported in the ventromedial prefrontal cortex (vmPFC) in previous studies. We therefore corrected for small volume with a sphere of 5mm centered on average coordinates of vmPFC activations from previous studies of decision-making reported by (Valentin et al., 2007). Consistent with these prior studies we found significant correlations (p_FWE < 0.05) in the vmPFC with the expected value of the chosen option.

Outcome value

Finally, we tested for regions encoding the value of the outcome. While the phasic effect of outcome value was not strong enough to survive a whole brain threshold, there is a large body of literature reporting activation of the ventral striatum in response to appetitive and aversive outcomes (Delgado et al., 2000, 2008; Elliott et al., 2000; O'Doherty et al., 2004). We therefore applied a small volume correction bilaterally at the ventral striatum using coordinates taken from (Di Martino et al., 2008) and found significant effects (p_FWE < 0.05) of outcome value at both left and right ventral striatum.

Prediction error modeling

In order to account for variance attributable to prediction error signaling (Montague et al., 1996; O'Doherty et al., 2004; Schultz et al., 1997) we ran an additional GLM which included expected value as a phasic modulator of activity at the time of cue onset and prediction error, derived from a fitted delta learning rule, as a phasic modulator at the time of outcome presentation. Using this model the results presented above remained significant at our whole-brain corrected threshold. In addition, we ran a separate analysis testing for the presence of an unsigned prediction error signal at the time of outcome presentation, but did not observe a response that survived our significance threshold.

Discussion

Uncertainty is an inherent feature of real-world interactions with the environment. While previous studies have revealed neural correlates of uncertainty, such studies have to date not determined the neural correlates of unexpected uncertainty in the brain, a metric that may mediate rapid adaptation to changes in the environment. Here, we localized brain activation correlating with unexpected uncertainty, carefully separating it from neural activity associated with risk and estimation uncertainty. We further separated this from activation arising from changes in the learning rate. By including all three uncertainty signals and learning rate in one model, we have ensured that experimental variance is appropriately assigned, thereby enabling the unique neural substrates of each to be identified.

We observed significant negative encoding of unexpected uncertainty in several brain regions at the time of outcome feedback: the posterior cingulate cortex, a region of post-central gyrus, a region of posterior insular cortex, left middle temporal gyrus and the left hippocampus. The presence of a specific unexpected uncertainty signal in a separate network of brain regions from that engaged by other forms of uncertainty provides direct experimental evidence in support of theoretical claims that this specific type of uncertainty is distinct from other forms of uncertainty such as risk and estimation uncertainty (Payzan-LeNestour and Bossaerts, 2011; Yu and Dayan, 2005). It is also important to note that a number of other studies have reported engagement of one or more of these brain areas in functions that may relate to or involve unexpected uncertainty, although this variable has not been explicitly measured in those past studies. For instance, unexpected uncertainty arguably relates to novelty detection, and the hippocampus has previously been found to play a role in classifying observations into categories of familiarity and novelty (Rutishauser et al., 2006). A recent experimental study of behavioral adaptation in humans (Collins and Koechlin, 2012) suggests that sometimes after a contextual change, humans retrieve from their memory similar contexts experienced in the past, and select the behavioral strategy that they previously learned to be optimal in that context. The unexpected uncertainty signalling we observe is unlikely to reflect the deployment of such a strategy because the unsignalled changes in our paradigm typically led to genuinely new situations.

We also observed a significant negative response to unexpected uncertainty in the noradrenergic brainstem nucleus locus coeruleus. This response was localized to locus coeruleus using an MR template of the human locus coeruleus (Keren et al., 2009), despite the decreased signal to noise ratio in the brainstem, resulting from the effects of cardiac pulsation and respiratory movement. The response is unlikely to be an artifact of motion attributable to increased physiological arousal as the BOLD effect observed is decreasing with increasing uncertainty. While previous studies have demonstrated sensitivity of neuronal responses in locus coeruleus to unexpected changes in reward contingencies in rats and nonhuman primates (Aston-Jones et al., 1997; Bouret and Sara, 2004) and have attributed phasic changes in pupil diameter in human subjects correlating with unexpected uncertainty to the action of locus coeruleus (Nassar et al., 2012; Preuschoff et al., 2011), this finding represents the first neural evidence in humans for the claim that brain regions containing noradrenergic neurons are involved in the representation of unexpected uncertainty (Yu and Dayan, 2005). The neurophysiological literature (Aston-Jones et al., 1999; Bouret and Sara, 2005) has noted a distinction between the phasic and tonic modes of LC activity. While the phasic mode has been associated with enhanced task engagement and performance, the tonic mode has been associated with increased distractibility, the shifting of attention and exploratory behavior (Aston-Jones and Cohen, 2005; Aston-Jones et al., 1994; Rajkowski et al., 1992). In addition, shifts from phasic to tonic LC mode have been noted during contingency changes in a target reversal task with non-human primates (Aston-Jones et al., 1997). In our paradigm however, a contingency change may not precipitate the shifting of attention to previously irrelevant task stimuli or engagement in exploratory behavior, as may be the case in a target-reversal paradigm; rather it is possible that the contingency change signaled by high unexpected uncertainty brings about increased engagement with the outcome stimuli for the purpose of learning, and thus recruitment of phasic LC mode, characterized by both relatively low baseline firing rate and high phasic responsiveness to task-relevant stimuli. Given that our BOLD signal appears to be more sensitive to baseline activity as opposed to phasic responsiveness, this effect could potentially manifest in the sustained decrease in BOLD signal that we observe under conditions of high unexpected uncertainty. Further investigation is required, however, to fully characterize how switching of LC mode relates to task demands and how it may influence the BOLD signal. Another key question for future research lies in determining which, if any, of the cortical representations of unexpected uncertainty observed here are dependent on efferent projection from locus coeruleus. It also remains to be seen whether unexpected uncertainty is computed in locus coeruleus or is projected to locus coeruleus from an upstream region; although it should be noted that in the current study we do not find evidence of unexpected uncertainty signaling in any of the prefrontal cortical regions suggested to project directly to locus coeruleus.

Estimation uncertainty at the time of cue presentation, as distinct from unexpected uncertainty and risk, correlated with activity in several brain structures, most notably in the anterior cingulate cortex, extending into posterior dorsomedial prefrontal cortex. The area of cingulate cortex found here overlaps with that described by Behrens et al. (2007) as correlating with volatility (i.e., the unconditional probability of a jump), as well as with estimation uncertainty. This may reflect the correlation between estimation uncertainty and volatility, as both are affected by the frequency at which the environment changes. However the two are conceptually distinct. In particular, one distinctive role of estimation uncertainty is to influence the trial-by-trial assessment of unexpected uncertainty (Payzan-LeNestour and Bossaerts, 2011).

In addition to responses at anterior cingulate and posterior dorsomedial prefrontal cortices, we observed encoding of estimation uncertainty bilaterally in dorsolateral prefrontal cortex. It should be noted that these regions, along with orbitofrontal cortex, comprise the limited set of cortical regions known to send strong direct projections to locus coeruleus in nonhuman primates (Arnsten and Goldman-Rakic, 1984; Aston-Jones et al., 2002; Jodo et al., 1998), although importantly, evidence for projections from posterior dorsomedial is weaker than that for other regions (Aston-Jones and Cohen, 2005). In the light of theoretical claims and empirical evidence that locus coeruleus may signal unexpected uncertainty through its noradrenergic efferents, allowing it to modulate the rate of learning (Nassar et al., 2012; Preuschoff et al., 2011; Yu and Dayan, 2005), our finding thus suggests a modulatory pathway through which representations of estimation uncertainty may influence unexpected uncertainty signaling. However, further research is required to directly test this hypothesis.

The presence of an estimation uncertainty signal in parts of the dorsomedial and dorsolateral frontal cortex is consistent with recent proposals that the prefrontal cortex provides estimation uncertainty signals that are used in directed exploration schemes (Badre et al., 2012; Cavanagh et al., 2012; Frank et al., 2009). In previous work (Payzan-LeNestour and Bossaerts, 2012), participants tended to direct exploration towards bandit arms with minimal level of estimation uncertainty as well as towards the options with maximal level of unexpected uncertainty. In the current learning task we did not find evidence of this directed exploration, which may be attributable to the task design; at most only two bandit arms were available for choice on each trial in the current task, versus six in the task of Payzan-LeNestour and Bossaerts (2012). Thus, although the neural representations of uncertainty we report may support such guided exploration, we could not directly examine this in the current study.

A region of inferior prefrontal lobule was also found to track estimation uncertainty. Such a finding relates to previous studies that have assessed neural correlates of ambiguity during economic decision-making (Bach et al., 2011; Huettel et al., 2006). In those studies, subjects were provided with partial information regarding the probabilities associated with obtaining a reward outcome and cannot improve their estimate of those probabilities through sampling. In contrast, in our case, estimation uncertainty reduces over trials as the number of samples of an option increases; provided there is no jump in the outcome probabilities. By showing that ambiguity and estimation uncertainty do appear to engage at least partly overlapping activations, and although findings of neural overlap must be treated with caution, our finding suggests that ambiguity and estimation uncertainty may engage similar underlying computational processes.

Now turning to risk, we found significant correlations with this variable in inferior frontal gyrus as well as a region of lingual gyrus bilaterally. Often in studies assessing risk perception, reward probabilities are presented explicitly in a descriptive fashion as opposed to being learned from trial-and-error experience (Christopoulos et al., 2009; Huettel et al., 2005b; Preuschoff et al., 2008), but see d' Acremont et al., 2009). In our task, neural representations of risk are acquired through direct sampling from a distribution of rewards as opposed to being constructed on the basis of descriptive information. In previous studies describing neural representations of risk, activity has been reported in the inferior frontal gyrus in some cases (Huettel et al., 2005b), and the adjacent anterior insula (Huettel et al., 2005b; Preuschoff et al., 2008). Other studies have reported activations in additional brain regions not found at our whole brain-corrected threshold, including the anterior cingulate cortex (Christopoulos et al., 2009) and the intraparietal sulcus. Furthermore, we found activity in the lingual gyrus, an area typically not found to correlate with risk per se, although Callan et al. (2009) found that lingual gyrus is involved in tracking resolution of uncertainty, and Bruguier et al. (2010) reported enhanced lingual gyrus activation when insider trading risk increased in a financial markets context. One potential account for the differences in activation patterns found here, is that because we are modeling other uncertainty components at the same time and therefore accounting for confounding variance, this confers a greater sensitivity to uncover signals specifically pertaining to risk on the present study, as opposed to those confounding variables. Furthermore, given that risk needs to be learned in our task, putative differences between neural systems involved in descriptive versus experiential learning may account partially for involvement of distinct brain areas to those found in studies on risk representations emerging from descriptive tasks.

Finally, we observed activity in cuneus correlating with the learning rate. Previous studies on the neurobiological bases of choice under uncertainty also reported cuneus activation (Huettel et al., 2005a; Schlund and Ortu, 2010; Volz et al., 2003), but the activation was not linked to parametric changes in the level of uncertainty or to changes in the learning rate induced by changes in uncertainty. One study by (Haruno et al., 2004) using an index of changes in behavior following reinforcement that could reflect in part learning rate, found activation correlating with cuneus activity. More generally, the cuneus has been identified in numerous studies as playing a role in visual attention and in orienting to stimuli in the environment (Carter et al., 1995; Corbetta, 1998; Hahn et al., 2006; Le et al., 1998; Talsma et al., 2010). Our finding may therefore reflect the modulation of visual attention in line with the rate of learning toward a particular stimulus. While the present study involved the presentation of stimuli exclusively in the visual domain, in future it would be informative to use cue stimuli in other modalities, such as the auditory domain, in order to ascertain whether brain systems involved in auditory attention are involved in setting the learning rate.

In conclusion, the present study goes substantially beyond previous studies on uncertainty representations by using a model-based fMRI procedure in combination with a Bayesian computational model to establish that each of three unique forms of uncertainty is encoded in the brain and depends on unique neural substrates. More specifically, we have identified, for the first time, specific regions that are involved in implementing unexpected uncertainty in the brain, centered on posterior cingulate, parietal cortex and the hippocampus, as well as the noradrenergic brainstem nucleus, locus coeruleus. This provides support for the theoretical proposal that unexpected uncertainty drives learning in unstable reward environments. We have also observed estimation uncertainty signals in prefrontal regions known to project directly to locus coeruleus, suggesting a neural pathway by which estimation uncertainty may modulate the noradrenergic representation of unexpected uncertainty, as required by our Bayesian learning algorithm. Our findings therefore demonstrate that the human brain has the capacity to disentangle uncertainty into its various components, here, risk, estimation uncertainty, or unexpected uncertainty. The resulting signals affect the learning rate differentially and optimally, in line with Bayesian learning.

Experimental Procedures

Procedures

Eighteen healthy young adults (mean age 22.5 years, standard deviation 2.81 years; 9 males) participated in our neuroimaging study. The imaging data from one female subject was discarded due to distortions. All participants provided written informed consent. The study was approved by the Research Ethics Committee of the School of Psychology at Trinity College Dublin.

Participants were directed to watch online instructions for the task before the experimental session¹. These instructions told participants that they would be performing a demanding decision task, described the task and stated that the experiment did not involve deception. Upon arrival in the lab, participants again watched the online instructions, after which they completed a multiple-choice questionnaire that checked their understanding of the task. Participants were also briefed on the payment procedure, including the fact that payment would be sensitive to task performance. Participants were told that they would complete four sessions of the task; one training session outside the MRI scanner and three experimental sessions inside the scanner. All participants acknowledged their understanding and acceptance of these procedures. Subsequently, participants completed the training session of the task outside the scanner, comprising 158 trials and lasting fifteen minutes. After a ten-minute break, participants performed the three in-scanner sessions of the task, each lasting approximately seventeen minutes. On average, participants completed 188 trials during the scanning runs. Participants received the accumulated outcomes from the four runs of the task minus an amount that was fixed before the session, but revealed to the subject only after the task was completed. This was intended to prevent well-established wealth effects from occurring during the task.

Task and Stimuli

The task (see Figure 1a) was an adaptation of a restless bandit task introduced in (Payzan-LeNestour and Bossaerts, 2011) and was presented using JAVA. Arm pairs were drawn from a selection of three yellow and three blue arms of differing shapes. On free-choice trials participants could choose between two displayed arms. On randomly interleaved forced-choice trials, only one arm was displayed for choice. Free choice trials comprised 95% of trials in the training session outside the scanner and 75% of trials in the scanner. This design was chosen to minimize potential confounding factors in our analysis of the neuroimaging data, because it allowed us to control for activations specific to the evaluation of non-chosen alternatives. Participants had 2s to indicate their choice and were penalized by €1 for each late or incorrect response. Four seconds after choice, the chosen arm probabilistically delivered a monetary gain (+€1), a monetary loss (-€1), or nothing. This outcome was displayed for 1.5s. Participants were not informed of the outcome probabilities of each arm. An inter-trial interval with a duration drawn from a uniform distribution with a minimum of 0.5s and a maximum of 14.5s followed each trial.

The outcome probabilities of the arms jumped (changed) regularly, without notice. Participants were informed that this would occur because previous work (Payzan-LeNestour and Bossaerts, 2011) suggests that without providing this information, subjects do not report detecting changes in contingencies. Participants were told that yellow arms had a higher jump probability than the blue but were not told the jump probabilities, which were 1/4 and 1/16 respectively. Participants were also informed that if the outcome probabilities had jumped for one arm, then they had jumped for all arms of the same color.

The yellow and blue groups each contained a high, a medium and a low risk arm, where risk refers to the entropy of the outcome probabilities of a arm. High-risk arms always had probability distributions with maximal entropy (1), meaning that the probabilities of its three outcome were equal. The low-risk, low entropy (0.5) arms had a single high probability outcome but the identity of this outcome changed with each jump in the probabilities. The medium-risk arm had entropy of 0.75. Participants were not told the risk levels of the arms but were told that the arms' risk levels were fixed across the task. Thus, when a jump occurred, the three outcome probabilities simply permuted within each arm.

Imaging Procedures

Magnetic resonance imaging was carried out with a Philips Achieva 3T scanner with an eight-channel SENSE (sensitivity encoding) head coil. T2*-weighted echo-planar volumes with BOLD (blood oxygen level dependent) contrast were acquired at a 30 degree angle to the anterior commissure-posterior commissure line, to attenuate signal dropout at the orbitofrontal cortex (Deichmann et al., 2003). Thirty-nine ascending slices were acquired in each volume, with an in-plane resolution of 3.5×3.5mm, and slice thickness of 3.85mm [TR: 2000ms; TE: 30ms; FOV: 224×224×150.15mm; matrix 64×64]. Data was acquired in three sessions, each comprising 520 volumes. Whole-brain high-resolution T1-weighted structural scans (voxel size: 0.9×0.9×0.9mm) were also acquired for each subject. To account for physiological fluctuations, subjects' cardiac and respiratory signals were recorded with a pulse oximeter and a pressure sensor placed on the umbilical region. Due to a technical problem, cardiac and respiratory information could not be collected from two subjects.

Behavioral Modeling

Choice was modeled using the softmax choice rule, which has been shown to capture exploration in restless multi-armed bandits (Daw et al., 2006). As inputs, the softmax choice rule uses differences in the estimated values of the available arms on each trial. We assume that these values are learned with a model-based Bayesian updating scheme. The Bayesian model used in this study is described in detail in (Payzan-LeNestour and Bossaerts, 2011) and for brevity is not reproduced here². According to this model, the decision maker uses the structure of our restless multi-armed bandit task to predict trial-by-trial outcomes for all options. Specifically, the decision maker adjusted the learning rate as a function of the strength of evidence in favor of a jump in a trial (the unexpected uncertainty). Our model-based Bayesian approach has the advantage of producing an explicit learning rate, unlike alternative Bayesian procedures. It has also been shown to fit choices well in our earlier study ((Payzan-LeNestour and Bossaerts, 2011) where participants had access to all six arms on every trial.

In order to check the goodness of fit of our Bayesian learning scheme, we benchmarked it against the fit of a simple reinforcement-learning (RL) model, using a Rescorla-Wagner update rule (Rescorla and Wagner, 1972). In the benchmark RL model, the estimated value of the chosen bandit was updated based on the reward prediction error (difference between outcome and predicted outcome values) and a constant learning rate. While the learning rate remained constant for a given arm, we allowed for differences across yellow (more volatile) and blue (less volatile) arms, in accordance with recent evidence that humans set different learning rates depending on jump frequency or volatility (Behrens et al., 2007). We also tried a learning approach whereby the learning rate changes proportionally with the size of the reward prediction error (Pearce and Hall, 1980) but this model performed more poorly and was discarded.

Both the Bayesian and benchmark RL models were fitted to participants' choices in the three runs in the scanner (141 free-choice trials) using maximum likelihood estimation. Estimated parameters were allowed to vary across participants. Only one parameter was needed to fit the Bayesian learning model, namely, the exploration intensity (temperature) of the softmax choice rule. In the case of the benchmark RL rule, two learning rates (one for each arm color group) were estimated, as well as the exploration intensity of the softmax choice rule. For each model we report the Bayesian Information Criterion (BIC), a model evaluation criterion that corrects the negative log-likelihoods for the number of free parameters.

fMRI Preprocessing

All image processing and analysis was performed using SPM5 (Wellcome Department of Imaging Neuroscience, Institute of Neurology, London, UK; available at http://www.fil.ion.ucl.ac.uk/spm). EPI images were slice-time corrected to TR/2 and realigned to the first volume. Each participant's T1-weighted structural image was co-registered with their mean EPI image and normalized to a standard T1 MNI template. The EPI images were then normalized using the same transformation, resampled to a voxel size of 2mm isotropic, smoothed with a Gaussian kernel (FWHM: 8mm) and high-pass filtered (128s).

In order to test for task-related BOLD signal at locus coeruleus, we adopted a specialized preprocessing and analysis procedure designed to mitigate difficulties arising from the size and position of locus coeruleus. Only results reported in LC were obtained using this procedure. The conventional normalization procedure in SPM5 seeks an optimal whole-brain deformation using a limited number of degrees of freedom. However, achieving a global optimum can come at the cost of regional accuracy, and as a consequence BOLD effects in small structures such as locus coeruleus may be underestimated or misattributed to neighboring regions; particularly if extensive Gaussian blurring is applied to the data. We therefore employed a two-stage normalization procedure designed to maximize intersubject registration, which followed the slice-timing and realignment steps described above. The first stage of this procedure comprised a whole-brain diffeomorphic normalization of the functional and anatomical data into MNI space using the DARTEL algorithm (Ashburner, 2007), which is not limited by a small number of degrees of freedom and is thus better at estimating local deformations than both conventional normalization in SPM, and regional weighting techniques (Yassa and Stark, 2009). This procedure resampled the functional data to a voxel size of 2mm isotropic and incorporated smoothing with a 1mm FWHM kernel. This minimal smoothing was employed in order to avoid aliasing of data. The second stage of the procedure was an ROI alignment (ROI-AL) (Yassa and Stark, 2009) procedure using a diffeomorphic implementation (Vercauteren et al., 2007) of Thirion's (Thirion, 1998) demons alignment algorithm in the MedINRIA software package (Version 1.9.0, ASCLEPIOS Research Team, France). Firstly, each subject's brainstem was manually delineated on his/her DARTEL-normalized anatomical scan. The ventral boundary of this ROI was set at the last axial slice on which the nodulus of the cerebellum was visible in the fourth ventricle, while the dorsal boundary was set on the most superior slice on which the crural cistern was visible. Our brainstem ROIs were then registered with the brainstem ROI of a single subject. The resulting registered brainstem ROIs were then averaged in SPM5 with ImCalc to create a first model. Subsequently, the original brainstem ROIs were registered with this model and the newly registered brainstem ROIs were averaged to create a second model. We repeated these two steps three more times to generate a more accurate model. The individual displacement fields resulting from the last iteration of this process were then applied to each subject's DARTEL-normalized functional and anatomical scans. The functional data was high-pass filtered (128s) before entering the statistical analysis.

fMRI StatisticalAnalysis

We analyzed the BOLD data using a parametric GLM. This GLM included parametric regressors constructed from trial-by-trial estimates of the learning rate and the three uncertainty signals obtained from the Bayesian learning model (see Figure S1 in supplemental materials for illustrations of the temporal dynamics of these signals). In our behavioral model, unexpected uncertainty measures the likelihood that a jump has occurred, given the current observation. Risk was measured as the entropy of the mean posterior outcome probabilities. Estimation uncertainty was measured as the entropy of the posterior distribution of the outcome probabilities.

The subject-specific design matrices used in the GLM comprised four onset regressors (see Figure 1c for a summary): a stick function at the time of cue presentation (“Phasic Cue”) modulated by three parametric regressors encoding the risk and estimation uncertainty of the chosen machine, and the trial type (free choice vs. forced choice); a boxcar regressor extending from the time of cue presentation to the time of outcome presentation (“Tonic Cue”) modulated by a parametric regressor encoding the model-derived expected value of the chosen machine; a stick function at the time of outcome presentation (“Phasic Outcome”) modulated by four parametric regressors encoding the value of the outcome displayed, the learning rate, the estimation uncertainty of the chosen machine and the trial type; and a boxcar regressor extending from the time of outcome presentation to the time of cue presentation on the following trial (“Tonic Outcome”) modulated by two parametric regressors encoding the learning rate and the unexpected uncertainty value of the chosen machine. Each of our regressors was convolved with a canonical haemodynamic response function after being entered into SPM5 to generate a design matrix. Motion parameters estimated during the realignment procedure were also included as regressors of no interest.

Task-related BOLD response in pontine structures may be attenuated by periodic physiologic noise arising from respiratory motion and cardiac pulsatility. In our analysis of LC activity, we therefore included 13 additional regressors of no interest in our GLM to account for physiological fluctuations (four related to heart rate, nine related to respiration) which were estimated using the Retrospective Image Correction (RETROICOR) method (Glover et al., 2000) with data recorded during the fMRI sequences.

In order to test for a BOLD response specific to unexpected and estimation uncertainty at outcome presentation, we orthogonalized these uncertainty regressors with respect to the learning rate regressor, with which they may be correlated. Thus the learning rate regressor captured all of the common variance between learning rate and the uncertainty signals, thereby ensuring that any variance loading on the uncertainty regressors could not be accounted for as reflecting an effect of learning rate per se. It should be noted that there is a functional relationship between the current level of unexpected uncertainty and the change of the learning rate - rather than the current level of the learning rate. This change in learning rate is a deterministic function of the estimated level of unexpected uncertainty, and updates of the latter depend on the level of risk and of estimation uncertainty.

Maps of the voxel-wise parameter estimates for the parametric regressors indicate how the BOLD activity scales with the computational signals. These subject-level linear contrasts were used in a between-subjects random effects analysis testing the effect of each regressor across the group. Each participant's model fit (log-likelihood) value was adjusted for the number of choice trials they completedand included as a covariate of no interest. Unless otherwise stated, we report statistics from whole-brain analyses corrected for multiple comparisons to p_FWE < 0.05, with a cluster spatial extent threshold of 186 voxels. This threshold was calculated using a Monte Carlo simulation of activation assuming the null hypothesis, implemented using 3DFWHMX and AlphaSim (AFNI, (Cox, 1996). In our analysis of LC activity we used an anatomical mask of human locus coeruleus in MNI space created by Keren et al. (2009) to verify that BOLD effects fall within the space of the LC.

For each of the areas where activation was found to covary significantly with a computational signal, we further analyzed whether the BOLD signal increased linearly in the computational signal. We reasoned that only a linear effect of an uncertainty measure on the BOLD signal would be evidence that the area encodes the uncertainty measure, and therefore plotted the average BOLD estimates (corrected for the effect of other regressors) across subjects on trials in which the uncertainty metric was low, medium, or high (Figures 2-5, 7). These plots were generated using the rfxplot toolbox for SPM5 (Gläscher, 2009). To avoid bias because of re-use of the same data, we used a leave-one-out cross-validation procedure: the group-level random effects model was re-estimated 17 times, omitting a different subject each time. For each subject, the trials were sorted into one of three bins (bins defined at 33rd, 66th, and 100th percentile) according to the value of the uncertainty signal. We extracted BOLD signals at the coordinates of the local maximum on the group-level from which the subject was omitted that were nearest to the coordinates of the full-group maximum. The plots illustrate the average parameter estimates across subjects.