Abstract
Recent advances in technology have allowed for the measurement of dynamic processes (re-alignment, crimp, deformation, sliding), but only a limited number of studies have investigated their relationship with mechanical properties. The overall objective of this study was to investigate the role of composition, structure, and the dynamic response to load in predicting tendon mechanical properties in a multi-level fashion mimicking native hierarchical collagen structure. Multiple linear regression models were investigated to determine the relationships between composition/structure, dynamic processes, and mechanical properties. Mediation was then used to determine if dynamic processes mediated structure-function relationships. Dynamic processes were strong predictors of mechanical properties. These predictions were location-dependent, with the insertion site utilizing all four dynamic responses and the midsubstance responding primarily with fibril deformation and sliding. In addition, dynamic processes were moderately predicted by composition and structure in a regionally-dependent manner. Finally, dynamic processes were partial mediators of the relationship between composition/structure and mechanical function, and results suggested that mediation is likely shared between multiple dynamic processes. In conclusion, the mechanical properties at the midsubstance of the tendon are controlled primarily by fibril structure and this region responds to load via fibril deformation and sliding. Conversely, the mechanical function at the insertion site is controlled by many other important parameters and the region responds to load via all four dynamic mechanisms. Overall, this study presents a strong foundation on which to design future experimental and modeling efforts in order to fully understand the complex structure-function relationships present in tendon.
Keywords: hierarchical, regression, supraspinatus tendon, mechanics
1 Introduction
To enable transmission of generated muscle force to bone, tendon exhibits nonlinear biomechanical behavior with an initial “toe-region” followed by the “linear-region” of a stress-strain curve (Connizzo et al., 2013b). In addition, tendons also display viscoelastic properties identified as stress relaxation, hysteresis, and creep (Woo et al., 2000). Clinically, the ability of tendon to demonstrate these properties allows for it to both guide movement (low stiffness) and provide stability (high stiffness). Additionally, the dynamic and viscoelastic properties emphasize the ability of tendon to structurally adapt to constant or cyclical loads in order to reach biomechanical equilibrium (Einhorn et al., 2007).
Mechanical function is modulated by dynamic processes that occur at the micro- and nanoscale during mechanical loading, specifically fiber uncrimping, fiber re-alignment, fibril deformation and fibril sliding. These mechanisms are thought to reduce strain on individual fibrils during the initial response to load and ultimately to prevent irreversible damage. Uncrimping has been implicated in the non-linear behavior observed in the toe-region of the stress-strain curve (Atkinson et al., 1999; Diamant et al., 1972; Miller et al., 2012b; Woo et al., 2000). In addition, collagen fibers are also capable of shifting their orientation towards the axis of loading, called re-alignment (Lake et al., 2009, 2010; Miller et al., 2012c). Finally, macroscopic extension is enabled by deformation and sliding mechanisms that simultaneously occur between fibers and fibrils, which have been cited as contributors to viscoelastic and dynamic behavior (Rigozzi et al., 2009; Rigozzi et al., 2011; Screen et al., 2005; Szczesny and Elliott, 2014).
The contribution of these dynamic processes to the mechanical response to load is thought to be dependent on region (insertion site versus midsubstance), alluding to the significance of extracellular matrix composition and structure in these processes. This matrix, comprised predominantly of collagen type I, is organized in a hierarchical manner spanning from individual collagen fibrils to full tendon (Birk et al., 1995; Birk et al., 1997). In addition to collagen I, the extracellular matrix is composed of minor collagens, proteoglycans with their associated glycosaminoglycans (GAGs), glycolipids, and cellular material (Woo et al., 2005). These elements all play a role in tendon mechanical function. Collagen orientation promotes high strength in the direction of fiber alignment, which is dependent on the underlying organizational structure. The extrafibrillar matrix, as well as cells, may also play a role in both quasi-static and dynamic mechanical function (Dourte et al., 2012; Dunkman et al., 2013; Grant et al., 2015; Henninger et al., 2015; Rigozzi et al., 2009) via their abilities to regulate fluid flow and stiffness of the interfibrillar tissue.
Despite previous studies (Ansorge et al., 2012; Best et al., 1993; Chan et al., 1998; Danielsen and Andreassen, 1988; Derwin and Soslowsky, 1999; Freedman et al., 2015; Hansen et al., 2010a; Haut et al., 1992; Parry, 1988; Robinson et al., 2004), current explanations of load sharing are insufficient, suggesting that the mechanical behavior cannot be explained solely by composition and structure. Recent advances have allowed for the measurement of dynamic parameters, but only a limited number of studies have investigated the relationships between the dynamic processes and mechanical properties (Lake et al., 2010; Miller et al., 2012a) or composition/structure (Connizzo et al., 2013a; Miller et al., 2012a; Miller et al., 2012b). Therefore, the purpose of this study was to investigate the role of composition, structure, and the dynamic response to load in predicting tendon mechanical properties in a multi-level fashion mimicking native hierarchical collagen structure. We hypothesized that dynamic responses to load would strongly predict mechanical properties and that composition/structure would predict dynamic responses. Our second hypothesis was that dynamic processes would act as a mediator of the relationship of composition/structure to mechanical properties, mimicking the native structural hierarchy.
2 Methods
2.1 Data Collection
Data analyzed in this study was gathered in recent studies (Connizzo et al., 2016; Connizzo et al., 2015) characterizing the multi-scale properties of mature supraspinatus tendons from wild type, collagen V heterozygous and tendon/ligament-specific collagen V null mice (Table 1). Briefly, mechanical parameters were measured in a series of mechanical studies (Connizzo et al., 2015; Connizzo et al., 2013a). Collagen fiber crimp was measured using quantitative polarized light microscopy from histological sections (Miller et al., 2012b). Collagen fiber re-alignment was measured using our integrated polarized light mechanical testing setup during mechanical testing (Connizzo et al., 2015; Lake et al., 2009; Miller et al., 2012a). Collagen fibril deformation and sliding were measured using a novel AFM-based technique (Connizzo et al., 2015; Connizzo et al., 2014b). Fibril morphology was measured using image analysis software from sections processed for transmission electron microscopy (Dourte et al., 2012; Dunkman et al., 2013). Cell morphology was measured in a similar software from images of histological sections (Thomas et al., 2014). Glycosaminoglycans (unpublished data, presented in Supplemental Data) and total collagen (Connizzo et al., 2016) was quantified with the DMMB and OHP assays, respectively (Connizzo et al., 2014a). Pyridinoline crosslinks were quantified with an ELISA kit and normalized to total collagen (Bjork et al., 2012; Cortes et al., 2013; Stevenson et al., 2014). All samples were analyzed at the insertion site and midsubstance of the tissue, defined by the first and second millimeter of the tissue, respectively, from the junction of tendon to bone.
Table 1.
Parameters utilized in study
| Parameter Measured | Experimental Method | Variable Name | |
|---|---|---|---|
| Composition/Structure | Total Collagen Content | Hydroxyproline Assay | COL |
| Glycosaminoglycan (GAG) Content | Dimethylmethylene Blue Assay | GAG | |
| Pyridinoline Content | Pyridinoline Serum ELISA | PYD | |
| Cell Shape | Paraffin Histology | CellShape | |
| Cell Density | Paraffin Histology | CellDens | |
| Fibril Diameter | Electron Microscopy | FibDiam | |
| Fibril Density | Electron Microscopy | FibDens | |
| Fibril Irregularity Factor | Electron Microscopy | FIF | |
| Fibril D-Period | Atomic Force Microscopy | Dperiod | |
| Fibril D-Period Variance | Atomic Force Microscopy | InitSlid | |
| Dynamic Processes | Amount of Re-Alignment | QPLM During Mechanical Testing | ReAlignAmount |
| Strain Required to Re-Align | QPLM During Mechanical Testing | ReAlignStrain | |
| Toe Region Re-Alignment | QPLM During Mechanical Testing | ToeReAlign | |
| Linear Region Re-Alignment | QPLM During Mechanical Testing | LinearReAlign | |
| Crimp Frequency | Histology+Polarized Light Imaging | CrimpFreq | |
| Crimp Amplitude | Histology+Polarized Light Imaging | CrimpAmp | |
| Fibril Deformation (0–1% Strain) | Atomic Force Microscopy | FibDef1 | |
| Fibril Deformation (0–3% Strain) | Atomic Force Microscopy | FibDef3 | |
| Fibril Deformation (0–5% Strain) | Atomic Force Microscopy | FibDef5 | |
| Fibril Deformation (0–7% Strain) | Atomic Force Microscopy | FibDef7 | |
| Fibril Sliding (0–1% Strain) | Atomic Force Microscopy | Slide1 | |
| Fibril Sliding (0–3% Strain) | Atomic Force Microscopy | Slide3 | |
| Fibril Sliding (0–5% Strain) | Atomic Force Microscopy | Slide5 | |
| Fibril Sliding (0–7% Strain) | Atomic Force Microscopy | Slide7 | |
| Mechanical Properties | Transition Strain | Dynamic Viscoelastic Testing | TransStrain |
| Transition Stress | Dynamic Viscoelastic Testing | TransStress | |
| Toe Modulus | Dynamic Viscoelastic Testing | ToeMod | |
| Linear Modulus | Dynamic Viscoelastic Testing | LinMod | |
| Maximum Stress | Dynamic Viscoelastic Testing | MaxStress | |
| Dynamic Modulus (6% Strain, 1Hz) | Dynamic Viscoelastic Testing | DynMod6 | |
| Tangent Delta (6% Strain, 1Hz) | Dynamic Viscoelastic Testing | TanDelta6 | |
| Stress Relaxation (6% Strain) | Dynamic Viscoelastic Testing | Relax6 | |
| Cycles to Failure | Fatigue Testing | FailCycle | |
| Peak Cyclic Strain (50% Fatigue Life) | Fatigue Testing | CycStrain50 | |
| Tangent Stiffness (50% Fatigue Life) | Fatigue Testing | TanStiff50 | |
| Hysteresis (50% Fatigue Life) | Fatigue Testing | Hyst50 | |
| Laxity (50% Fatigue Life) | Fatigue Testing | Lax50 | |
Note: Pyridinoline content was normalized to total collagen; QPLM = quantitative polarized light microscopy; Dynamic parameters were measured at 3 frequencies and 3 strain levels but only the values at 6% strain and 10 Hz were used in this study since results were similar across strains and across frequencies. Similarly, fatigue parameters were measured at multiple points during fatigue life but only the values at 50% fatigue life were used in the statistical studies since results were similar throughout fatigue life.
Statistical linear regression was performed on the data using each animal’s tissue as individual data points. To determine the sample size for multiple regression analysis, an a priori power analysis was performed based on 15 predictors (the largest number of predictors planned in the study) with an alpha set at 0.05, an anticipated R-squared of 0.8 and a desired statistical power of 0.8. The R2 was chosen based on an assumption that this study would better predict mechanical parameters than previous multiple regression analyses performed in our lab (Ansorge et al., 2012; Robinson et al., 2004). Based on this analysis, it was determined that a sample size of 16 tendons was sufficient, but a sample size of 20 tendons was used to account for experimental error and to remain conservative.
The regression analysis was “blind” to mouse genotype, allowing for the hypotheses to be tested by determining how variances in parameters affect mechanical properties, regardless of how those variances were achieved. The transgenic groups ensured a distribution of properties in addition to those achieved with normal biological variation. Bilateral samples from each mouse were analyzed to maximize the number of parameters measured from a single animal. However, it was not possible to obtain values for every dependent and independent parameter from a single specimen. To overcome and investigate this limitation, we performed all analyses on two data sets as a sensitivity analysis: (1) the complete data set (87% overall missing values), and a (2) ‘compact’ data set, in which the experimental data was compressed into 20 specimens (32% overall missing values). Imputation was performed on both data sets using the fully conditional specification method with 10 iterations for five imputations (White et al., 2011). Both data sets lead to the same overall conclusions so presented here are the results from the complete data set only. The results for the ‘compact’ data can be found in Supplemental Data for completeness and to further support the approach presented.
2.2 Multiple Regression Analysis
Summary statistics of all variables were examined to ensure that assumptions for linear regression analysis were met (Supplemental Data). This study consisted of three sets of defined variables: (1) dependent variables (mechanical properties), (2) dynamic processes (re-alignment, crimp, fibril deformation, fibril sliding), and (3) composition and structure (cell morphology, fibril morphology, initial d-period and variance, extracellular matrix composition). Pearson correlation coefficients were used to determine univariate relationships between predictor variables with significance set at p<0.05.
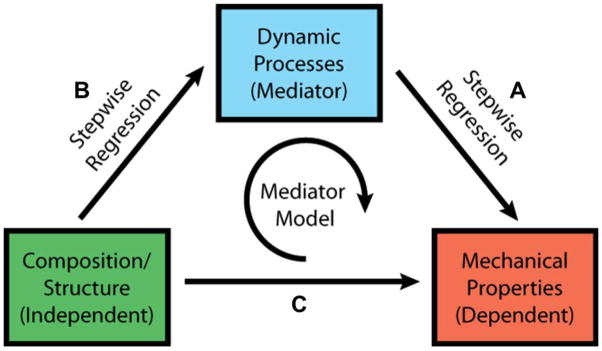
Multiple linear regression models were used to quantify the relationship: (A) between mechanical properties and dynamic processes, and (B) between composition/structure and dynamic processes (Fig. 1). The relationship between mechanical properties and composition/structure (C) was also determined to compare results with previous findings in the literature (Supplemental Data). A series of stepwise regression models using least-square estimation with forward elimination were used to predict these relationships. Variables were included in the model if they significantly improved the model via an F test with significance set at p<0.05.
Figure 1.
Model schematic depicting regression analyses. Stepwise linear regressions were performed between (A) dynamic process and mechanical properties and (B) composition/structure and dynamic processes. Regression between (C) composition/structure and mechanical properties was also performed and can be found in Supplemental Data. Mediator modeling was then used to determine if the dynamic processes mediate the relationships between composition/structure and mechanical properties.
2.3 Mediator Modeling
Mediator models have recently been used in a variety of fields to explain the relationship between correlated parameters (Baron and Kenny, 1986; Huang and Pan, 2015; Tripp et al., 2015; Wright and DeKemper, 2015). Traditional mediator models make several assumptions in addition to all of the standard assumptions of the general linear model, such as the independence of measured parameters and the lack of significant correlation between the independent variable and the mediator. In addition, this analysis was performed on imputed data (predicted values), which homogenizes the variance in the data. Nevertheless, this method tests the causal hypothesis that a third parameter, called the mediator, is contributing to the relationship between the independent and dependent variables and is capable of measuring the strength of that mediation. In other words, the mediator explains how or why a relationship exists between the independent and dependent variable. For all of the regression models that displayed strong relationships (R2>0.5), multiple mediator models were analyzed by defining all significant contributors of regression A as the mediators and the most important contributor of regression B as the independent variable (Hayes, 2013). This study only investigated a single independent variable for each dependent variable, although future studies should focus on investigating more complex models featuring multiple independent variables. Partial mediation was determined by comparing the difference between the mediated path and the direct path (Baron and Kenny, 1986). Significance was determined using the Sobel method (MacKinnon et al., 2002) with significance set at p<0.05.
3 Results
3.1 Correlations Between Independent Variables
Moderate to strong correlations between independent variables are displayed in Table 2. In both regions, fibril diameter and fibril density were strongly correlated. At the insertion site, pyridinoline (PYD) content was positively correlated with glycosaminoglycan (GAG) content and fibril irregularity (FIF). Fibril density was also positively correlated with cell density. At the midsubstance, fibril diameter was also positively correlated with PYD and FIF. FIF was also negatively correlated with fibril density. There were no significant correlations between any of the dynamic parameters.
Table 2.
Independent Variable Correlations
| Independent Variables | r | p | ||
|---|---|---|---|---|
| INS | FibDiam | FibDens | −0.83 | <0.0001 |
| FibDens | CellDens | 0.54 | <0.0001 | |
| PYD | GAG | 0.58 | <0.0001 | |
| FIF | PYD | 0.61 | <0.0001 | |
| MID | FibDiam | FibDens | −0.91 | <0.0001 |
| FibDiam | PYD | 0.57 | <0.0001 | |
| FIF | FibDiam | 0.58 | <0.0001 | |
| FIF | FIbDens | −0.51 | <0.0001 | |
Note: Moderate to strong observed correlations shown. r = Pearson correlation coefficient; p = correlation significance.
3.2 Regression of Mechanical Parameters on Dynamic Processes
Results from Regression A are presented in Table 3 and key findings will be discussed in the text that follows. Dynamic parameters (re-alignment, crimp, deformation, sliding) were strong predictors of mechanical properties, with R2 values reaching as high as 0.89. Tangent stiffness was the strongest predicted mechanical parameter in both regions. Transition strain and stress, as well as peak cyclic strain, cycles to failure, and laxity were the weakest predicted mechanical parameters in both regions, with all parameters having an R2 value less than 0.50. For complete transparency and reader interpretation, results from all regression models are shown in Table 3. However, it is important to note that major conclusions should only be drawn from the ‘strong’ relationships, those with R2 values greater than 0.50. At the insertion site, mechanical parameters were well predicted by linear combinations of all four dynamic parameters, with fibril sliding and deformation making the largest contributions. Crimp was a positive predictors of mechanical properties. The amount of re-alignment was also a positive predictor of mechanical properties and a negative predictor of viscoelastic properties (stress relaxation, tangent delta). Fibril deformation at 1% and 5% applied strain were positive predictors of mechanics while deformation at 3% and 7% strain did not predict any parameter strongly. Fibril sliding was a strong positive predictor at 1% strain and a strong negative predictor at 3% and 5% strain.
Table 3.
Mechanical Properties Regressed on Dynamic Processes
| Dependent Variable | R2 | Re-Alignment | Crimp | Deformation | Sliding | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S | RA | TR | LR | F | A | 1% | 3% | 5% | 7% | 1% | 3% | 5% | 7% | |||
| INSERTION | Transition Strain | 0.11 | P | N | N | N | ||||||||||
| Transition Stress | 0.32 | N | P | P | N | |||||||||||
| Toe Modulus | 0.57 | N | P | P | P | P | P | P | N | |||||||
| Linear Modulus | 0.65 | P | P | P | P | P | P | P | N | P | ||||||
| Max Stress | 0.72 | P | P | P | P | P | P | P | N | N | ||||||
| Dynamic Modulus | 0.55 | N | P | P | P | P | P | N | ||||||||
| Tangent Delta | 0.53 | N | N | N | N | N | N | N | P | |||||||
| Stress Relaxation | 0.59 | N | N | N | N | N | N | N | P | |||||||
| Cycles to Failure | 0.49 | P | P | P | P | P | N | |||||||||
| Peak Cyclic Strain | 0.11 | P | N | |||||||||||||
| Tangent Stiffness | 0.82 | P | P | P | P | P | P | P | P | N | N | |||||
| Hysteresis | 0.59 | P | P | P | P | P | N | N | ||||||||
| Laxity | 0.08 | P | ||||||||||||||
| MIDSUBSTANCE | Transition Strain | 0.27 | P | N | P | N | ||||||||||
| Transition Stress | 0.32 | P | N | P | N | P | N | N | ||||||||
| Toe Modulus | 0.61 | P | P | N | N | N | ||||||||||
| Linear Modulus | 0.61 | N | N | P | P | P | N | N | N | N | ||||||
| Max Stress | 0.82 | P | N | P | N | P | P | P | N | P | N | N | ||||
| Dynamic Modulus | 0.61 | P | N | N | N | P | N | P | N | |||||||
| Tangent Delta | 0.57 | P | N | N | P | N | N | P | P | |||||||
| Stress Relaxation | 0.73 | N | P | N | P | N | P | P | ||||||||
| Cycles to Failure | 0.47 | N | P | N | N | N | ||||||||||
| Peak Cyclic Strain | 0.14 | N | N | N | P | |||||||||||
| Tangent Stiffness | 0.89 | P | N | P | P | P | P | N | N | |||||||
| Hysteresis | 0.61 | P | P | P | N | N | N | |||||||||
| Laxity | 0.10 | N | P | N | ||||||||||||
|
| ||||||||||||||||
Note: S = ReAlignStrain, RA = ReAlignAmount, TR = ToeReAlign, LR = LinearReAlign, F = CrimpFreq, A = CrimpAmp; R2 = correlation coefficient of model; P = positive predictor, N = negative predictor; Darkness of color represents the importance of the contribution of each predictor to the overall model.
In contrast, the midsubstance mechanical parameters were best predicted by fibril deformation, with sliding and re-alignment playing more minor roles. Crimp amplitude and frequency were weak, negative predictors of mechanics. The strain required to fully re-align was a positive predictor of mechanical properties while the amount of re-alignment was not strongly predictive. Fibril deformation was a strong predictor of mechanics with the contribution increasing with strain level. Deformation from 1–5% strain was a positive predictor of mechanics while deformation at 7% strain was a negative predictor. Finally, fibril sliding was a positive predictor at 1% strain and a negative predictor at 3–7% strain.
3.3 Regression of Dynamic Processes on Composition and Structure
Results from Regression B are presented in Table 4 and will be discussed in the text that follows. Dynamic properties were moderately predicted by parameters of composition and structure, with R2 values reaching 0.69. Fibril deformation and sliding were the best predicted parameters, while realignment and crimp were only moderately predicted. The strain required to re-align and 7% fibril deformation were the weakest predicted variables at the insertion, while re-alignment (total and toe region), crimp amplitude and fibril sliding at 3% strain were weakest at the midsubstance (R2 values below 0.25). Results from all of the regression models are shown in Table 4. However, major conclusions should only be drawn from the ‘strong’ relationships, those with R2 values greater than 0.25.
Table 4.
Dynamic Processes Regressed on Composition and Structure
| Dependent Variable | R2 | FDi | FDe | FIF | COL | GAG | PYD | CS | CD | DP | IS | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| INSERTION SITE | ReAlignStrain | 0.12 | N | P | ||||||||
| ReAlignAmount | 0.44 | P | N | P | ||||||||
| ToeReAlign | 0.19 | P | N | |||||||||
| LinearReAlign | 0.28 | P | P | N | P | |||||||
| CrimpFreq | 0.31 | N | N | |||||||||
| CrimpAmp | 0.41 | P | N | N | N | |||||||
| FibDef1 | 0.53 | P | N | N | ||||||||
| FibDef3 | 0.59 | P | P | P | N | N | ||||||
| FibDef5 | 0.33 | P | N | |||||||||
| FibDef7 | 0.05 | N | P | |||||||||
| Slide1 | 0.69 | P | P | N | N | N | N | |||||
| Slide3 | 0.49 | P | N | P | N | N | N | |||||
| Slide5 | 0.69 | P | P | P | P | N | N | N | ||||
| Slide7 | 0.51 | P | P | P | N | N | ||||||
| MIDSUBSTANCE | ReAlignStrain | 0.31 | N | |||||||||
| ReAlignAmount | 0.07 | P | N | |||||||||
| ToeReAlign | 0.07 | N | P | |||||||||
| LinearReAlign | 0.19 | N | N | P | ||||||||
| CrimpFreq | 0.15 | N | N | P | ||||||||
| CrimpAmp | 0.20 | P | P | |||||||||
| FibDef1 | 0.62 | N | N | N | P | N | N | P | ||||
| FibDef3 | 0.35 | N | N | N | N | |||||||
| FibDef5 | 0.67 | N | N | N | P | N | N | N | ||||
| FibDef7 | 0.59 | N | N | N | P | N | N | P | ||||
| Slide1 | 0.22 | P | P | P | N | |||||||
| Slide3 | 0.16 | N | P | P | ||||||||
| Slide5 | 0.50 | P | P | P | ||||||||
| Slide7 | 0.60 | P | P | P | N | P | P | N | ||||
|
| ||||||||||||
Note: INS = Insertion Site, MID = Midsubstance; FDi = FibDiam, FDe = FibDens, CS = CellShape, CD = CellDens, DP = DPeriod, IS = InitSlid; R2 = correlation coefficient of model; Darkness of color represents the importance of the contribution of each predictor to the overall model.
Many parameters at the insertion site were strongly predicted by PYD, fibril density, and initial d-period variance. PYD was a negative predictor of re-alignment, crimp and fibril deformation, but a positive predictor of fibril sliding. Fibril density was a positive predictor of all dynamic processes. Initial d-period variance was a negative predictor of re-alignment and sliding. Weaker predictors included FIF, collagen and GAG, cell shape, and initial d-period. FIF and collagen were primarily positive predictors of dynamic processes while GAG, cell shape, and initial d-period were all negative predictors.
At the midsubstance, the strongest predictors of dynamic properties were fibril morphology and initial d-period length and variance. Fibril diameter and density were negative predictors of fibril deformation and positive predictors of fibril sliding. Fibril diameter also negatively predicted the strain required to realign and re-alignment in the linear region, and positively predicted crimp amplitude. Initial d-period variance was a positive predictor of re-alignment, crimp, and fibril deformation and a negative predictor of fibril sliding. Initial d-period was a positive predictor of crimp amplitude, while negatively predicted realignment and fibril deformation. Weaker predictors included cell shape and PYD, which were negative predictors of fibril deformation and positive predictors of fibril sliding, and collagen and GAG content, which were positive predictors of fibril deformation.
3.4 Mediator Modeling
Results of mediator modeling are presented in Table 5. Dynamic processes mediated structure-function relationships in almost every mechanical parameter, although there was no case in which all of the significant predictors were mediators. On average, approximately 35% and 44% of the dynamic processes were significant mediators at the insertion site and midsubstance, respectively (Table 5). Many of the strong predictors at the insertion site were not strong mediators of the relationship between PYD and mechanical properties. In contrast, the strongest predictors at the midsubstance were strong mediators of the relationship between fibril diameter and mechanical properties.
Table 5.
Multiple mediator modeling with a single independent variable
| Dependent Variable | Independent Variable | Re-Alignment | Crimp | Deformation | Sliding | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| S | RA | TR | LR | F | A | 1% | 3% | 5% | 7% | 1% | 3% | 5% | 7% | |||
| PYD | M | M | M* | M* | ||||||||||||
| Linear Modulus | PYD | M | M* | M | M* | |||||||||||
| Dynamic Modulus | PYD | M | M* | M* | M | M | M | M* | ||||||||
| Tangent Delta | PYD | M | M* | |||||||||||||
| Max Stress | PYD | M* | M | M* | ||||||||||||
| Stress Relaxation | PYD | M* | ||||||||||||||
| Tangent Stiffness | PYD | M | M | M* | M* | M | M* | |||||||||
| Hysteresis | PYD | M* | M* | M* | ||||||||||||
| MIDSUBSTANCE | Toe Modulus | FibDiam | M* | M* | M* | |||||||||||
| Linear Modulus | FibDiam | M | M | M* | M | M | M* | |||||||||
| Dynamic Modulus | FIbDens | M | M* | M* | M | |||||||||||
| Tangent Delta | FibDiam | M | M* | M* | M | |||||||||||
| Max Stress | FibDiam | M* | M | M | M | M | M* | M* | M | |||||||
| Stress Relaxation | FibDiam | M* | M | M* | M* | M | ||||||||||
| Tangent Stiffness | FibDiam | M | M* | M* | M* | |||||||||||
| Hysteresis | FibDiam | M | M* | M* | ||||||||||||
Note: PYD = pyridinoline content, FibDiam = fibril diameter; S = ReAlignStrain, RA = ReAlignAmount, TR = ToeReAlign, LR = LinearReAlign, F = CrimpFreq, A = CrimpAmp; P = predictor, M = mediator+predictor, M* = mediator+strong predictor (top 3 predictive properties)
4 Discussion
Correlations between independent parameters revealed relationships consistent with previous studies. The strongest relationships present were those between the morphological parameters, specifically fibril diameter and fibril density, where a larger fibril diameter correlated strongly with decreased fibril density as seen previously (Michna, 1984; Sanders and Goldstein, 2001). A moderate relationship between cell density and fibril density was also demonstrated in this study, suggesting a spatial organization of cells and assembled collagen structure. Finally, there was also a relationship between PYD and fibril morphology in both regions of the tendon, alluding to the complex and simultaneous processes of fibril assembly and collagen crosslinking (Couppe et al., 2009; Hansen et al., 2010b).
Mechanical properties were strongly predicted by dynamic processes, and the contribution of each process was location-dependent. Given that the insertion site experiences the highest strains (Shaw and Benjamin, 2007), it likely utilizes re-alignment, uncrimping, and sliding in order to delay the onset of direct deformation to the fibrils/fibers. Due to the increased organization and structure at the midsubstance, this region of the tissue likely responds primarily through deformation of the fibrils and fibers themselves. In both locations, elastic properties (moduli values) had opposite predictors from viscoelastic properties, alluding to the complex interplay between fluid flow and elasticity during the dynamic response to load (Ahmadzadeh et al., 2015; Buckley et al., 2013).
Re-alignment and crimp were stronger predictors at the insertion site than in the midsubstance. Since it is well established that the insertion site is more disorganized than the midsubstance, the importance of re-alignment at the insertion site is perhaps not surprising. Interestingly, the insertion site was best predicted by the amount of re-alignment, while the midsubstance was best predicted by the strain required to re-align, which could indicate strain transfer occurring from bone to muscle. Increased disorganization at the insertion site would require more re-alignment, and therefore increased time to perform that re-alignment, delaying midsubstance loading. Crimp frequency and amplitude were also positive predictors at the insertion site. Given that initial crimp frequency and amplitude are indicative of the potential for uncrimping, this suggests a reliance on uncrimping to delay deformation and subsequent damage.
Fibril deformation was a strong predictor of mechanical function in both regions, but the timing of the contribution revealed location-dependent mechanisms. At the insertion site, fibril deformation at 1% and 5% strain were positive predictors, which agrees with previous data showing a bimodal deformation response at the insertion site (Connizzo et al., 2014b) as well as function-dependent deformation mechanisms (Miller et al., 2012d; Screen et al., 2013). In contrast, the midsubstance displayed an increasing importance of fibril deformation with the strongest contributions at 7% strain. However, deformation was a negative predictor at 7% strain, which could suggest failure occurring.
In contrast to all of the other dynamic processes, fibril sliding displayed a similar role in prediction of mechanical properties at both regions although the contribution was stronger at the insertion site. Early sliding was a positive predictor of mechanical properties at both regions, advocating for sliding to protect fibrils/fibers from deformation. In contrast, fibril sliding later in the test was a negative predictor of mechanics, possibly alluding to failure due to fibrils pulling away from each other in shear. This work is in contrast to several recent studies showing continuously increasing fibril sliding during macroscopic loading (Gupta et al., 2010; Szczesny and Elliott, 2014). However, these studies investigated the response following relaxation which could account for differences as fibrils are not able to recover in the present work (Connizzo et al., 2014b).
Dynamic processes were moderately predicted by structure and composition. PYD was a strong predictor of dynamic properties at the insertion site, as a negative predictor for re-alignment, crimp and deformation but a positive predictor of fibril sliding. While the role of collagen crosslinks in these dynamic processes has not yet been studied, increased crosslink density is thought to increase mechanical properties (Alfredo Uquillas et al., 2012; Ng et al., 2013). Our model suggests that increasing PYD reduces the dynamic response to load and thus ultimately would result in early strain on the fibrils. If increased crosslinks also increase the brittleness of collagen fibrils (Buehler, 2008), this would result in early damage or failure.
Fibril morphology was a strong predictor of dynamic function at the midsubstance only. Since mechanical properties here were strongly predicted by fibril deformation, this is expected. Interestingly, fibril diameter and density were often both predictors in the same direction, which is in contrast to correlations found previously. While fibril diameter and fibril density are often negatively correlated, regression models suggest that isn’t the most efficient method for dynamic responses. However, while fibril deformation was predicted negatively by both and fibril sliding was predicted positively by both, perhaps these parameters are negatively correlated to balance these two responses which are crucial for mechanical function.
Given the hierarchical nature of tendon structure and therefore likely strain transfer during loading, we hypothesized that a model reflecting this innate structure would be able to better predict mechanical parameters than one directly regressing composition and structure with mechanics. If predictors of the mechanical properties were also found to be mediators of the structure-function relationship, denoted by an ‘M’ or M*’ in Table 5, this implied that the dynamic process explains the relationship between the independent and dependent parameter. For example, fibril deformation at the midsubstance was a strong mediator, indicating that fibril diameter is related to mechanical function due to fibril deformation. In general, the dynamic processes were mediators of the relationship between composition/structure and mechanical function, confirming our hypothesis. However, since we only analyzed relationships between a single independent parameter and each mechanical property, some of the dynamic processes that predict mechanics may mediate relationships with other compositional/structural parameters. It is also likely that mediation of these relationships is shared by many of the dynamic processes, particularly at the insertion site where all of these processes contribute significantly to mechanical function. The use of complex multi-mediator and multi-independent variable models would be necessary to fully explain these relationships.
While all of the assumptions of linear regression were met prior to analyses, it should be noted that there are several possible limitations that may exist with multiple regression analyses. First, inclusion of strongly correlated independent parameters could lead to false conclusions from regression modeling due to the possibility of multi-collinearity in the data. Therefore, it is important to use caution when drawing conclusions from these models. However, this possibility would only affect Regression B in our study as there were no correlations found between any of the dynamic processes used as independent parameters for Regression A and despite these correlations, our regression models did not exhibit multi-collinearity and therefore all of the assumptions for linear regression were met. It should also be noted that the complete data set was designed with a large amount of missing data, an inherent and unavoidable limitation. To address this limitation, the data was analyzed in two ways (‘complete’ and ‘compact’) as a sensitivity analysis of our conclusions. The data presented in the tables and text are analyses of the ‘complete’ dataset, however all of the conclusions presented in this work were also present in the ‘compact’ dataset, instilling confidence in the analyses that were performed (Supplemental Data). Nevertheless, while the imputed datasets in this study appeared to be efficient in capturing the real distribution of the data based on summary statistics, imputation can have unintended effects on interpretation of the analysis, such as the homogenization of the data, misrepresentation of the experimental data due to selection of imputed values from a normal distribution, and specific biases based on the imputation method, which must be considered.
Additionally, although a large number of parameters were measured in this study, there are still important properties that were not measured here. For example, initial crimp morphology is present in this analysis but uncrimping was not measured. Similarly there are a number of additional compositional elements that were not measured and could contribute to mechanical function, most notably elastin and fibrillins (Boregowda et al., 2008; Grant et al., 2013; Grant et al., 2015; Henninger et al., 2015), as well as other non-enzymatic and enzymatic collagen crosslinks (Hanada et al., 2014; Marturano et al., 2014; Takaluoma et al., 2007). Furthermore, while these studies separated the insertion site and midsubstance of the tissue as separate samples for simplicity, it should be noted that the locations are part of a continuously changing gradient of properties and that our analyses likely represent the extremes of this gradient.
In conclusion, the mechanical properties at the midsubstance of the tendon are controlled primarily by fibril structure and this region responds to load via fibril deformation and sliding, which we hypothesize would be similar to organized tendons such as tail or flexor tendons. Conversely, the mechanical function at the insertion site is more complicated, as it is controlled by many other important parameters and the region responds to load via all four dynamic mechanisms. Overall, this study presents a strong foundation on which to design future experimental and modeling efforts in order to fully understand the complex structure-function relationships in tendon.
Supplementary Material
Footnotes
All authors were fully involved in the study and preparation of this manuscript and the material within has not been and will not be submitted for publication elsewhere.
5 Conflict of Interest Statement
There are no known conflicts of interest associated with this publication or any of its authors and there has been no significant financial support for this work that could have influenced its outcome.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Ahmadzadeh H, Freedman BR, Connizzo BK, Soslowsky LJ, Shenoy VB. Micromechanical poroelastic finite element and shear-lag models of tendon predict large strain dependent Poisson’s ratios and fluid expulsion under tensile loading. Acta Biomater. 2015 doi: 10.1016/j.actbio.2015.04.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Alfredo Uquillas J, Kishore V, Akkus O. Genipin crosslinking elevates the strength of electrochemically aligned collagen to the level of tendons. J Mech Behav Biomed Mater. 2012;15:176–189. doi: 10.1016/j.jmbbm.2012.06.012. [DOI] [PubMed] [Google Scholar]
- Ansorge HL, Adams S, Jawad AF, Birk DE, Soslowsky LJ. Mechanical property changes during neonatal development and healing using a multiple regression model. J Biomech. 2012;45:1288–1292. doi: 10.1016/j.jbiomech.2012.01.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Atkinson TS, Ewers BJ, Haut RC. The tensile and stress relaxation responses of human patellar tendon varies with specimen cross-sectional area. J Biomech. 1999;32:907–914. doi: 10.1016/s0021-9290(99)00089-5. [DOI] [PubMed] [Google Scholar]
- Baron RM, Kenny DA. The moderator-mediator variable distinction in social psychological research: conceptual, strategic, and statistical considerations. J Pers Soc Psychol. 1986;51:1173–1182. doi: 10.1037//0022-3514.51.6.1173. [DOI] [PubMed] [Google Scholar]
- Best TM, Collins A, Lilly EG, Seaber AV, Goldner R, Murrell GA. Achilles tendon healing: a correlation between functional and mechanical performance in the rat. J Orthop Res. 1993;11:897–906. doi: 10.1002/jor.1100110617. [DOI] [PubMed] [Google Scholar]
- Birk DE, Nurminskaya MV, Zycband EI. Collagen fibrillogenesis in situ: fibril segments undergo post-depositional modifications resulting in linear and lateral growth during matrix development. Dev Dyn. 1995;202:229–243. doi: 10.1002/aja.1002020303. [DOI] [PubMed] [Google Scholar]
- Birk DE, Zycband EI, Woodruff S, Winkelmann DA, Trelstad RL. Collagen fibrillogenesis in situ: fibril segments become long fibrils as the developing tendon matures. Dev Dyn. 1997;208:291–298. doi: 10.1002/(SICI)1097-0177(199703)208:3<291::AID-AJA1>3.0.CO;2-D. [DOI] [PubMed] [Google Scholar]
- Bjork JW, Meier LA, Johnson SL, Syedain ZH, Tranquillo RT. Hypoxic culture and insulin yield improvements to fibrin-based engineered tissue. Tissue Eng Part A. 2012;18:785–795. doi: 10.1089/ten.tea.2011.0017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Boregowda R, Paul E, White J, Ritty TM. Bone and soft connective tissue alterations result from loss of fibrillin-2 expression. Matrix Biol. 2008;27:661–666. doi: 10.1016/j.matbio.2008.09.579. [DOI] [PubMed] [Google Scholar]
- Buckley MR, Sarver JJ, Freedman BR, Soslowsky LJ. The dynamics of collagen uncrimping and lateral contraction in tendon and the effect of ionic concentration. J Biomech. 2013;46:2242–2249. doi: 10.1016/j.jbiomech.2013.06.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buehler MJ. Nanomechanics of collagen fibrils under varying cross-link densities: atomistic and continuum studies. J Mech Behav Biomed Mater. 2008;1:59–67. doi: 10.1016/j.jmbbm.2007.04.001. [DOI] [PubMed] [Google Scholar]
- Chan BP, Fu SC, Qin L, Rolf C, Chan KM. Pyridinoline in relation to ultimate stress of the patellar tendon during healing: an animal study. J Orthop Res. 1998;16:597–603. doi: 10.1002/jor.1100160512. [DOI] [PubMed] [Google Scholar]
- Connizzo BK, Adams SM, Adams T, Birk DE, Soslowsky LJ. Collagen V expression is crucial in regional development of the supraspinatus tendon. Review at Journal of Orthopaedic Research. 2016 doi: 10.1002/jor.23246. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connizzo BK, Bhatt PR, Liechty KW, Soslowsky LJ. Diabetes alters mechanical properties and collagen fiber re-alignment in multiple mouse tendons. Ann Biomed Eng. 2014a;42:1880–1888. doi: 10.1007/s10439-014-1031-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connizzo BK, Han L, Birk DE, Soslowsky LJ. Collagen V-heterozygous and -null supraspinatus tendons exhibit altered dynamic mechanical behavior at multiple hierarchical scales. Royal Society Interface Focus. 2015 doi: 10.1098/rsfs.2015.0043. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connizzo BK, Sarver JJ, Han L, Soslowsky LJ. In situ fibril stretch and sliding is location-dependent in mouse supraspinatus tendons. J Biomech. 2014b;47:3794–3798. doi: 10.1016/j.jbiomech.2014.10.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connizzo BK, Sarver JJ, Iozzo RV, Birk DE, Soslowsky LJ. Effect of age and proteoglycan deficiency on collagen fiber re-alignment and mechanical properties in mouse supraspinatus tendon. J Biomech Eng. 2013a;135:021019. doi: 10.1115/1.4023234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connizzo BK, Yannascoli SM, Soslowsky LJ. Structure-function relationships of postnatal tendon development: a parallel to healing. Matrix Biol. 2013b;32:106–116. doi: 10.1016/j.matbio.2013.01.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cortes DH, Han WM, Smith LJ, Elliott DM. Mechanical properties of the extra-fibrillar matrix of human annulus fibrosus are location and age dependent. J Orthop Res. 2013;31:1725–1732. doi: 10.1002/jor.22430. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Couppe C, Hansen P, Kongsgaard M, Kovanen V, Suetta C, Aagaard P, Kjaer M, Magnusson SP. Mechanical properties and collagen cross-linking of the patellar tendon in old and young men. J Appl Physiol (1985) 2009;107:880–886. doi: 10.1152/japplphysiol.00291.2009. [DOI] [PubMed] [Google Scholar]
- Danielsen CC, Andreassen TT. Mechanical properties of rat tail tendon in relation to proximal-distal sampling position and age. J Biomech. 1988;21:207–212. doi: 10.1016/0021-9290(88)90171-6. [DOI] [PubMed] [Google Scholar]
- Derwin KA, Soslowsky LJ. A quantitative investigation of structure-function relationships in a tendon fascicle model. J Biomech Eng. 1999;121:598–604. doi: 10.1115/1.2800859. [DOI] [PubMed] [Google Scholar]
- Diamant J, Keller A, Baer E, Litt M, Arridge RG. Collagen; ultrastructure and its relation to mechanical properties as a function of ageing. Proc R Soc Lond B Biol Sci. 1972;180:293–315. doi: 10.1098/rspb.1972.0019. [DOI] [PubMed] [Google Scholar]
- Dourte LM, Pathmanathan L, Jawad AF, Iozzo RV, Mienaltowski MJ, Birk DE, Soslowsky LJ. Influence of decorin on the mechanical, compositional, and structural properties of the mouse patellar tendon. J Biomech Eng. 2012;134:031005. doi: 10.1115/1.4006200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dunkman AA, Buckley MR, Mienaltowski MJ, Adams SM, Thomas SJ, Satchell L, Kumar A, Pathmanathan L, Beason DP, Iozzo RV, Birk DE, Soslowsky LJ. Decorin expression is important for age-related changes in tendon structure and mechanical properties. Matrix Biol. 2013;32:3–13. doi: 10.1016/j.matbio.2012.11.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Einhorn TA, Buckwalter JA, O’Keefe RJ American Academy of Orthopaedic, S. Orthopaedic basic science : foundations of clinical practice. American Academy of Orthopaedic Surgeons; Rosemont, IL: 2007. [Google Scholar]
- Freedman BR, Zuskov A, Sarver JJ, Buckley MR, Soslowsky LJ. Evaluating changes in tendon crimp with fatigue loading as an ex vivo structural assessment of tendon damage. J Orthop Res. 2015 doi: 10.1002/jor.22875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grant TM, Thompson MS, Urban J, Yu J. Elastic fibres are broadly distributed in tendon and highly localized around tenocytes. J Anat. 2013;222:573–579. doi: 10.1111/joa.12048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grant TM, Yapp C, Chen Q, Czernuszka JT, Thompson MS. The Mechanical, Structural, and Compositional Changes of Tendon Exposed to Elastase. Ann Biomed Eng. 2015 doi: 10.1007/s10439-015-1308-5. [DOI] [PubMed] [Google Scholar]
- Gupta HS, Seto J, Krauss S, Boesecke P, Screen HR. In situ multi-level analysis of viscoelastic deformation mechanisms in tendon collagen. J Struct Biol. 2010;169:183–191. doi: 10.1016/j.jsb.2009.10.002. [DOI] [PubMed] [Google Scholar]
- Hanada M, Takahashi M, Suzuki D, Abe M, Matsuyama Y. A biochemical study of the distribution of collagen and its crosslinks in knee ligaments and the patellar tendon. Connect Tissue Res. 2014;55:378–383. doi: 10.3109/03008207.2014.957283. [DOI] [PubMed] [Google Scholar]
- Hansen P, Haraldsson BT, Aagaard P, Kovanen V, Avery NC, Qvortrup K, Larsen JO, Krogsgaard M, Kjaer M, Peter Magnusson S. Lower strength of the human posterior patellar tendon seems unrelated to mature collagen cross-linking and fibril morphology. J Appl Physiol. 2010a;108:47–52. doi: 10.1152/japplphysiol.00944.2009. [DOI] [PubMed] [Google Scholar]
- Hansen P, Haraldsson BT, Aagaard P, Kovanen V, Avery NC, Qvortrup K, Larsen JO, Krogsgaard M, Kjaer M, Peter Magnusson S. Lower strength of the human posterior patellar tendon seems unrelated to mature collagen cross-linking and fibril morphology. J Appl Physiol (1985) 2010b;108:47–52. doi: 10.1152/japplphysiol.00944.2009. [DOI] [PubMed] [Google Scholar]
- Haut RC, Lancaster RL, DeCamp CE. Mechanical properties of the canine patellar tendon: some correlations with age and the content of collagen. J Biomech. 1992;25:163–173. doi: 10.1016/0021-9290(92)90273-4. [DOI] [PubMed] [Google Scholar]
- Hayes AF. Introduction to Mediation, Moderation, and Conditional Process Analysis: A Regression-Based Approach. Guilford Press; 2013. [Google Scholar]
- Henninger HB, Valdez WR, Scott SA, Weiss JA. Elastin governs the mechanical response of medial collateral ligament under shear and transverse tensile loading. Acta Biomater. 2015;25:304–312. doi: 10.1016/j.actbio.2015.07.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huang YT, Pan WC. Hypothesis test of mediation effect in causal mediation model with high-dimensional continuous mediators. Biometrics. 2015 doi: 10.1111/biom.12421. [DOI] [PubMed] [Google Scholar]
- Lake SP, Miller KS, Elliott DM, Soslowsky LJ. Effect of fiber distribution and realignment on the nonlinear and inhomogeneous mechanical properties of human supraspinatus tendon under longitudinal tensile loading. J Orthop Res. 2009;27:1596–1602. doi: 10.1002/jor.20938. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lake SP, Miller KS, Elliott DM, Soslowsky LJ. Tensile properties and fiber alignment of human supraspinatus tendon in the transverse direction demonstrate inhomogeneity, nonlinearity, and regional isotropy. J Biomech. 2010;43:727–732. doi: 10.1016/j.jbiomech.2009.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- MacKinnon DP, Lockwood CM, Hoffman JM, West SG, Sheets V. A comparison of methods to test mediation and other intervening variable effects. Psychol Methods. 2002;7:83–104. doi: 10.1037/1082-989x.7.1.83. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marturano JE, Xylas JF, Sridharan GV, Georgakoudi I, Kuo CK. Lysyl oxidase-mediated collagen crosslinks may be assessed as markers of functional properties of tendon tissue formation. Acta Biomater. 2014;10:1370–1379. doi: 10.1016/j.actbio.2013.11.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Michna H. Morphometric analysis of loading-induced changes in collagen-fibril populations in young tendons. Cell Tissue Res. 1984;236:465–470. doi: 10.1007/BF00214251. [DOI] [PubMed] [Google Scholar]
- Miller K, Connizzo B, Soslowsky L. Collagen Fiber Re-Alignment in a Neonatal Developmental Mouse Supraspinatus Tendon Model. Annals of Biomedical Engineering. 2012a;40:1102–1110. doi: 10.1007/s10439-011-0490-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KS, Connizzo BK, Feeney E, Tucker JJ, Soslowsky LJ. Examining differences in local collagen fiber crimp frequency throughout mechanical testing in a developmental mouse supraspinatus tendon model. J Biomech Eng. 2012b;134:041004. doi: 10.1115/1.4006538. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KS, Connizzo BK, Soslowsky LJ. Collagen fiber re-alignment in a neonatal developmental mouse supraspinatus tendon model. Ann Biomed Eng. 2012c;40:1102–1110. doi: 10.1007/s10439-011-0490-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Miller KS, Edelstein L, Connizzo BK, Soslowsky LJ. Effect of preconditioning and stress relaxation on local collagen fiber re-alignment: inhomogeneous properties of rat supraspinatus tendon. J Biomech Eng. 2012d;134:031007. doi: 10.1115/1.4006340. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ng KW, Wanivenhaus F, Chen T, Abrams VD, Torzilli PA, Warren RF, Maher SA. Differential cross-linking and radio-protective effects of genipin on mature bovine and human patella tendons. Cell Tissue Bank. 2013;14:21–32. doi: 10.1007/s10561-012-9295-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Parry DA. The molecular and fibrillar structure of collagen and its relationship to the mechanical properties of connective tissue. Biophys Chem. 1988;29:195–209. doi: 10.1016/0301-4622(88)87039-x. [DOI] [PubMed] [Google Scholar]
- Rigozzi S, Muller R, Snedeker JG. Local strain measurement reveals a varied regional dependence of tensile tendon mechanics on glycosaminoglycan content. J Biomech. 2009;42:1547–1552. doi: 10.1016/j.jbiomech.2009.03.031. [DOI] [PubMed] [Google Scholar]
- Rigozzi S, Stemmer A, Muller R, Snedeker JG. Mechanical response of individual collagen fibrils in loaded tendon as measured by atomic force microscopy. J Struct Biol. 2011;176:9–15. doi: 10.1016/j.jsb.2011.07.002. [DOI] [PubMed] [Google Scholar]
- Robinson PS, Lin TW, Jawad AF, Iozzo RV, Soslowsky LJ. Investigating tendon fascicle structure-function relationships in a transgenic-age mouse model using multiple regression models. Ann Biomed Eng. 2004;32:924–931. doi: 10.1023/b:abme.0000032455.78459.56. [DOI] [PubMed] [Google Scholar]
- Sanders JE, Goldstein BS. Collagen fibril diameters increase and fibril densities decrease in skin subjected to repetitive compressive and shear stresses. J Biomech. 2001;34:1581–1587. doi: 10.1016/s0021-9290(01)00145-2. [DOI] [PubMed] [Google Scholar]
- Screen HR, Shelton JC, Chhaya VH, Kayser MV, Bader DL, Lee DA. The influence of noncollagenous matrix components on the micromechanical environment of tendon fascicles. Ann Biomed Eng. 2005;33:1090–1099. doi: 10.1007/s10439-005-5777-9. [DOI] [PubMed] [Google Scholar]
- Screen HR, Toorani S, Shelton JC. Microstructural stress relaxation mechanics in functionally different tendons. Med Eng Phys. 2013;35:96–102. doi: 10.1016/j.medengphy.2012.04.004. [DOI] [PubMed] [Google Scholar]
- Shaw HM, Benjamin M. Structure-function relationships of entheses in relation to mechanical load and exercise. Scand J Med Sci Sports. 2007;17:303–315. doi: 10.1111/j.1600-0838.2007.00689.x. [DOI] [PubMed] [Google Scholar]
- Stevenson DA, Rudser K, Kunin-Batson A, Fung EB, Viskochil D, Shapiro E, Orchard PJ, Whitley CB, Polgreen LE. Biomarkers of bone remodeling in children with mucopolysaccharidosis types I, II, and VI. J Pediatr Rehabil Med. 2014;7:159–165. doi: 10.3233/PRM-140285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Szczesny SE, Elliott DM. Interfibrillar shear stress is the loading mechanism of collagen fibrils in tendon. Acta Biomater. 2014;10:2582–2590. doi: 10.1016/j.actbio.2014.01.032. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Takaluoma K, Hyry M, Lantto J, Sormunen R, Bank RA, Kivirikko KI, Myllyharju J, Soininen R. Tissue-specific changes in the hydroxylysine content and cross-links of collagens and alterations in fibril morphology in lysyl hydroxylase 1 knock-out mice. J Biol Chem. 2007;282:6588–6596. doi: 10.1074/jbc.M608830200. [DOI] [PubMed] [Google Scholar]
- Thomas SJ, Sarver JJ, Yannascoli SM, Tucker JJ, Kelly JDt, Ahima RS, Barbe MF, Soslowsky LJ. Effect of isolated hyperglycemia on native mechanical and biologic shoulder joint properties in a rat model. J Orthop Res. 2014;32:1464–1470. doi: 10.1002/jor.22695. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tripp JC, Meshesha LZ, Teeters JB, Pickover AM, McDevitt-Murphy ME, Murphy JG. Alcohol craving and demand mediate the relation between posttraumatic stress symptoms and alcohol-related consequences. Exp Clin Psychopharmacol. 2015;23:324–331. doi: 10.1037/pha0000040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- White IR, Royston P, Wood AM. Multiple imputation using chained equations: Issues and guidance for practice. Stat Med. 2011;30:377–399. doi: 10.1002/sim.4067. [DOI] [PubMed] [Google Scholar]
- Woo SL, Debski RE, Zeminski J, Abramowitch SD, Saw SS, Fenwick JA. Injury and repair of ligaments and tendons. Annu Rev Biomed Eng. 2000;2:83–118. doi: 10.1146/annurev.bioeng.2.1.83. [DOI] [PubMed] [Google Scholar]
- Woo SL, Thay QL, Abramowitch SD, Gilbert TW. Structure and Function of Ligaments and Tendons, Basic orthopaedic biomechanics & mechano-biology. 3. Lippincott, Williams & Wilkins; Philadelphia [u.a.]: 2005. pp. 301–342. [Google Scholar]
- Wright CL, DeKemper D. Music as a mediator between ethnicity and substance use among college students. J Ethn Subst Abuse. 2015:1–21. doi: 10.1080/15332640.2015.1022627. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.