Abstract
The hand pattern (i.e., full-cycle hand path) used during manual wheelchair propulsion is frequently classified as one of four distinct hand pattern types: arc, single loop, double loop and semicircular. Current clinical guidelines recommend the use of the semicircular pattern, which is based on advantageous levels of broad biomechanical metrics implicitly related to the demand placed on the upper extremity (e.g., lower cadence). However, an understanding of the influence of hand pattern on specific measures of upper extremity muscle demand (e.g., muscle power and stress) is needed to help make such recommendations, but these quantities are difficult and impractical to measure experimentally. The purpose of this study was to use musculoskeletal modeling and forward dynamics simulations to investigate the influence of the hand pattern used on specific measures of upper extremity muscle demand. The simulation results suggest that the double loop and semicircular patterns produce the most favorable levels of overall muscle stress and total muscle power. The double loop pattern had the lowest full-cycle and recovery-phase upper extremity demand but required high levels of muscle power during the relatively short contact phase. The semicircular pattern had the second-lowest full-cycle levels of overall muscle stress and total muscle power, and demand was more evenly distributed between the contact and recovery phases. These results suggest that in order to decrease upper extremity demand, manual wheelchair users should use either the double loop or semicircular pattern when propelling their wheelchairs at a self-selected speed on level ground.
Keywords: Forward dynamics simulation, musculoskeletal model, propulsion pattern, biomechanics
Introduction
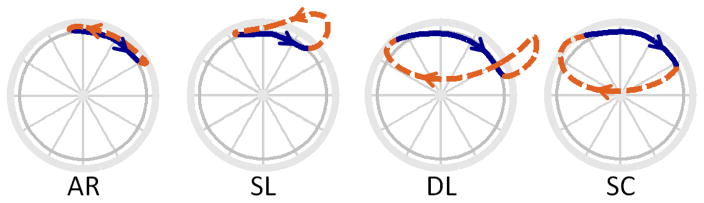
The manual wheelchair propulsion cycle can be divided into the contact phase, when mechanical power is delivered to the wheelchair via hand contact with the handrim, and the recovery phase, when the hand is repositioned in preparation for the next cycle (e.g., Kwarciak et al., 2009). During the contact phase, the hand is constrained to the arc of the handrim. However, during the recovery phase, the hand is much less constrained and can follow a number of different paths. The resulting hand patterns (i.e., full-cycle hand paths) are frequently classified into four distinct hand pattern types based on the shape of their projection onto the plane of the handrim: arc (AR), single loop (SL), double loop (DL) and semicircular (SC) (Fig. 1, e.g., Boninger et al., 2002). The hand pattern is a clinically visible indicator that can provide insight into an individual’s propulsion technique due to the close relationship between the movement of the hand and propulsion mechanics (e.g., Shimada et al., 1998).
Fig. 1.
Hand pattern definitions. The four hand pattern types are arc (AR), single loop (SL), double loop (DL) and semicircular (SC). The solid line denotes the contact phase, while the dashed line denotes the recovery phase. The arrows indicate the direction of hand motion and the direction of wheelchair propulsion is to the right.
Previous investigations have attempted to determine whether the choice of hand pattern influences the likelihood of developing upper extremity pain and injury (e.g., Boninger et al., 2002; de Groot et al., 2004; Kwarciak et al., 2012; Qi et al., 2014). Most of these studies have focused on the influence of hand pattern on broad biomechanical metrics that have been identified as risk factors (e.g., cadence, peak handrim force). Results suggest that SC produces lower cadence, larger contact percentages, larger contact angles, longer push distances and lower peak forces (e.g., Boninger et al., 2002; Kwarciak et al., 2012; Qi et al., 2014). SC also produces lower joint accelerations (Shimada et al., 1998) and results in a clearer separation between contact and recovery muscle activity timing (Qi et al., 2014). As a result, current clinical guidelines recommend the use of SC, citing many potentially advantageous levels of these biomechanical metrics (PVACSCM, 2005).
However, other hand patterns may also have favorable characteristics. Kwarciak et al. (2012) found that DL is associated with an increased contact angle, decreased cadence and decreased braking moment, leading them to recommend its use. DL and AR have also been shown to have the lowest integrated electromyography (iEMG) values among the hand patterns (Kwarciak et al., 2012). Others have found that AR is a more metabolically efficient hand pattern than SC (de Groot et al., 2004).
While previous investigations of hand pattern differences have been largely focused on broad biomechanical metrics that have been related to upper extremity demand (e.g., cadence, contact angle), a detailed investigation of how specific measures of upper extremity demand such as muscle power and stress vary across hand patterns could serve to further refine clinical propulsion technique training aimed at mitigating the negative consequences of increased shoulder loads during manual wheelchair propulsion.
Forward dynamics modeling and simulation techniques provide a powerful framework for examining the biomechanics of a task at the individual muscle level (e.g., Erdemir et al., 2007) and allow the quantification of the upper extremity demand placed on individual muscles. The purpose of this study was to use musculoskeletal modeling and forward dynamics simulations to examine the influence of the four common hand pattern types on specific measures of upper extremity muscle demand (i.e., individual muscle power and stress). Based on the previously reported biomechanical advantages (e.g., low handrim forces, low cadence, large contact angle, and large contact percentage), we expected that overall the SC simulation would also have the lowest muscle demand. These results will help provide rationale for designing propulsion training programs aimed at reducing upper extremity demand and development of overuse injuries and pain in manual wheelchair users.
Methods
Musculoskeletal model
An upper extremity musculoskeletal model and dynamic optimization framework that have been previously described in detail (e.g., Rankin et al., 2010; Rankin et al., 2011) were used in this study to generate forward dynamics simulations of manual wheelchair propulsion. The musculoskeletal model was based on the work of Holzbaur et al. (2005) and developed using SIMM (Musculographics, Inc., Santa Rosa, CA, USA). The model had six rotational degrees-of-freedom and included segments representing the trunk and right upper arm, forearm and hand. In addition to trunk lean, elbow flexion-extension and forearm pronation-supination, there were three degrees-of-freedom at the shoulder: plane-of-elevation, elevation angle and internal-external rotation (thoracohumeral angles). Scapulohumeral rhythm was defined using regression equations based on cadaver data (de Groot and Brand, 2001). Full-cycle trunk lean and contact-phase hand translations were prescribed based on experimentally-collected kinematic data. The dynamic equations-of-motion were generated using SD/FAST (Parametric Technology Corp., Needham, MA, USA). The major upper extremity muscles crossing the shoulder and elbow joints were represented by 26 Hill-type musculotendon actuators (see Slowik and Neptune, 2013) and governed by intrinsic muscle force-length-velocity and tendon force-strain relationships. Each actuator received a distinct excitation signal except the three latissimus dorsi actuators, the two sternocostal pectoralis major actuators, and the two actuators representing the lateral triceps and anconeus. Muscles within each of these groups received the same excitation signal. Muscle excitation-activation dynamics were modeled using a first order differential equation (Raasch et al., 1997) with muscle-specific activation and deactivation time constants (Happee and van der Helm, 1995; Winters and Stark, 1988). The musculotendon lengths and moment arms were determined using polynomial regression equations (Rankin and Neptune, 2012), and the product of each muscle moment arm and force was applied at the joint as a muscle moment. Passive torques were applied at the joints to represent ligaments and other passive joint structures that limit extreme joint positions (Davy and Audu, 1987).
Simulation and optimization framework
Each muscle excitation pattern was generated using a bimodal pattern defined by six parameters (e.g., Hall et al., 2011), resulting in a total of 132 optimization parameters. For each hand pattern type, the excitation parameters that produced a simulation that best emulated hand pattern subgroup-averaged experimental propulsion data (i.e., joint angle and 3D handrim force profiles; see Experimental data below) were identified using a simulated annealing optimization algorithm (Goffe et al., 1994) and an optimal tracking cost function (Neptune et al., 2001). To prevent excess co-contraction, an additional term was included in the cost function that minimized the muscle stress squared. Average power delivered to the handrim was kept constant (6 W) across simulations to allow for direct comparisons.
Experimental data
Experimental data was previously collected from 223 individuals with complete motor paraplegia while they propelled their wheelchair at a self-selected speed on a stationary ergometer that simulated level propulsion over a tile surface (e.g., Soltau et al., 2015). The subjects were recruited from outpatient clinics throughout the Rancho Los Amigos National Rehabilitation Center, and informed written consent was obtained in accordance with the governing Institutional Review Board. Further subject enrollment and inclusion criteria details are described elsewhere (Mulroy et al., 2015). The biomechanical data collection and processing procedures will be described briefly here. Subjects were allowed to acclimate until they felt comfortable, and then a ten-second trial was recorded following at least 30 seconds of propulsion to ensure near steady-state propulsion. Trunk, right side upper extremity and wheel kinematics were collected using a 4-scanner CODA motion analysis system (Charnwood Dynamics Ltd., Leicestershire, UK) with 15 active markers placed on landmarks on the body and right wheel (e.g., Lighthall-Haubert et al., 2009). Three-dimensional handrim kinetics were measured using an instrumented wheel (SmartWheel; Three Rivers Holdings, Mesa, AZ, USA).
Kinematic and kinetic data were low-pass filtered using a fourth-order zero-lag Butterworth filter with cutoff frequencies of 8 Hz and 10 Hz, respectively, in Visual3D (C-Motion, Inc., Germantown, MD, USA). Contact and recovery phases were delineated using a resultant handrim force threshold of 5 N. Contact and recovery-phase data for each cycle were time-normalized and averaged across propulsion cycles within each subject. A previously-described method (Rao et al., 1996) was used to locate the third metacarpophalangeal joint center (MCP3), and the hand pattern was defined as the average MCP3 path projected onto the plane of the handrim (e.g., Fig. 1). Hand patterns were characterized using a set of objective, quantitative parameters (see Slowik et al., 2015 for details), and this characterization was used to identify four groups of subjects that used each of the four hand pattern types. From these groups, twenty male subjects (five of each hand pattern type) were then identified such that differences between pattern-type group averages for age, time from injury, height, mass, body mass index and propulsion speed were minimized (Table 1). Mean subject data were then averaged across subjects within each pattern type group to create group-averaged hand pattern, joint angle and 3D handrim force profiles.
Table 1.
Mean values of subject and propulsion characteristics for the four hand pattern types: arc (AR), single loop (SL), double loop (DL) and semicircular (SC).
| Subject characteristics | Propulsion characteristics | ||||||||
|---|---|---|---|---|---|---|---|---|---|
|
| |||||||||
| Hand pattern type | Age (yr) | Time from injury (yr) | Height (m) | Mass (kg) | Body Mass Index (kg/m2) | Propulsion speed (m/s) | Cycle Time (s) | Contact Percentage (%) | Contact Angle (°) |
| AR | 39.4 | 9.3 | 1.77 | 77.3 | 24.97 | 0.97 | 0.95 | 45.8 | 73.2 |
| SL | 39.2 | 14.2 | 1.80 | 77.6 | 23.98 | 1.02 | 1.02 | 36.4 | 71.7 |
| DL | 32.7 | 12.9 | 1.73 | 81.1 | 26.86 | 0.97 | 1.43 | 34.7 | 86.6 |
| SC | 35.0 | 10.0 | 1.77 | 79.9 | 25.35 | 0.99 | 1.34 | 44.9 | 92.9 |
|
| |||||||||
| All 20 subjects | 36.6 | 11.6 | 1.77 | 79.0 | 25.29 | 0.99 | 1.19 | 40.5 | 81.1 |
Analysis
Three consecutive propulsion cycles were simulated for each hand pattern type, and the third cycle was analyzed to allow the simulation to reach steady-state. To assess how well each simulation tracked the experimental data, root-mean-square (RMS) differences between the simulated and experimental data were calculated. Individual muscle data at each time step were then obtained from the simulations and used to calculate specific measures of upper extremity muscle demand. Instantaneous muscle stress was calculated by dividing the instantaneous muscle force by the physiological cross-sectional area of the muscle, and time-averaged within the contact and recovery phases as well as across the full cycle. The full-cycle values were also decomposed into contributions during the contact and recovery phases, which enable additional comparisons across simulations that account for the differences in contact percentages.
Instantaneous muscle mechanical power was computed as the product of the instantaneous muscle force and velocity. Mean positive and negative power for the contact phase, recovery phase and full cycle were calculated by time-averaging the instantaneous positive and negative power, respectively. Mean total (absolute value sum) and net (linear sum) power were subsequently calculated. The full-cycle values were again decomposed into contributions from the contact and recovery phases. The individual muscle data from the 26 muscles were combined into 13 analysis groups based on a combination of anatomical location and muscle function (Table 2), with power data summed and stress data averaged within each muscle group. Overall measures of upper extremity demand were then calculated as the summed power and average stress of all 26 muscles.
Table 2.
Upper extremity muscle and group definitions.
| Muscle Group | Muscle | Compartment | Abbreviation |
|---|---|---|---|
| ADelt | Deltoid | Anterior | DELT1 |
|
|
|
||
| MDelt | Middle | DELT2 | |
|
|
|
||
| PDelt | Posterior | DELT3 | |
|
| |||
| Subsc | Subscapularis | ---------------------- | SUBSC |
|
| |||
| Supra | Supraspinatus | ---------------------- | SUPSP |
|
| |||
| Infra | Infraspinatus | ---------------------- | INFSP |
|
| |||
| Teres Minor | ---------------------- | TMIN | |
|
| |||
| PecMaj | Clavicular head | PECM1 | |
| Pectoralis major | Sternocostal head - sternum | PECM2 | |
| Sternocostal head - ribs | PECM3 | ||
|
| |||
| Coracobrachialis | ---------------------- | CORB | |
|
| |||
| Lat | Thoracic | LAT1 | |
| Latissimus dorsi | Lumbar | LAT2 | |
| Iliac | LAT3 | ||
|
| |||
| Teres Major | ---------------------- | TMAJ | |
|
| |||
| Tri | Long head | TRIlong | |
| Triceps brachii | Medial head | TRImed | |
| Lateral head | TRIlat | ||
|
| |||
| Anconeus | ---------------------- | ANC | |
|
| |||
| Bra | Brachialis | ---------------------- | BRA |
|
| |||
| Brachioradialis | ---------------------- | BRD | |
|
| |||
| Bic | Biceps brachii | Long head | BIClong |
| Short head | BICshort | ||
|
| |||
| Sup | Supinator | ---------------------- | SUP |
|
| |||
| Pro | Pronator teres | ---------------------- | PT |
|
| |||
| Pronator quadratus | ---------------------- | PQ | |
Results
Experimental data tracking
All four simulations resulted in propulsion mechanics that closely emulated the corresponding hand pattern type experimental joint kinematics and handrim forces (Table 3), with average RMS differences of 2.1° and 1.7 N, respectively. All RMS differences were well within one standard deviation of the experimental data.
Table 3.
Root-mean-square differences between simulated and experimental joint kinematics and handrim forces for the four hand pattern types: arc (AR), single loop (SL), double loop (DL) and semicircular (SC). For comparison, one standard deviation of the experimental data is provided in parentheses to indicate inter-subject variability.
| Tracking differences (simulation vs. experimental) | Simulations
|
||||
|---|---|---|---|---|---|
| AR | SL | DL | SC | ||
| Joint kinematics (degrees) | Elevation plane | 1.2 (10.3) | 1.8 (19.1) | 2.3 (13.3) | 3.3 (12.4) |
| Elevation angle | 0.7 (5.3) | 1.0 (7.3) | 0.9 (6.4) | 1.1 (8.2) | |
| Shoulder rotation | 1.0 (23.6) | 2.9 (32.4) | 2.3 (18.0) | 9.2 (26.0) | |
| Elbow flexion | 0.9 (18.5) | 0.7 (8.4) | 0.8 (8.6) | 0.8 (12.9) | |
| Pronation/supination | 4.2 (23.6) | 1.7 (12.0) | 1.2 (11.6) | 4.3 (22.5) | |
| All joints | 1.6 (16.3) | 1.6 (15.8) | 1.5 (11.6) | 3.7 (16.4) | |
|
| |||||
| Handrim forces (N) | Tangential | 0.9 (5.2) | 3.2 (3.8) | 1.0 (6.2) | 2.3 (5.5) |
| Radial | 3.3 (11.4) | 0.8 (5.8) | 1.9 (4.8) | 2.0 (10.1) | |
| Lateral | 0.7 (5.0) | 1.7 (3.0) | 1.7 (3.8) | 1.3 (4.1) | |
| All forces | 1.6 (7.2) | 1.9 (4.2) | 1.5 (4.9) | 1.9 (6.6) | |
Overall muscle power
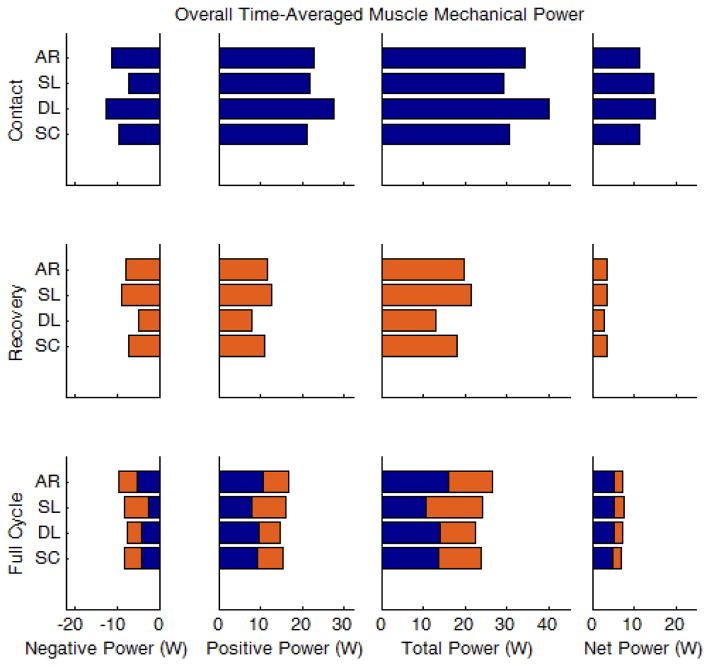
Full-cycle net muscle power was similar across hand pattern types, with the lowest power generated with SC and the highest power generated with SL (7.0 W vs. 7.6 W, Fig. 2). While contact-phase net muscle power was larger for SL and DL compared to AR and SC (14.6 W and 15.2 W vs. 11.4 W and 11.3 W, respectively), contact-phase contributions to the full-cycle net muscle power were similar across all hand pattern types (range: 5.1–5.3 W). There were larger differences in the total muscle power, with DL requiring the least full-cycle total power and AR requiring the most (22.5 W vs. 26.5 W). The contact and recovery phases had comparable amounts of negative (eccentric) muscle power. However, the contact phase consistently had greater amounts of positive (concentric) muscle power than the recovery phase. As a result, the contact phase also had consistently larger total and net muscle power than the recovery phase, although the net power was positive during both phases for all hand pattern types. While the recovery-phase contributions accounted for only a small portion of the full-cycle net power (26–30%), recovery-phase power accounted for a much larger portion of the full-cycle total power (37–57%).
Fig. 2.
Overall levels of time-averaged negative, positive, total and net power (summed across all muscles) for the four hand pattern types: arc (AR), single loop (SL), double loop (DL) and semicircular (SC). The top, middle and bottom rows correspond to the contact phase, recovery phase and full cycle, respectively. Contact and recovery-phase contributions are colored blue and orange, respectively.
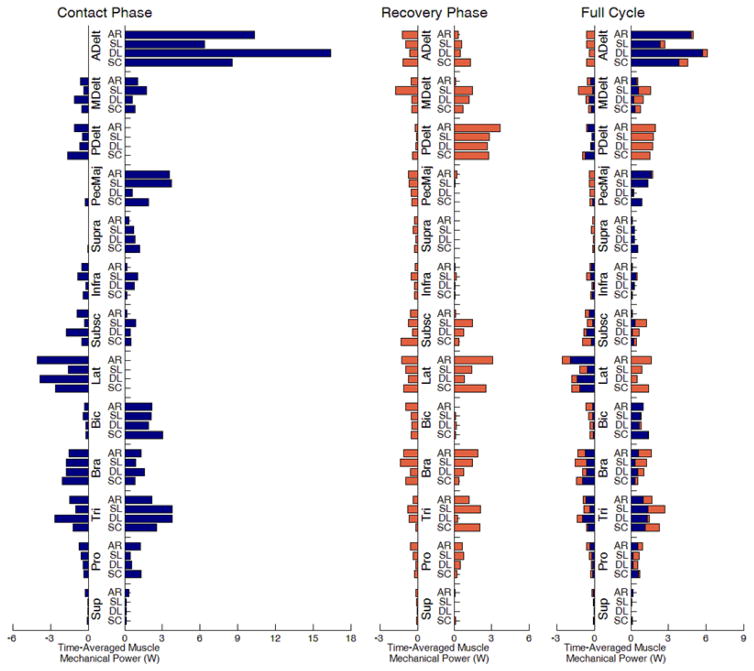
Individual muscle power
For all hand pattern types, ADelt and Tri were among the primary contributors to the full-cycle total and net muscle power (Fig. 3). The majority of this power was generated during the contact phase. Other large contributors to the full-cycle total muscle power included PDelt, Lat and Bra with AR; MDelt and Bra with SL; and Lat with SC.
Fig. 3.
Time-averaged positive and negative power generated by each muscle group for the four hand pattern types: arc (AR), single loop (SL), double loop (DL) and semicircular (SC). The left, center and right plots correspond to the contact phase, recovery phase and full cycle, respectively. Contact and recovery-phase contributions are colored blue and orange, respectively.
Comparisons between hand pattern types revealed a few differences in individual muscle power generation. Full-cycle Lat total power generation was increased with AR. Full-cycle MDelt total power generation was increased with SL, but full-cycle ADelt total power generation was decreased. Contact-phase ADelt and Tri total power generation was increased with DL, but contact-phase PecMaj and recovery-phase Lat total power generation was decreased. Total power generation was not notably higher or lower for any individual muscle group with SC relative to the other hand pattern types.
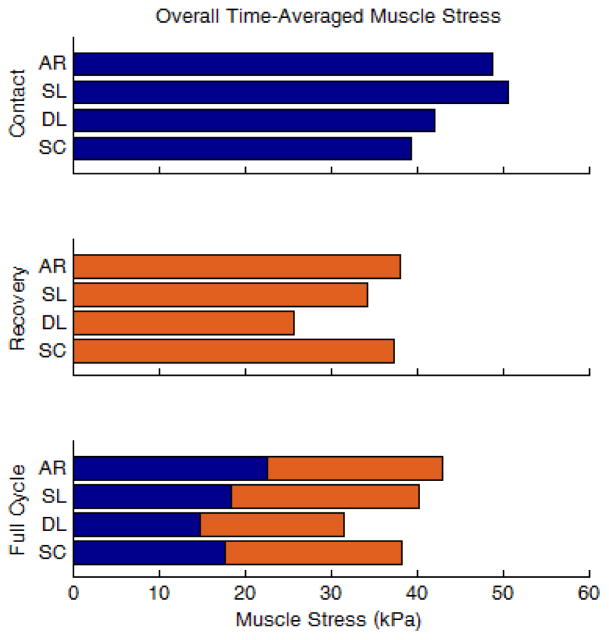
Overall muscle stress
Full-cycle muscle stress was lowest with DL and highest with AR (31.5 kPa vs. 43.0 kPa, Fig 4). Contact-phase stress was lowest with SC and highest with SL (39.4 kPa vs. 50.7 kPa). However, contact-phase contribution to the full-cycle muscle stress was lowest with DL and highest with AR (14.7 kPa vs. 22.6 kPa). Recovery-phase stress was lowest with DL and highest with AR (25.8 kPa vs. 38.0 kPa). While recovery-phase contribution to the full-cycle muscle stress was also lowest with DL, it was highest with SL (16.8 kPa vs. 21.9 kPa). Recovery-phase muscle stress was consistently lower than contact-phase muscle stress, with percent differences between contact and recovery values ranging from 5% (SC) to 48% (DL). However, the recovery phase consistently contributed approximately half of the full-cycle muscle stress (46–53%) due to the longer duration of this phase.
Fig. 4.
Overall levels of time-averaged muscle stress (averaged across all muscles) for the four hand pattern types: arc (AR), single loop (SL), double loop (DL) and semicircular (SC). The top, middle and bottom rows correspond to the contact phase, recovery phase and full cycle, respectively. Contact and recovery-phase contributions are colored blue and orange, respectively.
Individual muscle stress
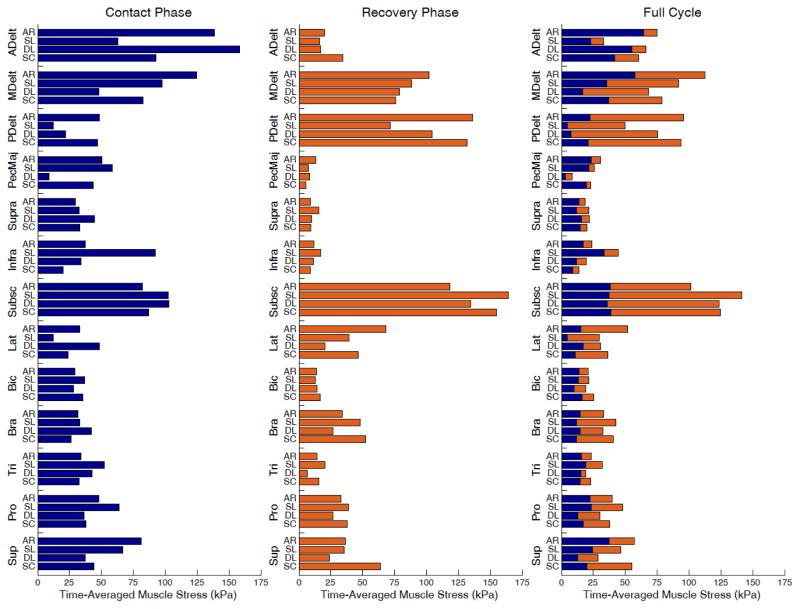
For all hand pattern types, Subsc, MDelt, PDelt and ADelt were among the muscle groups that experienced the highest full-cycle stress levels (Fig 5). The majority of the full-cycle ADelt stress was attributed to high stress during the contact phase, while the majority of the full-cycle PDelt and Subsc stresses were attributed to the high stresses during the recovery phase. The high full-cycle MDelt stress was attributed to high stresses during both phases. Other high full-cycle muscle stress values occurred in Lat and Sup with AR; Infra, Bra, Pro and Sup with SL; and Bra and Sup with SC.
Fig. 5.
Time-averaged individual muscle stress values for the four hand pattern types: arc (AR), single loop (SL), double loop (DL) and semicircular (SC). The left, center and right plots correspond to the contact phase, recovery phase and full cycle, respectively. Contact and recovery-phase contributions are colored blue and orange, respectively.
Comparisons between hand pattern types revealed a number of differences in individual muscle stress levels. AR experienced relatively high full-cycle MDelt stress due to contributions during both phases. AR also experienced high contact-phase stress from Sup and high recovery-phase stress from Lat. However, AR experienced low full-cycle stress from Subsc compared to other hand pattern types, primarily due to low stress during the recovery phase. SL experienced high full-cycle Infra stress, primarily due to the high stress during the contact phase. SL also experienced high full-cycle Subsc stress, due to high stress during the recovery phase. In addition, SL experienced high contact-phase Pro stress. However, SL experienced low full-cycle ADelt stress, primarily due to low stress during the contact phase. SL also experienced low full-cycle PDelt stress due to low stresses during both phases. In addition, SL experienced low contact-phase Lat stress. DL experienced high contact-phase ADelt and Lat stresses, but low full-cycle MDelt stress, primarily due to low stress during the contact phase. DL also experienced low full-cycle Sup stress (due to low stress during both phases), low contact-phase PecMaj stress and low recovery-phase Lat stress. SC only experienced high recovery-phase Sup stress.
Discussion
The purpose of this study was to identify the influence of wheelchair propulsion hand pattern on upper extremity muscle demand by developing forward dynamics simulations of the four distinct hand pattern types. Contrary to our expectation that the SC simulation would have the lowest muscle demand, the DL simulation exhibited lower overall levels of demand. However, the SC simulation typically had the second lowest levels, and the demand was more evenly distributed throughout the full cycle, as the DL simulation had a shorter and more demanding contact phase. In addition to these key findings, other potential differences between the four pattern types were identified in the propulsion characteristics and muscle demand measures. While the range of full-cycle total power values only spanned 4.0 W (26.5 W for AR vs. 22.5 W for DL), this represented a 16.5% difference between patterns. Furthermore, the range of full-cycle overall muscle stress values spanned 11.5 kPa (43.0 kPa for AR vs. 31.5 kPa for DL), which is a 30.9% difference. Since manual wheelchair users can generate thousands of propulsion cycles per day (e.g., Tolerico et al., 2007), the differences in these demand levels will likely accumulate over time, and thus optimizing propulsion technique to minimize the upper extremity demand will likely reduce the risk of upper extremity pain and injury (e.g., PVACSCM, 2005).
Propulsion characteristics
While the subjects were chosen such that the four hand pattern subgroups would have similar propulsion speeds (Table 1), there were differences in other propulsion characteristics that influenced the individual muscle power and stress quantities. SC had a long cycle time, large contact percentage and large contact angle (Table 1), which have all previously been suggested as favorable characteristics (e.g., PVACSCM, 2005). DL had a long cycle time and large contact angle, but a small contact percentage. AR had a large contact percentage, but a short cycle time and small contact angle. SL had a short cycle time, small contact percentage and small contact angle, which have all been suggested as unfavorable characteristics. The relative levels of these spatiotemporal variables across hand pattern types were consistent with previous studies (Boninger et al., 2002; Kwarciak et al., 2012), providing confirmation that the selected subjects appropriately represented the different hand pattern types.
Arc Pattern
Of the four hand pattern types, AR experienced the highest levels of overall upper extremity demand across the full cycle (i.e., total muscle power and muscle stress). This was primarily due to AR having the highest contributions during the contact phase, derived from both high contact-phase demand levels and a large contact percentage. However, AR did have the lowest full-cycle Subsc stress, which may reduce the risk of fatigue and injury in this rotator cuff muscle. As Subsc plays a critical role in stabilizing the shoulder (e.g., Ward et al., 2006), this may also prevent more extensive injuries. Although the most common location for a rotator cuff tear is within Supra (e.g., Akbar et al., 2010), a Supra tear and the resulting shift of demand to the other rotator cuff muscles often leads to tears in Infra and Subsc, all of which reduces the stability of the shoulder joint and greatly increases the risk of impingement in manual wheelchair users (van Drongelen et al., 2013).
Single Loop Pattern
SL experienced the second highest levels of overall upper extremity demand across the full cycle. SL had the highest recovery-phase contributions to the total power, but lowest contact-phase contributions, leading to the second highest full-cycle average total power. SL also experienced the highest contact-phase stress. However, due to its small contact percentage, it experienced only the second highest contact-phase contribution to full-cycle stress which resulted in the second highest overall full-cycle stress. SL also experienced high Infra and Subsc stress, which could increase the risk of fatigue and injury in these rotator cuff muscles. As Infra and Subsc help stabilize the shoulder (e.g., Ward et al., 2006), this could lead to more extensive injuries (e.g., rotator cuff tears and impingement).
Double Loop Pattern
Of the four hand pattern types, DL experienced the lowest levels of overall upper extremity demand across the full cycle. This was primarily due to a combination of the lowest recovery-phase demand levels and the smallest contact percentage. Despite high demand levels during the contact phase (including the highest contact-phase total power), time spent in this phase was relatively short, and as a result DL actually experienced the lowest contact-phase contribution to the full-cycle average muscle stress and only the second highest contact-phase contribution to the full-cycle power. While DL has greater ranges of motion during the recovery phase, it also has the longest recovery time (Table 1), allowing this greater motion to occur over a longer period of time. This also allows a prolonged and more gradual transition between propulsive and recovery tasks, thus reducing instantaneous muscle demand levels. The low recovery-phase demand levels for DL were consistent with previous work suggesting that using a low cadence technique could reduce muscle power requirements during the recovery phase (Rankin et al., 2012). One potential disadvantage of the DL technique is that it showed increased contact-phase ADelt power combined with decreased contact-phase PecMaj power, which could increase the risk of impingement (e.g., Burnham et al., 1993; Sharkey and Marder, 1995).
Semicircular Pattern
SC experienced the second lowest levels of overall upper extremity demand across the full cycle. SC consistently had the second lowest total power, for each individual phase and the full cycle. In addition, SC experienced the lowest contact-phase stress, but the second-highest recovery-phase stress. This led to the smallest percent difference between contact and recovery-phase stresses among the four hand pattern types, suggesting that upper extremity demand is most evenly distributed throughout the cycle when using SC. There were no individual muscles that appeared to be at a greater risk of injury during SC in comparison to the other hand pattern types.
Study limitations
A potential limitation of this study is that the experimental data was not collected overground but on a calibrated wheelchair ergometer. Ergometers and other stationary propulsion simulators do not perfectly replicate overground propulsion. However, they result in similar propulsion mechanics while providing greater control over experimental variables in a laboratory setting (Koontz et al., 2012).
In addition, the musculoskeletal model did not include the ability of the hand to produce a pure moment at the handrim because it did not include the wrist muscles and the wrist joint was fixed in the anatomical position. However, relative to shoulder and elbow moments, wrist moments are generally small (e.g., Robertson et al., 1996; Sabick et al., 2004). In addition, the influence of the fixed wrist on the other joints and study conclusions was minimized by using a consistent model across all simulations and requiring the optimized simulations to emulate the experimental joint kinematics and handrim forces.
Another potential limitation of this study is that it only examined level propulsion at a self-selected speed. Results of previous investigations suggest that people who use manual wheelchairs modify their hand pattern with changes in propulsion speed (Boninger et al., 2002; Slowik et al., 2015) and grade of incline (Richter et al., 2007; Slowik et al., 2015). Thus, future work should examine upper extremity demand during these other propulsion conditions.
Finally, only a single representative simulation was developed for each hand pattern type. This allowed the use of a computationally-intensive forward dynamics framework that included the time-dependent physiological nature of muscles, but as a result we were unable to assess the statistical significance of our identified differences. Furthermore, due to the scarcity of longitudinal studies of manual wheelchair propulsion, a threshold for clinical significance of demand levels is not yet well-defined. While these limitations should be considered when interpreting the study results, the clear differences between hand patterns support previous experimental findings that the double loop or semicircular patterns are preferred to minimize upper extremity demand and potentially prevent pain and injuries during manual wheelchair propulsion.
Summary
DL and SC produced the most favorable levels of upper extremity demand. While DL had the lowest full-cycle and recovery-phase demand values, it did require high levels of muscle power during its relatively short contact phase. The full-cycle demand levels of SC were the second-lowest, and the demand was more evenly distributed between the contact and recovery phases. These results suggest that when propelling their wheelchairs at a self-selected speed on level ground, individuals may want to consider using either the DL or SC pattern.
Acknowledgments
This study was supported by NIH Grant R01 HD049774 and a National Science Foundation Graduate Research Fellowship under Grant DGE-1110007.
Footnotes
Conflict of interest statement
The authors have no con ict of interest to declare.
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Akbar M, Balean G, Brunner M, Seyler TM, Bruckner T, Munzinger J, Grieser T, Gerner HJ, Loew M. Prevalence of rotator cuff tear in paraplegic patients compared with controls. Journal of Bone and Joint Surgery. 2010;92:23–30. doi: 10.2106/JBJS.H.01373. [DOI] [PubMed] [Google Scholar]
- Boninger ML, Souza AL, Cooper RA, Fitzgerald SG, Koontz AM, Fay BT. Propulsion patterns and pushrim biomechanics in manual wheelchair propulsion. Archives of Physical Medicine and Rehabilitation. 2002;83:718–723. doi: 10.1053/apmr.2002.32455. [DOI] [PubMed] [Google Scholar]
- Burnham RS, May L, Nelson E, Steadward R, Reid DC. Shoulder pain in wheelchair athletes. The role of muscle imbalance. The American Journal of Sports Medicine. 1993;21:238–242. doi: 10.1177/036354659302100213. [DOI] [PubMed] [Google Scholar]
- Davy DT, Audu ML. A dynamic optimization technique for predicting muscle forces in the swing phase of gait. Journal of Biomechanics. 1987;20:187–201. doi: 10.1016/0021-9290(87)90310-1. [DOI] [PubMed] [Google Scholar]
- de Groot JH, Brand R. A three-dimensional regression model of the shoulder rhythm. Clinical Biomechanics. 2001;16:735–743. doi: 10.1016/s0268-0033(01)00065-1. [DOI] [PubMed] [Google Scholar]
- de Groot S, Veeger HE, Hollander AP, van der Woude LH. Effect of wheelchair stroke pattern on mechanical efficiency. American Journal of Physical Medicine & Rehabilitation. 2004;83:640–649. doi: 10.1097/01.phm.0000133437.58810.c6. [DOI] [PubMed] [Google Scholar]
- Erdemir A, McLean S, Herzog W, van den Bogert AJ. Model-based estimation of muscle forces exerted during movements. Clinical Biomechanics. 2007;22:131–154. doi: 10.1016/j.clinbiomech.2006.09.005. [DOI] [PubMed] [Google Scholar]
- Goffe WL, Ferrier GD, Rogers J. Global Optimization of Statistical Functions With Simulated Annealing. Journal of Econometrics. 1994;60:65–99. [Google Scholar]
- Hall AL, Peterson CL, Kautz SA, Neptune RR. Relationships between muscle contributions to walking subtasks and functional walking status in persons with post-stroke hemiparesis. Clinical Biomechanics. 2011;26:509–515. doi: 10.1016/j.clinbiomech.2010.12.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Happee R, van der Helm FC. The control of shoulder muscles during goal directed movements, an inverse dynamic analysis. Journal of Biomechanics. 1995;28:1179–1191. doi: 10.1016/0021-9290(94)00181-3. [DOI] [PubMed] [Google Scholar]
- Holzbaur KR, Murray WM, Delp SL. A model of the upper extremity for simulating musculoskeletal surgery and analyzing neuromuscular control. Annals of Biomedical Engineering. 2005;33:829–840. doi: 10.1007/s10439-005-3320-7. [DOI] [PubMed] [Google Scholar]
- Koontz AM, Worobey LA, Rice IM, Collinger JL, Boninger ML. Comparison between overground and dynamometer manual wheelchair propulsion. Journal of Applied Biomechanics. 2012;28:412–419. doi: 10.1123/jab.28.4.412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kwarciak AM, Sisto SA, Yarossi M, Price R, Komaroff E, Boninger ML. Redefining the Manual Wheelchair Stroke Cycle: Identification and Impact of Nonpropulsive Pushrim Contact. Archives of Physical Medicine and Rehabilitation. 2009;90:20–26. doi: 10.1016/j.apmr.2008.07.013. [DOI] [PubMed] [Google Scholar]
- Kwarciak AM, Turner JT, Guo L, Richter WM. The effects of four different stroke patterns on manual wheelchair propulsion and upper limb muscle strain. Disability and Rehabilitation: Assistive Technology. 2012;7:459–463. doi: 10.3109/17483107.2011.650781. [DOI] [PubMed] [Google Scholar]
- Lighthall-Haubert L, Requejo PS, Mulroy SJ, Newsam CJ, Bontrager E, Gronley JK, Perry J. Comparison of shoulder muscle electromyographic activity during standard manual wheelchair and push-rim activated power assisted wheelchair propulsion in persons with complete tetraplegia. Archives of Physical Medicine and Rehabilitation. 2009;90:1904–1915. doi: 10.1016/j.apmr.2009.05.023. [DOI] [PubMed] [Google Scholar]
- Mulroy SJ, Hatchett P, Eberly VJ, Haubert LL, Conners S, Requejo PS. Shoulder Strength and Physical Activity Predictors of Shoulder Pain in People With Paraplegia From Spinal Injury: Prospective Cohort Study. Physical Therapy. 2015;95:1027–1038. doi: 10.2522/ptj.20130606. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neptune RR, Kautz SA, Zajac FE. Contributions of the individual ankle plantar flexors to support, forward progression and swing initiation during walking. Journal of Biomechanics. 2001;34:1387–1398. doi: 10.1016/s0021-9290(01)00105-1. [DOI] [PubMed] [Google Scholar]
- Paralyzed Veterans of America Consortium for Spinal Cord Medicine. Preservation of upper limb function following spinal cord injury: a clinical practice guideline for health-care professionals. Journal of Spinal Cord Medicine. 2005;28:434–470. doi: 10.1080/10790268.2005.11753844. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Qi L, Wakeling J, Grange S, Ferguson-Pell M. Patterns of Shoulder Muscle Coordination Vary Between Wheelchair Propulsion Techniques. IEEE Transactions on Neural Systems and Rehabilitation Engineering. 2014;22:559–566. doi: 10.1109/TNSRE.2013.2266136. [DOI] [PubMed] [Google Scholar]
- Raasch CC, Zajac FE, Ma B, Levine WS. Muscle coordination of maximum-speed pedaling. Journal of Biomechanics. 1997;30:595–602. doi: 10.1016/s0021-9290(96)00188-1. [DOI] [PubMed] [Google Scholar]
- Rankin JW, Kwarciak AM, Mark Richter W, Neptune RR. The influence of altering push force effectiveness on upper extremity demand during wheelchair propulsion. Journal of Biomechanics. 2010;43:2771–2779. doi: 10.1016/j.jbiomech.2010.06.020. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rankin JW, Kwarciak AM, Richter WM, Neptune RR. The influence of wheelchair propulsion technique on upper extremity muscle demand: A simulation study. Clinical Biomechanics. 2012;27:879–886. doi: 10.1016/j.clinbiomech.2012.07.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rankin JW, Neptune RR. Musculotendon lengths and moment arms for a three-dimensional upper-extremity model. Journal of Biomechanics. 2012;45:1739–1744. doi: 10.1016/j.jbiomech.2012.03.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rankin JW, Richter WM, Neptune RR. Individual muscle contributions to push and recovery subtasks during wheelchair propulsion. Journal of Biomechanics. 2011;44:1246–1252. doi: 10.1016/j.jbiomech.2011.02.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rao SS, Bontrager EL, Gronley JK, Newsam CJ, Perry J. Three-dimensional kinematics of wheelchair propulsion. IEEE Transactions on Rehabilitation Engineering. 1996;4:152–160. doi: 10.1109/86.536770. [DOI] [PubMed] [Google Scholar]
- Richter WM, Rodriguez R, Woods KR, Axelson PW. Stroke pattern and handrim biomechanics for level and uphill wheelchair propulsion at self-selected speeds. Archives of Physical Medicine and Rehabilitation. 2007;88:81–87. doi: 10.1016/j.apmr.2006.09.017. [DOI] [PubMed] [Google Scholar]
- Robertson RN, Boninger ML, Cooper RA, Shimada SD. Pushrim forces and joint kinetics during wheelchair propulsion. Archives of Physical Medicine and Rehabilitation. 1996;77:856–864. doi: 10.1016/s0003-9993(96)90270-1. [DOI] [PubMed] [Google Scholar]
- Sabick MB, Kotajarvi BR, An KN. A new method to quantify demand on the upper extremity during manual wheelchair propulsion. Archives of Physical Medicine and Rehabilitation. 2004;85:1151–1159. doi: 10.1016/j.apmr.2003.10.024. [DOI] [PubMed] [Google Scholar]
- Sharkey NA, Marder RA. The rotator cuff opposes superior translation of the humeral head. The American Journal of Sports Medicine. 1995;23:270–275. doi: 10.1177/036354659502300303. [DOI] [PubMed] [Google Scholar]
- Shimada SD, Robertson RN, Boninger ML, Cooper RA. Kinematic characterization of wheelchair propulsion. Journal of Rehabilitation Research and Development. 1998;35:210–218. [PubMed] [Google Scholar]
- Slowik JS, Neptune RR. A theoretical analysis of the influence of wheelchair seat position on upper extremity demand. Clinical Biomechanics. 2013;28:378–385. doi: 10.1016/j.clinbiomech.2013.03.004. [DOI] [PubMed] [Google Scholar]
- Slowik JS, Requejo PS, Mulroy SJ, Neptune RR. The influence of speed and grade on wheelchair propulsion hand pattern. Clinical Biomechanics. 2015 doi: 10.1016/j.clinbiomech.2015.07.007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Soltau SL, Slowik JS, Requejo PS, Mulroy SJ, Neptune RR. An Investigation of Bilateral Symmetry During Manual Wheelchair Propulsion. Frontiers in Bioengineering and Biotechnology. 2015;3:86. doi: 10.3389/fbioe.2015.00086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tolerico ML, Ding D, Cooper RA, Spaeth DM, Fitzgerald SG, Cooper R, Kelleher A, Boninger ML. Assessing mobility characteristics and activity levels of manual wheelchair users. Journal of Rehabilitation Research and Development. 2007;44:561–571. doi: 10.1682/jrrd.2006.02.0017. [DOI] [PubMed] [Google Scholar]
- van Drongelen S, Schlussel M, Arnet U, Veeger D. The influence of simulated rotator cuff tears on the risk for impingement in handbike and handrim wheelchair propulsion. Clinical Biomechanics. 2013;28:495–501. doi: 10.1016/j.clinbiomech.2013.04.007. [DOI] [PubMed] [Google Scholar]
- Ward SR, Hentzen ER, Smallwood LH, Eastlack RK, Burns KA, Fithian DC, Friden J, Lieber RL. Rotator cuff muscle architecture: implications for glenohumeral stability. Clinical Orthopaedics and Related Research. 2006;448:157–163. doi: 10.1097/01.blo.0000194680.94882.d3. [DOI] [PubMed] [Google Scholar]
- Winters JM, Stark L. Estimated mechanical properties of synergistic muscles involved in movements of a variety of human joints. Journal of Biomechanics. 1988;21:1027–1041. doi: 10.1016/0021-9290(88)90249-7. [DOI] [PubMed] [Google Scholar]