A CLINICAL METHOD FOR MAPPING AND QUANTIFYING BLOOD STASIS IN THE LEFT VENTRICLE

Abstract

In patients at risk of intraventricular thrombosis, the benefits of chronic anticoagulation therapy need to be balanced with the pro-hemorrhagic effects of therapy. Blood stasis in the cardiac chambers is a recognized risk factor for intracardiac thrombosis and potential cardiogenic embolic events. In this work, we present a novel flow image-based method to assess the location and extent of intraventricular stasis regions inside the left ventricle (LV) by digital processing flow-velocity images obtained either by phase-contrast magnetic resonance (PCMR) or 2D color-Doppler velocimetry (echo-CDV). This approach is based on quantifying the distribution of the blood Residence Time (T_R) from time-resolved blood velocity fields in the LV. We tested the new method in illustrative examples of normal hearts, patients with dilated cardiomyopathy and one patient before and after the implantation of a left ventricular assist device (LVAD). The method allowed us to assess in-vivo the location and extent of the stasis regions in the LV. Original metrics were developed to integrate flow properties into simple scalars suitable for a robust and personalized assessment of the risk of thrombosis. From a clinical perspective, this work introduces the new paradigm that quantitative flow dynamics can provide the basis to obtain subclinical markers of intraventricular thrombosis risk. The early prediction of LV blood stasis may result in decrease strokes by appropriate use of anticoagulant therapy for the purpose of primary and secondary prevention. It may also have a significant impact on LVAD device design and operation set-up.

Introduction

Cardiovascular diseases are the leading cause of mortality worldwide and are projected to cause more than 20 million deaths per year by 2030. Cardioembolic stroke is one of the most devastating consequences of cardiac diseases, both in terms of mortality and disability. Amongst all causes of stroke, the cardioembolic etiology is associated with the highest mortality rate and reaches 20% in some prospective series (Arboix & Alio 2010).

Three major mechanisms promote intracardiac thrombosis and embolism in cardiac diseases. First, endocardial injury, due to surgery, chronic stretch or ischemic necrosis, activates clot formation by exposing pro-coagulation factors of the basal membrane. Additionally, cardiac diseases are frequently associated with chronic inflammation, and increased catecholamine and inflammatory cytokine levels, which induce a systemic hypercoagulable state. Finally, blood flow stagnation triggers the activation of the coagulation system. These three predisposing factors are classically known as “Virchow’s triad” (Lowe 2003). Diseases such as atrial fibrillation, myocardial infarction, dilated and hypertrophic cardiomyopathies are well-established conditions that increase the risk of cardiac embolisms by a combination of these three mechanisms.

Anticoagulation therapy has proven to be effective for decreasing the risk of cardioembolic events. However, the benefits of anticoagulation are frequently neutralized by the increased hemorrhagic risk associated with this therapy (Massie et al 2009). In fact, most clinical trials assessing the efficacy of primary prevention of anticoagulation therapy in non-AF cardioembolic diseases have been negative or neutral (Bakalli et al 2013, Homma et al 2012). These trials have been based on clinical risk factors and demographic variables, because precision individualized risk assessment methods are lacking. We hypothesize that imaging-based biomarkers are particularly well suited for this purpose.

Mechanical left-ventricular-assisted-devices (LVADs) are being used as temporary and destination therapies in an increasing number of patients with end-stage heart failure (HF) (Toeg et al 2014). However, intraventricular thrombosis is a well-recognized complication of LVADs and may lead to device malfunction and embolism. A quantitative and individualized topologic assessment of the chamber regions at particular risk for thrombus development may help to define the ideal locations for the insertion of the LVAD cannulas on a patient-specific basis and, to optimize the device operating settings.

Flow in the heart involves complex fluid transport and mixing processes (Bermejo et al 2015). Intracardiac transport and mixing depends on convoluted trajectories of flow inside the chambers (Kilner et al 2000, Wigstrom et al 1999, Zhang et al 2012) as well as on the dynamical interactions between incoming flow and residual flow from preceding cycles (Bolger et al 2007). In the healthy heart, these phenomena result in a small residual volume with no associated blood stasis. However, intraventricular flow patterns are significantly altered by disease (Bermejo et al 2014, Eriksson et al 2013, Hong et al 2008, Rodriguez Munoz et al 2013). How these disturbed flow dynamics may lead to increased blood stasis is only beginning to be understood (Eriksson et al 2013, Hendabadi et al 2013).

Currently, there are no tools capable of a high-throughput measurement of flow stasis in the clinical setting. There have been only a few attempts to define indices of intraventricular blood stasis using in vitro and computational models (Quaini et al 2011, Wong et al 2014). However, most of these indices are based on Eulerian flow metrics and therefore fail to capture the intricate unsteady nature of blood flow transport, as well as the mixing between the blood volume entering the LV each heart beat and the residual volume from preceding ones (Hendabadi et al 2013).

The present study was designed to implement a novel method for measuring and mapping blood stasis in the heart. The purpose was to obtain individual quantitative metrics of global and regional stasis from flow-velocity measurements in the LV. The feasibility of the method was first tested in a high-resolution three-dimensional dataset of LV flow velocity obtained in a large animal by phase-contrast magnetic resonance (PCMRI). To generalize the applicability of the tool we also adapted the method to work with ultrasound data. We analyzed data from healthy and diseased LVs, as well as before and after LVAD implantation. We demonstrate the unique ability of the tool to identify and track the regions at risk of blood stagnation, providing qualitative and topological assessments of blood stasis in the LV.

Methods

Study Population

The present study is based on the following data: 1) high-resolution 3D PCMRI data from a pig scanned under highly controlled heart and respiratory rates, and 2) color-Doppler ultrasound datasets from 2 patients with non-ischemic dilated cardiomyopathy (NIDCM), one healthy volunteer without known heart disease and no cardiovascular risk factors, and one patient with end-stage HF both before and after LVAD implantation. Ultrasound datasets were randomly selected from a large database of two-dimensional velocity maps recruited at our institutions. The study protocol was approved by the local institutional review committee and all subjects provided written informed consent for this study. Clinical data are summarized in Table 1.

TABLE 1.

Clinical data of the studied cases.

ID	Age	Gender	Regional Wall Motion	H.R. (b.p.m.)	EDV (mL)	ESV (mL)	EF (%)
HEALTHY	51	F	Normal	64	98	31	68
NIDCM-1	47	M	Inferior & posterior akinesis	80	81	62	24
NIDCM-2	64	F	Global hypokinesis	76	154	117	24
PRE-LVAD	63	F	Inferior & septal akinesis	68	156	111	29
POST-LVAD	63	F	LVAD	100	84	63	25
PIG	1	M	Normal	76	---	----	----

H.R: Heart rate, EDV: End-Diastolic Volume, ESV: End-Systolic Volume, EF: Ejection fraction, HEALTHY: healthy volunteer; NIDCM: non-ischemic dilated cardiomyopathy; LVAD: left ventricle assist device.

3d PCMRI, Image acquisition and PROCESSING

A high-resolution 3D PCMRI of the LV together with its corresponding 3D anatomical images were obtained in a male Large White pig under anesthesia, using a 3T magnet (Achieva-Tx, Philips Medical Systems, Best, the Netherlands), equipped with a 32-channel cardiac phased-array surface coil. Images were acquired during spontaneous ventilation using retrospective electrocardiographic gating. 3D PCMRI images were planned in a standard 4 and 2-chamber view to cover the entire LV from the level of the mitral annulus to the apex. The following imaging parameters were used: FOV 240×240 mm, voxel size 2×2×4 mm, 1 NEX, SENSE 2, reconstructed heart phases 25 corresponding to a time resolution of 34 ms, PC flow directions RL-AP-FH, act. TR/TE (ms) = 6.0 / 3.7 and VENC of 100 cm/s, as similarly reported (Garcia-Alvarez et al 2013). The velocity field inside the ventricle was obtained from the phase data after correcting for phase-aliasing artifacts through phase unwrapping of closed regions with abnormal intensity gradient. Each anatomical image was post processed using a semi-automatic volume segmentation tool in order to obtain the ventricle boundary surface throughout the cardiac cycle. The segmentation method is based on a multi-resolution level-set active contour optimized for heart segmentation (Gonzalez et al 2015).

2d Image acquisition, analysis and processing

Comprehensive 2-dimensional (2D) B-mode and color-Doppler echocardiographic examinations were performed using a Vivid 7 scanner and 2–4 MHz transducers (General Electric Healthcare). The LV myocardial wall was segmented, and its longitudinal and transversal strain were measured from the apical long-axis B-mode sequences to delineate the endocardial boundary (EchoPac v.110.1.2, General Electric Healthcare). We reconstructed the 2D+t flow field inside the LV using 2D echo color Doppler velocimetry (echo-CDV), as previously described and validated in vitro (Garcia et al 2010) and in vivo (Bermejo et al 2014). The 2D flow velocity fields together with the LV segmentation were used to integrate the unit-forced transport equation and to calculate the spatio-temporal evolution of blood residence time inside the LV (see below). Conventional Doppler-echocardiographic data was recorded following current recommendations (Lang et al 2015).

Residence Time

EVOLUTION EQUATION FOR RESIDENCE TIME

The time spent by a blood particle inside the LV can be evaluated by a scalar magnitude known as Residence Time (T_R). Using a Lagrangian approach, T_R evolution can be described by the advection equation with unit forcing,

$${\partial }_t{T}_R+\nabla ·({\overrightarrow{\upsilon }}_{\mathit{\text{inc}}}{T}_R)=1,$$ (1)

where ${\overrightarrow{\upsilon }}_{\mathit{\text{inc}}}$ is the velocity field. Previous works have considered a similar equation with a non-zero mass diffusivity term (Esmaily-Moghadam et al 2013, Jozsa & Kramer 2000, Mangual et al 2012), but we note that the self-diffusivity of blood is negligible compared to its advective fluxes inside the LV (Bermejo et al 2015, Tarbell 2003). The full derivation of equation (1) can be found in Appendix I. In the absence of a diffusive term, equation (1) can be completed with Dirichlet boundary conditions at the inlet, S_in, when the blood coming from the left atrium enters the ventricle domain V_LV. Equation (1) was numerically integrated on a Cartesian grid using a second-order Finite Volume discretization, in which T_R and ${\overrightarrow{\upsilon }}_{\mathit{\text{inc}}}$ were respectively interpolated at each cell’s center and faces. We used a Total Variation Diminishing (TVD) flux limiting scheme (LeVeque 2002) to avoid the numerical oscillations that would appear at the sharp interfaces created by the transport process, particularly between fresh blood entering the LV each cycle and the residual blood from previous cycles. A second-order time integration scheme was adopted keeping the Courant–Friedrichs–Lewy (CFL) number below 0.5 throughout the whole integration and using a variable time step, Δt, bounded between 5-0.3 ms for the 2D-echo-CDV and 33-0.5 ms for the 3D PCMRI data. The velocity field at each integration step was obtained by linearly interpolating in time the previous and the successive velocity acquisition data frames.

Spatio-temporally connected pixels with high residence time (e.g. T_R > 2 sec) were clustered and stored for further analysis using in-house algorithms. Clusters smaller than 2% LV volume (area in 2D) and clusters that did not span the whole cardiac cycle were discarded and were not analyzed further.

PCMRI VELOCITY CORRECTION FOR MASS CONSERVATION

Similar to other flow measurement techniques, PCMRI provides velocity fields with noise that usually do not satisfy mass conservation (i.e. $\nabla ·{\overrightarrow{\upsilon }}_{\mathit{\text{inc}}}\ne 0$). Although noise can be minimized by appropriate fine-tuning during data acquisition, appreciable errors remain in current state-of-the-art PCMRI measurements (Busch et al 2013). Errors in mass conservation are particularly troublesome for the purpose of analyzing blood transport and residence time because they introduce a spurious source term equals to $-T_R\nabla ·{\overrightarrow{\upsilon }}_{\mathit{\text{inc}}}$ in the transport equation (1). This spurious term can generate undesired variations in T_R that are not caused by convective blood transport.

In this work, we apply a solenoidal projection method to enforce the condition that the PCMRI velocity field is incompressible (Chorin 1967). Note that, since the echo-CDV fields are derived by enforcing mass conservation (Garcia et al 2010), they automatically satisfy this condition. Briefly, a velocity field derived from a potential function φ is added to the original field, ${\overrightarrow{\upsilon }}_0:{\overrightarrow{\upsilon }}_{\mathit{\text{inc}}}={\overrightarrow{\upsilon }}_0+\nabla \phi$. Imposing that ${\overrightarrow{\upsilon }}_{\mathit{\text{inc}}}$ is divergence-free allows for calculating φ by solving a Poisson’s equation with non-homogeneous Neumann boundary conditions at the LV walls. This problem was solved using a custom Multi-Grid method developed in FORTRAN, interpolating the original domain onto a Cartesian grid. The moving boundary was defined independently of the Cartesian grid by using a sharp interface immersed boundary method (Mittal et al 2008).

GRID SENSITIVITY ANALYSIS

While time-resolved 3D PCMRI provides invaluable information about the multi-dimensional flow transport and stasis patterns in the LV, the moderate spatio-temporal resolution (Δx=Δy= 0.94 mm, Δz= 2 mm & Δt= 33 ms) of this technique could pose a potential limitation. To rule out this possibility, we performed a sensitivity analysis of the dependence of the T_R maps on the time and space resolution in the echo-CDV data, which is better resolved (Δx= 0.5 mm & Δt= 5 ms). We progressively deteriorated the resolution of N=3 echo-CDV datasets and computed the average L2 norm of the error in the T_R fields as a function of Δx and Δt. Table 2 summarizes the results of this analysis, and suggests that the resolution of the PCRMI data used in this work was sufficient to accurately resolve the spatiotemporal evolution of the residence time.

TABLE 2.

Sensitivity analysis over 6 beats (6T): mean ± standard deviation, of the L2 norm of the error, defined below, compared to the reference frame in 3 different cases.

$${\Vert \mathit{\text{err}}\Vert }_2=\sqrt{{\int }_{t=0}^{t=6T}{\int }_{\Omega }{(\widetilde{T_R}-T_R)}^{2}dxdydt/{\int }_{t=0}^{t=6T}{\int }_{\Omega }{\widetilde{T_R}}^{2}dxdydt}$$
	dt [ms]	3.9±0.4	7.8±0.7	15.7±1.5	39.2±3.8	78±7.5
	Number of input frames	200	100	50	20	10
Nx × Ny, dx [mm]	256×256, 0.35±0.02	Reference: $\widetilde{T_R}$	0.022 ± 0.015	0.121 ± 0.02	0.15 ± 0.039	0.297 ± 0.104
	128×128, 0.70±0.04	0.123 ± 0.018	0.124 ± 0.018	0.154 ± 0.02	0.173 ± 0.029	0.28 ± 0.092
	64×64, 1.42±0.08	0.212 ± 0.027	0.21 ± 0.028	0.218 ± 0.03	0.227 ± 0.024	0.282 ± 0.075
	32×32, 2.88±0.16	0.295 ± 0.028	0.293 ± 0.029	0.293 ± 0.029	0.296 ± 0.028	0.32 ± 0.049
	16×16, 5.96±0.32	0.394 ± 0.035	0.395 ± 0.036	0.401 ± 0.041	0.406 ± 0.055	0.396 ± 0.035

Results and Discussion

Residence Time in 3d

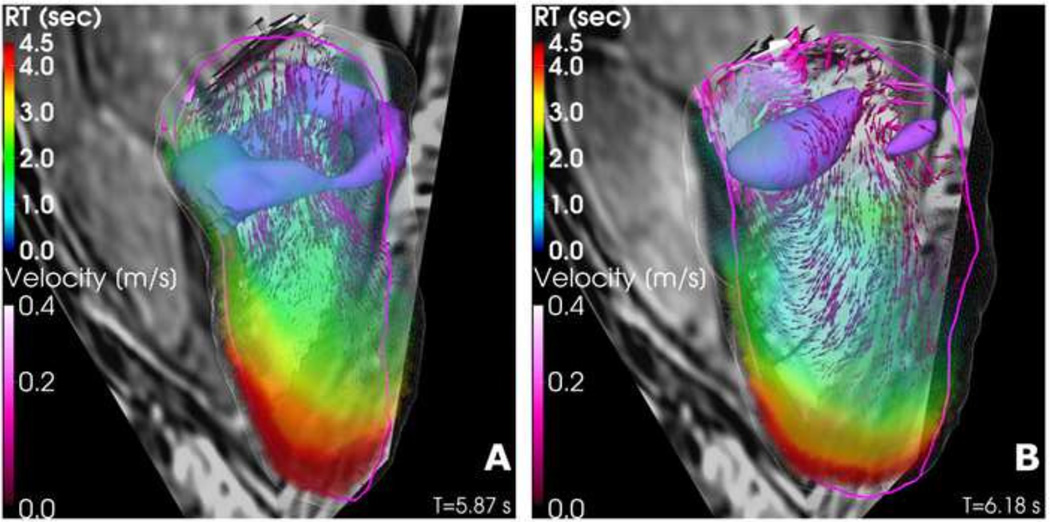
The 3D+t spatiotemporal distribution of T_R in the LV was calculated from PCMRI data. Figure 1 displays 3D renderings of T_R at mitral valve opening and at isovolumic contraction. The velocity field shows the strong diastolic jet and associated vortex ring that characterizes LV filling flow (Bermejo et al 2015). In this ventricle the region of highest T_R is located close to the apex, and extends towards the aortic tract along the anteroseptal wall. This residence time pattern agrees well with the pattern observed in normal human LVs (see example in Figure 2A). The three-dimensionality of the T_R field is evident in Figure 1, and is caused by the complexity of intraventricular blood flow and transport during the cardiac cycle. However, the main features of this field are relatively well captured in the three-chamber view (delineated by the magenta contour in Figure 1), particularly the maximum value of T_R and its apical location. This result is important because our approach to estimate T_R using conventional echocardiography is performed from velocity fields acquired in the three-chamber view.

FIGURE 1.

3-D intraventricular velocity field and residence time map in a pig at mitral valve opening (A) and at the end of filling (B). The wireframe contour depicts the LV volume segmentation. The magenta and contour lines identify the long-axis plane that contains the mitral valve, apex and aortic valve. The vortical structures in purple are visualized by isosurfaces of λ_ci (imaginary part of the complex conjugate eigenvalue of ∇υ).

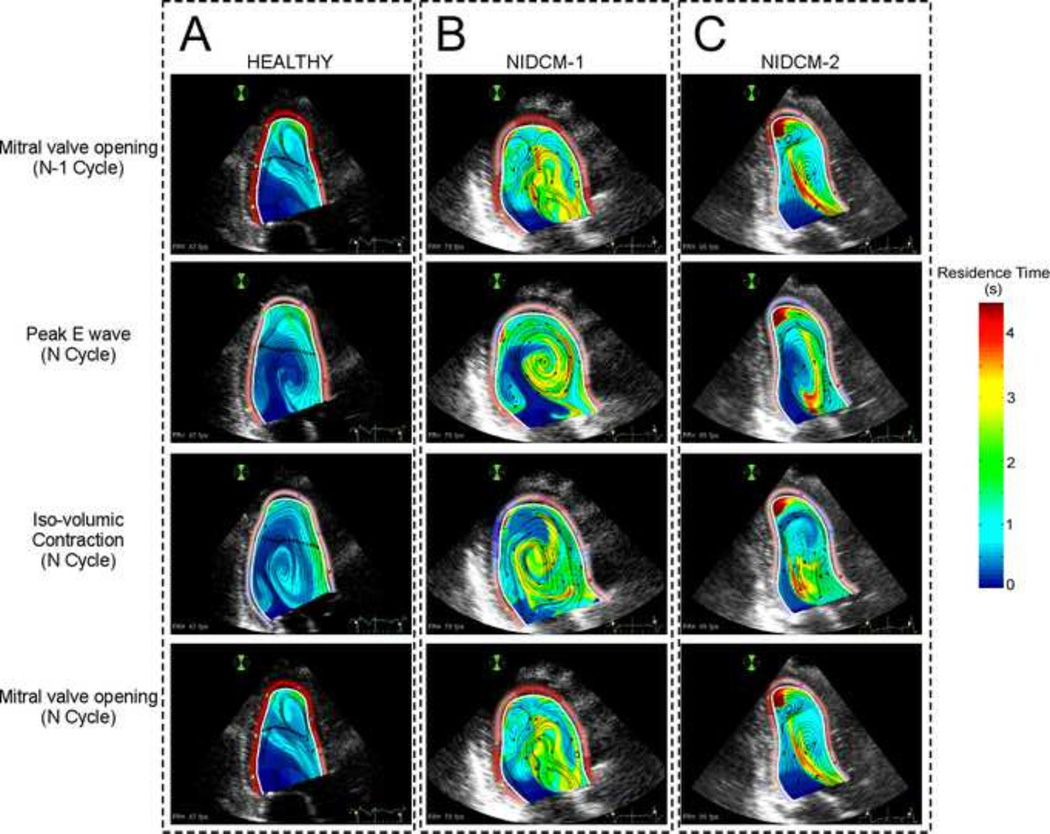
FIGURE 2.

Snapshots of 2-D intraventricular residence time along the cardiac cycle in a healthy heart (A) and in two different examples of dilated cardiomyopathy (NIDCM) patients (B & C). 1^st row: Residence Time mapping at the mitral valve opening in the converged N-l cycle. 2^nd row: Residence Time mapping at peak E-wave in the last computed cycle. 3^rd row: Residence Time mapping at the iso-volumetric contraction in the last computed cycle. 4^th row: Residence Time mapping at mitral valve opening in the last cycle. Notice that in both NIDCMs there coexist different regions with high T_r.

LV Residence Time in NON-ISCHEMIC DILATED CARDIOMYOPATHY

Dilated cardiomyopathy is a condition associated with increased risk of intraventricular thrombosis. The normal LV flow pattern has been reported to recycle the blood volume inside the left ventricle every 2–3 beats (Figure 2A) (Bolger et al 2007, Eriksson et al 2010, Hendabadi et al 2013, Watanabe et al 2008). However, blood transport is significantly altered in patients with NIDCM by the large swirling flow patterns that are typical of this condition (Figure 2B–C) (Bermejo et al 2014, Hendabadi et al 2013). In these patients, blood is trapped inside long-lasting vortices and undergoes rotation throughout most of the cardiac cycle (see supplementary movie 1). Thus, proper assessment of intraventricular stasis should consider factors such as the distortion of fluid particles and their kinetic energy density in addition to T_R The kinetic energy density of a fluid particle, defined as K = (u² + v²)/2, can be used together with T_R as an intuitive indicator of stasis. However, kinetic energy is not a Galilean invariant and it could be possible for a fluid parcel to have high values of K while moving with little distortion, similar to a rigid solid. The distortion of a fluid particle can be quantified by the second invariant of the symmetric strain tensor S_ij = (∂_xj u_i + ∂_xi u_j)/2. For an incompressible flow, the first invariant of S_ij is zero and the second invariant is defined as ${\mathrm{Q}}_{\mathrm{s}}=\text{trace}({\mathrm{S}}_{\mathrm{i}\mathrm{j}}^2)/2$. Note that Q_s has dimensions of squared inverse of time, so it can be used to define a second stasis timescale ${\mathrm{T}}_{\mathrm{S}}={\mathrm{Q}}_{\mathrm{S}}^{-1/2}$ in addition to T_R.

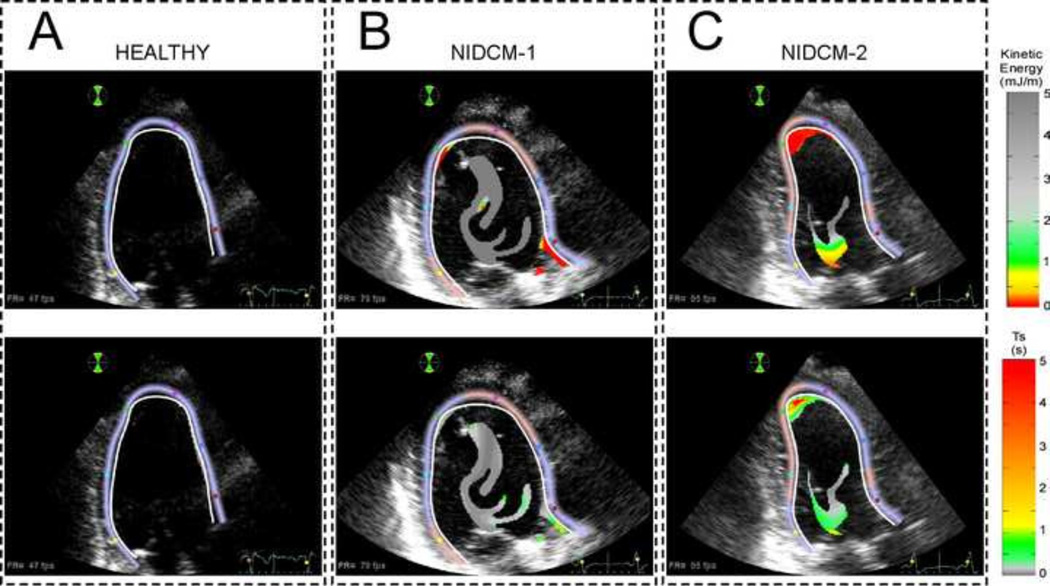
Figure 3 shows the spatial distributions of K and T_s in the regions with T_R > 2 s for the same ventricles of figure 2, at the end of diastole. As expected, the normal LV (Figure 3A) does not show any significant region with T_R > 2 s. There is a small cluster located near the endocardium but it has relatively high K and low T_s. Interestingly, both dilated LVs (Figure 3B–C) show large regions with T_R > 2 s located at the center of the chamber but these regions are associated with high values of K and low values of T_s. This indicates that blood is continuously being stirred by the LV flow patterns in this centrally located region despite having high T_R. By contrast, the second diseased LV (Figure 3C) shows a separate, apically located region with T_R > 2 sec that also has low K and high T_s, and is therefore stagnant. These results illustrate how the combined analysis of the spatio-temporal Lagrangian patterns of residence time and Eulerian measures of fluid motion and distortion can provide clinically accessible information about intraventricular blood stasis from conventional color-Doppler datasets.

FIGURE 3.

Snapshots of 2-D K and T_s before mitral valve opening in the last converged cardiac cycle in a healthy heart (A) and in two different examples of NIDCM (B & C). 1^st row: Kinetic energy density (K) mapping in the regions with in the regions with T_R > 2 s. 2^nd row: Distortion time (T_s) in the regions with T_R > 2 s. The NIDCM-2 case is at risk of apical blood stasis given the combination of low K and large T_s.

Changes in Blood Stasis After LVAD Implantation

Implantable cardiac assist devices, particularly LVADs, are considered to alter the physiological blood flow patterns in the heart, leading to increased risk of thrombosis (Bluestein 2004, Wong et al 2014). Among the three elements of Virchov’s triad, abnormal flow patterns present the most complex challenge to improve device design and post-implantation patient management (Kormos 2015). However, blood stasis has not been previously measured in the patients implanted with LVADs.

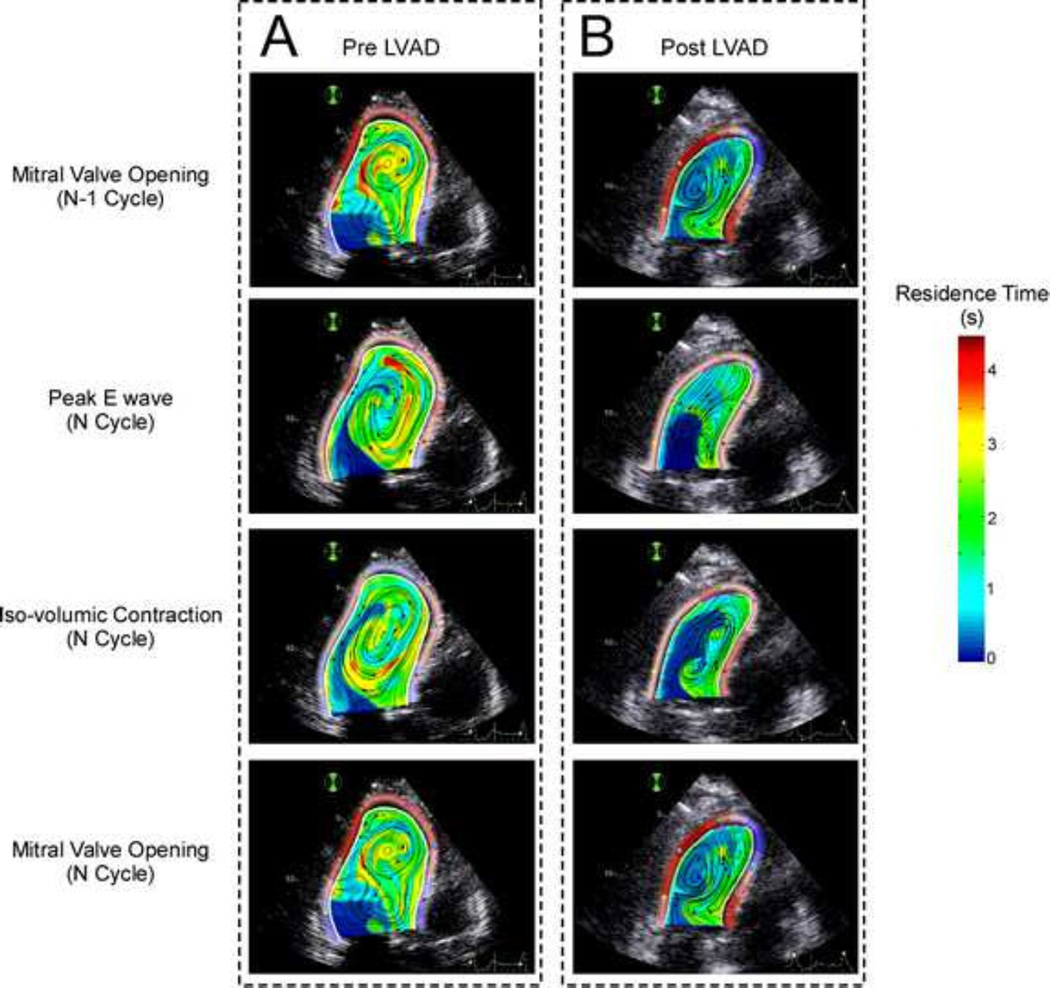
Figure 4 shows residence time maps along a cardiac cycle in a patient with NIDCM, mitral regurgitation and end-stage HF before and 1 month after LVAD implantation. The pre-LVAD condition (Figure 4A) shows a large region with T_R > 2 s located at the center of the chamber, which is caused by the large swirling region that is sustained during most of the cardiac cycle in this dilated heart. This large swirling pattern is indicated by the circular instantaneous streamlines in Figure 4A. Consistent with the results presented in Figure 3, this region is associated with relatively high values of kinetic energy density and low values of T_s, implying that this region is not stagnant. However, this flow and stasis pattern are significantly altered after LVAD implantation, as the flow is channeled from the mitral annulus to the LVAD inflow cannula located at the LV apex, instead of transiting towards the outflow tract (magenta line in Figure 4B). As a result, a region with high residence time, moderate low kinetic energy and moderate low fluid distortion (moderately high T_s) appears near the LV outflow tract. These factors combined are the hallmark of blood stasis, suggesting a hemodynamic explanation for clinical reports of mural thrombosis in the LV outflow tract of LVAD-implanted patients (May-Newman et al 2013). These in vivo results are in agreement with previous in vitro experiments performed using a cardiac simulator (Wong et al 2014), although it should be noted that the drastic LV volume unloading caused by LVAD implantation was not modeled in the in vitro study.

FIGURE 4.

Snapshots of 2-D intraventricular residence time along the cardiac cycle in a patient before (A) and after (B) LVAD implantation. The apically located inflow LVAD cannula is represented in magenta. 1^st row A: Residence Time mapping at the mitral valve opening in the converged N-l cycle. 2^nd row: Residence Time mapping at E-wave peak in the last computed cycle. 3^rd row: Residence Time mapping at the onset of isovolumic contraction in the last computed cycle. 4^th row: Residence Time mapping at mitral valve opening in the last cycle.

Simplified Residence Time Indices

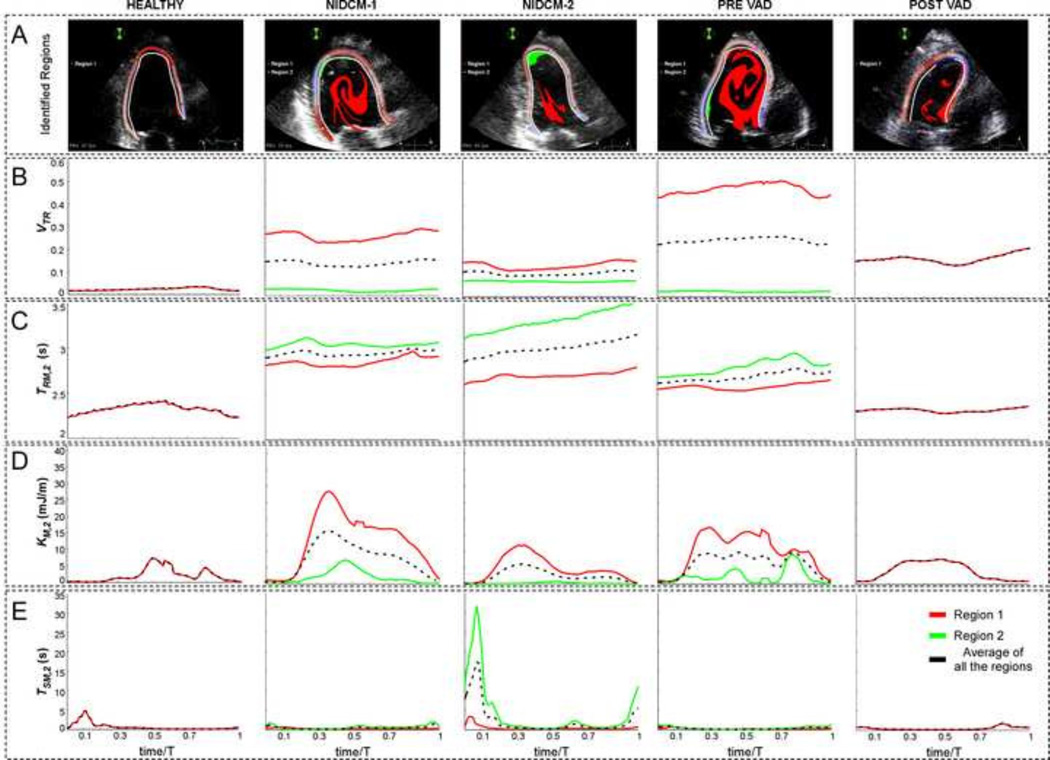
An additional challenge in introducing clinically relevant indices of LV blood stasis is to incorporate metrics that integrate the spatio-temporal nature of the T_R distributions, together with additional parameters such as K or T_s, into simple metrics that can be used to compare values between patients. Therefore, we identified Lagrangian clusters of residual volume formed by spatiotemporally connected pixels with T_R > 2 sec (Figure 5A and supplementary movie 2), and plotted the following indices as a function of time for each Lagrangian cluster: 1) Relative LV volume (area in 2D) occupied by each cluster (V_TR, Figure 5B), 2) spatially-averaged value of T_R in each cluster (T_RM,2, Figure 5C), 3) spatially-averaged value of K in each cluster (K_M,2, Figure 5D), and 4) spatially-averaged value of T_s in each cluster (T_SM,2, Figure 5E).

FIGURE 5.

Example of region tracking (A) and time evolution of V_TR (B), T_M,2 (C), K_M,2 (D), T_SM,2 (E) along the last converged cycle in all the 2-D studied cases: Healthy heart (1^st col), NIDCM-1 (2^nd col), NIDCM-2 (3^rd col), Pre-VAD (4^th col) and Post-VAD (5^th col). Line colors correspond to each of the tracked regions (row A) and their average (black).

The temporal profiles of V_TR varied periodically, implying that the numerical integration of eq. 1 achieved numerical convergence. Consistent with the instantaneous maps in Figure 2, the diseased hearts showed higher values of V_TR than the healthy volunteer throughout the cardiac cycle. Remarkably, in the NIDCM cases, the profiles of T_RM,2 increased from beat to beat, indicating that there is a persistent residual volume of blood that does not mix with incoming blood in these ventricles. Conversely, T_RM,2 varied periodically for the healthy case, suggesting that blood is not indefinitely trapped in healthy ventricles. Separate analysis of each T_R>2 s Lagrangian cluster for diseased LVs showed that the apically located residual volume in NIDCM case 2 had significantly higher values of T_SM,2 and significantly lower values of K_M,2 than all other residual volumes in NIDCM cases 1 and 2. These data suggest that it is possible to derive simplified indices of stasis from the Doppler-derived spatio-temporal maps of T_R, T_s and K. Furthermore, our results indicate that individual analyses of intraventricular residual volumes help to unmask blood stasis in patients with more than one residual volume region.

To further simplify the potential clinical application of these stasis indices, we considered temporally averaging the time-varying indices defined above for each Lagrangian cluster of residual volume. The time-averaged indices are denoted with an overline (e.g. $\overline{{\mathrm{V}}_{\mathrm{T}\mathrm{R}}}$) and are summarized in Table 3 for the subjects analyzed in this pilot study. To facilitate the identification of each cluster, its normalized average apical location, $\overline{{\mathrm{X}}_{\mathrm{A}}}$, is included in the table (0 indicates basal and 1 indicates apical). Despite the small number of cases, we found marked differences in time-averaged stasis indices in patients with NIDCM and healthy volunteers, as well as in the patient with HF before and after LVAD implantation. The values of $\overline{{\mathrm{V}}_{\mathrm{T}\mathrm{R}}}$ in the diseased LVs ranged between 20% and 50%, much higher than the healthy case which had less than 2.5%. The secular variation of T_RM,2 in the diseased cases rendered $\overline{{\mathrm{T}}_{\mathrm{R}\mathrm{M},2}}$ meaningless in those cases. Conversely, the values of $\overline{{\mathrm{K}}_{\mathrm{M},2}}$ and $\overline{{\mathrm{T}}_{\mathrm{S}\mathrm{M},2}}$ were not relevant in the healthy case and for the secondary residual volumes of cases NIDCM 1, NIDCM2 and the pre-LVAD case, which had insignificant size. Consistent with the results presented in the previous sections, the apical residual volume of NIDCM case 2 had an appreciable size $(\overline{{\mathrm{V}}_{\mathrm{T}\mathrm{R}}}\approx 70\%)$, its value of $\overline{{\mathrm{K}}_{\mathrm{M},2}}$ was considerably low and its value of $\overline{{\mathrm{T}}_{\mathrm{S}\mathrm{M},2}}$ was considerably high. Likewise, in the LVAD patient, $\overline{{\mathrm{V}}_{\mathrm{T}\mathrm{R}}}$ $\overline{{\mathrm{K}}_{\mathrm{M},2}}$, and $\overline{{\mathrm{T}}_{\mathrm{S}\mathrm{M},2}}$ reflect the increase of blood stasis risk near the outflow tract after LVAD implantation. These results suggest that the time-averaged stasis indices were able to capture the subtle differences in the spatio-temporal stasis patterns found in those two ventricles. Further analysis with larger patient populations and validation with patient outcomes (e.g. incidence of LV thrombus formation) are required to confirm these trends.

TABLE 3.

Time-averaged stasis indices for the cases under study

CASE	# Residual volumes (TR > 2 s clusters)	Cluster	$\overline{{\mathrm{V}}_{\mathrm{T}\mathrm{R}}}$ (nor.)	$\overline{{\mathrm{T}}_{\mathrm{R}\mathrm{M},2}}$ (sec)	$\overline{{\mathrm{T}}_{\mathrm{S}\mathrm{M},2}}$ (sec)	$\overline{{\mathrm{K}}_{\mathrm{M},2}}$ (mJ/m3)	$\overline{{\mathrm{X}}_{\mathrm{A}}}$ (nor.)	$\overline{{\mathrm{V}}_{\mathrm{T}\mathrm{R}0}}$ (nor.)	$\overline{{\mathrm{T}}_{\mathrm{R}\mathrm{M},20}}$ (s)	$\overline{{\mathrm{T}}_{\mathrm{s}\mathrm{M},20}}$ (s)	$\overline{{\mathrm{K}}_{\mathrm{M},20}}$ (mJ/m3)
HEALTHY	1	1	0.023	2.33	0.64	2.0	0.92
NIDCM-1	2	1	0.26	secular	0.25	13.4	0.43	0.14	Secular	0.34	7.74
		2	0.025	secular	0.43	2.1	0.85
NIDCM-2	2	1	0.14	secular	0.48	4.8	0.28	0.10	Secular	2.36	2.49
		2	0.068	secular	4.3	0.19	0.86
PRE-VAD	2	1	0.47	secular	0.28	10.0	0.51	0.25	secular	0.47	4.03
		2	0.023	secular	0.66	2.2	0.40
POST-VAD	1	1	0.17	secular	0.45	4.0	0.32

HEALTHY: healthy volunteer; NIDCM: non-ischemic dilated cardiomyopathy; LVAD: left ventricle assist device. $\overline{{\mathrm{V}}_{\mathrm{T}\mathrm{R}}}$: Normalized fraction of chamber volume (Area in 2D) occupied by blood with T_R >2 s, averaged over the cardiac cycle. $\overline{{\mathrm{T}}_{\mathrm{R}\mathrm{M},2}}$: Mean residence time in the region with T_R > 2 s, averaged over the cardiac cycle. $\overline{{\mathrm{T}}_{\mathrm{S}\mathrm{M},2}}$: Mean distortion time scale in the region with T_R >2 sec, averaged over the cardiac cycle. $\overline{{\mathrm{K}}_{\mathrm{M},2}}$: Mean kinetic energy density in the region with T_R >2 s, averaged over the cardiac cycle. $\overline{{\mathrm{X}}_{\mathrm{A}}}$: Normalized average cluster apical location. Subindex 0 denotes the average of all the regions with T_R >2 s.

Conclusions And Study Limitations

In this paper, implement an in vivo method to generate multi-dimensional spatio-temporal maps of LV blood stasis. We also derive simplified patient-specific stasis metrics that integrate these maps and can be used to guide personalized clinical decision-making. This new method is based on the quantification of the residence time spent by blood particles inside the LV since entering the chamber, which is obtained by integrating a transport equation with unit forcing. A residence time threshold can be used to automatically segment and label residual blood volumes that do not mix with the fresh blood entering the LV each cardiac cycle, and which are potentially stagnant. By analyzing the kinetic energy and the rate of distortion of each one of these residual volumes we were able to discern if blood is stagnant inside of them. This semi-Lagrangian categorization has been shown to anticipate thrombogenic regions in a pilot study in patients with acute myocardial infarction (Devesa et al 2015).

To illustrate the residence time mapping methodology, we assessed intraventricular blood stasis in several representative examples. The healthy LV presented residual volumes of small size in comparison to NIDCM patients. Conversely, we often observed large residual volumes inside the persistent swirling flow patterns that develop in dilated LVs (Bermejo et al 2014). These results are concordant with previous studies based on echo-CDV and PCMRI (Bolger et al 2007, Eriksson et al 2010, Eriksson et al 2011, Hendabadi et al 2013).

Further analysis of the fluid’s kinetic energy and rate of distortion suggests that, although the blood inside these residual volumes barely mixes with fresh blood entering the LV each cardiac cycle, it is continuously stirred by the surrounding fluid. Therefore, we conclude that the large swirling flow pattern that develops in dilated LVs does not necessarily induce blood stasis. In addition to this frequent pattern, some diseased LVs had other regions of high residence time that were also associated with low kinetic energy and low rates of distortion, and which were effectively stagnant. Thus, the new method proposed in this paper allows clinicians to assess the degree of intraventricular blood stasis on an individualized basis. Future trials are obviously necessary to address whether this method is suitable to predict the risk of intraventricular thrombosis and, eventually, cardioembolic events. The possibility of Lagrangianly tracking and analyzing each residual volume inside the LV at low computational costs is instrumental for this purpose.

By combining echo-CDV and residence time mapping, we obtained the first quantification of intraventricular blood stasis in patients with LVADs. Our results suggest that intraventricular blood stasis in the LVAD-assisted heart can be higher than prior to implanting the device, particularly near the left ventricular outflow tract, a region reported to be thrombogenic during continuous LVAD support (May-Newman et al 2013). Mapping methods as the one proposed herein show an excellent potential to correlate stagnant regions with local and global wall motion abnormalities. This type of analysis may be useful in optimally choosing the insertion sites for the LVAD cannulas on a per-patient basis.

The proposed methodological framework relies on clinical access to time-resolved LV velocity fields but is independent of the imaging modality employed to measure intraventricular velocity. In this work, we exploited this flexibility to obtain T_R maps from both 3D+t PCMRI and 2D+t echo-CDV velocity fields. This allowed us to use each modality to evaluate the limitations of the other, namely the spatiotemporal resolution in PCMRI and the planar flow simplification in echo-CDV. The analysis of residence time maps derived from 3D+t PCMRI showed that both the key spatial features and numerical values of T_R are well represented in the long-axis three-chamber plane imaged by 2D echo-CDV. We performed a sensitivity analysis on echo-CVD data with progressively coarsened spatial and temporal resolutions, concluding that the resolution of the PCRMI velocity fields used in this work was adequate to accurately quantify intraventricular blood stasis. However, we noticed that this method may be sensitive to low-scale velocities. Future clinical studies are needed to optimize the adjustments of the VENC scale (PCMRI) and the Nyquist limit (Doppler) for the purpose of quantifying stasis.

Currently, LV blood stasis is not assessed in the clinical setting. Echo-CDV has important practical advantages, as it is fast, clinically feasible, does not require infusion of contrast agents, and it can be safely performed in patients implanted with LVADs. A limitation of this approach is that it neglects the presence of intraventricular anatomical elements such as papillary muscles and endocardial trabeculae, which can locally increase mixing (Bermejo et al 2015). This may be particularly important at the endocardial surface, where our approach predicts high residence time values. This limitation could be addressed by including a mass-diffusivity term in eq. (1) with a spatially varying coefficient that would need to be determined from high-resolution anatomical imaging. Additionally, there is no doubt that the planar flow simplification may lead to inaccuracies in the estimation of LV blood transport. However, the impact of these and other technical issues needs to be balanced against the potential clinical benefit offered by the new method. In this context, a pilot study suggests that echo-CDV-derived indices of blood stasis may be able to predict LV thrombus formation in patients with acute myocardial infarction (Devesa et al 2015), a condition in which an individualized assessment of the risk of thrombosis is particularly necessary. If these promising results are confirmed in further trials, it is possible that the clinical information provided by the quantitation of stasis using conventional ultrasound outweighs by far the technical limitations of the method.

In summary, we have implemented a method to quantify and map intraventricular stasis from flow-velocity measurements which is suitable for bedside clinical application. Using this method, important physiological consequences of a number of cardiovascular procedures can now be addressed. Interventions such as valve replacement, resynchronization therapy, correction or palliation of congenital cardiac defects, and surgical ventricular restoration are all known to heavily disturb physiological flow dynamics. Why and to what extent these procedures may impact stasis can be clarified. Spatial, temporal and velocity resolution of current imaging modalities are rapidly increasing, potentially allowing this type of analyses in other cardiac chambers. The final objective of obtaining a reliable individual assessment of the risk of cardiac thrombosis, useful for tailoring anticoagulant therapy and programming cardiac interventions such as LVADs on a patient specific basis, seems therefore achievable in the near future.

Appendix I

Derivation of the Residence time equation

In this section, we derive the continuum equation for the residence time of a fluid parcel based on the stochastic analysis of the residence time of its constituent particles. The stochastic derivation is done in 1D without loss of generality.

We consider a fluid particle with position, x, which varies as the particle moves with local flow velocity,υ, and due to Brownian fluctuations. The Langevin equations for the particle’s position and residence time, T, are

$$\frac{dx}{dt}=\upsilon +2\sqrt{k}\xi (t),$$ (2)

$$\frac{dT}{dt}=1,$$ (3)

where ξ(t) is a random forcing with a Dirac delta correlation function, and k is the diffusivity of the fluid particle within the rest of the fluid (Gardiner 2004). From these equations, it is straightforward to derive the Fokker-Planck equation for the probability density function, p(x,T,t),

$$\frac{\partial p}{\partial t}=-\frac{\partial (\upsilon p)}{\partial x}-\frac{\partial p}{\partial T}+k\frac{{\partial }^{2}p}{\partial x^2}.$$ (4)

Notice that the relevant coefficient in equation (4) is diffusivity and not the viscosity, as at a microstructural level mass diffusion between two instants of time requires change of position while momentum diffusion requires particle collision, which can occur without change of position. To obtain an equation for the continuum residence time, one can multiply by T equation (4), yielding to

$$\frac{\partial (Tp)}{\partial t}=-\frac{\partial (T\upsilon p)}{\partial x}-T\frac{\partial p}{\partial T}+k\frac{{\partial }^2(Tp)}{\partial x^2}.$$ (5)

This equation can be integrated in T between ± infinity to obtain a governing equation for the ensemble average of T,

$$T_R(x,t)={\int }_{-\infty }^{\infty }Tp(x,T,t)dT,$$ (6)

which is the residence time of the fluid parcel at each position and instant of time. The only non-trivial term when integrating eq. (5) is

$${\int }_{-\infty }^{\infty }T\frac{\partial p}{\partial T}dT,$$ (7)

which can be handled by parts resulting in

$${\int }_{-\infty }^{\infty }{T\frac{\partial p}{\partial T}dT=Tp]}_{-\infty }^{\infty }-{\int }_{-\infty }^{\infty }pdT=-1.$$ (8)

It is straightforward to see that the first term in the right-hand-side of equation (8) needs to be zero if p is integrable, and that the integral of p must be equal to 1 since p is a probability density function. Thus, combining equations (5), (6) and (8), one arrives at:

$$\frac{\partial (T_R)}{\partial t}=-\frac{\partial (\upsilon T_R)}{\partial x}-(-1)+k\frac{{\partial }^2(T_R)}{\partial x^2}.$$ (9)

The mass diffusivity of blood is customarily considered much smaller than its kinematic viscosity, and it is not expected to play an important role in influencing particle trajectories, platelet-surface contact frequency and dissociative binding phenomena under flow at physiological shear rates (Fournier 2012, Leonard et al 1972, Mody & King 2007, Peattie 2013). Therefore, we set k = 0, which is analogous to previous studies of LV blood transport based on the deterministic integration of fluid particle trajectories (Hendabadi et al 2013, Wigstrom et al 1999). Under these premises, equation (9) becomes

$$\frac{\partial (T_R)}{\partial t}+\frac{\partial (\upsilon T_R)}{\partial x}=1,$$ (10)

which is the 1D analogous of equation (1).