Light acclimation of photosynthesis in two closely related firs (Abies pinsapo Boiss. and Abies alba Mill.): the role of leaf anatomy and mesophyll conductance to CO₂

Abstract

Leaves growing in the forest understory usually present a decreased mesophyll conductance (g_m) and photosynthetic capacity. The role of leaf anatomy in determining the variability in g_m among species is known, but there is a lack of information on how the acclimation of g_m to shade conditions is driven by changes in leaf anatomy. Within this context, we demonstrated that Abies pinsapo Boiss. experienced profound modifications in needle anatomy to drastic changes in light availability that ultimately led to differential photosynthetic performance between trees grown in the open field and in the forest understory. In contrast to A. pinsapo, its congeneric Abies alba Mill. did not show differences either in needle anatomy or in photosynthetic parameters between trees grown in the open field and in the forest understory. The increased g_m values found in trees of A. pinsapo grown in the open field can be explained by occurrence of stomata at both needle sides (amphistomatous needles), increased chloroplast surface area exposed to intercellular airspace, decreased cell wall thickness and, especially, decreased chloroplast thickness. To the best of our knowledge, the role of such drastic changes in ultrastructural needle anatomy in explaining the response of g_m to the light environment has not been demonstrated in field conditions.

Introduction

The variation in light quality and availability is among the most outstanding features of plant canopies (Niinemets et al. 2015). The strategies of the trees for coping with the environmental conditions imposed by the forest canopy have long been associated with changes in the morphology of leaves and shoots (Carpenter and Smith 1981, Givnish 1988, Abrams and Kubiske 1990, Niinemets and Sack 2006). For instance, to maximize light capture, plants increase the allocation of carbon toward leaf production at the expense of roots and stems (Givnish 1988, Landhäusser and Lieffers 2001, Pearcy 2007, Niinemets 2010).

Niinemets et al. (2015) stated that the worldwide variation across plant functional types in leaf structural and physiological traits in response to changes in light availability (from high light environments in the upper canopy to typical light environments in the understory) tends to be smaller in conifers. Regardless of this general trend, several studies have found morphological and functional acclimation to understory environments in several conifer species (Niinemets et al. 2001, 2002, 2007, Cescatti and Zorer 2003, Mori et al. 2008). Within this context, it is interesting that Abies pinsapo Boiss.—a relict conifer that occurs in some restricted areas of the Mediterranean mountain ranges in Spain and Morocco—displays a great plasticity in response to drastic changes in light availability (Sancho-Knapik et al. 2014). When grown in the open field, A. pinsapo increases water transport efficiency to the transpiring needles, whereas when grown in the forest understory, it develops shoots for maximizing light capture. Despite these canopy adjustments, at the leaf level, A. pinsapo grown in the understory showed decreased photosynthetic capacity when compared with trees grown in the open field (Sancho-Knapik et al. 2014). Although the decreased photosynthetic capacity is considered a common phenomenon in plants growing in the understory (Montpied et al. 2009), there is currently limited understanding of the extent to which different structural and/or anatomical traits control photosynthetic acclimation (Niinemets et al. 2015).

One of the key traits that determine the maximum photosynthetic rate is the mesophyll conductance (g_m), which under certain conditions can be the most significant photosynthetic limitation (Flexas et al. 2012). In fact, leaves growing in the forest understory usually present lower g_m values than sun leaves (Hanba et al. 2002, Warren et al. 2007, Flexas et al. 2008), but the number of studies investigating g_m acclimation to growth light is still very limited (Niinemets et al. 2009). Recently, several studies have quantitatively determined the importance of several leaf anatomical traits in determining the variability in g_m and photosynthetic capacity among species. Among others, g_m can be influenced by the leaf thickness, the packing of mesophyll cells relative to the distance and position of stomata, the chloroplast-exposed surface area facing intercellular air spaces, the thickness of the mesophyll cell walls and the chloroplast size (see Tomás et al. 2013 and references therein). Regarding conifers, Peguero-Pina et al. (2012), when comparing A. pinsapo with its congeneric Abies alba Mill., found that the two species growing in the open field in high light conditions displayed contrasting leaf anatomical characteristics (mainly cell wall thickness and chloroplast size), with important consequences for g_m and photosynthetic CO₂ assimilation. Given that interspecific differences in the responses of the functional anatomy of leaves to changes in light availability can have major implications for g_m and the overall leaf photosynthetic performance (Terashima et al. 2011), possible differences in light-dependent plasticity in foliage structure can further importantly modify the photosynthetic acclimation between the congeneric firs.

To the best of our knowledge, there is a lack of information on how the acclimation of g_m and main photosynthetic parameters to shade conditions is mostly driven by changes in ultrastructural mesophyll traits that ultimately determine different carbon gain performance. Moreover, how far the plasticity of these traits to changes in growth light is species dependent is a matter that deserves further research. In this regard, the aim of the present study is to contribute a better knowledge on this topic. This is explored by means of the following specific objectives: (i) to analyze the phenotypic response of A. pinsapo individuals to low light regime beneath a forest canopy, in terms of mesophyll ultrastructural traits and photosynthetic parameters, and (ii) to compare the magnitude of this response with its congeneric species A. alba.

Materials and methods

Study sites

The study was carried out in an A. pinsapo forest on a NE facing slope of the southern ‘Sistema Ibérico’ range (Orcajo, Spain; 41°05′N, 01°30′W; 1150 m above sea level (a.s.l.)) (Sancho-Knapik et al. 2014). The forest was planted in 1913, and since then had developed a vigorous naturally regenerated fir understory. On the other hand, we selected a stand located in the western Spanish Pyrenees (Gamueta, 42°52′N, 0°49′W, 1350 m a.s.l.) for A. alba measurements (Peguero-Pina et al. 2007). Precipitation was higher in Gamueta (A. alba), whereas temperature and atmospheric vapor pressure deficit were higher in Orcajo (A. pinsapo) (see meteorological data in Peguero-Pina et al. 2011). Measurements were made in 10 isolated individuals in the open field (denoted as OI) and in 10 understory individuals (denoted as UI) for both A. pinsapo and A. alba.

The mean daily quantum flux density (Q_int, mol m⁻² day⁻¹) was calculated for both sites in the open field and in the understory during the growing season (April–September). To do this, we used hemispherical photographs obtained with a digital camera with a fish-eye conversion lens providing a focal length equivalent to 8 mm in a 35 mm format (Esteso-Martínez et al. 2010). A total of 25 photographs per site were analyzed with the Gap Light Analyzer software version 2.0 (GLA V2.0, Frazer et al. 1999). Mean Q_int values were 38.0 ± 1.4 and 8.3 ± 0.5 mol m⁻² day⁻¹ for A. pinsapo and 42.0 ± 1.2 and 6.2 ± 0.4 mol m⁻² day⁻¹ for A. alba, for the open field and the understory, respectively. Furthermore, the leaf area index (LAI, m² m⁻²) was calculated for the canopies of both stands. Mean LAI values were 1.52 ± 0.08 and 2.30 ± 0.09 m² m⁻² for the canopies of A. pinsapo and A. alba, respectively.

Leaf mass to area ratio

Leaf mass to area ratio (LMA, mg cm⁻²) was measured on 10 current-year shoots of A. alba and A. pinsapo collected from OI and UI trees. Total needle dry mass for each shoot was estimated after drying the plant material in a ventilated oven at 60 °C for 48 h. Total shoot leaf area for each shoot was determined using Ballotini balls (Thompson and Leyton 1971). Leaf mass to area ratio was calculated as the ratio between the dry mass of the needles and the total shoot leaf area.

Anatomical measurements

Anatomical measurements were made in A. alba and A. pinsapo needles collected from OI and UI trees. Transverse slices of 1 × 1 mm were cut from needles and quickly fixed under vacuum with 2% p-formaldehyde (2%) and glutaric aldehyde (4%) in 0.1 M phosphate buffer solution (pH = 7.2) and postfixed 1 h in 1% osmium tetroxide. Samples were dehydrated in (i) a graded ethanol series and (ii) propylene oxide and subsequently embedded in Embed-812 embedding medium (EMS, Hatfield, PA, USA). Semi-thin (0.8 μm) and ultrathin (90 nm) cross sections were cut with an ultramicrotome (Reichert & Jung model Ultracut E). Semi-thin cross sections were stained with 1% toluidine blue and viewed under a light microscope (Optika B-600TiFL, Optika Microscopes, Ponteranica, Italy). Ultrathin cross sections were contrasted with uranyl acetate and lead citrate and viewed under a transmission electron microscope (TEM H600, Hitachi, Tokyo, Japan). Anatomical characteristics were derived from the micrographs with ImageJ software (http://rsb.info.nih.gov/nih-image/). Light microscopy images were used to determine the mesophyll thickness between the two epidermal layers (t_mes, µm), the fraction of the mesophyll tissue occupied by the intercellular air spaces (f_ias) (Patakas et al. 2003) and the mesophyll (S_m/S) and chloroplast (S_c/S) surface area facing intercellular air spaces per leaf area (Evans et al. 1994, Syvertsen et al. 1995, Tomás et al. 2013). All parameters were analyzed in at least four different fields of view and at three different sections. Electron microscopy images were used to determine the cell wall thickness (T_cw), cytoplasm thickness (T_cyt), chloroplast length (L_chl) and chloroplast thickness (T_chl) (Tomás et al. 2013). Three different sections and four to six different fields of view were used for measurements of each anatomical characteristic.

Mesophyll conductance modeled on the basis of anatomical characteristics

Leaf anatomical characteristics were used to estimate the g_m as a composite conductance consisting of within-leaf gas and liquid components, according to the 1D gas diffusion model of Niinemets and Reichstein (2003) as applied by Tosens et al. (2012a):

$$g_{\mathrm{m}}=\frac{1}{(1/g_{\mathrm{ias}})+[(R\cdot T_{\mathrm{k}})/(H\cdot g_{\mathrm{liq}})]}$$ (1)

where g_ias is the gas-phase conductance inside the leaf from substomatal cavities to outer surface of cell walls, g_liq is the conductance in liquid and lipid phases from outer surface of cell walls to chloroplasts, R is the gas constant (Pa m³ K⁻¹ mol⁻¹), T_k is the absolute temperature (K) and H is the Henry's law constant for CO₂ (Pa m³ mol⁻¹). g_m is defined as a gas-phase conductance, and thus, H/(RT_k), the dimensionless form of the Henry's law constant, is needed to convert g_liq to corresponding gas-phase equivalent conductance (Niinemets and Reichstein, 2003).

The intercellular gas-phase conductance (and the reciprocal term, r_ias) was obtained according to Niinemets and Reichstein (2003) as:

$$g_{\mathrm{ias}}=\frac{1}{r_{\mathrm{ias}}}=\frac{D_{\mathrm{A}}\cdot f_{\mathrm{ias}}}{\mathrm{\Delta }{L}_{\mathrm{ias}}\cdot \tau }$$ (2)

where ΔL_ias (m) is the average diffusion pathway to mesophyll cells (the gas-phase thickness), τ is the diffusion path tortuosity (1.57 m m⁻¹, Syvertsen et al. 1995), D_A is the diffusivity of the CO₂ in the air (1.51 × 10⁻⁵ m² s⁻¹ at 25 °C) and f_ias is the fraction of intercellular air spaces. ΔL_ias was taken as the half of the mesophyll thickness for A. alba and for UI of A. pinsapo, while ΔL_ias was taken as the average thickness of mesophyll ellipsoid up to the surface of the central cylinder for OI of A. pinsapo (about a quarter of the mesophyll thickness, Peguero-Pina et al. 2012). Total liquid-phase conductance (g_liq) from the outer surface of cell walls to the carboxylation sites in the chloroplasts is the sum of serial conductances in the cell wall, plasmalemma and inside the cell (Tomás et al. 2013):

$$g_{\mathrm{liq}}=\frac{S_{\mathrm{m}}}{(r_{\mathrm{cw}}+r_{\mathrm{pl}}+r_{\mathrm{cel},\mathrm{tot}})\times S}$$ (3)

The conductance of the cell wall was calculated as previously described in Peguero-Pina et al. (2012) but using a porosity value fixed at 0.028 for both species. This porosity value corresponds to that used by Tomás et al. (2013) for several species with cell wall thickness very similar to those found in the present study but a bit lower than those previously used in Peguero-Pina et al. (2012) (see Table S1 available as Supplementary Data at Tree Physiology Online). For the conductance of plasma membrane, we used an estimate of 0.0035 m s⁻¹ as previously suggested (Tosens et al. 2012a). The conductance inside the cell was calculated following the methodology described in Tomás et al. (2013), considering two different pathways of CO₂ inside the cell: one for cell wall parts lined with chloroplasts and the other for interchloroplastial areas (Tholen et al. 2012).

Needle gas exchange and chlorophyll fluorescence measurements

Needle gas exchange parameters were measured simultaneously with measurements of chlorophyll fluorescence using an open gas exchange system (CIRAS-2, PP-Systems, Amesbury, MA, USA) fitted with an automatic conifer cuvette (PLC-C, PP-Systems) with an FMS II portable pulse amplitude modulated fluorometer (Hansatech Instruments Ltd, Norfolk, UK). Six CO₂ response curves were obtained from OI and UI trees of A. pinsapo and from UI trees of A. alba. In light-adapted mature shoots, photosynthesis measurements started at a CO₂ concentration surrounding the shoot (C_a) of 400 μmol mol⁻¹, and a saturating photosynthetic photon flux density (PPFD) of 1500 μmol m⁻² s⁻¹ for OI shoots and 1000 μmol m⁻² s⁻¹ for UI shoots. Needle temperature was maintained at 25 °C during all measurements. Once steady-state gas exchange rate was reached under these conditions (usually 30 min after clamping the leaf), net assimilation rate (A_N), stomatal conductance (g_s) and the effective quantum yield of PSII were estimated. Thereafter, C_a was decreased stepwise down to 50 μmol mol⁻¹. Upon completion of measurements at low C_a, C_a was increased again to 400 μmol mol⁻¹ to restore the original value of A_N. Then, C_a was increased stepwise to 1800 μmol mol⁻¹. Leakage of CO₂ in and out of the cuvette was determined for the same range of CO₂ concentrations with a photosynthetically inactive shoot enclosed (obtained by heating the shoot until no variable chlorophyll fluorescence was observed), and used to correct measured leaf fluxes (Flexas et al. 2007a).

The effective photochemical efficiency of photosystem II (Φ_PSII) was measured simultaneously with A_N and g_s. For Φ_PSII, the steady-state fluorescence (F_S) and the maximum fluorescence during a light-saturating pulse of ∼8000 μmol m⁻² s⁻¹ $(F_{\mathrm{M}}^{\mathrm{\prime }})$ were estimated, and Φ_PSII was calculated as $(F_{\mathrm{M}}^{\mathrm{\prime }}-F_{\mathrm{S}})/F_{\mathrm{M}}^{\mathrm{\prime }},$ following the procedures of Genty et al. (1989). The photosynthetic electron transport rate (J_flu) was then calculated according to Krall and Edwards (1992), multiplying Φ_PSII by PPFD and by α (a term that includes the product of leaf absorptance and the partitioning of absorbed quanta between photosystems I and II). α was previously determined for each species as the slope of the relationship between Φ_PSII and ${\mathrm{\Phi }}_{\mathrm{C}{\mathrm{O}}_2}$ (i.e., the quantum efficiency of CO₂ fixation) obtained by varying light intensity under nonphotorespiratory conditions in an atmosphere containing <1% O₂ (Valentini et al. 1995). Five light curves from OI and UI trees of A. pinsapo and from UI trees of A. alba were measured to determine α.

Estimation of mesophyll conductance by gas exchange and chlorophyll fluorescence

Mesophyll conductance (g_m) was estimated according to the method of Harley et al. (1992), as follows:

$$g_{\mathrm{m}}=\frac{A_{\mathrm{N}}}{C_{\mathrm{i}}-[{\mathrm{\Gamma }}^{\ast }(J_{\mathrm{F}}+8(A_{\mathrm{N}}+R_{\mathrm{L}}))]/(J_{\mathrm{F}}-4(A_{\mathrm{N}}+R_{\mathrm{L}}))}$$ (4)

where A_N and the substomatal CO₂ concentration (C_i) were taken from gas exchange measurements at saturating light, and Γ* (the chloroplastic CO₂ photocompensation point in the absence of mitochondrial respiration) and R_L (the respiration rate in the light) were estimated for each species according to the Laisk (1977) method, following the methodology described in Flexas et al. (2007c). The values of g_m obtained were used to convert A_N–C_i into A_N–C_c curves (where C_c is the chloroplastic CO₂ concentration) using the equation C_c = C_i − A_N/g_m. The maximum carboxylation and J_flu capacities (V_c,max and J_max, respectively) were calculated from the A_N–C_c curves, using the Rubisco kinetic constants and their temperature dependence described by Bernacchi et al. (2002). The Farquhar model was fitted to the data by applying iterative curve-fitting (minimum least-square difference) method using the Solver tool of Microsoft Excel.

Estimation of g_m by a curve-fitting method

The estimation of g_m according to Ethier and Livingston (2004) is based on fitting A_N–C_i curves with a nonrectangular hyperbola version of the Farquhar's biochemical model of leaf photosynthesis (Farquhar et al. 1980). This is based on the hypothesis that presence of a finite g_m reduces the curvature of the Rubisco-limited portion of an A_N–C_i response curve. The method has been successfully used in several studies, showing a good agreement with other independent estimates of g_m (Niinemets et al. 2005, Warren and Dreyer 2006, Flexas et al. 2007b, Kodama et al. 2011). Values of the Rubisco Michaelis–Menten constant for CO₂ (K_c) and oxygen (K_o) and Γ*, and their temperature responses, were obtained from the C_c-based in vivo values of Bernacchi et al. (2002). The C_i cutoff point was determined based on the method proposed by Ethier et al. (2006).

Analysis of quantitative limitations of A_N

To separate the relative controls on A_N resulting from limited stomatal conductance (l_s), mesophyll diffusion (l_m) and limited photosynthetic capacity (l_b), we used the quantitative limitation analysis of Grassi and Magnani (2005) as applied in Tomás et al. (2013). Different fractional limitations, l_s, l_m and l_b (l_s + l_m + l_b = 1), were calculated as:

$$l_{\mathrm{s}}=\frac{g_{\mathrm{tot}}/g_{\mathrm{s}}\cdot \mathrm{\partial }{A}_{\mathrm{N}}/\mathrm{\partial }{C}_{\mathrm{c}}}{g_{\mathrm{tot}}+\mathrm{\partial }{A}_{\mathrm{N}}/\mathrm{\partial }{C}_{\mathrm{c}}}$$ (5)

$$l_{\mathrm{m}}=\frac{g_{\mathrm{tot}}/g_{\mathrm{m}}\cdot \mathrm{\partial }{A}_{\mathrm{N}}/\mathrm{\partial }{C}_{\mathrm{c}}}{g_{\mathrm{tot}}+\mathrm{\partial }{A}_{\mathrm{N}}/\mathrm{\partial }{C}_{\mathrm{c}}}$$ (6)

$$l_{\mathrm{b}}=\frac{g_{\mathrm{tot}}}{g_{\mathrm{tot}}+\mathrm{\partial }{A}_{\mathrm{N}}/\mathrm{\partial }{C}_{\mathrm{c}}}$$ (7)

where g_s is the stomatal conductance to CO₂, g_m is the mesophyll conductance according to Harley et al. (1992, Eq. (4)) and g_tot is the total conductance to CO₂ from ambient air to chloroplasts (sum of the inverse CO₂ serial conductances g_s and g_m). ∂A_N/∂C_c was calculated as the slope of A_N–C_c response curves over a C_c range of 50–100 µmol mol⁻¹. At least five curves were used for OI and UI trees of A. pinsapo and for UI trees of A. alba, and average estimates of the limitations were calculated.

Quantitative analysis of partial limitations of g_m

The determinants of g_m were divided between the component parts of the diffusion pathway (Eqs (1–3)) as in Tomás et al. (2013). The proportion of g_m determined by limited gas-phase conductance (l_ias) was calculated as:

$$l_{\mathrm{ias}}=\frac{g_{\mathrm{m}}}{g_{\mathrm{ias}}}$$ (8)

The share of g_m by different components of the cellular phase conductances (l_i) was determined as:

$$l_{\mathrm{i}}=\frac{g_{\mathrm{m}}}{g_{\mathrm{i}}(S_{\mathrm{m}}/S)}$$ (9)

where l_i is the component limitation in the cell walls, the plasmalemma and inside the cells, and g_i refers to the component diffusion conductances of the corresponding diffusion pathways.

Determination of leaf total soluble protein and Rubisco contents

Abies pinsapo needles from OI and UI were ground in 500 µl of ice-cold extraction buffer containing 50 mM Bicine–NaOH (pH = 8.0), 1 mM ethylenediaminetetraacetic acid, 5% polyvinyl pyrrolidone, 6% polyethylene glycol (PEG₄₀₀₀), 50 mM β-mercaptoethanol, 10 mM dithiothreitol and 1% protease-inhibitor cocktail (Sigma-Aldrich Co. LLC., St. Louis, MO, USA). The extracts were centrifuged at 14,000 × g for 1 min at 4 °C and the total soluble protein (TSP) concentration in supernatant was determined by the method of Bradford (1976). The concentration of Rubisco was determined with the gel electrophoresis method (Suárez et al. 2011, Bermúdez et al. 2012) using known concentrations of purified Rubisco from wheat as a standard for calibration.

Shoot hydraulic conductance

As an additional measurement, the whole shoot hydraulic conductance (K_shoot, mmol m⁻² s⁻¹ MPa⁻¹) was estimated for OI and UI trees of A. pinsapo in order to explore the existence of a coordinated response between K_shoot, A_N and g_m, as previously reported by Flexas et al. (2013). Shoot hydraulic conductance was calculated following the methodology described by Brodribb et al. (2005). Six sun-exposed branches from six trees per species were collected at 07:00–08:00 h (solar time), minimizing the possibility for midday K_shoot depression (Brodribb and Holbrook 2004). The branches were enclosed in sealed plastic bags to prevent water loss, and stored in the dark for a period of at least 1 h until stomatal closure, so that all shoots from the same branch could reach the same water potential. It is assumed that this is the water potential of the shoots prior to rehydration (Ψ₀). Once this value was obtained, one shoot per branch was cut under water to prevent air entry and allowed to take up water for 120–300 s. The water potential after rehydration was subsequently obtained (Ψ_f). The whole shoot hydraulic conductance was calculated according to the following equation:

$$K_{\mathrm{shoot}}=\frac{C_{\mathrm{l}}\ln ({\mathrm{\Psi }}_0/{\mathrm{\Psi }}_{\mathrm{f}})}{t}$$ (10)

where C_l (mol MPa⁻¹ m⁻²) is the leaf capacitance for each species. C_l was calculated as the initial slope of the pressure–volume relationships, normalized by the leaf area of the shoot (Brodribb et al. 2005). Pressure–volume relationships for A. pinsapo grown in the open field and in the understory were determined in six shoots, following the free-transpiration method described in previous studies (Vilagrosa et al. 2003).

Statistical analysis

Data are expressed as means ± standard error (SE). Student's t-tests were used to compare the trait values between OI and UI trees of A. alba and A. pinsapo. All statistical analyses were carried out using SAS version 8.0 (SAS, Cary, NC, USA).

Results

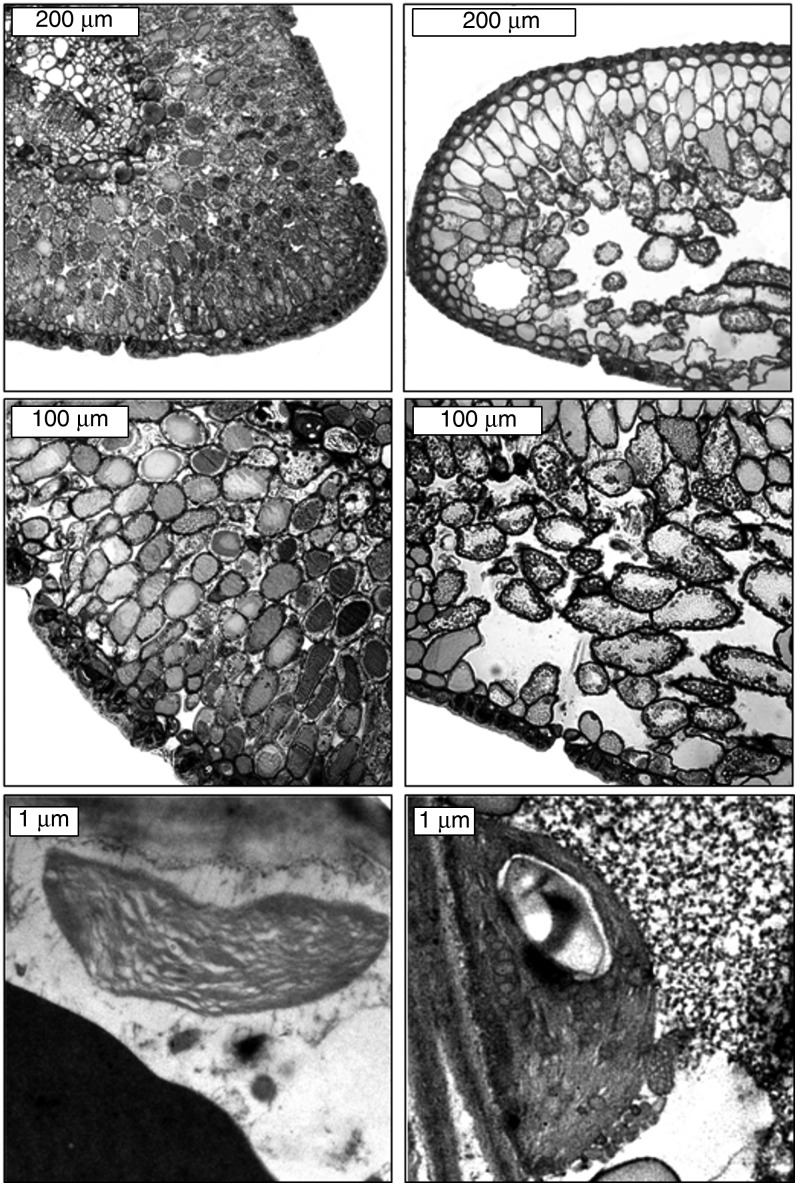
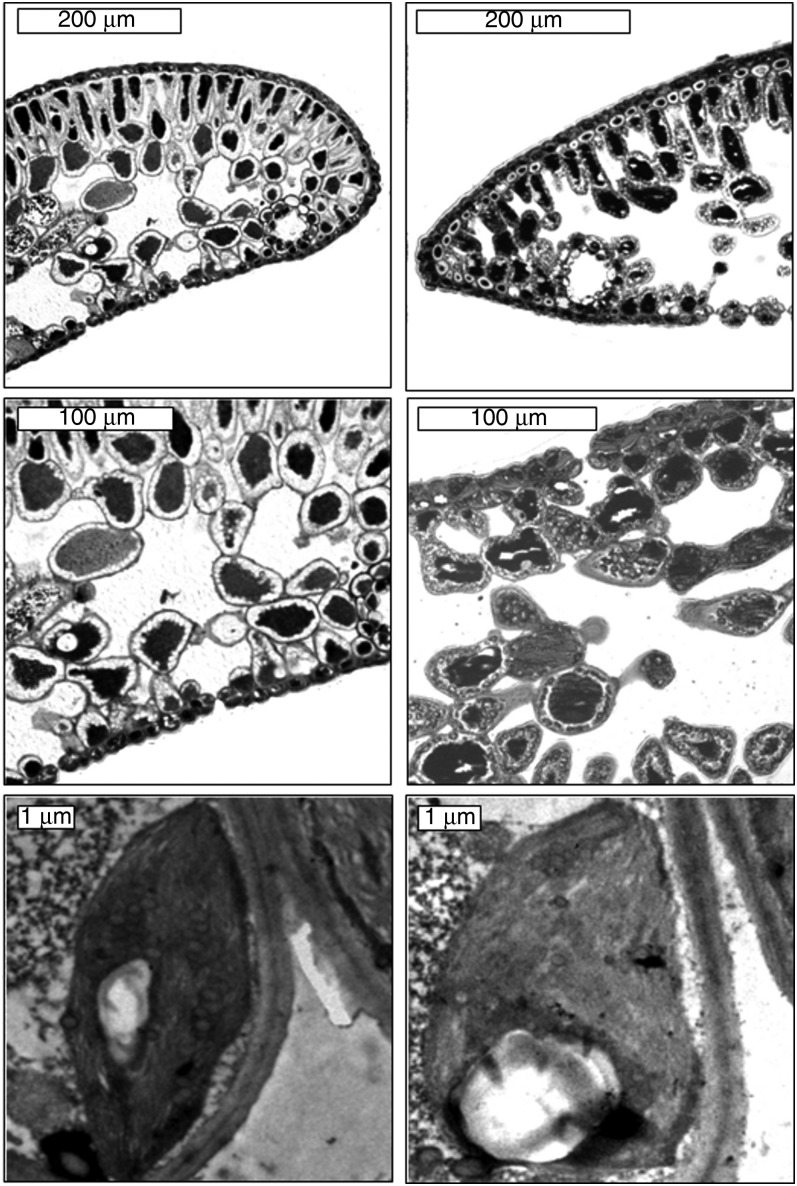
The needles of A. pinsapo grown in the open field (OI) and in the understory (UI) showed contrasting anatomical features at the leaf and cell levels (Figure 1, Table 1). The needles of A. pinsapo were amphistomatous in OI and hypostomatous in UI. The mesophyll thickness, LMA, S_m/S and S_c/S were higher in OI of A. pinsapo, whereas f_ias was higher in UI of A. pinsapo (Table 1). The ratio S_c/S_m did not differ between OI and UI of A. pinsapo. Moreover, T_cw, L_chl and T_chl were higher in UI of A. pinsapo, whereas no differences were found in T_cyt (Table 1). In contrast, the anatomical parameters of A. alba did not exhibit differences (P > 0.05) between OI and UI, with the exception of L_chl, which was higher in OI (Figure 2, Table 1). In fact, regardless of the light environment, the anatomical parameters of A. alba were very similar to those measured in UI of A. pinsapo.

Figure 1.

Transverse section of the mesophyll and mesophyll cells of A. pinsapo grown in the open field (OI, left) and in the understory (UI, right).

Table 1.

Needle type, LMA, mesophyll thickness, fraction of the mesophyll tissue occupied by the intercellular air spaces (f_ias), mesophyll surface area exposed to intercellular airspace (S_m/S), chloroplast surface area exposed to intercellular airspace (S_c/S), the ratio S_c/S_m, cell wall thickness (T_cw), cytoplasm thickness (T_cyt), chloroplast length (L_chl) and chloroplast thickness (T_chl) in A. pinsapo and A. alba grown in the open field (OI) and in the understory (UI). Data are mean ± SE (n = 6). Different letters indicate statistically significant differences (P < 0.05) between OI and UI within the same species.

	A. pinsapo OI	A. pinsapo UI	A. alba OI	A. alba UI
Needle type	Amphistomatous	Hypostomatous	Hypostomatous	Hypostomatous
LMA (mg cm−2)	25.1 ± 2.5 a	17.4 ± 2.1 b	14.8 ± 1.9 a	13.7 ± 2.3 a
Mesophyll thickness (µm)	809 ± 15 a	446 ± 9 b	428 ± 13 a	408 ± 14 a
fias	0.13 ± 0.05 a	0.35 ± 0.07 b	0.40 ± 0.06 a	0.45 ± 0.08 a
Sm/S (m2 m−2)	40.5 ± 3.9 a	25.3 ± 3.1 b	24.8 ± 2.4 a	22.7 ± 3.4 a
Sc/S (m2 m−2)	31.2 ± 2.8 a	17.4 ± 2.1 b	17.8 ± 1.9 a	15.9 ± 2.3 a
Sc/Sm	0.78 ± 0.08 a	0.69 ± 0.10 a	0.72 ± 0.06 a	0.70 ± 0.8 a
Tcw (µm)	0.236 ± 0.008 a	0.350 ± 0.011 b	0.343 ± 0.018 a	0.319 ± 0.014 a
Tcyt (µm)	0.230 ± 0.086 a	0.166 ± 0.047 a	0.169 ± 0.053 a	0.185 ± 0.021 a
Lchl (µm)	4.75 ± 0.24 a	6.86 ± 0.20 b	6.16 ± 0.26 a	5.57 ± 0.16 b
Tchl (µm)	1.37 ± 0.08 a	3.06 ± 0.21 b	3.69 ± 0.42 a	3.83 ± 0.32 a

Figure 2.

Transverse section of the mesophyll and mesophyll cells of A. alba grown in the open field (OI, left) and in the understory (UI, right).

Estimation of different components of the CO₂ transfer resistances relative to total mesophyll resistance showed that g_ias was much lower in OI of A. pinsapo (Table 2), reflecting the low value of f_ias found in these individuals (Table 1). Regarding the liquid phase, the results demonstrated that OI of A. pinsapo showed much higher values of predicted CO₂ transfer conductance (g_liq) than UI of A. pinsapo and OI and UI of A. alba (Table 2). This can be attributed to the lower values of T_cw, and T_chl found in OI of A. pinsapo (Table 1). This strong difference found in g_liq counterbalanced the lower g_ias in OI of A. pinsapo, and overall resulted in a much higher estimated value of g_m in OI of A. pinsapo than those estimated for UI of A. pinsapo and for OI and UI of A. alba (Table 2). Both g_ias and g_liq did not exhibit significant differences (P > 0.05) between OI and UI of A. alba (Table 2).

Table 2.

CO₂ transfer conductances across the intercellular air space (g_ias, m s⁻¹), the liquid phase (g_liq, m s⁻¹) and the mesophyll conductance for CO₂ (g_m, mol m⁻² s⁻¹) calculated from anatomical measurements in A. pinsapo and A. alba needles grown in the open field (OI) and in the understory (UI). Data are mean ± SE (n = 6). Different letters indicate statistically significant differences (P < 0.05) between OI and UI within the same species.

	A. pinsapo OI	A. pinsapo UI	A. alba OI	A. alba UI
gias (m s−1)	0.0074 ± 0.0004 a	0.0153 ± 0.0011 b	0.0179 ± 0.0013 a	0.0212 ± 0.0016 a
gliq (m s−1)	0.0053 ± 0.0005 a	0.0022 ± 0.0003 b	0.0021 ± 0.0002 a	0.0020 ± 0.0002 a
gm (mol m−2 s−1)	0.117 ± 0.016 a	0.077 ± 0.010 b	0.074 ± 0.012 a	0.072 ± 0.010 a

In A. pinsapo, g_m estimated by gas exchange and chlorophyll fluorescence was higher in OI than in UI irrespective of the method used (Table 3), confirming the differences in the values of g_m predicted on the basis of needle anatomical traits. A_N and g_s were also higher in OI (11.5 µmol CO₂ m⁻² s⁻¹ and 0.105 mol H₂O m⁻² s⁻¹, respectively) than in UI (5.2 µmol CO₂ m⁻² s⁻¹ and 0.043 mol H₂O m⁻² s⁻¹, respectively), so that intrinsic water use efficiency (A_N/g_s) was very similar for both low and high light grown A. pinsapo trees (Table 3). Parameterization of the Farquhar et al. (1980) model of photosynthesis yielded higher values for V_{c,max_Cc} and J_flu in OI of A. pinsapo (Table 3). The analysis of the quantitative limitations of photosynthesis revealed that A_N in A. pinsapo was mainly limited by the stomatal conductance (l_s = 44 and 50% for OI and UI, respectively), whereas l_m accounted for 33 and 31%, and l_b for 23 and 19%, for OI and UI, respectively.

Table 3.

Mean ± SE (n = 6) values for the photosynthetic parameters analyzed for A. pinsapo and A. alba grown in the open field (OI) and in the understory (UI). A_N, net photosynthesis; g_s, stomatal conductance; g_m, mesophyll conductance to CO₂; V_{c,max_Cc} and J_{max_Cc}, maximum velocity of carboxylation and maximum capacity for electron transport calculated from gas exchange on a C_c basis; J_flu, electron transport rate estimated by chlorophyll fluorescence. Different letters indicate statistically significant differences (P < 0.05) between OI and UI within the same species. ¹Data obtained from Peguero-Pina et al. (2012).

	A. pinsapo OI	A. pinsapo UI	A. alba OI1	A. alba UI
AN (µmol CO2 m−2 s−1)	11.5 ± 0.7 a	5.2 ± 0.1 b	7.3 ± 0.4 a	7.7 ± 0.3 a
gs (mol H2O m−2 s−1)	0.105 ± 0.011 a	0.043 ± 0.004 b	0.116 ± 0.010 a	0.098 ± 0.012 a
AN/gs (µmol mol−1)	115.5 ± 10.8 a	122.0 ± 11.5 a	63.4 ± 3.7 a	77.6 ± 5.2 b
gm Harley (mol CO2 m−2 s−1)	0.137 ± 0.016 a	0.071 ± 0.028 b	0.068 ± 0.004 a	0.073 ± 0.006 a
gm Ethier (mol CO2 m−2 s−1)	0.151 ± 0.010 a	0.078 ± 0.019 b	0.081 ± 0.011 a	0.065 ± 0.009 a
Vc,max_Cc Harley (µmol m−2 s−1)	158 ± 12 a	134 ± 7 b	117 ± 6 a	105 ± 9 a
Vc,max_Cc Ethier (µmol m−2 s−1)	171 ± 11 a	123 ± 13 b	113 ± 14 a	117 ± 10 a
Jmax_Cc Harley (µmol m−2 s−1)	221 ± 17 a	201 ± 9 a	138 ± 10 a	130 ± 12 a
Jmax_Cc Ethier (µmol m−2 s−1)	203 ± 11 a	188 ± 10 a	158 ± 14 a	139 ± 11 a
Jflu (µmol m−2 s−1)	171 ± 12 a	138 ± 6 b	134 ± 16 a	102 ± 8 b
Jmax_Cc : Vc,max_Cc Harley	1.39 ± 0.09 a	1.49 ± 0.05 a	1.18 ± 0.04 a	1.24 ± 0.07 a
Jmax_Cc : Vc,max_Cc Ethier	1.18 ± 0.10 a	1.52 ± 0.08 b	1.38 ± 0.07 a	1.20 ± 0.09 a

In A. pinsapo, the concentration of TSP per needle area in UI needles was 53% lower than that in OI. The decrease in the Rubisco concentration per needle area in UI with respect to OI was of similar magnitude (57%), so that the ratio Rubisco/TSP was kept constant between the treatments (0.20 and 0.23 in OI and UI, respectively).

The values of K_shoot for A. pinsapo showed trends consistent with those described above for photosynthetic parameters: the value for OI (6.21 ± 0.24 mmol m⁻² s⁻¹ MPa⁻¹) was higher than that for UI (1.81 ± 0.15 mmol m⁻² s⁻¹ MPa⁻¹) (P < 0.05).

In contrast to A. pinsapo, photosynthetic traits of A. alba needles did not differ between UI and OI, irrespective of the method used (Table 3). This is in agreement with the lack of significant differences in the estimated values of g_m based on needle anatomical traits (Table 2). In A. alba, A_N was mainly limited by the mesophyll (l_m = 51 and 44% for OI and UI, respectively), whereas l_s accounted for 30 and 32% and l_b accounted for 19 and 24%, for OI and UI, respectively (data not shown).

Discussion

Photosynthetic acclimation to growth light in A. pinsapo as driven by anatomy

In this study, we have shown that an increase in Q_int of about five times in the open field of the studied population of A. pinsapo causes a sharp increase in the photosynthetic capacity of OI when compared with UI of this species (Table 3). While photosynthetic traits like V_c,max and J_max were significantly different in OI and UI plants, these differences were small compared with those in g_m, for which the latter was largely responsible for phenotypic plasticity of A_N. Strong differences in g_m found between OI and UI of A. pinsapo can be attributed to the great phenotypic response found in needle anatomical traits, i.e., needle type (amphistomatous vs hypostomatous), S_c/S, the cell wall thickness and especially the chloroplast thickness (Table 1, Figure 1). The drastic phenotypic response of A. pinsapo to changes in growth light has been reported previously by Sancho-Knapik et al. (2014) in terms of plant capacity to supply water to the needles, i.e., the plasticity in shoot hydraulic conductance parameters in response to the limitations imposed by growing in a Mediterranean forest understory (low light and high vapor pressure deficit). However, the changes reported in this new study in terms of mesophyll anatomical traits and their implications in g_m constitute a new insight into the functional acclimation to variations in environmental conditions in conifers.

Previous studies have evidenced the role of these traits in determining the specific variability in g_m across species (Tosens et al. 2012b, Tomás et al. 2013) or among plant functional types (Carriquí et al. 2015). In this regard, Peguero-Pina et al. (2012) found that differences in g_m and photosynthesis between A. pinsapo and A. alba were related to changes in needle anatomical traits. Nevertheless, this early study was focused on the interspecific differences between both species without taking into consideration the role of drastic environmental changes such as growth light. Within species, effects of growth light have been investigated in laboratory conditions (e.g., Tosens et al. 2012a), but to the best of our knowledge, the role of such drastic changes in ultrastructural needle traits in explaining the response of g_m to the light environment has not been demonstrated in field conditions. Although the relationship between the variations in g_m and some anatomical traits observed in our study may not be enough to establish causality, the fact that the anatomy-based estimates of g_m closely resemble the estimates made by in vivo measurements strongly suggests that there must be at least a partial causality between changes in anatomy and changes in g_m.

Few studies have specifically dealt with the role of the chloroplast size in the performance of the photosynthetic apparatus. Li et al. (2012) showed that, under water stress conditions, the downsizing of chloroplasts in Oryza sativa L. restrained the g_m and photosynthetic rate. These authors attributed this phenomenon to the decrease in the surface area of chloroplasts exposed to intercellular air spaces (S_c/S). However, this does not seem to be the case of A. pinsapo, with OI having smaller chloroplasts (lower T_chl and L_chl) but higher S_c/S in OI than in UI (Table 1).

When compared with OI, the needles of A. pinsapo grown in the forest understory showed a higher fraction of the mesophyll occupied by intercellular air spaces (f_ias) (Table 1), which is a common response of plants grown under low light conditions (Terashima et al. 2011). Higher f_ias correlated with a decreased CO₂ transfer resistance across the air phase (Table 3), as already reported by other authors (Galmés et al. 2013). In spite of this, the ∼2.5-fold increases in the CO₂ transfer resistance across the liquid phase—mainly imposed by the cell wall and the chloroplast stroma (Table S2 available as Supplementary Data at Tree Physiology Online)—constrained the overall needle CO₂ transfer capacity of UI, resulting in a decreased g_m when compared with OI of A. pinsapo (Table 2). It is possible, however, that the effect of stroma thickness on the overall resistance is somewhat overestimated due to the facilitation effect of carbonic anhydrase and even by Rubisco itself as it can enhance the stromal CO₂ diffusion gradients (Terashima et al. 2011, Tholen and Zhu 2011). However, for noncompartmentalized systems such as chloroplast stroma, quantitative evidence of the involvement of carbonic anhydrase in altering g_m and A_N remains elusive, for which it is difficult to evaluate its quantitative contribution to diffusion gradients (reviewed by Flexas et al. 2008, 2012). In addition, Weise et al. (2015) have shown recently in arc mutants with fewer but larger chloroplasts that g_m is indeed reduced by 25–50% by increased stromal pathway. Therefore, following Tosens et al. (2012a), we did not include the potential effect of carbonic anhydrase in our analysis, although we acknowledge that this may result in some overestimation of the stromal size effect.

Our results show a coordinated response between leaf g_m and shoot hydraulic conductance (K_shoot). We suggest that such a correlation reflects the coordination of stomatal conductance (g_s) with K_shoot (Brodribb and Feild 2000, Brodribb et al. 2007) and coordination between g_s and g_m, which is partly due to the fact that water and CO₂ share a significant portion of their respective pathways in the mesophyll (Flexas et al. 2013). Ultimately, these correlations are expected to result in a general coordination among photosynthetic capacity and K_shoot (Brodribb and Feild 2000, Brodribb et al. 2007). Thus, we argue that this coordination may help determining the maximum rates of photosynthesis of A. pinsapo growing under shifting environmental conditions, as it may be at least partially responsible for the observed coordination between g_s and g_m, which in turn results in maximizing the total leaf conductance to CO₂. In this regard, the differences found in g_m between OI and UI of A. pinsapo did not have additional consequences in limiting net photosynthesis, mainly because changes in g_s were of higher magnitude and constituted the main limiting factor for A_N in this species.

How does the needle light acclimation differ between the two congeneric Abies species?

In contrast to A. pinsapo, A. alba did not show significant differences either in needle anatomical traits (Table 2, Figure 2) or in photosynthetic parameters (Table 3) between OI and UI trees, even with an increase in Q_int (about seven times) slightly higher than that measured for the studied population of A. pinsapo (about five times). A narrow photosynthetic plasticity of A. alba to high PPFD was previously described by Grassi and Bagnaresi (2001). In this sense, the limited response of A. alba in needle structural and physiological traits to changes in light availability points in the same direction as the general trend found by Niinemets et al. (2015) in conifers when compared with other plant functional types. On the other hand, Cescatti and Zorer (2003) observed a larger within-canopy plasticity in A. alba and Robakowski et al. (2003) found a plastic response to different levels of irradiance in seedlings of A. alba. Therefore, there is a lack of consensus about the plasticity of A. alba to changing irradiance, which is a matter that deserves further investigation. It is also plausible that the low photosynthetic plasticity of A. alba observed here and in the study of Grassi and Bagnaresi (2001), both conducted at the southern drier limits of A. alba dispersal, might reflect population-level differentiation of the fragmented populations at the range margins. Stronger intraspecific competition in denser stands within more favorable parts of species' bioclimatic distribution is likely to favor greater plasticity as observed in several studies conducted on A. alba in its center of dispersal (Aussenac 1973, Cescatti and Zorer 2003, Robakowski et al. 2003).

Conclusions

This study confirms the high plasticity showed by A. pinsapo to changes in light availability, in accordance with a previous paper dealing with the light acclimation of this species in terms of water transport to the atmosphere (Sancho-Knapik et al. 2014). In this new study, we explore the changes in some anatomical traits in the needle mesophyll, revealing that the plasticity of this Mediterranean fir operates at different levels in a coordinated way. We conclude that A. pinsapo experienced profound modifications in needle anatomy to drastic changes in Q_int that ultimately led to differential photosynthetic performance between OI and UI trees. However, A. alba did not show differences either in needle anatomy or in photosynthetic parameters between OI and UI trees. The increased g_m values found in OI trees of A. pinsapo can be explained by occurrence of amphistomatous needles, increased S_c/S, decreased T_cw and, especially, decreased T_chl. To the best of our knowledge, the role of such drastic changes in ultrastructural needle anatomy in explaining the response of g_m to the light environment has not been demonstrated in field conditions.

Supplementary data

Supplementary data for this article are available at Tree Physiology Online.

Conflict of interest

None declared.

Funding

This study was partially supported by projects AGL2009-07999 awarded to J.G. and BFU2011-23294 awarded to J.F. (Ministerio de Ciencia e Innovación, Spain). Financial support from Gobierno de Aragón (H38 research group) is also acknowledged. Work of D.S.-K. is supported by a DOC-INIA contract co-funded by the Spanish National Institute for Agriculture and Food Research and Technology (INIA) and the European Social Fund (ESF).