Skip to main content
PMC home page
NIHPA Author Manuscripts logoLink to NIHPA Author Manuscripts
. Author manuscript; available in PMC: 2017 Apr 1.
Published in final edited form as: J Biomed Inform. 2016 Jan 28;60:114–119. doi: 10.1016/j.jbi.2016.01.012

Generating a Robust Statistical Causal Structure Over 13 Cardiovascular Disease Risk Factors Using Genomics Data

Azam Yazdani 1,*, Akram Yazdani 1, Ahmad Samiei 2, Eric Boerwinkle 1
PMCID: PMC4886234  NIHMSID: NIHMS759852  PMID: 26827624

Abstract

Understanding causal relationships among large numbers of variables is a fundamental goal of biomedical sciences and can be facilitated by Directed Acyclic Graphs (DAGs) where directed edges between nodes represent the influence of components of the system on each other. In an observational setting, some of the directions are often unidentifiable because of Markov equivalency. Additional exogenous information, such as expert knowledge or genotype data can help establish directionality among the endogenous variables. In this study, we use the method of principle component analysis to extract information across the genome in order to generate a robust statistical causal network among phenotypes, the variables of primary interest. The method is applied to 590,020 SNP genotypes measured on 1,596 individuals to generate the statistical causal network of 13 cardiovascular disease risk factor phenotypes. First, principal component analysis was used to capture information across the genome. The principal components were then used to identify a robust causal network structure, GDAG, among the phenotypes. Analyzing a robust causal network over risk factors reveals the flow of information in direct and alternative paths, as well as determining predictors and good targets for intervention. For example, the analysis identified BMI as influencing multiple other risk factor phenotypes and a good target for intervention to lower disease risk.

Keywords: Causal Network, Data Integration, Cardiovascular Disease Risk Factors, Partial Correlation, Conditional Independency, Granularity DAG

Graphical Abstract

graphic file with name nihms759852u1.jpg

Introduction

Interindividual variation in disease susceptibility is influenced by genetic variants, which can be organized into a defined biologic pathways or data-driven associative networks [1–3]. By identifying variables correlated with the primary endpoint of interest, we are able to classify individuals and predict future disease. Going beyond partial correlations and evaluating causal relationships among variables plays an essential first step in risk prediction, thereby promoting more efficacious treatment of current disease and prevention of future disease. By changing the level of a causal variable (e.g. LDL-cholesterol levels), we are able to change the risk of future disease (e.g. coronary heart disease), which may not be the case for mere associated variables (e.g. HDL-cholesterol levels) [4]. In the case of a randomized intervention, such as a clinical trial, identification of causation is conceptually straight forward. However, in observational studies, which represent the majority of most large-scale epidemiologic studies, causal inference is more complex. In most applications, especially “big data” applications, causal inference is embodied in Directed Acyclic Graphs (DAG), where any inference is based on an estimated graph (i.e. nodes and edges). DAGs are illustrations of causal relationships among the variables. Mendelian randomization is an established approach to identify causal relationships [5–8] and it is natural in a biomedical setting to integrate genomics and phenotypic information to help establish directionality within a network of phenotypes. We apply this technique in large data sets from different granularities to achieve robust causal graphs (i.e. DAGs). In the present context, granularities are defined as hierarchical levels with different quiddity that the causal relationship between them is known, e.g. they are reflecting different levels of biologic organization and measurement (genomic and phenotypic, [4]). In the application shown here, we use data from a deeper granularity, the genome, to generate a robust statistical causal network among 13 risk factor phenotypes. Inclusion of genotypes in the analysis of phenotypes (e.g. plasma glucose levels) provides two advantages: first, genotypes are assumed to be measured without error, and second, there is a natural order between these granularities (genome variation → phenotype variation; G→P) and this knowledge helps identify robust directionality in the upper granularity.

Using genome information is a promising approach to identify directionality that is less susceptible to confounding. Previous applications in data integration using gene expression data and genotypes have followed a similar logic [9–12]. For example, Mehrabian et al., [9] integrated genotypic and phenotypic data in a segregating mouse population to generate causal relationships. Aten et al., [11] introduced an algorithm to estimate directionality among nodes in a DAG by applying information from selected single nucleotide polymorphisms (SNPs). In this study, we apply the concept of granularity in a comprehensive manner and extract information from a deeper granularity, here the genome, to achieve a robust causal network among variables of interest in the upper level of granularity, here cardiovascular risk factor phenotypes. To go beyond using a sample of SNPs, which are incomplete and may introduce instability in the study results [13], the method of principal components is used to extract information across the genome. Integration of genome information embedded in the deeper granularity and captured using principal component analysis with phenotype information in the upper granularity results in a robust causal network among the phenotypes, and we call this algorithm granularity directed acyclic graph (GDAG).

We first briefly review the theory of graphical causal inference and introduce the granularity framework and the GDAG algorithm. The utility of this approach is introduced by application to a data set including 13 cardiovascular disease risk factors and 590,020 SNP genotypes measured on 1,596 individuals and then the estimated structure is further interpreted. Use of information from the genome level of granularity allowed us to robustly generate the statistical causal network among the phenotypes. A discussion of the GDAG algorithm and the results is provided.

1 Background

Assume a DAG D = (v,ε) where v is a set of nodes with p elements which corresponds to a set of p random variables and ε is a set of edges which connect the nodes and shows the partial correlation between two corresponding variables. The existence of a directed edge between two nodes shows the causal relationship between the corresponding variables. Assume P is a joint probability distribution over the variables corresponding to the nodes in DAG D = (v,ε). The underlying assumption for a DAG is the Markov condition over D and P [14]. D and P must satisfy the Markov condition: every variable Yi, i ∈ v is independent of any subset of its predecessors conditioned on a set of variables, corresponds to parents/immediate causes of node i,

Yi⊥{Yk;i&k∈v\pa(i)}∣Ypa(i),

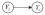where Yk occurs before Yi and parental set pa(i) = paD(.) denotes the set of parents of node i relatives to the underlying structure of DAG D. For j ∈ pa(i), we denote j → i or Inline graphic.

A topology or skeleton of a DAG is a graph without direction and is obtained by identification of conditional (in)dependencies, see section “Identification the Topology of Nodes” below. Identification of directions is however a challenging problem due to the Markov equivalent property of observational data. Analysis of data in the upper granularity can identify only v-structures, two nonadjacent nodes pointing inward toward a third node. A complete assessment of directionality (i.e. statistical causal relationships) usually cannot be determined from such data alone, resulting in Markov equivalent DAGs [15–16]. Different DAGs on the same set of nodes are Markov equivalent (ME DAGs) if and only if they have the same topology and the same v-structures [17]. When the number of nodes grows, the number of ME DAGs can grow super-exponentially [18]. Complete determination of directionality over the corresponding set v is not, however, possible in most of cases.

2 The GDAG Method

Identifying robust and complete directionality and showing flow of information is a difficult task, but can be facilitated by integration of different data types (i.e. granularities) where we know the direction of effect is from one granularity to the other. Assume we are seeking a DAG between two phenotypes Y1 and Y2. For this example, assume genome-wide information, related to the set (Y1,Y2) is captured in the variable X1. Based on the results of an analysis assessing conditional independencies, we find that X1 is correlated to Y1 and is independent of Y2 given Y1, by notationY2⊥X1|Y1. Since genome sequence variation is a causal factor in phenotypic differences (and not the other way around), the direction of the effect is from X1 to Y1, as shown in DAG A in Figure 1. Knowing the relationship between X1 and Y1 helps generate the directionality between Y1 andY2 based on the property Y2 ⊥ X1|Y1, and the direction shows the flow of information is from Y1 toY2, as shown in DAG B in Figure 1. If we obtain X1 ⊥ Y2 & X1 ⊥̸ Y2|Y1 by analysis of the data, then the direction of effect would be from Y2 to Y1, as shown in DAG C in Figure 1, which represents a v-structure at Y1.

Figure 1.

Figure 1

Open in a new tab

DAG A is a representation of three connected variables as well as the knowledge about direction of the effect between two granularities where variable X1 is from a deeper granularity. DAG B and DAG C represent direction identification based on analysis of data.

To identify the direction among three variables in ME DAGs 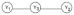Inline graphic, we need to have at least two variables from the genome (i.e. a lower level of granularity, where G→P) influencing Y1 and Y2 or one variable from the genome influencing Y3. By integrating multi-omics data from different granularities, we are able to derive causal inference that is less susceptible to confounding and, as a result, estimate causal networks robustly and uniquely. Partial information from a deeper granularity creates weak instrumental variables and may result in unstable structures in the upper granularity [13], and we may not be able to find a genome variable strongly associated with every phenotype under study [19]. Therefore, we go beyond inclusion of a sample of SNP marker genotypes and extract comprehensive information across the genome by application of principal component analysis (PCA) to reduce the dimensionality of the data while retaining most of the variation in the data set. Since PCA is an unsupervised approach, it avoids increasing false discovery using the same data twice. The steps of the GDAG algorithm are summarized as follows:

The GDAG Algorithm: Steps to identify a Granularity Directed Acyclic Graph (GDAG) over a set of variables of interest, Y, using data from a deeper granularity, X

  1. Extract genome information by principal component analysis. Select the principal components responsible for a majority of genome variation, set X.

  2. Estimate a topology over sets Y and X.*

  3. If a variable in set X is linked to a variable in set Y, draw an arrow from the former to the latter.

  4. Use the established directions from step 3, generate other directions using partial correlations recorded in step 2.**

  5. If there is an undirected link between Ys, use rules in [20] to identify directionality.***

Open in a new tab
*

Topology estimation is detailed in the following section

**

Presented at the beginning of this section.

***

The supplementary information provides further details.

To make the algorithm feasible, we assume the underlying network is sparse. A sparse network is a network with fewer numbers of links than the maximum possible number of links within the same network [21]. Under the sparsity assumption, the run-time of the algorithm is reduced to a polynomial and as a result the number of nodes can grow with the sample size. This assumption is reasonable and is often considered in most biomedical applications [22–25].

When applying the GDAG algorithm, we are primarily interested in the causal relationships among nodes in the upper granularity, not among nodes in the deeper granularity or the relationship between the deeper and upper granularities. In the current application, genome information summarized by PCAs is applied to identify a robust statistical causal network structure among cardiovascular risk factor phenotypes in upper granularity. In genetics and epidemiology, application of PCA for summarizing genome information is frequent [e.g. 26–29].

3 Identification the Topology of Nodes

In this manuscript, generating the basic topology among nodes and then assessing directionality are carried out by finding conditional independencies in the framework of data integration. One statistical approach to estimate conditional independencies under a Gaussian assumption is assessing partial correlations [30–32]. Conditioning only on one variable, the partial correlation is defined as

ρyiyj.yk=ρyiyj-ρyiykρyjyk(1-ρyiyk2)(1-ρyjyk2),

where ryiyj=cov(yi,yj)/var(yi)var(yj) is the Pearson product-moment correlation coefficient. Fisher’s Z transform is used to assess the statistical significance of the sample correlation coefficient, r. If the partial correlation between two variables Yi and Yj given variables corresponding to a subset s ⊆v\{i,j} is not determined to be significantly different from zero at some significance threshold, then the corresponding nodes i and j are not connected with an edge. On the other hand, there is an edge between nodes i and j if and only if given all subsets s ⊆ v\{i, j}, Yi and Yj are significantly correlated (see [33] prop. 5.2). Assessing all partial correlations in the case of multivariate normal distribution to estimate conditional independencies is computationally unfeasible. Therefore, a sparsity assumption is employed, meaning that each node is connected to only some but not all of the nodes in the network.

4 Results

Application to Simulated Data

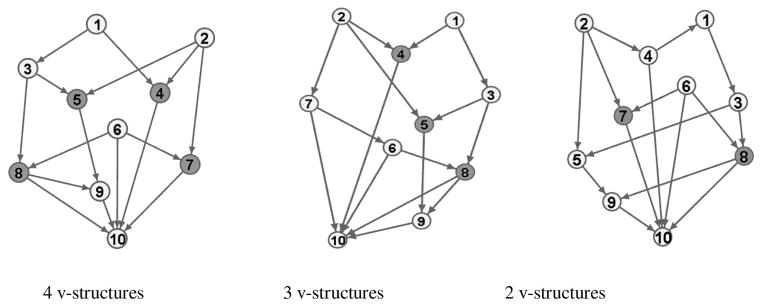
To evaluate the properties of the GDAG algorithm, we used simulated data. We estimated the simulated DAG without genomic information and separately with the GDAG algorithm incorporating the genomic information. We then compared the frequency of false discoveries (FD), which are the number of wrong directions, and non-discoveries (ND), which are the number of non-directed edges, estimated by each method. Since the performance of the algorithms depends on the number of v-structures in the underlying causal graph, we considered DAGs with different numbers of v-structures. The underlying models of the simulations are depicted in Figure 2.

Figure 2.

Figure 2

Open in a new tab

Three truth sets. The underlying graph on the left has 4 v-structures (at nodes 4, 5, 7, and 8), the middle has 3 v-structures (at nodes 4, 5, and 8), and on the right has 2 v-structures (at nodes 7 and 8). The nodes that v-structures are formed in are highlighted in the graphs.

In order to have genotype data with a realistic linkage disequilibrium structure, we generated 10,000 SNPs for 2000 individuals on the basis of a coalescent model that mimics the linkage disequilibrium (LD) (i.e. non-random association of alleles at different loci) pattern, local recombination rate and the population history of African American and European American using a previously validated demographic model [34].

Phenotype values were generated using the structural model

Zi=∑j=1i-1λijZj+∑k=1qγikXk+εi,

for j < i, where the phenotypes (Zj) in the model are compatible with the graphs in Figure 2. For each scenario, SNPs were selected randomly from the larger set of generated SNPs. The εi in the model was assumed to be Gaussian with unit variance. The value of non-zero genome effects were randomly sampled from a U (−0.9, − 0.5) and U (0.5,0.9) and the value of the non-zero phenotype effects were sampled from a uniform U (− 1.9, − 1.0) and U (1.0,1.9). The values of these extreme points were based on preliminary analyses. While other studies such as [32] considered only positive effects, we considered both negative and positive effect sizes.

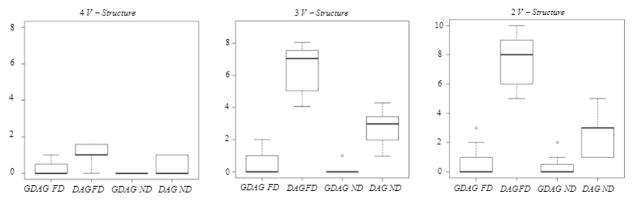
The simulated data were analyzed considering only the phenotypic data using the PC-algorithm [35] which is implemented with polynomial complexity in high-dimensional sparse setting [32]. The simulated data were also analyzed using the GDAG algorithm based on both phenotypic and genomic data. To apply the GDAG algorithm, we extended the PC-algorithm to analyze data from different granularities. We extracted information from the generated SNPs using principal component analysis and selected the first 110 principal components responsible for almost 90% of variation to form the set X in the GDAG algorithm. Result of the comparison of the performance of the PC and the GDAG algorithms based on fifty repetitions is summarized in figure 3, which shows the number of false discoveries (FD) and non-discoveries (ND) under different scenarios.

Figure 3.

Figure 3

Open in a new tab

Comparison of the performance of the GDAG and PC algorithms by comparing False Discoveries (FD) and Non Discoveries (ND) under different numbers of v-structures.

The GDAG algorithm has fewer FDs and NDs compared to a simple DAG application without the genome information. As can be seen in Figure 3, the performance of the PC-algorithm is improved dramatically by adding information from a deeper granularity. There have been other attempts to improve the PC-algorithm’s characteristics. For example, de Campos et al. [36] improved the PC-algorithm by employing three types of structural restrictions, and Shojaei et al. [25] achieved better performance using a penalization approach.

The GDAG Performance for Different Numbers of Samples and Significance Levels

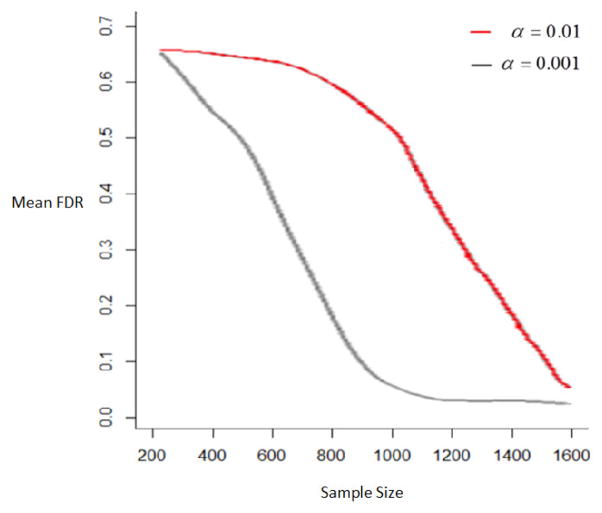
The GDAG algorithm can generate directionality robustly because it leverages information from a deeper granularity. Here, we examine the performance of the GDAG algorithm for different numbers of observations and two significance levels. We simulated different number of individuals and 40 replicates for each sample size for an underlying network with directionality. Using data from a deeper granularity, the GDAG algorithm was used to generate the topology and directionality for each replication. Therefore, when assessing the GDAG performance across different scenarios, showing either the false discovery rate (FDR) or true discovery rate are sufficient. The mean FDRs across the 40 replicates for each sample size were calculated. A smooth line over mean of FDRs is depicted in Figure 4. The red line shows the mean FDRs at the significance α =0.01 and the black at α =0.001.

Figure 4.

Figure 4

Open in a new tab

Mean FDRs for different sample sizes and different significant levels: α =0.01, the red line, and α = 0.001, the black line

Examination of the FDR rate in Figure 4 indicates unsatisfactory rates of false discovery at small sample sizes (e.g. <600 for alpha =0.001 and <1200 for alpha =0.01) and satisfactory rates at larger sample size at both significance levels. For sample sizes between 600 and 1200, alpha=.001 provides more reliable result than alpha=.01.

Application to Genotype and Risk Factor Data

As an application of the GDAG algorithm, we identified causal relationships among 13 chronic disease risk factor phenotypes: BMI (body mass index), SB (systolic blood pressure), DB (diastolic blood pressure), FG (fasting glucose), FS (fasting insulin), HDL (high density lipoprotein), LD (low density lipoprotein), TRIG (triglyceride), TC (total cholesterol), FIBR (Fibrinogen), PLT (Platelet count), as well as electrocardiogram measurements QT and QRS. The data set includes 590,020 measured genotypes in sample of 1,596 non-Hispanic white individuals from the National Heart Lung and Blood Institute (NHLBI) GO-ESP, which is an ancillary study of the Atherosclerosis Risk in Communities (ARIC) study [37], the Cardiovascular Health Study (CHS) [38], and the Framingham Heart Study [39]. The data were obtained from dbGAP [40], and this analysis is part of ongoing studies having local Institutional Review Board approval. The following steps were undertaken in order:

  1. Prior to calculation of the principle components, we identified a subset of informative SNPs using hierarchical clustering and the r2 measure of linkage disequilibrium, where r2 is the square of correlation between two SNPs [41].

  2. Since chromosomes are assumed to be independent, we applied principal component analysis over each chromosome separately and selected the first principal components responsible for approximately 90% of the variation. Over all of the chromosomes, 586 principal components were selected.

  3. The topology of the network was determined over the 13 risk factor phenotypes and the principal components. 130 genome wide principal components remained in the model at significant level 0.01.

  4. The direction of effect was assumed to be from the genome-wide principal components to the risk factor phenotypes (and not the other way around).

  5. Use partial correlations to estimate the Markov properties among the risk factor phenotypes and directions in step 4, the directionality of the network is determined. Details can be found in the supplementary materials.

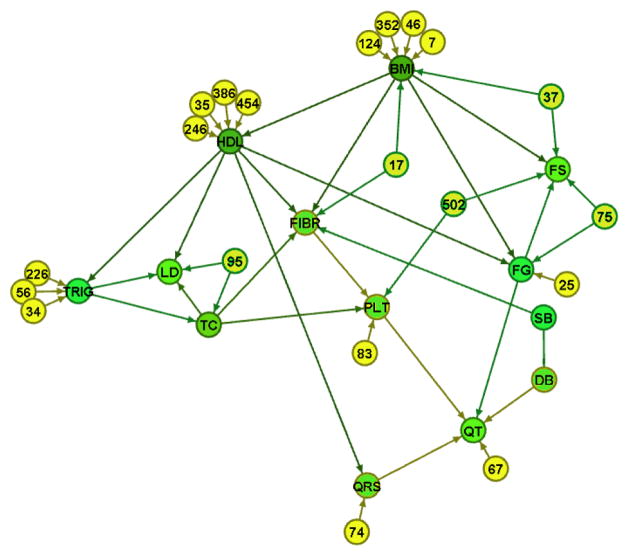
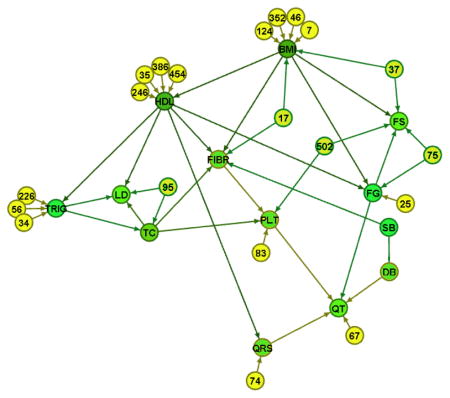
The resulting GDAG among the risk factor phenotypes is shown in Figure 5.

Figure 5.

Figure 5

Open in a new tab

A robust GDAG among 13 cardiovascular risk factor phenotypes using information across the genome embodied in 130 principal components remained in the model. Only some of them are depicted here (numbered nodes) so as to better highlight the structure among the phenotypes.

As was shown in the simulated data, use of information from the genome embedded in the principal components allowed us to estimate the causal network among the phenotypes. Some of the relationships in Figure 5 are expected, such as those among the lipid phenotypes. The analysis identified a causal link between BMI and HDL-cholesterol and an indirect effect of BMI on triglycerides. The relationship between fibrinogen and platelets underscores the important role of fibrinogen in platelet aggregation and function [42]. It is important to note the effect of BMI throughout the network.

Discussion

DAGs are illustrations of causal relationships among a set of related variables. To definitively identify causal relationships, interventions are required. However, interventions, even in some parts of the graph, are not possible in most human observational studies. Data analysis alone does not robustly identify causal relationships, except in very special cases for non-Gaussian distributions [43]. As shown here, application of domain expert knowledge and data from another granularity is helpful for identifying causal networks, including the direction of arrows and estimating the magnitude of effect sizes. In a granularity framework, we take advantages of genotype information to identify a robust statistical causal network structure among phenotypes (i.e. GDAG), which provides a high degree of certainty about finding causal relationships. Any algorithm for DAGs can be extended in the granularity framework to be able to achieve causal inference that is less susceptible to confounding by hidden variables and, as a result, estimate robust statistical causal networks which are well anchored to domain knowledge. In previous applications, a priori biologic candidate gene variation has been used to analyze phenotypes [11], but a comprehensive approach to the concept of granularity has not been used. Leveraging eQTLs identified from previous association studies to reduce the number of Markov equivalence classes among phenotypes is well-established [2–3&12] but distinct from the concept of granularity. To the best of our knowledge, there is no report using PCAs derived from genome-wide SNP information to identify the causal network structure among phenotypes. In the proposed granularity framework, the domain knowledge “genome variation causes phenotypic differences” is used along with objective dependencies in the data to estimate causal relationships.

The concept of granularity can be applied to reduce the running time of the GDAG algorithm. Since the primary interest is generating a causal network structure over the variables Y in the upper level of granularity, the topology of the causal network can be estimated only over the variables Y. After the topology is established, the GDAG algorithm seeks partial correlations between any two variables, one from X and the other from Y. Since the variables in set X, the genome-wide principal components, are independent of one another, the GDAG algorithm does not require estimating the partial correlations between the Xs. This results in further reduction of the running time.

To implement the granularity framework, we extended the Peter and Clark (PC) algorithm because it is computationally feasible and often fast for sparse problems having many nodes (variables) [32]. This method can be applied to generate network structures among many variables and reveal patterns in complex systems. A robust statistical causal network reveals patterns in the underlying structure, thereby identifying good targets for intervention and prediction. The total effects among phenotypes can be estimated by structural equations while a sufficient set of confounders identified graphically are in the model [44]. We applied the GDAG algorithm to 13 risk factor phenotypes and genome-wide principal components as the deeper granularity. Visualization of the phenotype GDAG shown in Figure 5 provides opportunities for improved disease prediction and identifying targets for risk factor intervention. Nodes with a high in-degree (i.e. number of arrows pointing into a node) correspond to variables influenced by multiple other risk factors. These nodes may be good predictors of disease since they capture information from multiple risk factors. On the other hand, nodes with a high out-degree (i.e. number of arrows pointing out of a node) correspond to variables having influences on multiple other risk factors. These nodes may be good intervention targets to lower risk and influence clinical outcomes. For example, according to the GDAG in Figure 5, a good disease predictor may be fibrinogen (FIBR) since it is influenced by multiple other risk factors. BMI may be a good intervention target since it has a high impact on the other risk factor levels, such as fibrinogen, HDL, glucose, and insulin. Changes in BMI are predicted to yield changes in the majority of the network of risk factors. In conclusion, generating a robust statistical causal network among risk factor phenotypes and using this directionality, we are able to identify good candidates for future manipulation.

Supplementary Material

supplement

Highlights.

Understanding causal relationships among large numbers of variables is a fundamental goal of biomedical sciences and can be facilitated by Directed Acyclic Graphs (DAGs) where directed edges between nodes represent the influence of components of the system on each other. In an observational setting, some of the directions are often unidentifiable because of Markov equivalency. Additional exogenous information, such as expert knowledge or genome data can help establish directionality among the endogenous variables. In this study, we use the method of principle component analysis to extract information across the genome in order to generate a robust statistical causal structure among phenotypes, our variables of interest. The method is applied to 590,020 SNP genotypes measured on 1596 individuals to generate the structure on a set of 13 cardiovascular disease risk factor phenotypes. First, principal component analysis was used to capture information across the genome. The principal components were then used to identify a robust causal structure, GDAG, among the phenotypes. Analyzing a robust causal structure over risk factors reveals the flow of information in direct and alternative paths, as well as determining predictors and good targets for intervention. For example, the analysis identified BMI as influencing multiple other risk factor phenotypes and potentially a good target for intervention to lower disease risk.

Acknowledgments

Azam Yazdani is supported in part by a training fellowship from the Keck Center for Interdisciplinary Bioscience Training of the Gulf Coast Consortia (CPRIT Grant No. RP140113). Funding for GO ESP was provided by the National Heart, Lung, and Blood Institute (NHLBI) grants RC2 HL-103010 (HeartGO) and RC2 HL-102924 (WHISP). The exome sequencing was performed through NHLBI grants RC2 HL-102925 (BroadGO) and RC2 HL-102926 (SeattleGO).

Footnotes

Disclaimer: The content is solely the responsibility of the authors and does not necessarily represent the official views of the Cancer Prevention and Research Institute of Texas.

Author Disclosure Statement: The authors declare that no conflict of interests exists.

Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.

References

  • 1.Rodin S, Boerwinkle E. Mining genetic epidemiology data with Bayesian networks I: Bayesian networks and example application (plasma APOE levels) Bioinformatics. 2005;21(15):3273–3278. doi: 10.1093/bioinformatics/bti505. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 2.Cai X, Bazerque JA, Giannakis GB. Inference of Gene Regulatory Networks with Sparse Structural Equation Models Exploiting Genetic Perturbations. 2013 doi: 10.1371/journal.pcbi.1003068. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 3.Logsdon BA, Mezey J. Gene Expression Network Reconstruction by Convex Feature Selection when Incorporating Genetic Perturbations. PLoS Comput Biol. 2010;6(12):e1001014. doi: 10.1371/journal.pcbi.1001014. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Voight BF, Peloso GM, Orho-Melander M, et al. Plasma HDL cholesterol and risk of myocardial infarction: a Mendelian randomization study. Lancet. 2012;380(9841):572–80. doi: 10.1016/S0140-6736(12)60312-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Thomas DC, Conti DV. Commentary: The concept of ‘Mendelian randomization’. International Journal of Epidemiology. 2004;33:21–25. doi: 10.1093/ije/dyh048. [DOI] [PubMed] [Google Scholar]
  • 6.Clayton D, McKeigue PM. Epidemiological methods for studying genes and environmental factors in complex diseases. Lancet. 2001;358:1356–1360. doi: 10.1016/S0140-6736(01)06418-2. [DOI] [PubMed] [Google Scholar]
  • 7.Kulp DC, Jagalur M. Causal inference of regulator-target paris by gene mapping of expression phenotypes. BMC Genomics. 2006;7:125. doi: 10.1186/1471-2164-7-125. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Thompson JR, Minelli C, Abrams KR, Tobin MD, Riley RD. Metaanalysis of genetic studies using Mendelian randomization-a multivariate approach. Stat Med. 2005;24:2241–2254. doi: 10.1002/sim.2100. [DOI] [PubMed] [Google Scholar]
  • 9.Mehrabian M, Allayee H, Stockton J, Lum PY, Drake TA, Castellani LW, Suh M, Armour C, Edwards S, Lamb J, Lusis AJ, Schadt EE. Integrating genotypic and expression data in a segregating mouse population to identify 5-lipoxygenase as a susceptibility gene for obesity and bone traits. Nat Genet. 2005;37:1224–1233. doi: 10.1038/ng1619. [DOI] [PubMed] [Google Scholar]
  • 10.Zhu J, Zhang B, Smith EN, Drees B, Brem RB, Kruglyak L, … Schadt EE. Integrating large-scale functional genomic data to dissect the complexity of yeast regulatory networks. Nature genetics. 2008;40(7):854–861. doi: 10.1038/ng.167. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Aten JE, Fuller TF, Lusis AJ, Horvath S. Using genetic markers to orient the edges in quantitative trait networks: the NEO software. BMC Systems Biology. 2008;2:34. doi: 10.1186/1752-0509-2-34. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Neto EC, Keller MP, Attie AD, Yandell BS. Causal graphical models in systems genetics: a unified framework for joint inference of causal network and genetic architecture for correlated phenotypes. The annals of applied statistics. 2010;4(1):320. doi: 10.1214/09-aoas288. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Burgess S, Thompson S. Avoiding bias from weak instruments in Mendelian randomization studies. International journal of epidemiology. 2011;40(3):755–764. doi: 10.1093/ije/dyr036. [DOI] [PubMed] [Google Scholar]
  • 14.Pearl J. Causality: Models, Reasoning, and Inference. Cambridge University Press; New York: 2009. [Google Scholar]
  • 15.Dawid AP. Research Report. Vol. 279. Department of Statistical Science, University College London; 2007. Fundamentals of statistical causality. [Google Scholar]
  • 16.Lauritzen SL, Dawid AP, Larsen BN, Leimer HG. Independence Properties of Directed Markov Fields. Networks. 1990;20:491–505. [Google Scholar]
  • 17.Verma T, Pearl J. Causal Networks: Semantics and Expressiveness. In: Shachter RD, Levitt TS, Kanal LN, Lemmer JF, editors. Uncertainty in Artificial Intelligence. Vol. 4. North-Holland; Amsterdam: 1990. pp. 69–76. [Google Scholar]
  • 18.Robinson RW. Counting labeled acyclic digraphs. In: Haray F, editor. New Directions in the Theory of Graphs; Proc. of the Third Ann Arbor Conf. on Graph Theory; 1971; NY: Academic Press; 1973. pp. 239–273. [Google Scholar]
  • 19.Inouye M, Kettunen J, Soininen P, Silander K, Ripatti S, Kumpula LS, … Peltonen L. Metabonomic, transcriptomic, and genomic variation of a population cohort. Molecular Systems Biology. 2010;6:441. doi: 10.1038/msb.2010.93. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 20.Verma T, Pearl J. An Algorithm for Deciding if a Set of observational Independencies Has a Causal Explanation. In: Dubois D, Wellman MP, D’Ambrosio B, Smets P, editors. Proceedings of the Eight Conference on Uncertainty in Artificial Intelligence. Morgan Kaufmann; 1992. pp. 323–330. [Google Scholar]
  • 21.Sprites P, Cooper G. An experiment in causal discovery using a pneumonia database. In: Heckerman D, Whittaker J, editors. Processing of the Seventh International Workshop on Artificial Inteligence and Statistics. Morgan Kaufmann; 1999. [Google Scholar]
  • 22.Meinshausen N, Bühlmann P. High dimensional graphs and variable selection with the lasso. Annals of Statistics. 2006;34:1436–1462. [Google Scholar]
  • 23.Friedman Jerome, Hastie Trevor, Tibshirani Robert. Sparse inverse covariance estimation with the graphical lasso. Biostatistics. 2008;9(3):432–441. doi: 10.1093/biostatistics/kxm045. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Hsieh Cho-Jui, et al. Sparse inverse covariance matrix estimation using quadratic approximation. Advances in Neural Information Processing Systems. 2011 [Google Scholar]
  • 25.Shojaie Ali, Michailidis George. Penalized likelihood methods for estimation of sparse high-dimensional directed acyclic graphs. Biometrika. 2010;97(3):519–538. doi: 10.1093/biomet/asq038. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 26.Ringnér M. What is principal component analysis? (2008) Nature biotechnology. 2008;26(3):303–304. doi: 10.1038/nbt0308-303. [DOI] [PubMed] [Google Scholar]
  • 27.Alter O, Brown P, Botstein D. Singular Value Decomposition for Genome-Wide Expression Data Processing and Modeling. Proceedings of the National Academy of Sciences. 2000;97:10101–10106. doi: 10.1073/pnas.97.18.10101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Price Alkes L, et al. Principal components analysis corrects for stratification in genome-wide association studies. Nature genetics. 2006;38(8):904–909. doi: 10.1038/ng1847. [DOI] [PubMed] [Google Scholar]
  • 29.Hastie T, Tibshirani R, Eisen M, Brown P, Ross D, Scherf U, Weinstein J, Alizadeh A, Staudt L, Botstein D. ‘gene Shaving’ as a Method for Identifying Distinct Sets of Genes With Similar Expression Patterns. Genome Biology. 2000;1:1–21. doi: 10.1186/gb-2000-1-2-research0003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 30.Freudenberg Jan, et al. Partial correlation analysis indicates causal relationships between GC-content, exon density and recombination rate in the human genome. BMC bioinformatics. 2009;10(Suppl 1):S66. doi: 10.1186/1471-2105-10-S1-S66. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Baba Kunihiro, Shibata Ritei, Sibuya Masaaki. Partial correlation and conditional correlation as measures of conditional independence. Australian & New Zealand Journal of Statistics. 2004;46(4):657–664. [Google Scholar]
  • 32.Kalisch M, Bühlmann P. Estimating high-dimensional directed acyclic graphs with the PC-algorithm. The Journal of Machine Learning Research. 2007;8:613–636. [Google Scholar]
  • 33.Lauritzen S. Graphical Models. Oxford University Press; 1996. [Google Scholar]
  • 34.Schaffner SF, Foo C, Gabriel S, Reich D, Daly MJ, Altshuler D. Calibrating a coalescent simulation of human genome sequence variation. Genome Res. 2005;15:1576–1583. doi: 10.1101/gr.3709305. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Spirtes P, Glymour C, Scheines R. Causationn, Prediction, and Search. Springer-Verlag; 2000. [Google Scholar]
  • 36.de Campos LM, Castellano JG. Bayesian network learning algorithms using structural restrictions. International Journal of Approximate Reasoning. 2007;45(2):233–254. [Google Scholar]
  • 37.The ARIC Investigators. The Atherosclerosis Risk in Communities (ARIC) Study: design and objectives. The ARIC investigators. American Journal of Epidemiology. 1989;129(4):687–702. [PubMed] [Google Scholar]
  • 38.http://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000287.v3.p1
  • 39.http://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs000401.v9.p10
  • 40.ncbi.nlm.nih.gov/gap
  • 41.Yazdani A, Dunson DBD. A hybrid Bayesian approach for genome-wide association studies on related individuals. Bioinformatics. 2015:btv496. doi: 10.1093/bioinformatics/btv496. [DOI] [PubMed] [Google Scholar]
  • 42.Bennett Joel S. Platelet-Fibrinogen Interactions. Annals of the New York Academy of Sciences. 2001;936(1):340–354. doi: 10.1111/j.1749-6632.2001.tb03521.x. [DOI] [PubMed] [Google Scholar]
  • 43.Shimizu S, Hoyer P, Hyvarinen A, Kerminen A. A linear non-Gaussian acyclic model for causal discovery. Journal of Machine Learning Research. 2006;7:2003–2023. [Google Scholar]
  • 44.Yazdani A, Boerwinkle E. Causal Inference in the Age of Decision Medicine. J Data Mining Genomics Proteomics. 2014;6:163. doi: 10.4172/2153-0602.1000163. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

supplement
NIHMS759852-supplement.docx (65.2KB, docx)

RESOURCES