Abstract
In recent years, there have been significant advances in our understanding of the mechanisms underlying chemically directed motility by eukaryotic cells such as Dictyostelium. In particular, the LEGI model has proven capable of providing a framework for quantitatively explaining many experiments that present Dictyostelium cells with tailored chemical stimuli and monitor their subsequent polarization. In their natural setting, cells generate their own directional signals via the detection and secretion of cAMP. Here, we couple the LEGI approach to an excitable medium model of the cAMP wave-field that is propagated by the cells and investigate the possibility for this class of models to enable accurate chemotaxis to the cAMP waveforms expected in vivo. Our results indicate that the ultra-sensitive version of the model does an excellent job in providing natural wave rectification, thereby providing a compelling solution to the “back-of-the-wave paradox” during cellular aggregation.
I. INTRODUCTION
The aggregation of individual cells of Dictyostelium Discoideum (henceforth Dicty) to form rudimentary multicellular organisms has long been a fascinating subject for biologists and physicists alike [1–3]. In this process, 104–105 cells generate a chemical roadmap via the formation, over several hours, of a self-organized wave pattern of the small organic molecule cAMP [4]. The aggregation locations are determined by the organizing centers of the wave pattern (either target sources or spiral cores) [5] as the wave emanating from a center directs nearby cells to move towards these points. This self-organization process has been extensively studied both experimentally [6, 7] and theoretically [8–11] and is reasonably-well understood.
This wave system fundamentally arises from the excitable nature of the individual cells. Cells respond to an above-threshold value of cAMP in their vicinity by manufacturing and secreting more cAMP, hence relaying the wave. There is also a needed recovery time before the cells can repeat this response in order to avoid a runaway behavior due to the autocatalytic response to cAMP. There have been numerous attempts [12–15] to create mathematical models of this nonlinear behavior starting from underlying assumptions regarding the interactions of the responsible biomolecules. Yet, it is fair to say that none of these are completely satisfactory, especially with regard to accurately mirroring what is known about these interactions. For our purposes, we will utilize the Martiel-Goldbeter (MG) model [13] and its extensions, which serves to quantitatively capture well most of the established wave phenomenology – namely, relay of cAMP signal via intracellular cAMP-synthesis, refractory period between successive responses and realistic wave speeds and cAMP levels. Later, we will discuss which features of the MG model are truly essential in allowing the waves to function as the needed directional roadmap.
Of course, the roadmap properties of the wave field are only of use if they can be interpreted by individual cells so as to direct their motion. Many cells in differing organisms have a chemotactic capability, namely, they can bias their motility via detection of chemical gradients in their environment, and much effort has gone into understanding how this is accomplished through the action of signal transduction pathways [16–19]. Of particular note here is that for chemotaxis to be useful in this context, cells must move directionally toward wave sources, necessarily responding more forcefully to the rising segment as opposed to the falling one (“back-of-the-wave paradox”). As pointed out in [20], this can be more difficult than sensing a static gradient.
It has become clear in recent years that a good modeling paradigm for gradient sensing comes from the concept of LEGI - local excitation and global inhibition [21–24]. In this formulation, the incoming signal from ligand-receptor binding activates excitatory and inhibitory pathways that converge on a downstream effector. In Dicty, a good working assumption posits that the effector is a RAS protein whose activation (by an exchange factor, aka a GEF) drives the physical motility apparatus and whose inactivation (by a GAP) prevents this from happening. The fact that the inhibitor molecule is assumed to diffuse rapidly through the cytoplasm means that the steady-state response of the effector is given by the local value of the excitation minus its global average. One way to reliably distinguish the front and back of the cell is to make the effector response ultra-sensitive [25] with a threshold at the equilibrium value of the activated effector. Since the model circuit perfectly adapts to any uniform stimulus, as has been verified experimentally [24], this equilibrium is unique and the cell can detect and amplify gradients independent of any background mean concentration.
It has been argued that the LEGI model in its ultra-sensitive version can help solve the aforementioned wave detection problem [26, 27]. The reason for this is that with the proper parameter choices the response kinetics is highly different for rising versus falling concentrations. For the former, the positive temporal gradient and the slower response of inhibitor versus activator gives rise to a large transient effector activation and possibly a large front-back asymmetry; no such effect is seen when the concentration is falling, since then there is an excess of inhibitor which takes a while to disappear and which will prevent a significant response. In addition, recent experiments [27] have indicated other types of memory, lasting for longer than that of the LEGI inhibitor. Whether or not this extra module is needed to further resolve the traveling wave problem or is useful for some other aspect of the aggregation behavior is at present uncertain.
Given that we have working models for both the waves and the chemotactic response, we can combine them to address the question of whether the LEGI model can explain the directed motility response to natural waveforms. In this work, we will present a computational approach that encompasses both an MG and a LEGI module to accomplish this task. We will discuss how to drive LEGI dynamics with output variables from MG and we will discuss how to tackle the inherently multi-scale challenge of solving reaction-diffusion systems simultaneously on the individual cell and multicellular pattern scales. We will show that for the waves created by the MG model, the ultra-sensitive LEGI does an excellent job of resolving the direction of the wave source. These findings are complementary to those obtained for artificial waves generated in micro-fluidic devices. At the end, we will present two directions for future work; one involves allowing the cells to physically translocate based on their LEGI output and one which involves studying the role of developmental time in establishing the needed properties of the coupled system.
II. MODEL
A. Wave Propagation Model
The Martiel-Goldbeter (MG) model [13] consists of the following interacting chemical components: a membrane-bound receptor species, cytosolic as well as extracellular cyclic adenosine monophosphate (cAMP), adenylyl cyclase (ACA, which acts as an enzyme in the production of cAMP) within the cytosol, as well as cytosolic adenosine triphosphate (ATP) which acts as substrate in the cellular production of cAMP. The receptor can be in one of two possible states; phosphorylated or de-phosphorylated, which act as the inactive and active forms respectively. An inactive receptor may be activated in its free state or its ligand-bound state, as is the case for inactivation of the active receptor. What is important is that the bound receptor gets phosphorylated at a faster rate and de-phosphorylated at a slower rate compared to the free receptor.
Extracellular cAMP binds to membrane bound receptors with a higher binding rate for active receptors than for inactive receptors. A key assumption of the model is that two ligand-bound active receptors are then needed to activate each molecule of ACA, which produces cAMP at a much higher rate than non-activated ACA. The nonlinearity of this step is ultimately what allows the model to mimic the excitability of the cell. Intracellular cAMP can then be transported outside the cell, while cAMP hydrolysis occurs both within and outside the cell. This assumed mechanism leads to a system of nine coupled ODEs. Assuming that binding of receptor to ligand, activation of ACA and association of ACA with ATP are all fast processes, the system can be reduced to 4 equations. The experimental observation that ATP concentration remains more or less steady during early aggregation, which is also verified by directly simulating the 4-variable model, provides another simplification. The final, simplified MG model thus consists of three variables; total active receptor fraction (ρT, which includes both bound and unbound forms), normalized intracellular cAMP (β) and normalized extracellular cAMP (γ).
| (1) |
| (2) |
| (3) |
where is the ligand-bound active receptor fraction. The quantities L1, L2 are combinations of fundamental kinetic rates and the s parameters in addition depend on intracellular versus extracellular volumes; see the original paper for a detailed discussion.
Equation 1 describes the phosphorylation and de-phosphorylation of the receptor in its bound and unbound forms. Equation 2 describes the intracellular production of cAMP (the squared term comes from the fact that two ligand-bound active receptors are required to activate one ACA molecule) and its transport from and hydrolysis within the cell. Finally, Equation 3 describes the addition of intracellular cAMP to the extracellular environment, its hydrolysis as well as diffusion through extracellular space.
This model has been successfully used to simulate wave pattern formation in 2-dimensions[28], as well as to explain single cell behaviors, including oscillatory response and the formation of supra-threshold pulses[13]. We will use the parameter set employed by Tyson et. al. to simulate spiral waves [28], given in Table I (Set A). ATP values are normalized by KM (Michaelis constant for ACA), cAMP values are normalized by KR (dissociation constant of cAMP-receptor complex in active state) and RT is the total cAMP receptor concentration per cell. We should note that our choice of the MG model is motivated by its ability to capture the essential non-linear nature of the cell response and its relative simplicity.
TABLE I.
MG Parameters. Set A is used by Tyson et. al. to produce spiral waves in a 2D spatially-extended system [28]. Set B is used to produce wider waves for cell-populations with half the number density used for Set A. Space and time units are normalized using and tScale = 1/k1 respectively, where ke is the rate of dissociation of cAMP in the extracellular environment, Dγ is the diffusion coefficient for extracellular cAMP and k1 is the rate of phosphorylation of active free receptor. In order to increase wave-width, we increased the rate of transport of intracellular cAMP by 10% while decreasing the rate of extracellular phosphodiasterase (ke) by a factor of 2.3 such that the space-scale is unchanged (implying the diffusion coefficient (Dγ) increases by a factor of 2.3). This results in a change in the Tyson parameters s1, s2, ε′ and ε. The doubled time-scale in Set B implies that all rate parameters are actually halved in physical units. This was done to maintain a realistic wave speed in our simulation to test the effect of spatial size of the wave on LEGI response.
| Parameter | Set A | Set B |
|---|---|---|
| κ | 18.5 | 18.5 |
| L1 | 10 | 10 |
| L2 | 0.005 | 0.005 |
| c | 10 | 10 |
| λ1 | 0.001 | 0.001 |
| λ2 | 2.4 | 2.4 |
| s1 | 950 | 906.8182 |
| s2 | 0.05 | 0.1265 |
| ε′ | 0.019 | 0.0181 |
| ε | 0.01 | 0.023 |
| KM | 4 × 10−4 M | 4 × 10−4 M |
| KR | 1 × 10−7 M | 1 × 10−7 M |
| RT | 3 × 10−8 M | 3 × 10−8 M |
| tScale | 8.3 min | 16.6 min |
| xScale | 4.5 mm | 4.5 mm |
Typically, simulations of the MG model treat cells as points on a grid where each of the dynamical variables obey ODEs and where the extracellular cAMP concentration is solved using the diffusion term. This is sufficient to study wave propagation which has length scales much larger than individual cell size. However, it is not sufficient if we wish to simultaneously simulate directional sensing in cells as a response to spatiotemporal gradients across the body of the cell. For this we clearly need finite-sized cells. This involves de-coupling the variables for the cell from the variables that live on the overall grid, namely extracellular cAMP, and will be discussed in Section III: Numerical Methods.
B. Direction Sensing Model
As discussed above, our direction sensing model is based on the local-excitation global inhibition (LEGI) concept, which has been shown to capture experimental observations concerning front-back asymmetries in response to spatiotemporal stimuli. Our LEGI-based model consists of a membrane-bound activator species (A) which is activated by the input signal (Y) and decays at some fixed rate. Note that this is the same variable that activates ACA in the MG module. There is also an inhibitory species which may be diffusing through the cytosol (ICyt), or recruited to the membrane (IMem). In our formulation, the cytosolic species is produced in response to the external signal and the membrane species can decay; none of those precise details matter. We have assumed that the diffusion constant is sufficiently large that we can assume the cytosolic concentration obeys the Laplace equation in the bulk. This then means that the experimentally observed delay in inhibitor versus activator rise, responsible for the transient response to a spatially uniform stimulus, must arise from the production kinetics and not the transport. We have chosen this version of the LEGI concept so as to avoid having to solve the time-dependent diffusion equation inside the cell; instead we will approximately solve the Laplace equation analytically, as described in Section III C.
In detail, the model consists of the following equations:
| (4) |
| (5) |
where ICyt is the solution to Laplace’s equation
with boundary condition
| (6) |
where n̂ is the unit vector normal to perimeter of the cell, pointing out.
The effector molecules (E) are also membrane-bound, and are “de-activated” by membrane-bound inhibitor while the reverse process is mediated by the activator species. The assumed mechanics for the activation/inactivation of effector leads to two forms of the LEGI model; first-order kinetics leads to the basic LEGI model (Equation 7a) while Michaelis-Menten kinetics leads to the ultra-sensitive LEGI model (Equation 7b). This latter version can lead to large amplification of the response as compared to the linear effector kinetics version, as long as the parameters KA and KI are small compared to the values of E in the resting state.
| (7a) |
| (7b) |
Our model is most similar to that of Takeda et. al. [24], and the parameters used are taken from that work and are shown in Table II. In order to combine MG and LEGI, space-time normalization and units of parameters should be consistent across the two models. To this purpose, we convert all dimensions to units of mm and min and use the MG scaling factors to make space and time dimensionless. Concentrations of LEGI variables are normalized by RT from Table I, which is also assumed to be the total effector concentration in the cell (as is assumed in [24]). Here, we have chosen the parameters KA and KI to give a large response, based on testing a variety of choices. The dependence of gradient detection on these parameters will be discussed later.
TABLE II.
LEGI Parameters: Second column contains the parameters used for the basic LEGI model. Parameters in the third column are used in the ultra-sensitive LEGI model; along with the introduction of Michaelis-Menten constants for activator and inhibitor species, the rates of activation (k+) and inactivation (k−) need to be altered due to the changes in the precise formulation of the model.
| Parameter | Basic LEGI | Ultra-sensitive LEGI |
|---|---|---|
| λA | 2.4 min−1 | 2.4 min−1 |
| dA | 24 min−1 | 24 min−1 |
| λI | 0.6 min−1 | 0.6 min−1 |
| dI | 0.18 mm min−1 | 0.18 mm min−1 |
| dIMem | 6.0 min−1 | 6.0 min−1 |
| DI | 0.0018 mm2min−1 | 0.0018 mm2min−1 |
| k+ | 23400 min−1 | 351 min−1 |
| k− | 187560 min−1 | 375.12 min−1 |
| KA | – | 0.015 |
| KI | – | 0.002 |
| RC | 5 μm | 5 μm |
III. NUMERICAL METHODS
A. Finite Cells in MG Model
A common feature of early numerical simulations of the MG model was that every point on the numerical grid used to solve the cAMP diffusion equation is taken to be a single cell; as such, integration in time simply involves updating all the MG variables for each grid point. Changes in cell density are accommodated by changing the parameters, not by computing a new grid. This, of course, misses several details, such as the difference between intercellular and extracellular space and the possibility of spatial variation in the external cAMP concentration on scales smaller than the cell-cell spacing. Upon consideration of cell motion, researchers proceeded with a hybrid strategy of solving the internal MG variables (all except γ) for individual cells located at arbitrary points and then having these cells act as localized sources for the cAMP diffusion solved on a fixed grid. This is a clear improvement as now the density becomes a true dynamically determined variable and the system can deal with phenomena such as the formation of high-density streams. To address coupling of MG and LEGI, however, we need to treat the cell as an extended object, allowing the cAMP to vary along the cell membrane so as to provide input to the LEGI model. To do this, we maintain a cAMP grid and embed cells at positions within the grid, with each cell having its own MG variable set. Essentially, we are maintaining two separate grids, one for the extracellular environment where every grid point has an associated cAMP concentration, while the other grid maintains cell variables (receptor fractions, intracellular cAMP and all the LEGI variables). In two dimensions, we will use 4 points evenly distributed around the cell’s circumference to represent the cell (see Figure 1b). The situation is simpler in one spatial dimension, where each of the cell-bound variables takes on values at two points, representing the left and right edges of the cell (Figure 1a). The intracellular cAMP concentration is assumed to diffuse sufficiently rapidly so that it takes on a uniform value throughout the cell and hence can be treated as a single dynamical variable.
FIG. 1.
(a) 1D Numerical Grid. Each cell is represented by a line bounded by two membrane-points (orange diamonds) placed in between two grid points (blue ovals). (b) 2D Numerical Grid. The points on the cell perimeter marked (1–4) denote the actual points tracked in our simulation; all cellular variables are tracked at only these points for a cell (with the exception of cytosolic cAMP, which has one value per cell).
When integrating in time, we need to deal separately with the cell-bound variables and the external cAMP. To update the internal variables, we need to know that value of the extracellular cAMP at the cell grid points. This is done by direct interpolation using the values at the nearby grid points. In detail, for 1D, we use a simple linear interpolation method utilizing the nearest grid points for a given cell-edge to calculate the cAMP value at that edge. In 2D, we pick four perimeter points as shown in Figure 1b and use the value of cAMP at the four neighboring grid points to interpolate the perimeter values using Equation 8. These formulae can obviously be simply extended to computations which utilize more than four perimeter grid points.
| (8) |
with coefficients {ai} given in terms of grid cAMP values,
| (9) |
The bilinear interpolant p(x, y) evaluates extracellular cAMP exactly at the grid nodes in Figure 1b and interpolates the value at perimeter nodes for the bounded cell. The equations are integrated using a forward Euler method and after each update of the grid cAMP values, we use this interpolation to determine the perimeter cAMP values for each cell, which are in turn needed to evaluate time derivatives for the next time-step.
B. Secretion of cAMP from Cells
When integrating the MG equations, we use the mean cAMP-bound active receptor fraction for the internal cAMP production equation, since these fractions are different at the different perimeter points; this is because we assume rapid internal cAMP diffusion. Given β at a time t, then the amount of cAMP secreted by that cell at next time-step is s2/εβΔt (Δt being the time-step). In our calculations this amount is secreted uniformly; although biological evidence indicates that cAMP is preferentially secreted at the back of the cell [29], we find the MG model is capable of producing reasonable traveling waves without this feature. This secreted amount is then distributed to the nearby grid positions, weighted such that closer points get more of the cAMP and further points get less; but all of the secreted cAMP makes it to the nearest grid nodes. In general, these weights can be (1 − |xCell − xGrid|/ds) in 1D, and (0.5 − |xCell − xGrid|.|yCell − yGrid|/ds2) in 2D. As long as our cells are stationary and our density uniform, we can choose to place them equidistant from their neighboring grid nodes, such that the weights are simply 1/2 and 1/4 for 1D and 2D respectively, i.e. cAMP is uniformly distributed to nearest grid points. Once the secreted cAMP has been distributed, the remaining terms in the external cAMP equation are treated in standard fashion. The MG parameters given in Table I allow the cells to respond to an increase in extracellular cAMP concentration by producing and secreting intracellular cAMP; the cells do not exhibit intracellular cAMP oscillations, which can be achieved using a different set of parameters and is studied by Martiel and Goldbeter [13]. Hence our cells are stably propagating a wave created initially by perturbing the boundary conditions (see later).
C. Solving for Steady-State Cytosolic Inhibitor
Although we have grid points distributed along the cell perimeter, we do not have a grid inside each individual cell and hence do not solve numerically for the diffusion of inhibitor in the cytosol. Doing this directly is extremely cumbersome, since for every cell within the extracellular grid, we would need a finer grid describing the interior and perimeter of cell to integrate the inhibitor diffusion equations. Instead, we simplify the problem by finding an analytical solution to Equation 6, thereby reducing the LEGI model to a system of three coupled ODEs, which can be easily integrated numerically. In one dimension, the problem of finding an analytical solution to Equation 6 is trivial; a general solution for Laplace’s equation is just a linear function (Equation 10) and one needs only to solve for the unknown coefficients using the boundary conditions on a cell of radius RC (xCell ∈ [−RC, RC]).
| (10) |
Using boundary conditions in Equation 6 to solve for {A0, A1}, we get
| (11) |
Hence, the steady-state cytoslic inhibitor concentrations at the two edges of the cell can be expressed in terms of the LEGI parameters and the active ligand-bound receptor fraction at the two edges, as follows:
| (12a) |
| (12b) |
In two dimensions we cannot exactly solve the boundary condition for the entire perimeter, since we do not have the LEGI input for the entire perimeter of the cell (either as a set of discrete points or as a function of angle); the perimeter is represented by just a finite number of points, which in this work we will limit to just 4. Now, the general solution for Laplace’s equation in 2D polar coordinates, under the condition that the solution is well behaved near the center of the cell, is given by:
| (13) |
where the coefficients {Ci, Di} are found by solving the boundary condition in Equation 6.
In order to solve this boundary condition, we need to express the ligand-bound active receptor fraction Y(x, y) as a function of {r, θ} in the reference frame of the cell. We can express the interpolant from Equation 8 in terms of θ by realizing that positions in the coordinate system of the grid {x, y} is related to the cell’s polar coordinate as follows: x = xC + Rc cos θ and y = yC + Rc sin θ where {xC, yC } is the center of the cell in grid coordinate system, θ is the azimuthal angle around the center of the cell. We then fit the values at the four points to a four term Fourier series, thereby uniquely determine the coefficients. We find
| (14) |
where the coefficients are given as functions of perimeter values of Y(θ)
| (15) |
where the subscripts on Y correspond with perimeter-node indices in Figure 1b.
Using Equation 14 as an approximation for the ligand-bound active receptor fraction on the membrane, we can solve boundary condition in Equation 6 to solve for the coefficients in Equation 13. Thus, the cytosolic inhibitor on the perimeter is given by:
| (16) |
where the coefficients are given in terms of the coefficients of interpolant in Equation 15 and LEGI parameters, as follows,
| (17) |
We can now substitute for ICyt in Equation 5 using Equations 16 and 17.
To integrate in time, we use the forward-Euler method with a time-step of 0.12 seconds for the MG model, with each MG integration step containing 45 LEGI integration steps; we have checked that this is long enough to ensure convergence. We used a grid-spacing of 0.045 mm for the extracellular grid, with cells centered in between all grid points.
IV. RESULTS
A. Traveling Waves in 1D
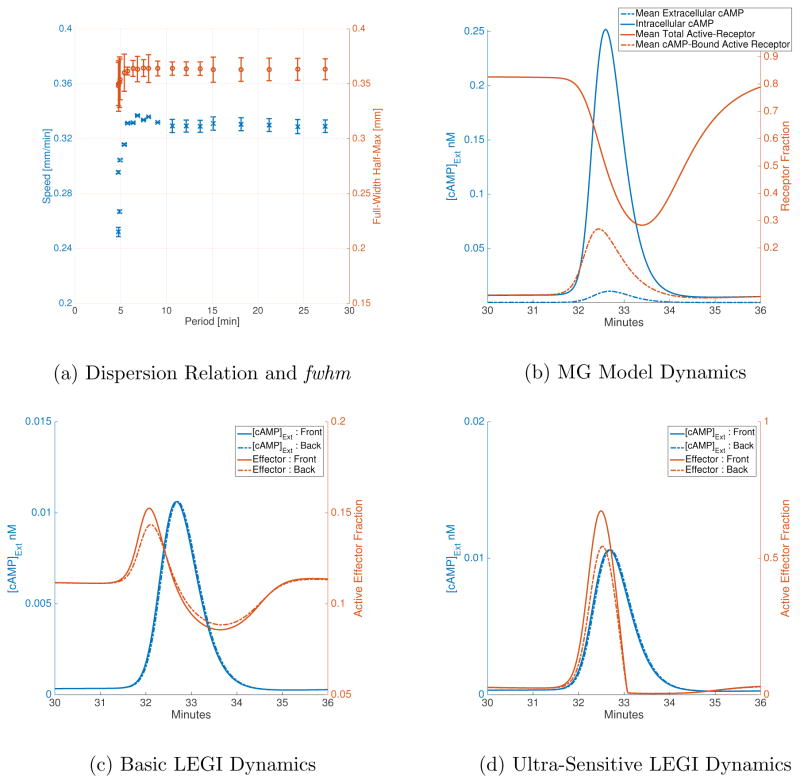
Using the MG parameters given in Table I (Set A), we study the dispersion of waves in 1D. For the first 1.5 minutes of simulation time, we hold the right edge of the grid at 0.1 μM and the left edge at 0 μM to allow the cellular variables to reach a steady-state; we then reverse the boundary conditions to induce a single wave traveling left to right. The cells on the left edge respond to the increase in extracellular cAMP in their vicinity by producing and secreting cAMP till their receptors get de-sensitized, at which point cellular cAMP production stops and hydrolysis of cAMP dominates the dynamics; in this way a single wave is produced. The wave propagates due to the receptor dynamics; the cells in the front of the wave have higher levels of de-phosphorylated receptors which induce cAMP production while those in the back of the wave have higher levels of phosphorylated receptors which do not induce cAMP production. We use periodic boundary conditions to allow the wave to transit over the grid several times. By changing the overall length of the grid (and therefore the period of the wave) we can numerically determine the dispersion relation for the 3-variable MG model (Figure 2a). For a grid-length of 2.7 mm (61 grid points, 60 cells), we find that the wave speed is about 0.34 mm/min with a period of about 8.04 min (averages are calculated ignoring the first 10-minutes of simulation), which is in the range of experimentally observed spirals [28]. We also found that these waves have a full-width half-max (fwhm) of about 0.364 mm, with very little deviation over the range of speeds allowed by the model (over a range of 0.25–0.33 mm/min, fwhm does not drop below 0.32 mm and does not exceed 0.37 mm; see Figure 2a). In addition, we find that the MG model cannot accommodate waves with a period shorter than about 4.8 min, which is consistent with the 5 min limit proposed by Tyson et al.
FIG. 2.
(a) Wave speed and full-width half-max for different periods allowed by the MG model. Data is averaged skipping the first 10 minutes of simulation time for all grid lengths. Speed is calculated for a single cell at 3/4 of grid length. Waves with period less than 4.8 min cannot be sustained by the MG model. Full-width half-max does not vary greatly for allowed periods, staying between 0.32 and 0.37 mm. The error-bars mark ±1 standard deviation from the mean. (b) The blue lines are cAMP concentrations (solid → β, dashed → γ) and the orange lines are average receptor fractions (solid → ρT, dashed → ρTγ/(1 + γ)). Extracellular cAMP is scaled by a factor of 10 to make it visible on the same axis as intracellular cAMP. (c), (d) The effector response (in orange) is plotted for the front of the cell (solid line) and the back of the cell (dashed line) along with the corresponding extracellular cAMP conc. (blue lines).
The basic output of the MG model for a single cell (at 2.0025 mm on a 2.7 mm grid) as a cAMP wave passes over it is shown in Figure 2b, which presents the average total active receptor fraction, the average cAMP-bound active receptor fraction and the intra-cellular cAMP concentration as functions of time. When extracellular cAMP increases at around the 31 minute mark, the active receptor fraction drops as active bound receptor fraction increases, the latter accelerating intracellular cAMP production. The recovery of the active receptor depends on the kinetic parameters for the receptor phosphorylation/de-phosphorylation steps; this recovery is slower in the presence of cAMP. As such, any stimulus experienced before the active receptor levels are fully recovered will not incite the same amplified response in cytosolic cAMP production. This sets the minimum limit on wave transit period for relaying cells. All told, our results are in agreement with previous simulations.
We then proceed to couple the LEGI model to this wave system. As discussed in the introduction, the basic question we wish to investigate is the extent to which this model effectively deals with wave rectification, i.e. succeeds in creating a large asymmetry between the response of the cell during the rising phase and the falling phase of the signal. As such, we focus on the difference in effector values between the front and back of the cell (front being the left edge). Successful rectification implies a higher difference at the front than at the back of the wave. Furthermore, as experiments have shown a significant asymmetry in the distribution of fluorescent-marked labels in the presence of a wave, we also want the actual effector concentrations to be significantly different across the cell at any given point when the cell experiences the rising phase of the wave. In order to quantify the model’s ability to resolve the “back-of-the-wave paradox”, we calculate the ratio of the magnitude of peak difference in active effector levels in response to the rising phase vs. that in response to the falling phase of the wave. A high ratio implies a higher polarization in response to the front of the wave compared to the back of the wave. For a given cell with radius RC, this “asymmetry” is given as follows:
| (18) |
Figure 2c and Figure 2d show the LEGI response (orange line) to MG input in the case of first-order and ultra-sensitive kinetics for effector species, respectively. In the case of the basic LEGI model, as the rising phase of the wave hits the cell, the front experiences higher local concentrations of cAMP than the back. This results in faster activation of effector levels at the front than at the back. The inhibitor species counters this activation process, but it needs to catch up to the activation process since it needs to be recruited to the membrane to de-activate active effectors. As the cell enters the falling phase, the back experiences higher levels of cAMP, which results in higher local activation at the back than the front. However, the net response is lower than the rising phase since there is cytosolic inhibitor left from the response to the rising phase. In the ultra-sensitive case, the striking difference compared to the basic model is the muted response to the falling phase of the wave: this is a result of the zeroth-order ultra-sensitivity and the diffusion of active inhibitor. In the rising phase of the wave, local activation is initially faster than inhibition due to diffusion inhibitor. However, in the falling phase, local activation is balanced by cytosolic active inhibitors remaining from the rising phase of the wave.
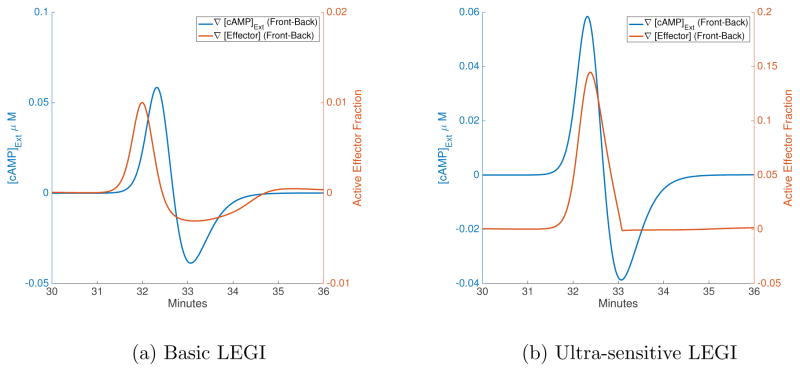
To elucidate the model’s ability to distinguish between the front and back of the traveling wave, we plot the difference in extracellular cAMP levels and effector concentrations across a single cell as a function of time (Figure 3). ∇[cAMP]Ext is the difference in extra-cellular cAMP between the front and back of the cell (which is positive for the rising phase and negative for the falling phase), while ∇[Effector] is the corresponding difference in active effector levels between front and back of the cell (given as a fraction of the total effector concentration). The effector concentrations and differences in cAMP and effector levels across cells for regular waves are also given in Table III, which also contains corresponding data for wider waves (see Section IV C). Using the ultra-sensitive LEGI model (Equation 7b) with a cAMP wave of period 13.64 min, the maximum polarization in the cAMP field was found to be ~1.5 times stronger for the rising phase on average, whereas the same polarization in the effector levels is ~136.4 times stronger on average for the front of the wave (compared to the falling phase of the wave). With the basic LEGI model for the same wave period, the maximum polarization in the effector levels was ~3.3 times stronger on average during the rising phase than the falling phase (about 44 times weaker than the ultra-sensitive version). The effector levels are higher in general for the ultra-sensitive model (see Table III). In agreement with what has been argued for the LEGI response to artificial waves made in a micro-fluidics device [26, 27], the ultra-sensitive LEGI model does an extremely good job in allowing for wave chemotaxis.
FIG. 3.
Time-series of gradients in cAMP and effectors across a cell. The blue lines are the difference in extracellular cAMP conc. between front and back edges of a cell, while the orange line is the corresponding difference in effector levels. When the blue line is positive, the cell is exposed to the rising phase, while the falling phase corresponds to negative difference in cAMP. While the basic LEGI model (a) has a noticeable response in the back of the wave, this response is muted for the ultra-sensitive model (b).
TABLE III.
The first and second rows are the basic and ultra-sensitive response respectively, to a cAMP wave with speed 0.34 mm/min, period of 8.04 min and full-width half-max of 0.364 mm. The third and fourth rows are the basic and ultra-sensitive response respectively, to a cAMP wave with speed 0.284 mm/min, period of 12.75 min and full-width half-max of 0.783 mm. The final row is the ultra-sensitive response to the same wide wave when all the rate parameters in Table II are increased by a factor of 3. Empty cells imply the same values as the corresponding cells in the preceding row. Comparing the first two rows, the ultra-sensitive model has a three-fold advantage over the basic LEGI model. Firstly, the difference in effectors is higher for the rising phase while in the falling phase of the wave this difference is lower, compared to the basic model. Secondly, the active effector levels achieved are also higher for both edges, while the difference in peak active effector levels also increases compared to the basic model. Comparing the first and third rows, we can say that for an almost 4-fold decrease in the cAMP gradient across the cell, the difference in effectors for the rising phase drops more significantly than the difference during falling phase for the wider waves in comparison to the regular waves. The ultra-sensitive model improves the response for the wider waves in a similar fashion to the regular wives, namely, increasing the asymmetry in effector difference between rising and falling phases, increasing peak active effector levels at both edges while increasing the difference in the peak effector levels. Increasing the LEGI rate parameters results in a more effective inactivation, which causes effector levels to drop. The faster LEGI dynamics for the same MG dynamics results in a greater polarization in active effector levels in the falling phase of the wave while the rising phase response is comparable to the preceding case.
| Peak Difference in cAMP [nM]
|
Peak Difference in Effector [a.u.]
|
Peak Effector (Front) [a.u.] | Peak Effector (Back) [a.u.] | ||
|---|---|---|---|---|---|
| Rising Phase | Falling Phase | Rising Phase | Falling Phase | ||
| 5.846 | −3.865 | 0.01 | −0.0031 | 0.152 | 0.143 |
| — | — | 0.145 | −0.001 | 0.674 | 0.544 |
| 1.506 | −1.087 | 0.002 | −0.001 | 0.13 | 0.128 |
| — | — | 0.047 | −0.0007 | 0.335 | 0.288 |
| — | — | 0.043 | −0.0015 | 0.109 | 0.067 |
B. Parameters for Ultra-Sensitive LEGI Model
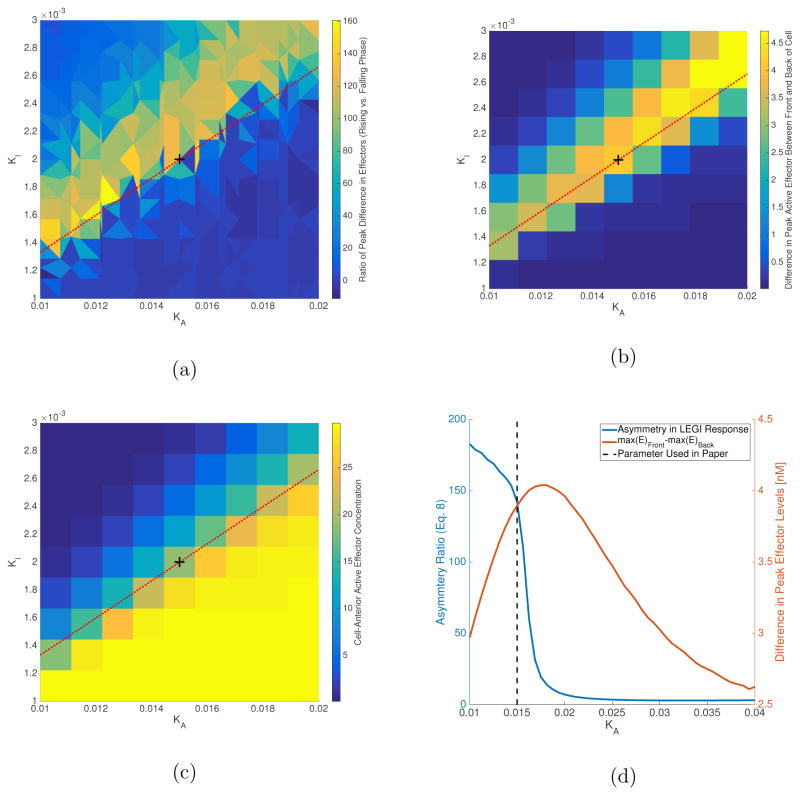
We now wish to investigate the effect of varying the ultrasensitivity parameters. We start with the values from the basic LEGI model (Table II) as determined in a previous study [24]. We then redefine coefficients k+ and k− as (k+KA) and (k−KI) respectively, such that the ultra-sensitive model reduces to the basic model for large values of KA and KI. We vary KA and KI, keeping the ratios k+/KA and k−/KI constant, and determine the values which maximizes the asymmetry (Equation 18); simulations were run on a 2.7 mm grid for 120 minutes, and asymmetry in spatial gradient of effectors was averaged for the last 108 minutes of simulation for a cell at 2.0025 mm (the method is identical to that introduced in Section IV A). The results are shown in Figure 4; the asymmetry in polarization is larger in the parameter region KA ∈ [0.01, 0.02] and KI ∈ [0.001, 0.003]. In the results presented above, we chose parameters that maximize the asymmetry in polarization between rising and falling phases, while maintaining a large difference in the peak effector levels between front and back of the cell (i.e. the front of the cell had a higher active effector level than the back). The largest asymmetries (bright yellow spots in Figure 4a) in the parameter region shown were found to lie close to a line with slope KI/KA = 2/15, shown in Figures 4a, 4b and 4c as a red dashed line. Figure 4d shows the asymmetry in response and difference in peak active effectors for parameters on this line. The last column in Table II contains the values for KA and KI we found using this procedure.
FIG. 4.
(a) Parameter region for large asymmetry in LEGI response. Results from a sampling of 100 parameter combinations were used to interpolate results shown here. We used a biharmonic spline interpolation available in MATLAB®. (b) Difference in peak active effector levels between front and back of the cell. Total effector concentration is assumed to be 30 nM, same as total receptor concentration. Results are shown for 100 simulations. (c) Peak effector values at cell-front for sampled parameter space. Above the red-dashed line, peak effector levels drop below 50% of total effector levels, while below the line it reaches almost full activation. The peak effector levels at the back of the cell (not shown here) exhibit a similar trend. (d) Asymmetry and difference in peak effector levels along red-dashed line. Asymmetry gets large for KA values less than 0.02, however, the difference in peak active effector levels starts to drop in this region. The value for KA is selected such that we can get high asymmetry while maintaining a difference in peak effectors close to maximum achievable along the red-dashed line (~4 nM). The black dashed-line marks the parameter values used in this paper. These parameters are also marked in Figures 4a–4c with a black plus-sign.
C. Response to Wider Waves
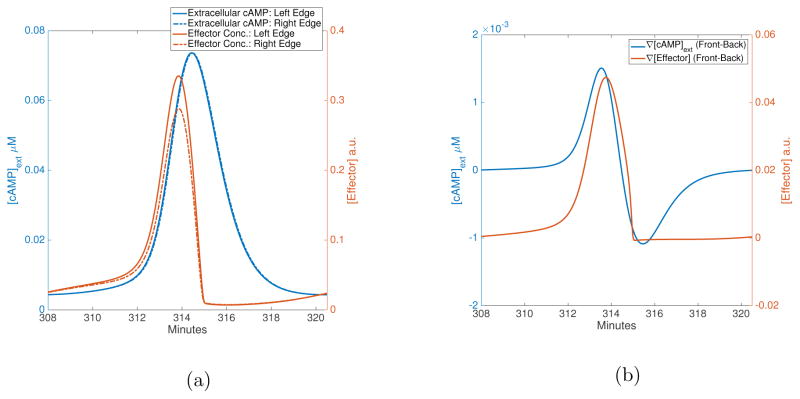
The LEGI response should depend on the duration of the wave as experienced by the cell which depends on the full-width half-max of the spatial waveform. Figure 2a shows that the full-width half-max does not vary significantly over wave-periods allowed by the MG model, hence we do not expect the LEGI response to vary for waves with these parameters. In order to study the effect of wider waves on the LEGI response, we ran 1-D simulations with cells centralized on every other grid spacing, thereby halving the number density from the preceding case. In order to get traveling waves in this sparser system, we had to increase both the transport of cAMP from cells and the diffusion coefficient for extracellular cAMP while decreasing the rate of extracellular cAMP degradation (Table I Set B). In order to get waves with similar speeds as the regular MG model, we double the time-scale. The simulation is run, for 5 hours, on a 9 mm grid using constant input of 0.1 μM at the left boundary and perfect absorption at the right. This model creates waves with fwhm = 0.763 mm and a speed of 0.284 mm/min, with the distance between two consecutive cAMP peaks being 3.625 mm. The results for a cell at 6.73 mm on the grid are shown in Figure 5. With the ultra-sensitive LEGI parameters same as in Table II, we find the cAMP difference between the two cell-edges is ~1.4 times stronger for the rising phase of the cAMP wave with the corresponding effector difference ~70 times stronger for the rising phase compared to the falling phase (roughly 2 times weaker than the preceding case), which can be seen in Figure 5b. Figure 5a shows the effector response (in red) along with the extracellular cAMP concentration (blue) at the front and back edges of a cell at 6.73 mm on a 9 mm grid. This decrease in response is due to the slowing of the wave dynamics. In agreement with this notion, we also find that the response starts dropping as we increase the LEGI rate parameters by a constant factor; for a three-fold increase in LEGI parameters, the peak effector polarization is ~28 times stronger for the rising phase compared to the falling phase, almost a 2.5-fold drop from the wide-wave case. Our results show that as the inhibitor field can better keep up with the wave dynamics, the LEGI model becomes less able to use its temporal response to effect good rectification. As the wave gets wider, it takes longer for it to transit over a cell, allowing the inhibition dynamics to catch up with activation earlier than the case of the regular wave, resulting in lower active effector levels. The effector levels reach below pre-stimulus levels before the peak of the wave transits the cell, as a result there is a small polarization in effector levels in the falling phase of the wave which is larger than the response to the wide waves using regular LEGI parameters. Essentially, as the wave gets wider, the rising and falling phases are far enough apart in time that the LEGI response in each phase do not affect each other as much as in the regular wave case. These results are consistent with what has been observed for artificial waves with varying periods [26, 27] (it is worth noting that the in vivo response of cells to inverse waves is carried out by exposing the cells to an artificially created wave and this response is well explained by the LEGI model as shown by Nakajima et. al. [26]. We expect our model would have a similar response with MG parameters that might sustain an inverse wave since the downstream LEGI model is identical).
FIG. 5.
LEGI response to wide waves. (a) The extracellular cAMP (blue) waves at the front (solid line) and the back of the cell (dashed line) are shown along with the corresponding effector values (red lines). Compared to the ultra-sensitive LEGI model with regular waves (fwhm=0.3 mm, Figure 2d), the response in effector drops to zero almost exactly as the rising phase of the wave ends. This is even clearer in (b), which shows the difference in cAMP levels (blue) and effector values (red) for the same cell. The difference returns to zero almost concurrently with the beginning of the falling phase of the wave. Essentially, the wider wave is slow enough that the LEGI model reaches saturation before the cAMP wave peak completely passes the front of the cell.
D. 2D Spiral Wave
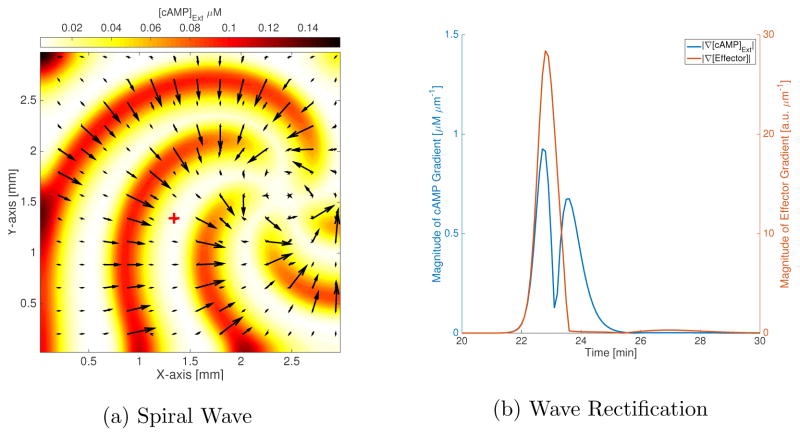
The MG parameters in Table I have been shown to produce spiral patterns in two dimensions with wave speed and wavelength that match experimental observations[28]. Here we wish to demonstrate how the LEGI model induces front-back asymmetry in response to such a spiral. For this purpose, we simulate a 3 mm by 3 mm grid using a grid-spacing of 45 μm and a time-step of 0.12 seconds, with cells placed within the grid as shown in Figure 1b. In order to form a spiral, we start with linear gradients in extracellular cAMP (γ) and active-receptor fraction (ρT) along two orthogonal axes. We use the difference in the effector concentration between front and back of the cell in each coordinate direction as the signal that picks a motility direction. In the case of the basic LEGI model (data not shown), we find that the gradient is smaller in the back of the wave than the front, by a maximum factor of ~3 (we took average asymmetry for each cell over all times and found the average asymmetry among all cells, ignoring a region 5 grid-spacings wide near each edge). The effector levels (and effector polarization) is highly muted in the back of the wave in the case of the ultra-sensitive LEGI model; the magnitude of the gradient (|∇[Effector]|) is at most ~140 times bigger in the rising phase of the wave compared to the falling phase (see Figure 6b). The effector gradient successfully picks the normal to the wave-front (against the direction of the wave propagation in the front of the wave; Figure 6a). We find that the cells away from the core of the spiral are polarized in a radially-inward fashion with respect to the spiral curvature (aligned with the cAMP gradient (not shown), pointing from yellow→red), while those near the core point around the core with a large azimuthal component and not aligned with the cAMP gradient (in Figure 6a, the effector gradient vectors (black arrows) point towards the core far from the spiral-core and around the core close to it). This is expected since the wave is not homogenous in space, and cAMP gradients are smaller near the spiral core than farther away in the grid. Combined with a motility model, this can lead to circular motion of cells about the aggregation center (the spiral core).
FIG. 6.
Spiral waves in 2D. (a) The colorbar indicates the extracellular cAMP concentrations (in units of μM), which are shown with filled contours. The black arrows are the mean effector gradient across the cell using a Cartesian grid. The wave travels radially outwards, normal to the curvature of spiral. We have shown the spiral at 5 different times (starting with the small tip at the right edge and going clock-wise, the respective times are 14.4 min, 16.9 min, 19.4 min, 21.9 min and 24.4 min), along with vectors for the effector gradients corresponding to each time-step superimposed over one another (this results in some of the larger black arrows having smaller arrows at their base which corresponds to a different point in time). The response in the falling phase of the wave is suppressed; cells are only responding significantly to the rising phase of the wave (the arrows are small everywhere but on the wave-front). The gradients are perfectly aligned with the normal to the spiral, except at the tips of the spiral. (b) The magnitude of effector gradient (red) and cAMP gradient (blue) at cell position (1.34mm,1.34mm), shown as a cross in (a). The dip in the cAMP gradient magnitude corresponds to the peak in the cAMP wave at cell position, the left of the dip is the rising phase while to the right lies the falling phase of the cAMP wave. There is a large effector gradient in response to the cAMP gradient, with its peak within 6 seconds of the cAMP gradient peak, for the rising phase of the wave. In the falling phase of the wave, the peak in cAMP gradient does not elicit a strong response in the effector gradient. The effector gradient peak for the rising phase is ~140 times stronger than the effector gradient 6 seconds after the cAMP gradient peak in the falling phase.
V. DISCUSSION
We have been able to successfully incorporate the receptor levels as determined from the MG wave model as the input to a LEGI model to create a chemotaxis model capable of both wave generation and directional sensing for the dictyostelium system. We simulate this system in both one and two dimensions, using an approximate scheme to avoid having to create an intracellular grid on a much finer scale than that needed for the extracellular grid. We found the asymmetry in response to the rising and falling phases of the cAMP wave was significantly better for the ultra-sensitive LEGI model than for the basic model, hence this version of the model essentially solves the “back-of-the-wave” problem. Nothing depends on the wave period as the waveform is not significantly changed with period variation, the extra time being taken up by adding time to the recovery phase between pulses. The combined model can also be applied to a sparser population of cells, leading to wider waves being formed. This results in a somewhat less efficient rectification by both the simple, and ultra-sensitive LEGI models, the asymmetry in response between front and back of the wave dropping two-fold for a doubling of the wave full-width half-max.
One issue that is quantitatively hard to address is the event to which the waveform formed by the MG dynamics is a good representation of the actual cAMP signal in the aggregation process. Unfortunately, there still does not exist any direct method for measuring extracellular cAMP, and connecting this needed field to measures of intracellular cAMP is model-dependent. One point worth mentioning is that in the excitable wave regime, changing the period of the waves in the MG model does not very much change the form of the cAMP pulse seen by the cells; instead the length of time for receptor recovery is lengthened as the period lengthens., This is very different than the role of wave period in artificial wave devices where, at least to date, waves of longer period are made by just slowing down the entire process and hence do directly change the pulse shape.
In two-dimensions, using the ultra-sensitive LEGI model, we confirmed that our combined model continues to work well with off-grid cells containing membrane dynamics at only four points on each cell’s perimeter. We can check that a 2D plane wave replicates the 1D results even with this more complex cell discretization. In the case of spiral waves, the model still highly suppresses the effector response of cells exposed to the falling phase of the wave. Our model picks the chemotaxis direction perfectly by the gradient direction of the front of the wave, aligned with the normal to the wave opposite to the direction of wave velocity. With this computationally tractable 2D chemotaxis model, it is now feasible to add a phenomenological motility model so as to obtain a full model for Dicty aggregation. This will be reported on in the future.
As we proceed to a full aggregation model, there is one additional aspect of the Dicty system that must be taken into account. Starting from starvation, it takes 3–5 hours for cells to self-organize the wave-field pattern. As discussed elsewhere [30–32], this process is strongly influenced by the feedback between the cAMP system and the expression of genes responsible for the production of the various proteins needed for the system. This idea is based on the experimental observation that many of these genes are inactive in the vegetative state and become fully activated only in response to the receipt of pulsatile cAMP signals by the individual cells. One mystery that persists is that during early aggregation, cells are in fact not able to rectify the nascent wave-field and instead move back-and-forth, remaining in place on average. Recently, it has been suggested [26] that perhaps early cells have much weaker ultra-sensitivity and also, it is expected due to the lowered excitability that the waves themselves are slower and lower in amplitude. Taking into account both lower ultra-sensitivity (Section IV A) and response to wider waves (Section IV C), these changes mean that our model shows that these cells would indeed be significantly poorer rectifiers and would hence help explain the aforementioned mystery. A related question has to do with the role of the longer term memory demonstrated in a recent paper [27]. If this memory is not needed to rectify typical waves, perhaps it has a role in locking a cell’s motion into a particular aggregation center when the wave-field is first getting established. All this can be tested with a full simulation of the actual aggregation.
Acknowledgments
This work was supported by National Institutes of Health Grant P01 GM078586.
References
- 1.Nanjudiah V. J Theor Biol. 1973;42:63–105. doi: 10.1016/0022-5193(73)90149-5. [DOI] [PubMed] [Google Scholar]
- 2.Loomis WF. The development of Dictyostelium discoideum. Academic Press; New York: 1982. [Google Scholar]
- 3.Levine H, Rappel W-J. Physics today. 2013:66. doi: 10.1063/PT.3.1884. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Alcantara F, Monk M. J Gen Microbiol. 1975;85:321. doi: 10.1099/00221287-85-2-321. [DOI] [PubMed] [Google Scholar]
- 5.Lee KJ, Cox EC, Goldstein RE. Physical Review Letters. 1996;76:1174–7. doi: 10.1103/PhysRevLett.76.1174. [DOI] [PubMed] [Google Scholar]
- 6.Tomchik K, Devreotes P. Science. 1981;212:443. doi: 10.1126/science.6259734. [DOI] [PubMed] [Google Scholar]
- 7.Sawai S, Thompson PA, Cox EC. Nature. 2005;433:323. doi: 10.1038/nature03228. [DOI] [PubMed] [Google Scholar]
- 8.Kessler DA, Levine H. Physical Review E. 1993;48:4801. doi: 10.1103/physreve.48.4801. [DOI] [PubMed] [Google Scholar]
- 9.Vasiev B, Hogeweg P, Panfilov A. Physical Review Letters. 1994;73:3173. doi: 10.1103/PhysRevLett.73.3173. [DOI] [PubMed] [Google Scholar]
- 10.Hofer T, Sherratt JA, Maini PK. Proceedings of the Royal Society of London B: Biological Sciences. 1995;259:249–257. doi: 10.1098/rspb.1995.0037. [DOI] [PubMed] [Google Scholar]
- 11.Palsson E, Othmer HG. Proc Natl Acad Sci U S A. 2000;97:10448–10453. doi: 10.1073/pnas.97.19.10448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Goldbeter A, Segel LA. Differentiation. 1990;17:127–35. doi: 10.1111/j.1432-0436.1980.tb01090.x. [DOI] [PubMed] [Google Scholar]
- 13.Martiel J, Goldbeter A. Biophys J. 1987;52:807. doi: 10.1016/S0006-3495(87)83275-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Tang Y, Othmer HG. Math Biosci. 1994;120:25–76. doi: 10.1016/0025-5564(94)90037-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Laub MT, Loomis WF. Mol Biol Cell. 1998;9:3521–3532. doi: 10.1091/mbc.9.12.3521. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Janetopoulos C, Jin T, Devreotes P. Science. 2001;291:2408–2411. doi: 10.1126/science.1055835. [DOI] [PubMed] [Google Scholar]
- 17.Firtel RA, Meili R. Curr Opin Genet Devel. 2000;10:421–427. doi: 10.1016/s0959-437x(00)00107-6. [DOI] [PubMed] [Google Scholar]
- 18.Manahan CL, Iglesias PA, Long Y, Devreotes PN. Annu Rev Cell Dev Biol. 2004;20:223–253. doi: 10.1146/annurev.cellbio.20.011303.132633. [DOI] [PubMed] [Google Scholar]
- 19.Sasaki AT, Chun C, Takeda K, Firtel RA. J Cell Biol. 2004;167:505–518. doi: 10.1083/jcb.200406177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Goldstein RE. Phys Rev Lett. 1995;77:775–8. doi: 10.1103/PhysRevLett.77.775. [DOI] [PubMed] [Google Scholar]
- 21.Parent CA, Devreotes PN. Science. 1999;284:765–770. doi: 10.1126/science.284.5415.765. [DOI] [PubMed] [Google Scholar]
- 22.Levchenko A, Iglesias PA. Biophys J. 2002;82:50–63. doi: 10.1016/S0006-3495(02)75373-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Krishnan J, Iglesias PA. Bull Math Biol. 2003;65:95–128. doi: 10.1006/bulm.2002.0323. [DOI] [PubMed] [Google Scholar]
- 24.Takeda K, Shao D, Adler M, Charest PG, Loomis WF, Levine H, Groisman A, Rappel W-J, Firtel RA. Science signaling. 2012;5:ra2. doi: 10.1126/scisignal.2002413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Levine H, Loomis WF, Rappel W-J. In: Eukaryotic chemotaxis and its limitations due to stochastic sensing. Sivaloganathan S, editor. American Mathematical Society; 2010. pp. 1–19. [Google Scholar]
- 26.Nakajima A, Ishihara S, Imoto D, Sawai S. Nature communications. 2014;5:5367. doi: 10.1038/ncomms6367. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Skoge M, Yue H, Erickstad M, Bae A, Levine H, Groisman A, Loomis WF, Rappel WJ. Proceedings of the National Academy of Sciences. 2014;111:14448–14453. doi: 10.1073/pnas.1412197111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Tyson JJ, Alexander KA, Manoranjan VS, Murray JD. Physica D. 1989;34:193–207. [Google Scholar]
- 29.Kriebel PW, Barr VA, Rericha EC, Zhang G, Parent CA. The Journal of cell biology. 2008;183:949–961. doi: 10.1083/jcb.200808105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Levine H, Aranson I, Tsimring L, Truong TV. Proc Nat Acad Sci USA. 1996;93:6382–6. doi: 10.1073/pnas.93.13.6382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Lauzeral J, Halloy J, Goldbeter A. Proc Natl Acad Sci U S A. 1997;94:9153–9158. doi: 10.1073/pnas.94.17.9153. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Falcke M, Levine H. Physical Review Letters. 1998;80:3875–8. doi: 10.1103/PhysRevLett.84.5664. [DOI] [PubMed] [Google Scholar]