Monovar: single nucleotide variant detection in single cells

Abstract

Current variant callers are not suitable for single-cell DNA sequencing (SCS) as they do not account for allelic dropout, false-positive errors, and coverage non-uniformity. We developed Monovar, a novel statistical method for detecting and genotyping single nucleotide variants in SCS data. Evaluation based on an isogenic fibroblast cell line and three different human tumor datasets showed substantial improvement of Monovar over standard algorithms for identifying driver mutations and delineating clonal substructure.

Next-generation sequencing (NGS) technologies have vastly improved our fundamental understanding of the human genome and its variation in normal populations and diseases such as cancer. However, most NGS datasets are composed of admixtures that represent genomes derived from millions of cells, and therefore mask genomic variations within the tissue sample. Recently, single cell sequencing (SCS) methods have emerged as powerful tools for resolving genomic variation in complex admixtures of cells, and measuring genomic information in rare subpopulations¹. SCS tools have had a major impact on diverse fields of biology, including cancer research, neurobiology, microbiology, immunology and development². In cancer research, SCS methods have greatly improved our understanding of intratumor heterogeneity and clonal evolution in human cancers³.

While substantial progress has been made in the development of new technologies for single cell DNA and RNA sequencing, the computational tools are severely lacking^2,3. While some progress has been made in computational methods for estimating DNA copy number^4,5 and RNA expression^6,7 in single cells, the methods for calling single nucleotide variants (SNVs) have not yet been developed. In most studies to date^8–10, standard NGS variant callers such as GATK¹¹, Samtools¹², SOAPsnp¹³, SNVMix2¹⁴, and Varscan2¹⁵ have been applied. These variant callers, designed for bulk tissue samples, make many assumptions regarding the underlying properties of the data. This is problematic for SCS data, which have inherent properties and technical errors due to whole genome amplification (WGA), including non-uniform coverage depth, allelic dropout (ADO) events, false-positive (FP) errors and false-negative (FN) errors, making it difficult to call SNVs accurately¹⁶. Consequently, these studies have been challenged by a large number of FP and FN errors, which require extensive orthogonal validation.

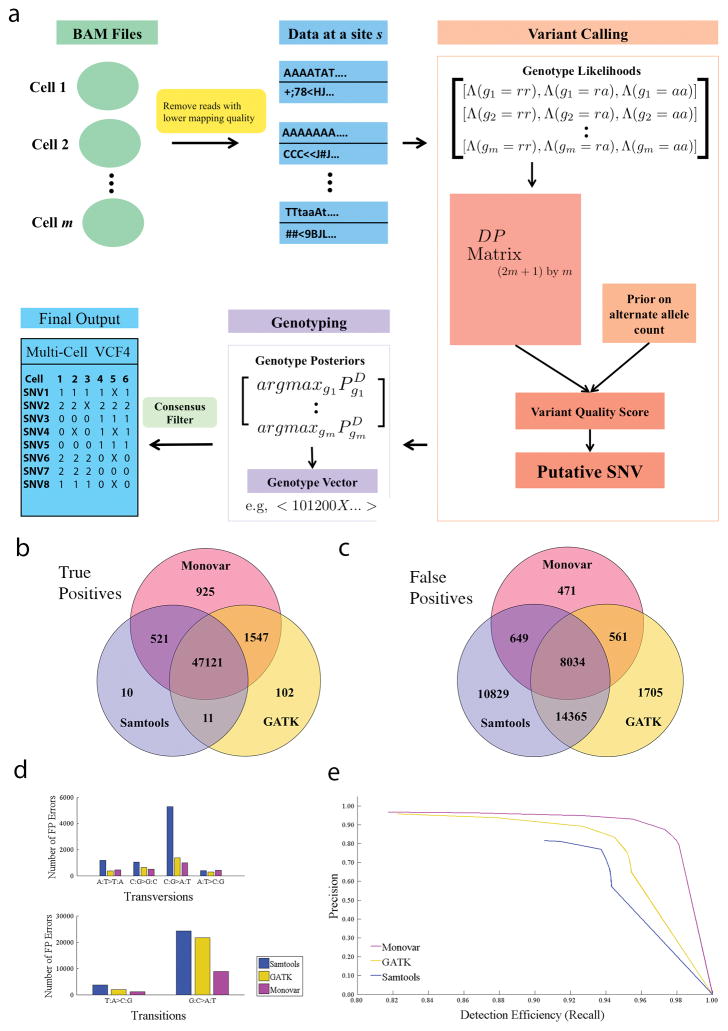
To improve the detection of SNVs in SCS datasets, we developed a novel statistical method called Monovar (Fig. 1a and Online Methods), which leverages data from multiple single cells to discover SNVs with high confidence and mitigates the effects of uneven or low coverage. Monovar independently analyzes each locus of the DNA, assuming data coming from different loci to be independent. For a particular locus, the input data consists of an array of observed bases from multiple single cells and the corresponding base quality scores. Monovar calculates the posterior probability of the locus containing a variant, P_sSNV = Pr(s = SNV|D) and based on this probability, the locus is classified as SNV or not. To calculate the posterior probability P_sSNV, Monovar applies Bayes’ rule and uses the likelihood values λ(l) of alternate allele count, l, for every value of l in the set {0,..,2m}, where m is the number of single cell samples. Calculation of λ(l) requires summation of genotype likelihoods over all possible combinations of genotype conformations of the single cells that result in the corresponding alternate allele count and these values are efficiently estimated using a dynamic programming algorithm given a prior distribution of allele frequency. Monovar models the effects of WGA specific FP errors in the calculation of genotype likelihoods for homozygous genotypes. For heterozygous genotypes, effects of both ADO and FP errors are accounted for. After a locus is classified as SNV, the j^th cell is genotyped based on the posterior probability of the genotype, $P_{g_j}^D$, calculated using a dynamic programming algorithm. An optional consensus-filtering step follows genotyping, where variants with support from only one cell are filtered. The final output is a VCF4 file in which each SNV is a different row followed by a genotype vector with length equal to the number of single cells (Fig. 1a).

Figure 1. Monovar Algorithm and Performance in a Normal Cell Line.

(a) Monovar variant detection flowchart. (b)–(e) Evaluation of Monovar, GATK and Samtools for the detection of SNVs in a single cell exome sequencing dataset generated from a normal isogenic fibroblast cell line. (b) Venn diagram showing the number of TPs called by different algorithms. (c) Venn diagram showing the number of FPs called by different algorithms. (d) Comparison of the SNV spectrum for FP errors detected using different variant detection algorithms. (e) Precision vs Detection Efficiency (Recall) curve for Monovar.

We first evaluated the performance of Monovar on three simulated SCS datasets (Online Methods and Supplementary Note), which showed that Monovar achieved higher precision compared to Samtools, GATK UnifiedGenotyper and GATK HaplotypeCaller (Supplementary Table 1). To validate Monovar’s performance on real datasets, we analyzed 12 single cell exome sequencing data (mean coverage depth 65X and breadth 92.7%), generated by a method called single nucleus exome sequencing (SNES) from an isogenic fibroblast cell line (SKN2)¹⁶. Exome sequencing of reference population sample at high coverage depth (59×) and breadth (99.76%) was used for constructing a reference set of variants (Supplementary Note). We compared Monovar against Samtools and GATK (HaplotypeCaller) for multi-sample SNV callset on the basis of precision and detection efficiency. Detection efficiency (or recall) of an algorithm is defined as the percentage of true SNVs that are discovered in the single cells. Precision of an algorithm denotes the fraction of SNV calls that are true positives. Monovar achieved substantially higher precision (0.8376) compared to GATK (0.6641) and Samtools (0.5845) with some improvement in the detection efficiency (Supplementary Table 2). Such improvement was particularly evident, when inspecting the true-positive (TP) and the false-positive (FP) SNVs called jointly or uniquely by the 3 callers (Fig. 1b–c). These data showed a major improvement in the reduction of specific FP classes, such as C:G > T:A transitions, which are the most prominent class of FP errors that arise during WGA in SCS experiments¹⁶ (Fig. 1d, Supplementary Fig. 1b).

Monovar also achieved the highest dbSNP precision, i.e., 83.02% of the SNVs detected by Monovar, 67.55% by GATK and 60.71% by Samtools were found in dbSNP (v138), respectively (Supplementary Table 3). Precision-recall curve obtained by varying the threshold used for calling SNV revealed Monovar’s superior performance over GATK and Samtools regardless of the choice of threshold used for calling SNV (Fig. 1e, Supplementary Fig. 1a). In addition, Monovar achieved consistently better results as compared to GATK HaplotypeCaller, when we down-sampled SKN2 data to various coverage depths (Supplementary Note and Supplementary Fig. 2). Monovar was able to detect a high percentage of true mutations with high precision in minor subclones created by intermixing (Online Methods) in silico subsets of normal SKN2 single cells with subsets of tumor cells from a triple negative breast cancer patient (TNBC) data⁸ (Supplementary Note and Supplementary Fig. 3).

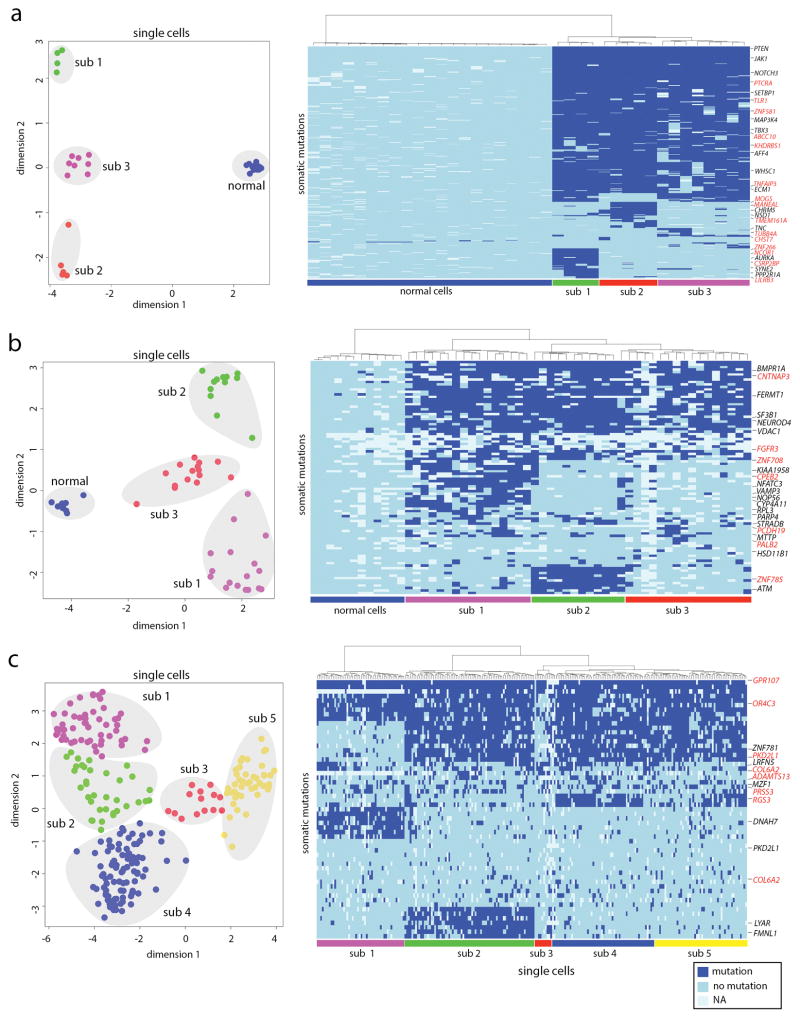
We applied Monovar to detect somatic mutations and delineate the clonal substructure of three human tumor samples: a TNBC patient⁸, a muscle invasive bladder cancer patient¹⁷ and a childhood acute lymphoblastic leukemia (ALL) patient¹⁸ (Fig. 2). In the TNBC patient, Monovar was applied to single cell exome data from 16 tumor and 20 normal cells, resulting in the detection of 120 synonymous and 282 nonsynonymous somatic SNVs (Supplementary Table 4.1). Hierarchical clustering and multi-dimensional scaling (MDS) identified three major tumor subpopulations that shared a common genetic lineage (Fig. 2a) as evidenced by 269 shared founder mutations that arose early in tumor evolution and unique subclonal mutations in SYNE2 and PPP2R1A (sub 1), CHRM5 and NSD1 (sub 2) and TNC (sub 3). In addition to the previously reported mutations⁸, Monovar also detected an additional 163 clonal somatic mutations in genes including PTCRA, TLR1, ZNF581, ABCC10, KHDRBS1, TNFAIP3, in addition to subclonal mutations in ZNF266, NCOR1, CSRP2BP, LILRB3 (sub 1), MOGS, MANEAL and TMEM161A (sub 2), and TUBB4A and CHST7 (sub 3) (Supplementary Table 5.1).

Figure 2. Application of Monovar to Human Tumor Samples.

Monovar was applied to detect somatic mutations in datasets from three human tumor samples, including a triple-negative breast cancer (a), a muscle-invasive bladder cancer (b) and a childhood acute lymphoblastic leukemia patient (c). Multi-dimensional Scaling analysis (left panels) and hierarchical clustering (right panels) were performed using the single cell genotype matrices to identify subpopulations of single cells that shared common sets of somatic mutations. Mutations in genes that were previously detected in these studies are listed in black, while new mutations identified by Monovar are listed in red.

Monovar was then applied to single cell exome data from 42 tumor cells and 11 normal cells from a muscle-invasive bladder carcinoma¹⁷ and detected 94 somatic mutations. Hierarchical clustering and MDS analysis identified three major subpopulations of tumor cells (sub 1, sub 2, sub 3) in addition to the normal cell population. Additionally, Monovar detected 54 subclonal mutations that were unique to each subpopulation, including mutations in KIAA1958, NFATC3, VAMP3, NOP56, CYP4A11, RPL3, PARP4 (sub 1), ZNF785 and ATM (sub 2), and PALB2 and MTTP (sub 3) (Supplementary Table 4.2). Importantly, Monovar identified 42 additional somatic mutations that were not detected in the original study¹⁷, including clonal cancer gene mutations in FGFR3, CNTNAP3 and ZNF708 and subclonal cancer gene mutations in PCDH19 (sub 1), ZNF785 (sub 2) and PALB2 (sub 3) (Supplementary Table 5.2).

We also applied Monovar to targeted single cell DNA sequencing data from a pediatric ALL patient¹⁸ (patient #3) to analyze 255 single cells. Hierarchical clustering and MDS analysis of somatic SNVs identified 5 major subpopulations (Fig. 2c). In total, Monovar discovered 57 somatic mutations (Supplementary Table 4.3), including 28 new somatic SNVs (Supplementary Table 5.3). Monovar identified significant mutations in OR4C3 and GPR107 (all subclones), LRFN5, PKD2L1 and ZNF781 (present in sub 2, 4, 5), DNAH7 (sub 1), LYAR and FMNL1 (sub 2), RGS3 (sub 4, 5), and ADAMTS13, PRSS3, and PKD2L1 (sub 2, 3, 4, 5). Among these mutations, the clonal mutations in OR4C3 and GPR107, and the subclonal mutations in PKD2L1, ADAMTS13, PRSS3 and RGS3 were not identified in the original study¹⁸ (Supplementary Table 5.3).

In summary, these data show that Monovar is a major advance for calling SNVs in SCS datasets, compared to standard NGS variant callers. With the recent innovations in high-throughput SCS methods to analyze thousands of single cells in parallel for RNA analysis^19,20 (which will soon be extended to DNA analysis) the need for accurate DNA variant detection algorithms will continue to grow. Monovar is capable of analyzing large-scale datasets, and handling different WGA protocols, therefore it is well suited for such studies. Although this study focused mainly on cancer datasets, Monovar can also be applied to SCS datasets in broad fields of biology, including neurobiology, microbiology, immunology, development and tissue mosaicism⁵. In the near future, as SCS methods move into the clinic, we expect that Monovar will have important translational applications in cancer diagnosis and treatment, personalized medicine and pre-natal genetic diagnosis, where the accurate detection of SNVs is critical for patient care.

ONLINE METHODS

Software availability

Monovar was implemented in Python. The source code and instructions for running Monovar are available at https://bitbucket.org/hamimzafar/monovar.

Monovar Algorithm

Monovar is a multi-sample SNV calling method that takes as input aligned read data from multiple single cells. Monovar quantifies the likelihood values of alternate allele count in the population of single cells and utilizes those values to detect the presence of SNV at a particular site. The calculation of the likelihood values of alternate allele count requires summing over all possible combinations of genotype conformations necessitating the quantification of genotype likelihood values for each cell. Each single cell is assigned the genotype with the highest value of the posterior probability calculated via a dynamic programming algorithm.

Model assumptions

In a single cell sample, sequence data at different sites are assumed to be completely independent. This assumption follows what is practiced by most of the state-of-the-art NGS SNV callers for the sake of simplicity. Sequencing and mapping being context dependent, this assumption might not hold always for real data²¹. But this assumption should not affect our analysis, as we are interested in calling point mutations. We also assume that the data coming from different single cells are independent. At a genomic site, the mapping and sequencing errors of different reads are assumed to be independent. Since we are interested in finding SNVs, we assume that the variants are bi-allelic (triallelic SNVs are rare, ~0.2%²²).

Calculation of genotype likelihood

In each single cell, the sequencing data at a site contains an array of bases observed on the sequenced reads and the corresponding base qualities. Considering the variants to be bi-allelic, we denote the reference allele as r and alternate allele as a at a site. For homozygous reference and variant genotypes (g = 0(rr) and g = 2(aa) respectively), the likelihood calculation does not require the effect of allelic dropout (ADO). For the case pertaining to g = 1(ra) (heterozygous variant genotype), we need to account for allelic dropout. At a genomic site s, for a single cell having sequencing data d consisting of n reads, the likelihood of g = 0 and g = 2 can be calculated as

$$\mathrm{\Lambda }(g=0)=p(d\mid g=0)=\prod _{i=1}^{n}p(d_i\mid g=0)=\prod _{i=1}^n[e_i(1-p_{d_i}^{rr})/3+(1-e_i)p_{d_i}^{rr}]$$ (1)

$$\mathrm{\Lambda }(g=2)=p(d\mid g=2)=\prod _{i=1}^{n}p(d_i\mid g=2)=\prod _{i=1}^n[e_i(1-p_{d_i}^{aa})/3+(1-e_i)p_{d_i}^{aa}]$$ (2)

For the heterozygous genotype (g = 1), the effect of allelic dropout is considered while calculating the genotype likelihood. We assume that the preferential non-amplification due to an ADO event can affect either of the alleles with equal probability. At a particular site, ADO affects all the reads as amplification precedes sequencing. The likelihood of g = 1 can be calculated as

$$\mathrm{\Lambda }(g=1)=p(d\mid g=1)=P_{ad}p(d\mid g=1,\mathit{ADO}=\mathit{True})+(1-p_{ad})p(d\mid g=1,\mathit{ADO}=\mathit{False})$$ (3)

where,

$$\begin{array}{ll}\hfill p(d\mid g=1,\mathit{ADO}=\mathit{True})& =\frac{1}{2}[p(d\mid g=0)+p(d\mid g=2)]\hfill \\ \hfill p(d\mid g=1,\mathit{ADO}=\mathit{False})=\overline{p}(d\mid g=1)& =\prod _{i=1}^n[e_i(1-p_{d_i}^{ra})/3+(1-e_i)p_{d_i}^{ra}]\hfill \end{array}$$ (4)

In Equations (1) to (4), d_i represents the observed base in the i^th read. $p_{\beta }^{g^{[1]}{g}^{[2]}}$ represents the probability of β being the ‘intermediate allele’ given the genotype g = g^[1]g^[2]. β is a variable that takes value from {A,T,G,C}. The term ‘intermediate allele’ refers to the allele which is called after amplification. In the absence of any amplification errors, β should be either g^[1] or g^[2]. Due to the errors introduced during preparation of the sample, β can differ from both g^[1] and g^[2]. In the context of single cell sequencing data, β accounts for the FP errors introduced during the amplification process. β is a latent random variable and we assume that it follows a discreet four point distribution with parameter p_e(Supplementary Table 6). p_e represents a prior probability that β equals an allele different from the haplotypes of the given genotype. This type of distribution has been previously proposed²³ in the context of bulk sequencing data. p_ad is the prior probability of allelic dropout.

Variant Calling

Assuming diploid single cells, m single cells contain 2m chromosomes at a site. The posterior probability of the site being a SNV, P_sSNV = p(s = SNV | D) is given by the probability, that at least one among 2m chromosomes contains an allele which is different from the reference allele. We introduce a random variable l, named alternate allele count, which gives us the number of chromosomes containing allele different from the reference allele. l can vary from 0 to 2m.

$$P_{s_{\mathit{SNV}}}=p(s=\mathit{SNV}\mid D)=1-p(l=0\mid D)$$ (5)

p(l = 0 | D) can be calculated using Bayes’ rule as

$$p(l=0\mid D)=\frac{p(D\mid l=0)p(l=0)}{{\displaystyle \sum _{l^{\prime }=0}^{2m}}p(D\mid l^{\prime })p(l^{\prime })}.$$ (6)

The sequencing data vector is given by D = {D₁,.., D_m}. For a random genotype vector for m cells g⃗ = {g₁,.., g_m}, the likelihood of alternate allele count l is evaluated by

$$\mathrm{\Lambda }(l)=p(D\mid l)=\frac{1}{\left(\begin{array}{c}2m\\ l\end{array}\right)}\sum _{g_1}\dots \sum _{g_m}{\delta }_{l,a_m(\overrightarrow{g})}\prod _i\left(\begin{array}{c}2\\ g_i\end{array}\right)\mathrm{\Lambda }(g_i).$$ (7)

δ_l,k is the Kronecker delta function which equals 1 if l = k and equals 0 otherwise. $a_m(\overrightarrow{g})={\displaystyle \sum _{i=1}^m}{g}_i$ is the number of alternate alleles in the genotype vector g⃗ = {g₁,.., g_m}.

To employ dynamic programming for the efficient computation of these likelihood values, we define h_l,j as follows:

$$h_{l,j}=\{\begin{array}{ll}\sum _{g_1=0}^2\dots \sum _{g_j=0}^2{\delta }_{l,a_j(\overrightarrow{g})}\prod _{i=1}^j\left(\begin{array}{c}2\\ g_i\end{array}\right)\mathrm{\Lambda }(g_i)\hfill & \mathit{for}0\le l\le 2j\hfill \\ 0\hfill & \mathit{otherwise}.\hfill \end{array}$$ (8)

h_l,j can be iteratively calculated using

$$h_{l,j}=h_{l,j-1}p(D_j\mid g_j=0)+2h_{l-1,j-1}p(D_j\mid g_j=1)+h_{l-2,j-1}p(D_j\mid g_j=2).$$ (9)

The base cases are as follows

$$h_{0,1}=p(D_1\mid g_1=0),h_{1,1}=2p(D_1\mid g_1=1),h_{2,1}=p(D_1\mid g_1=2).$$

Likelihood of alternate allele count can be obtained from h_l,j values using:

$$\mathrm{\Lambda }(l)=\frac{h_{l,m}}{\left(\begin{array}{c}2m\\ l\end{array}\right)}.$$ (10)

This type of dynamic programming approach has previously been explored^{21, 24} in the context of NGS data on a population of individuals.

The prior distribution on the alternate allele count is inspired by a population genetic prior

$$p(l)=\{\begin{array}{ll}\frac{\theta }{l}\hfill & 0<l<2m\hfill \\ \frac{1}{2}(1-\theta \sum _{i=1}^{2m-1}\frac{1}{i})\hfill & \mathit{otherwise}\hfill \end{array}$$ (11)

In equation 11, θ represents population level mutation rate, which is set to 0.001²⁴. Higher prior probability was assigned to alternate allele frequency of 0 or 1, because we expect that at the vast majority of sites, a population of single cell genomes will have identical homozygous genotypes. This prior can help limit false positives introduced by whole genome amplification and sequencing, which occur randomly at single cell level.

If the value of p(l = 0 | D) is smaller than 0.05, then the site is called as variant. The variant quality score in Phred scale is computed as

$$Q_{\mathit{var}}=-10{\mathit{log}}_{10}p(l=0\mid D)$$ (12)

Genotyping of single cells

After a site is declared to be a variant, each single cell is genotyped. For a variant site with reference allele r and alternate allele a, the genotype of a single cell can be either of {rr,ra,aa} corresponding to v ∈ {0,1,2}, indicating the number of alternate alleles. The posterior probability for the genotype of j^th single cell, $P_{g_j}^D$ is given by

$$\begin{array}{l}{P}_{g_j}^D=p(g_j=v\mid D)=\frac{p(D,g_j=v)}{p(D)}\\ =\frac{p(d_j\mid g_j=v)p(D\backslash d_j\mid g_j=v)}{p(D)},\\ =\frac{p(d_j\mid g_j=v){\displaystyle \sum _{l=v}^{2m-2+v}}{c}_{l,v}p(l)h_{l-v,m}^{j^{\ast }}}{{\displaystyle \sum _{l^{\prime }=0}^{2m}}p(D\mid l^{\prime })p(l^{\prime })}\end{array}$$ (13)

where, c_l,v is given by

$$c_{l,v}=\{\begin{array}{ll}\frac{\left(\begin{array}{c}l\\ v\end{array}\right)\left(\begin{array}{c}2m-l\\ 2-v\end{array}\right)}{\left(\begin{array}{c}2m\\ 2\end{array}\right)}\hfill & \hfill ifv\le l\\ 0\hfill & \hfill \mathit{otherwise}.\end{array}$$

$h_{l,m}^{j^{\ast }}$ is the value of h_l,m calculated for m − 1 cells excluding j^th cell, {1,2,…, j − 1, j + 1,…,m}. For the estimation of the posterior genotype probabilities of the single cells, the values of $h_{l,m}^{j^{\ast }}$ are recalculated for all m possible subsets found by excluding one cell from the data. The genotype with the highest posterior probability is assigned to the single cell. A similar genotyping approach has been used previously ²⁵ for bulk sequencing data. The genotyping results are stored as a string, called genotype vector that contains one character corresponding to one single cell. The character corresponding to a single cell can be ‘0’: homozygous reference, ‘1’: heterozygous variant, ‘2’: homozygous variant and ‘×’: insufficient coverage depth.

Consensus filtering using multiple cells

To achieve a higher quality call set, a filtering step is introduced after genotyping. The consensus filter removes low quality variants that have lower support. Depending on the genotype vector, the SNVs that are detected only in one single cell are removed as low quality. This step helps to remove spurious FP errors that occur at random positions in the single cell dataset. This step is optional but recommended for achieving a high quality call set.

Computational complexity of variant and genotype calling

The variant calling and genotyping step contributes to the major computational complexity of Monovar. For the variant discovery process for a site of the genome, s, the dynamic programming algorithm comprises most of the computation. Let us assume, we have m single cell samples. The average number of reads per single cell is denoted by $\overline{n_a}$. If the total number of reads at site s combining all cells is denoted by N_s, $N_s={\displaystyle \sum _{i=1}^m}{n}_i$, then $\overline{n_a}=\frac{N_s}{m}$. During the dynamic programming, for each single cell, amount of calculation is $O(m+\overline{n_a})$. The genotype likelihood calculation for each cell is $O(\overline{n_a})$ and for each single cell, we need to fill O(m) entries of the DP matrix. We need to do this for m single cells. Therefore, the asymptotic complexity of the variant discovery algorithm for a single site is $O(m^2+m\overline{n_a})$ i.e., O(m² + N_s). N_s varies over different sites and the variant discovery has linear complexity on the size of N_s. In the genotyping step, Monovar genotypes each single cell at the site s, where a variant has been discovered. To genotype a single cell, we need to find the genotype likelihood, which is $O(\overline{n_a})$. Also we need to redo the dynamic programming excluding the current single cell. Therefore, cost of genotyping a single cell is $O(\overline{n_a}(m^2+N_s))$. Asymptotic complexity of genotyping m single cells is given by $O(m\overline{n_a}(m^2+N_s))$ i.e., O(N_s (m² + N_s)). If we store the genotype likelihood values found in the variant discovery process, then the asymptotic complexity of genotyping of each single cell is O(1).O(m²) i.e., O(m²). Therefore, asymptotic complexity of genotyping m single cells is O(m³).

Simulation of single cell sequencing dataset

A 1 Mbp region of chromosome 20 of human genome (hg19) was chosen as the reference genome. Assuming n_cell to be the number of single cells in the population, n_cell synthetic genomes were constructed from the reference genome. The SNVs introduced in synthetic single cell genomes are the true SNVs. 1,000 SNVs (SNV rate 0.001/bp) were introduced in the reference region and those were shared by the single cells. These 1,000 SNVs served as the gold standard set. 1/3^rd of the SNVs were present in all the cells. Other 1/3^rd SNVs were present in half of the single cells. The rest of the SNVs had frequency other than 0.5 or 1 in the population and were either shared by a number of single cells or present as singletons in different single cells. Amplification errors were introduced in the single cell genomes. Allelic drop out rate was set to 20%⁸ and false positive error rate was set to 3.2e− 5¹⁶. Paired end sequencing reads were generated for each single cell using program dwgsim (http://davetang.org/wiki/tiki-index.php?page=DWGSIM). Sequencing error rate was set to 0.01% while generating the reads. dwgsim also simulated base quality scores for each sequenced nucleotide. Reads were discarded at random intervals to emulate the coverage variation in single cell sequencing data. The coverage depth of the simulated data was 24×. Three datasets varying in the number of cells (10, 15 and 20) were generated.

Isogenic cell line data

Single cell sequencing data from an isogenic fibroblast cell line (SKN2) was used for the validation of Monovar. SKN2 is an isogenic human fibroblast cell line that was obtained from the Cold Spring Harbor Laboratory (Dr. Michael Wigler). SKN2 was cultured using Dulbecco’s Modified Eagle Medium with 10% fetal bovine serum, penicillin/streptomycin and L-glutamine. The data consisted of exome sequencing data from 12 single cells and bulk sequencing data (reference population) from millions of cells.

Sequencing data from human tumor samples

We applied Monovar to three different human tumor samples that were previously published: a triple-negative breast cancer (TNBC) patient⁸, a muscle invasive bladder cancer patient¹⁷ and a childhood acute lymphoblastic leukemia (ALL) patient¹⁸.

Sequence alignment and data processing

For the simulated dataset, raw fastq files were aligned to the reference genome using BWA-MEM (v0.7.12)²⁶. For SKN2 dataset, BWA-MEM (v0.7.12)²⁶ was used to align the raw reads (FASTQ files) to the human genome (hg19). For all three human tumor datasets, sequenced reads in FASTQ format were mapped to the human genome assembly US National Center for Biotechnology Information (NCBI) build 36 (hg18) using the Burrows-Wheeler alignment tool (BWA version 0.7.12)²⁶ with default parameters and sampe option to create SAM files with correct mate pair information, and read group tag that includes sample name. Samtools (0.1.19)¹² was used to convert SAM files to compressed BAM files and sort the BAM files by chromosome coordinates. The reads with lower mapping quality (≤ 40) were removed from the BAM files. This removes about 5% of the total reads. For the SKN2 and TNBC datasets, the Genome Analysis Toolkit (GATK v1.4–37)¹¹ was used to locally realign the BAM files at intervals that have indel mismatches before PCR duplicate marking with Picard (version 1.56) (http://picard.sourceforge.net/).

Comparison of algorithms for performance evaluation

For the simulated data and SKN2 data, Monovar’s performance was compared against GATK¹¹ (v3.5) and Samtools¹² (v0.1.19), two widely used NGS SNV callers. Monovar was run with default parameter values (https://bitbucket.org/hamimzafar/monovar) on pileup data obtained from the bam files of all single cells in the dataset. For GATK, we used two variant callers UnifiedGenotyper and HaplotypeCaller. Each of them were run with default parameters as per GATK best practices recommendation (https://www.broadinstitute.org/gatk/guide/tooldocs/org_broadinstitute_gatk_tools_walkers_genotyper_UnifiedGenotyper.php, https://www.broadinstitute.org/gatk/guide/tooldocs/org_broadinstitute_gatk_tools_walkers_haplotypecaller_HaplotypeCaller.php). For the experiments with SKN2 data, HaplotypeCaller was used in most comparisons as per GATK best practices recommendation. For Samtools, Samtools mpileup command was used followed by bcftools for detecting variants. Maximum read depth for calling SNV was set to 10,000. For each dataset, each algorithm was run on data pooled from all single cells in the dataset.

Construction of the validation set for SKN2 data

For the SKN2 data, the gold standard variant set was constructed based on the results of GATK and Monovar on the reference population sequencing data. A union of the variant sets called by GATK and Monovar consisting of 51,154 SNVs was used as the gold standard variant set. 50,374 (98.5%) SNVs in the gold standard set were called by both GATK and Monovar. The rationale for computing the union is to have a gold standard variant set that is unbiased towards any variant calling algorithm, ensuring a fair comparison. The set of variants that Samtools discovered from the reference population sample was a subset of the gold standard variant set.

Down-sampling experiments

DownsampleSam program of the Picard toolkit (version 1.56) (http://picard.sourceforge.net/) was used to down sample the exome sequencing data from SKN2 single cells. DownsampleSam allows a user to randomly extract a certain percentage of reads from the original input BAM file. For example, the following command extracts 37.7% of the reads from the input sample, which has an average coverage depth of 53 ×, to generate a downsampled BAM file that has a coverage depth of 20 ×.

$ java -jar DownsampleSam.jar I= SKN2.bam O=SKN2.20X.bam P=0.377

Each single cell in the SKN2 dataset was down-sampled to 40 ×, 30 ×, 20 × and 10 × respectively. Monovar and GATK HaplotypeCaller were run on each down-sampled dataset. Precision and detection efficiency were measured for each algorithm for each down-sampled dataset.

Tumor-Normal Mixing experiments

6 in silico mixed datasets were prepared by mixing subset of normal SKN2 cells with subset of tumor cells from triple-negative breast cancer (TNBC) patient⁸. Such mixed datasets mimic a heterogeneous DNA sample where set of SKN2 cells forms a subclone. The SKN2 subclone size was varied from 7.6% (i.e. 7.6% of the cells in the population are normal SKN2 cells) to 50%. More specifically, the number of SKN2 cells were 1, 2, 3, 6, 9, 12 respectively in the 6 mixed datasets while keeping the number of TNBC cells fixed at 12. Monovar was run on pooled data from all the cells for each dataset. Monovar’s precision and detection efficiency were measured for each dataset.

Calling somatic mutations in human tumor datasets

For the human tumor datasets, from the set of SNVs called by Monovar, somatic mutations were identified by filtering the germline variants. The bulk normal tissue sequencing data worked as the source of germline variants for the triple-negative breast cancer⁸ and the muscle invasive bladder cancer¹⁷ datasets. For the acute lymphoblastic leukemia dataset¹⁸, germline variants were obtained from highly targeted amplicon sequencing data.

Clustered filtering

A common technical artifact that occurs in single cell sequencing data is genomic regions with clusters of false-positive (FP) mutations. These regions correlate with known areas of the human genome that have poor mappability and repetitive elements. To remove these FP artifacts from human tumor datasets, we filtered ‘clustered regions’ from the VCF files in which more than 1 SNV is detected within a 10bp window using a custom Perl script.

Genotype passcodes

In order to subset mutations, a binary string ‘passcode’ is added to each line in the VCF file that represents the genotype of each sample for each mutation: homozygous variant (2), heterozygous variant (1), absence of mutation (0) and insufficient coverage depth (×). For tumor samples or normal single cells, the minimum coverage we use is 10 × and the minimum number of reads required to call a variant is 3. However, to correct for high coverage samples, we use different thresholds depending on the coverage depth. When coverage is more than 20 × and less than 100 ×, we require a variant allele frequency of 15%. When coverage is more than 100 ×, we require a variant allele frequency of at least 10%. For the matched normal population sample, we require a more stringent cut off, coverage depth at least 6 × and at least 2 variant alleles - to detect germline mutations during the filtering steps. The ‘passcode’ also indicates whether a mutation resides within the targeted region or exome region or not. An example ‘passcode’ is <E01X02101X21120>. Here ‘<’ and ‘>’ represent the start and end of the ‘passcode’ respectively. ‘E’ indicates that this mutation is within the exome or targeted region, or alternatively ‘N’ indicates that the variant is present outside the targeted region. The number and order of samples in a ‘passcode’ is the same as the sample number and order at the VCF header.

Annotation of somatic mutations

Mutations were annotated with ANNOVAR²⁷ (http://annovar.openbioinformatics.org/en/latest/) to integrate multiple databases and classify mutations as non-synonymous, synonymous, intergenic and non-coding mutations. We then determined if mutations intersect with known cancer genes using the ‘intersect’ function of BEDTools²⁸ (http://bedtools.readthedocs.org/en/latest/). The cancer gene list was compiled from multiple sources including the Cosmic²⁹ (http://cancer.sanger.ac.uk/cosmic) database and cancer gene census³⁰ (http://cancer.sanger.ac.uk/census). We developed a custom Perl script that reads a VCF file as input and runs through the annotation steps automatically and combines all annotation results into one tab-delimited text output file. Another Perl script was used to extract ‘passcode’ and allele frequency information of each sample from the input VCF file. The final annotation output can then be imported into Microsoft Excel, R or MatLab for statistic analysis or for visualization by building a heatmap.

Predicting damaging impact of mutations

To evaluate whether a mutation is likely to affect protein structure or function, we used two databases: Polyphen³¹ (http://genetics.bwh.harvard.edu/pph2) and SIFT³² (http://sift.jcvi.org/). Mutations with Polyphen score > 0.5 and SIFT score < 0.05 were considered to be significant. We considered mutations that were predicted to be significant by both databases as protein structure/function damaging.

Multi-dimensional scaling (MDS) analysis

Non-synonymous and synonymous mutations were parsed from the VCF file containing single cell exome and targeted variant data to construct a binary distance matrix for sites where coverage depth was ≥ 6 ×. Hamming distance was used as the distance metric and missing values with no coverage were replaced by value 0.5. The resulting binary matrix was used to perform multi-dimensional scaling (MDS) analysis in R (http://www.r-project.org). The MDS coordinates 1 and 2 were plotted on the X and Y axes respectively to identify clusters of cells with similar genotypes or mutations.

Hierarchical clustering and heatmaps

A binary matrix was calculated using non-synonymous and synonymous mutations from the single cell genotype ‘passcode’ strings. Heterozygous and homozygous mutation sites were converted to a value of 1. For sites without mutations, we used a value 0. Sites with coverage depth less than 6 × were assigned value 0.5. The heatmap was generated using the heatmap.2 function in R and 2-dimensional hierarchical clustering was performed using both rows (mutations) and columns (cells).