Abstract
The lifespan of red blood cells (RBCs) plays an important role in the study and interpretation of various clinical conditions. Yet, confusion about the meanings of fundamental terms related to cell survival and their quantification still exists in the literature. To address these issues, we started from a compartmental model of RBC populations based on an arbitrary full lifespan distribution, carefully defined the residual lifespan, current age, and excess lifespan of the RBC population, and then derived the distributions of these parameters. For a set of residual survival data from biotin-labeled RBCs, we fit models based on Weibull, gamma, and lognormal distributions, using nonlinear mixed effects (NLME) modeling and parametric bootstrapping. From the estimated Weibull, gamma, and lognormal parameters we computed the respective population mean full lifespans (95% confidence interval): 115.60 (109.17–121.66), 116.71 (110.81–122.51), and 116.79 (111.23–122.75) days together with the standard deviations of the full lifespans: 24.77 (20.82–28.81), 24.30 (20.53–28.33), and 24.19 (20.43–27.73). We then estimated the 95th percentiles of the lifespan distributions (a surrogate for the maximum lifespan): 153.95 (150.02–158.36), 159.51 (155.09–164.00), and 160.40 (156.00–165.58) days, the mean current ages (or the mean residual lifespans): 60.45 (58.18–62.85), 60.82 (58.77–63.33), and 57.26 (54.33–60.61) days, and the residual half-lives: 57.97 (54.96–60.90), 58.36 (55.45–61.26), and 58.40 (55.62–61.37) days, for the Weibull, gamma, and lognormal models respectively. Corresponding estimates were obtained for the individual subjects. The three models provide equally excellent goodness-of-fit, reliable estimation, and physiologically plausible values of the directly interpretable RBC survival parameters.
Keywords: RBC lifespan, mathematical model, survival functions, direct and indirect RBC survival models
Introduction
The survival of red blood cells (RBCs) has been studied for nearly a century [3] because of its importance in clinical medicine and translational research. To cite three examples, the mean RBC lifespan and production rate determine the steady-state hemoglobin (Hb) concentrations in both healthy and diseased individuals [41]; variation in mean RBC lifespan is sufficient to result in clinically important differences in HbA1c among diabetics with the same mean blood glucose level [13]; and reduced mean RBC lifespan contributes to the anemia of chronic renal failure [47, 65]. Equally important is the role of the RBC lifespan in establishing criteria for stored RBCs for transfusion, elucidation of the physiology and pathophysiology of erythropoiesis, and the design of therapies for anemia and other hematological conditions [4, 19, 46].
Confusion and a lack of proper quantification of various aspects of RBC survival still exist in the literature. Before discussing these issues we describe the two approaches, direct and indirect, commonly used to study RBC survival and the types of RBC samples used in such studies [45]. We then provide a brief literature review.
Direct and indirect models of RBC survival
The direct approach [45] involves observing and quantifying the disappearance of a population of labeled RBCs from the circulation. Direct models fall primarily into two categories: 1) empirical models for simple curve fitting [9, 13, 32, 42, 44, 46, 53, 65], and 2) “phenomenological” models accounting for macroscopic phenomena such as random destruction of the cells, lifespan-based elimination of the cells, neocytolysis (selective hemolysis of young RBCs under conditions of RBC excess when acutely exposed to increased tissue oxygen content), etc., and method-specific phenomena such as radioactive decay of the label, elution, vesiculation, etc. in the case of labeling by 51Cr [8, 9, 16, 17, 24, 35, 36, 45, 61].
Instead of the direct measurement of RBC survival, the indirect approach [45] relies on native Hb, glycosylated Hb, or other pharmacokinetic/pharmacodynamic (PK/PD) information over time to make inferences about the RBC lifespan [22, 41, 45, 59, 62, 64]. Indirect models are lifespan-based compartmental PK/PD models (e.g., lifespan-based indirect response or LIDR models [38]), of which transit compartment (TC) models are a special case [37]. A series of transit compartments, each compartment with a PDF representing the lifespan distribution of the cells in that compartment [30, 37, 45] is a hallmark of TC models.
As the name indicates, LIDR models are “indirect” models. Direct models, in which the survival of labeled RBCs is tracked over time, are based on the residual survival function (SF), which is derived here as a consequence of the LIDR model.
Random and cohort samples
Direct RBC survival studies can be conducted in two ways depending on the type of sample of RBCs used [19]. A random (or population) sample consists of a mixture of RBCs of all ages, such as that obtained by a venous blood draw. In contrast, a cohort sample consists of RBCs that are all approximately the same age [19]. Random sample methods are more easily performed and thus more widely used in RBC survival studies [19, 53]. In such studies, RBCs in blood drawn from a donor are labeled and transfused into a recipient (possibly the same person), and their disappearance is followed [19]. The time at which the sample is collected is called the index time, and the corresponding RBC population (in the circulation plus in the sample) at that time is the index population.
For a random sample study, the sampling of blood and transfusion of labeled RBCs back into the subject should ideally happen at the index time and within a time interval insignificant in comparison to the shortest lifespan of all but a negligible fraction of the RBCs; further, the transfused RBCs should be distributed homogeneously in the circulation immediately. The concentration of labeled RBCs in the circulation at that instant would serve as the baseline concentration. In practice, the labeled RBC enrichment at day 1 is taken as the baseline to minimize artifacts from RBCs that are damaged and consequently removed during the first 24 h in circulation [28]. Blood samples are subsequently drawn at sufficient intervals after the labeled RBC transfusion to permit determination of RBC survival parameters. The ratio of the concentration of labeled RBCs in the later samples to the baseline concentration gives the survival data at each time. A plot of these measurements against time constitutes the random sample (residual) survival curve.
Labeling with radioactive 51Cr is the current de facto gold standard for RBC survival studies [53], despite the fact that it exposes subjects to radiation and despite the analytical complications due to radioactive decay, elution of 51Cr from cells, and loss of label by vesiculation [34]. Recently, Mock et al. [52] demonstrated that random sample survival data for normal adults obtained using nonradioactive biotin labeled RBCs (bioRBCs) can be used in RBC survival studies with results similar to those from 51Cr. Rather than measuring the radioactivity of hemoglobin bound 51Cr in the blood samples, which is inevitably confounded by radioactive decay, vesiculation, and elution, individual cells are enumerated by flow cytometry after separation from unlabeled RBCs based on fluorescence intensity due to binding of fluorescent-labeled streptavidin to the biotin label on the RBCs. Thus, this method is free from the problems of elution and vesiculation. Moreover, biotinylation at lower densities appears not to affect the RBC lifespan [53].
Brief literature survey
Mathematical descriptions of RBC survival are broadly based on the direct or indirect method described above. Direct models are based on the theory for transfused RBCs developed early on [7, 9, 14, 60]. Some quantitative descriptions developed later focused on fitting a curve to the survival curve and quantifying the mean lifespan and half-life [7, 8, 17, 24, 32, 65]. Complicated phenomenological models were also used [8, 9, 16, 17, 24, 34–36, 61]. Some authors used simple linear or cubic curve-fitting of the survival curve to estimate the mean age at the time of labeling [13, 53]. Many studies use the maximum RBC lifespan (Tmax), a term that is difficult to quantify [13, 32, 44] in a plausible manner.
A direct PK/PD model including RBC survivor functions of various complexity was presented by Uehlinger et al. [64]. A new lifespan based compartmental PK/PD model paved the way to an indirect and compartmental approach to quantify RBC/reticulocyte mean lifespan [39]. Earlier works based on this approach assumed that all cells in a compartment survived for a fixed time, which introduced a time-delay in the input/output models thus representing the lifespan of the cells in a compartment by a point distribution [1, 38, 39, 41, 57, 59]. The theory was expanded later to represent the RBC lifespan distribution by possibly time-varying continuous PDF [21–23, 40, 61]. These indirect methods do not involve direct measurement of random sample cell survival data. But Lledó-García et al. [45] presented a somewhat “hybrid” approach that used a TC model to estimate mean lifespan from a set of biotin-labeled random sample RBC survival data previously published by Cohen et al. [13].
There exist confusions in the literature primarily due to failure to distinguish between various survival functions and survival parameters and subtle disconnects in the theoretical relationships developed. Furthermore, some models have a large number of unknown parameters, which creates identifiability issues.
Objectives
In this paper, starting with a LIDR model based on an arbitrary lifespan distribution, we derive the relations between the residual lifespan distribution, which is the basis of observations in the direct method, and the full lifespan distribution; these are expressed through the survival functions corresponding to each distribution. Further, we derive survival functions for the current age distribution (distribution of ages in the index RBC population) and the excess lifespan distribution (distribution of remaining lifespan of cells in the index population that have survived beyond a specified time te past the index time). Other RBC survival descriptors (mean lifespan, mean current age, etc.) are then easily obtained.
We apply these results to analyze a set of bioRBC data [53] using the NLME framework. We consider three models, based on the Weibull, gamma, and log-normal distributions, respectively, for the full RBC lifespan. The PDFs for these distributions are given in Appendix A. These distributions are widely used in reliability theory [5, 49, 55], survival analysis [43], and studies of aging and lifespan for both mechanical and biological systems using a reliability theory approach [6, 10, 25, 26, 33]. Although the Weibull is widely used as a failure distribution [5], aside from the papers by Friese et al. [22, 23], ours is the only use of the Weibull as an RBC lifespan distribution to our knowledge. In RBC survival studies the gamma distribution arises in transit compartment models [37] with a fixed, specified integer-valued shape parameter, a restriction we avoid in this work.
Based on observations of the residual survival function provided by the experimental data, the estimated structural parameters of each model are used to compute the survival functions for the full lifespan, current age, and excess lifespan distributions. From these it is easy to estimate many RBC survival descriptors at both the population and individual levels; as examples we use the mean lifespan, the standard deviation of the lifespan distribution, τ95 (as a surrogate for maximum lifespan), mean current age, and residual half-life. The definitions of these terms are provided later in the text.
The process of RBC aging and the eventual death is an issue of special scientific and clinical interest [2, 29, 31]. The RBC lifespan distribution may provide information of clinical and research relevance in understanding the type of red cell elimination taking place in normal individuals and in those with specific diseases. For example, these models can potentially be used to determine whether elimination is primarily driven by an intrinsic lifespan-based mechanism or is the result of extrinsic factors acting independently of the RBC lifespan.
Post-transfusion survival of stored RBC has important implications in determination of the shelf life of RBCs [46, 63]. Excess lifespan of RBC can potentially be used to better quantify the post-transfusion survival of stored RBC.
A potential use of current age and excess lifespan distributions is to help identify morphological and/or physiological attributes of RBCs that correlate to the RBC age distribution, shedding light on the mechanism of RBC aging and eventual death in health and disease [20]. For example, it has been shown that the surface area and hemoglobin amount generally resemble lognormal distribution and the distribution changes in a time dependent manner as the membrane continues to be shed [27]. Time dependent changes in the density distribution of biotin-labeled sickle RBC have been studied in [18]. If we are able to accurately measure the current age or excess lifespan distributions based on some morphological or physiological attributes of RBCs, then it would potentially allow the quantification of full RBC survival descriptors discussed in this paper with a single random sample of blood instead of multiple consecutive random samples over the period of up to 4 months as in the most commonly used residual lifespan data.
Mathematical Model
The birth time of an RBC is the time when a reticulocyte transitions to a fully matured and hemoglobinized RBC after losing the ribosomes and mitochondria. By death time of RBC we mean the moment of elimination of the RBC from the circulation. At birth time t = −u, each RBC is assumed to be endowed with a full lifespan τ. Consider the index time t = 0 when the RBC sample is collected and labeled. The age of an RBC in the index population at this time is the current age, τc = u, which is the amount of time already spent by it in circulation since its “birth.” The residual lifespan of the RBC is the time τr that it remains in the circulation before its “death”. Thus
Given a fixed, specified time te after the index time, the remaining lifespan of the RBC is excess lifespan of the RBC, τe = τ − te. Not all RBCs are born with the same lifespans. The full lifespan and hence the residual lifespan, the current age, and the excess lifespan can be represented by respective continuous probability density functions (PDFs). In general the RBC survival distributions for different people will not be the same.
We assume that the RBCs in healthy individuals survive independently of each other. We assume the internal environment of the study subject is stable in the sense that the RBC lifespan distribution is time-invariant and that there is no abnormal blood loss or other significant intercurrent event (e.g., events leading to hemolysis).
Full lifespan distribution
The (full) lifespan distribution in the population of RBCs in a given individual is represented by a PDF p(t), t ≥ 0. The corresponding full SF is the probability that the lifespan is > t; more explicitly,
| (1) |
The mean lifespan μ is then given by the well-known formulae
| (2) |
In principle, if we could isolate a sample of newly produced RBCs released into the circulation (i.e., a cohort sample), label them, and transfuse them into the recipient, the survival curve obtained by tracking the labeled RBCs would provide an estimate of the full SF P̄(t).
RBC compartmental model
We start with the LIDR compartmental model previously studied by several other groups [1, 21, 38, 40, 57]. In brief the model specifies that
| (3) |
where r(t) denotes the number of cells in the RBC compartment at time t, k(t) is the RBC production rate, which is the rate of entry of cells into the RBC compartment, and p(t) is the full RBC lifespan PDF, which can be a completely arbitrary PDF on the positive real numbers. The integral term in equation (3) is the rate at which cells leave the compartment, i.e., the rate of RBC death due to senescence or hemolysis [40]. We assume k(t) is bounded and nonnegative, 0 ≤ k(t) ≤ M < ∞ for all t, −∞ < t < ∞, and that the mean lifespan μ (equation (2)) is < ∞. Integrating equation (3) from 0 to t > 0, we obtain
Because k(t) is bounded, both integrals are finite. After exchanging the order of integration in the double integral, letting r0 = r(0) be the size of the index population (i.e., the RBC population that was present at time t0 = 0, which is the index time as described above), and some algebraic manipulation, we find
| (4) |
where
| (5) |
and
| (6) |
The integral in (4) represents the RBC population due to past production, that is, during t < 0, that is present at time t0 = 0. This can be seen by noting that k(−u)du is the number of cells produced during the time interval −u to −u + du, and P̄(u) is the fraction of cells that survive for time u > 0, and the integral is the sum of these quantities over all u > 0. For a person with a stable internal environment, this will be the RBC population at time 0, thus r0 and the integral cancel each other in equation (4) and we are left with
| (7) |
The term r0(t) represents the part of the index population that has survived until time t > 0, whereas r1(t) is the portion of the RBC population that is present at time t > 0 that was produced between times 0 and t.
Residual lifespan distribution
The survival time after t = 0 of a cell in the index population is called the residual lifespan of the cell. The residual survival function (RSF), P̄r(t), is the proportion of the index population that has survived at least until time t > 0 (equivalently, the probability of residual lifespan > t), P̄r(t) = r0(t)/r0(0). From equation (5),
| (8) |
Survival curves reported in studies of random RBC samples are in fact estimates of the RSF.
The RSF depends on the past production rate k(t) for times t < 0, as indicated in equation (8). If k(t) can be assumed constant for t < 0 (which is consistent with the assumption that the subjects had a stable intravascular environment), P̄r reduces to the familiar form
| (9) |
Note the similarity between equations (9) and (1). The corresponding PDF of the residual lifespan is
| (10) |
Integration by parts of gives the mean residual lifespan μr, which is different from mean full lifespan:
| (11) |
where E(·) signifies expected value, and μ and σ2 are the mean and variance of the full RBC lifespan τ.
Current age distribution
The members of the index population that have age > t ≥ 0 at time 0 are those that were produced at some time u before time −t and have survived for an additional time −u; as in the case of equation (4), this is given by
The fraction of the index population of age > t, namely,
| (12) |
is the SF of the current age distribution, which is the distribution of ages in the cell population at the index time t0 = 0. It reduces to equation (9) if the past production rate is constant; in this specific situation, but not in general, the current age distribution is the same as the residual lifespan distribution and hence mean current age, μc= mean residual lifespan, μr.
Excess lifespan distribution
Consider the subpopulation of the index population that is still present at a specified time te > 0; these are the cells that were produced at some time −u < 0 and survived for a time te + u. The excess lifespan distribution corresponds to the SF P̄e(t), which is the fraction of this subpopulation of age > te + t, where t > 0 is called the excess lifespan. By an argument similar to that following equation (4), the subpopulation of age > te + t consists of those cells that were produced at some time some time −u < 0 and have survived for time te + t + u; the number of such cells is . The entire subpopulation present at time te corresponds to t = 0 in this expression. Thus the fraction of those present at time te that are of age> te + t is the ratio
| (13) |
This is the conditional probability that the lifespan of an RBC in the index population is > t + te given that it is > te. Given a constant past production rate it reduces to
| (14) |
and this can be estimated from the observed residual survival curve. The corresponding PDF of excess lifespan distribution is given by
| (15) |
Note that, for te = 0, the excess lifespan SF is the same as the current age SF and consequently is the same as the residual lifespan SF in the case under consideration.
Relation (2) holds for any probability distribution, including the full lifespan, residual lifespan, current age, and excess lifespan distributions. We can use equations (8), (12), and (14) to compute the mean residual lifespan (μr), mean current age (μc) in the index population, and the mean excess lifespan (μe) in the surviving part of the index population at any time te > 0. These results generalize those of Lindsell et al. [44], without the questionable assumption of a stable, stationary, and closed population [54].
Methods and Statistical Analysis
We used a nonlinear mixed effects (NLME) model [58] to analyze data obtained from 8 healthy adults who received autologous biotin-labeled RBCs [53]. Parametric bootstrap analysis was performed to confirm the results of NLME analysis because the number of subjects is small. The NLME model analysis was conducted using the nlmefit function in the Statistics toolbox of MATLAB software [48]. All computations and simulations were conducted using the same software. A personal computer with a 4 GB RAM and a 2 core Intel© (R) Core(TM) i3M 370 @ 2.40GHz processor was used for all computations.
We analyzed the lowest density bioRBC data from Mock et al. [53] as biotinylation at lower densities has negligible effect on the RBC lifespan [53]. Details of the experimental design and data collection are provided in [53]. Briey, each of eight healthy subjects was transfused with autologous bioRBCs labeled at a biotinylation reagent density of 6μg/mL of packed RBC. Post-transfusion residual RBC survival data were collected. Since even microliter blood samples contain many RBCs, the laws of large numbers from probability theory imply that such samples will replicate the residual lifespan distribution of the whole circulation at a given time within measurement error; this is the basis of the statistical analysis of random blood samples. Since the flow cytometric instrumentation allows tracking of the disappearance of at least 97 % of bioRBCs [53], we excluded values of the survival curves smaller than 0.03. The bioRBC concentration at day 1 was used as the baseline value.
We performed separate analyses for the Weibull, gamma, and lognormal models. For each model, the nonlinear mean-value terms are the RSFs as in equation (9), but with the appropriate survival functions; thus,
| (16) |
where W̄r, Ḡr, and L̄r denote the RSFs, W̄, Ḡ, and L̄ denote the full SFs, and μw, μg, and μl denote the mean full lifespans (see Appendix A) in the Weibull, gamma, and lognormal models, respectively. The same letters α and β are used for all of the Weibull, gamma, and lognormal parameters for brevity in presentation, but we emphasize that they are entirely unrelated. We refer to α and β as the structural parameters on the original scale.
Just as P̄r(t) is the ratio of the surviving part of the index population relative to the size of the index population, the observed residual survival curve, is the ratio of the measured concentration of the surviving part of the labeled RBCs at time t > 0 relative to the concentration at index time t = 0. In standard mixed effects model notation, the models in equation (16) are
| (17) |
where W̄ij, Ḡij, and L̄ij denote the observed residual survival curve corresponding to the Weibull, gamma, and lognormal models, respectively, M = 8 is the number of subjects, ni is the number of observations on the ith subject, tij is the time of the jth observation on the ith subject, and εij is an additive random error term, assumed normal N(0, ϕ2) (we use ϕ2 to denote variance of the random error to not confuse with σ2 used to denote the variance of the full lifespan distribution). Thus W̄ij = W̄ (tij), for example, is the observed residual survival curve for the ith subject at the jth time using the Weibull model. To ensure the parameter estimates are > 0 we write
| (18) |
and rewrite the models as
| (19) |
| (20) |
We call ai and bi the individual structural parameters on the log scale; this well known “log trick” [58] allows the use of unconstrained optimization techniques. af (= log(αf)) and bf (= log(βf)) denote the fixed effects, representing the average values of the parameters (in log scale) over the whole population from which the subjects in the sample are drawn (the reference population), and ari and bri denote random effects, which represent the deviations of an individual’s parameters from the population average [58]. “Mixed effects” refers to the presence of both fixed and random effects in (20). The random effects vector (ari, bri) is modeled as multivariate normal, N(0, Ψ), independent of the measurement errors εij, and independent between subjects; likewise, the errors are assumed independent between and within subjects [58].
For the distribution specified by the corresponding PDF, the derived parameters for each individual are the functions of corresponding αi and βi and for the population (fixed effects estimates) are the functions of corresponding αf and βf. For the corresponding full lifespan distribution, the mean full lifespan (or simply mean lifespan) μ and the standard deviation σ are the derived parameters that can be computed easily using the formula provided in Appendix A. Other derived parameters describing RBC survival of potential clinical importance are
τ95, defined as the 95th percentile of the full lifespan distribution, a surrogate for the maximum lifespan,
the mean current age, μc, defined as the mean of the current age distribution, which is equal to the mean of the residual lifespan distribution or the mean of the excess lifespan distribution at index time t = 0 assuming constant past production rate, and
the residual half-life, T50, defined as the median of the residual lifespan distribution. Note that we use the term half-life irrespective of whether or not the distribution is exponential.
The values of τ95 and T50 have to be obtained numerically as they cannot generally be expressed in closed form; any modern statistical software has a facility to do this. An exception is that τ95 is easily obtained for the Weibull distribution: τ95 = β(log(20))1/α (all logarithms in this paper are natural logarithms). The closed form expressions for μc for the corresponding PDFs are presented in Appendix B. Formulas for mean residual lifespan and steady state mean full lifespan are provided in Appendix B. Mathematical manipulations for efficient computation of the different survival functions based on the Weibull, gamma, and lognormal PDFs are also provided therein.
Results
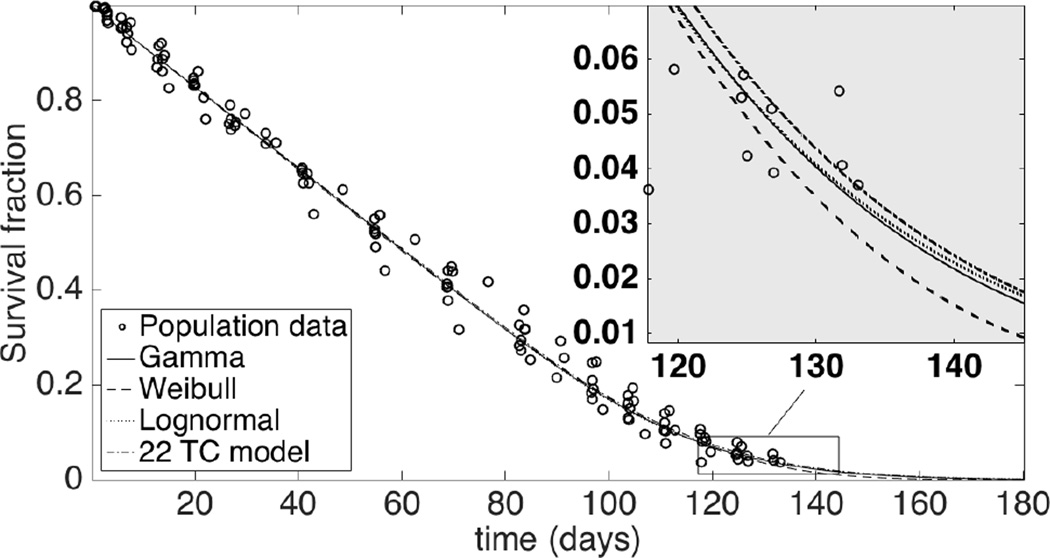
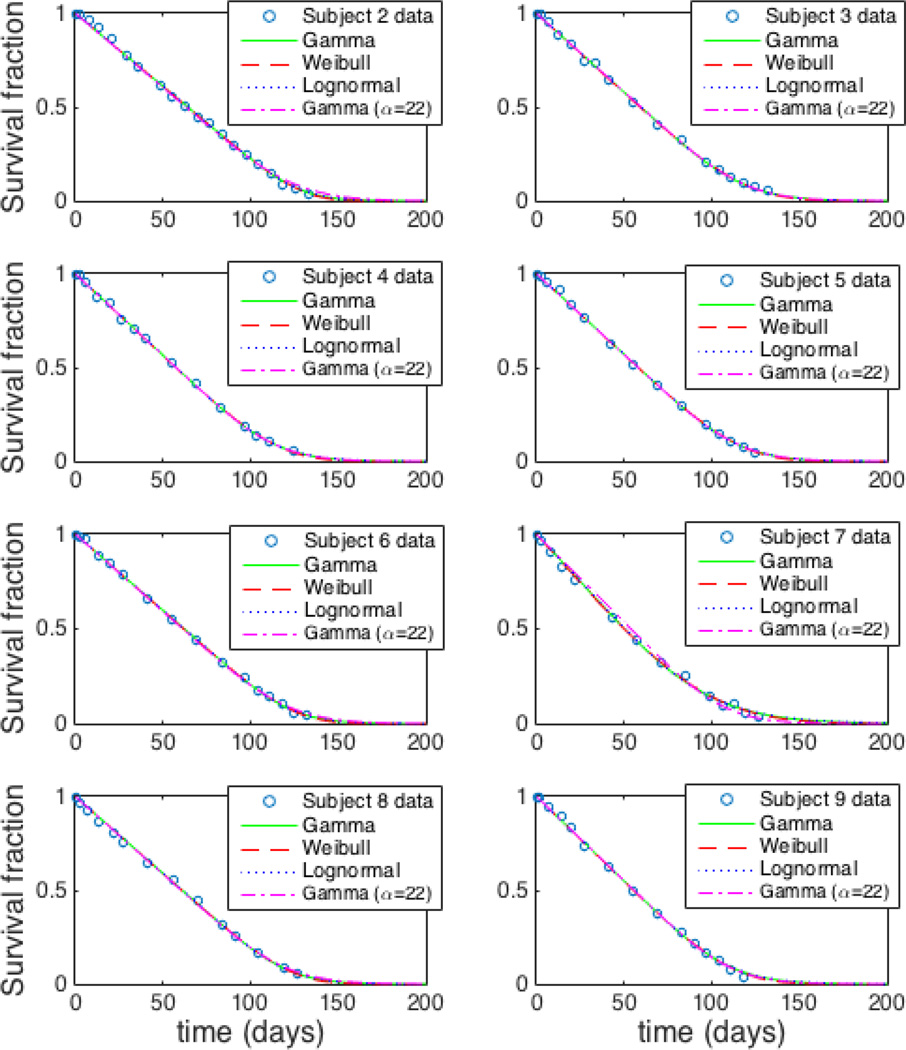
Figure 1 shows the population fits for the 8 study subjects using the 3 different models. Residual survival data for each subject along with the respective individual fits using the Weibull, gamma, and lognormal models are shown in Figure 2. The group values of root mean square errors (RMSEs) are 0.0120, 0.0126, and 0.0129 for Weibull, gamma, and lognormal models, respectively. Corresponding fractional RMSE (RMSE/average response value) are 0.023, 0.024, and 0.025 respectively. The log likelihood (logl) values are 358, 354, and 351 respectively. The RMSE and logl values are shown in Table 1.
Fig. 1.
Fitted population-level residual survival curves for data of all 8 study subjects. Insert: tail region where the models differ the most.
Fig. 2.
Fitted individual-level residual survival curves for data of all 8 study subjects.
Table 1.
Goodness-of-fit and model selection criteria. RMSE: Root mean squared error. logl: loglikelihood.
| Goodness of fit |
Weibull | Model Gamma |
Lognormal |
|---|---|---|---|
| RMSE | 0.0120 | 0.0126 | 0.0129 |
| logl | 358 | 354 | 351 |
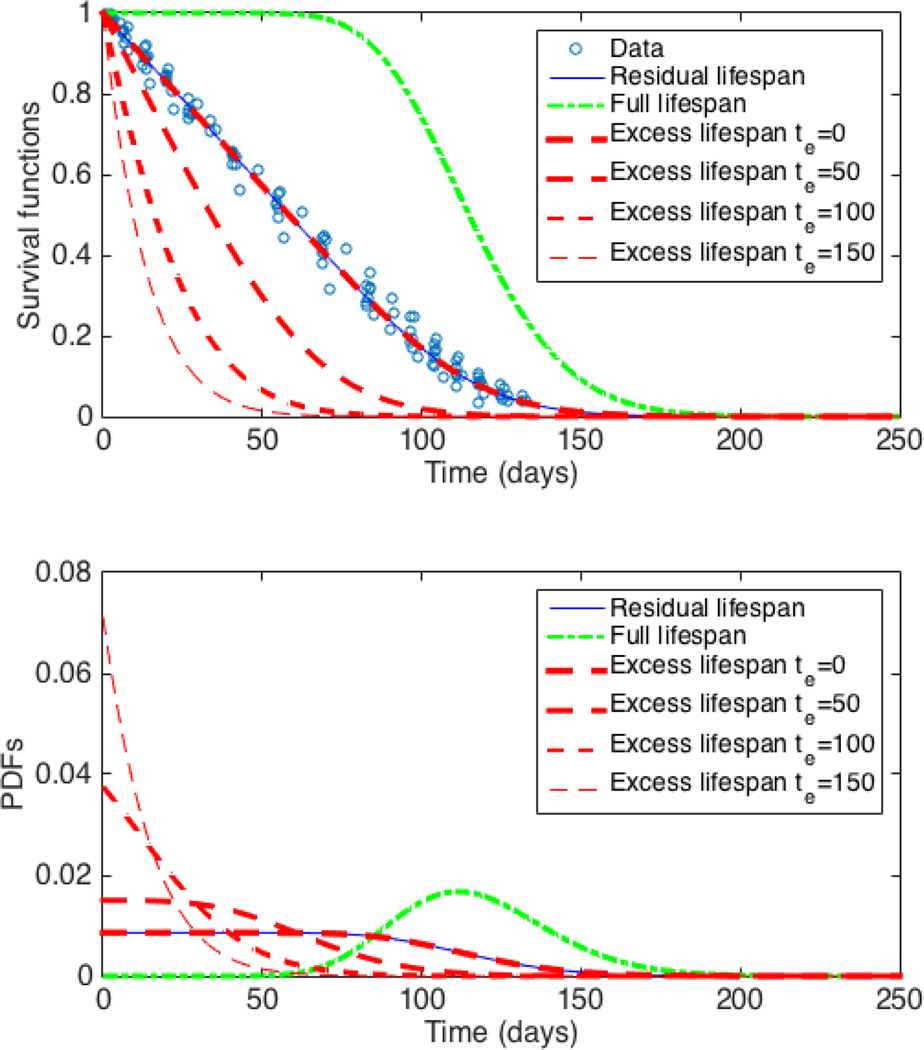
The individual weighted residuals, population weighted residuals, and conditional weighted residuals for all of the models were consistent with normality based on normal probability plots (not shown) and Shapiro-Wilk tests (P ≥ 0.05). The population fit for the RSF along with the computed full lifespan, current age, and excess lifespan (at different times te after index time) SFs and corresponding PDFs using the gamma model are shown in Figure 3 top and bottom panels respectively. Such a graph can easily be computed for individual subjects too (not shown). Similarly, the population and individual survival functions and the corresponding PDFs can easily be computed using the Weibull and lognormal models as well (not shown).
Fig. 3.
Population survival functions (top panel) and PDFs (bottom) based on gamma model. For constant past production rate the residual lifespan, current age, and excess lifespan (for te = 0) SFs and PDFs coincide. Note the changes in excess lifespan SF and PDF depending on the choice of te.
Population-level (fixed effects) estimates of the structural parameters on the original scale, αf and βf, for all the models are given in Table 2. For each of the three models, Table 3 gives maximum likelihood estimates (top), mean of the bootstrap estimates (middle), and the bootstrap 95% CI of the population derived parameters μ, σ, τ95, μc, and T50. The predicted values of the individual structural parameters on original scale are shown in Table 4 and the values of the individual derived parameters of the RBC survival are shown in Table 5.
Table 2.
Estimated population-level structural parameters αf and βf on original scale (subscript f indicates fixed effects); The parameters in the Weibull, gamma, and lognormal models have different meanings and are neither related nor comparable. i) Maximum likelihood estimates of the population fixed effects parameters on log scale are obtained from the NLME analysis; exponentials of the estimates give the values in original scale. Confidence intervals (CIs) on original scale are given by exp(fixed effect estimate on log scale ± 1.96SE) ii) Bootstrap estimates of αf and βf are the means of the NLME estimates of 1000 virtual experiments.
| Bootstrap | Parameter | Weibull | Model Gamma |
Lognormal |
|---|---|---|---|---|
| NLME | αf | 5.38 | 23.02 | 4.74 |
| 95%CI | (4.17, 6.58) | (13.99, 32.05) | (4.68, 4.80) | |
| unit | - | - | - | |
| βf | 125.38 | 5.06 | 0.0421 | |
| 95%CI | (119.75, 131.01) | (3.31, 6.81) | (0.0272, 0.0571) | |
| unit | day | day | - | |
| Bootstrap | αf | 5.42 | 23.54 | 4.74 |
| 95%CI | (4.32, 6.81) | (15.45,34.95) | (4.68, 4.80) | |
| unit | - | - | - | |
| βf | 125.39 | 5.15 | 0.0428 | |
| 95%CI | (119.88, 130.64) | (3.49,7.21) | (0.0282, 0.0593) | |
| unit | day | day | - | |
Table 3.
Population estimates and confidence intervals for derived parameters, μf mean of the full lifespan distribution (or mean full lifespan), σf standard deviation of the full lifespan distribution, τ95f : 95th percentile of the full lifespan distribution, μcf mean of the current age distribution (or mean current age), and T50f median of the residual lifespan distribution (or residual half-life). All the units are in days. Top: maximum likelihood estimate (computed from NLME estimates of structural parameters); middle: bootstrap estimate; bottom: 95% bootstrap confidence interval. Subscript f indicates fixed effect.
| Derived Parameters |
Parameter Info |
Weibull | Model Gamma |
Lognormal |
|---|---|---|---|---|
| μf | NLME | 115.60 | 116.57 | 116.64 |
| Bootstrap | 115.62 | 116.71 | 116.79 | |
| (CI) | (109.17, 121.66) | (110.81, 122.51) | (111.23, 122.75) | |
| σf | NLME | 24.77 | 24.30 | 24.19 |
| Bootstrap | 25.84 | 24.38 | 24.28 | |
| (CI) | (20.82, 28.81) | (20.53, 28.33) | (20.43, 27.73) | |
| τ95f | NLME | 153.76 | 159.20 | 160.07 |
| Bootstrap | 153.95 | 159.51 | 160.40 | |
| (CI) | (150.02, 158.36) | (155.09, 164.00) | (156.00, 165.58) | |
| μcf | NLME | 60.45 | 60.82 | 57.26 |
| Bootstrap | 60.51 | 60.93 | 57.32 | |
| (CI) | (58.18, 62.85) | (58.77, 63.33) | (54.33, 60.61) | |
| T50f | NLME | 57.94 | 58.29 | 58.32 |
| Bootstrap | 57.97 | 58.36 | 58.40 | |
| (CI) | (54.96, 60.90) | (55.45, 61.26) | (55.62, 61,37) | |
Table 4.
Estimated individual-level (mixed effects) structural parameters αi and βi on original scale. Units are the same as in Table 2. The parameters in the Weibull, gamma, and lognormal models have different meanings and are neither related nor comparable. Subscript i indicates individual parameter.
| Model | Parameter | Subject | Mean | CV (%) |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||
| Weibull | αi | 8.07 | 4.99 | 5.33 | 5.38 | 6.62 | 2.86 | 6.41 | 4.99 | 5.58 | 27.24 |
| βi | 135.87 | 128.11 | 123.96 | 125.17 | 132.51 | 109.37 | 130.34 | 119.70 | 125.63 | 6.61 | |
| Gamma | αi | 46.38 | 21.01 | 21.99 | 22.79 | 33.92 | 7.83 | 31.51 | 19.28 | 25.59 | 45.13 |
| βi | 2.77 | 5.65 | 5.23 | 5.10 | 3.67 | 12.72 | 3.87 | 5.75 | 5.59 | 54.83 | |
| Lognormal | αi | 4.84 | 4.76 | 4.72 | 4.74 | 4.81 | 4.56 | 4.79 | 4.68 | 4.74 | 1.87 |
| βi | 0.023 | 0.042 | 0.045 | 0.042 | 0.029 | 0.113 | 0.032 | 0.052 | 0.047 | 59.42 | |
Table 5.
Individual-level (mixed effects) estimates of derived RBC survival parameters, μi mean full lifespan; σi standard deviation of the full lifespan; τ95i : 95th percentile of the full lifespan distribution; μci mean current age; T50i residual half-life. All the units are in days. Subscript i indicates individual parameter.
| Model | Derived Parameter |
Subject | Mean (days) |
CV (%) |
|||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | ||||
| Weibull | μi | 128.01 | 117.61 | 114.23 | 115.42 | 123.58 | 97.47 | 121.36 | 109.89 | 115.95 | 8.10 |
| σi | 18.84 | 26.99 | 24.68 | 24.72 | 21.87 | 36.97 | 22.12 | 25.21 | 25.18 | 21.41 | |
| τ95i | 155.65 | 159.64 | 152.30 | 153.48 | 156.40 | 160.51 | 154.67 | 149.15 | 155.22 | 1.41 | |
| μci | 65.39 | 61.91 | 59.78 | 60.35 | 63.73 | 55.7 | 62.69 | 57.84 | 60.93 | 5.18 | |
| T50i | 64.02 | 59.01 | 57.26 | 57.85 | 61.84 | 50.08 | 60.74 | 55.14 | 58.24 | 7.41 | |
| Gamma | μi | 128.42 | 118.69 | 114.98 | 116.23 | 124.33 | 99.63 | 122.02 | 110.77 | 116.88 | 7.63 |
| σi | 18.86 | 25.90 | 24.52 | 24.35 | 21.37 | 35.59 | 21.72 | 25.25 | 24.70 | 20.22 | |
| τ95i | 160.93 | 164.24 | 158.05 | 158.96 | 161.40 | 164.48 | 159.83 | 155.27 | 160.39 | 1.93 | |
| μci | 65.59 | 62.17 | 60.10 | 60.66 | 64.0 | 56.18 | 62.94 | 58.26 | 61.24 | 5.03 | |
| T50i | 64.21 | 59.36 | 57.50 | 58.12 | 62.17 | 50.29 | 61.01 | 55.41 | 58.51 | 7.34 | |
| Lognormal | μi | 128.37 | 119.30 | 115.14 | 116.46 | 124.47 | 100.95 | 122.09 | 110.97 | 117.22 | 7.31 |
| σi | 19.51 | 24.69 | 24.61 | 24.20 | 21.36 | 34.98 | 22.04 | 25.55 | 24.62 | 18.81 | |
| τ95i | 162.87 | 163.78 | 159.38 | 160.01 | 162.43 | 165.72 | 161.12 | 157.14 | 161.56 | 1.68 | |
| μci | 63.50 | 58.56 | 56.47 | 57.16 | 61.41 | 48.62 | 60.17 | 54.29 | 57.52 | 8.04 | |
| T50i | 64.19 | 59.66 | 57.58 | 58.23 | 62.24 | 50.65 | 61.05 | 55.49 | 58.64 | 7.36 | |
The range of individual μ was 97.5 – 128.0 days for the Weibull, 99.6 – 128.4 days for the gamma, and 100.95 – 128.37 days for the lognormal model. The range of σ was 18.84 – 36.97 days for the Weibull, 18.86 – 35.59 days for gamma, and 19.51 – 34.98 for the lognormal model. For τ95 the ranges were 149.2 – 160.1, 155.3 – 164.5, and 157.14 – 165.72 days, for μc they were 55.7 – 65.39, 56.18 – 65.59, and 48.62 – 63.50 days, and for T50 they were 50.1 – 64.0, 50.3 – 64.2, and 50.65 – 64.19 days, for the Weibull, gamma, and lognormal, respectively.
Discussion
Various distributions have been used for the full RBC lifespan in the literature, including the homogeneous lifespan model [40, 41, 59, 64], in which each of the cells has the same fixed lifespan, and the Weibull [22, 23], gamma [40], and lognormal [15] distributions. A more complicated model, a mixture of two Weibulls (a socalled bathtub-shaped distribution), was used by Korell et al. [32, 34–36]. (Note that there is a misplaced minus sign in equation (1) in both [36] and [34]). By judicious choice of the parameters its shape can be made to mimic senescence, random destruction, and neocytolysis. This is a phenomenological model in the sense mentioned earlier.
In the present paper three separate models, using the Weibull, gamma, and lognormal distributions, were employed to analyze the bioRBC data from 8 healthy adult subjects. The nonlinear mixed effects approach provided a framework for analysis of both population and individual variability of the structural and derived parameters. Because of the large number of parameters in their model, the authors in [32, 34–36] were unable to estimate all of them simultaneously and thus found it necessary to fix several of them in the analysis. By contrast, we were able to carry out complete analyses with the Weibull, gamma, and lognormal models, each with only 2 structural parameters, without fixing any parameter in advance.
The fits appear excellent visually (Figures 1 and 2). The fractional RMSEs (RMSE/ average response value) of 0.023, 0.024, and 0.025 respectively for Weibull, gamma, and lognormal models together with the fact that the residuals are consistent with normality support the use of the NLME methodology.
In addition to routine model diagnostics we performed a parametric bootstrap simulation (details in [61]) to confirm the results from the NLME software (MATLAB [48]), which are based on asymptotic theory for maximum likelihood and require the number of subjects to be large. The bootstrap simulation utilizes the NLME information from the reference population to generate a large number of virtual datasets that duplicate the random mechanism that generated the original data set. The confidence intervals (CIs) of structural parameters obtained from the bootstrap analysis are similar to those from the NLME analysis. This shows that parameter estimation by the NLME software is reliable even with the small number of subjects (M = 8) in our dataset. Since analytical expressions for the standard errors (SEs) of the derived parameters are not available, we also used the bootstrap results to quantify their SEs in order to compute the resulting 95% CIs (= estimate ±1.96×SE).
All three models give physiologically plausible values for the parameters μ, σ, τ95, μc, and T50 for both the population and the individual subjects. The agreement between the three models is almost exact for μ, σ, μc, and T50, but the gamma and lognormal models give consistently greater values (approximately 3%) for τ95 than the Weibull. The reason is that the full lifespan distributions are very similar in their midranges but diverge towards the long survival tail, where the data are sparse, and τ95 is a property of the tail. We speculate that a data set with more reliable measurements in the tail region of the residual survival curve might provide a stronger basis for deciding which (if any) of the models is significantly better than the others. Techniques for more accurately enumerating bioRBCs after removal of 95% of the initial population are currently being developed by some of the authors (JAW, DMM, PV-P).
Because of the small sample size there is no statistical criterion by which to decide confidently which is the “best” of the three models entertained here. For some purposes the choice of any particular model is immaterial, and in this case the three models are about equally mathematically and computationally tractable; see Appendix B. One advantage of the gamma model in certain applications is that a clean state space representation exists when α is an integer. We presented such a gamma-based erythropoiesis model that is physiologically relevant and demonstrated its applicability using clinical data [12].
Recently, Lledo-Garcia et al. [45] gave extensive comparisons of three common RBC lifespan models: homogeneous lifespan, random destruction (RD), and transit compartment (TC) models. The TC model contains a series of compartments connected by first order cell transfer rates [37]. The TC model with one compartment is the RD model. A TC model with infinitely many compartments converges to the homogeneous lifespan model [37]. The TC model with 12 compartments was found by Lledo-Garcia et al. to describe the data best based on likelihood functions (in the form of the objective function value or OFV, defined as minus twice the loglikelihood) and visual predictive checks. The mean full lifespan for the 12 TC model was found to be 91.8 days for healthy subjects, which is substantially shorter than the normally accepted value of around 120 days.
There can be difficulties with likelihood-based model selection [11], especially for non-nested models [66] as occur in [45] and in the present paper. Unless the data satisfy the technical requirements, such as normality or independence, for several models, as must be determined from model diagnostics, a comparison based on likelihood may be questionable, as the likelihood function is then just a criterion function that is not the same for different models. Even when such requirements are met, it is not always clear what such a comparison means. To say, as is often done, that the model with the higher likelihood ”explains the data better” is circular, because, without some discussion of the mechanism behind the data, the only sense in which the data are ”explained” in this situation is by the higher likelihood. Unfortunately the probabilistic justification of a comparison by likelihood will also be inapplicable if the sample size is small, as is the case in some of the studies discussed in [45] and here.
The gamma model in the current paper is equivalent to TC model with α compartments if α is a positive integer. For comparison we conducted NLME analyses of our bioRBC data with 1 to 50 compartments, namely, by taking α = 1 to 50 and estimating only β in each case. The smallest RMSE (= 0.0151), fractional RMSE (= 0.029), and largest loglikelihood (= 336), all occurred for the 22-compartment TC model (α = 22), as shown in Figure 3. These values were less favorable than those for the unconstrained Weibull, gamma, and lognormal models; in particular, the loglikelihood for the lognormal model (= 351), which was the smallest loglikelihood for our three models, was considerably larger than that of the 22-compartment TC model.
It is accepted in the literature that RBC lifespan values are tightly dispersed around a mean value for healthy individuals. There are many diseases which impact RBC lifespan, e.g., sickle cell disease, diabetes, chronic kidney disease, etc. In such cases, information about the whole distribution of RBC lifespan, in particular the mean (μ) and the standard deviation (σ), may be helpful in distinguishing between health and disease. A simultaneous estimation of μ and σ of the RBC lifespan distribution has never been done to the best of our knowledge. Typically, RBC survival studies have been focused on quantifying an average description, e.g., mean age (i.e mean current age according to our definition) of circulating RBCs [13], RBC survival (meaning the half life of the 51Cr disappearance from the circulation) [65], half-life [47], mean lifespan [32, 36, 45, 51], mean potential lifespan (MPL) [53], mean remaining life span [42] (this is similar to mean excess lifespan at te = 0 according to our definition), etc.
The concepts of residual lifespan, current age, and excess lifespan have often appeared in the literature, but are not named explicitly and sometimes not treated rigorously [13, 14, 20, 46, 54, 63]. Outside of RBC survival literature, the concepts of current age and excess lifespan appear in renewal theory [56] but have not previously been used in compartmental models, which are conceptually different from renewal theory.
In the literature, the maximum RBC lifespan Tmax is defined as the time when all of the labeled RBCs disappear from the circulation [13, 32, 44]. Taken literally, this means Tmax is the time at which the residual survival curve decreases to zero. The determination of that time is highly dependent on the sensitivity of the method and associated analytical instrumentation because the proportion of labeled RBCs becomes very small towards the tail region. Tmax is often estimated as the time at which a linear or nonlinear curve fitted to the residual survival curve intersects the time axis. When a linear fit of the entire residual survival curve is used, this intersection is actually an estimate of the mean lifespan rather than the maximum [14, 52]. When a nonlinear fit is used [13, 44], the estimate is strongly dependent on the last sample time of the residual survival curve. The final 2 points of the residual survival curve were extrapolated to the time axis to estimate the maximum RBC lifespan in [13]; such an estimate will also depend on the distance between the last two measurement points.
We used the 95th percentile τ95 of the lifespan distribution as a surrogate for the maximum lifespan; by definition, τ95 is the value such that 95% of the RBC lifespans are < τ95. (The Weibull, gamma, and lognormal distributions extend to infinity in the positive direction; hence have no true maximum value.) The choice of 95% is arbitrary and is used here only for illustration. Any other percentile could be used; in practice the choice would likely be dictated by the nature of the application. The estimated population values of τ95 are in physiologically plausible ranges.
Recently, a new clinically relevant parameter to assess the quality of transfused red blood cells called Mean Remaining Lifespan (MRL) has been introduced [42]. MRL is analogous to the area under the curve (AUC) or mean residence time (MRT) in PK studies. It is defined as the AUC of the fraction of the transfused RBCs remaining in the circulation versus time [42]. This is in fact an estimate of mean residual lifespan described in the current paper . Measurement of MRL as described in the paper [42] again runs into the problem of determining when the last of the transfused RBCs have left the circulation. For practical purposes, MRL is replaced by MRL0.95, which is defined as the area under the curve until the time, t0.95, when 95% of the transfused cells have disappeared from the circulation. t0.95 is estimated by interpolation of the curve [42]. The accuracy of MRL0.95 depends on the frequency of sampling around t0.95 and the last sample must wait until at least 95% of the transfused cells have disappeared, which takes approximately 3 to 4 months in healthy individuals.
As shown by Dornhorst [14], it follows from equation (9) that the mean RBC lifespan μ is given by the negative reciprocal of the slope of the RSF at t = 0, a result that holds for any lifespan distribution, assuming the past production rate is constant. Thus the MPL (mean potential lifespan) described in [53] is actually an estimate of μ for each individual (note that we use the data from [53]). The average MPL for the eight subjects given in [53] was 115 ± 8 days, which is very close to our population values of μ = 116 ± 3 for Weibull and 117 ± 3 for both the gamma and lognormal (mean ± SE). Similarly, the time to disappearance of 50% of the labeled RBCs from the circulation, denoted by T50 and given as 58 ± 4 days in [53], is very close to the population residual half-lives T50 found here (58±1.5 for all models).
Why use a complicated method like NLME when the simple MPL method gives similar results? There are both statistical and practical reasons. From the statistical point of view, first, the average MPL in [53] is the average of the individual MPLs obtained by simple linear regression for each subject separately. This approach yields an overestimate of the variability among individuals, and hence the SD of the MPLs, based on only 8 subjects, is likely too large. By contrast, NLME gives estimates and standard errors at both the population and individual levels [58]. Second, the MPL does not model the full lifespan distribution and, therefore, is incapable of providing quantitative information about other survival parameters such as the longest lifespans in the distribution as reflected in τ95. Information about the whole distribution may be helpful in distinguishing between health and disease (e.g., sickle cell disease). Third, the NLME framework provides standard methodology to include covariates such as sex, age, ethnicity, etc. in the analysis. Fourth, NLME is well-suited to the situation of sparse samples, which is usually the case in clinical settings. The results of a NLME analysis can be used to determine the minimum number, optimal timing, and the last time point of measurement for measurements in a new subject when only a few measurements are possible [50, 61], e.g., in infants or sick patients.
Our results in Appendix B allow complete, rigorous, and computationally efficient analyses of the models considered here (parameter estimation took under a second for Weibull and just over a second for the gamma and lognormal models on a personal computer). Further, there are no constraints on parameters during the estimation process, as in other published models [34, 36, 45], or computational constraints, such as the inability of the software to handle more than 30 compartments described by Lledó-García et al. [45].
Conclusions
Starting with definitions of index population, which has previously not been made explicit, and of birth time, death time, full lifespan, residual lifespan, current age, and excess lifespan, we provided mathematical descriptions of RBC survival parameters, which remove the lack of clarity often found in the literature. We exhibit the connections between a compartmental (or LIDR) model for the RBC population based on a given lifespan distribution and the residual lifespan, current age, and excess lifespan distributions, not available previously in the literature. We gave analytical expressions for mean full lifespan, mean residual lifespan, mean current age, and steady-state mean full lifespan, and indicated how to compute RBC half-life and 95th percentile of the RBC lifespan distribution (τ95). The use of τ95 (or other percentiles) avoids the questionable concept of Tmax often used in the literature.
Employing nonlinear mixed effects modelling, we analyzed residual survival data from biotin-labeled RBCs using models based on the Weibull, gamma, and lognormal distributions. The three models fit the data closely and gave equally physiologically plausible estimates of clinically interpretable RBC survival parameters at population and individual levels.
Our modelling framework could be useful in studying RBC lifespans in various diseases that affect RBC survival, especially in situations with strongly non-linear survival curves (e.g., sickle cell anemia). The model cannot be used if the assumption of “stability” of the subject’s internal environment is not satisfied, as may occur in the case of blood loss and/or other significant intercurrent events (e.g., events leading to hemolysis). The framework also lends itself to analyzing richer data sets containing covariates such as age, gender, and weight.
Acknowledgments
This work was supported in part by a grant from National Institutes of Health/National Institute of Diabetes and Digestive and Kidney Diseases K25DK096006 (YC); an Amgen award #20090067 (YC, MG, CVH, JH); The United States Public Health Service NIH Grant P01 HL046925 (JAW, DMM, PV-P); The Thrasher Research Fund 0285-3 (JAW, DMM, PV-P); The National Center for Research Resources, a part of the NIH, Grant Numbers UL1RR024979, UL1TR000039, and 1S10 RR027219 (JAW, DMM, PV-P). The funding sources did not have any role in the study design; collection, analysis, or interpretation of the data; writing the report; or the decision to submit the report for publication.
APPENDICES
A Weibull, Gamma, and lognormal PDFs
The PDF of the Weibull distribution, denoted by w(t; α, β), is given by
| (21) |
The Weibull parameters α and β are both > 0 and are called the shape and scale parameters, respectively. The mean and variance for the Weibull are
| (22) |
The PDF of the gamma distribution with parameters α, β > 0 is
| (23) |
(Γ denotes the Euler gamma function). Note that we write g instead of p for the PDF of the gamma distribution. The parameters α and β are again called the shape and scale parameters, respectively. The mean and variance are
| (24) |
Let X ~ N(α, β2), i.e., normal with mean α and variance β2, and Y = eX. Then Y has the lognormal distribution with parameters α and β, and PDF
| (25) |
The mean and variance for the lognormal are
| (26) |
The same letters α and β are used for the Weibull, gamma, and lognormal parameters for brevity in presentation, but we emphasize that the parameters in the three distributions are entirely unrelated. The PDFs represent the full RBC lifespan distributions in the Weibull, gamma, and lognormal models respectively and the means correspond to the full RBC lifespan.
B Survival functions for Weibull, gamma, and lognormal lifespan distributions
For any lifespan distribution we have
| (27) |
Interchanging the order of integration yields
| (28) |
The full survival functions (equation (1)), in the case of gamma, Weibull, and lognormal lifespan distributions are given by
| (29) |
| (30) |
and
| (31) |
respectively, where N(x) is the CDF for the standard normal Z ~ N(0, 1). Thus using equations (9) and (28), we obtain the residual survival function in the case of the gamma lifespan distribution
| (32) |
Similarly, from equation (14) we obtain the excess lifespan survival function for the gamma lifespan distribution
| (33) |
Given α and β, the survival functions in equations (32) and (33) are readily calculated by numerical integration in most statistical packages, including MATLAB [48]; equations (32) and (33) show that the survival functions of the residual lifetime and the current and excess lifespan distributions are no more difficult to calculate than the full survival function. It also follows from equations (32) and (2) that the mean residual lifespan and mean current age are both equal to (α + 1)β/2: the integral from 0 to 1 of Ḡ(t; α + 1, β) equals (α + 1)β and the integral of tḠ(t; α, β) equals αβ2(1 + α)/2, as shown u = Ḡ(t; α, β), dv = tdt.
The survival functions Ḡr and Ḡc of the residual lifetime and current age distributions, for the gamma lifespan distribution cannot be expressed in closed form, but there is a closed form when α is an integer ≥ 1. The gamma distribution with α = 2 has been used [12] in an erythropoiesis model for chronic kidney disease patients.
Although the Weibull survival function (30) has a simple form, the corresponding residual survival function does not. The integral in equation (9) can be expressed in terms of the gamma survival function:
| (34) |
The residual, current age, and excess lifespan survival functions, W̄r, W̄c, and W̄e, can now be written for the Weibull model as follows:
| (35) |
| (36) |
Using equations (9), (14), (28) and (31), the residual, current age, and excess lifespan survival functions, L̄r, L̄c, and L̄e for the lognormal model can be written as follows:
| (37) |
| (38) |
From equations (2) and (9) the mean residual lifespans for the gamma, Weibull, and lognormal distributions are given by , and , respectively (using equation (11)); these are obviously different from the corresponding mean full lifespans (Appendix A). We also note that, in equilibrium, the steady state residual lifespan distribution has PDF pr,ss(t) = P̄(t)/μ, which is the same as the transient residual lifespan distribution. The steady state full lifespan has PDF pss(t) = tp(t)/μ [15]. Thus the mean residual and mean full lifespans in steady state are respectively (σ2 + μ2)/2μ (equation (11)) and (σ2 + μ2)/μ. In steady state, therefore, the mean residual lifespan is one half the mean full lifespan. For the gamma, Weibull, and lognormal the steady state mean full lifespans equal μg,ss = (α + 1)β, μw,ss = 2βΓ(2/α)/Γ(1/α), and μw,ss = exp(μ + 3β2/2), respectively. For an individual in stable condition, these distributions are what would be seen for RBCs in the circulation.
References
- 1.Al-Hunity NH, Widness JA, Schmidt RL, Veng-Pedersen P. Pharmacodynamic analysis of changes in reticulocyte subtype distribution in phlebotomy-induced stress erythropoiesis. Journal of Pharmacokinetics and Pharmacodynamics. 2005;32(3):359–376. doi: 10.1007/s10928-005-0009-3. [DOI] [PubMed] [Google Scholar]
- 2.Antonelou MH, Kriebardis AG, Papassideri IS. Aging and death signalling in mature red cells: from basic science to transfusion practie. Blood Transfusion. 2010;8(3):s39–s47. doi: 10.2450/2010.007S. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ashby W. The determination of the length of life of transfused blood corpuscles in man. J Exp Med. 1921;29:267–281. doi: 10.1084/jem.29.3.267. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Banks HT, Bliss KM, Tran H. Modeling red blood cell and iron dynamics in patients with chronic kidney disease. Internat J Pure Appl Math. 2012;75 [Google Scholar]
- 5.Barlow RE, Proschan F. Statistical Theory of Reliability and Life Testing: Probability Models. New York, NY: Holt, Rinehart and Winston; 1975. [Google Scholar]
- 6.Birnbaum ZW, Saunders SC. A statistical model for life-length of materials. J Am Stat Assoc. 1958;53 [Google Scholar]
- 7.Brown GM, Hayward OC, Powell EO, Witts LJ. The destruction of transfused erythrocytes in anaemia. The Jounal of Pathology and Bacteriology. 1944;56(1):81–94. [Google Scholar]
- 8.Brown IW, Jr, Eadie GS. An analytical study of in vivo survival of limited populations of animal red blood cells tagged with radioiron. The Journal of General Physiology. 1953;36(3):327–343. doi: 10.1085/jgp.36.3.327. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Callender ST, Powell EO, Witts LJ. The lifespan of the red cell in man. The Journal of Pathology and Bacteriology. 1945;57(1):129–139. doi: 10.1002/path.1700590402. [DOI] [PubMed] [Google Scholar]
- 10.Castorina P, Blanchard P. Unified approach to growth and aging in biological, technical and biotechnical systems. SpringerPlus. 2007;1:7–. doi: 10.1186/2193-1801-1-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Cavanaugh JE. Model Selection Lecture XIV: The Application of Model Selection Criteria. [Accessed: Jun 2015]; url: http://myweb.uiowa.edu/cavaaugh/ms_lec_14_ho.pdf. [Google Scholar]
- 12.Chait Y, Horowitz J, Nichols B, Shrestha RP, Hollot CV, Germain MJ. Control-relevant erythropoiesis modeling in end-stage renal disease. IEEE Trans Biomed Eng. 2014;61(3):658–664. doi: 10.1109/TBME.2013.2286100. [DOI] [PubMed] [Google Scholar]
- 13.Cohen RM, Franco RS, Khera PK, Smith EP, Lindsell CJ, Ciraolo PJ, Palascak MB, Joiner CH. Red cell life span heterogeneity in hematologically normal people is sufficient to alter HbA1c. Blood. 2008;112(10):4284–4291. doi: 10.1182/blood-2008-04-154112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Dornhorst AC. The interpretation of red cell survival curves. Blood. 1951;6:1284–1292. [PubMed] [Google Scholar]
- 15.Dowling MR, Milutinović D, Hodgkin PD. Modeling cell lifespan and proliferation: is likelihood to die or to divide independent of age? JR Soc Interface. 2005;2 doi: 10.1098/rsif.2005.0069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Eadie GS, (Tor) MB, Brown IW., Jr Analytical review: red blood cell survival studies. Blood. 1953;8(12):1110–1136. [PubMed] [Google Scholar]
- 17.Eadie GS, Brown IW, Jr, Curtis WG. The potential life span and ultimate survival of fresh red blood cells in normal healthy recipients as studied by simultaneous Cr51 tagging and differential hemolysis. J Clin Invest. 1955;34(4):629–636. doi: 10.1172/JCI103112. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Franco RS. Time-dependent changes in the density and hemoglobin f content of biotin-labeled sickle cells. The Journal of Clinical Investigation. 1998;101(12):2730–2740. doi: 10.1172/JCI2484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Franco RS. The measurement and importance of red cell survival. American Journal of Hematology. 2009;84:109–114. doi: 10.1002/ajh.21298. [DOI] [PubMed] [Google Scholar]
- 20.Franco RS. Measurement of red cell lifespan and aging. Transfusion Medicine and Hemotherapy. 2012 doi: 10.1159/000342232. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Freise KJ, Widness JA, Schmidt RL, Veng-Pederson P. Pharmacodynamic analysis of time-variant cellular disposition: reticulocyte disposition changes in phlebotomized sheep. Journal of Pharmacokinetics and Pharmacodynamics. 2007;34:519–547. doi: 10.1007/s10928-007-9056-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Freise KJ, Schmidt RL, Widness JA, Veng-Pedersen P. Pharmacodynamic modeling of the effect of changes in the environment on cellular lifespan and cellular response. J Pharmacokinet Pharmacodyn. 2008;35:527–552. doi: 10.1007/s10928-008-9100-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Freise KJ, Widness JA, Schmidt RL, Veng-Pederson P. Modeling time variant distributions of cellular lifespans: increases in circulating reticulocyte lifespans following double phlebotomies in sheep. Journal of Pharmacokinetics and Pharmacodynamics. 2008;35:285–323. doi: 10.1007/s10928-008-9089-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Garby L, Mollison PL. Deduction of mean red-cell life-span from 51Cr survival curves. British journal of haematology. 1971;20(1):527–536. doi: 10.1111/j.1365-2141.1971.tb07068.x. [DOI] [PubMed] [Google Scholar]
- 25.Gavrilov LA, Gavrilova NS. The Biology of Life Span: a Quantitative Approach. NY: Harwood Academic Publisher; 1991. [Google Scholar]
- 26.Gavrilov LA, Gavrilova NS. The reliability theory of aging and longevity. J Theor Biol. 2001;213 doi: 10.1006/jtbi.2001.2430. [DOI] [PubMed] [Google Scholar]
- 27.Gifford SC, Derganc J, Shevkoplyas SS, Yoshida T, Bitensky MW. A detailed study of time-dependent changes in human red blood cells: from reticulocyte maturation to erythrocyte senescence. British Journal of Haematology. 2006;135:395–404. doi: 10.1111/j.1365-2141.2006.06279.x. [DOI] [PubMed] [Google Scholar]
- 28.Glynn SA. The red blood cell storage lesion: a method to the madness. Transfusion. 2001;50:1164–1169. doi: 10.1111/j.1537-2995.2010.02674.x. [DOI] [PubMed] [Google Scholar]
- 29.Greenwalt TJ, Dumaswala UJ. Effect of red cell age on vesiculation in vitro. British Journal of Hematology. 1988;68:465–467. doi: 10.1111/j.1365-2141.1988.tb04237.x. [DOI] [PubMed] [Google Scholar]
- 30.Hamren B, Bjork E, Sunzel M, Karlsson M. Models for plasma glucose, hba1c, and hemoglobin interrelationships in patients with type 2 diabetes following tesaglitazar treatment. Clin Pharmacol Ther. 2008;84(2):228–235. doi: 10.1038/clpt.2008.2. [DOI] [PubMed] [Google Scholar]
- 31.Handelman GJ, Levin NW. Red cell survival: relevance and mechanism involved. Journal of Renal Nutrition. 2010;20(5):S84–S88. doi: 10.1053/j.jrn.2010.06.007. [DOI] [PubMed] [Google Scholar]
- 32.International Committee for Standardization in Hematology. Recommended method for radioisotopic red-cell survival studies. British Journal of Haematology. 1980;45:659–666. doi: 10.1111/j.1365-2141.1980.tb07189.x. [DOI] [PubMed] [Google Scholar]
- 33.Juckett DA, Rosenberg B. Comparison of the Gompertz and Weibull functions as descriptors for human mortality distributions and their intersections. Mech Ageing Dev. 1993;69 doi: 10.1016/0047-6374(93)90068-3. [DOI] [PubMed] [Google Scholar]
- 34.Korell J, Coulter CV, Dufful SB. Evaluation of red blood cell labelling methods based on a statistical model for red blood cell survival. Journal of Theoretical Biology. 2011;291:88–98. doi: 10.1016/j.jtbi.2011.09.016. [DOI] [PubMed] [Google Scholar]
- 35.Korell J, Coulter CV, Dufful SB. A statistical model for red blood cell survival. Journal of Theoretical Biology. 2011;268:39–49. doi: 10.1016/j.jtbi.2010.10.010. [DOI] [PubMed] [Google Scholar]
- 36.Korell J, Vos FE, Coulter CV, Schollum JB, Walker RJ, Dufful SB. Modeling red blood cell survival data. J Pharmacokinet Pharmacodyn. 2011;38:787–801. doi: 10.1007/s10928-011-9220-6. [DOI] [PubMed] [Google Scholar]
- 37.Krzyzanski W. Interpretation of transit compartments pharmacodynamic models as lifespan based indirect response models. J Pharmacokinet Pharmacodyn. 2011;38:179–204. doi: 10.1007/s10928-010-9183-z. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Krzyzanski W, Ruixo JJP. Lifespan based indirect response models. J Pharmacokinet Pharmacodyn. 2012;39:109–123. doi: 10.1007/s10928-011-9236-y. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Krzyzanski W, Ramakrishnan R, Jusko WJ. Basic pharmacodynamic models for agents that alter production of natural cells. Journa of Pharmacokinetics and Biopharmaceutics. 1999;27(5):467–489. doi: 10.1023/a:1023249813106. [DOI] [PubMed] [Google Scholar]
- 40.Krzyzanski W, Woo S, Jusko WJ. Pharmacodynamic models for agents that alter production of natural cells with various distributions of lifespan. Journal of Pharmacokinetics and Pharmacodynamics. 2006;33(2):125–166. doi: 10.1007/s10928-006-9007-3. [DOI] [PubMed] [Google Scholar]
- 41.Krzyzanski W, Perez-Ruixo JJ, Vermeulen A. Basic pharmacodynamic models for agents that alter the lifespan distribution of natural cells. J Pharmacokinet Pharmacodyn. 2008;35:349–377. doi: 10.1007/s10928-008-9092-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Kuruvilla DJ, Nalbant D, Widness JA, Veng-Pedersen P. Mean remaining life span: a new clinically relevant parameter to assess the quality of transfused red blood cells. Transfusion. 2014;41 doi: 10.1111/trf.12562. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Lee ET. Statistical Methods for Survival Data Analysis. Wadsworth, Belmont, CA: 1980. [Google Scholar]
- 44.Lindsell CJ, Franco RS, Smith EP, Joiner CH, Cohen RM. A method for the continuous calculation of the age of labeled red blood cells. American Journal of Hematology. 2008;83:454–457. doi: 10.1002/ajh.21148. [DOI] [PubMed] [Google Scholar]
- 45.Lledó-García R, Kalicki RM, Uehlinger DE, Karlsson MO. Modeling of red blood cell life-spans in hematologically normal populations. J Pharmacokinet Pharmacodyn. 2012;39 doi: 10.1007/s10928-012-9261-5. [DOI] [PubMed] [Google Scholar]
- 46.Luten M, Roerdinkholder-Stoelwinder B, Schapp NPM, J de Grip W, Bos HJ, Bosman GJCGM. Survival of red blood cells after transfusion:a comparison between red cells concentrates of different storage periods. Transfusion. 2008;48 doi: 10.1111/j.1537-2995.2008.01734.x. [DOI] [PubMed] [Google Scholar]
- 47.Ly J, Marticorena R, Donnelly S. Red blood cell survival in chronic renal failure. American Journal of Kidney Disease. 2004;44(4):715–719. [PubMed] [Google Scholar]
- 48.MATLAB. MATLAB and Statistics Toolbox Release 2010a. Natick, Massachusetts, USA: Mathworks Inc.; 2010. [Google Scholar]
- 49.Meeker WQ, Escobar LA. Statistical Methods for Reliability Data. New York, NY: Wiley; 1998. [Google Scholar]
- 50.Merrill S, Horowitz J, Traino AC, Chipkin SR, Hollot CV, Chait Y. Accuracy and optimal timing of activity measurement in estimating absorbed dose of radioiodine in the treatment of graves’ disease. Physics in Medicine and Biology. 2011;56:1–11. doi: 10.1088/0031-9155/56/3/003. [DOI] [PubMed] [Google Scholar]
- 51.Mitlyng BL, Singh JA, Furne JK, Ruddy J, Levitt MD. Use of breath carbon monoxide measurements to assess erythrocyte survival in subjects with chronic diseases. American Journal of Hematology. 2006;81:432–438. doi: 10.1002/ajh.20644. [DOI] [PubMed] [Google Scholar]
- 52.Mock DM, Lankford GL, Widness LF, Burmiester DK, Strauss RG. Measurement of red cell survival using biotin-labeled red cells: validation against 51Cr-labeled red cells. Transfusion. 1999;39:156–162. doi: 10.1046/j.1537-2995.1999.39299154729.x. [DOI] [PubMed] [Google Scholar]
- 53.Mock DM, Matthews NI, Zhu S, Strauss RG, Schmidt RL, Nalbant D, Cress GA, Widness JA. Red blood cell (RBC) survival determined in humans using RBCs labeled at multiple biotin densities. Transfusion. 2011;51:1047–1057. doi: 10.1111/j.1537-2995.2010.02926.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Müller H, Wang J, Carey JR, Caswell-Chen EP, Chen C, Papadopoulos N, Yao F. Demographic window to aging in the wild: constructing life tables and estimating survival functions from marked individuals of unknown age. Aging Cell. 2004;3:125–131. doi: 10.1111/j.1474-9728.2004.00096.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Nachlas JA. Reliability Engineering: Probabilistic Models and Maintenance Methods. Boca Raton, FL: Taylor and Francis; 2005. [Google Scholar]
- 56.Parzen E. Stochastic processes. San Francisco, CA: Holden-Day; 1967. [Google Scholar]
- 57.Pérez-Ruixo JJ, Krzyzanski W, Hing J. Pharmacodynamic analysis of recombinant human erythropoietin effect on reticulocyte production rate and age distribution in healthy subjects. Clin Pharmacokinet. 2008;47(6):399–415. doi: 10.2165/00003088-200847060-00004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Pinheiro JC, Bates DM. Mixed-Effects Models in S and S-PLUS. New york: Springer; 2000. [Google Scholar]
- 59.Ramakrishnan R, Cheung WK, Wacholtz MC, Minton N, Jusko WJ. Pharmacokinetic and pharmacodynamic modeling of recombinant human erythropoietin after single and multiple doses in healthy volunteers. The Journal of Clinical Pharmacology. 2004;44:991–1002. doi: 10.1177/0091270004268411. [DOI] [PubMed] [Google Scholar]
- 60.Schiødt E. On the duration of life of the red blood corpuscles. Acta Medica Scandinavica. 1938:49–79. [Google Scholar]
- 61.Shrestha RP. PhD Dissertation. Amherst, MA: University of Massachusetts; 2012. Modeling the lifespan of red blood cells. [Google Scholar]
- 62.Sun YN, Jusko WJ. Transit compartments versus gamma distribution function to model signal transduction processes in pharmacodynamics. J Pharm Sci. 1998;87:732–737. doi: 10.1021/js970414z. [DOI] [PubMed] [Google Scholar]
- 63.Tinmouth A, Fergusson D, Ian Yee CP, Hébert C Investigators A, the Canadian Critical Care Trials Group. Clinical consequences of red cell storage in the critically ill. Transfusion. 2006;46(11):2014–2017. doi: 10.1111/j.1537-2995.2006.01026.x. [DOI] [PubMed] [Google Scholar]
- 64.Uehlinger DE, Gotch FA, Sheiner LB. A pharmacodynamic model of erythropoietin therapy for uremic anemia. Clin Pharmacol Ther. 1992;51 doi: 10.1038/clpt.1992.10. [DOI] [PubMed] [Google Scholar]
- 65.Vos FE, Schollum JB, Coulter CV, Doyle TC, Duffull SB, Walker RJ. Red blood cell survival in long-term dialysis patients. Am J Kidney Dis. 2011;58:591–598. doi: 10.1053/j.ajkd.2011.03.031. [DOI] [PubMed] [Google Scholar]
- 66.Vuong QH. Likelihood ratio tests for model selection and non-nested hypotheses. Econometrica. 1989;57 [Google Scholar]