An unbiased metric of antiproliferative drug effect in vitro

Abstract

In vitro cell proliferation assays are widely used in pharmacology, molecular biology, and drug discovery. Using theoretical modeling and experimentation, we show that current antiproliferative drug effect metrics suffer from time-dependent bias, leading to inaccurate assessments of parameters such as drug potency and efficacy. We propose the drug-induced proliferation (DIP) rate, the slope of the line on a plot of cell population doublings versus time, as an alternative, time-independent metric.

MAIN TEXT

Evaluating antiproliferative drug activity on cells in vitro is a widespread practice in basic biomedical research^1–3 and drug discovery^4–6. Typically, quantitative assessment relies on constructing dose–response curves⁷ (Supplementary Note and Supplementary Fig. 1). Briefly, a drug is added over a range of concentrations and the effect on the cell population is quantified with a metric of choice⁸. The de facto standard metric is the number of viable cells 72 h after drug addition^4,6,8,9. Being a single-time-point measurement, we refer to this as a “static” drug effect metric. The data is then fit to the Hill equation¹⁰, a four-parameter log-logistic function, to produce a sigmoidal dose–response curve that summarizes the relationship between drug effect and concentration. Parameters extracted from these curves include the maximum effect (E_max), the half-maximal effective concentration (EC₅₀), the half-maximal inhibitory concentration (IC₅₀), area under the curve (AUC), and activity area (AA)^4,6,8,9 (Supplementary Fig. 1 and Supplementary Table 1). These are useful for quantitatively comparing various aspects of drug activity across drugs and cell lines.

We contend that dose–response curves constructed using current standard metrics of drug effect can result in erroneous and misleading values of drug-activity parameters, skewing data interpretation. This is because they suffer from time-dependent bias, i.e., the metric value varies with the time point chosen for experimental measurement. We identify two specific sources of time-dependent bias: (i) exponential growth, and (ii) delays in drug effect stabilization. The former can lead to erroneous conclusions, e.g., that a drug is increasing in effectiveness over time, while the latter requires shifting the window of evaluation to only include data points after stabilization has been achieved (Supplementary Fig. 2).

To overcome this problem of bias, we propose as an alternative drug effect metric the drug-induced proliferation (DIP) rate^11,12, defined as the steady-state rate of proliferation of a cell population in the presence of a given concentration of drug. Previously, with related approaches, we quantified clonal fitness¹² and heterogeneous single-cell fates¹¹ within cell populations responding to perturbations. Here, we show that DIP rate is an ideal metric of antiproliferative drug effect because it naturally avoids the bias afflicting traditional metrics, it is easily quantified as the slope of the line on a plot of cell-population doublings versus time (Supplementary Fig. 2), and it is interpretable biologically as the rate of regression or expansion of a cell population.

To theoretically illustrate the consequences of time-dependent bias in standard drug effect metrics, we constructed a simple mathematical model of cell proliferation that exhibits the salient features of cultured cell dynamics in response to drug (Online Methods, Supplementary Note, Supplementary Fig. 3, and Supplementary Table 2). The model assumes that cells experience two fates, division and death, and that the drug modulates the difference between the rates of these two processes, i.e., the net rate of proliferation. Drug action may occur immediately or gradually over time, depending on the chosen parameter values. In all cases, a stable DIP rate is eventually achieved, and when calculated over a range of drug concentrations a sigmoidal dose–response relationship emerges (Supplementary Note and Supplementary Fig. 3).

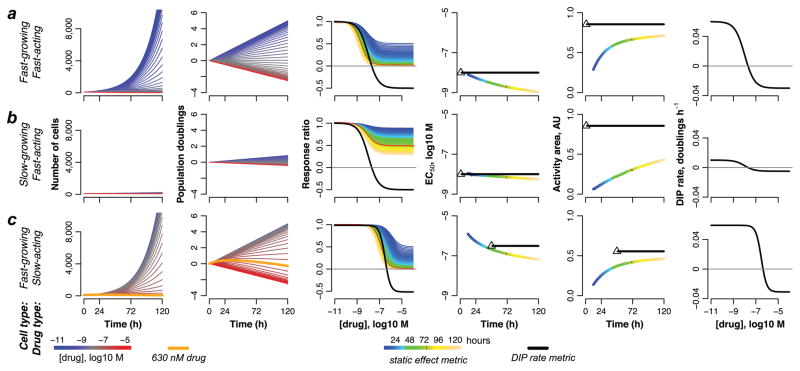
We model three scenarios: treatment of a fast-proliferating cell line with a fast-acting drug (Fig. 1a), a slow-proliferating cell line with a fast-acting drug (Fig. 1b), and a fast-proliferating cell line with a delayed-action drug (Fig. 1c). In each case, we generate simulated growth curves in the presence of increasing drug concentrations (Fig. 1, columns 1 and 2) and from these produce static dose–response curves by taking cell counts at single time points between 12h and 120h (Fig. 1, column 3). As expected, in each scenario the shape of the dose–response curve varies depending on the time of measurement. Consequently, parameter values extracted from these curves (EC₅₀ and AA) also vary (Fig. 1, columns 4 and 5). Similar results are obtained for an alternative drug effect metric proposed by the U.S. National Cancer Institute’s Developmental Therapeutics Program¹³ (Supplementary Note and Supplementary Fig. 4). In contrast, DIP rate, being the slope of a line, is independent of measurement time. Using it as the drug effect metric gives a single dose–response curve (Fig. 1, columns 3 and 6) and single values of the extracted drug-activity parameters (Fig. 1, columns 4 and 5).

Figure 1. Theoretical illustration of bias in dose–response curves based on static metrics of drug effect.

Computational simulations of the effects of drugs on: (a) a fast-growing cell line treated with a fast-acting drug; (b) a slow-growing cell line treated with a fast-acting drug; (c) a fast-growing cell line treated with a slow-acting drug. In all cases, in silico growth curves, plotted in linear (column 1) and log₂ (column 2) scale, are used to generate static- (column 3) and DIP rate-based (columns 3 and 6) dose–response curves, from which values of EC₅₀ (column 4) and activity area (AA; column 5) are extracted. For DIP rate-based values of EC₅₀ and AA, the black triangle denotes the first time point used to calculate the DIP rate (i.e., after the drug effect has stabilized; see Online Methods); the black dashed line signifies that the value remains constant for all subsequent time points. Note that the “response ratio” (column 3) and “direct effect” (column 6) versions of the DIP rate-based dose–response curves (Supplementary Fig. 1) convey complementary information about the activity of a drug on a cell line (see Supplementary Note for further discussion).

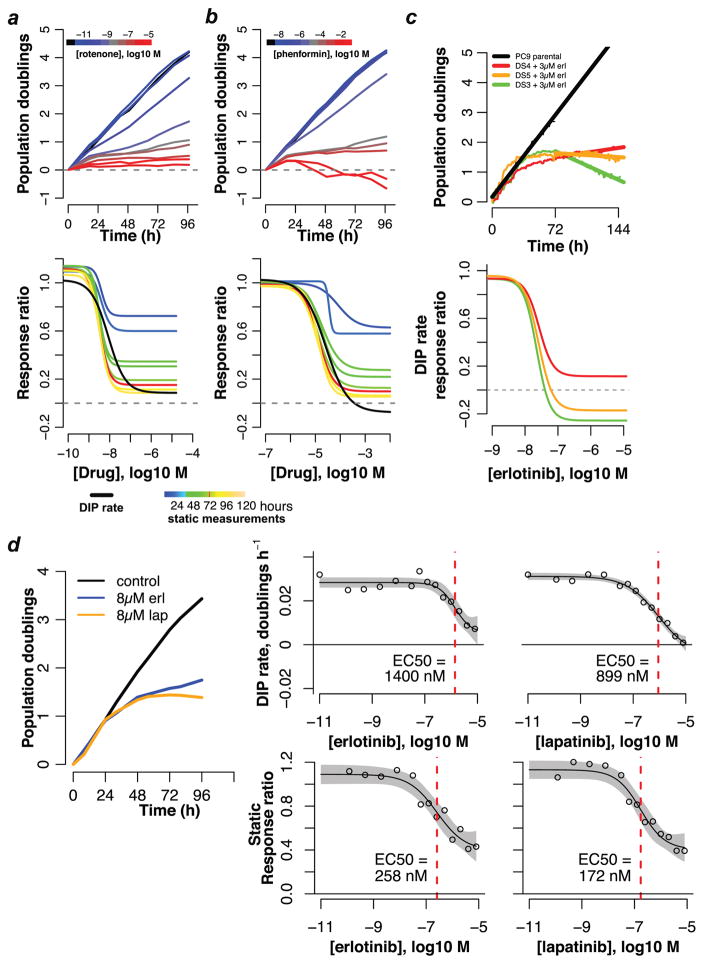
As a first confirmation of our theoretical findings, we subjected triple-negative breast cancer cells (MDA-MB-231) to the metabolic inhibitors rotenone (Fig. 2a) and phenformin (Fig. 2b). Using fluorescence microscopy time-lapse imaging^11,12,14 (Online Methods), we quantified changes in cell number over time for a range of drug concentrations^18,19. For both drugs, we observe a rapid stabilization of the drug effect (<24h delay) and stable exponential proliferation thereafter, reminiscent of the growth dynamics of the theoretical cell lines treated with fast-acting drugs (Fig. 1a,b). We generated dose–response curves from these data using the standard static effect metric and DIP rate for various drug exposure times. Consistent with our theoretical results, the shape of the static-based dose–response curve strongly depends on the time point at which cell counts are taken, an illustration of time-dependent bias. The DIP rate, on the other hand, is free of time-dependent bias and produces a single dose–response curve in both cases.

Figure 2. Experimental illustration of time-dependent bias in dose–response curves for drug-treated cancer cells.

Population growth curves (log₂ scaled) and derived dose–response curves (static- and/or DIP rate-based) for (a) MDA-MB-231 triple-negative breast cancer cells treated with rotenone; (b) MDA-MB-231 cells treated with phenformin; (c) three single-cell-derived drug-sensitive (DS) clones of the EGFR mutant-expressing lung cancer cell line PC9 treated with erlotinib; (d) HCC1954 HER2-positive breast cancer cells treated with erlotinib and lapatinib. Data for (a) and (b) are from single experiments with technical duplicates; data in (c) are from individual wells for two experiments containing technical duplicates (growth curves) and from a single experiment with technical duplicates (dose–response curves); data in (d) are sums of technical duplicates from a single experiment (growth curves) and mean values (circles) with 95% confidence intervals (gray shading) on the log-logistic model fit (dose–response curves; n=4, 6 for erlotinib and lapatinib, respectively).

These DIP rate-based dose–response curves produce interesting insights (Fig. 2a,b). For example, they indicate that while rotenone is much more potent than phenformin (EC₅₀ ≅ 8.5 nM versus 25 μM), phenformin is more effective (E_max/E₀ ≅ −0.1 versus 0.1). The ordering of potencies (rotenone ≫ phenformin) could have been garnered from the static dose–response curves, but not the ordering of efficacies, i.e., the static drug effect metric obscures the crucial fact that at saturating concentrations phenformin is cytotoxic (causes cell population regression) while rotenone is partially cytostatic (cell populations continue to expand slowly). This information is obviously critical to studies assessing drug mechanism of action. This example illustrates the perils of biased drug effect metrics and the ability of DIP rate to produce reliable dose-response curves from which accurate quantitative and qualitative assessments of antiproliferative drug activity can be made.

To illustrate the confounding effects that a delay in the stabilization of the drug effect can have, we examined single-cell derived clones of the lung cancer cell line PC9, which is known to be hypersensitive to erlotinib¹⁵, an epidermal growth factor receptor (EGFR) kinase inhibitor. Consistent with our previous report¹¹, three drug-sensitive PC9-derived clones (DS3, DS4, DS5) each respond to 3 μM erlotinib with nonlinear growth dynamics over the first 48–72h, followed by stable exponential proliferation thereafter (Fig. 2c). These dynamics are reminiscent of those for the theoretical fast-proliferating cell line with a delayed-action drug (Fig. 1c). Due to the delay in drug action, all three clones have nearly identical population sizes 72h after drug addition for all concentrations considered. The static 72h metric thus produces essentially identical dose–response curves for all clones (Supplementary Fig. 5). In contrast, dose–response curves based on DIP rate make a clear distinction between the clones in terms of their long-term response to drug, i.e., erlotinib is cytotoxic (negative DIP rate) for two of the clones but partially cytostatic (positive DIP rate) for the other (Fig. 2c).

We then investigated the effects of erlotinib and lapatinib (a dual EGFR/human EGFR 2 (HER2) kinase inhibitor) on HER2-positive breast cancer cells (HCC1954; delay ~48h; Fig. 2d). In each case, DIP rate-based dose–response curves produce EC₅₀ values more than five-fold larger than their static counterparts, i.e., by the static drug effect metric the drugs appear significantly more potent than they actually are. Taken together with the PC9 results (Fig. 2c), these data illustrate the importance of accounting for delays in drug action when assessing antiproliferative drug activity and further emphasize the ability of the DIP rate metric to produce accurate drug-activity parameters and qualitative conclusions about drug-response dynamics.

Within the last several years, a number of studies have been published reporting drug responses for hundreds of cell lines derived from various cancer types^4,6,9,16,17 and organ sites^8,18,19. Raw data are available for the responses of over 1000 cancer cell lines to a panel of 24 drugs in the Cancer Cell Line Encyclopedia (CCLE)⁶ and for over 1200 cell lines treated with 140 drugs in the Genomics of Drug Sensitivity in Cancer (GDSC) project⁹. These data are largely based on static measurements of cell number after 72h of drug exposure, a metric that we have shown here contains time-dependent bias.

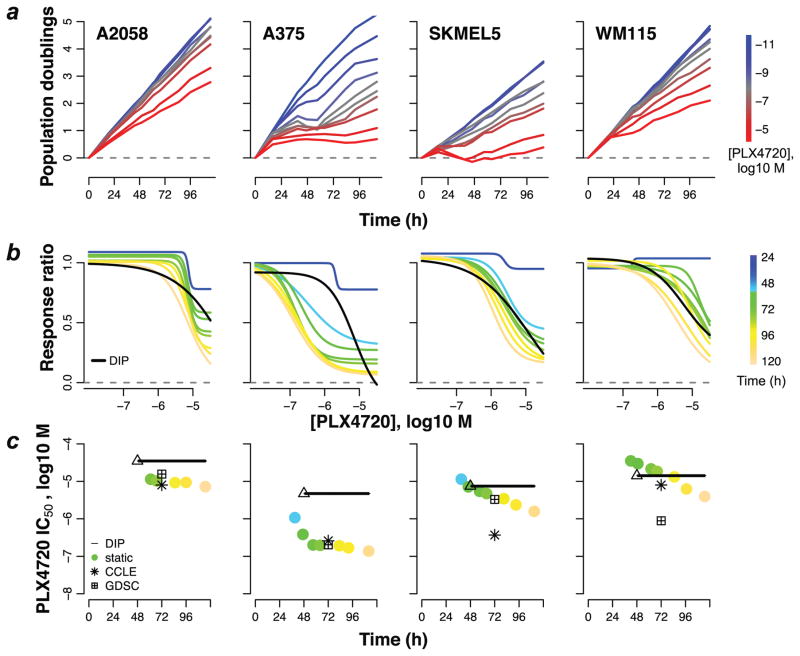
To investigate bias in these datasets, we treated four BRAF^{V600E or D}-expressing melanoma cell lines with various concentrations of the BRAF-targeted agent PLX4720, an analog of vemurafenib. We produced experimental growth curves (Fig. 3a), static- and DIP rate-based dose–response curves (Fig. 3b), and extracted IC₅₀ values for each cell line and compared these to IC₅₀ values obtained from the CCLE and GDSC data sets (Fig. 3c). In all cases, our IC₅₀ values correspond closely to the value from at least one of the public data sets. While in three cases the static- and DIP rate-based IC₅₀ values correspond within an order of magnitude, in one case (A375) they differ by nearly two orders of magnitude. This discrepancy can be traced to a period of complex, non-linear dynamics (brief regression followed by rebound) observed for this cell line between 24h and 72h post-drug addition (Fig. 3a). This result is particularly intriguing because it shows that, based on DIP rate, this cell line is not much different in terms of drug sensitivity than the other three. Using the biased static drug effect metric, however, one would be led to the incorrect conclusion that it is significantly more sensitive. It is very likely that cases like this abound within these and other similar data sets^16,17 and illustrates the critical need for new antiproliferative drug effect metrics.

Figure 3. Bias in potency metrics from publicly available data sets.

(a) Population growth curves (log₂ scaled) for four select BRAF-mutant melanoma cell lines treated with various concentrations of the BRAF inhibitor PLX4720; (b) dose–response curves based on the static effect metric (colored lines) and DIP rate (black line); (c) static- (circles) and DIP rate-based (triangle+line) estimates of IC₅₀ for each measurement time point. IC₅₀ values obtained from public data sets (CCLE: Cancer Cell Line Encyclopedia; GDSC: Genomics of Drug Sensitivity in Cancer), based on the static 72h drug effect metric, are included for comparison. The triangle denotes the first time point used in calculating the DIP rate and the black line signifies that the value remains constant for all subsequent time points. Data shown are from a single experiment with technical duplicates. Experiment has been repeated at least twice with similar results.

Current protocols for cell proliferation assays are based on informal ‘rules of thumb’, for example, counting cells after 72 h of treatment to ameliorate the impact of complex dynamics and delays in drug response. However, these de facto standards have no theoretical basis and, as demonstrated here, they suffer from time-dependent bias that leads to erroneous conclusions. In light of the widespread applications of cell proliferation assays in oncology, pharmacology, and basic biomedical science²⁰ (for example, to assess activity of cytokines, cell surface receptors, altered signaling pathways, gene overexpression and silencing, or cell metabolic adaptation to varied microenvironmental conditions), it is imperative that the quality of the metric for antiproliferative assays be improved. Toward this end, we have proposed DIP rate as a viable, unbiased alternative antiproliferative drug effect metric. DIP rate overcomes time-dependent bias by log-scaling cell count measurements to account for exponential proliferation and by shifting the time window of evaluation to accommodate lag in the action of a drug, changes that do not substantially alter experimental design (Supplementary Note and Supplementary Figs. 6–9). Moreover, DIP rate is an intuitive, biologically interpretable metric with a sound basis in theoretical population dynamics, and it faithfully captures, within a single value, the long-term effect of a drug on a cell population.

ONLINE METHODS

Dose–response curve fitting

All drug-response data (theoretical and experimental) were fit with a four-parameter log-logistic function (Supplementary Note) using nonlinear least-squares regression²¹ within the R statistical programming environment (http://R-project.org). Fitting was performed using the drm function of the drc R library²². Ninety-five percent confidence intervals for each parameter were obtained using the delta method assuming asymptotic variance²¹, as implemented within the confint function of the stats R library. EC₅₀ is a fit parameter of the model. IC₅₀ is the concentration at which E_drug = E₀/2 (Supplementary Fig. 1 and Supplementary Table 1), independent of the value of E_max, and is obtained using the ED function of the drc library. Activity area (AA; Supplementary Fig. 1) is calculated as

$$\text{AA}=-{\sum }_{i=1}^N(E_{\mathit{drug},i}/E_0-1)/N$$ (1)

where E_drug,i is the value of the effect metric at the i-th drug concentration and N is the total number of concentrations considered.

A simple two-state model of drug action on an exponentially proliferating cell population

We assume that cells can exist in two states, a “no-drug” and a “drug-saturated” state, and that cells in each state can experience two fates, division and death, with kinetic rate constants that are characteristic of the state, i.e., reflecting the effect of the drug (visual representation of the model is provided in Supplementary Fig. 3a). In the presence of drug, cells can transition from the no-drug to the drug-saturated state at a rate proportional to the concentration of drug. Reverse transitions occur at a rate independent of drug. If Cell is the number of cells in the no-drug state and Cell* is the number of cells in the drug-saturated state, then the temporal dynamics of the drug-treated cell population is described by the following pair of coupled ordinary differential equations,

$$\frac{\mathit{dCell}}{dt}=(k_{\mathit{div}}-k_{\mathit{death}}-k_{on}\mathit{Drug})·\mathit{Cell}+k_{\mathit{off}}·{\mathit{Cell}}^{\ast }$$ (2)

$$\frac{d{\mathit{Cell}}^{\ast }}{dt}=(k_{di{v}^{\ast }}-k_{{\mathit{death}}^{\ast }}-k_{\mathit{off}})·{\mathit{Cell}}^{\ast }+k_{on}·\mathit{Drug}·\mathit{Cell}$$ (3)

where k_div (k_div^*) and k_death (k_death^*) are the rate constants for cellular division and death, respectively, in the no-drug (drug-saturated) state, Drug is the drug concentration, k_on is the rate constant for the transition from the no-drug to the drug-saturated state, and k_off is the rate constant for the reverse transition.

At a given drug concentration (assumed to be constant, i.e., drug is neither consumed, removed, nor degraded), a population of cells will eventually reach a dynamic equilibrium in terms of the number of cells in each state. The effective DIP rate of a cell population is then the weighted average of the net proliferation rates (i.e., the difference between the division and death rate constants) of the two individual states (Supplementary Fig. 3b). With increasing drug concentration, the equilibrium shifts increasingly towards the drug-saturated state, asymptotically approaching 100% occupancy. The result is a sigmoidal dose–response relationship between DIP rate and drug concentration (Supplementary Fig. 3c,d). If the values of the rate constants governing the interconversion between the no-drug and drug-saturated state (k_on and k_off) are “large” (effectively infinite), then the dynamic equilibrium between states is achieved immediately upon drug addition. This is known as the partial equilibrium assumption (PEA)^23,24. Mathematically, the PEA asserts that

$$k_{on}·\mathit{Drug}·\mathit{Cell}=k_{\mathit{off}}·{\mathit{Cell}}^{\ast }$$ (4)

Under this assumption, an analytical solution for the total number of cells, Cell_T = Cell + Cell*, can be obtained as a function of time,

$$ln\frac{{\mathit{Cell}}_T(t)}{{\mathit{Cell}}_T(0)}=\frac{\frac{k_{\mathit{off}}}{k_{\mathit{on}}}(k_{\mathit{div}}-k_{\mathit{death}})+\mathit{Drug}(k_{\mathit{div}}^{\ast }-k_{\mathit{death}}^{\ast })}{\frac{k_{\mathit{off}}}{k_{\mathit{on}}}+\mathit{Drug}}·t$$ (5)

where Cell_T(0) is the initial number of cells. All theoretical results shown in Figure 1a,b were obtained using equation (5). For the results in Figure 1c and Supplementary Figure 4, numerical integration of equations (2) and (3) was necessary since the values of k_on and k_off were set such that the PEA does not hold (Supplementary Table 2), i.e., there is a delay in the stabilization of the drug effect. Numerical integration was performed in R using the deSolve package²⁵. For further details of the model, see Supplementary Note; for all parameter values used in this work, see Supplementary Table 2.

Cell lines

The PC9 cell line was originally obtained from William Pao (Vanderbilt University). WM115 cells were from Meenhard Herlyn (Wistar Institute). All other cell lines were obtained from the American Type Culture Collection (www.atcc.org). All cell lines are regularly tested for mycoplasma using a PCR-based method (MycoAlert, Lonza, Allendale, NJ) and any positive cultures are immediately discarded. Cell line authentication is provided by ATCC. Authenticity of PC9 and WM115 have not been verified.

Time-lapse fluorescence microscopic imaging

Time-lapse fluorescence microscopy of cells expressing histone H2B conjugated to monomeric red fluorescent protein (H2BmRFP) to facilitate automated image analysis for identifying and quantifying individual nuclei was performed as previously described^11,12,14. Briefly, cells are engineered to express H2BmRFP using recombinant, replication-incompetent lentiviral particles and flow sorted for the highest 20% intensity. Cells are seeded at ~2,500 cells per well in 96-well imaging microtiter plates (BD Biosciences) and fluorescent nuclei are imaged using a BD Pathway 855 with a 20× objective in 3×3 montaged images per well at ~15 min intervals for 5 days. Alternatively, fluorescent cell nuclei are imaged twice daily using a Synentec Cellavista High End with a 20× objective and tiling of nine images. DIP rate-based dose–response curves shown in Figure 2c were generated from a single experiment performed at the Vanderbilt High-Throughput Screening Core on a Molecular Devices ImageXpress using similar imaging parameters. The experiment had two technical replicates per condition and images were obtained at 0, 24, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96,100,104,108, and 112 hours after addition of erlotinib at each of eight different concentrations or dimethyl sulfoxide (DMSO) control.

Other statistical considerations and code availability

Estimates of DIP rate are determined within an experiment using the sum of cells across all technical replicates at a given time point and obtaining the slope of a linear model of log2(cell number) ~ time for time points greater than the observed delay. Minimum delay time is estimated by visual inspection of log-growth curves for the time at which they become approximately linear (for an automated method of estimating the stabilization time point, see Supplementary Note and Supplementary Figs. 6 and 7). All data analysis was performed in R (version 3.2.1) and all raw data and R analysis code is freely available at github.com/QuLab-VU/DIP_rate_NatMeth2016.

Publicly available data sets

Drug-response data were obtained from the Genomics of Drug Sensitivity in Cancer (GDSC) project^4,9 website at ftp://ftp.sanger.ac.uk/pub/project/cancerrxgene/releases/release-5.0/gdsc_drug_sensitivity_raw_data_w5.zip and from the Cancer Cell Line Encyclopedia (CCLE)⁶ website at http://www.broadinstitute.org/ccle/ in the data file CCLE_NP24.2009_Drug_data_2015.02.24.csv (user login required).