Medial-Lateral Postural Control in Older Adults Exhibits Increased Stiffness and Damping

Abstract

Older adults often exhibit increased co-contraction in response to a balance perturbation. This response is generally thought to enhance stability by increasing joint stiffness. We investigated the issue of increased stiffness in postural control by exposing seven older (75 ±5 y) and ten young (24 ± 3 y) adults to pseudo-random medial-lateral (ML) floor tilts, and then fitting the measured ML body sway data to a previously-developed postural control model that includes stiffness and damping parameters. Significant increases were found in both parameters in the older adults compared to the young adults. This concurrent increase in stiffness and damping is more stabilizing than an increase in stiffness alone, which can lead to resonances.

I. Introduction

Aging is known to negatively impact the ability to maintain stable upright posture. Studies have shown that older adults have generally different stiffness than young adults and, in addition, older adults with a history of falls exhibit greater ankle stiffness compared to non-fallers [1]. Co-contraction has been shown to be one mechanism for older adults to increase stiffness when exposed to changes in sensory information [2]. Other studies have suggested that passive properties of muscle fibers and tendons also impact stiffness and damping properties [3], [4]. Ishida et al. [4] showed that the frequency characteristics of ankle impedance (ratio of external torque to ankle angle) changed with perturbation amplitude (small vs large) and available sensory information (eyes open vs closed). These frequency-dependent changes were interpreted by the authors as evidence that increased low frequency impedance (mainly stiffness) is effective for enhancing stability in response to slowly changing perturbations, but as the perturbations become more rapid, one should investigate ankle impedance over a broad frequency range and consider factors in addition to stiffness alone [4].

From a biomechanics and control viewpoint, increased stiffness alone is not necessarily stabilizing. Consider, for example, the linearized, second order, stable inverted pendulum model of upright balance, with stiffness K, damping B, mass m, center-of-mass height h_COM and moment of inertia J. In response to an external impulsive perturbation applied at time t = 0 which moves the pendulum away from stable upright, the angle θ(t) of the pendulum with respect to vertical will return to the upright position (θ = 0) over time according to

$$\theta (t)=A_1{e}^{s_{1}t}+A_2{e}^{s_{2}t},t\ge 0,s_1\ne s_2$$ (1)

where

$$s_{1,2}=\frac{-B}{2J}\pm \sqrt{{\left(\frac{B}{2J}\right)}^2-\frac{K-{\mathit{mgh}}_{\mathit{COM}}}{J}}$$ (2)

are the poles of the system, and A₁, A₂ are constants. Note that if the damping B is held fixed, increasing K will eventually cause the term under the square root to become negative, resulting in complex poles and hence an oscillatory (i.e., underdamped) response to a perturbation. From a stability standpoint, such an oscillatory response is not necessarily desirable. A concurrent increase in the damping would reduce the magnitude of these oscillations and moreover result in a faster settling time to steady state after a perturbation.

We provide new experimental results and model-based interpretations that complement and add to previous studies. Specifically, we show that older adults employ increased active stiffness and damping as a means of improving stability in response to platform perturbations, which is more effective than increasing stiffness alone. Although the human postural control system is not linear time-invariant (LTI), for small perturbations the response is approximately linear and, in addition, an input-output transfer function based analysis has been found to be useful in studying and understanding differences in postural control [5], [6]. We follow this approach here.

II. Experimental Methods

All subjects gave their informed consent to participate in this study, and the experimental protocol was approved by the Institutional Review Board at the University of Pittsburgh. Prior to experimental tests, subjects completed standard screening examinations to ensure absence of any balance abnormality. Data were obtained from seven older adults (three males and four females, ages 68 to 81 years (mean 75± 5 years SD)) and ten young adults (four male and six females, ages 21 to 30 years (mean 24 ± 3 years SD)).

Platform perturbations and data acquisition were accomplished using a dynamic posturography platform (NeuroTest, Neurocom International, Inc., Clackamas, OR). Subjects wore a harness during tests to prevent injury from possible falls. The harness did not impede sway, or give any positional feedback to the subject. Body sway in response to the rotational platform perturbations was measured with a magnetic tracking device (Fastrak, Polhemus, Colchester, VT) with a sensor positioned on the lower back, at the height of the iliac crest.

For the data used in modeling stiffness and damping, subjects were exposed to movements of the underfoot platform. The platform (termed the support surface (SS)) perturbation consisted of a randomly moving platform driven by a pseudo-random ternary sequence (PRTS-SS). Subjects stood on the platform such that the platform rotated about an anterior-posterior axis in between the medial malleoli, thus inducing medial-lateral (ML) sway. During the PRTS-SS condition, the platform rotated pseudo-randomly according to the integral of a PRTS, with peak-to-peak amplitude of 4°and a cycle duration of 48.4 s (see [5], [6] for details). Recorded postural sway in response to the platform perturbations was used to estimate dynamic properties of the postural control system over a range of frequencies (0.02 – 2.80 Hz). The PRTS-SS condition allows for an input-output analysis and estimation of model parameters. To ensure adequate steady-state conditions for this analysis, three consecutive cycles of the PRTS-SS were presented during a trial, for a total perturbation interval of 145.2 s.

Anthropometric measurements were taken for each subject so that the body inertia (J), mass (m), and height (h) used in the model could be obtained [7]. During experimental testing, subjects stood upright, with eyes closed, on the posturography platform while performing the trials. All subjects were instructed to “maintain a relaxed upright stance position with your eyes closed and arms folded across your chest.” Three trials were conducted per subject. The duration of each trial was 205.2 s, consisting of a 145.2 s perturbation interval (PRTS-SS motion) preceded and followed by a 30 s quiet stance period on a fixed SS.

III. Data Measurement, Analysis and Modeling

Medial-lateral (ML) hip displacement measured with the electromagnetic sensor was used to calculate body sway (BS) angle in the frontal plane by using the small angle approximation, 10 cm, corresponding to Hip_ML (t) = h_COM sin BS(t) ≈ h_COM BS(t). For the hip excursions we observed (less than ± BS angle of less than ±6° for h_COM = 100 cm), the error in this approximation is negligible. Body sway (BS) and angular platform rotation (SS) measurements during the 145.2 s of pseudo-random platform motion were each divided into three segments corresponding to the three PRTS-SS cycles of 48.4 s duration. For each segment, the power spectrum, and the cross-power spectrum between SS and BS, were estimated via the discrete Fourier transform (DFT), and then ensemble averaged across the three segments. Further spectral smoothing was also applied to reduce variability in the spectral estimates, especially at higher frequencies, as described in [5], [6]. The resulting smoothed power and cross-power estimates had 17 data points ranging from 0.021 to 2.79 Hz, evenly spaced in a log scaled frequency axis (Fig. 2). From these smoothed ensemble averages, the experimental frequency response was computed by taking the ratio of the cross-power spectrum to the power spectrum of the support surface.

Fig. 2.

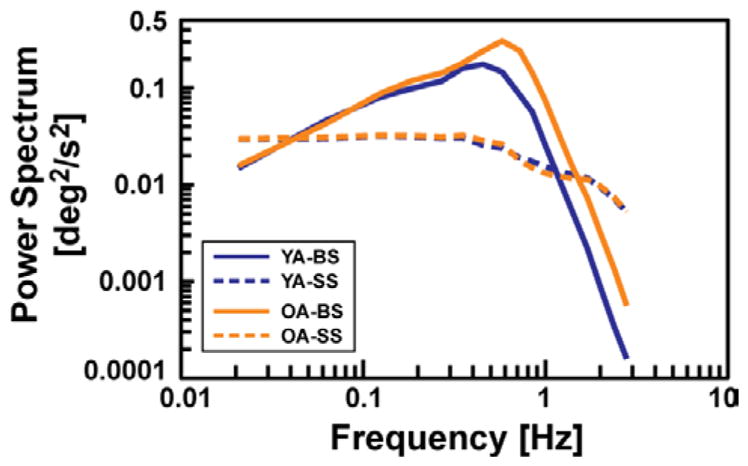
Mean experimental power spectra of input (SS) and output (BS) for young adult (YA) and older adult (OA) age groups.

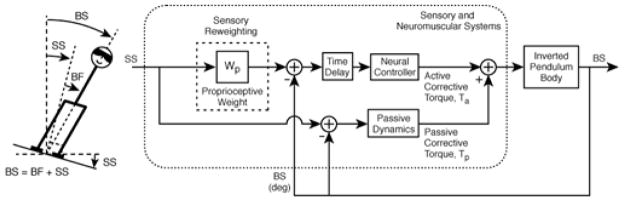
A least-squares fit of the experimental frequency response was made to a previously developed and validated feedback postural control model (Fig. 1), which has been shown to produce simulations in good agreement with postural data under a variety of experimental conditions, including ones similar to our experiments [5], [6], [8]–[11]. The transfer function of the model is:

$$\frac{BS(s)}{SS(s)}=\frac{w_P·(K_D{s}^2+K_{P}s+K_I)·e^{-T_{D}s}+B{s}^2+Ks}{J{s}^3+(K_D{s}^2+K_{P}s+K_I)e^{-T_{D}s}+B{s}^2+(K-{\mathit{mgh}}_{\mathit{COM}})s}$$ (3)

where s is the Laplace variable, and the parameters of the model include active stiffness (K_P) and damping (K_D), which are the proportional and derivative gains, respectively, of a PID controller with integral gain (K_I); passive stiffness (K) and damping (B); a lumped time-delay (T_D) that accounts for neural transmission, sensory processing, and muscle activation delays in the postural control system; and proprioceptive sensory gain (w_P). The model also includes gravitational acceleration (g = 9.81 m/s²), and the (measured) moment of inertia (J), mass (m) and height-to-center-of-mass (h_COM) of the subject. In this closed-loop control model, the body is modeled as a single-link inverted pendulum with small angle deviations, thus allowing a linear time-invariant representation. Least-squares curve fits of the postural control model frequency response function (s=jω) to the experimental frequency response function were made as in [9], [11] to obtain the parameter values for each subject.

Fig. 1.

Diagram of postural control model corresponding to eq.3. (Adapted from)

A mixed-factor repeated-measures ANCOVA was performed on all model parameters, using a significance level of α=0.05, with independent factor of Age (Young and Older Adults) and covariate J (moment of inertia). This covariate was included in our statistical analysis because body size differences are known to be correlated with stiffness and damping [5], and thus any observed differences in these parameters may be explained by differences in body size. This statistical approach was used to determine if the postural control model parameters change significantly with age, while accounting for differences in body size between the subject groups.

IV. Results

The mean group (young vs old) experimental frequency response gain and phase curves of BS to PRTS-SS are shown in Fig. 3. Observe that below about 0.3 Hz, there is little difference between the two groups, but above 0.3 Hz, the gain is higher for the older adults compared to the young and exhibits a slight peak around 0.7 Hz. No apparent systematic differences between young and old were observed for the phase.

Fig. 3.

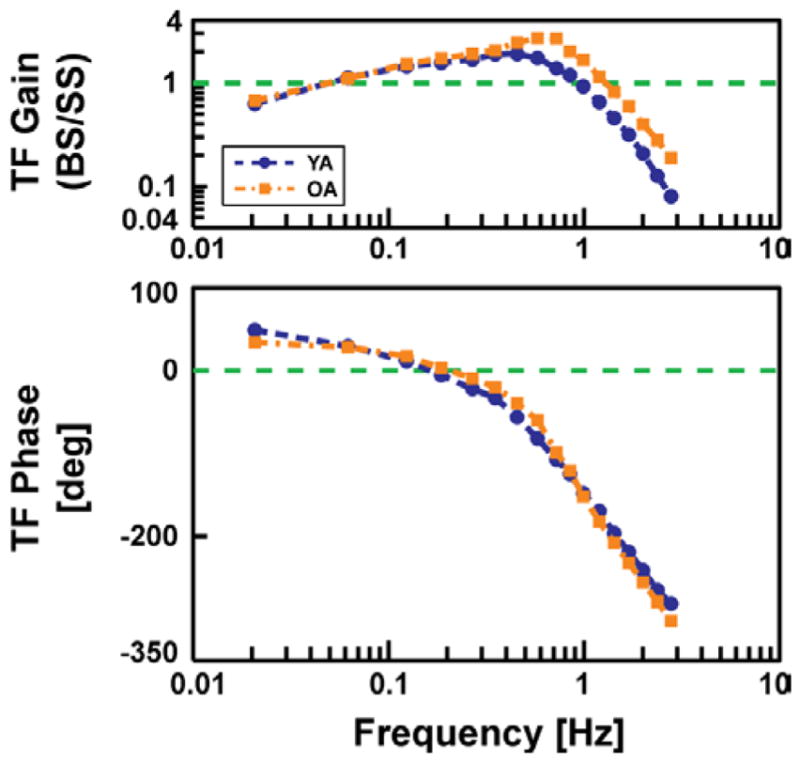
Mean experimental frequency response (gain and phase) for young adult (YA) and older adult (OA) age groups. Note higher gain above 0.3 Hz, including a slight peak around 0.7 Hz, for the OA group.

The model fits to each subject’s experimental frequency response further quantified differences between the young and older groups, in terms of the mean model parameter values (Table I). In particular, the active stiffness K_P and damping K_D were both significantly larger in the older adults compared to the young adults, after adjusting for the covariate J, as was the integral gain parameter K_I. Thus these differences in parameter values between young and old cannot be attributed to differences in body size between the two groups. Further analysis by normalizing the parameters by J confirmed this result. Passive stiffness and damping control parameters (K and B) tended to be smaller in value than the corresponding active parameters. Moreover, no significant age effect was found in the passive parameters. No significant age effect on the time delay (T_D) parameter was found. The proprioceptive sensory weight parameter (w_p) was significantly larger in the older adults than in the young adults. The last column in Table Ishows a measure of goodness-of-fit (mean-square-error) of the model to the mean frequency response of each subject group.

Table I.

Estimated model parameters (mean±SD) for young and older adult groups.

	KP [N·m·rad−1]	KD [N·m·s·rad−1]	KI [N·m·rad−1·s−1]	K [N·m·rad− 1]	B [N·m·s·rad−1]	TD [ms]	wp	mse [%]
Young	898 ± 215	288 ± 71	182 ± 110	157 ± 165	34 ± 40	172 ± 27	0.44 ± 0.13	3.25 ± 0.79
Older	1225 ± 299	370 ± 86	359 ± 163	99 ±166	44 ± 49	173 ± 24	0.64 ± 0.17	3.25 ± 1.19
p-value	0.005	0.042	0.032	0.195	0.943	0.818	0.011	0.984

IV. Discussion

As adults age, there is increasing degradation in motor and sensory function which impacts balance function [12], [13], [14], with significant changes starting in the 6^th and 7^th decade of age [15]. These degradations may lead to changes in postural control strategies employed by older adults to maintain balance. For example, it is generally felt that older adults are “stiffer,” exhibiting increased co-contraction of muscles during challenging balance tasks or in response to balance perturbations [16]. However, from a control systems standpoint, increased stiffness alone is not necessarily a good compensatory response, as noted in the Introduction. Our experimental results showed that, indeed, older adults are stiffer than young adults, but that they also have increased damping, which, based on a simple inverted pendulum description of postural control, should have the beneficial effect of reducing oscillations in response to external perturbations.

In our model based analysis, we were able to estimate stiffness and damping and furthermore to distinguish between active and passive factors. We found that active stiffness and damping dominated the response to external perturbations in both young and older adults, compared to the corresponding passive properties, consistent with previous findings in young adults [5], [6]. Moreover, we found increases in both active stiffness and damping, relative to body size, in older adults compared to young adults.

V. Conclusion

We conducted balance experiments on young and older adults, with model-based analysis of the data, to investigate postural control changes with age. In particular, we were interested in the view that older adults are “stiffer” in response to balance perturbations, which is often interpreted as having a stabilizing influence. Our experimental and modeling results revealed that, in response to medial-lateral small amplitude pseudo-random floor tilts, older adults indeed had significantly higher stiffness for postural control than young adults, but they also had increased damping as well. The combination of increased stiffness and damping is theoretically more stabilizing than an increase in stiffness alone. We also observed larger frequency response gain above 0.3 Hz and a more pronounced peak around 0.7 Hz in older adults compared to young adults, suggesting that, even with their increased stiffness and damping, older adults would experience a more oscillatory response to fast occurring perturbations than they would for slow perturbations, compared to young adults. Thus, older adults may be at greater risk for balance loss in situations where they could experience rapid floor movements, such as on a bus, train, or escalator.