Detecting and quantifying parasite-induced host mortality from intensity data: method comparisons and limitations

Abstract

Parasites can significantly impact animal populations by changing host behavior, reproduction and survival. Detecting and quantifying these impacts is critical for understanding disease dynamics and managing wild animal populations. However, for wild hosts infected with macroparasites, it is notoriously difficult to quantify the fatal parasite load and number of animals that have died due to disease. When ethical or logistical constraints prohibit experimental determination of these values, examination of parasite intensity and distribution data may offer an alternative solution. In this study we introduce a novel method for using intensity data to detect and quantify parasite-induced mortality in wildlife populations. Using simulations, we show that this method is more reliable than previously proposed methods while providing quantitative estimates of parasite-induced mortality from empirical data that are consistent with previously published qualitative estimates. However, we stress that this method, and all techniques that estimate parasite-induced mortality from intensity data alone, have several critical assumptions that limit their applicability in the real world. Due to these limitations, these methods should only be used as an exploratory tool to inform more rigorous studies of parasite-induced host mortality.

Introduction

Infectious agents can impact on animal populations through changing population dynamics and stability (Dobson & Hudson 1992), altering predator-prey interactions (Joly & Messier 2004), and even causing species’ decline and extinction (De Castro & Bolker 2005; McCallum 2012). Accurately estimating the impact of these infectious agents in wildlife is critical to understanding what regulates host and parasite populations, making predictions about disease transmission, and managing disease outbreaks (Langwig et al. 2015). The impact of microparasite pathogens, such as rabies (Coyne et al. 1989), bovine tuberculosis (Cox et al. 2005), and rinderpest (Tillé et al. 1991), are typically modeled based on the presence or absence of disease, and host survival is not a function of the number of infectious agents present. In contrast, for macroparasites, pathology increases with parasite burden and host survival probability must be treated as a function of infection intensity. Helminths exhibiting this intensity-dependent pathology have significant impacts on human health (Brooker et al. 2004), domestic livestock economics (Roeber et al. 2013), and wildlife survival (Kirk 2003; Logiudice 2003). While it is generally assumed that some fraction of wild host populations succumb to parasitic infection, it is notoriously difficult to actually quantify parasite-induced host mortality (PIHM) in wild animal populations because it is difficult to observe the dead or dying hosts most impacted by parasitism (McCallum 2000).

Ideally, parasite-induced host mortality is quantified by experimentally infecting and tracking individual hosts in the wild population; however, for logistical and ethical reasons this method is rarely feasible (McCallum 2000). Snapshot data of parasite intensities across multiple hosts is much easier to collect and has often been used to identify the presence of PIHM (Crofton 1971; Lester 1977, 1984; Lanciani & Boyett 1989; Royce & Rossignol 1990; Ferguson et al. 2011) and to quantify the relationship between infection intensity and host mortality (Adjei et al. 1986).

Crofton (1971) first proposed that PIHM could be identified from parasite intensity data by comparing the observed parasite distribution in sampled hosts to the distribution predicted in the absence of parasite-induced mortality. This method assumes that, prior to host mortality, infection intensity in the host population follows a negative binomial distribution and the tail of the distribution is truncated as intensity dependent pathology removes the most heavily infected hosts. Assuming mortality occurs only in heavily infected hosts, evidence of this parasite-induced mortality should then be detectable by iteratively fitting a negative binomial distribution to hosts with lower and lower parasite intensities, and comparing these truncated predicted distributions to the corresponding truncated observed parasite data (Figure 1, see Supplementary Material (SI) 1 for additional detail).

Figure 1.

A schematic representation of the iterative approach of the Crofton Method. A) The light gray shows the pre-mortality distribution that the Crofton Method is trying to estimate from the dark grey post-mortality distribution. The Crofton Method proceeds by truncating the post-mortality data at different levels (t_i, e.g. i = 0,…, 5) and finding the parameters pre-mortality host population size (N_p), pre-mortality mean parasite intensity (μ_p), and pre-mortality parasite aggregation (k_p) that best fit the truncated data. B) The parameter N_p is then plotted against the truncation level t_i to determine if a “kink” occurs in the parameter values (Lester 1984). This “kink” indicates that PIHM is occurring in the system. In the above example, PIHM is occurring in the system as visualized by the distinct “kink” at t₃.

While the Crofton Method detects the presence of PIHM, it makes no attempt to quantify the relationship between infection intensity and host survival probability; an important relationship for determining the potential impact of a parasite on host dynamics (Anderson & May 1978; Barbour & Pugliese 2000). Adjei et al. (1986) suggested that this relationship could be calculated by first using the Crofton Method to estimate the pre-mortality parasite distribution and then using this distribution to calculate the probability of host survival with increasing parasite intensity. To do this, Adjei et al. (1986) modeled host survival as a logistic function and then used a generalized linear model (GLM) to estimate the parameters of the host survival function (see SI 2 for a technical description of the Adjei Method). Adjei et al. noted that this survival function could provide useful information such as the parasite intensity at which a host has a greater than 50% chance of suffering parasite-induced mortality. However, if mean infection intensity is high or sample sizes are small the observed intensity data must be subjectively binned into intensity ranges in order to fit the GLM framework. Furthermore, for the Adjei Method to work, any observed intensity values greater than predicted values must be modified and set equal to the predict values (see SI 2 for details); a questionable act of data manipulation. These manipulations may introduce bias, reduce the precision and limit the power of this method to detect and quantify parasite-induced host mortality.

After 30 years, and despite clear limitations (McCallum 2000), these methods (particularly the Crofton Method) are still discussed among parasitologists and are the primary techniques for examining population-level impacts of parasitism using parasite intensity data. In these methods, PIHM can only be identified by visually examining plots of the pre-mortality parameters predicted by Crofton Method and determining whether they show a “kink” over a range of truncation values (Figure 1B; Lester 1984; Ferguson et al. 2011). This qualitative criteria makes it difficult to compare PIHM between studies and a more rigorous and quantitative method is needed to both detect and quantify host mortality. The survival function given by the Adjei Method may be used to do this; however, it requires manipulating the original data and its accuracy remains untested.

In this study, we propose a novel method for detecting and quantifying PIHM that ameliorates many of the aforementioned deficiencies of the previous methods. Our method does not require data alteration, is highly generalizable, and uses standard statistical techniques to quantitatively determine whether PIHM is occurring in a system. We use simulations to compare our method with the Adjei Method to test the ability of both to (1) detect occurrence of PIHM and (2) estimate the host survival function. We then apply both methods to real datasets previously used in PIHM analyses and compare the results. Finally, we discuss the limitations of inferring PIHM from intensity data and the place of any of these methods in modern quantitative parasitology.

Methods

A novel, likelihood-based method for estimating PIHM

Our method (henceforth the Likelihood Method) begins with the same assumptions as the Adjei Method: namely that infection has occurred and hosts with fatal parasite loads have died prior to the population sampling. As discussed by Adjei et al., this is not necessarily an unrealistic as some parasite infections occur primarily in younger hosts with parasite-induced mortality occurring soon after infection (e.g. Schotthoefer et al. 2003; Johnson & McKenzie 2008).

The Likelihood Method then assumes that prior to mortality the parasite distribution can be described by the distribution g(x; ϕ), which specifies the probability of a host having x parasites when it is observed. ϕ is a vector of parameters that describes the shape of this distribution. The method then assumes that the probability of a host surviving with x parasites from infection until sampling is given by the host survival function h(survival; x, θ) where θ specifies any additional parameters needed to define the host survival function.

With these two assumptions, we can define a distribution that gives the probability of having a parasite load of x parasites conditional on host survival, P (x|survival). Using standard rules of conditional probability this distribution can be written as

$$P(x\mid \text{survival})=\frac{P(\text{survival}\mid x)\ast P\left(x\right)}{P\left(\text{survival}\right)}$$ (1)

P (survival|x) is the survival function h(survival; x, θ), P (x) is the pre-mortality parasite distribution g(x; ϕ) and P(survival) = ${\Sigma }_{x=0}^{\infty }$ P (survival|x) * P(x) = ${\Sigma }_{x=0}^{\infty }$ h(survival; x, θ) * g(x; ϕ). Thererfore, equation 1 can be written as

$$P(x\mid \text{survival})=\frac{h(\text{survival};x,\theta )\ast g(x;\varphi )}{\sum _{x=0}^{\infty }h(\text{survival};x,\theta )\ast g(x;\varphi )}$$ (2)

Using this probability distribution, one can then find the parameters θ and ϕ that maximize the likelihood of an observed host-parasite dataset. To estimate the significance of PIHM in a host-parasite system, a likelihood ratio test can be used in which the full model is given by equation 2 and the reduced model is given by the pre-mortality distribution g(x; ϕ). If PIHM is not significant in the system, the resulting likelihood ratio statistic should approximately follow a χ² distribution with degrees of freedom equal to the number of parameters in the full model with parasite-induced mortality minus the number of parameters in the reduced model without parasite-induced mortality (Bolker 2008).

The parameterization of equation 2 depends on the parasite system of interest. Here, we assume that the pre-mortality parasite distribution g(x; ϕ) follows a negative binomial distribution with the parameters mean parasite intensity (µ_p) and aggregation (k_p) before mortality (smaller k_p indicates more aggregation) (Crofton 1971; Anderson & May 1978; Adjei et al. 1986). A variety of different biological and statistical assumptions can result in an equilibrium parasite distribution that follows a negative binomial distribution (Kendall 1948; Boswell & Patil 1970; Calabrese et al. 2011). Furthermore, the negative binomial distribution is an incredibly flexible distribution that fits many host-parasite systems even when the underlying mechanisms determining the empirical distribution are unknown (Shaw et al. 1998).

The function for h(survival; x, θ) is also system specific. Many theoretical models of parasite-induced host mortality assume that the parasite-induced death rate of hosts is a linear function of parasite intensity (Anderson & May 1978; Dobson & Hudson 1992; Barbour & Pugliese 2000). In systems where there is truly a linear relationship between infection intensity and survival probability it will be nearly impossible to use intensity data to detect parasite-induced host mortality (Lanciani & Boyett 1989). However, there is substantial empirical evidence that host-parasite systems do not universally exhibit linear host-survival functions (Benesh 2011), suggesting a linear form for h(survival; x, θ) is not always the most reasonable.

To compare the Likelihood Method and the previously proposed Adjei Method, we adopt the host-survival function used in the earlier study and assume it is non-linear and follows a logistic function given by

$$h(\text{survival};x,a,b)=\frac{e^{a-b\text{log}\left(x\right)}}{1+e^{a-b\text{log}\left(x\right)}}$$ (3)

Generally, a larger b leads to a more rapid decline in the probability of host survival as parasite intensity increases, with the maximum rate of decline having a value of b/4 (SI 2). b is in many ways analogous to the the pathogenicity parameter in classic macroparasite models which gives the rate at which host death rate changes with increasing parasite intensity (Anderson & May 1978; Isham 1995). When b is held constant, a larger a allows for hosts to tolerate larger parasite intensities before experiencing parasite-induced mortality. More specifically, for every one unit increase in a the log parasite intensity at which any percent of hosts survive (e.g. 99% of hosts survive) increases by 1/b (SI 2).

The equation exp(a/b) can also be used to calculate the parasite LD₅₀, here defined as the infection intensity above which a host has greater than 50% probability of dying. Equation 3 is commonly used in toxicology and has the useful properties of being bounded between 0 and 1 and being differentiable for all x (Collet 2002). That being said, it is phenomenological and there is little theoretical justification to use it rather than it tends to fit survival data. However, given that a goal of these analyses is to compare the Likelihood Method’s results to the Adjei Method, it is natural to adopt the same host-survival function to facilitate comparison. When applying the Likelihood Method to other systems more mechanistic host-survival functions can be used in place of equation 3.

Evaluating the Adjei and Likelihood Methods

Question 1: Can we detect PIHM?

We tested the ability of the Adjei and the Likelihood Methods to identify the presence of PIHM on simulated data with known pre-mortality parameters. Consistent with the model assumption that parasite infection, host mortality, and population sampling are temporally separate events, we first created a pre-mortality host population by drawing N_p randomly infected hosts from a negative binomial distribution with parameters μ_p and k_p. This represents a host population that has become infected but not yet experienced parasite-induced mortality (Adjei et al. 1986). In the Adjei Method and Crofton Method, N_p is a necessary parameter defined as the number of hosts in the population before parasite-induced mortality. More accurately, N_p is the number of hosts that would have been sampled had parasite-induced host mortality not occurred. This parameter is not necessary when using the Likelihood Method because, unlike the Adjei Method and Crofton Method which estimate parasite-induced mortality using absolute numbers of hosts, the Likelihood Method estimates parasite-induced mortality using probabilities. However, to compare the results of the Likelihood Method with the Adjei Method, we specified a value for N_p for all simulations.

We next chose values of a and b for the host survival function and calculated the probability of survival for all N_p hosts using equation 3. Then, to simulate the period in which hosts died due to infection, for each host we drew a random number from a uniform distribution between 0 and 1 and if the calculated host survival probability was less than this random number, the host experienced parasite-induced mortality. The surviving individuals represent the post-mortality hosts that would be sampled in the field.

We then used these simulated pre-mortality and post-mortality datasets to test the ability of both methods to correctly determine whether or not PIHM was occurring when the parameters N_p, μ_p and k_p were known. Although the parameters N_p, μ_p, and k_p are always unknown in real systems, a method that fails under these ideal simulation conditions with known parameters will certainly also fail when these values must be estimated from empirical data. In practice, for the Adjei Method, N_p, μ_p, and k_p are estimated using the Crofton Method (Adjei et al. 1986), while μ_p and k_p in the Likelihood Method can be estimated jointly with a and b or via the Crofton Method.

We compared the two methods using three different mean parasite intensity values (μ_p = 10, 50, 100) and three different host survival functions (gradual, moderate, and steep decreases in the host survival with increasing parasite intensity, Figure 2A). For a given μ_p, each survival function had the same LD₅₀ ([μ_p = 10, LD₅₀ = 7.39], [μ_p = 50, LD₅₀ = 35.57], [μ_p = 100, LD₅₀ = 77.3]), but different values of a and b. We examined each μ_p-survival function pair at three levels of parasite aggregation, k_p = 0.1, 0.5, and 1 — realistic values of parasite aggregation in natural populations (Shaw et al. 1998). For each of these 27 parameter combinations we simulated 150 datasets and tested the probability of each method correctly identifying PIHM in the post-mortality dataset (power) and incorrectly identifying PIHM in the pre-mortality dataset (Type I error). For each method, we used a likelihood ratio test to determine whether the full model with PIHM provided a significantly better fit than the reduced model without PIHM at significance level of 0.05. We also examined the impact of sample size by simulating each parameter for pre-mortality sample sizes of N_p = [50, 100, 200, 300, 400, 500]. Wild host populations were assumed to be sampled after PIHM has occurred, thus we calculated the sample size in the power simulations as the average number of surviving hosts over all 150 simulations for each parameter combination.

Figure 2.

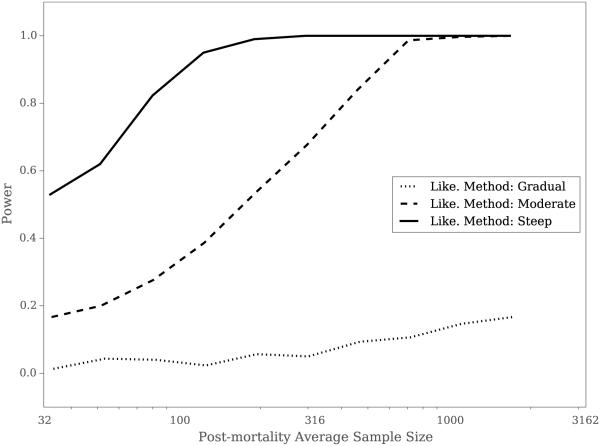
A) Five potential shapes for a host-survival functions. In the simulations we used a gradual survival function (dotted line), and moderate survival function (dashed line), and a steep survival function (solid line). The linear and immediate survival functions represent two potential extremes that we do not include in the simulations. For each of these survival functions and the parameter combinations described in the main text, we tested the Type I error and power of the Likelihood (Like.) Method and Adjei Method. B) Gives the Type I error of each method over a range of pre-mortality sample sizes with a pre-mortality mean parasite intensity (μ_p) of 50 and pre-mortality parasite aggregation (k_p) at 0.5. The red line shows the pre-set significance level of 0.05. C) Gives the power of each method for detecting PIHM over a range of post-mortality sample sizes for μ_p = 50 and k_p = 0.5. In general, the Likelihood Method has higher power and lower Type I error than the Adjei Method. See the SI 3 Fig 1 - 3 for Type I Error and power results for all parameter combinations.

We then tested the ability of the Likelihood Method to correctly identify PIHM under the more realistic condition of unknown pre-mortality parameters. Based on the first set of simulations, we excluded the Adjei Method and only examined the power of the Likelihood Method under “best-case” scenario parameter values, setting μ_p = 10 and k = 1 because PIHM is most detectable when parasites are less clumped and mean intensity is low. We examined the impact of survival function shape and sample size on the Likelihood Method’s ability to identify PIHM when the pre-mortality parameters μ_p and k_p and the survival function parameters a and b needed to be estimated. We performed 500 simulations over a range of different samples sizes for gradual, moderate, and steep survival functions, following the simulation procedure described above.

Question 2: Can we estimate properties of the host survival function?

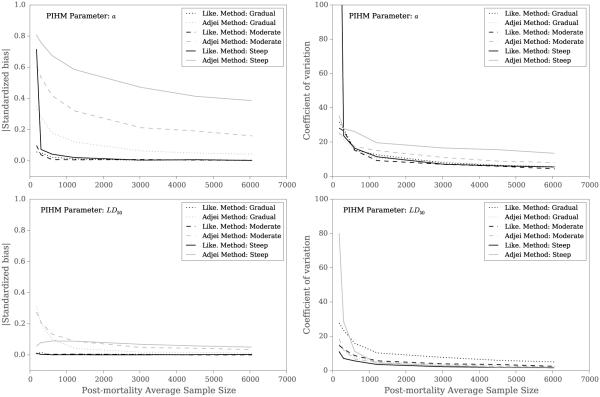
In the previous section we compared the ability of the Adjei Method and the Likelihood Method to provide a “yes” or “no” answer for whether or not PIHM was occurring in a system. In this section we compared the ability of the Adjei Method and the Likelihood Method to estimate properties of the survival function such as the parameters a, b and LD₅₀. Using the same simulation procedure and parameter combinations described above, we simulated 150 datasets, estimated a, b, and LD₅₀ and calculated the standardized bias and precision for these estimates (Walther & Moore 2005). Because estimating properties of the host survival function requires more information than simply detecting PIHM, we used larger values of N_p for this simulation (N_p = [300, 500, 1000, 2000, 5000, 7500, 10000]). We used the average number of surviving hosts for each set of 150 simulated datasets as our measure of sample size. Although both a and b are necessary to estimate LD₅₀, the two parameters showed similar patterns of bias and precision so we only show the results for a.

Application to real data

We tested the ability of the Adjei Method and the Likelihood Method to identify PIHM in six host-parasite datasets given in Crofton (1971) and four datasets given in Adjei et al. (1986) (Table 2). Crofton analyzed infection patterns in the snail Gammarus pulex infected with the acanthocephalan Polmorphus minutus. Adjei et al. analyzed males and females of two species of lizard fish Saurida tumbil and S. undosquamis that were infected by the cestode Callitetrarhynchus gracilis.

Table 2.

Comparison of the PIHM predictions of previously used host-parasite datasets to those given by the Adjei Method and the Likelihood Method. The first column specifies the identity of the dataset, the second column specifies whether or not the authors indicated that PIHM was occurring in the system based on a qualitative assessment, the third column indicates whether or not the Likelihood Method with pre-mortality parameters estimated from the Crofton Method detects significant PIHM, and the final column indicates whether the Adjei Method with pre-mortality parameters estimated from the Crofton Method detects PIHM. If a method detected significant PIHM the predicted LD₅₀ is given in parentheses.

Data Set (sample size)	Author detected PIHM?	Likelihood Method?	Adjei Method?
Crofton, Station 1 (n = 538)	Yes	Yes (7.27)	Yes (9.33)
Crofton, Station 2 (n = 507)	Yes	Yes (6.92)	Yes (14.95)
Crofton, Station 3 (n = 633)	Yes	Yes (5.93)	Yes (5.98)
Crofton, Station 4 (n = 486)	No	No	Yes (7.99)
Crofton, Station 5 (n = 276)	No	No	Yes (10.58)
Crofton, Station 6 (n = 191)	No	No	No
Adjei, S. tumbil female (n = 446)	Yes (5.7)	No	Yes (6.37)
Adjei, S. tumbil male (n = 452)	Yes (3.4)	Yes (3.42)	Yes (3.66)
Adjei, S. undosquamis female (n = 2573)	Yes (3.2)	Yes (3.04)	Yes (3.11)
Adjei, S. undosquamis male (n = 2440)	Yes (1.8)	Yes (1.83)	Yes (1.78)

In both earlier studies, the authors reported PIHM in some of the datasets and we tested whether the Adjei Method and/or the Likelihood Method also predicted PIHM. For the six datasets from Crofton (1971), we used the general conclusions of the author and truncated the data at four parasites, applied the Crofton Method to estimate the pre-mortality distribution, and then ran the Likelihood Method and Adjei Method using these pre-mortality parameters. For the Adjei et al. (1986) datasets, we followed the same procedure as the authors and first truncated the data at two parasites and then fit the Crofton Method for the female fish of both species. Then, following the original authors’ methods, we parameterized the male pre-mortality distributions for each species with the results from the females. Finally, we applied the Adjei Method and the Likelihood Method to determine whether or not PIHM was significant for these species and compared our results to those given by the authors. All code for the analyses is provided in SI 4.

Results

Question 1: Detecting presence of PIHM

The power of the Adjei Method to detect PIHM in a system was close to unity for larger sample sizes and tended to decrease as sample size decreased for all survival functions (Figure 2C; SI 3 Figs 1-3). The Likelihood Method had a power close to unity for all parameter combinations and sample sizes considered. With gradual survival functions, the power of the Likelihood Method decreased slightly for small samples sizes (Fig. 2C, SI 3 Figs 1-3).

The Adjei Method showed highly inflated Type I error rates (i.e. falsely detected PIHM) for all parameter combinations that we considered (Fig. 2B; SI 3 Figs 1-3). This method also showed the unintuitive pattern of decreasing Type I error rate with decreasing sample size. This occurred because, at small samples sizes, intensity data must be binned before the Adjei Method can be used (SI 2). In contrast, the Likelihood Method showed a Type I error rate at or near the pre-set level of 0.05 for all parameter combinations and sample sizes considered (Fig. 2B; SI 3 Figs 1-3).

When all parameters were jointly estimated, the Likelihood Method showed highly context-dependent results even when detecting PIHM under the best-case scenario of μ_p = 10 and k_p = 1. For steep survival curves, PIHM could be detected with a power of greater than 0.8 from a sample of less than 100 hosts (Fig 4). However, for moderate survival functions over 400 hosts had to be sampled to achieve the same power and for gradual survival functions, no tested sample size ever achieved a power greater than 0.8 (Fig 4).

Figure 4.

The power of the Likelihood Method (Like.) to detect PIHM for gradual, moderate, and steep survival functions when all four parameters μ_p, k_p, a, and b were jointly estimated. The curves were generated from 500 simulations for 10 pre-mortality sample sizes, N_p.

Question 2: Estimating the LD₅₀ and survival function

The Likelihood Method gave asymptotically unbiased estimates of the LD₅₀ for all combinations of parameters examined in this study (Fig. 3, SI 3 Figs 4-6). Even for the smallest sample sizes we considered, the Likelihood Method’s estimate of LD₅₀ was largely unbiased, with small biases occurring for gradual host survival functions. The precision of the Likelihood Method’s LD₅₀ estimates decreased (increasing coefficient of variation) as sample size decreased for all parameter combinations we examined (Fig 3, SI 3 Figs 4-6).

Figure 3.

Bias and precision (coefficient of variation) for the Likelihood Method (Like.) and Adjei Method estimates of the a parameter and the LD₅₀ of the host survival function based on simulated PIHM data over a range of post-mortality sample sizes. As the coefficient of variation increases, precision decreases. The pre-mortality parameters for this simulation were μ_p = 50 and k_p = 0.5. The figure shows the simulations for three different host survival functions (gradual, moderate, and steep), each with the same LD₅₀. Bias and precision results of LD₅₀ and a for all other parameter combinations can be found in SI 3 Fig 4 - 9.

The Adjei Method produced biased estimates of the LD₅₀ across nearly all parameter combinations, tending to underestimate the true value of the parameter (Fig 3, SI 3 Figs 4-6). For μ_p = 10, the LD₅₀ estimates from the Adjei Method were largely unbiased for large samples sizes, but as μ_p increased, the Adjei Method produced biased estimates of LD₅₀ across all sample sizes, with bias increasing as sample size decreased (Figure 3, SI 3 Fig 4-6). The LD₅₀ estimates from the Adjei Method also showed large decreases in precision with the steepest survival function across all values of μ_p (Figure 3, SI 3 Fig 4-6).

In terms of the host survival function, the Likelihood Method gave unbiased estimates of survival function parameter a when sample sizes were large, however as sample size decreased these estimates became severely biased (Fig. 3, SI Fig 7 - 9) The Adjei Method produced biased estimates of the host survival function across all sample sizes, with the bias consistently being larger when the survival function was steeper and μ_p was larger (Fig 3, SI 3 Figs 7-9).

Application to real data

The previous authors qualitatively detected PIHM in 7 of the 10 datasets considered (Table 2). The Likelihood Method parameterized from the pre-mortality parameters of the Crofton Method detected significant PIHM in 6 of these 7 datasets at a significance level of 0.05. The only dataset in which the Likelihood Method did not detect a significant effect of PIHM was the Adjei dataset for female S. tumbil. For this dataset there was a marginally significant effect of PIHM (${\chi }_{df=2}^2$ = 5.34; p = 0.069). The Adjei Method detected PIHM in 9 of the 10 datasets (Table 2), consistent with our simulation results showing that the Adjei Method has a high Type I error rate.

Discussion

Our likelihood-based method to estimate parasite-induced host mortality from observed parasite intensity data is a significant improvement over the previous methods. In simulations, it had greater power for detecting PIHM over a wider range of parameter values and also exhibited fewer false detection events (Type I errors) in both simulations and when applied to published datasets previously used in PIHM analyses. The Likelihood Method was also generally less biased and more precise when quantifying parasite-induced mortality via the host survival function for the parameters we considered. The superior performance of the Likelihood Method over the Adjei Method can be attributed to its fewer parameters, its lack of unnecessary data alteration, and its applicability across a variety of different parameter combinations. In short, the Likelihood Method is a better method for detecting and quantifying PIHM than the previously proposed Adjei Method.

Although superior to the Adjei Method, the Likelihood Method still cannot be applied to all real datasets. For host-parasite systems where host mortality occurs as a steep, non-linear function of parasite intensity only 80 hosts must be sampled to have an 80% power in detecting PIHM. However, as the maximum slope of the survival function decreases and the function becomes somewhat linear, hundreds, or possibly thousands of hosts would have to be sampled to achieve the same result. This is consistent with previous studies which illustrate the difficulty of detecting PIHM from linear host survival functions (Lanciani & Boyett 1989). While it may be feasible to sample several hundred invertebrates or small fish, even the smallest sample sizes are completely unfeasible for many vertebrates, particularly the species of conservation concern where addressing the impact of parasitism would be most important. An even larger sample size would be required to identify PIHM when parasites are highly aggregated, mean infection intensity is high, or parasite prevalence is low, all of which are common in many parasitic helminths. Moreover, while linear functions make PIHM undetectable, at the other extreme, steep, non-linear survival curves produce severely biased estimates of the survival function. Give the interaction between all of these different factors, the Likelihood Method is probably limited to detecting PIHM in systems where greater than 100 hosts can be collected, parasites are common and only moderately aggregated, and substantial host mortality occurs at relatively low parasite intensity.

While we have improved on the existing methods for quantifying PIHM from parasite intensity data, all such methods require several fundamental, and potentially problematic assumptions. Nearly all current methods derive from Crofton (1971) (but see Ferguson et al. 2011) and assume that, prior to any PIHM, parasites are distributed in the host population following a negative binomial distribution. But, it is fundamentally impossible to know what the pre-mortality parasite distribution was in a wild host population and it is widely recognized that different processes can lead to a variety of parasite distributions in hosts (Anderson & Gordon 1982; Duerr et al. 2003). However, the negative binomial is extremely flexible and there is substantial empirical and theoretical evidence to support the assumption that, prior to any PIHM, parasite distributions can be fit by a negative binomial distribution (Shaw & Dobson 1995; Shaw et al. 1998; Wilson et al. 2002).

Unfortunately, this flexibility in the distribution may also reduce our ability to detect PIHM. If a negative binomial can be fit to the observed post-mortality parasite distribution then, regardless of how lethal the parasite was, it will be impossible to detect PIHM because there is no need for a more complex model. Most observed parasite distributions are well fit by the negative binomial distribution (Shaw et al. 1998), suggesting that systems where these methods are applicable may be more the exception than the rule. Furthermore, even when truncation of the negative binomial distribution is detected, it may be caused by other processes such as within host density dependence, age dependent variation in host resistance and/or heterogeneous infection rates (McCallum 2000; Anderson & Gordon 1982; Rousset et al. 1996). This means that in the event that PIHM is detected, it may actually not be the result of PIHM.

Given these numerous caveats, is there a place in parasitology for methods that estimate PIHM from intensity data? As suggested by Lester (1984) these methods for estimating PIHM can provide preliminary insight into whether or not PIHM is worth further exploration. However, we stress that these methods should only be used as an exploratory tool when assessing the role of PIHM in a system, and potential users should critically evaluate whether they think they have a large enough sample size and an appropriate host survival function/post-mortality distribution for the methods developed in this paper to be applicable. Even if they are applicable, inferring PIHM from distributional data is no substitute for field experiments and an in depth understanding of the natural history of the host-parasite system under consideration.

Table 1.

Definition of parameters and functions used in the main text

Parameter	Definition
μp	Pre-mortality mean parasite intensity
kp	Pre-mortality parasite aggregation
Np	Pre-mortality host sample size
x	Number of parasites in a given host
g(x; μp, kp)	Pre-mortality negative binomial parasite distribution
h(survival; x, a, b)	The probability of host survival given a parasite load x and logistic parameters a and b
b/4	The maximum rate of decline in host survival probability with increasing parasite intensity
a	When b is held constant a one unit increase in a leads to a 1/b increase in the log parasite intensity at which some percent of hosts survive
LD 50	exp(a/b), parasite intensity above which a host has a greater than 50% chance of dying