Improving pulse detection in multibin photon-counting detectors

Abstract.

Energy-discriminating, photon-counting (EDPC) detectors are attractive for their potential for improved detective quantum efficiency and for their spectral imaging capabilities. However, at high count rates, counts are lost, the detected spectrum is distorted, and the advantages of EDPC detectors disappear. Existing EDPC detectors identify counts by analyzing the signal with a bank of comparators. We explored alternative methods for pulse detection for multibin EDPC detectors that could improve performance at high count rates. The detector signal was simulated in a Monte Carlo fashion assuming a bipolar shape and analyzed using several methods, including the conventional bank of comparators. For example, one method recorded the peak energy of the pulse along with the width (temporal extent) of the pulse. The Cramer–Rao lower bound of the variance of basis material estimates was numerically found for each method. At high count rates, the variance in water material (bone canceled) measurements could be reduced by as much as an order of magnitude. Improvements in virtual monoenergetic images were modest. We conclude that stochastic noise in spectral imaging tasks could be reduced if alternative methods for pulse detection were utilized.

1. Introduction

Energy-discriminating, photon-counting (EDPC) detectors have been proposed for use in diagnostic computed tomography (CT) scanners.¹ Compared to conventional, energy-integrating detectors, EDPC detectors promise several benefits. These detectors may be virtually immune to electronic noise by virtue of the pulse height threshold. They could improve contrast-to-noise characteristics for all material types but especially for high atomic number contrast agents using appropriate weighting of energy bins.^2,3 Finally, these detectors introduce the possibility of simultaneous imaging of multiple contrast agents. EDPC detectors have been studied in several early prototype systems.^4,5

For spectral tasks such as material decomposition, it is well known that an ideal EDPC detector (i.e., one with perfect energy resolution and no count losses) outperforms existing approaches such as fast kVp switching, dual-source, or dual-layer detector systems.⁶ However, current implementations of EDPC detectors suffer from a variety of nonidealities, including K-escape, charge sharing, and pulse pileup. K-escape, the departure of characteristic fluorescence photons from the detector material, is a fundamental limitation that cannot be corrected. With K-escape, the detected energy will be the original photon energy minus the energy of the characteristic photon. Charge sharing refers to the distribution of charge from one incident x-ray photon into more than one detector pixel. Rather than counting a single photon at the correct energy, the system will count multiple events at lower energies. Pulse pileup occurs when multiple photons arrive in close spatial and temporal proximity that together are indistinguishable from a single, higher-energy photon. Charge sharing is aggravated with smaller pixel sizes, whereas pulse pileup effects become more significant with larger pixel sizes and at high flux. Charge sharing compensation mechanisms are promising for improving performance^7–9 but increase the effective pixel size and associated pileup effects.

Photon-counting detectors are commonly parameterized by a dead time or its inverse, the characteristic count rate.¹⁰ The characteristic count rate is well defined in model systems such as the ideal paralyzable or nonparalyzable detector and can be loosely defined in real systems as the maximum count rate that the detector electronics support for events arriving at a perfectly constant rate. As the count rate incident on the detector becomes comparable to the characteristic count rate, photon counts are lost and the detected spectrum is distorted because of pileup effects. It has been estimated that if the incident count rate is more than 20% of the characteristic count rate, an otherwise ideal EDPC detector will be outperformed by conventional dual-energy CT.¹¹ Many currently available detectors are not ideal, and even at very low incident flux may still be outperformed by conventional systems due to charge sharing.⁶ However, performance at low flux is expected to improve substantially with newer technologies such as charge sharing compensation.^8,9

The performance of EDPC detectors at moderate count rates is further compromised by the method of signal analysis and pulse detection that is typically used. Most existing detectors rely on a bank of comparators to analyze the signal from the detector. While comparators are simple to implement and effective in the low-flux regime, at moderate flux the performance of the comparator system suffers. The purpose of this work was to examine alternative approaches for pulse detection and to assess their performance in EDPC detectors at higher count rates.¹²

2. Methods

2.1. Pulse Detection in Energy-Discriminating, Photon-Counting Detectors

Most x-ray EDPC detectors operate using a semiconductor substrate that directly converts incident, high-energy x-ray photons into electron and hole charge clouds. These charge clouds are swept into the readout electronics and are preprocessed using pulse shaping circuitry, yielding a signal such as the example in Fig. 1. This signal is then analyzed using pulse-detection logic such as the bank of comparators. This pulse-detection logic condenses and summarizes the events received on the detector, but some information is lost in the process. In this work, we adopted the triangular bipolar pulse shape described in Ref. 13, based on a fit to experimental measurements of a photon-counting detector. The shape consisted of a short, tall positive triangle followed by a long, shallow, and negative tail. The pulse was not constrained to have integral zero but to best match the experimental data.

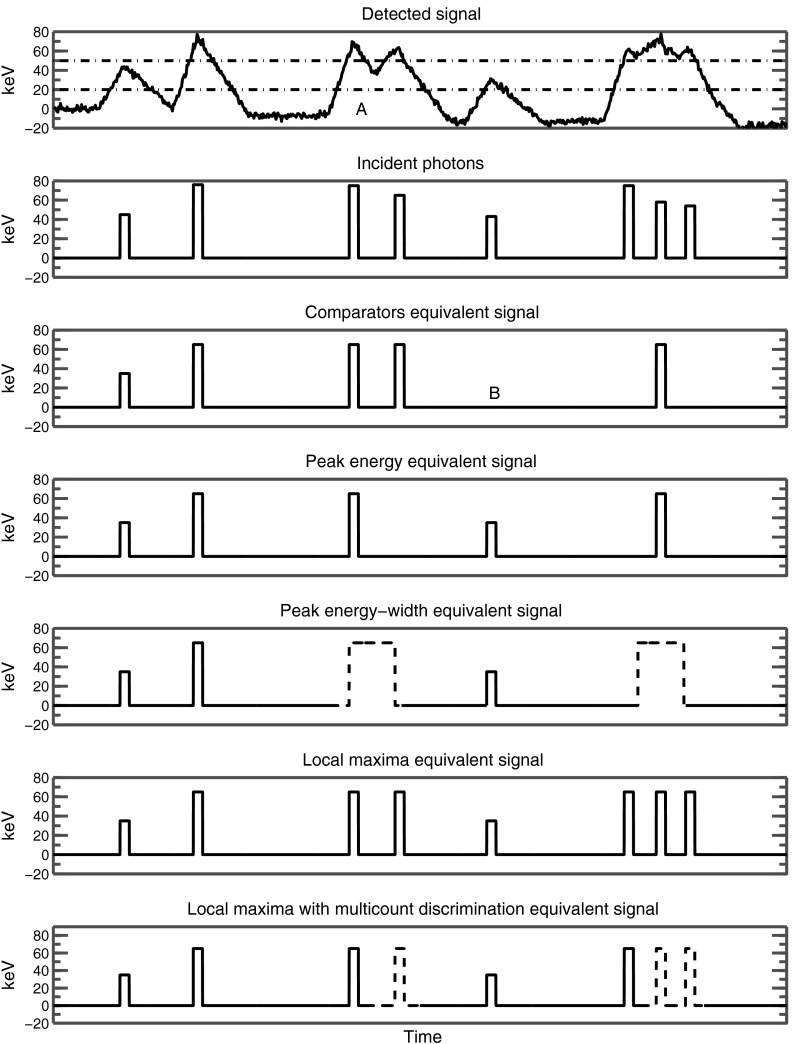
Fig. 1.

Example of different pulse-detection mechanisms. The “detected signal” plot is simulated from the incident photons, convolved with the bipolar detector response shape. Noise is added in this plot but absent in actual simulations. In the detected signal plot, two horizontal lines are drawn, representing energy thresholds for the comparators. Because of pileup, the signal contributions from different photons sometimes overlap and become difficult to separate. Each of the pulse-detection mechanisms loses different types of counts. For each mechanism, we draw an equivalent signal that can be compared against the incident photons to show which photons are lost. See text for details.

These comparators are simple circuits that compare the detector signal to a reference voltage and increment a counter when the signal rises above the reference voltage. A high-energy photon will yield a pulse that triggers several comparators in sequence. At low count rates a bank of comparators effectively bins incident photons, and hence the system is able to infer the number of events within each bin by taking differences. For example, if the detector uses two comparators at a lower energy $E_L$ and a higher energy $E_H$, which are triggered $n_L$ and $n_H$ times, respectively, it can be inferred that there were $n_H$ photons with energies exceeding $E_H$ and ($n_L-n_H$) photons with energies between $E_L$ and $E_H$.

As the incident count rate increases, this simple interpretation breaks down and it is no longer clear what the bank of comparators is counting. For example, two photons, arriving in quick succession, may trigger the $E_H$ comparator twice but the $E_L$ comparator only once. According to the simple interpretation, this is equivalent to two counts with energies above $E_H$ and a nonphysical, negative count between $E_L$ and $E_H$. This occurs in Fig. 1 and is denoted in region A and results in the elimination of one of the counts at $E_L$ (at B). We hypothesized that other pulse-detection schemes could be more robust than the comparator at high count rates. We investigated five alternative pulse-detection schemes that are described as follows.

2.1.1. Peak-energy counting

Peak-energy counting is a simple extension of the conventional bank of comparators. Suppose again that a pair of photons arrives in close succession, crossing the $E_H$ comparator twice but the $E_L$ comparator once. Peak-energy counting prohibits double counting of the higher-energy threshold. Once the lowest energy threshold $E_L$ is crossed from below, the higher energy threshold is only allowed to count once until the $E_L$ threshold is crossed again from above. Conceptually, peak-energy counting accepts missed counts to improve reliability. It divides the incident signal into a number of segment “pulses,” where each pulse is defined as regions above $E_L$. Within each pulse, peak-energy counting is able to identify the highest energy, and it bins the entire pulse as a single event with that highest energy.

In this pulse-detection logic, as with other logics described later, there is a special dependence on the lowest energy threshold $E_L$ to segment the detected signal into multiple pulses. We will return to this point in Sec. 4.

2.1.2. Peak, width two-dimensional binning

A refinement on peak-energy counting is to additionally record the width, or time duration, of the pulse, and not just its peak energy. Pulse pileup would be expected to lengthen the pulse, defined as the time for which the signal is above the lowest energy threshold $E_L$. A pulse that is longer than normal might therefore indicate corruption. In Fig. 1, long pulses are denoted by wider rectangles and also dashed outlines to denote their possible corruption.

The length of the pulse might be recorded using a time-to-amplitude converter. For the purpose of this work, we sought to provide only an upper bound on the performance, and analytically divided the detector signal into a series of pulses. Each pulse was binned into one of three length bins as well as into an energy bin corresponding to the peak energy of the pulse. For $n$ energy thresholds, the data corresponding to this pulse-detector logic was therefore $3n$ integers instead of $n$ integers for the regular bank of comparators.

2.1.3. Local maxima detection

Another mechanism for detecting pulses, aimed at capturing the maximum quantity of events, is to bin individual local maxima in the detector signal. This was not a problem in simulations, which were noiseless and used a perfect bipolar triangular pulse for each individual photon. In this case, it was possible to analytically identify local maxima and bin them accordingly. We did this to explore the upper bound performance of this method, but in practice, identifying local maxima in noisy data may be difficult.

2.1.4. Local maxima with multicount discrimination

A further refinement on the detection of local maxima is to further bin the detected local maxima into two categories: “first” local maxima and “subsequent” local maxima. A first local maximum is the first maximum detected after the crossing of the lowest energy threshold $E_L$ from below. In the presence of pulse pileup, we anticipated that the first such maximum in the pulse was the one most likely to be accurate, with subsequent maxima corrupted by the effects of preceding photons. In a two energy threshold system, there are now four outputs, $n_L^{\text{first}}$, $n_H^{\text{first}}$, $n_L^{\text{subsequent}}$, and $n_H^{\text{subsequent}}$. In Fig. 1, subsequent pulses are denoted by dashed outlines to denote their possible corruption.

2.1.5. Local maxima with multicount discrimination using comparators

As we previously described, it may be impractical to identify local maxima in a signal that is corrupted with noise. Therefore, we designed a variant of the local maxima counter that operated on the same data present with the traditional bank of comparators. Here, the local maxima were inferred only from the up-crossings and down-crossings of the energy thresholds.

A local maximum is identified by an up-crossing of any energy threshold, followed by a down-crossing of the same threshold without a crossing of any other threshold. Multicount threshold detection is provided by special logic on the lowest threshold $E_L$. The first maximum detected in a pulse increments the “first” counter corresponding to the energy of the maximum. Afterward, the first counter is locked and all future maxima increment the “subsequent” counter instead. The lock on the first counter is released upon the crossing of the $E_L$ threshold from above.

2.2. Monte Carlo Simulations

The relationship between the various counts in the simulated systems and the desired values of basis material amounts is very complicated. In real systems, one would need an algorithm to produce estimates of the basis material amounts from the measured counts. The Cramer–Rao lower bound (CRLB) uses an information theoretic inequality to provide a lower bound on the variance of any unbiased estimator. Therefore, it allows us to bind the performance of an estimator without having developed such an algorithm. The CRLB needs only data on the derivative of the signals with respect to the estimated quantities and knowledge of the statistics of the data.

The variance of EDPC detectors is difficult to analyze in the general case, although with certain assumptions, analytic approximations are available.^13,14 In the presence of pileup, detector statistics are not Poissonian and the measurements from the various bins become correlated. Monte Carlo simulations were therefore used to estimate the covariance matrix with each pulse-detection logic.

Following Refs. ¹¹ and ¹⁵, we assume that the measurements from each pixel follow a multivariate Gaussian distribution. For short frame times (i.e., few detected counts), readouts from a pixel may not be Gaussian. However, a readout with a sufficiently long frame time can be approximately treated as a sum of readouts for short integration times, and the central limit theorem implies that the resulting readout should follow a multivariate Gaussian distribution. We estimate the mean and standard deviation of this Gaussian using Monte Carlo trials. In each trial, the arrival times of incident photons are randomly chosen following Poisson arrival times, and their energies are determined by sampling the incident spectrum. We used 10,000 trials, with each trial having an integration time that was 10,000 times the mean time between arrival of photons. For all of the pulse-detection mechanisms, we used six energy bins, with thresholds at 30, 45, 65, 85, 105, and 125 keV. These energy bins were not optimized.

We then estimated the changes in the mean and covariance matrix as the two basis materials, water and bone, were varied by a small amount. This information was used to calculate the Fisher information matrix as follows:¹⁶

$${\mathcal{F}}_{ij}={\left[\frac{\partial \mu (\mathbf{m})}{\partial m_i}\right]}^{\mathrm{T}}{\mathrm{\Sigma }}^{-1}(\mathbf{m})\left[\frac{\partial \mu (\mathbf{m})}{\partial m_j}\right]+\frac{1}{2}\mathrm{Tr}[{\mathrm{\Sigma }}^{-1}(\mathbf{m})\frac{\partial \mathrm{\Sigma }(\mathbf{m})}{\partial m_i}{\mathrm{\Sigma }}^{-1}(\mathbf{m})\frac{\partial \mathrm{\Sigma }(\mathbf{m})}{\partial m_j}],$$

where $\mu (\mathbf{m})$ and $\mathrm{\Sigma }(\mathbf{m})$ refer to the mean and covariance matrix as a function of the basis material thicknesses $\mathbf{m}$. The CRLB of the variance is the inverse of the Fisher information matrix.

We repeated this process five times to calculate the standard deviation of our numerically estimated CRLB.

2.3. Experiments

A 120-kVp incident spectrum was generated from using the Spektr toolkit^17,18 and was passed through a variable amount of water and bone. We neglected scatter and assumed that only primary radiation reached the detector. The arrival times of photons and their energies were randomly sampled from this spectrum on a small area detector pixel and represented as a series of delta functions on the detector signal. Because of various detector imperfections, the energy deposited on the detector is not always proportional to the energy of the incident photons. We analyzed two cases: in the first case, we assumed an ideal energy response with a deposited energy equal to the incident photon; and in the second case, the energy deposited was first degraded using the energy response functions measured in Ref. 4. The energy response of EDPC detectors is implementation dependent, and the detector response in Ref. 4 was used only to illustrate one possible case. Features such as charge sharing compensation can greatly improve the energy response.⁸

The deposited signal spikes were then convolved with a bipolar pulse shape.¹³ The pulse shaping circuitry is again implementation dependent, but we choose the bipolar pulse shape because it has been proposed and validated for one specific detector. A real detector may show different pulse shapes depending on the depth of interaction in the substrate. We used a fixed bipolar shape throughout, as described in Ref. 13.

We examined two possible spectral tasks: material decomposition imaging and equivalent monoenergetic imaging. Material decomposition is a popular application of spectral imaging systems, enabling the clinician to, e.g., retrospectively subtract out iodine contrast from a postcontrast image to produce a virtual noncontrast image. In material decomposition, the data are used to estimate an equivalent thickness of two basis materials such as soft tissue and iodine.¹⁹ In our work, we used water and bone as the basis materials. Equivalent monoenergetic images are equivalent to a linear combination of the water and bone basis materials, with coefficients equal to the attenuation coefficients of the basis materials at a chosen energy, so the combination mimics an image with a truly monoenergetic spectrum at that energy.

We use linear systems theory to propagate the noise from individual projections to the noise in CT images. To a good approximation, the variance of a CT image is proportional to the unfiltered backprojection of the variance of individual projections.²⁰ Estimating the noise for each ray in the sinogram using Monte Carlo techniques would be computationally prohibitive. Instead, we precomputed the variance on a grid at 2.5-cm water length increments and 1-cm bone length increments. The variance for other rays was determined using bilinear interpolation from this precomputed table. We assumed that the CT system used a beam-shaping filter but no tube current modulation. The beam-shaping filter was approximated to be water-like with a shape given in Ref. 21. Although real beam-shaping filters are not composed of water, they are often designed to be similar to water to reduce the complexity of the beam hardening correction.

We estimated raw data for a CT system by forward projection of an anonymized clinical image. We assumed a parallel beam system, and decomposed the clinical image into water and bone equivalents by assuming $\text{voxels}<100\mathrm{HU}$ were composed of water of the appropriate density, and $\text{voxels}>100\mathrm{HU}$ were composed of water and cortical bone in the correct mixture to produce the observed CT number.

For propagation of noise into CT images, the output of the tube was assumed to be $5\times {10}^8\text{counts}/{\mathrm{mm}}^2\mathrm{s}$ at the detector before the bowtie filter or the object. After the bowtie filter, the effective tube output was reduced. This corresponds roughly to a scan technique of 120 kVp and 200 mA, although the precise mapping from tube current to counts is scanner dependent. The characteristic count rate of the detector was assumed to be $1\times {10}^7\text{counts}/{\mathrm{mm}}^2\mathrm{s}$, following the bipolar pulse shape described in Ref. 13.

3. Results

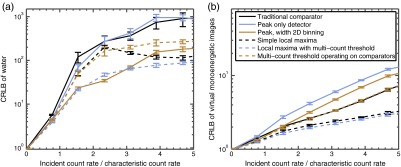
Figure 2 shows the CRLB for the ideal detector energy response. The incident spectrum passes through 1 cm of bone and 20 cm of water. The left plot is the CRLB of the water component of the water–bone decomposition. The right plot is the CRLB of the equivalent monoenergetic image with the lowest variance. The response of an ideal detector that is immune to pileup effects would have a flat response on this curve, because the effect of increasing flux has been normalized out. The performance of all the systems degrades with increasing count rate. When the count rate is substantially less than the characteristic count rate, all the systems perform similarly, but at higher rates the difference in performance when measuring the water component is more than an order of magnitude, with the simple comparator being among the poorest performers. The effect of count rate on the equivalent monoenergetic image is smaller.

Fig. 2.

Relative CRLB of the variances for different pulse-detection logics, assuming ideal energy response. The $x$-axis corresponds to the incident flux normalized by the characteristic count rate, but the variances are reported at constant dose, so the measurement time decreases as the incident flux is increased. Within each plot, the CRLB has been normalized to performance at very low count rates. Hence, both axes are unitless. Error bars represent 95% confidence intervals. (a) Water material. (b) Equivalent monoenergetic imaging.

Curiously, the performance of the simple local maxima method improves at high flux. At low flux, the output of the simple local maxima method corresponds directly with detected photons. For example, bone provides greater contrast in the low energy bins, and water provides greater contrast in high-energy bins. We observed that, at high flux, these interpretations break down, with water providing greater contrast at lower bins and bone providing greater contrast at higher bins. A possible explanation for this behavior is that individual bins experience transition points between these two regimes and become ineffective at discriminating between the two basis materials, leading to a local maximum in variance. Continuing to increase the incident count rate past the limit of Fig. 2 does eventually lead to decreasing performance of the simple local maxima method.

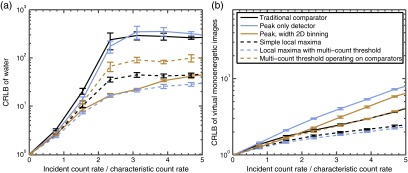
Figure 3 shows a similar plot, but with the imperfect detector energy response reported in Ref. 4. The improvements of the alternatives still exist with imperfections in the detector response.

Fig. 3.

The same variance plots as in Fig. 2, but assuming a degraded energy response following that of Ref. 4. (a) Water material. (b) Equivalent monoenergetic imaging. Note that the $y$-axis is normalized to the CRLB of the degraded energy response at low count rate, which is a different normalization factor than used in Fig. 2.

Figure 4 illustrates propagation of variance into CT images for a thorax and an abdomen. The propagation of variance was performed by backprojecting the variance, as estimated using the CRLB, of each ray in the sinogram. As pointed out in Ref. 20, this method is effective at producing images of the variance (or variance maps) in reconstructed images under the approximation that the ramp filter is local. Currently, an estimation algorithm that is efficient both in noise performance and computation time for material decomposition, and that compensates for distortion due to pulse pileup, charge sharing, etc., does not exist. However, should it be developed, backpropagation of the CRLB would provide an estimate of the variance maps that such an efficient estimator would produce. In these variance maps, higher brightness indicates larger variance. In both cases, we constrain the analysis to three systems: the traditional bank of comparators, the local maxima with multicount threshold detection constrained to operate on the bank of comparators, and peak/width two-dimensional (2-D) binning. In the water material images, variance is markedly reduced in the lung field and in the region outside the patient by the more complex pulse-detection mechanisms.

Fig. 4.

Effect of different comparators in the noise of CT images. These are variance maps, with the brightness of pixel proportional to the variance in the reconstruction. The variance maps are for (top row) equivalent monoenergetic images and (bottom row) virtual noncontrast or water material images. The window widths and levels are constant within each row but different from row to row; the equivalent monoenergetic images have had their noise multiplied by 40 to display them on the same scale. The columns correspond to (left) the traditional bank of comparators, (middle) peak-width 2-D binning, and (right) local maxima detection with multicount distinction operating on the comparator signals.

4. Discussion

At low count rates, the EDPC detector did not suffer from pileup and all proposed pulse-detection mechanisms operated equally well. As the count rates increased, many of the alternatives outperformed the simple comparator, and some by more than a factor of three on material decomposition images. The best schemes were able to identify a subset of events in which one may have more confidence (e.g., the shorter pulses in peak/width binning, or the “first” detections with multicount discrimination) because they were less contaminated from pileup. Presumably, the CRLB was able to use these higher-quality events to produce better estimates of the basis material amounts.

Equivalent monoenergetic imaging was much less sensitive to pulse pileup than basis material decomposition. It is well known that the noise in basis material decompositions is strongly anticorrelated. With spectral distortion, the noise increases and becomes even more anticorrelated. In equivalent monoenergetic imaging, when the target photon energy is in the middle of the spectrum, the two basis materials are combined in a way that exploits this anticorrelation and produces images of minimal noise. We note that in Figs. 2 and 3, we select the energy for equivalent monoenergetic imaging expressly to minimize the noise. In some applications, the clinician may choose a lower energy than the minimum-noise energy, such as the energy that maximizes the iodine contrast-to-noise ratio. In these cases, the anticorrelations are not fully exploited and the resulting images will have variance that is intermediate between the equivalent monoenergetic images shown here and the basis material images. The local maxima with multicount discrimination performs very well in equivalent monoenergetic imaging, presumably because it is able to detect photons that cannot be discerned with other methods, such as those that rely on comparators. It would be difficult to realize these advantages in a real system.

Our simulations involved several assumptions. Each photon arriving onto an EDPC detector deposits charge only into one pixel, and the amount of charge deposited is deterministic. In practice, a single photon may undergo several interactions within the detector substrate, including possible scattering into neighboring pixels. The detected signal may be a function of the depth of interaction. Electronic noise will introduce additional uncertainties. Perhaps more importantly, our simulations neglected real-world effects such as material polarization, charge trapping, and voltage drift. The bank of comparators is simple and robust. More sophisticated pulse-dependent logic could be fragile, particularly in its dependence on the lowest energy threshold, $E_L$, which served as a “reset” marker in many of our proposed schemes. It may be possible to build alternative pulse-detection logic that is more robust in the presence of these nonidealities, but this is beyond the scope of our work.

Scatter effects were not modeled in this work because the amount of scatter depends on several factors beside object thickness, including the cone angle of the scanner, the bowtie filter used, and the design of the antiscatter grid. However, photons scattered in the object will introduce additional degradation. It has previously been shown that scatter contamination of the lower energy bins, even if the scatter were perfectly estimated and suppressed, would still increase the variance of these bins.²² Scattered photons would degrade the energy response of the detector, which (as seen in Figs. 2 and 3) may diminish the advantages of new pulse-detection logic. However, it would also increase the effective incident count rate on the detector and could lead to benefits at lower tube current.

These concerns notwithstanding, we believe that the choice of pulse-detection logic is an important and often overlooked design consideration in EDPC detectors. While the comparator has become the standard method for extracting counts from EDPC detectors, it is not the only possibility and some of the alternatives that we investigated here have the potential to reduce stochastic noise in spectral imaging tasks.

Biographies

Scott S. Hsieh is an instructor at Stanford University. He works on improving mechanisms to improve the image quality and dose efficiency in computed tomography scanners. He received a PhD degree in electrical engineering from Stanford University.

Norbert J. Pelc is a chair of the Department of Bioengineering at Stanford University. His primary research interests are in the physics, engineering, and mathematics of diagnostic imaging and the development of applications of this imaging technology. He is a member of the National Academy of Engineering and a fellow of the American Association of Physicists in Medicine, the International Society for Magnetic Resonance in Medicine, and the American Institute of Medical and Biological Engineering.